Transition State Asymmetry in C–H Bond Cleavage by Proton-Coupled Electron Transfer

Abstract

The selective transformation of C–H bonds is a longstanding challenge in modern chemistry. A recent report details C–H oxidation via multiple-site concerted proton–electron transfer (MS-CPET), where the proton and electron in the C–H bond are transferred to separate sites. Reactivity at a specific C–H bond was achieved by appropriate positioning of an internal benzoate base. Here, we extend that report to reactions of a series of molecules with differently substituted fluorenyl-benzoates and varying outer-sphere oxidants. These results probe the fundamental rate versus driving force relationships in this MS-CPET reaction at carbon by separately modulating the driving force for the proton and electron transfer components. The rate constants depend strongly on the pK_a of the internal base, but depend much less on the nature of the outer-sphere oxidant. These observations suggest that the transition states for these reactions are imbalanced. Density functional theory (DFT) was used to generate an internal reaction coordinate, which qualitatively reproduced the experimental observation of a transition state imbalance. Thus, in this system, homolytic C–H bond cleavage involves concerted but asynchronous transfer of the H⁺ and e⁻. The nature of this transfer has implications for synthetic methodology and biological systems.

Graphical Abstract

INTRODUCTION

The selective transformation of C–H bonds remains one of the primary challenges facing modern chemistry. The practical and fundamental interest in manipulating these inert bonds has stimulated decades of research from the organometallic, synthetic, biological, inorganic, and physical organic chemistry communities.¹ Many methods have been developed to overcome the inertness of C–H bonds, including the use of activating and directing groups, selective catalysts, and supramolecular recognition.

Hydrogen atom transfer (HAT) is the classical mechanism for C–H bond activation, central to combustion, free-radical halogenation, and many other processes.² HAT is one kind of proton-coupled electron transfer (PCET) process, in which a hydrogen atom, a proton and electron (H⁺ + e⁻ ≡ H^•), is transferred from one group to another in a single kinetic step.³ HAT mechanisms for C–H bond activation have a strong intrinsic selectivity and can be harnessed in a number of ways for processes from petrochemical scale to synthetic organic transformations.^2e,4

Most enzymatic oxidations of unactivated C–H bonds are described as HAT processes, including heme and nonheme iron and copper enzymes.⁵ Many of these and other biological reactions, however, might be better described as multiple-site concerted proton–electron transfer (MS-CPET). MS-CPET reactions occur when electrons and protons are transferred to or from disparate sites or cofactors.³ In cytochrome P450 oxidations, for example, C–H bonds are cleaved by proton transfer to the oxo group concerted with electron transfer to a heme/thiolate-based orbital.⁶ HAT and MS-CPET are widely utilized, from biological to energy to synthetic processes, as the concerted transfer of protons and electrons can avoid high energy, charged intermediates.⁷

Well-characterized examples of MS-CPET, in both synthetic and biological contexts, have occurred nearly exclusively at polar bonds, typically at O–H or N–H bonds. In these systems, MS-CPET proceeds through the preformation of a hydrogen bond, which serves to align the proton transfer coordinate.⁸ The canonical biological example of MS-CPET is the oxidation of Tyr_Z in photosystem II, where the phenolic bond is cleaved by proton transfer to a proximal histidine ligand accompanied by long-range electron transfer to P₆₈₀⁺⁹. Similarly, MS-CPET reactions in small-molecule model systems¹⁰ and synthesis reactions¹¹ all occur at polar bonds.

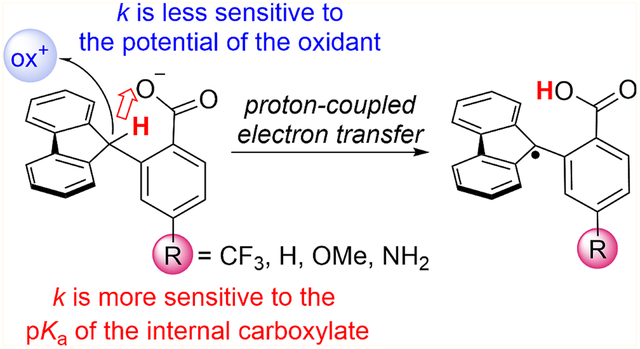
We recently demonstrated that MS-CPET can occur directly at the C–H bond in the absence of classical hydrogen-bonding interactions.¹² In the fluorenyl-benzoate shown in Scheme 1, Flr(H)CO₂⁻, the fluorenyl C–H bond is oxidized by proton transfer to an internal carboxylate concerted with electron transfer to an outer-sphere oxidant (Scheme 1). Use of MS-CPET as a strategy for activating C–H bonds relies on the appropriate positioning of a basic cofactor to provide the necessary kinetic setting for proton transfer.¹²

Scheme 1. MS-CPET at Fluorenyl-benzoates Flr(R)CO.

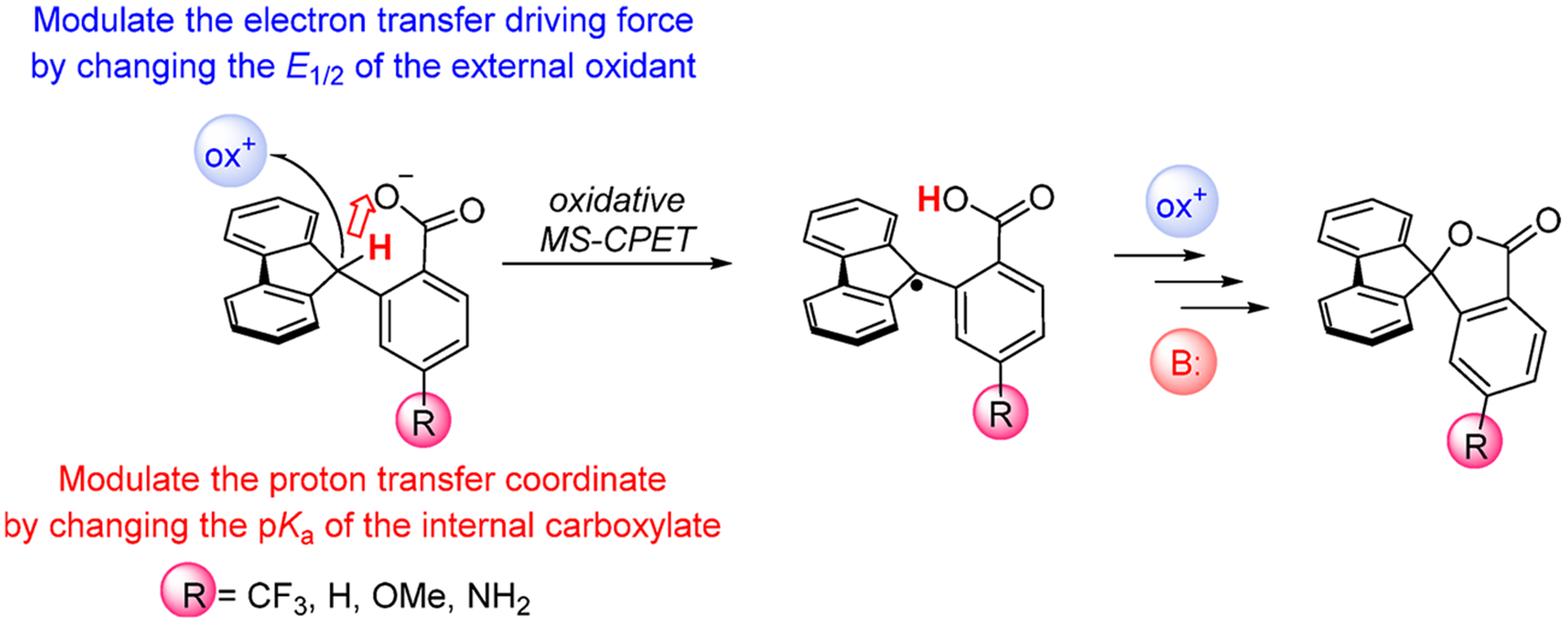
₂⁻, R = CF₃, H, OMe, NH₂^a

^aThe driving forces for proton and electron transfer can be modulated by changing the pK_a of the internal base and the E_1/2 of the external oxidant, respectively. Oxidation leads to the formation of the carbon centered radical, which is subsequently converted to the corresponding lactone.

Our previous report examined the variation in the rate constant for oxidation of Flr(H)CO₂⁻ with various outer-sphere oxidants. The rate versus driving force relationship upon changing the oxidant was found to be very shallow: ∂ ln(k)/∂ ln(K_eq) = ∂(ΔG^‡)/∂(ΔG°) = α = 0.2. Semiclassical Marcus-theory type treatments predict an α of 0.5, and this is what has typically been observed in both HAT and MS-CPET reactions.^2a,3,13 The small α shows that the reaction rate constants are not greatly affected by the nature of the outer-sphere oxidant.

We hypothesized that the shallow dependence on the potential of the oxidant could be due to an asynchronous or imbalanced transition state. Transition state imbalances have been extensively described for E2 elimination reactions¹⁴ and deprotonation of nitroalkanes,¹⁵ and have been observed in many classes of bond breaking and forming reactions.¹⁶ Jencks invoked imbalanced transition states in describing structure–reactivity coefficients in the 1970s; these ideas were developed into the widely used visualizations presented in More O’Ferrall–Jencks plots.¹⁷ Building on this framework, Bernasconi introduced his Principle of Nonperfect Synchronization (PNS) to describe elementary reactions that involve multiple concurrent processes, for example, bond formation/ cleavage and electronic localization/delocalization. Differences in the progression of these processes at the transition state are called imbalances.^16,18 Complementary multidimensional analyses have been developed by Grunwald¹⁹ and Guthrie.²⁰ Asynchronicity has very recently been discussed for metal-mediated HAT reactions of C–H bonds, which can occur through multiple mechanisms.²¹ Asynchronicity is important from a practical perspective because when different thermochemical parameters affect transition state energetics differently, rates and selectivities can be modulated by the choice of reagents.

The fluorenyl-benzoate system (Flr(R)CO₂⁻) is an ideal model to study fundamental aspects of MS-CPET at C–H bonds. Herein, we demonstrate that independently modulating the proton transfer and electron transfer portions of the reaction result in very different rate versus driving force relationships (Scheme 1). The observed discrepancies in the rate/driving force relationships suggest an imbalanced or asynchronous transition state, where electronic reorganization and proton transfer have occurred to different extents. Density functional theory (DFT) methods were used to contextualize the experimental results and were analyzed in the context of Bernasconi’s PNS. Overall, the results inform how the rate of C–H bond oxidation can be controlled by changes to the electron or proton transfer reaction coordinates, and suggest how selectivity could be achieved in synthetic and biological contexts.

RESULTS

Synthesis/Characterization.

The compounds shown in Scheme 1 were synthesized via a Pd-catalyzed coupling reaction between fluorene and the corresponding para-substituted methyl 2-bromobenzoate in DMF.²² The carboxylic acid derivatives Flr(R)CO₂H were obtained from the respective methyl esters via base hydrolysis (see Supporting Information section 2 for details).

The carboxylic acids were deprotonated in situ using a slightly substoichiometric amount of tetrabutylammonium hydroxide (TBAOH, as a 1 M solution in MeOH). Oxidation reactions of the carboxylates were performed with various para-substituted aminium (NAr_X^•+) and ferrocenium (Fc⁺) oxidants. The driving force for reactions with this series of oxidants spans 1.2 V. Oxidations of the carboxylates each gave good yields of the corresponding lactone with regeneration of protonated starting material, as described previously for the R = H derivative (see the Supporting Information).¹²

Kinetics of Oxidation Reactions.

The kinetics of oxidation were measured for all four carboxylates with up to seven different aminium and ferrocenium oxidants in MeCN solvent (Figure 1A, Table 1). The carboxylate was generated in situ immediately before the reaction by deprotonating with 0.9 equiv of tetrabutylammonium hydroxide (TBAOH, as a solution in MeOH). Reactions were performed with an excess of carboxylate relative to the oxidant (3–30 equiv). The time-courses of the oxidations were monitored optically using a stopped-flow instrument, following the disappearance of the colored oxidants (Figure 1B). Each full set of absorbance spectra over time was fit using SpecFit global-fitting software.²³ The rate constant for the C–H bond oxidation step, k_MS‑CPET, is one-half of the measured rate constants (k₂ in Table 1) because 2 equiv of the oxidant is consumed in the total reaction, although the MS-CPET step is rate-limiting.¹² The data for the R = H compound (α_ET(H) line in Figure 1C) were reported in our previous study.¹²

Figure 1.

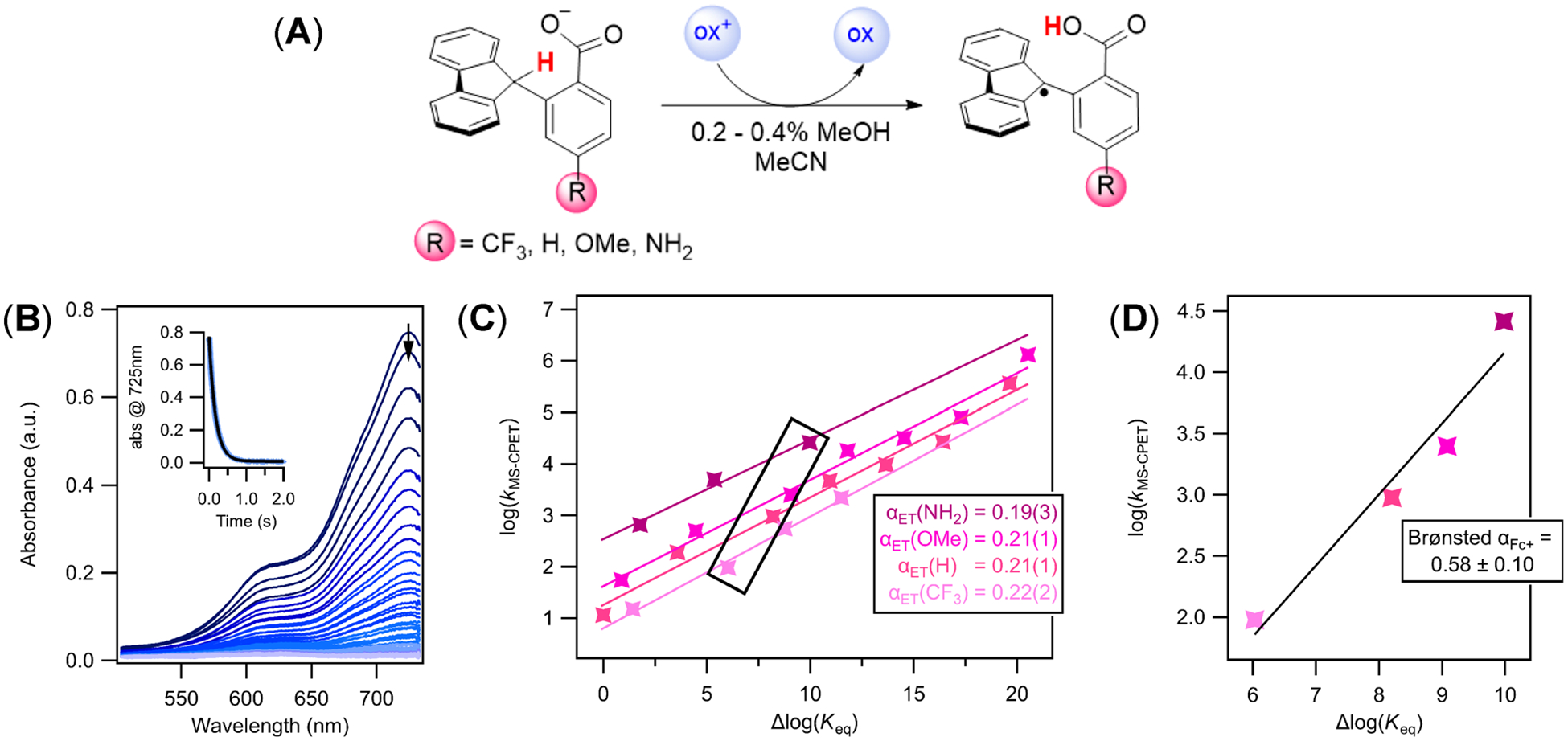
(A) General reaction scheme for the oxidation of Flr(R)CO₂⁻ substrates. Reactions were performed with an excess of carboxylate, generated in situ with TBAOH (as a solution in MeOH). Absorbance spectra were monitored on a stopped-flow following the disappearance of the colored aminium and ferrocenium oxidants. (B) Representative absorbance versus time data set monitoring the reaction of N(Ar_OMe)₃^•+ with Flr(OMe)CO₂⁻. The inset shows the absorbance at the λ_max of the oxidant, 752 nm, versus time, and the fit to an exponential function using SpecFit global fitting software. (C) Plot of the logarithm of the MS-CPET rate constants (k_MS‑CPET = k₂/2) versus changes in driving force for all substrates over a range of oxidants. Δlog(K_eq) = −ΔΔG°_rxn/2.303RT and ΔΔG°_rxn = ΔBDFE_CH(CO₂H) − 1.37ΔpK_a(CO₂H) − 23.06E_ox (see text and Scheme 2). The Δlog(K_eq) for the reaction of the R = H compound with FeCp*₂⁺ has been set equal to zero,¹² and all other values are relative to that based on changes in BDFE_CH and pK_a,COOH (see the Supporting Information for all values). Uncertainty in the last decimal is shown in parentheses. (D) Plot of MS-CPET rate constants versus changes in driving force for the four substrates with a single oxidant (FeCp₂⁺).

Table 1.

Second-Order Rate Constants for the Reactions of Carboxylates with Oxidants of Varying Potential (Eox) in MeCN^a

entry	oxidantb	Eox (V)c	Flr(NH2)CO2− k2 (M−1 s−1)d	Flr(OMe)CO2− k2 (M−1 s−1)d	Flr(H)CO2− k2 (M−1 s−1)d,e	Flr(CF3)CO2−k2 (M−1 s−1)d
1	N(ArBr)3•+	0.67	nd	2.6 × 106	7.2 × 105	nd
2	N(ArOMe)(ArBr)•+	0.48	nd	1.6 × 105	5.4 × 104	nd
3	N(ArOMe)2(ArBr)•+	0.32	nd	6.3 × 104	1.9 × 104	4.4 × 103
4	N(ArOMe)3•+	0.16	nd	3.6 × 104	9.5 × 103	1.1 × 103
5	FeCp2+	0.00	5.2 × 104	5.0 × 103	1.9 × 103	1.9 × 102
6	FeCp*Cp+	−0.27	1.0 × 104	1.0 × 103	3.8 × 102	3.0 × 101
7	FeCp*2+	−0.48	1.3 × 103	1.1 × 102	2.3 × 101	nd

^aCarboxylates generated in situ from carboxylic acids using 0.9 equiv of TBAOH (1 M in CH₃OH); nd = not determined.

^bAr_X = p-C₆H₄-X; Cp = η⁵-C₅H₅; Cp* = η⁵-C₅Me₅; all oxidants are PF₆⁻ salts.

^cE_1/2 versus FeCp₂^+/0 in MeCN.

^dIn MeCN with 0.2 vol % MeOH (NAr₃^•+) or 0.4 vol % MeOH (Fc⁺); uncertainties in k₂ ca. ±10%.

^eData previously reported in ref 12.

Reactions of the carboxylates with the oxidants fit well to a second-order kinetic model, with a few exceptions. Reactions of both the NH₂- and the CF₃-derivatives with the stronger aminium oxidants (e.g., N(Ar_OMe)(Ar_Br)₂^•+ display deviations from the second-order model, likely due to oxidant/base incompatibilities.²⁴ The most electron-rich and the most electron-poor of these series of benzoates have undesirable side reactions that occur with stronger oxidants (Supporting Information section 3). These incompatibilities can be mitigated by using the weaker ferrocenium oxidants, as these are less susceptible to nucleophilic attack by the carboxylate, for example.

Bimolecular rate constants for the reactions of Flr(OMe)CO₂⁻, Flr(H)CO₂⁻, and Flr(CF₃)CO₂⁻ with N^•+(Ar_OMe)₃ were measured at different temperatures. Using data from −40 to 15 °C for the first two compounds, and from −20 to 15 °C for the CF₃ derivative, the Eyring parameters in Table 2 were obtained (Supporting Information section 3.4). The data show that the free energies of activation are enthalpy controlled.

Table 2.

Activation Parameters for Oxidations of Flr(R)CO2− by N•+(ArOMe)3^a

compound	ΔH‡	ΔS‡
Flr(OMe)CO2−b	14.4 ± 0.1	11.8 ± 0.5
Flr(H)CO2−b	15.2 ± 0.3	11.6 ± 1.0
Flr(CF3)CO2−c	16.3 ± 0.2	12.2 ± 0.8

^aSee Supporting Information section 3.4. ΔH^‡ in kcal mol⁻¹; ΔS^‡ in cal K⁻¹ mol⁻¹. Uncertainties are one standard deviation (1σ).

^bBased on k_MS‑CPET from −40 to 15 °C.

^cBased on k_MS‑CPET from −20 to 15 °C.

Thermochemical Analysis.

The driving forces for the various C–H bond oxidation reactions were determined using the thermochemical cycle in Scheme 2. The relative pK_a’s of Flr(R)CO₂H in MeCN (eq 2) were determined experimentally by equilibration of each carboxylate with 4-trifluoromethylbenzoic acid (TFBA) and monitoring by ¹H and ¹⁹F NMR spectroscopies in CD₃CN, using a previously described method.^10d Absolute values were determined by equilibrating TFBA with benzoic acid (pK_a = 21.5).²⁵ The experimental pK_a’s vary over a range of 1.7 units (Table 3). While the MS-CPET processes should initially form the E-isomers of the carboxylic acids, not the more stable Z-forms, the relative energetics of these isomers varies only slightly with substituents (based on computational studies).²⁶ Thus, the differences in the measured pK_a values should be sufficient for the relative MS-CPET free energy calculation in Scheme 2.

Scheme 2. Thermochemical Cycle To Determine the Relative Free Energies of MS-CPET Oxidation of the Fluorenyl C–H Bonds.

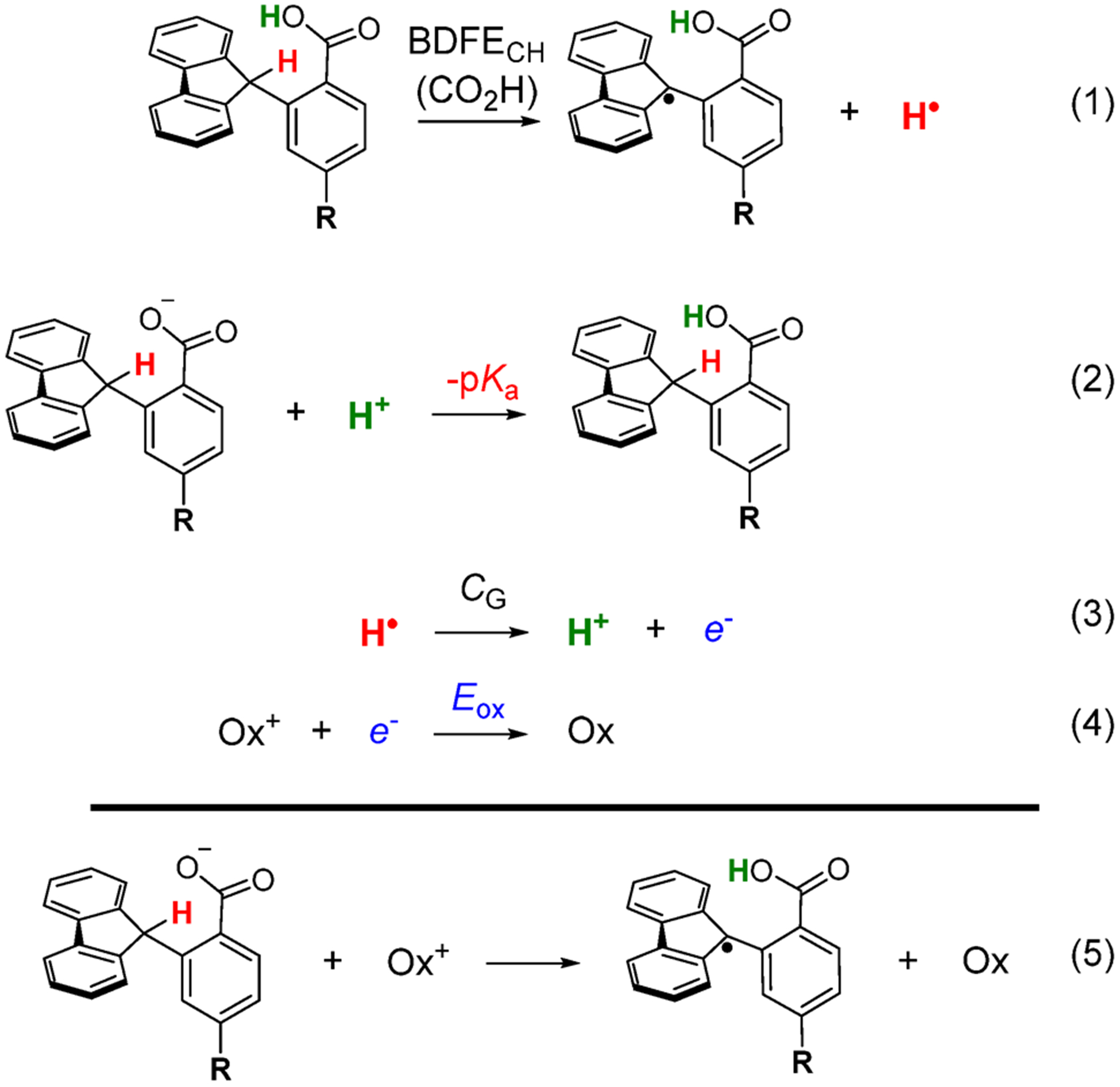
Table 3.

Changes in Thermodynamic Parameters with Substituent for Substituted Fluorenyl-benzoates, from Experiment and DFT Calculations^a

R	pKa(CO2H) expt	ΔpKa(CO2H) expt	ΔBDFECH(CO2−)b (kcal mol−1)
NH2	22.0	+0.8	−0.06
OMe	21.5	+0.3	0.22
H	21.2	0	0
CF3	20.3	−0.9	0.83

^aRelative values are versus the R = H compound.

^bDifferences in the DFT-computed bond dissociation free energies (BDFEs) for the carboxylate fluorenyl C–H bond (B3LYP/def2-TZVP with PCM = MeCN).

The relative C–H bond dissociation free energies (BDFEs, eq 1) for Flr(R)CO₂⁻ and Flr(R)CO₂H were determined computationally, as described below (see also Supporting Information section 4.1). The reaction being studied involves cleavage of the C–H bond in the carboxylate form (Figure 1A), so those values are used in the Discussion and are in Table 3. However, the thermochemical cycle to determine the overall driving force uses the BDFE_CH(CO₂H) for the carboxylic acid because that allows the use of the experimental pK_a values (Scheme 2) (Supporting Information section 4.1). The free energy to separate H^• into e⁻ and H⁺ (eq 3) is constant over the series,⁷ and the reduction potentials of the oxidants (eq 4) were taken from previous reports.^10d,27

The relative bond dissociation free energies of the fluorenyl C–H bond (ΔBDFE_CH) for the carboxylate with different R substituents were computed using Density Functional Theory (DFT). The computations used B3LYP/def2-TZVP with a polarized continuum model (PCM) in acetonitrile solvent. Free energies were calculated for isodesmic reactions between the carbon radical of one carboxylate species and the C–H bond of a second carboxylate compound (Supporting Information section 4.2). The change in BDFE with substituent is given in Table 3 relative to the R = H compound. The BDFE_CH(CO₂⁻) changes by less than 1 kcal mol⁻¹ with changes to R, presumably because the substituents are meta to the radical center.²⁸

Rate versus Driving Force Relationships.

The values in Table 3 and the analysis in Scheme 2 give the relative free energies (eq 6) and equilibrium constants, Δlog(K_eq) = −ΔΔG°/2.303RT, for all of the C–H bond cleavage reactions. The rate constants can be compared to the Δlog(K_eq) values to examine rate versus driving force linear free energy relationships (LFERs). The full set of rate versus driving force data for the four derivatives studied, with various oxidants, is shown in Figure 1C. Most sets of single-step reactions such as those studied here follow a single linear free energy relationship (LFER), such as eq 7.^17c The slope of this relationship α indicates how the logarithm of the rate constant changes with a given change in Δlog(K_eq).

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\mathrm{r}\mathrm{x}\mathrm{n}}^{\circ }=\mathrm{\Delta }{\text{BDFE}}_{\mathrm{C}\mathrm{H}}\left(\mathrm{C}{\mathrm{O}}_2\mathrm{H}\right)-1.37\mathrm{\Delta }\mathrm{p}{K}_{\mathrm{a}}-23.06E_{\mathrm{O}\mathrm{X}}$$ (6)

$$\mathrm{\Delta }\text{log}\left(k_{\mathrm{M}\mathrm{S}-\text{CPET}}\right)=\alpha \mathrm{\Delta }\text{log}(K_{\mathrm{e}\mathrm{q}})$$ (7)

The data set in Figure 1C is interesting because the dependence of log(k_MS‑CPET) on Δlog(K_eq) cannot be fit by a single LFER. Even though the compounds and reactions are very similar, a given value of Δlog(K_eq) corresponds to four different log(k_MS‑CPET) values, for the four different substrates. The four MS-CPET rate constants at the same Δlog(K_eq) differ by almost 2 orders of magnitude.

Two different sets of LFERs are needed to describe the results. The dependence of log(k_MS‑CPET) on Δlog(K_eq) for a single substrate over a series of oxidants will be termed the electron transfer α, α_ET, because the K_eq is changed only by using outer-sphere oxidants with different reduction potentials. The α_ET value reports on how the rate constants respond to changes in the electron transfer component of MS-CPET. As shown in Figure 1C, all of the substrates have α_ET ≅ 0.2, as found for Flr(H)CO₂⁻ in our previous report.¹² The rate constants are much larger for the substrates with the more basic carboxylates; for instance, the rate constants for the −NH₂ compound are on average an order of magnitude larger than those for −OMe.

The LFERs for reactions of a single oxidant with the four differently substituted compounds have much steeper slopes. This is shown in Figure 1C by the box surrounding the four data points for reactions with Fc⁺. These four points are plotted in Figure 1D and show a slope of 0.58. We term this the Brønsted α_Fc+, to indicate that it reflects changes in the reactivity of the R-substituted fluorenes with Fc⁺. For five of the seven different oxidants studied, the Brønsted α_ox+ values are within the uncertainty of this 0.58 value (0.48–0.61); N(Ar_OMe)₂ (Ar_Br)^•+ (0.36) and Br FeCp*₂⁺ (0.99) are a bit different (Supporting Information section 3.3, uncertainties ~ ±0.1). All of the α_ox+ values are substantially larger than the α_ET for changes in the oxidant with a given substituted compound (2–5 times larger).

The rate constants are much more sensitive to changes in K_eq that result from changing the benzoate substituent versus changes in K_eq from different outer-sphere oxidants (Figure 1C vs D). In the set of oxidations by FeCp₂⁺, for instance, the rate constant for Flr(NH₂)CO₂⁻ is 270 times faster than that of Flr(CF₃)CO₂⁻ for a difference in the equilibrium constants of 10⁴ (Figure 1D). In contrast, changing the oxidant from FeCp₂⁺ to FeCp*Cp⁺ , a change in K_eq of 3.5 × 10⁴ results in a change in k_MS‑CPET of only a factor of 5. These data highlight the large difference in slope between these two LFERs.

DFT Calculated Potential Energy Surfaces.

A computational investigation was undertaken to understand the origin of the very different dependencies on changing the oxidant versus changing the substituent in these MS-CPET reactions. In particular, we aimed to understand what features of the reaction coordinate might account for this distinction. To do this, we have calculated the internal reaction coordinate (IRC). This is defined as the minimum energy reaction pathway that connects a transition state (TS) to the reactants and products of a reaction. We take the IRC to be a reasonable description of the potential energy surface (PES).

Our approach to analyzing these reactions follows the computational studies of PT at carbon centers by Bernasconi.²⁹ While such adiabatic DFT calculations are not the best approach to a reaction with an outer-sphere electron transfer component, we believe that this side-by-side comparison of PT and MS-CPET provides valuable insights. There are much more sophisticated theoretical treatments of proton-coupled electron transfer reactions.³⁰ In particular, Sayfutyarova, Goldsmith, and Hammes-Schiffer have very recently reported a study of the oxidations of Flr(H)CO₂⁻ that treats the proton as a quantum particle and emphasizes the importance of vibrational excited states.³¹

Our goal with these DFT studies was to connect with the prior physical-organic literature on proton transfers from C–H bonds and its emphasis on imbalanced transition states. To that end, we first describe computations of the intramolecular proton transfer (PT) from the fluorenyl C–H to the carboxylate in Flr(H)CO₂⁻. We then use the same methodology to explore the more complicated MS-CPET reactions between Flr(H)CO₂⁻ and N(Ar_Br)₃^•+ and N(Ar_H)₃^•+.

The IRCs for intramolecular PT and MS-CPET were calculated using B3LYP/def2-SVP, because the MS-CPET calculation with the def2-TZVP basis set was prohibitively expensive. Both used a PCM solvent model with acetonitrile solvent. First, the geometries of the substrate and the product were optimized. Best guess structures for the TS then were used as a starting point for transition state calculations. The true TS structures (at this level of theory) were identified (i) by having a single imaginary frequency along the appropriate reaction coordinate (proton transfer between the fluorenyl carbon and the carboxylate oxygen) and (ii) by IRC calculations of the minimum energy pathway giving the optimized reactant and products (Supporting Information sections 4.2, 4.3, and 4.5). The degree of proton transfer and electronic reorganization (vide infra) were then quantified along the IRC and at the TS.

For both PT and MS-CPET, progress along the proton transfer coordinate was defined as the distance between the fluorenyl proton and carboxylate oxygen. For MS-CPET, the extent of electron transfer was determined from the change in the natural bond orbital (NBO) charge on the nitrogen atom of the oxidant. Although the charge is delocalized into the phenyl rings of the oxidant, the nitrogen atom undergoes the largest change in charge and thus provides a good measure of electron transfer.

The calculations were also used to indicate the progress of the Bernasconi-type “electronic reorganization” within the fluorenyl group along this reaction coordinate.³² We chose to use the pyramidalization of the fluorenyl carbon as a measure of this reorganization, because it reflects the extent of rehybridization from the starting saturated sp³ center to the sp² carbanion or radical product of PT or MS-CPET, respectively. This choice follows Bernasconi’s calculations of the deprotonation of acetaldehyde showing that pyramidalization of the α-carbon lags significantly behind proton transfer to form the enolate.^18c,29a In our analysis, the sum of the CCC bond angles around the fluorenyl carbon showed the progress as it varied from 338° in the sp³ reactant to 358° in the sp² products.

For intramolecular proton transfer in Flr(H)CO₂⁻, PT is computed to be endoergic, with ΔE = +5.8 kcal mol⁻¹ and ΔG° = +6.5 kcal mol⁻¹ (Figure 2). The highest energy point along the IRC, the TS, occurs when the proton transfer has made 76% progress toward the product. At this point, analysis of the TS structure shows that the sum of the fluorenyl CCC bond angles is 349°, which is only 45% progress toward the planar product (Figure 2C and E). This indicates that for the PT reaction, PT is ahead of fluorenyl rehybridization, or electronic reorganization. This observation has been made for many other deprotonation reactions at carbon, as discussed below.

Figure 2.

Comparison of the DFT-computed internal reaction coordinates and transition states for intramolecular PT in Flr(H)CO₂⁻ (A, C, and E) and for the MS-CPET reaction of Flr(H)CO₂⁻ and N(Ar_Br)₃^•+ (B, D, and F). (A and B) The transition state occurs at x = 0 along the reaction coordinate. Proceeding to negative values along the x-axis leads toward reactants, while proceeding to positive values leads to products. Black “○” show potential energy (ΔE) along the reaction coordinate. (C and D) Red “□” show the distance between the fluorenyl proton and the carboxylate oxygen along the reaction coordinate, which is a measure of proton transfer. For intramolecular PT, the fluorenyl proton has proceeded 76% toward the carboxylate oxygen. For MS-CPET, the fluorenyl proton has proceeded 44% toward the carboxylate oxygen. (E and F) Blue “Δ” show the sum of the CCC bond angles along the fluorenyl carbon along the reaction coordinate, which is a measure of electronic reorganization. For intramolecular PT, the sum of the fluorenyl CCC bond angles has proceeded 45% toward the final geometry. For MS-CPET, the sum of the fluorenyl CCC bond angles has proceeded 29% toward the final geometry.

In comparison, the potential energy surface for MS-CPET between Flr(H)CO₂⁻ and N(Ar_Br)₃^•+ is highly exoergic, with ΔE = −17 kcal mol⁻¹ and ΔG° = −20.5 kcal mol⁻¹, and has a small barrier. The NBO charge on the nitrogen atom of the oxidant stays constant until the TS, then abruptly becomes more positive and stays constant for the remainder of the reaction (Supporting Information section 4.3). Thus, at this level of theory, the ET component of the reaction occurs at the TS. At the TS, the proton transfer has made 44% progress toward the product, while the sum of the fluorenyl CCC bond angles is 344°, only 29% progress toward the product (Figure 2D and F). As in the computations of the PT reactions, the TS shows greater progress in PT than in the electronic rearrangement of the fluorenyl group. A similar result was found for the 2.1 kcal mol⁻¹ less exoergic MS-CPET reaction of Flr(H)CO₂⁻ with N(Ar_H)₃^•+ (Supporting Information section 4.5). (Calculations with ferrocenium oxidants were found to be too computationally expensive.) As expected from Hammond’s postulate, the less exoergic reaction has proceeded farther along the reaction coordinate, but the asymmetry is still observed. In this case, PT has made 50% progress toward the product, while the sum of the fluorenyl CCC bond angles has made only 31% progress toward the product.

Both the MS-CPET and the PT reactions proceed with significantly more proton transfer from the C–H bond than electronic reorganization within the fluorenyl group. In both cases, electronic reorganization lags far behind the proton transfer at the transition state. In the MS-CPET cases, it is striking that, despite the strongly exoergic nature of the reaction, the proton has moved roughly halfway along its coordinate.

DISCUSSION

Presented here is a detailed kinetic study of the factors that affect the cleavage of the C–H bond in four fluorenyl-benzoate compounds by multiple-site concerted proton–electron transfer (MS-CPET). As emphasized in our initial study of the oxidation of the R = H compound, these reactions proceed via concerted transfer of e⁻ and H⁺ because the alternative initial PT or initial ET steps are highly unfavorable.¹² The data presented herein show that the rates of this reaction are very sensitive to substituents para to the benzoate base, but quite insensitive to the reduction potential of the outer-sphere oxidant.

The dependence of the rate constants on driving force for this series of similar MS-CPET reactions cannot be described by a single linear free energy relationship (LFER). There is not a one-to-one correspondence of log(k_MS‑CPET) with the changes in the free energies of the reaction, described by Δlog(K_MS‑CPET). LFERs of very different slopes are observed, depending on whether the driving force is changed via changes in the outer-sphere oxidant or the benzoate substituent (Figure 1C vs D).

Traditionally, experimental studies of MS-CPET (and other types of PCET reactions) have used a Marcus theory approach.³ Most PCET reactions that have been studied at this level of detail show sensitivities similar to those of ET and PT driving forces and α’s close to 0.5.^10a,d,33,34 We have argued that such results imply synchronous transfer of the e⁻ and H⁺, with balanced transition states. A recent study by the Knowles group of ketone reductions found a shallow α, with the rate constants responding equally to changes in the PT and ET portions.³⁵ These reactions therefore proceed via synchronous PCET. Goetz and Anderson recently reported HAT reactions that are more dependent on the pK_a of the substrate than the C–H BDFE.^21b There are also PCET reactions that do not show simple correlations of rate with driving force.³⁶

The results reported here do not fit a simple Marcus-type model. The observation that k_MS‑CPET does not simply correlate with ΔG°_MS‑CPET, the presence of two LFERs for the same range of driving forces, would require that the intrinsic barriers vary substantially with substituent. This seems very unlikely given the similarity of the compounds and because the same α_ET is seen for each compound.

There are a number of other possible approaches that could be used to interpret the apparent dual dependence of log(k_MS‑CPET) on log(K_{eq‑MS‑CPET}). A very recent study of Sayfutyarova, Goldsmith, and Hammes-Schiffer analyzed the oxidation of Flr(H)CO₂⁻ with an approach that includes the quantum mechanical nature of the transferring proton.³¹ They found significant contributions from vibrational excited states in the reactant and product.

In this study, we have chosen to use an adiabatic DFT model with a classical proton. While this cannot capture some effects, it allows a direct comparison with classical physical-organic studies of proton transfer from C–H bonds. In this model, the discrepancy between the LFERs suggests that the H⁺ and e⁻ transfer in a concerted but asynchronous manner. DFT calculations indicate that proton transfer is much more advanced at the transition state than electronic reorganization, as observed in many proton transfer reactions at carbon.^16,32,37 In this Discussion, we identify the dominant effect of the substituents and then contextualize the results in terms of precedent in the physical organic chemistry literature. The strong analogies found between PT and MS-CPET at C–H bonds are an important conclusion of this study.

Disentangling Substituent Effects.

Varying the outer-sphere oxidant has the same effect for each of the four compounds (Figure 1C): the rate constants show a shallow dependence on the change in the equilibrium constant. The α_ET, defined as Δlog(k_MS‑CPET)/Δlog(K_eq), is 0.2 in all four cases. Analysis of the effects of the different substituents is more complicated, however, because the changes in substituent affect multiple properties of the fluorenyl-benzoate molecules.

Our analysis takes the following conceptual approach. We consider that the fluorenyl radical is formed by homolytic cleavage of the C–H bond, with the proton and electron formed by this cleavage being transferred to the carboxylate and the oxidant, respectively. This approach is related to Savéant’s theory of electron transfer concerted with bond cleavage, which emphasizes the strength of the bond being cleaved, for example, in electrochemical carbon–halogen and peroxide O–O bond cleavages.^38,39

For the Flr(R)CO₂⁻ compounds, changing the R-group affects both the basicity of the carboxylate and the C–H BDFE. The larger effect is on the basicity, which experimentally shifts by 1.7 pK_a units, corresponding to a change in ΔG° of 2.3 kcal mol⁻¹. Shifts also occur in the ΔBDFE_C–H’s for the fluorenyl C–H bonds in Flr(R)CO₂⁻, computed to vary by 0.9 kcal mol⁻¹ (Table 2). The CF₃ compound has the strongest C–H bond and is the slowest-reacting substrate. However, the pattern of reactivity does not otherwise follow the small changes in computed ΔBDFEs. Additionally, the −OMe compound reacts 3 times faster than even the R = H compound, although the R = OMe is computed to have a slightly stronger C–H bond. While these comparisons may approach the limit of relative computational accuracy, the changes in the C–H BDFEs with benzoate substituent do not appear to be the major contributor to the large variation of k_MS‑CPET with substituent.

The data indicate that the effects of the benzoate substituents are primarily based on changes in the basicity of the carboxylate acceptor. The spacing of the LFER lines in Figure 1C, for instance, generally echoes differences in experimental pK_a values for Flr(R)CO₂H (ΔpK_a,COOH, Table 2), within the accuracy of the measurements. The large Brønsted α_ox+ values thus suggest a great sensitivity to the strength of the base, and to the proton transfer portion of the MS-CPET reaction.

Imbalanced Transition States.

The computed proton potential energy surfaces for the MS-CPET reactions described above suggest imbalanced transition states for the MS-CPET reactions. In particular, proton transfer appears to be more advanced than expected from a simple Hammond postulate analysis. Even though the reactions of Flr(H)CO₂⁻ and N(Ar_Br)₃^•+ or N(Ar_H)₃^•+ are strongly exoergic, at the TS the proton transfer has progressed roughly halfway to the product. PT is more advanced than the electronic reorganization within the fluorenyl unit to accommodate the incipient radical (for MS-CPET) or carbanion (for simple PT). The calculations are consistent with the experimental observation of two Brønsted α values. In many cases, the Brønsted α is taken as a rough measure of the transition state position.^17c,40 The larger α_ox+ values for changes in substituents should therefore imply a transition state that is later, more product like, along the proton transfer coordinate. We believe that these analyses provide a qualitative rationale for the high sensitivity of our MS-CPET reactions to the basicity of the carboxylate.

Reactions with imbalanced transition states have long been discussed in the physical organic literature. In particular, Bernasconi has argued that this is a very common situation, as enunciated in his Principle of Nonperfect Synchronization (PNS).^{18a,b,c,29a,b,41} Others have developed similar ideas in different formalisms, including Marcus,⁴² Kresge,^15,40 More O’Ferrall, Jencks, Grunwald, Guthrie,^19,20,43 and Bordwell.¹⁵ One classic example is the deprotonation of nitroalkanes, where C–H bond cleavage is more pronounced at the TS than the electronic delocalization of the π system.^15,37d

The DFT analysis shows that pure proton transfer in Flr(H)CO₂⁻ behaves similarly to traditional C–H bond deprotonations, for example, in aldehydes or nitroalkanes.^16,18c The Flr(H)CO₂⁻ PT transition state is imbalanced, with proton transfer being farther along than the electronic reorganization within the fluorene, as indicated by the planarization of the incipient radical.

The imbalance of the proton transfer in Flr(H)CO₂⁻ is illustrated in Figure 3A by a traditional More O’Ferrall–Jencks plot.^17a,44 The horizontal axis represents progress along the PT coordinate, and the vertical axis represents progress along the internal electronic reorganization coordinate. A synchronous reaction would be indicated by progress along the diagonal of the square. The asynchrony of PT in Flr(H)CO₂⁻ is indicated by the curved line that connects the reactant to the product (bottom left to top right corners). Because the transition state has more progress along the proton transfer coordinate than the electronic reorganization coordinate, the lines are curved toward the bottom right corner.

Figure 3.

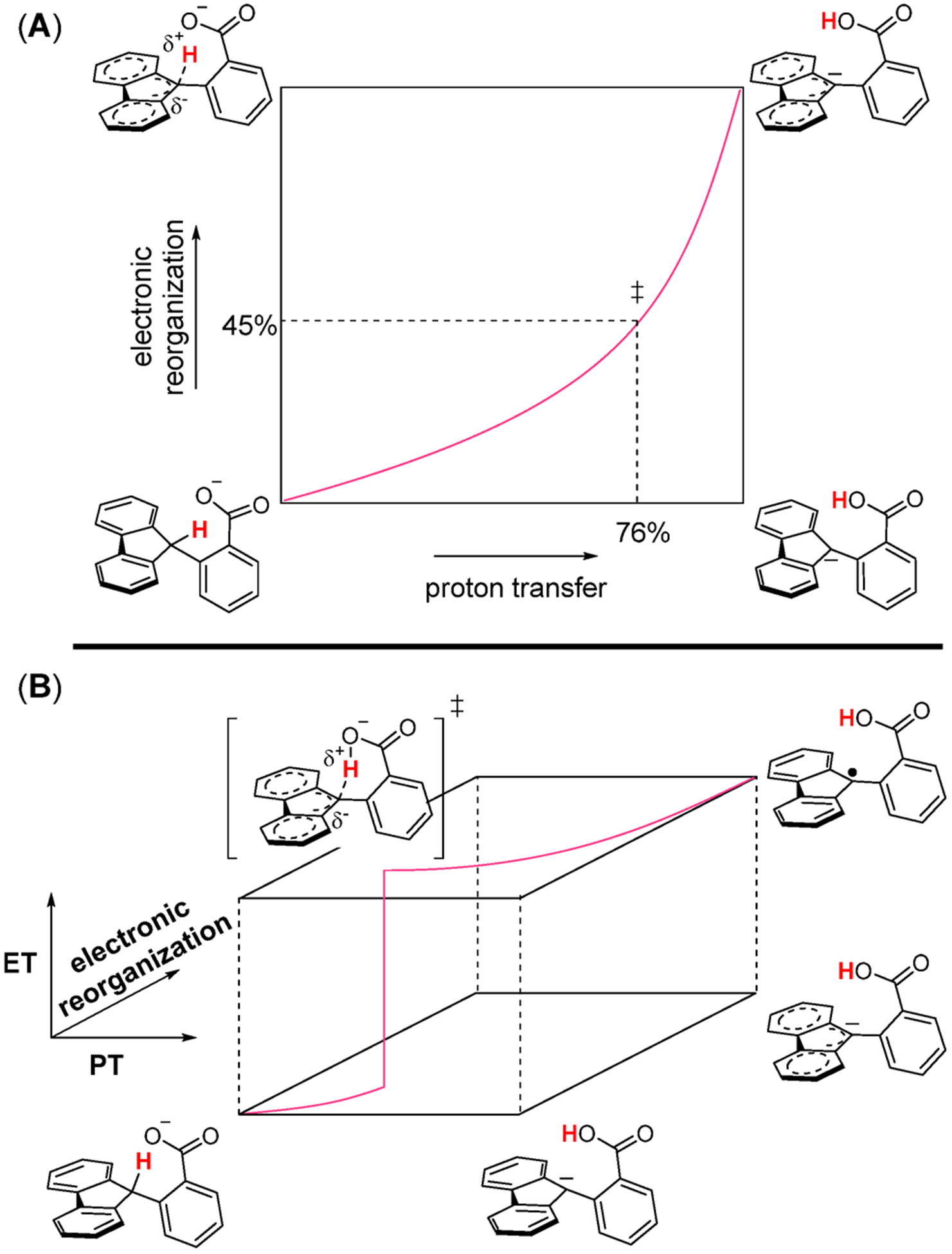
(A) A More O’Ferrall–Jencks plot for intramolecular proton transfer in Flr(H)CO₂⁻. The progress of the proton transfer and electronic reorganization at the transition state (‡) are noted with dashed lines. (B) A double More O’Ferrall–Jencks plot for the MS-CPET reaction of Flr(H)CO₂⁻ with an outer-sphere oxidant. As in part (A), each of the two horizontal planes illustrates the progress in the proton transfer coordinate and in the electronic reorganization coordinate. The jump from the bottom to the top plane represents the electron transfer to the oxidant, an essentially instantaneous step that takes the system from one electronic state to another.

Extending Bernasconi’s PNS to MS-CPET requires thinking not only about proton transfer and electronic reorganization but also about the electron transfer portion of the reaction. The adiabatic DFT calculations used here are not the preferred treatment for electron transfer processes, which can be nonadiabatic.³⁰ Still, the DFT analysis provides valuable insights into the structure of the MS-CPET transition state. This transition state is both the highest point along the proton reaction coordinate and the point where the electron transfers from Flr(R)CO₂⁻ to the oxidant (see above). The parallels between the DFT description of MS-CPET with the PT case are quite strong. Again, PT is farther along the reaction coordinate than would be expected from the Hammond postulate. Electronic reorganization within the fluorene lags behind the proton transfer.

One way to visualize MS-CPET in the Bernasconi PNS formalism is to represent the two electronic states as two More O’Ferrall–Jencks planes, as shown in Figure 3B. The bottom plane shows the nuclear reorganization to arrive at the transition state. Electron transfer for the MS-CPET reaction is shown by a “jump” from one plane to another, because it occurs instantaneously on the time scale of nuclear motions (the Franck–Condon principle).^5a,30,31 This takes the system to the upper plane where the nuclear reorganization is completed to form the product. This description is supported by the DFT calculations, which show that the NBO charge on the nitrogen atom of the oxidant sharply changes at the transition state, while the nuclear motions proceed smoothly before and after the transition state.

The late position of proton transfer along the reaction coordinate provides a rationale for the larger Brønsted α upon changing the substituent than the oxidant. It is, however, more challenging to use this model to understand the small dependence of the rate constants on the reduction potential of oxidant (α_ET = 0.2). In a simple Marcus theory formalism, a small α would normally indicate a strongly exoergic reaction, with −ΔG° approaching λ. This is not consistent with our estimates that MS-CPET is close to isoergic for the oxidation of Flr(H)CO₂⁻ with FeCp*₂⁺.¹² In addition, this explanation would require curvature of the log(k_MS‑CPET) versus log(K_{eq‑MS‑CPET}) plots, which is not seen in Figure 1C. The TS for the MS-CPET is early only in the “electronic reorganization” coordinate, and this refers to π bond rearrangement in the developing fluorenyl radical, not electron transfer to the oxidant. Understanding the small α likely requires a more complete treatment, as reported recently by Sayfutyarova, Goldsmith, and Hammes-Schiffer.³¹

CONCLUSIONS

Reported here is a detailed study of the fundamental properties of oxidative cleavage of C–H bonds, by multiple-site concerted proton–electron transfer (MS-CPET). This mechanism is a new addition to the arsenal of C–H bond functionalization reactions. Kinetic studies of a series of fluorenyl-benzoate substrates show that the second-order rate constants are much more sensitive to substituents on the benzoate than to changes in the reduction potential of the oxidant. This shows, surprisingly, that the k_MS‑CPET values do not simply correlate with the reaction driving force (K_{eq‑MS‑CPET}). The k_MS‑CPET values vary much more dramatically when the K_eq is changed via the substituent (Brønsted α_Fc+ = 0.6) than when K_eq is changed with changes in the oxidant (α_ET = 0.2). Experimental and computational analyses indicate that these differences reflect a higher sensitivity to the pK_a of the base rather than the oxidizing power of the oxidant.

Computational experiments show that the MS-CPET transition state (TS) is later on the proton transfer reaction coordinate than would be expected from the Hammond postulate. In addition, the TS shows significantly more progress along the proton transfer coordinate than along a coordinate that describes electronic reorganization of the π bonding within the fluorenyl group. Similar features were observed in DFT analysis of intramolecular proton transfer (PT) within the same substrate. These studies indicate strong analogies between PT and MS-CPET, despite the latter reaction involving an outer-sphere electron transfer component. The description of these reactions is reminiscent of classical physical organic analyses of proton transfer from C–H bonds, such as Bernasconi’s Principle of Nonperfect Synchronization.

The results reported here are, to our knowledge, the first examples of MS-CPET reactions that show such a clear differentiation between changes in the electron transfer and the proton transfer reaction coordinates. Because this is the only example that involves a C–H bond, we tentatively suggest that this asymmetry could be characteristic of MS-CPET of C–H bonds, just as it is for simple deprotonation of C–H versus N–H or O–H bonds. This asynchrony of the concerted e⁻/H⁺ transfer should have implications for broader development of MS-CPET as a mechanism for C–H bond activation, for instance, in selectivity enforcement in synthetic reactions and enzymatic processes.

EXPERIMENTAL SECTION

General Considerations.

Reagents were typically purchased from Sigma-Aldrich, Alfa Aesar, or Acros and used as received. Solvents were obtained from Fisher, while deuterated solvents were from Cambridge Isotope Laboratories. Unless otherwise noted, experiments were performed in an N₂-filled glovebox using solvents that were sparged with argon and plumbed directly into the glovebox. Dimethylformamide was purified using a Glass Contour Solvent Purification System (Pure Process Technology, LLC, Nashua, NH). Acetonitrile was Burdick Jackson low water grade and used without additional drying. All oxidants used were hexafluorophosphate (PF₆⁻) salts. Aminium^27a and ferrocenium^10d oxidants were prepared as described previously. NMR samples following MS-CPET reactions were prepared in an N₂-filled glovebox using degassed, deuterated solvents dried over activated 3 Å molecular sieves. NMR spectra were collected on Agilent DD2 400, 500, or 600 MHz spectrometers.

DFT Calculations.

All calculations were performed using the Gaussian 16 software package. All optimized geometries were confirmed to be local minima by vibrational analysis (no imaginary frequencies). Geometry optimizations and frequency calculations were performed at the B3LYP/def2-SVP or B3LYP/def2-TZVP level of theory. Cartesian coordinates of the optimized geometries of all species are given in the Supporting Information.

Synthesis.

The carboxylic acids were generated by basic hydrolysis from the corresponding methyl ester. The methyl ester compounds were synthesized using a modified procedure from a previous report.²² Fluorene (1.2 equiv), the appropriate methyl ester (1.0 equiv), Pd(OAc)₂ (2 mol %), PCy₃·HBF₄ (4 mol %), and Cs₂CO₃ (1.5 equiv) were added to a microwave vial that was equipped with a stir bar. The vial was evacuated and backfilled with N₂ on a Schlenk line. DMF was taken directly from the solvent system inside the glovebox and syringed into the reaction vial. The reaction then was heated at 110 or 130 °C overnight (~16 h). The reaction was cooled to room temperature and diluted with 1 M HCl. The aqueous layer was extracted with Et₂O (3 × 20 mL), and then the organic layer was washed with 1 M HCl (2 × 20 mL), H₂O (2 × 20 mL), and brine (20 mL). The organic layer was dried over MgSO₄ and solvent evaporated. The crude reaction mixture was purified on a silica gel column in 5% EtOAc:hexanes eluent. The methyl ester products generated via the above procedure were then treated with basic hydrolysis to yield the corresponding carboxylic acid. The isolated methyl ester was added to a degassed solution of ethanol and 3 M aqueous KOH. This solution was brought to reflux until a TLC revealed consumption of the methyl ester starting material (usually in about 15–30 min). The reaction mixture was cooled to room temperature and diluted with 1 M HCl_aq and washed with Et₂O to afford the carboxylic acids as white or off-white solids.

Experimental pK_a Measurements.

Measurements of the pK_a’s were performed in analogy to a previous report.^10d In a typical experiment, a fluorenyl substrate was deprotonated with 1.0 equiv of 1,8-diazabicyclo[5.4.0]undec-7-ene (DBU) in an N₂-filled glovebox in CD₃CN. Next, 4-trifluoromethyl benzoic acid (TFBA) was added to the solution, the mixture was allowed to equilibrate, and ¹H/¹⁹F NMR spectra were measured to determine the chemical shifts of chosen hydrogen and fluorine atoms at equilibrium. The acid/base pair for each material is in rapid equilibrium, so only an averaged signal was observed for each. The chemical shifts of the averaged signal give the ratio of acid to carboxylate for that species, allowing determination of the quotient of the K_a’s of the two acids in solution. These data were used to construct a relative pK_a scale. The relative pK_a between TFBA and benzoic acid was also measured, which gives the relative scale an absolute anchor because the pK_a of benzoic acid in MeCN is known.

Kinetics.

Kinetic measurements were recorded on an OLIS-RSM 1000 single mixing stopped-flow spectrophotometer in Burdick & Jackson low water acetonitrile that was sparged with argon and plumbed directly into an N₂-filled glovebox. Measurements at different temperatures were made on a TgK double mixing stopped-flow instrument at temperatures ranging from −40 to 15 °C.