Measured and predicted resting energy expenditure in wheelchair rugby athletes

Abstract

Objective: Report measured resting energy expenditure (REE) in wheelchair rugby athletes and evaluate agreement between REE and the prediction models of Chun, Cunningham, Harris-Benedict, Mifflin, Nightingale and Gorgey, and Owen.

Design: Cohort-based validation study.

Setting. Paralympic team training camp.

Participants: Fourteen internationally competitive athletes who play wheelchair rugby, 13 of whom had cervical spinal cord injuries (SCI).

Outcome Measures: A portable metabolic analyzer was used to measure REE following an overnight fast and dual-energy X-ray absorptiometry (DXA) was used to assess lean body mass for the prediction equations.

Results: REE in the current sample was 1735 ± 257 kcal × day⁻¹ ranging from 1324 to 2068 kcal × day⁻¹. Bland–Altman analyses revealed negative mean bias but similar limits of agreement between measured REE and scores predicted by Chun, Cunningham, Mifflin, Nightingale and Gorgey, and Owen models in elite athletes who play wheelchair rugby.

Conclusion: Prediction models regressed on persons with and without SCI under-predicted REE of competitive wheelchair rugby athletes. This outcome may be explained by the higher REE/fat-free mass (FFM) ratio of current athletes compared to less active samples. Findings from the current study will help practitioners to determine nutrient intake needs on training days of varied intensity.

Introduction

Wheelchair sport (WS) is expanding physical activity options, and associated benefits, to athletes with physical impairments.¹ Sport has become extremely important to this population because individuals with physical impairments typically engage in minimal physical activity, experience greater barriers to activity participation, and have a greater prevalence of chronic disease than the general population.^2,3 Wheelchair rugby is a popular team sport and, although it is available to individuals with varied physical impairments in both upper and lower limbs, it is primarily played by persons with a cervical spinal cord injury (SCI; i.e. tetraplegia).^4,5

Specific to athletes with SCI, Price identified resting energy expenditure (REE) as a primary research need.⁶ This need exists because, compared to the general population, persons with SCI have less active muscle mass and atypical sympathetic nervous stimulation, dramatically affecting metabolic rate during rest and physical activity.^6–8 Specifically, REE is 14–27% lower in persons with SCI compared to persons without and wheelchair rugby requires approximately 26% of the energy demand required for standing rugby.^9–13 Without a clear understanding of REE in this population, there is no evidence-based model to prescribe appropriate energy intake during training or competition. This gap in practice is problematic since insufficient energy intake during training decreases exercise capacity, impairs power output, reduces the body’s ability to recover between training sessions, and ultimately increases the risk of injury and illness in athletes with physical impairments.¹⁴ Conversely, excess energy intake increases body fat levels which may diminish performance and health. Therefore, the primary purpose of this study was to measure REE in wheelchair rugby athletes, a sport primarily played by athletes with SCI.

Predicted versus measured REE in persons with SCI

Among sport populations, REE has been measured via indirect calorimetry or predicted from regression equations developed on persons with and without physical disabilities.^7,10,13 Indirect calorimetry requires considerable expense and data collector expertise, yielding the use of prediction equations as a more practical method for those working with athletes. To determine if prediction equations are suitable alternatives to measured REE, empirical examination must support their usage. Among athletes with physical impairments, six models have been validated for persons with tetraplegia or empirically examined for their agreement with a measure of resting metabolism (either REE or basal metabolic rate) (see Table 1).

Table 1. Regression models used to predict resting energy expenditure (REE).

Model	Equation for REE (kcal × day−1)	Note
Chun et al.16	REE = 244 + 24.5 × FFM	Regressed on 50 adults with motor complete paraplegia or tetraplegia
Cunningham17	REE = 500 + 22 × FFM	Regressed on Harris-Benedict sample
Harris-Benedict20	REE = 66.47 + 13.75 × WT + 5 × HT + 6.67 × Age	Classic prediction formula developed in 1919 on healthy, normal weight males
Mifflin et al.21	REE = 413 + 19.7 × FFM	Default formula in DXA; Regressed on 498 normal weight and obese males and females
Nightingale and Gorgey18	REE = 294.330 + 23.469 × FFM	Regressed on 30 men with motor complete paraplegia or tetraplegia
Owen et al.22	REE = 290 + 22.3 × FFM	Sample comprised healthy and obese males

Note. FFM, fat free mass; WT, weight; HT, height.

Bland–Altman plots¹⁵ have been used to evaluate the agreement of three of these models with measured REE. Chun and colleagues¹⁶ examined the consistency between their own prediction model regressed on adults with SCI (paraplegia and tetraplegia) with measured REE. They reported strong agreement within measures (ICC = 0.87) and published limits of agreement from – 229 to 233 kcal × day⁻¹ (or – 18.5 to 20.6%). These authors also used Bland–Altman techniques to evaluate the consistency between prediction scores from the Cunningham model to measured REE in persons with SCI.¹⁷ Despite using a model regressed on the general population, Chun et al.¹⁶ reported good agreement within measures (ICC = 0.85) and limits of agreement of −230 to 241 kcal × day⁻¹ (−18.5 to 22%). Nightingale and Gorgey¹⁸ developed multiple regression equations on basal metabolic rate (BMR) in 30 males with motor complete paraplegia and tetraplegia. These authors reported that fat free mass (FFM) explained 69% of the variance in BMR with a prediction error of approximately 100 kcal × day⁻¹. Using Bland–Altman analyses, these authors reported a mean bias for the FFM model to be −84 kcal × day⁻¹ with limits of agreements from −346 to 178 kcal × day⁻¹.

Correlation and regression have also been used to examine agreement, or consistency, between predicted and measured REE. For example, Barco and colleagues¹⁹ reported a strong relationship between measured and predicted BMR using an adjusted Harris-Benedict equation²⁰ among 11 men with tetraplegia in an inpatient setting (r = .74–.79 across 4 weeks of observation). In their study, the adjustment to the Harris-Benedict score included a 10% increment as an activity correction and a 20% increment as an injury adjustment. The general equations developed by Mifflin et al.²¹ and Owen et al.²² have also been examined in wheelchair sport populations and have demonstrated strong relationships to measured REE in athletes with physical impairments.^7,23 FFM explains a great deal of variation in REE,²⁴ which in turn, explains why equations using FFM as a predictor, such as Chun et al., Cunningham et al., Mifflin et al., Nightingale and Gorgey, and Owen et al., may be useful for athletes who play wheelchair rugby.

The need to describe REE and evaluate agreement with prediction models is paramount for wheelchair rugby athletes as these individuals typically have a greater physical impairment, greater sympathetic impairment, and less active muscle mass than most wheelchair sport athletes. A better understanding of REE and the agreement of predictive models with REE may improve sport science applications for this population. Therefore, the purposes of this study were to: (a) report measured REE (not basal metabolic rate) in elite wheelchair rugby athletes, and (b) evaluate agreement between previously validated prediction equations and REE in these athletes.

Methods

Participants

Data from 15 male international-level wheelchair rugby athletes were examined during a team training camp. Inclusion criteria included homeostatic diet (no deliberate calorie restriction), body weight (within 2.5 kg over the past 6 mo), heart rate and blood pressure at the time of data collection. One prospective participant was restricting caloric intake to lose weight at the time of data collection and was excluded from data analyses. Demographic data from the remaining 14 athletes are reported in Table 2. Eleven athletes in the sample had an incomplete cervical SCI, two athletes had a complete cervical SCI, and one athlete had an alternative physical impairment that affected both upper and lower limbs. Although many clinicians use the American Spinal Injury Association Impairment Scale to describe functional ability in this population, we used a more ecologically valid assessment, namely each athlete’s sport classification score, to describe the motor function of the sample. Sport classification scores are based on the athlete’s functional abilities and range from 0.5 (most significant limitation) to 3.5 (least significant). Four athletes were classified ≤1.0, 6 athletes were classified as 1.5–2.0, and three athletes were ≥2.5 according to the international wheelchair rugby classification system.²⁵ Institutional Review Board and team approval were obtained for analysis of retrospective data for research purposes. Data are available through a figshare repository (10.6084/m9.figshare.7,673,618).

Table 2. Sample demographics (N = 14).

	Mean ± SD	Min	Max
Age (yrs)	31 ± 6	22	42
Weight (kg)	66.43 ± 10.45	52.27	84.14
Fat free mass (kg)a	47.50 ± 7.74	36.55	57.91
Body fat (%)a	25.44 ± 5.81	16.20	34.50
REE (kcal × day−1)	1735 ± 257	1324	2068
REE/WT (kcal × kg−1 × day−1)	26 ± 2	23	29
REE/FFM (kcal×kg−1 × day−1)	37 ± 2	33	41

Note. REE, resting energy expenditure; WT, weight; FFM, fat free mass.

^aDenotes assessments made via DXA.

Procedures

Indirect calorimetry was undertaken using a portable gas analyzer (Fitmate^® Pro, Cosmed, Rome, Italy) to assess REE. The device was calibrated using room air before each test. The accuracy of the oxygen analyzer (±0.02%) and flowmeter (±2%) were both within industry standards. A silicon facemask was fitted over the participants’ mouth and nose upon waking in the athletes’ bed (6–7am) following an overnight fast and at least 10 h since the previous exercise bout. Rooms remained dimly lit and quiet during data collection but room temperature varied based on participant preference. Oxygen consumption was measured breath-by-breath and averaged for each minute while participants rested in a supine position for 30 min and REE was computed as the average oxygen consumption score across the final 20 steady-state minutes. Participants were monitored to ensure they did not fall asleep during data collection and that no participant interruptions occurred. The average minute expenditure was then extrapolated to a 24-hour REE score (kcal × day⁻¹).^7,26 Research has shown the Fitmate^® Pro to be valid and reliable system for the measurement of parameters of respiration.²⁷

Once assessment of REE was complete, athletes were pushed in their everyday chair to the DXA instrument and scans were performed using procedures specific to elite wheelchair athletes.²⁸ Specifically, each athlete was asked to lie supine with arms and legs straight. The arms were placed at their sides with palms turned in toward the body. The midline of the scan field was aligned with the midline of the participant’s body, and, if necessary, a knee or foot strap was used to maintain a neutral position of the lower body as recommended for these athletes.²⁸ Body composition and bone mass were assessed using the Lunar Prodigy Primo DXA scanner (GE Healthcare, Wisconsin, USA) set to standard scan mode. The instrument was calibrated daily based on manufacturer recommendations. Participants were instructed to fast overnight and a minimum of 12 h passed between their previous meal and total body scan. This delimitation was made to maximize the accuracy of body composition assessment for athletes.²⁹ All scans were completed with Lunar software (enCORE version 15) and data collection included FFM (lean tissue mass plus bone mineral content) and fat mass. Body fatness percentage was determined from the ratio of total fat (g) to total tissue (g).

Analysis

To address the primary research purpose, exploratory data analysis was done on measured REE in wheelchair rugby athletes. Data for each variable met the assumption for normality as confirmed by visual inspection and the Kolmogorov–Smirnov Test. To examine the agreement of each prediction model with REE in wheelchair rugby athletes, the following analyses were conducted. First, intraclass correlation coefficients (ICC₂) were run to examine the consistency between predicted and measured REE. If the agreement was strong (ICC ≥ 0.70), equivalence testing between predicted and measured REE scores was conducted.^7,23,30 An a priori decision was made that ± 100 kcal × day⁻¹ was a suitable agreement in practice to confirm two measures as equivalent REE scores. These values were derived from standard deviations of REE mean difference scores reported for varied prediction models of REE in persons with SCI.^16,18 Equivalency testing required testing two null hypotheses: difference scores were >100 kcal × day⁻¹ (H_A = difference scores ≤ 100) and difference scores were < −100 kcal × day⁻¹.

Once conducted, Bland–Altman plots were generated to evaluate mean bias and precision of each prediction model.¹⁵ Mean absolute percent error (MAPE) was then determined.^16,26,31 Assumptions for normality (difference scores in Bland–Altman plots) and homoscedasticity (examination of standardized residual and predicted scores) were met. IBM SPSS 22 (Armonk, NY, USA) and Microsoft Excel 2016 (Redmond, WA, USA) software were used to compute all statistics.

Results

REE in the current sample was 1735 ± 257 kcal × day⁻¹ ranging from a low score of 1324 to a high score of 2068 kcal × day⁻¹. Regarding agreement with previously validated equations, there was an acceptable agreement between each prediction model and measured REE in wheelchair rugby athletes (ICC > 0.70; Table 3). Predicted scores from the Chun et al.¹⁶, Cunningham¹⁷, Mifflin et al.²¹, Nightingale and Gorgey¹⁸, and Owen et al.²² models were statistically equivalent to measured REE within ± 100 kcal × day⁻¹ (Table 3). The Harris-Benedict model²⁰, however, was not statistically equivalent relative to the null hypothesis for difference scores >100 kcal × day⁻¹.

Table 3. Intraclass correlation coefficients (ICC) and equivalency test statistics between prediction models and measured resting energy expenditure (REE).

Prediction model	ICC	Upper limit t-statistic	p	Lower limit t-statistic	p
Chun et al.	0.94	7.72	.000	14.54	.000
Cunningham	0.92	2.81	.007	9.089	.000
Harris-Benedict	0.78	−0.94	.180	3.00	.005
Mifflin et al.	0.91	7.03	.000	12.98	.000
Nightingale and Gorgey	0.93	7.45	.000	14.04	.000
Owen et al.	0.92	9.05	.000	15.39	.000

Note. Upper and lower-limit t-values reflect equivalency with measured REE within ± 100 kcal × day⁻¹.

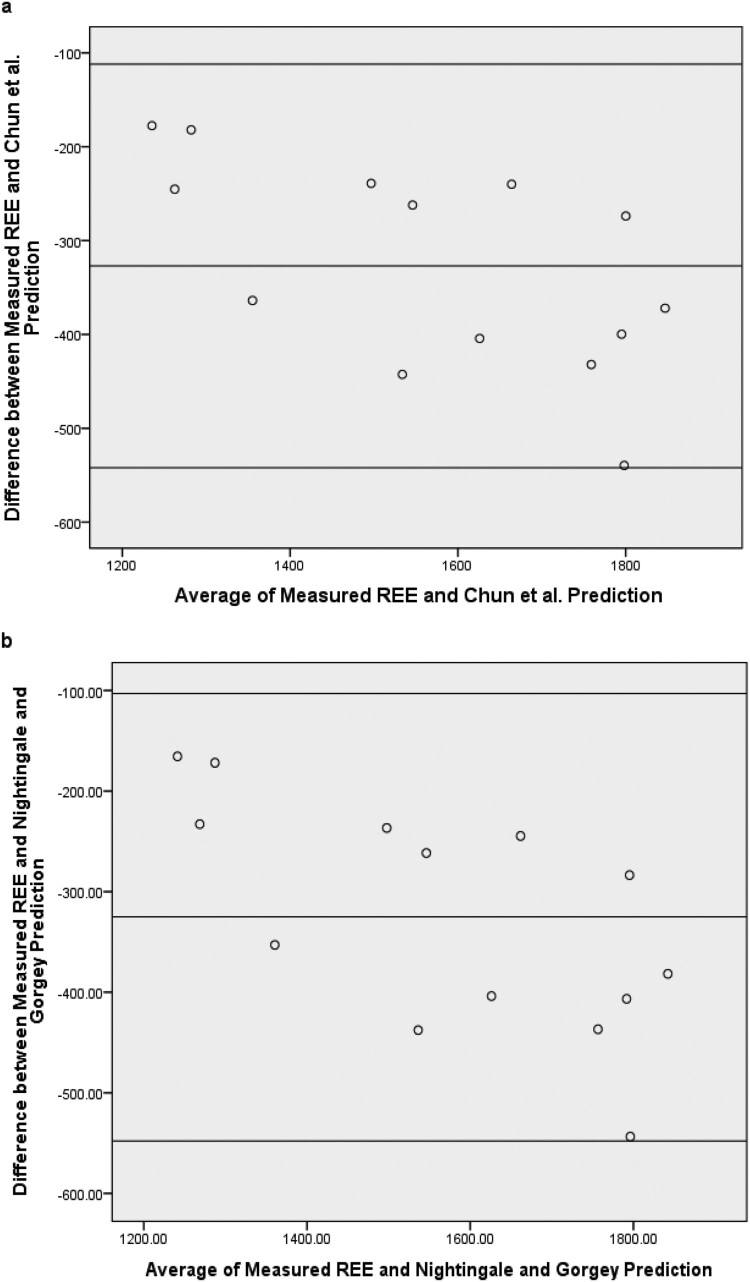
The Bland–Altman plots for the Chun et al., Cunningham, Mifflin et al., Nightingale and Gorgey, and Owen et al. models are presented in Fig. 1. For each of the aforementioned models, the mean of the predicted score and REE, plotted against difference scores between the two, all fell within limits of agreement (Table 4). This finding is important but must be interpreted within the context of each model’s precision with REE (i.e. range between limits of agreement). Additionally, each model demonstrated a negative bias to measured REE, indicating that these models all under-predicted REE in the wheelchair rugby sample. Proportional bias was also evident, indicating greater underestimation with higher calorie expenditure scores. Mean absolute percentage error scores ranged from 10% to 22% across these models (Table 4). Results for the Harris-Benedict model were different as there were much lower bias and smaller error scores than the other models but much larger upper and lower limits of agreement. Based on these findings, the Chun et al., Cunningham, Mifflin et al., Nightingale and Gorgey, and Owen et al. models may be used to estimate REE in similar samples but adjustment for mean bias should be considered.

Figure 1.

Interpretation of Bland-Altman Plots for evaluation of agreement. Graphs reflect bias, upper limit of agreement, and lower limit of agreement scores between measured REE and predicted scores from the (a) Chun et al. equation, (b) Nightingale and Gorgey equation, (c) Cunningham equation, (d) Harris-Benedict equation, (e) Mifflin et al. equation, and (f) Owens et al. equation.

Table 4. Agreement of prediction models with measured resting energy expenditure.

	Chun et al.	Cunningham	Harris-Benedict	Mifflin et al.	Nightingale and Gorgey	Owen et al.
Kcal × day−1 (mean ± s)	1408 ± 189	1545 ± 170	1682 ± 186	1398 ± 161	1409 ± 182	1349 ± 173
Bias (kcal × day−1)	−326	−190	−52	−336	−325	−385
Upper limit of agreement (kcal × day−1)	−112	44	321	−90	−103	−154
Lower limit of agreement (kcal × day−1)	−542	−424	−425	−583	−548	−617
Mean absolute percent error	18.6%	10.3%	9.7%	18.9%	18.4%	21.9%

Discussion

REE continues to decline over time in persons with SCI;³² however, lean body mass is greater in active persons with SCI than sedentary matched controls.⁸ These findings may explain why the mean REE in the current study, 1735 kcal × day⁻¹, is distinct from norms in non-athletic samples with SCI. Specifically, the REE for the current sample exceeds REE ranges of 1200–1500 kcal × day⁻¹ reported by others.^32–34

Fat mass percentage in the current sample was meaningfully different from less active samples of persons with motor complete SCI (Table 2).^16,18 This distinction could be used to rationalize that individuals with less fat mass in turn have a greater amount of FFM which explains increased REE. This assumption would be logical as wheelchair rugby training results in decreased fat mass and increased FFM percentages.³⁵ However, mean FFM in the current sample (47.5 kg) was actually lower than the non-sport sample examined by Nightingale and Gorgey (51.3 kg). When examining the data in more detail, the ratio of REE/FFM provides a better explanation of elevated REE in the current sample. Mean REE relative to FFM, in the Chun et al.¹⁶ and Nightingale and Gorgey¹⁸ samples, was approximately 30 kcal × kg⁻¹ × day⁻¹. This consistency between the two studies is not surprising considering that both samples comprised adults with paraplegia or tetraplegia who had motor complete injuries. However, mean REE in the current sample, expressed relative to FFM, was 37 kcal × kg⁻¹ × day⁻¹. This finding is consistent with the value of 34 kcal × kg⁻¹ × day⁻¹ reported for nationally competitive athletes with spinal cord injury.⁷ More research is needed to confirm but it seems likely that activity level, in conjunction with injury type (i.e. incomplete), explains a great deal of variability in REE demonstrated across persons with SCI.

Evaluation of Agreement Chun et al.¹⁶ and Nightingale and Gorgey¹⁸ used FFM among individuals with motor complete SCI to predict REE and BMR, respectively. Both models demonstrated strong agreement with measured REE in the current study (ICC = 0.94 and 0.93, respectively) and were statistically equivalent to measured REE. Additionally, negative mean bias was present in both models as each under-predicted REE in the current study by approximately 325 kcal × day⁻¹ (Table 4). This bias is explained by the aforementioned REE/FFM differences between our athletic sample and the non-athletic samples evaluated by Chun et al.¹⁶ and Nightingale and Gorgey.¹⁸

However, limits of agreement (Fig. 1(a) and 1(b)), or the range where 95% of difference scores fall, were very similar between our use of Chun et al. and Nightingale and Gorgey models to predict REE and their original validation studies (range of ∼450 kcal × day⁻¹). Chun and colleagues¹⁶ evaluated this spread as lacking sufficient precision when applied at the individual level for persons with SCI. We agree that precision can be improved, possibly through appropriate scaling or algorithmic adjustments for athletes, to make usage more effective at the individual level. Mean absolute percent errors (MAPE) in the current study were almost identical to the error reported by Chun et al.¹⁶ for the original validation equation but higher than that reported by Nightingale and Gorgey.¹⁸ This difference could be due to the fact that we measured REE whereas Nightingale and Gorgey assessed BMR.

Despite being regressed on an able-bodied non-athlete population, the prediction model developed by Cunningham was also equivalent to measured REE in wheelchair rugby players (Table 3). Similar to the Chun et al. and Nightingale and Gorgey models, all difference scores, plotted against mean differences, fell within limits of agreement (Fig. 1(c)). The precision of the Cunningham model¹⁷ was also similar to the Chun et al. and Nightingale and Gorgey models (Table 4). The Cunningham model systematically under-predicted REE but the MAPE was smallest for the Cunningham model among all those examined. The Cunningham equation was developed on 223 healthy adults (120 males, and 103 females) who were subjects in the classic metabolic study performed by Harris and Benedict.²⁰ Through regression analysis, Cunningham determined that the best single predictor of REE from multiple anthropometric variables, regardless of sex, was FFM. It seems possible that our sample demonstrated an REE/FFM rate that was more similar to the general population than less active individuals with SCI reported in prior research; hence, prediction accuracy was better.

Our findings on the agreement between Cunningham scores and measured REE in persons with SCI are consistent with the literature. Pelly and colleagues⁷ reported no significant mean differences between measured and Cunningham-predicted REE scores in seven athletes with paraplegia but reported greater prediction error (209 kcal × day⁻¹). The stronger relationship in the current study (ICC = 0.92) compared to the relationship strength in the Pelly article (ρ = 0.14) explains the discrepancy. It seems likely that the more stratified sample in the current study (i.e. persons with tetraplegia) reflects a more metabolically-similar sample than the group examined by Pelly et al.⁷ This supposition is supported by the minimal variance in REE when expressed relative to weight or FFM in the current sample (Table 2). Additionally, Chun and colleagues¹⁶ reported an ICC of 0.85 between Cunningham-predicted and measured REE in persons with motor complete tetraplegia or paraplegia.

The Harris-Benedict model²⁰ has been used for over a century in the estimation of REE in the able-bodied population. Despite its overestimation of measured REE in the general population by 7–14%,²² this model slightly underestimated REE in the current sample (bias score = −52 kcal × day⁻¹). Evaluation of this model reveals less statistical equivalency with REE than the other models (Table 3) but there was a smaller error rate (Table 4). Current findings are similar to those reported by Pelly and colleagues.⁷ Unlike our study, however, Pelly et al.⁷ reported that the Harris-Benedict formula over-predicted REE. Our findings are less consistent with those of Barco and colleagues¹⁹ who reported a strong relationship between BMR and Harris-Benedict scores among 11 men with tetraplegia (r = 0.74–0.79). These authors also reported lower error rates as BMR values were 95–100% of the Harris-Benedict predicted score. The distinction could be due to the fact that our study did not adjust for bed rest and altered metabolism due to injury as done by Barco and colleagues.

We also found the Mifflin et al.²¹ and Owen et al.²² models to be statistically equivalent to measured REE but, similar to the Chun et al. and Nightingale and Gorgey models, less precise than what is desired at the individual level. Pelly et al.⁷ reported no significant mean difference between Mifflin et al.-predicted and measured REE scores but did find differences using the Owen et al. model in seven male athletes with SCI. Additionally, these authors reported that the model developed by Mifflin et al. had the strongest relationship to measured REE across 5 regression models in their sample (including Cunningham and Harris-Benedict). However, Juzwiak and colleagues²³ reported that the Owen et al. equation was the best predictor of BMR in athletes with visual impairments and cerebral palsy. These authors reported prediction errors of 104 and 125 kcal × day⁻¹ for athletes with visual impairments and cerebral palsy, respectively, using Root Mean Squared Prediction Error. Our findings are very similar as the Owen et al. equation in the current study had a prediction error of 107 kcal × day⁻¹ in wheelchair rugby athletes. And similar to other prediction models, these estimates were statistically equivalent, within ± 100 kcal × day⁻¹, to measured REE despite systematic under-prediction.

Worth noting, REE during rest and activity are related to lesion level but the relationship is only moderate.¹¹ This outcome is likely due to multiple system influences on REE (e.g. sympathetic activity) which will vary more by completeness or incompleteness of injury rather than strict lesion level. In the current study, there was a very weak relationship between lesion level and REE (r = 0.09). It is likely that the limited variation of SCI level in the current study (tetraplegia) improved the agreement with models used to predict REE. In general, regression equations developed for the general population have overestimated REE in non-athletes with SCI. This trend is thought to be due to the reduced lean body mass in this population.^24,36 However, active individuals with SCI seem to exhibit a higher REE/FFM ratio which compensates for less FFM.

Limitations of this study are worth noting. One, the scope of the sample limits the generalizability of findings to a narrow population of elite athletes. The majority of research participants were persons with SCI but wheelchair rugby is open to persons with varied upper and lower mobility impairments. It is important to determine if these equations are robust and truly applicable to all persons who participate in wheelchair rugby. Additionally, the small sample size must provide context for the mean bias and limits of agreement reported in the current sample. Sample size was dictated by the population but allows for potentially large variations in our estimates across other samples. Finally, scores were collected during a training camp and participants were active prior to test day which, in turn, may have affected REE. Future research should determine the appropriate scaling for these formulas as all models under-estimated REE (but in a systematic fashion that may be remedied by appropriate scaling).

Conclusion

Measured REE of competitive wheelchair rugby players was 1735 ± 257 kcal × day⁻¹. Results of the current study support the statistical equivalency of Chun et al., Cunningham, Mifflin et al., Nightingale and Gorgey, and Owen et al. models as an alternative to measured REE with the Cunningham model demonstrating the best precision. Therefore, practitioners can use these models to develop nutrient intake planning for light-, moderate-, and vigorous-intensity training days for these athletes. Caution is warranted, however, as these models under-predicted REE and had error rates that could be improved, especially when applied at the individual level.

Disclaimer statements

Contributors None.

Funding None.

Conflicts of interest The authors report no conflict of interest and no funding support for this work.

Correction Statement

This article has been republished with minor changes. These changes do not impact the academic content of the article.

Acknowledgements

The authors would like to thank the national wheelchair rugby team for their participation in this research and Dr Xiuyan Guo for her statistical consultation.

ORCID

J.P. Barfield http://orcid.org/0000-0003-1692-9650