Abstract
This paper presents a Stage 3 validation of the recently released Collection 6 NASA MCD64A1 500 m global burned area product. The product is validated by comparison with Landsat 8 Operational Land Imager (OLI) image pairs acquired 16 days apart that were visually interpreted. These independent reference data were selected using a stratified random sampling approach that allows for probability sampling of Landsat data in both time and in space. A total of 558 Landsat 8 OLI image pairs (1116 images), acquired between March 1st, 2014 and March 19th , 2015, were selected and used to validate the MCD64A1 product. The areal accuracy of the MCD64A1 product was characterized at the 30 m resolution of the Landsat independent reference data using standard accuracy metrics derived from global and from biome specific confusion matrices. Because a probability based Stage 3 sampling protocol was followed, unbiased estimators of the accuracy metrics and associated standard errors could be used. Globally, the MCD64A1 product had an estimated 40.2% commission error and 72.6% omission error; the prevalence of omission errors is reflected by a negative estimated bias of the mapped global area burned relative to the Landsat independent reference data (−54.1%). Globally, the standard errors of the accuracy metrics were less than 6%. The lowest errors were observed in the boreal forest biome (27.0% omission and 23.9% estimated commission errors) where burned areas tend to be large and distinct, and remain on the landscape for long periods, and the highest errors were in the Tropical Forest, Temperate Forest, and Mediterranean biomes (estimated > 90% omission error and > 50% commission error). The product accuracy was also characterized at coarser scale using metrics derived from the regression between the proportion of coarse resolution grid cells detected as burned by MCD64A1 and the proportion mapped in the Landsat 8 interpreted maps. The errors of omission and commission observed at 30 m resolution compensate to a considerable extent at coarser resolution, as indicated by the coefficient of determination (r2 > 0.70), slope (> 0.79) and intercept (−0.0030) of the regression between the MCD64A1 product and the Landsat independent reference data in 3 km, 4 km, 5 km, and 6 km coarse resolution cells. The Boreal Forest, Desert and Xeric Shrublands, Temperate Savannah and Tropical Savannah biomes had higher r2 and slopes closer to unity than the Temperate Forest, Mediterranean, and Tropical Forest biomes. The analysis of the deviations between the proportion of area burned mapped by the MCD64A1 product and by the independent reference data, performed using 3 km × 3 km and 6 km × 6 km coarse resolution cells, indicates that the large negative bias in global area burned is primarily due to the systematic underestimation of smaller burned areas in the MCD64A1 product.
Keywords: Fire, Burned area, Validation, MODIS, Landsat, MCD64A1, Accuracy, Probability sampling
1. Introduction
While it is well established by the scientific community that fire is a key process in the terrestrial carbon cycle, fire management is also increasingly recognized as a significant aspect of public policy (Bowman et al., 2009, 2017; Bloom et al., 2016; Le Quéré et al., 2018; Lipsett-Moore et al., 2018). There is therefore a growing need for long term, spatially-and temporally explicit global burned area data sets that are consistent and well characterized. The advent of NASA’s Terra and Aqua satellites, launched respectively in 1999 and 2002, enabled, for the first time, systematic production of multi-year, global active fire and burned area products using Moderate Resolution Imaging Spectroradiometer (MODIS) observations (Justice et al., 2002a). The NASA MODIS fire products have been used in the scientific literature more than any other global fire dataset (Mouillot et al., 2014), both by the global modeling community and by the fire applications community (e.g., van der Werf et al., 2010; Granier et al., 2011; Giglio et al., 2013; Archibald et al., 2013; Hantson et al., 2015; Jolly et al., 2015; Di Giuseppe et al., 2016; Andela et al., 2017; Abatzoglou et al., 2018; Turco et al., 2018; Zubkova et al., 2019).
The NASA MCD64A1 global burned area product (Giglio et al., 2018a) was released recently as part of the most recent reprocessing of the science-quality NASA MODIS Land Product suite (Justice et al., 2002b). The MCD64A1 product is defined for the global land surface from November 2000 to present, in the equal area sinusoidal projection in approximately 1200 × 1200 km tiles, and is distributed as a monthly product that classifies each 500 m pixel as burned (with indication of the estimated day of burning), unburned, or unmapped if insufficient data were available to determine the burnt/unburned status (Giglio et al., 2018b). The Collection 6 burned area product, hereafter referred to as MCD64A1, supersedes the previous Collection 5.1 NASA MODIS burned area MCD64A1 and MCD45A1 products. It uses a refined algorithm designed to increase the detection of small burns, reduce the uncertainty in the temporal detection of the day of burning, and reduce the extent of unmapped areas in regions with high cloud cover (Giglio et al., 2018a).
Satellite product performance information is required to enable users to select and use products appropriately (Roy et al., 2002; Morisette et al., 2002). Quantitative product accuracy information may be derived by product comparison with a sample of independent reference data that has minimal or no error; this is termed validation (Justice et al., 2000; Stehman, 2001; Baret et al., 2006; Morisette et al., 2006). Product performance information may also be derived by examination of product examples at different temporal and spatial scales and by intercomparison with other products that have similar accuracy; this is often termed quality assessment (Roy et al., 2002). Product quality assessment is necessary for global products given the large number of factors that can adversely affect their quality (for a detailed discussion see Roy et al., 2002), and because over large areas product quality issues, such as stripes at input image granule boundaries, or anomalous temporal and spatial burning patterns (for examples see Humber et al., 2018), may remain undetected by validation activities that necessarily rely on a limited sample of independent reference data. The Collection 6 MCD64A1 product development involved significant product quality assessment, and some quality assessment results were reported in the literature. For example, systematic comparisons with the previous Collection 5.1 MCD64A1 burned area products showed that the Collection 6 MCD64A1 identified more area burned (26%) but similar spatial and temporal patterns at regional to global scales (Humber et al., 2018; Giglio et al., 2018a). These quality assessment activities do not, however, describe the product accuracy.
This paper quantifies the areal accuracy of the Collection 6 MCD64A1 burned area product. The validation approach used to derive the product accuracy information follows the methods presented in Boschetti et al. (2016), and it conforms with the Stage 3 requirements defined by the Committee on Earth Observation Satellites (CEOS) Land Product Validation subgroup (Morisette et al., 2006) that were defined to broadly document the representativeness of product validation results:
Stage 1 Validation: Product accuracy has been estimated using a small set of independent reference data obtained from selected locations and time periods.
Stage 2 Validation: Product accuracy has been assessed using independent reference data selected over a widely distributed set of locations and time periods that are representative of the full range of conditions present in the product.
Stage 3 Validation: Product accuracy has been assessed, and the uncertainties in the product established via independent measurements made in a statistically robust way, at multiple locations and time periods that represent the full range of conditions present in the product, and is characterized by the selection of independent reference data via probability sampling.
Stage 4 Validation: Validation results for Stage 3 are systematically updated when new product versions are released, or when the time coverage of existing products expands.
Previously, we undertook a Stage 2 validation of the Collection 6 MCD64A1 product using an independent reference dataset composed of only 192 globally distributed Landsat Thematic Mapper (TM) and Landsat 7 Enhanced Mapper Plus (ETM+) images, acquired between 2003 and 2010, that were visually interpreted into 30 m burned, unburned, and unmapped classes (Giglio et al., 2018a). We found a 24% commission error and a 37% omission error with respect to the 30 m Landsat data, and a 0.88 linear regression slope (0.82 r2) between the burn fraction in the MCD64A1 product and the Landsat reference data in 5 km grid cells (Giglio et al., 2018a). In addition, the temporal difference between the MCD64A1 reported day of burning and the dates of MODIS active fire detections was assessed with improved temporal reporting accuracy over the previous collection NASA MODIS burned area products (Boschetti et al., 2010a). These Collection 6 MCD64A1 validation results are Stage 2 and so do not reliably reflect the global MCD64A1 product accuracy. Specifically, no unbiased estimators of the accuracy metrics could be used, and no standard errors for the accuracy metrics could be derived as the independent reference data were not selected via probability sampling.
In this paper, one year of the Collection 6 MCD64A1 product starting on March 1st 2014 was validated to Stage 3 by comparison with independent reference data derived from 558 Landsat 8 Operational Land Imager (OLI) image pairs. This period was used because an annual fire year definition starting March 1st results in more consistent annual burned area reporting than a conventional calendar year definition (Boschetti and Roy, 2008), and because Landsat 8 was launched February 2013 (Roy et al., 2014). Pairs of Landsat 8 OLI images sensed over the same location 16 days apart were visually interpreted according to the Global Burned Area Satellite Validation Protocol (Boschetti et al., 2010b) endorsed by the Land Product Validation subgroup of the Committee on Earth Observation Satellites (CEOS-LPV, http://lpvs.gsfc.nasa.gov/), and used as independent reference data that were compared with MCD64A1. Burned area validation is a specific case of land cover change validation: the rare and impermanent nature of burned areas requires the implementation of a sampling scheme that considers both the spatial and temporal dimension of the burned area products (Stehman and Foody, 2019). The Landsat 8 OLI images of the independent reference dataset were randomly extracted in space and time following the stratified sampling scheme presented in Boschetti et al. (2016). Initial analysis in Boschetti et al. (2016), further expanded by Padilla et al. (2017), demonstrated that this sampling scheme is statistically rigorous, i.e., it follows the design-inference framework defined by Särndal et al. (1992). Furthermore, it possesses the desirable properties of a sampling scheme (Stehman, 1999, 2009) for burned area product validation, namely, it enables unbiased estimation of accuracy and area metrics with associated standard errors, and it is practical to implement.
The paper is organized as follows. Sections 2 and 3 present the methods and results respectively. Section 2.1 describes the protocol employed for the generation of the independent reference data through interpretation of pairs of Landsat 8 OLI images. Section 2.2 summarizes the sampling scheme proposed in Boschetti et al. (2016), and describes how it was implemented to randomly select Landsat 8 OLI image pairs. Section 2.3 presents the accuracy metrics employed to document MCD64A1 product accuracy, derived from the confusion matrix evaluated at 30 m resolution (Section 2.3.1) and regression metrics evaluated using coarse resolution cells (Section 2.3.2). Section 3.1 presents the global and per-biome confusion matrices and the accuracy metrics with their standard errors. Section 3.2 presents the global and perbiome results of the regression analyses.
2. Methods
2.1. Independent reference data generation
The independent reference data used to quantify the MCD641 product accuracy were derived from a large number of Landsat 8 Operational Land Imager (OLI) 30 m images. Landsat 8 OLI images were used because they have greater global acquisition availability than older Landsat sensors (Loveland and Irons, 2016; Wulder et al., 2016) and they do not have the Landsat 7 Enhanced Thematic Mapper Plus (ETM+) 22% missing pixel problem (Markham et al., 2004). The recently processed Collection 1 Landsat 8 OLI images defined in the Universal Transverse Mercator (UTM) projection were used (Dwyer et al., 2018). Each OLI image covers approximately 180 × 185 km and is referenced by a unique path/row coordinate in the Worldwide Reference System (WRS). Nominally, each Landsat satellite can sense the same path/row every 16 days, i.e., 22 or 23 times per year, depending on the first January overpass date (Kovalskyy and Roy, 2013).
Pairs of Landsat 8 OLI images acquired 16 days apart over each path/row were used to generate interpreted burned area maps that define, at each 30 m Landsat pixel location, if the pixel burned between the Landsat 8 OLI image acquisition dates, or if the pixel was unburned. Pixel locations that could not be interpreted, or that were unobserved in one or both images (e.g., due to clouds or shadows), were labeled as unmapped. The Landsat Collection 1 30-m cloud and shadow masks were used as a guide but supplemented by visual checking and refinement as needed as they are not always reliable, which has been observed by other researchers (Qiu et al., 2019; Egorov et al., 2019). The visual interpretation was undertaken by experts following the protocol developed originally by members of the GOFC/GOLD Southern African Fire Network (SAFNet) (Roy et al., 2005) and adopted by the CEOS-LPV as best practice for coarse resolution burned area product validation (Boschetti et al., 2010b). The burned perimeters were digitized onscreen, taking into account any unburned islands within the fire; the minimum mapping unit was 60 m (i.e. all burned areas with small axis dimension of 60 m or greater were mapped), which is lower than the 240 m minimum mapping unit specified in Roy et al. (2005), due to the better radiometric resolution and geolocation of Landsat 8 OLI data relative to the Landsat 7 ETM + used for the original SAFNet protocol. Two interpreters were involved in the generation of the reference burned area map from each Landsat 8 OLI image pair: one interpreter undertook the digitization, and the other checked the results and modified them if appropriate after discussion. We note that in previous burned area validation exercises (e.g., Boschetti et al., 2006; Roy and Boschetti, 2009; Padilla et al., 2014; Padilla et al., 2015; Giglio et al., 2018a), the pairs of pre- and post-fire Landsat images were not always selected 16 days apart and that they were selected usually to ensure that any burning occurring between the acquisitions was discernable in the post-fire image. This is reasonable, as burned areas are discernable in satellite images for intervals from weeks to years depending on factors including the vegetation cover and vegetation regrowth; for example, a recent MODIS analysis indicates a global median persistence time of 29 days (Melchiorre and Boschetti, 2018), but this introduces an element of non-randomness in the temporal selection of the reference images.
2.2. Sampling design
To provide a statistically rigorous Stage 3 validation, Landsat 8 OLI image pairs acquired 16 days apart were selected randomly following a global stratified random sampling scheme that allows for the use of unbiased accuracy and burned area estimators (Boschetti et al., 2016; Padilla et al., 2017). The sampling scheme is based on random extraction in space and time. It uses a tri-dimensional sampling grid that is defined spatially by the irregular hexagons of the Thiessen Scene Area (TSA) tessellation of the Landsat path/row locations (Gallego, 2005; Cohen et al., 2010; Kennedy et al., 2010), and temporally by the 16-day Landsat acquisition calendar at each path/row. The grid defines non-overlapping sampling units, where each sampling unit is a voxel uniquely identified by three coordinates u = {p,r, t}, where p is the WRS path, r is the WRS row, and t is the 16-day Landsat acquisition interval. At each TSA hexagon, 23 voxels, i.e., 23 16-day periods (368 days) from the day of the first Landsat 8 overpass on or after March 1st, 2014, were considered. Among the global TSA hexagons the first Landsat 8 overpass date varied from March 1st, 2014 to March 16th, 2014. Thus, the global MCD64A1 product from March 1st, 2014 to March 19th, 2015 was considered.
The grid of voxels was stratified spatially into seven aggregated biomes, derived from the Olson global ecoregion map (Olson et al., 2001) (Fig. 1 top). Permanent water and ice surfaces were excluded because they do not burn. The voxels in each biome were further stratified temporally into low or high fire activity strata, taking into account the timing of burning within the year. In each voxel {p,r,t}, the number of active fire detections is derived as the MODIS active fire 1 km2 pixels detected within the TSA hexagon {p,r} over the 16-day interval {t}. The voxels assigned to the ‘high fire activity’ stratum are those with more active fire detections than a biome-specific threshold, and the remainder were assigned to the ‘low fire activity’ stratum (e.g., Fig. 1, bottom). The threshold was set as the 20th quantile of the cumulative distribution of the number of active fire detections in all the biome voxels. Thus, the union of the ‘high fire activity’ voxels in the biome comprises 80% of the biome active fire detections over the fire year. The active fire detections were defined by the MODIS Terra (MOD14A1) and Aqua (MYD14A1) day and night detection products (Giglio et al., 2003), with permanent fires, for example due to gas flares, removed using a pre-computed permanent fire mask (Giglio et al., 2018c). The adoption of the voxel stratification in space and time takes into account the seasonality of fire distribution: voxels acquired at the same TSA location will generally belong to the high fire activity stratum during the fire season and to the low fire activity stratum outside the fire season when no burning occurs.
Fig. 1.
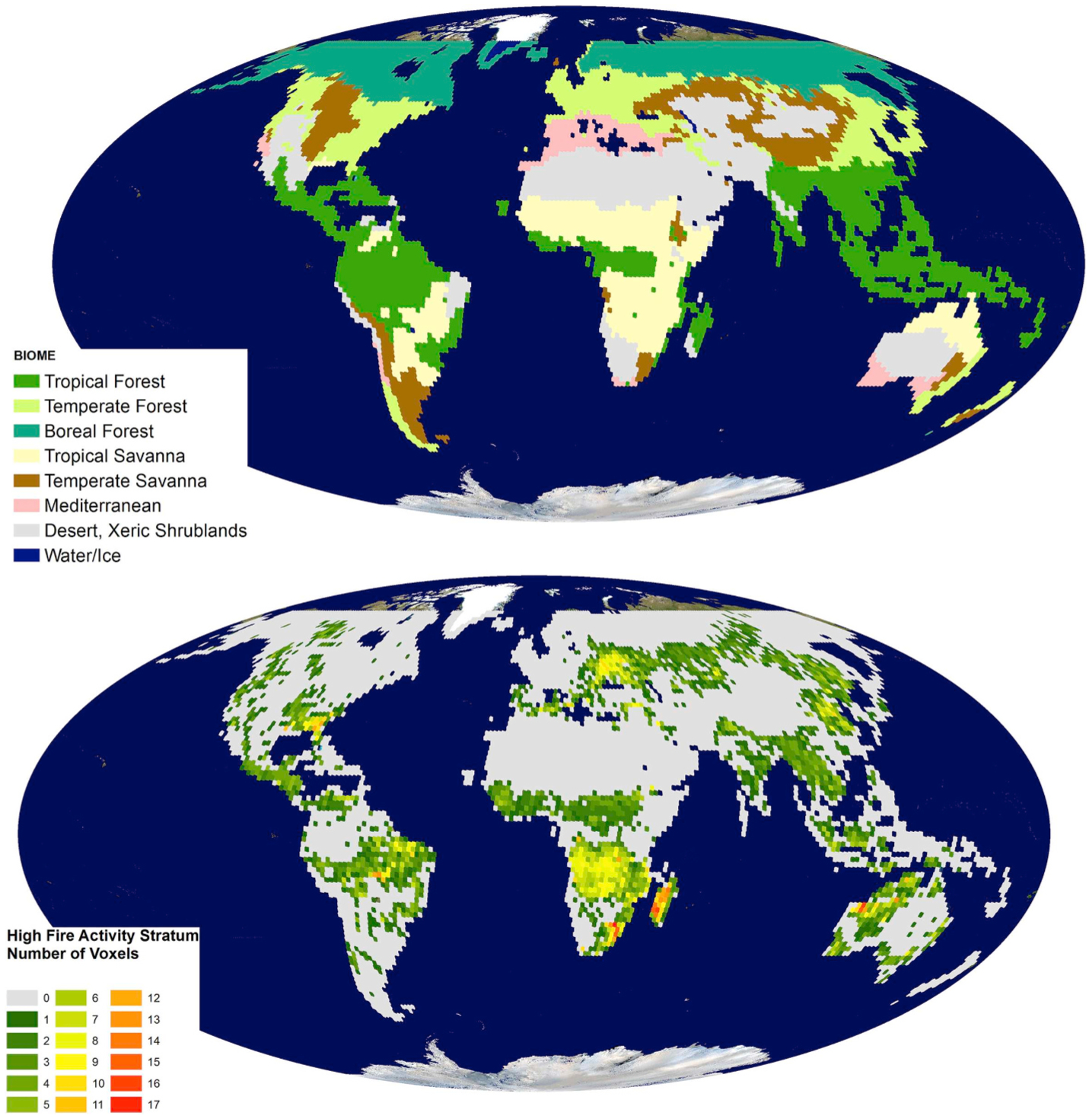
Illustration of the global stratified tri-dimensional grid, defined spatially by the Thiessen Scene Area (TSA) tessellation of the Landsat path/row locations (hexagons) and temporally by the Landsat 16-day acquisition calendar at each path/row (Boschetti et al., 2016). Top: stratification of the TSA hexagons based on seven aggregated biomes derived from the Olson et al. (2001) terrestrial ecosystem map; the analysis is performed between 70° S and 70° N because the MCD64A1 product is not generated at higher latitude, all TSAs covering exclusively water and permanent ice are excluded. Bottom: global spatial distribution of the high fire activity voxels for the 2014 to 2015 fire year; at each TSA location the map displays the number of voxels assigned to the high fire activity stratum based on the number of MOD14/MYD14 active fire detections.
There are 7805 TSA hexagons on land between 70° S and 70° N; combined with the 23 Landsat overpasses in the fire year, they define a global total of 179515 voxels. The number of voxels in the 14 combined biome and fire activity strata is summarized in Table 1. As discussed in Boschetti et al. (2016), for a global year of data, only a minority of the voxels have high fire activity, in this case only 4.27% of the voxels (Table 1). This implies that if a global simple random sample is implemented for the selection of independent reference data then approximately 95% of the sampled voxels would be low fire activity voxels. With a limited sample size, this would likely result in a validation dataset that produces high standard errors of the accuracy and area estimators.
Table 1.
Summary of the tri-dimensional grid stratification over the fire year (March 1st, 2014 to March 19th, 2015) showing for each biome and globally the number of TSA hexagons, the number of voxels, the number of low and high fire activity voxels, and the total burned area detected by MCD64A1 over the fire year.
| Biome | Number of TSA hexagons | Number of voxels | Number of high fire voxels | Number of low fire voxels | MCD64A1 total burned area [km2] |
|---|---|---|---|---|---|
| Tropical Forest | 1352 | 31096 | 1963 | 29133 | 374366 |
| Temperate Forest | 1142 | 25898 | 1562 | 24704 | 123664 |
| Boreal Forest | 2070 | 47610 | 364 | 47246 | 97955 |
| Tropical Savanna | 851 | 19573 | 1621 | 17952 | 2815146 |
| Temperate Savanna | 785 | 17825 | 953 | 17102 | 184535 |
| Mediterranean | 258 | 5934 | 350 | 5584 | 18031 |
| Deserts/Xeric Shrublands | 1347 | 30981 | 860 | 30121 | 204505 |
| Global | 7805 | 179515 | 7673 | 171842 | 3818410 |
Boschetti et al. (2016) demonstrated that stratified random sampling from the tri-dimensional combined biome and fire activity strata reduces the standard errors of the accuracy and area estimators compared to simple random sampling, by ensuring an adequate sample size at locations and times when burning occurs. Different stratified sampling allocation schemes were considered but equal allocation of the samples among the strata was found to be the most effective in reducing the standard errors. Thus, in this study, a random number generator was used to select voxels at random without replacement from the population of each stratum. If one or both images in each pair was not available in the U.S. from the archive or had cloud cover > 70% based on the image metadata, then the voxel was discarded from the validation analysis. A total of 100 voxels per biome were selected, 50 in the low and 50 in the high fire activity biome voxels, providing a global total of 700 voxels. Thus, 700 Landsat 8 OLI image pairs sensed 16 days apart over globally distributed TSA hexagons, in periods of both low and high fire activity, were downloaded. Following a preliminary inspection of the Landsat 8 OLI images, 142 voxels were discarded because of poor data quality, when the interpreters could not unambiguously identify burned and unburned areas in the Landsat 8 image pairs. This was primarily due to cloud cover, when the image metadata reported cloud cover < 70% but the portion of the images within the TSA footprint hexagon was completely cloudy in one or both images, or to high aerosol conditions that were not reflected by the cloud cover metadata and made the image interpretation impossible. The remaining 558 voxels, i.e., a total of 1116 Landsat 8 images, constitute the independent reference dataset and were used to generate the Landsat 8 interpreted burned area maps composed of 30 m burned, unburned, and unmapped classes. Fig. 2 illustrates their spatial and temporal distribution, showing the locations of the Landsat 8 image pairs acquired 16 days apart for each selected voxel and the date of the first image acquisition. The independent reference data are globally distributed, with between 77 and 88 voxels per biome and an approximately equal proportion in the low and high fire activity strata in each biome (Table 2).
Fig. 2.
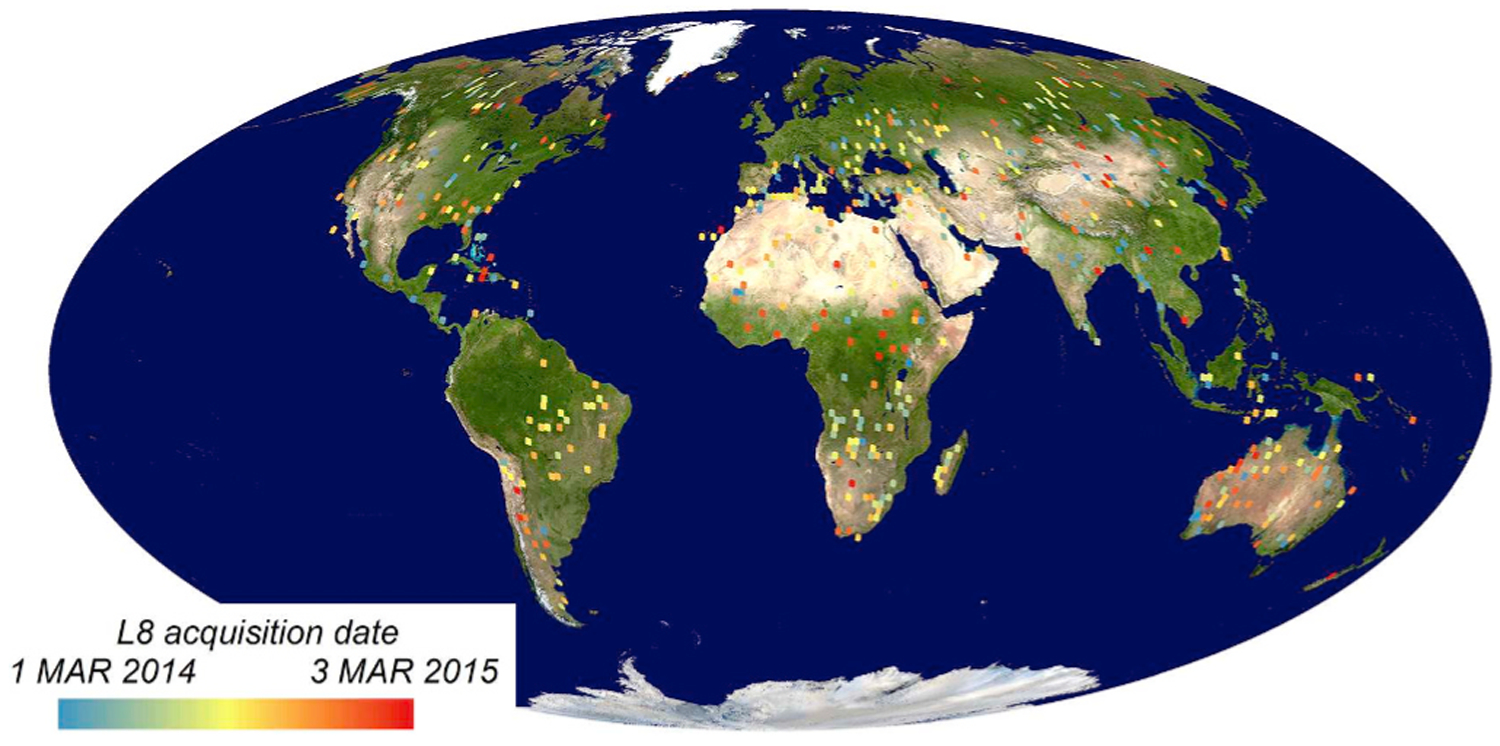
Spatial and temporal distribution of the 558 voxels used to assess the MCD64A1 product accuracy. Each voxel is defined by a pair of Landsat 8 images acquired 16 days apart, interpreted as burned, unburned or unmapped (Section 2.1). The acquisition date of the first Landsat 8 image is displayed with a rainbow color scale.
Table 2.
Summary of the distribution across strata of the 558 voxels (Fig. 2) used to assess the MCD64A1 product accuracy.
| Biome | Number of Voxels | ||
|---|---|---|---|
| High fire activity stratum | Low fire activity stratum | Total | |
| Tropical Forest | 36 | 41 | 77 |
| Temperate Forest | 40 | 42 | 82 |
| Boreal Forest | 37 | 41 | 78 |
| Tropical Savanna | 43 | 39 | 82 |
| Temperate Savanna | 41 | 42 | 83 |
| Mediterranean | 36 | 43 | 79 |
| Deserts/Xeric Shrublands | 36 | 41 | 77 |
| Global | 269 | 289 | 558 |
2.3. MODIS burned area product accuracy assessment
2.3.1. Confusion matrix and derived accuracy metrics
2.3.1.1. Overview and notation.
Conventionally, satellite burned area product accuracy is derived using confusion matrices that summarize the proportions of agreement and disagreement of the burned and unburned classes compared to independent reference data. The confusion matrices were derived by comparison of the contemporaneous MCD64A1 and Landsat 8 interpreted burned area maps for each sampled voxel. The MCD64A1 product was reprojected from the MODIS sinusoidal projection to the appropriate Landsat 8 UTM projection and zone, and the MCD64A1 500 m pixels were nearest-neighbor resampled to 30 m to allow direct comparison with the 30 m Landsat interpreted burned area maps.
Table 3 illustrates a burned area product confusion matrix to introduce the conventions and notation used in this paper. The confusion matrix considers only the burned and unburned classes: adopting the same simplifying assumption made by Padilla et al. (2014), it is assumed that the proportions of agreement and disagreement observed over the mapped areas of the validation dataset are the same for the unmapped areas.
Table 3.
Confusion matrix used to assess burned area product accuracy, where the matrix elements describe either the area Aij [m2] or the proportion (pii) [0–1] of agreement and disagreement of burned and unburned area between the classified data, and the reference data. If expressed as area, the four elements sum to A, the total spatial extent of the product; if expressed as proportions, the four elements sum to unity.
| Reference data | |||
|---|---|---|---|
| Burned | Unburned | ||
| Classified data | Burned | A11 (p11) | A12 (p12) |
| Unburned | A21 (p21) | A11 (p22) | |
Because the independent reference dataset was extracted using a probability sampling design, it is used to estimate the global and perbiome confusion matrices (Section 2.3.1.2), accuracy metrics (Section 2.3.1.3) and area burned (Section 2.3.1.4) with the associated standard errors. A more comprehensive discussion on the estimation of the confusion matrix and associated accuracy metrics using the tri-dimensional voxel sampling grid is presented in Boschetti et al. (2016), with the difference that in Boschetti et al. (2016) the standard errors are computed from the full population data available, whereas in the present work, as in (Padilla et al., 2014), the standard errors are estimated from the sample data. The estimators used are unbiased, and take into account the population and sample size in each biome and fire activity stratum (Boschetti et al., 2016; Padilla et al., 2017). Using standard statistical terminology, we denote N as the size of the population of all voxels, i.e., the total number of voxels in space and time; for example, for the global fire year N = 179515 (Table 1). The N voxels are partitioned in H non-overlapping strata; globally there are 7 biomes, each further partitioned into low and high fire activity strata, providing a total of H = 14 strata. The population in a specific stratum h is composed of Nh voxels, and nh voxels are sampled from the Nh voxels. For example, the strata {tropical forest; high fire activity} and {tropical forest; low fire activity} have populations composed of 1963 and 29133 voxels respectively (Table 1) and under the sampling protocol described in Section 2.2, a sample of equal size (nh = 50) is extracted from each.
2.3.1.2. Estimation of the global and per-biome confusion matrices.
A confusion matrix was computed at 30 m resolution for each Landsat 8 interpreted burned area map and the contemporaneous MCD64A1 product, i.e., a confusion matrix was derived for each sampled voxel u. The elements pu,ij ofthe confusion matrix are defined as:
| [1] |
| [2] |
where is the area of agreement and disagreement between the MCD64A1 product and the Landsat 8 interpreted burned area map, and is the total area of voxel u that was interpreted as burned or unburned in both products.
The elements of the per-biome and global confusion matrices are estimated from the sample using an unbiased estimator:
| [3] |
| [4] |
where is the estimated value of pij, and pu,ij are the elements of the confusion matrix for each sample voxel u calculated as [1], H is the total number of strata, nh is the sample size in stratum h, Nh is the population size in stratum h, and πh is the inclusion probability for stratum h. The inclusion probability is the probability that a voxel belonging to stratum h is included in the sample; under stratified random sampling, πh is the same for all the voxels in the stratum, and thus is defined as [4], i.e., as the ratio between the sample and the population sizes (Cochran, 1977).
The biome confusion matrix elements are derived considering H = 2 strata (one low and one high fire activity stratum) in the biome, and the global confusion matrix elements are derived considering H = 14 strata (seven biomes, each with low and high fire activity strata). The sample sizes of each stratum are the values reported in Table 2, and the population sizes are the values reported in Table 1.
2.3.1.3. Estimation of global and per-biome accuracy metrics.
Four accuracy metrics often used for burned area validation (Padilla et al., 2014, 2017; Boschetti et al., 2016) were considered, namely the Overall Accuracy (OA), the Omission Error Ratio of the burned area class (OE), the Commission Error Ratio of the burned area class (CE), and the bias of the total mapped area burned relative to the total estimated independent reference area burned (relB). The accuracy metrics are estimated globally and for each biome as:
| [5] |
| [6] |
| [7] |
| [8] |
where are the elements of the confusion matrix estimated respectively for each biome and globally from the sampled voxels defined as [3].
The standard errors of the four accuracy metrics [5–8] can be estimated using standard formulae for ratio estimators (Cochran, 1977). Generically, a ratio estimator is one where the parameter R (the population ratio) can be estimated as:
| [9] |
where and are the population means of two quantities x and y. In the case of the four accuracy metrics, by rearranging the terms of their standard formulation [5–8], the quantities x and y are defined for each voxel u as:
Overall accuracy (OA):
(interpreted area of voxel u)
(area of agreement for voxel u)
Omission error (OE):
(area burned determined from the reference data for voxel u)
(area burned determined from the reference data but not mapped as burned in the classified product for voxel u)
Commission error (CE):
(area mapped as burned in the classified product for voxel u)
(area mapped as burned in the classified product but not burned as determined from the reference data for voxel u)
Relative bias (relB):
(area burned determined from the reference data for voxel u)
(difference between the area mapped as burned in the reference data, and the area mapped as burned in the classified product for voxel u)
The standard error of each accuracy metric is estimated, for each biome and globally, as (Cochran, 1977):
| [10] |
where H is the total number of strata under consideration (H = 2 for per-biome estimations, H = 14 for the global estimation), Nh is the population size in stratum h, nh is the sample size in stratum h, is the estimated value as in [5–8], , and are the sample mean and variances of x and y in stratum h, and sxyh is the sample covariance of x and y in stratum h.
2.3.1.4. Estimation of global and per-biome total burned area.
The estimated total area burned can be derived for each biome and globally from the estimated confusion matrix as:
| [11] |
where is the estimated total area burned, , are the elements of the first column of the confusion matrix defined as [3], and A is the summed area of each TSA hexagon multiplied by 23 (as 23 16-day temporal intervals define the voxel population). The per-biome and global estimates of are derived using , from the per-biome and the global confusion matrices respectively, and using A defined as the sum of the areas of all the voxels in the biome and globally respectively.
can be also directly estimated from the sample by reformulating Equation [11] as:
| [12] |
where H is the total number of strata under consideration (H = 2 for per-biome estimations, H = 14 for the global estimation), Nh is the population size in stratum h, nh is the sample size in stratum h, and is the burned area mapped in the independent reference dataset within the TSA footprint and 16 day time period of voxel u.
The estimated standard error of the total area burned is (Cochran, 1977):
| [13] |
where H is the total number of strata under consideration (H = 2 for per-biome estimation, H = 14 for the global estimation), Nh is the population size in stratum h, nh is the sample size in stratum h, and is the sample variance of bu in stratum h. For ease of interpretation, the unitless coefficient of variation is reported:
| [14] |
where the standard error and the area are estimated as [13] and [11] (or [12]) respectively.
2.3.2. Coarse resolution regression metrics
Due to the different spatial resolutions of the Landsat 8 reference data (30 m) and the MODIS MCD64A1 product (500 m), some errors of omission and commission will occur due solely to the presence of mixed pixels at the MODIS resolution (Boschetti et al., 2004). The confusion matrix, evaluated at 30 m resolution, cannot be used to discriminate between errors of omission and commission occurring in the immediate vicinity of burned areas mapped in the independent reference dataset, likely due to the coarse resolution of the MCD64A1 product, and MCD64A1 misclassification errors. For this reason, the error matrix and the derived accuracy metric results were complemented by an accuracy assessment based on coarse resolution regression metrics (Boschetti et al., 2003; Roy and Boschetti, 2009).
The proportion of coarse resolution grid cells detected as burned by MCD64A1 was compared to the proportion labeled as burned in the Landsat 8 independent reference data. Coarse grid cells with side dimensions of 3 km, 4 km, 5 km, and 6 km were considered. These four grid cells dimensions, also used in a recent study that compared MCD64A1 with 30 m burned areas mapped over southern Africa using a Landsat-8 Sentinel-2A multi-temporal change detection algorithm (Roy et al., 2019), are many times larger than the 500 m MODIS pixel dimension but small enough to minimize the occurrence of cells with similar burned-area proportions in both products but with burns mapped at different locations within the cell (Roy and Boschetti, 2009; Roy et al., 2019). Only grid cells with < 5% unmapped data were considered. Regression lines were fitted through the data; the slope and intercept of the regression line are an indication of the accuracy of the burned area detection, whereas the coefficient of determination (r2) is an indication of the precision i.e., is indicative of the quality of coherence or repeatability (Boschetti et al., 2003). A regression line slope equal to unity with a zero intercept indicates that the burned area detection is accurate at the coarse resolution cell scale. A coefficient of determination equal to one indicates that the variability of the data is fully explained by the linear model (all the points fall on the regression line), while a coefficient of determination equal to zero indicates that there is no relationship between the linear model and the variability of the data (Roy and Boschetti, 2009).
To quantify the compensation between omission and commission errors in coarse resolution cells, the distribution of the deviations between the Landsat 8 independent reference data and the MCD64A1 product was characterized as a function of the proportion of area burned in the reference data. In order to investigate whether any overall areal differences between the MCD64A1 product and the independent reference data are due to large errors in relatively few cells, or to systematic overestimation or underestimation of smaller burned areas, the total difference in burned area was also computed as a function of the proportion of area burned in the reference data.
3. Results
3.1. Estimated confusion matrices and confusion matrix based accuracy metrics
The Landsat 8 pairs defining each of the 558 voxels of the independent reference dataset were interpreted into 30-m maps, with burned, unburned, or unmapped classes (Section 2.1). The Landsat 8 independent reference data cover over 12 million km2, including 0.12 million km2 of visually interpreted burned areas and almost 8 million km2 of unburned area.
Table 4 presents the estimated global and per-biome confusion matrices; the elements of the matrices are estimated as in [3] from the 558 independent reference data voxels, and taking into account the strata sample and population sizes. These results are reported for completeness and to ensure transparency for the calculation of the estimated accuracy metrics that are shown in Table 5.
Table 4.
Estimated global and per-biome confusion matrices, reported both in terms of area and in terms of proportions (in parentheses), using the same row, column conventions as in Tables 2 and 4 Globally a total of 558 voxels considered. The proportions are estimated taking into account the strata sample and population sizes as [3]; the areas are derived by multiplying each by the total area A of all the voxels of each biome.
| Biome | ||||
|---|---|---|---|---|
| Tropical Forest | 249910 (0.0005) | 435447 (0.0009) | 2397674 (0.0052) | 4.56 108 (0.9933) |
| Temperate Forest | 17550 (0.0001) | 22055 (0.0001) | 301734 (0.0009) | 3.32 108 (0.9990) |
| Boreal Forest | 100772 (0.0003) | 31695 (0.0001) | 37259 (0.0001) | 3.85 108 (0.9996) |
| Tropical Savanna | 1547709 (0.0037) | 840401 (0.0020) | 2386575 (0.0057) | 4.16 108 (0.9886) |
| Temperate Savanna | 135805 (0.0005) | 52443 (0.0002) | 234781 (0.0008) | 2.88 108 (0.9985) |
| Mediterranean | 7211 (0.0001) | 10287 (0.0002) | 116962 (0.0019) | 0.64 108 (0.9979) |
| Deserts/Xeric Shrublands | 34966 (0.0001) | 15529 (< 0.0001) | 64632 (0.0001) | 5.52 108 (0.9998) |
| Global | 2093922 (0.0008) | 1407857 (0.0006) | 5539617 (0.0022) | 2.49 109 (0.9964) |
Table 5.
Estimated global and per-biome accuracy metrics and total burned area, and associated standard errors derived from the Table 4 estimated confusion matrices. See Equations [5–8] for the accuracy metric definitions and equation [10] for the associated standard errors. See equations [11–12] for the total burned area estimation, and equations [13–14] for the associated coefficient of variation.
| Biome | [%] | [%] | [%] | [%] | [%] | [%] | [%] | [%] | [km2] | [%] |
|---|---|---|---|---|---|---|---|---|---|---|
| Tropical Forest | 99.4% | 0.4% | 90.6% | 1.5% | 63.5% | 8.0% | −74.1% | 4.2% | 2647584 | 14.5% |
| Temperate Forest | 99.9% | 0.1% | 94.5% | 2.1% | 55.7% | 7.9% | −87.6% | 3.5% | 319284 | 23.3% |
| Boreal Forest | 99.9% | 0.1% | 27.0% | 9.8% | 23.9% | 3.9% | −4.0% | 9.1% | 138031 | 34.6% |
| Tropical Savanna | 99.2% | 0.1% | 60.7% | 5.6% | 35.2% | 2.5% | −39.3% | 7.6% | 3934283 | 13.8% |
| Temperate Savanna | 99.9% | 0.1% | 63.4% | 11.8% | 27.9% | 7.9% | −49.2% | 11.1% | 370586 | 22.8% |
| Mediterranean | 99.8% | 0.1% | 94.2% | 8.2% | 58.8% | 10.6% | −85.9% | 16.1% | 124173 | 42.4% |
| Deserts/Xeric Shrublands | 99.9% | < 0.1% | 64.9% | 6.4% | 30.8% | 6.0% | −49.3% | 7.54% | 99598 | 18.1% |
| Global | 99.7% | < 0.1% | 72.6% | 3.9% | 40.2% | 2.4% | −54.1% | 5.3% | 7633539 | 8.9% |
Table 5 reports the estimated global and per-biome accuracy metrics, the estimated total area burned, and the associated standard errors derived from the Table 4 confusion matrices. The estimated Overall Accuracy , Omission Error , Commission Error and the Relative Bias are computed as [5–8], and the estimated total Landsat 8 burned area is computed as in [11–12]. The estimated standard errors of the four accuracy metrics, computed as [10] and the estimated coefficient of variation of the estimated burned area computed as [13–14] are also shown.
The is high globally (99.7%) and in each biome is greater than 90%, but as noted above, this reflects the generally low occurrence of burned areas in either product. Globally, the is 75.6% and the is 40.2%, with the prevalence of omission error reflected by a of −54%. The accuracy metric values are variable among the biomes, with the lowest and in Boreal Forest , and the highest errors in the Tropical Forest, Temperate Forest, and Mediterranean biomes . The values are negative in all biomes, and range from −4% in Boreal Forest, to −87% in Temperate Forest. Globally, the standard errors of the four accuracy metrics are less than 6% with , , , . At the biome level all standard errors are less than 12% with the sole exception of the standard error of in the Mediterranean biome, which is 16.1%. The estimated annual area burned , which is estimated solely from the Landsat 8 independent reference data (section 2.3.1.4), is 7.6 million km2 globally. The coefficient of variation ranges in the biomes from 14.5% (Tropical Savannah) to 42.4% (Mediterranean), and is 8.9% globally.
3.2. Coarse resolution regression metrics
Fig. 3 shows the regression analyses of the proportion of grid cells labeled as burned by the MCD64A1 product against the proportions labeled as burned by the Landsat 8 independent reference data using 5 km × 5 km coarse resolution cells. Per-biome and global scatterplots and regression results are presented; it should be noted that the density plots and the regression coefficients are derived by considering all coarse resolution cells in the independent resolution dataset without taking into account the inclusion probabilities. The negative intercepts and slopes smaller than one for all seven biomes indicate that the MODIS product always maps a smaller proportion of the landscape as burned than the Landsat 8 independent reference dataset. Globally, the high correlation (r2 = 0.74), the slope close to unity (0.81) and small negative intercept (−0.0031) indicate that the errors of omission and commission significantly compensate at relatively local scales. Only in some biomes the relationship between the two datasets can be meaningfully characterized with a regression analysis. There is a clear distinction between four biomes (Boreal Forest, Desert and Xeric Shrublands, Temperate Savannah and Tropical Savannah) where high correlations (r2 from 0.68 to 0.82) and slopes closer to unity (from 0.69 to 0.91) are observed, and the remaining three biomes (Temperate Forest, Mediterranean, Tropical Forest) where the correlations are lower (r2 from 0.17 to 0.38) and the slopes are further from unity (from 0.11 to 0.52). These results indicate that in the former four biomes, which account for the majority of the mapped burned area (Table 1), the omission and commission errors affecting the MCD64A1 500 m product largely compensate within the 5 km × 5 km cells. In the latter three biomes, which account only for 13.5% of the total global burned area mapped by the MCD64A1 product (Table 1), omission errors are prevalent, due to small burned areas entirely missed by the MCD64A1 product.
Fig. 3.
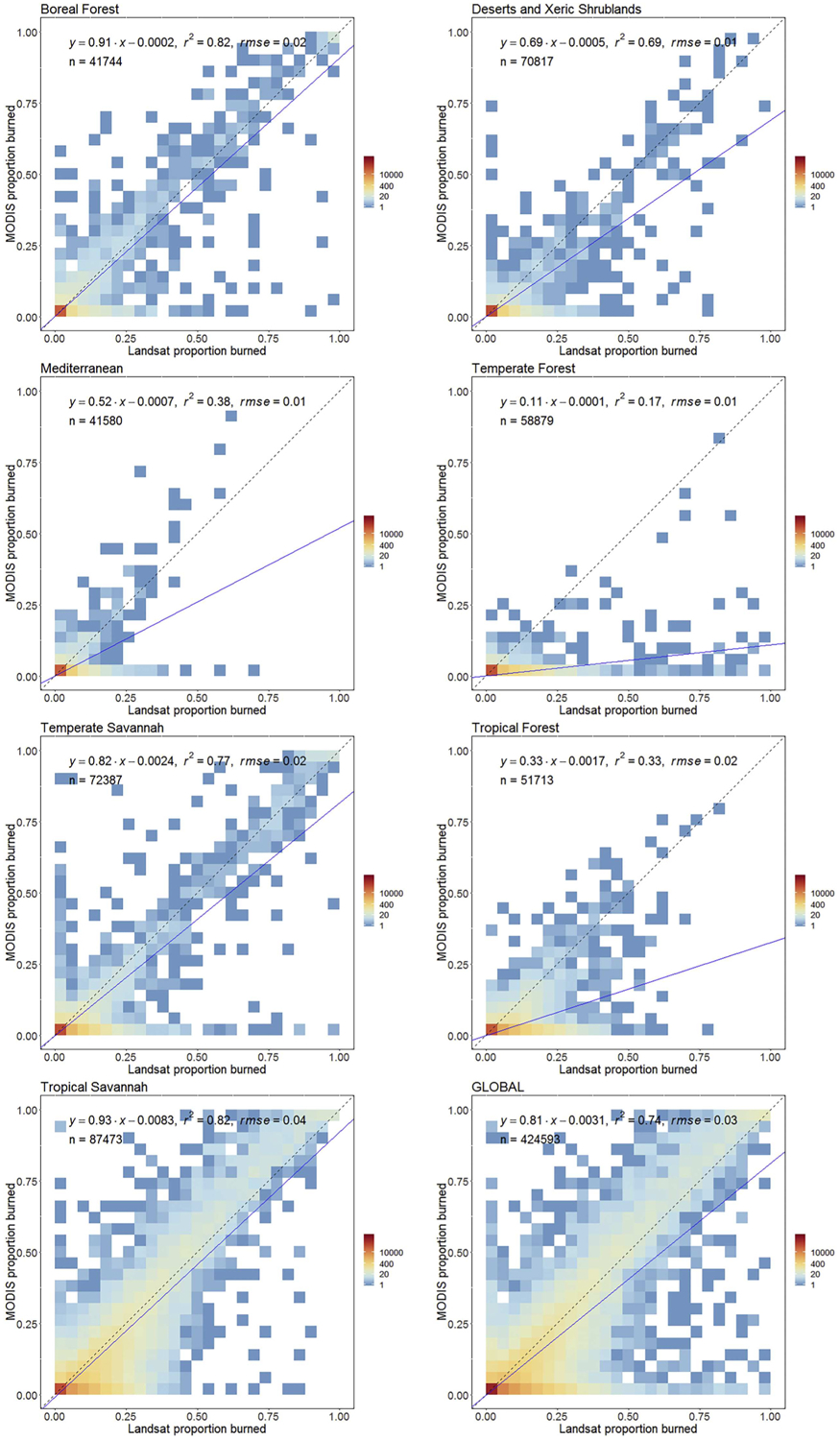
Scatter plot of the proportions of coarse resolution 5 km × 5 km cells labeled as burned by the MCD64A1 product, plotted against the proportion labeled as burned by the Landsat 8 independent reference dataset, combining the voxel results for each biome and globally. The point density distribution is calculated using a 25 × 25 quantization of the plot axes, and is displayed with a logarithmic color scale. The blue lines show the ordinary least squares regression of the proportion data; the dashed 1:1 lines are shown as reference.
Fig. 4 shows similar global results as Fig. 3 but for coarse grid cells with 3 km, 4 km, and 6 km side dimensions (the 5 km results are also shown for ease of comparison). The correlation between the MCD64A1 and the Landsat 8 cell proportions increases monotonically with the cell size, from r2 = 0.70 (3 km cells) to r2 = 0.75 (6 km cells). The slopes also increase monotonically with the cell size, and become progressively closer to unity, varying from 0.795 (3 km cells) to 0.818 (6 km cells) reflecting how the omission and commission errors compensate each other in progressively coarser cells (Roy and Boschetti, 2009). The intercepts are small (−0.0030 to −0.0031) but, because of the large number of cells with little or no burned area, point to a systematic burned area underestimation by the MCD64A1 product, consistently with the negative presented in Section 3.1. The relatively small size of the burned areas is reflected by the density plots: for all four cell sizes, the majority of points (yellow and red colors) correspond to low burning proportions, and noticeably at the coarser 6 km resolution very few cells are fully burned.
Fig. 4.
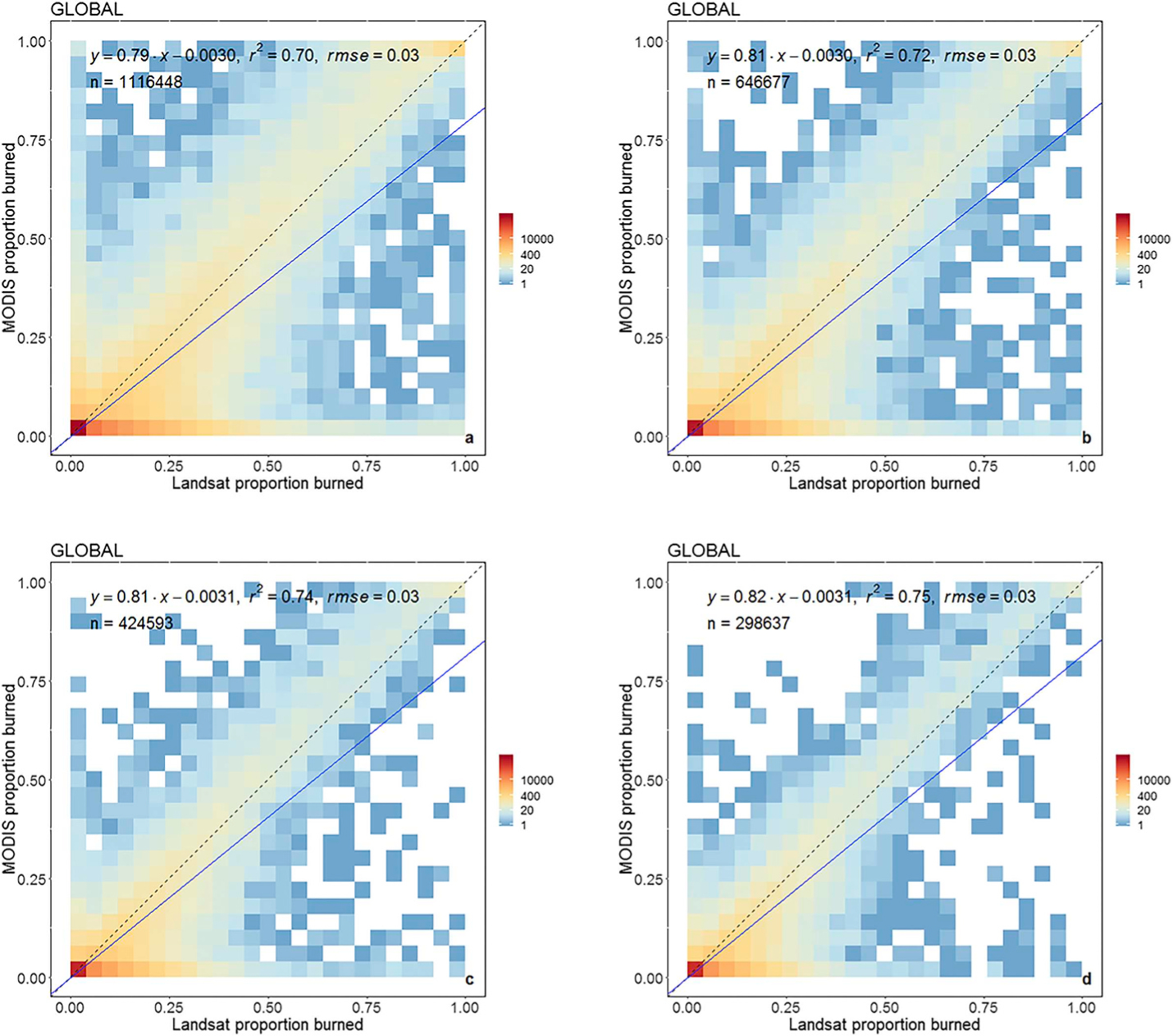
Global scatterplot results, as Fig. 3, considering coarse resolution (a) 3 km × 3 km, (b) 4 km × 4 km, (b) 5 km × 5 km, and (d) 6 km × 6 km grid cells.
The distribution of the deviations between the cell proportions labeled as burned by the Landsat 8 independent reference data and the cell proportions labeled as burned by the MCD64A1 product is summarized in Fig. 5 (top), and the histogram of the cell proportions labeled as burned by the Landsat 8 independent reference data is reported in Fig. 5 (bottom), for 3 km × 3 km and 6 km × 6 km coarse resolution grids. The median, interquantile range and minimum/maximum of the deviations are reported as a function of the Landsat proportion burned, quantized in 0.05 increments. The deviation median and interquantile range values initially increase with the Landsat proportion burned, with the greatest median deviations occurring for a Landsat proportion burned of 0.20 (3 km × 3 km cells) and 0.25 (6 km × 6 km cells), and then decrease for higher proportions, reaching values close to zero for proportions greater than 0.6 for both cell resolutions. This indicates that the MCD64A1 product systematically underestimates the reference area burned in cells with smaller burned areas (i.e. omission errors prevail on commission errors), and correctly identifies the area burned in cells with larger burned areas (i.e. omission and commission errors compensate).
Fig. 5.

Summary parameters of the distribution of the deviations between the proportions of area burned mapped by the Landsat 8 reference data and the proportion of area burned mapped by the MCD64A1 product, reported as a function of the Landsat proportion burned quantized in 5% intervals. As in Fig. 4, all global voxels are combined. Because the differences between the distributions obtained with the four grid cell sizes of Fig. 4 are nearly identical, only the smallest and largest grid cell sizes are reported (right column: 3 km × 3 km results; left column: 6 km × 6 km results). Top row: median (solid circles), interquantile range (lines) and minimum/maximum (open circles) of the deviations. Bottom row: total number of cells in which a given proportion of area burned is observed in the Landsat reference data. In all plots the Landsat proportion burned is quantized in 21 intervals, defined as {[0.00]; (0.00,0.05]; (0.05,0.10] … (0.90,0.95]; (0.95,1.00]}.
The deviations observed for cells with a small proportion of area burned have a significant impact on the overall areal discrepancy between the MCD64A1 product and the Landsat reference data, because the histogram of the cell proportion is highly skewed, with a clear prevalence of cells with low fractions of area burned. When the total areal difference between the MCD64A1 product and the Landsat 8 OLI reference data is quantized by Landsat proportion burned (Fig. 6, left), the largest errors are observed in cells with very low burned area. The maximum difference is observed in cells with burned area proportion in the (0.00, 0.05] interval when considering 3 km × 3 km grid cells and in the (0.05, 0.10] interval when considering 6 km × 6 km grid cells, and the difference is negligible for all intervals above 0.60 (3 km × 3 km grid cells) and 0.45 (6 km × 6 km grid cells). When considering the cumulative distribution of the differences (Fig. 6, right), 90% of the area difference is due to cells with burned area proportion below 0.25 and 0.30 in 3 km × 3 km and 6 km × 6 km grid cells respectively.
Fig. 6.
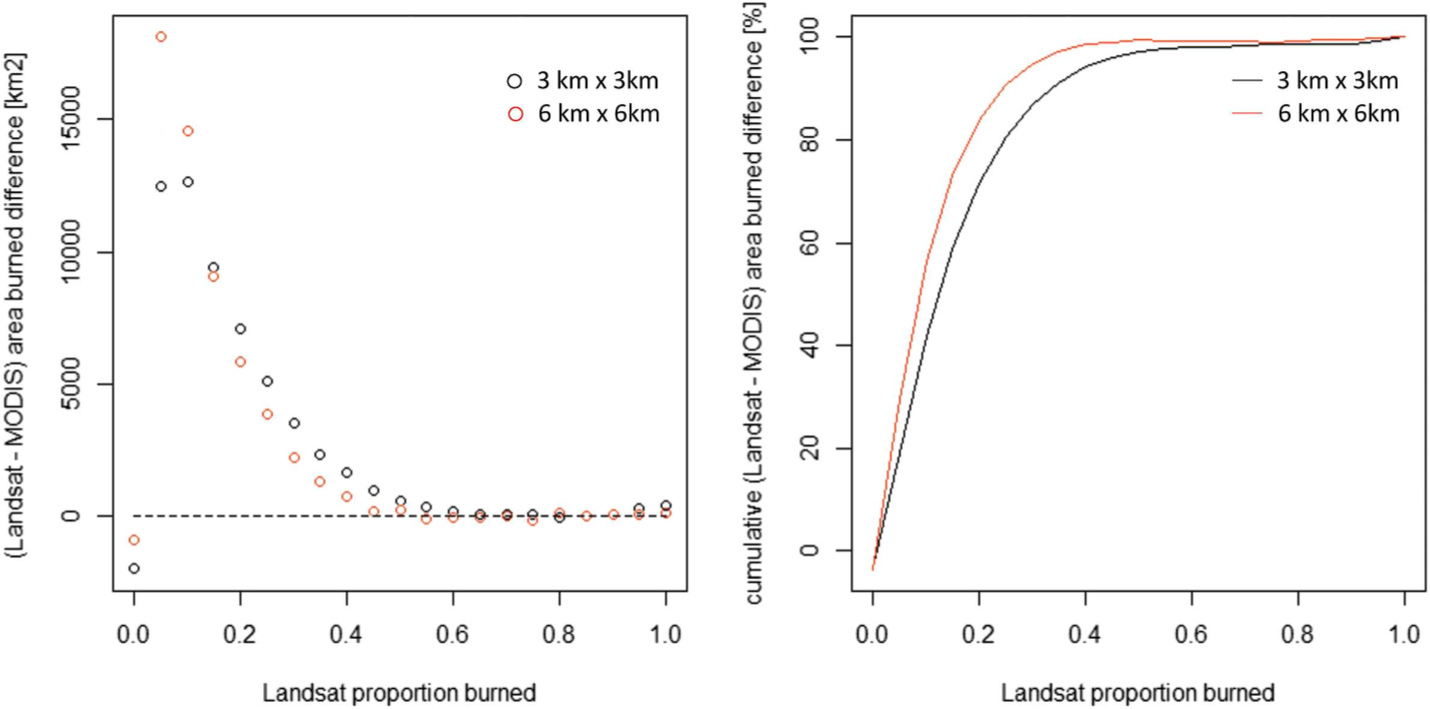
Area burned difference between the Landsat reference data and the MCD64A1 product, computed in 3 km × 3 km (red circles and lines) and 6 km × 6 km (black circles and lines) coarse resolution grid cells, reported as a function of the Landsat proportion burned, quantized with the same 21 intervals of Fig. 5. Left: burned area difference [km2] computed by summation of the Landsat-MODIS burned area deviations in all the global cells with a given Landsat proportion burned. Right: cumulative distribution of the areal differences, reported as percentage of the total difference between the Landsat reference data and the MCD64A1 product in all global voxels.
4. Conclusions
This paper presents the Stage 3 global validation of the Collection 6 NASA MODIS MCD64A1 product, implementing the sampling scheme for global burned area validation described in Boschetti et al. (2016). Independent reference data were generated from the interpretation of Landsat 8 OLI image pairs, selected in time and space according to a probability sampling design consistent with the Committee on Earth Observation Satellites (CEOS) Stage 3 Validation protocol (Morisette et al., 2006). The independent reference dataset consisted of 558 Landsat 8 image pairs, acquired 16 days apart.
Globally, the MCD64A1 product had an estimated Commission Error of 40.2% and an estimated Omission Error of 72.6%. These errors are similar to those reported for the MCD64A1 product by Chuvieco et al. (2018) in a multi-year validation exercise . They used a similar sampling design (Padilla et al., 2017) to generate a Landsat 5, 7 and 8 independent reference dataset covering 12 years (2003–2014), but with smaller sample size per year than the present study (100 sample voxels per year rather than 558), and only a 20 km × 30 km subset of each Landsat image pair, rather than the entire TSA footprint, was interpreted. Inconsistent Landsat acquisition and archiving prior to the launch of Landsat-8 (Kovalskyy and Roy, 2013; Wulder et al., 2016) also meant that in certain regions the availability of Landsat image pairs for the 2003–2013 period was limited (Padilla et al., 2017). Given the effort required in the generation of independent reference data, the different strategy adopted in the present paper compared to Chuvieco et al. (2018) points to the tradeoff between covering a single year with more sample voxels and single stage sampling (i.e. interpreting the entire voxels) to obtain more precise accuracy estimates, or covering multiple years with fewer sample voxels in each year and two stage sampling (i.e. interpreting only a subset of the voxel) to obtain multitemporal accuracy estimates, but with potentially higher standard errors on individual years. The issue is particularly relevant for biome-level accuracy estimates, as the sample size allocated to each biome may be small if the global sample size is not large.
We note that the errors are higher than those reported by Giglio et al. (2018b) in our Stage 2 validation (CE = 24%, OE = 37%). By definition, the Stage 2 validation did not follow a probability sampling design, and so the resulting CE and OE accuracy metrics were derived from the summation of the confusion matrices of the individual independent reference burned area maps, without taking into account any inclusion probabilities and so are biased estimators. In contrast, the Stage 3 Landsat independent reference dataset was selected following a probability sampling design and provides unbiased estimators of the accuracy metrics, i.e., and are estimated by considering the population and sample size in each stratum, as opposed to the biased CE and OE of a Stage 2 validation. In addition, the Landsat image pairs used in the Stage 2 validation were selected by interpreters who chose pairs that they could interpret easily and so were implicitly biased towards selecting image pairs covering distinct burned areas. Further, the Stage 2 validation used fewer Landsat images, i.e., 192 images (84 image pairs and 24 single scenes), with a predominance of images located in Tropical Savannah and Boreal Forest, whereas the Stage 3 validation reported in this paper used 1116 images (558 image pairs) equally distributed among biomes.
The global annual burned area estimated from the Landsat independentreference data , computed by taking into account the population and sample size in each stratum, was 7.6 million km2, approximately twice the 3.8 million km2 global annual burned area mapped by MCD64A1. This discrepancy is reflected in the 72.6% estimated Omission Error and in the −54.1% estimated relative bias metrics. The regression analysis between the proportions of area burned in coarse resolution cells showed high correlation (r2 between 0.698 and 0.751), slopes close to unity (0.795–0.818) and small intercepts (−0.0030 to −0.0031) considering grid cell resolutions from 3 km to 6 km, and indicated significant compensation of the MCD64A1 errors of omission and commission at local scale. The analysis of the deviations between the Landsat and MCD64A1 burned area proportion in coarse resolution cells indicated that the MCD64A1 product systematically underestimates the area burned in cells with smaller proportion of area burned (< 0.6 both at 3 km and 6 km grid cell resolution), whereas the estimates are correct for greater proportions of are burned. Because of the prevalence of cells with very small area burned, the total areal difference between the MCD64A1 product and the Landsat reference data can be largely attributed to cells with very small proportions of area burned: 90% of the area difference is due to cells with less than 0.25 and 0.30 proportion of area burned, when considering 3 km and 6 km resolution grid cells respectively. Evidently, small and spatially fragmented burned areas that are discernable at 30 m Landsat scale are not mapped by MCD64A1 at 500 m scale.
Both the confusion matrix and regression accuracy estimation approaches revealed that the accuracy of the MCD64A1 product varied significantly among biomes. The lowest errors were observed in Boreal Forest, Tropical Savanna and Temperate Savanna, while the highest errors were observed in the Tropical Forest, Temperate Forest and Mediterranean biomes. The reasons for this are complex but certainly the major proportion of the MCD64A1 mapped burned areas in the Boreal Forest, Tropical Savanna and Temperate Savanna biomes are spatially extensive, are often distinct in MODIS data, and can persist on the landscape for long periods and so their detection in cloudy conditions is still possible (Fraser et al., 2004; Silva et al., 2005; Roy et al., 2002, 2008; Lyons et al., 2008; Archibald et al., 2010; Melchiorre and Boschetti, 2018). In the Tropical Forest, Temperate Forest and Mediterranean biomes burned areas are often small and temporally nonpersistent (Bucini and Lambin, 2002; Miettinen and Liew, 2009; Viedma et al., 2009; Alonso-Canas and Chuvieco, 2015; Hantson et al., 2015; Vanderhoof et al., 2017; Melchiorre and Boschetti, 2018). In these latter biomes small cropland burns may also account for a large fraction of the fire activity (Korontzi et al., 2006; Roy et al., 2008; Magi et al., 2012), and the poor performance of the MCD64A1 product and other global burned area products over croplands has been observed in previous studies (Roy et al., 2008; Padilla et al., 2015; Hall et al., 2016; Lasko et al., 2017). Beyond the stratification by biome, a rigorous characterization of the errors as a function of land cover, seasonality, shape and spatial distribution of the burned areas is a priority for future work.
The Stage 3 Landsat independent reference dataset will be used for the validation of the forthcoming science-quality Suomi National Polarorbiting Partnership (S-NPP) Visible Infrared Imaging Radiometer Suite (VIIRS) VNP64A1 burned area product. It is anticipated that the validation exercise will be repeated in the course of the VIIRS mission to assess the performance of the VNP64A1 burned area product. As discussed in Boschetti et al. (2016) and Padilla et al. (2017), one of the advantages of the voxel sampling grid is that it makes it straightforward to extend the temporal period of study by adding complete years, thus making it possible to incrementally augment the independent reference dataset, achieving Stage 4 validation once the full duration of the mission is covered. Recommended research is to expand the independent reference data sampling scheme to include Sentinel 2 imagery that is also able to map burned areas (Huang et al., 2016; Roy et al. 2019; Roteta et al., 2019) and has higher temporal resolution than Landsat 8 (Li and Roy, 2017).
Acknowledgements
This research was funded by NASA grants number 80NSSC18K0739, NNX14AI68G, NNX14AP70A, NNX11AF39G, and NNX13AP48G. The authors gratefully acknowledge Andrea Melchiorre, Lian-Zhi Huo, and Aaron Sparks (Department of Forest, Rangeland and Fire Sciences, University of Idaho), and Sanath Kumar and Pedro Oliveira (South Dakota State University) for their technical work supporting this research.
Footnotes
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Abatzoglou JT, Williams AP, Boschetti L, Zubkova M, Kolden CA, 2018. Global patterns of interannual climate-fire relationships. Glob. Chang. Biol 24 (11), 5164–5175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alonso-Canas I, Chuvieco E, 2015. Global burned area mapping from ENVISAT-MERIS and MODIS active fire data. Remote Sens. Environ 163, 140–152. [Google Scholar]
- Andela N, Morton DC, Giglio L, Chen Y, van der Werf GR, Kasibhatla PS, … Bachelet D, 2017. A human-driven decline in global burned area. Science 356 (6345), 1356–1362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archibald S, Lehmann CER, Gomez-Dans JL, Bradstock RA, 2013. Defining pyromes and global syndromes of fire regimes. Proc. Natl. Acad. Sci. U.S.A 110 (16), 6442–6447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Archibald S, Scholes RJ, Roy DP, Roberts G, Boschetti L, 2010. Southern African fire regimes as revealed by remote sensing. International Journal of Wildland Fire 19 (7), 861–878. [Google Scholar]
- Baret F, Morissette JT, Fernandes RA, Champeaux JL, Myneni RB, Chen J, … Nickeson JE, 2006. Evaluation of the representativeness of networks of sites for the global validation and intercomparison of land biophysical products: proposition of the CEOS-BELMANIP. IEEE Trans. Geosci. Remote Sens 44 (7), 1794–1803. [Google Scholar]
- Bloom AA, Exbrayat JF, van der Velde IR, Feng L, Williams M, 2016. The decadal state of the terrestrial carbon cycle: global retrievals of terrestrial carbon allocation, pools, and residence times. Proc. Natl. Acad. Sci 113 (5), 1285–1290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boschetti L, Roy DP, 2008. Defining a fire year for reporting and analysis of global interannual fire variability. J. Geophys. Res.: Biogeosciences 113, G03020. [Google Scholar]
- Boschetti L, Brivio PA, Gregoire JM, 2003. The use of Meteosat and GMS imagery to detect burned areas in tropical environments. Remote Sens. Environ 85 (1), 78–91. [Google Scholar]
- Boschetti L, Flasse SP, Brivio PA, 2004. Analysis of the conflict between omission and commission in low spatial resolution dichotomic thematic products: the Pareto Boundary. Remote Sens. Environ 91 (3–4), 280–292. [Google Scholar]
- Boschetti L, Brivio PA, Eva Hugh D., Gallego J, Baraldi A, Grégoire J-M, 2006. A sampling method for the retrospective validation of global burned area products. IEEE Trans. Geosci. Remote Sens 44, 1765–1773. [Google Scholar]
- Boschetti L, Roy DP, Justice CO, Giglio L, 2010a. Global assessment of the temporal reporting accuracy and precision of the MODIS burned area product. Int. J. Wildland Fire 19 (6), 705–709. [Google Scholar]
- Boschetti L, Roy DP, Justice CO, 2010b. CEOS international global burned area satellite product validation protocol, Part I - production and standardization of validation reference data. available online. https://lpvs.gsfc.nasa.gov/PDF/BurnedAreaValidationProtocol.pdf.
- Boschetti L, Stehman SV, Roy DP, 2016. A stratified random sampling design in space and time for regional to global scale burned area product validation. Remote Sens. Environ 186, 465–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowman DM, Balch JK, Artaxo P, Bond WJ, Carlson JM, Cochrane MA, … Johnston FH, 2009. Fire in the Earth system. Science 324 (5926), 481–484. [DOI] [PubMed] [Google Scholar]
- Bowman DM, Williamson GJ, Abatzoglou JT, Kolden CA, Cochrane MA, Smith AM, 2017. Human exposure and sensitivity to globally extreme wildfire events. Nat. Ecol. Evol 1, 0058. [DOI] [PubMed] [Google Scholar]
- Bucini G, Lambin EF, 2002. Fire impacts on vegetation in Central Africa: a remote-sensing-based statistical analysis. Appl. Geogr 22 (1), 27–48. [Google Scholar]
- Chuvieco E, Lizundia-Loiola J, Pettinari ML, Ramo R, Padilla M, Tansey K, Mouillot F, Laurent P, Storm T, Heil A, Plummer S, 2018. Generation and analysis of a new global burned area product based on MODIS 250m reflectance bands and thermal anomalies. Earth Syst. Sci. Data Discuss 512, 1–24. [Google Scholar]
- Cochran WG, 1977. Sampling Techniques, third ed. Wiley, New York, pp. 413. [Google Scholar]
- Cohen WB, Yang Z, Kennedy R, 2010. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync-tools for calibration and validation. Remote Sens. Environ 114 (12), 2911–2924. [Google Scholar]
- Di Giuseppe F, Pappenberger F, Wetterhall F, Krzeminski B, 2016. The potential predictability of fire danger provided by numerical weather prediction. J. Appl. Meteorol. Climatol 55, 2469–2491. [Google Scholar]
- Dwyer JL, Roy DP, Sauer B, Jenkerson CB, Zhang HK, Lymburner L, 2018. Analysis ready data: enabling analysis of the Landsat archive. Remote Sens. 10 (9), 1363. [Google Scholar]
- Egorov AV, Roy DP, Zhang HK, Li Z, Yan L, Huang H, 2019. Landsat 4, 5 and 7 (1982 to 2017) analysis ready data (ARD) observation coverage over the conterminous United States and implications for terrestrial monitoring. Remote Sens. 11 (4), 447. [Google Scholar]
- Fraser RH, Hall RJ, Landry R, Lynham T, Raymond D, Lee B, Li Z, 2004. Validation and calibration of Canada-wide coarse-resolution satellite burned-area maps. Photogramm. Eng. Remote Sens 70 (4), 451–460. [Google Scholar]
- Gallego FJ, 2005. Stratified sampling of satellite images with a systematic grid of points. ISPRS J. Photogrammetry Remote Sens 59 (6), 369–376. [Google Scholar]
- Giglio L, Descloitres J, Justice CO, Kaufman YJ, 2003. An enhanced contextual fire detection algorithm for MODIS. Remote Sens. Environ 87, 273–282. [Google Scholar]
- Giglio L, Randerson JT, van der Werf GR, 2013. Analysis of daily, monthly, and annual burned area using the fourth generation Global Fire Emissions Database (GFED4). J. Geophys. Res.: Biogeosciences 118. [Google Scholar]
- Giglio L, Boschetti L, Roy DP, Humber ML, Justice CO, 2018a. The Collection 6 MODIS burned area mapping algorithm and product. Remote Sens. Environ 217, 72–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giglio L, Boschetti L, Roy DP, Hoffman AA, Humber M, Hall JV, 2018b. Collection 6 MODIS Burned Area Product User’s Guide. http://modis-fire.umd.edu/files/MODIS_C6_BA_User_Guide_1.2.pdf, Version 1.2.
- Giglio L, Schroeder W, Hall JV, Justice CO, 2018c. MODIS Collection 6 Active Fire Product User’s Guide. Revision B. University of Maryland, Department of Geographical Sciences, pp. 1–62. Available online at: http://modis-fire.umd.edu/guides.html. [Google Scholar]
- Granier C, Bessagnet B, Bond T, D’Angiola A, Van Der Gon HD, Frost GJ, Heil A, Kaiser JW, Kinne S, Klimont Z, 2011. Evolution of anthropogenic and biomass burning emissions of air pollutants at global and regional scales during the 1980–2010 period. Clim. Change 109, 163–190. [Google Scholar]
- Hall JV, Loboda TV, Giglio L, McCarty GW, 2016. A MODIS-based burned area assessment for Russian croplands: mapping requirements and challenges. Remote Sens. Environ 184, 506–521. [Google Scholar]
- Hantson S, Pueyo S, Chuvieco E, 2015. Global fire size distribution is driven by human impact and climate. Glob. Ecol. Biogeogr 24 (1), 77–86. [Google Scholar]
- Huang H, Roy DP, Boschetti B, Zhang HK, Yan L, Kumar SS, Gomez-Dans J, Li J, 2016. Separability analysis of Sentinel-2A multi-spectral instrument (MSI) data for burned area discrimination. Remote Sens. 8 (10), 873. [Google Scholar]
- Humber ML, Boschetti L, Giglio L, Justice CO, 2018. Spatial and temporal intercomparison of four global burned area products. Int. J. Digit. Earth 1–25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jolly WM, Cochrane MA, Freeborn PH, Holden ZA, Brown TJ, Williamson GJ, Bowman DM, 2015. Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun 6, 7537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Justice C, Belward A, Morisette J, Lewis P, Privette J, Baret F, 2000. Developments in the ‘validation’ of satellite sensor products for the study of the land surface. Int. J. Remote Sens 21 (17), 3383–3390. [Google Scholar]
- Justice CO, Giglio L, Korontzi S, Owens J, Morisette JT, Roy DP, … Kaufman Y, 2002a. The MODIS fire products. Remote Sens. Environ 83 (1–2), 244–262. [Google Scholar]
- Justice CO, Townshend JRG, Vermote EF, Masuoka E, Wolfe RE, Saleous N, … Morisette JT, 2002b. An overview of MODIS Land data processing and product status. Remote Sens. Environ 83 (1–2), 3–15. [Google Scholar]
- Kennedy RE, Yang Z, Cohen WB, 2010. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr-temporal segmentation algorithms. Remote Sens. Environ 114 (12), 2897–2910. [Google Scholar]
- Korontzi S, McCarty J, Loboda T, Kumar S, Justice C, 2006. Global distribution of agricultural fires in croplands from 3 years of Moderate Resolution Imaging Spectroradiometer (MODIS) data. Global Biogeochemical Cycles 20 (2). [Google Scholar]
- Kovalskyy V, Roy DP, 2013. The global availability of Landsat 5 TM and Landsat 7 ETM+ land surface observations and implications for global 30 m Landsat data product generation. Remote Sens. Environ 130, 280–293. [Google Scholar]
- Lasko K, Vadrevu KP, Tran VT, Ellicott E, Nguyen TT, Bui HQ, Justice C, 2017. Satellites may underestimate rice residue and associated burning emissions in Vietnam. Environ. Res. Lett 12 (8), 085006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Quéré C, Andrew RM, Friedlingstein P, Sitch S, Hauck J, Pongratz J, … Arneth A, 2018. Global carbon budget 2018. Earth Syst. Sci. Data 10, 2141–2194. [Google Scholar]
- Li J, Roy DP, 2017. A global analysis of sentinel-2A, sentinel-2B and Landsat-8 data revisit intervals and implications for terrestrial monitoring. Remote Sens. 9 (9), 902. [Google Scholar]
- Lipsett-Moore GJ, Wolff NH, Game ET, 2018. Emissions mitigation opportunities for savanna countries from early dry season fire management. Nat. Commun 9 (1), 2247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loveland TR, Irons JR, 2016. Landsat 8: the plans, the reality, and the legacy. Remote Sens. Environ 185, 1–6. [Google Scholar]
- Lyons EA, Jin Y, Randerson JT, 2008. Changes in surface albedo after fire in boreal forest ecosystems of interior Alaska assessed using MODIS satellite observations. J. Geophys. Res.: Biogeosciences 113 (G2). [Google Scholar]
- Magi BI, Rabin S, Shevliakova E, Pacala S, 2012. Separating agricultural and nonagricultural fire seasonality at regional scales. Biogeosciences 9 (8), 3003–3012. [Google Scholar]
- Markham BL, Storey JC, Williams DL, Irons JR, 2004. Landsat sensor performance: history and current status. IEEE Trans. Geosci. Remote Sens 42 (12), 2691–2694. [Google Scholar]
- Melchiorre A, Boschetti L, 2018. Global analysis of burned area persistence time with MODIS data. Remote Sens. 10 (5), 750. [Google Scholar]
- Miettinen J, Liew SC, 2009. Burn-scar patterns and their effect on regional burnt-area mapping in insular South-east Asia. Int. J. Wildland Fire 18 (7), 837–847. [Google Scholar]
- Morisette JT, Baret F, Privette JL, Myneni RB, Nickeson JE, Garrigues S, … Kalacska M, 2006. Validation of global moderate-resolution LAI products: a framework proposed within the CEOS land product validation subgroup. IEEE Trans. Geosci. Remote Sens 44 (7), 1804–1817. [Google Scholar]
- Morisette Jeffrey T., Privette Jeffrey L., Justice Christopher O., 2002. A framework for the validation of MODIS land products. Remote sensing of environment 83 (1–2), 77–96. [Google Scholar]
- Mouillot F, Schultz MG, Yue C, Cadule P, Tansey K, Ciais P, Chuvieco E, 2014. Ten years of global burned area products from spaceborne remote sensing-a review: analysis of user needs and recommendations for future developments. Int. J. Appl. Earth Obs. Geoinf 26, 64–79. [Google Scholar]
- Olson DM, Dinerstein E, Wikramanayake ED, Burgess ND, Powell GV, Underwood EC, D’Amico JA, Itoua I, Strand HE, Morrison JC, Loucks CJ, Allnutt TF, Ricketts TH, Kura Y, Lamoreux JF, Wettengel WW, Hedao P, Kassem KR, 2001. Terrestrial Ecoregions of the World: a New Map of Life on Earth A new global map of terrestrial ecoregions provides an innovative tool for conserving biodiversity. Bioscience 51 (11), 933–938. [Google Scholar]
- Padilla M, Stehman SV, Chuvieco E, 2014. Validation of the 2008 MODIS-MCD45 global burned area product using stratified random sampling. Remote Sens. Environ 144, 187–196. [Google Scholar]
- Padilla M, Stehman SV, Ramo R, Corti D, Hantson S, Oliva P, Alonso-Canaz I, Bradley AV, Tansey K, Mota B, Pereira JM, Chuvieco E, 2015. Comparing the accuracies of remote sensing global burned area products using stratified random sampling and estimation. Remote Sens. Environ 160, 114–121. [Google Scholar]
- Padilla M, Olofsson P, Stehman SV, Tansey K, Chuvieco E, 2017. Stratification and sample allocation for reference burned area data. Remote Sens. Environ 203, 240–255. [Google Scholar]
- Qiu S, Lin Y, Shang R, Zhang J, Ma L, Zhu Z, 2019. Making Landsat time series consistent: evaluating and improving Landsat analysis ready data. Remote Sens. 11 (1), 51. [Google Scholar]
- Roteta E, Bastarrika A, Padilla M, Storm T, Chuvieco E, 2019. Development of a Sentinel-2 burned area algorithm: generation of a small fire database for sub-Saharan Africa. Remote Sens. Environ 222, 1–17. [Google Scholar]
- Roy DP, Boschetti L, 2009. Southern Africa validation of the MODIS, L3JRC, and GlobCarbon burned-area products. IEEE Trans. Geosci. Remote Sens 47, 1032–1044. [Google Scholar]
- Roy DP, Lewis PE, Justice CO, 2002. Burned area mapping using multi-temporal moderate spatial resolution data-a bi-directional reflectance model-based expectation approach. Remote Sens. Environ 83 (1–2), 263–286. [Google Scholar]
- Roy DP, Frost PGH, Justice CO, Landmann T, Le Roux JL, Gumbo K, Makungwa S, Dunham K, Du Toit R, Mhwandagara K, Zacarias A, Tacheba B, Dube OP, Pereira JMC, Mushove P, Morisette JT, Vannan SKS, Davies D, 2005. The Southern Africa Fire Network (SAFNet) regional burned-area product validation protocol. Int. J. Remote Sens 26, 4265–4292. [Google Scholar]
- Roy DP, Boschetti L, Justice CO, Ju J, 2008. The collection 5 MODIS burned area product - global evaluation by comparison with the MODIS active fire product. Remote Sens. Environ 112, 3690–3707. [Google Scholar]
- Roy DP, Wulder MA, Loveland TR, Woodcock CE, Allen RG, Anderson MC, Scambos TA, 2014. Landsat-8: science and product vision for terrestrial global change research. Remote Sens. Environ 145, 154–172. [Google Scholar]
- Roy DP, Huang H, Boschetti L, Giglio L, Yan L, Zhang HK, Li Z, 2019. Landsat-8 and Sentinel-2 burned area mapping - a combined sensor multi-temporal change detection approach. Remote Sens. Environ 231, 111254. [Google Scholar]
- Särndal C-E, Swensson B, Wretman J, 1992. Model-Assisted Survey Sampling. Springer-Verlag, New York, N.Y., pp. 694. [Google Scholar]
- Silva JM, Sá AC, Pereira JM, 2005. Comparison of burned area estimates derived from SPOT-VEGETATION and Landsat ETM+ data in Africa: influence of spatial pattern and vegetation type. Remote Sens. Environ 96 (2), 188–201. [Google Scholar]
- Stehman SV, 1999. Basic probability sampling designs for thematic map accuracy assessment. Int. J. Remote Sens 20, 2423–2441. [Google Scholar]
- Stehman SV, 2001. Statistical rigor and practical utility in thematic map accuracy assessment. Photogramm. Eng. Remote Sens 67, 727–734. [Google Scholar]
- Stehman SV, 2009. Sampling designs for accuracy assessment of land cover. Int. J. Remote Sens 30, 5243–5272. [Google Scholar]
- Stehman SV, Foody GM, 2019. Key issues in rigorous accuracy assessment of land cover products. Remote Sens. Environ 231, 111199. [Google Scholar]
- Turco M, Jerez S, Doblas-Reyes FJ, AghaKouchak A, Llasat MC, Provenzale A, 2018. Skilful forecasting of global fire activity using seasonal climate predictions. Nat. Commun 9, 2718. 10.1038/s41467-018-05250-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Werf G, Randerson J, Giglio L, Collatz J, Kasibhatla P, Morton D, Defries R, 2010. The improved Global Fire Emissions Database (GFED) version 3: contribution of savanna, forest, deforestation, and peat fires to the global fire emissions budget. In: EGU General Assembly Conference Abstracts, vol. 12. pp. 13010. [Google Scholar]
- Vanderhoof MK, Brunner N, Beal YJG, Hawbaker TJ, 2017. Evaluation of the US Geological survey Landsat burned area essential climate variable across the conterminous US Using commercial high-resolution imagery. Remote Sens. 9 (7), 743. [Google Scholar]
- Viedma O, Angeler DG, Moreno JM, 2009. Landscape structural features control fire size in a Mediterranean forested area of central Spain. Int. J. Wildland Fire 18 (5), 575–583. [Google Scholar]
- Wulder MA, White JC, Loveland TR, Woodcock CE, Belward AS, Cohen WB, … Roy DP, 2016. The global Landsat archive: status, consolidation, and direction. Remote Sens. Environ 185, 271–283. [Google Scholar]
- Zubkova M, Boschetti L, Abatzoglou J, Giglio L, 2019. Changes in fire activity in Africa from 2002 to 2016 and their potential drivers. Geophys. Res. Lett 10.1029/2019GL083469. [DOI] [PMC free article] [PubMed]


