The Increase in Oxygen Demand During Severe Intensity Exercise Must be Included in Calculation of Oxygen Deficit

Abstract

A contentious element in the traditional method of calculating accumulated oxygen deficit (AOD) is the assumption that the oxygen demand remains constant throughout a bout of exercise. The purpose of this study was to investigate the appropriateness of this assumption. Twelve women and eight men volunteered for the study and completed cycle ergometer tests that resulted in exhaustion after ~4 min and ~8 min. In each test, AOD was calculated by subtracting accumulated oxygen uptake (in mL·kg⁻¹) from estimated total oxygen cost (in mL·kg⁻¹), which was estimating two ways: (i) assuming that oxygen demand (in mL·kg⁻¹·min⁻¹) increases over the course of the exercise bout and (ii) assuming it remains constant. Values for AOD in the 4-min and 8-min tests were expected to be the same (maximal). Mean values for AOD in the 4-min and 8-min tests were similar (79.1 ± 7.6 mL·kg⁻¹ and 79.6 ± 8.3 mL·kg⁻¹) when calculated assuming an increase in oxygen demand, but different (71.0 ± 7.9 mL·kg⁻¹ and 42.5 ± 7.6 mL·kg⁻¹) when the demand was kept constant. These results support the hypothesis that oxygen demand increases during exhaustive severe intensity cycling exercise. This increase must be included in calculation of AOD.

INTRODUCTION

The accumulated oxygen deficit (AOD) was proposed as a measure of anaerobic contribution by Krogh and Lindhard (13), re-introduced by Hermansen (6), and popularized by Medbø and colleagues (14). Conceptually, it represents the difference between the estimated total oxygen cost of exercise and the measured accumulated oxygen uptake. Although a large number of studies have accepted AOD as a measure of anaerobic contribution (17), questions have arisen regarding its utility.

Most concerns about AOD as a measure of anaerobic contribution, or of maximal AOD (MAOD) as a measure of anaerobic capacity, are not about the theoretical construct. Rather, they are about the methods for determining the oxygen cost (in mL or mL·kg⁻¹) of severe intensity exercise (1, 2, 17, 19, 21). It has long been assumed, and incorporated into calculation of the AOD by traditional methods (14), that the oxygen demand (in mL·min⁻¹ or mL·kg⁻¹·min⁻¹) is constant throughout a bout of severe intensity exercise. While this assumption has been challenged (2, 6, 11, 12, 15), it has also been supported by recent work (20).

The present study focuses on the methodology of calculating AOD. Thus, there are direct applications to sport and exercise physiologists for whom the measurement of anaerobic contribution (AOD) or anaerobic capacity (MAOD) is important. Importantly, methodology is based on physiology. Understanding the impact of using different methods, or identifying the most appropriate methods, gives information about the underlying physiology. In this case, understanding how to accurately determine the oxygen cost of exercise can give insight into factors related to efficiency and fatigue, and into the significance of the slow component of the VO₂ response.

The purpose of the present study was to test the assumption that oxygen demand remains constant (or exercise efficiency remains constant) during severe intensity exercise, by comparing values of AOD in exhaustive tests of ~4 min and ~8 min duration. These durations were selected to ensure that maximal anaerobic contributions would be elicited in all tests. The values for AOD were calculated using the ‘traditional method’, which assumes that oxygen demand is constant (i.e., that exercise efficiency is constant) over the course of an exercise bout, and using an ‘alternate method’, which assumes that the oxygen demand is increasing (i.e., that efficiency is decreasing) over the course of the exercise bout. The hypothesis was that AOD values in these two exhaustive severe intensity tests would be the same (i.e., equal to MAOD) only if calculated using the alternate method.

METHODS

Participants

A power analysis conducted using G*Power 3.1.9.4 for Mac OS X (Düsseldorf, Germany) determined that 16 participants were needed in the present study for a power of 0.80, with an effect size of 1.0 and an alpha level of 0.05. In anticipation of a 20% dropout rate, we recruited 20 individuals. In fact, we had a 0% dropout rate. Participants were twelve women (mean ± SD, age 21 ± 1 y, height 168 ± 7 cm, and mass 71.2 ± 9.7 kg) and eight men (age 22 ± 2 y, height 178 ± 9 cm, and mass 80.0 ± 13.5 kg). All participants were involved in recreational sport or fitness activities, but not organized sport activities. This research was carried out fully in accordance to the ethical standards of the International Journal of Exercise Science (16). This study was approved by the Institutional Review Board for the Protection of Human Subjects and conducted in accordance with the latest Declaration of Helsinki. All participants provided written informed consent after the procedures, risks, and benefits of the study had been explained to them.

Protocol

Each participant made six visits to the Applied Physiology Laboratory, at the same time of day (± 1 h). All tests were performed under similar conditions in a temperature-controlled laboratory (20 °C to 22 °C; ~50% relative humidity), with no distractions. Testing sessions were separated by at least 48 hours and were completed within a 21-day period. Participants did not alter their usual exercise, diet, or sleep habits over the course of the study.

In the first session, after consent was obtained, the participant was screened using the PAR-Q (23) and a brief medical history, and then familiarized with testing procedures. Participants were instructed to avoid strenuous activity, abstain from drinking alcohol the day preceding and day of session, avoid caffeinated beverages, refrain from consuming carbonated beverages, “get a good night’s sleep” before each testing session, and eat lightly before testing but not within two hours immediately before testing. Participants were excluded if they were a smoker, had donated blood or plasma during the two months preceding the study, or reported an illness during the course of the study.

In the second and third sessions, participants performed incremental tests. Prior to each test, participant compliance with all instructions was verified. The exercise tests were performed on a Lode Excalibur (Groningen, Netherlands) cycle ergometer, using a pedaling cadence of ~80 revolutions per min (rev·min⁻¹). The initial work rates ranged from 30 W to 60 W in one test and from 40 W and 70 W in the other. In each case, work rates were increased 20 W to 30 W each 2 minutes. Work rates and increments were individually selected by the senior investigator based on his experience performing exercise testing with the pool of kinesiology majors from which the participants in the present study were drawn. The incremental tests were terminated when the participant allowed the pedaling cadence to drop below 75 rev·min⁻¹ for 5 seconds, despite strong verbal encouragement.

In the fourth, fifth, and sixth sessions, participants performed constant power tests. Unbeknownst to participants, the first constant power test (session four) was a practice trial, and data were not used in analyses. The second and third constant power tests (done in sessions five and six) were performed at work rates that were individually selected by the primary investigator, based on each participant’s performance in the incremental tests. Before each test, the participant was reminded to exercise for as long as possible and he or she was told that test duration would be about 5 min (at the 4-min work rate) or about 10 min (at the 8-min work rate); however, no feedback about exercise duration was provided during or after the tests. These durations were selected because exercise that leads to exhaustion in 4 min or 8 min is of an intensity appropriate for attainment of maximal anaerobic contribution (8, 11, 12, 15). Testing order was assigned using randomization.

Expired gases were analyzed on a breath-by-breath basis during each test using a MedGraphics (St. Paul, MN, USA) CardiO₂ metabolic system. In the incremental tests, the 30-s VO₂ at the end of each stage was reported as the steady state value; the highest 30-s VO₂ in each test was recorded, with the highest of these two values reported as the VO_2max. In the constant power tests, the highest 30-s VO₂ in each test was reported as the VO_2peak. Heart rate (HR) data were obtained using a Polar telemetry system (Lake Success, NY, USA), and a rating of perceived exertion (RPE) was obtained using the 6 to 20 scale (4), near the end of each stage and immediately prior to test termination.

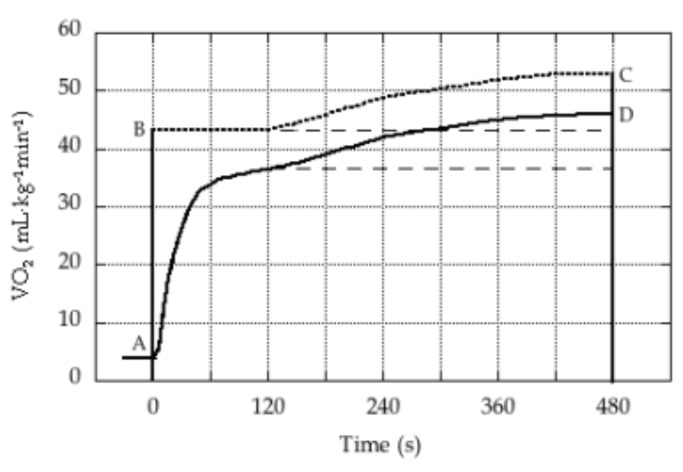
The AOD was calculated using data from each constant power cycling test. Using SPSS v22 (IBM, Armonk, NY, USA) linear regression analysis on software and data from all of the stages in the incremental tests for which the respiratory exchange ratio (VCO₂·VO₂⁻¹) was less than 1.00, the relationship between VO₂ and work rate was used to extrapolate the individual’s oxygen demand (in mL·kg⁻¹·min⁻¹) at the work rates used in the constant-power tests. Then, AOD were determined using the alternate method and the traditional method, which are depicted in Figure 1 and explained below.

Figure 1.

Responses in an exhaustive bout of severe intensity exercise. The solid curve (AD) represents the VO₂ response, while the dotted curve (BC) represents the oxygen demand. The area described by ABCD is the oxygen deficit. Dashed lines identify responses had there been no increase in oxygen demand and no increase in VO₂, and illustrate the effect of assuming that the oxygen demand does in fact increase during the exercise bout.

The alternate method was based on the assumption that oxygen demand increases (i.e., exercise efficiency decreases) during severe intensity exercise. Therefore, for the alternate method, total oxygen cost (in mL·kg⁻¹) was calculated as oxygen demand (in mL·kg⁻¹·min⁻¹) × exercise duration (in min) plus the excess oxygen cost (in mL·kg⁻¹). The value for the excess oxygen cost arising from the falling efficiency during the exercise is quantified by the oxygen uptake attributable to the slow component. AOD is the difference between the total oxygen cost and the total accumulated oxygen uptake. Calculations of the total accumulated oxygen uptake and the excess oxygen uptake are described in the next section.

The traditional method is based on the assumption that oxygen demand is constant during severe intensity exercise (14). Therefore, for the traditional method, the total oxygen cost (in mL·kg⁻¹) was calculated as oxygen demand (in mL·kg⁻¹·min⁻¹) × exercise duration (in min).

For each constant power test, breath-by-breath VO₂ data were reduced to rolling 5-breath averages. Parameters of the VO₂ response profile beginning at the onset of exercise were determined using nonlinear regression on KaleidaGraph 4.50 (Reading, PA, USA), by fitting responses to a model with two exponential terms (Equation 1):

$${\text{VO}}_2(\text{t})={\text{A}}_{\text{baseline}}+{\text{A}}_{\text{fast}}\times (1-{\text{e}}^{-(\text{t}-\text{TDfast})/\text{taufast}})+{\text{A}}_{\text{slow}}\times (1-{\text{e}}^{-(\text{t}-\text{TDslow})/\text{tauslow})}).$$

VO₂(t) is the value for VO₂ at time = t; A_baseline is the baseline VO₂; A_fast and A_slow are the asymptotic amplitudes for the two exponential terms; tau_fast and tau_slow are the respective time constants; and TD_fast and TD_slow are the time delays. The total area under the VO₂ response curve (i.e., total accumulated oxygen uptake, which represents the aerobic contribution) and the area under the curve of the fast phase of the VO₂ response were calculated using KaleidaGraph. The difference between these two areas, which represents the excess oxygen uptake attributable to the slow component, was determined by subtraction.

Statistical Analysis

The values for AOD were compared using a two-way analysis of variance (ANOVA), with repeated measures across method (alternate vs traditional) and test duration (4 min vs 8 min), using SPSS software. Initially, the analysis was carried out with a three-way (method × duration × gender) ANOVA. However, results of this analysis revealed no evidence of a significant interaction effect involving gender. Therefore, data were collapsed across gender and the two-way ANOVA was used. Significance for all analyses was set at p < 0.05. A one-way ANOVA was used to compare VO_2max and the two VO_2peak values. Values from the 4-min and 8-min tests were compared using paired-means t-tests. In addition, correlations between the various AOD values were determined. Values are presented in this paper as means ± SD.

The comparisons of interest were (i) alternate method AOD from 4-min tests versus alternate method AOD from 8-min tests and (ii) traditional method AOD from 4-min tests versus traditional method AOD from 8-min tests. The first hypothesis was that the first comparison, (i) above, would not be significant, that the alternate method would produce values for AOD that were not significantly different from each other (i.e., not different from the MAOD), regardless of duration of the exhaustive tests. The hypothesis was that the second comparison, (ii) above, would be significant, that the traditional method would produce values for AOD from the two exhaustive tests that were significantly different from each other (i.e., not both representative of MAOD). When these comparisons suggested that means were not different, Bland-Altman (3) plots were created to evaluate the similarity of the values from the two tests.

RESULTS

The mean value for VO_2max from the incremental tests was 44.9 ± 6.7 mL·kg⁻¹·min⁻¹, and it was associated with RER, 1.24 ± 0.03; RPE, 19 ± 1; and HR, 196 ± 8 bt·min⁻¹. The mean work rate in the 4-min tests was 320 ± 59 W (4.2 ± 0.2 W·kg⁻¹); duration, 246 ± 22 s (4.1 ± 0.4 min); RER, 1.30 ± 0.04; RPE, 19 ± 1; and HR, 195 ± 6 bt·min⁻¹. The VO_2peak was 44.6 ± 6.5 mL·kg⁻¹·min⁻¹. The excess oxygen uptake attributable to the slow component was 8.1 ± 4.0 mL·kg⁻¹.

The mean work rate in the 8-min tests was 247 ± 47 W (3.3 ± 0.3 W·kg⁻¹); duration, 490 ± 24 s (8.2 ± 0.4 min); RER, 1.33 ± 0.04; RPE, 20 ± 1; and HR, 196 ± 6 bt·min⁻¹. The VO_2peak was 45.7 ± 6.6 mL·kg⁻¹·min⁻¹. The excess oxygen uptake attributable to the slow component was 37.1 ± 8.0 mL·kg⁻¹.

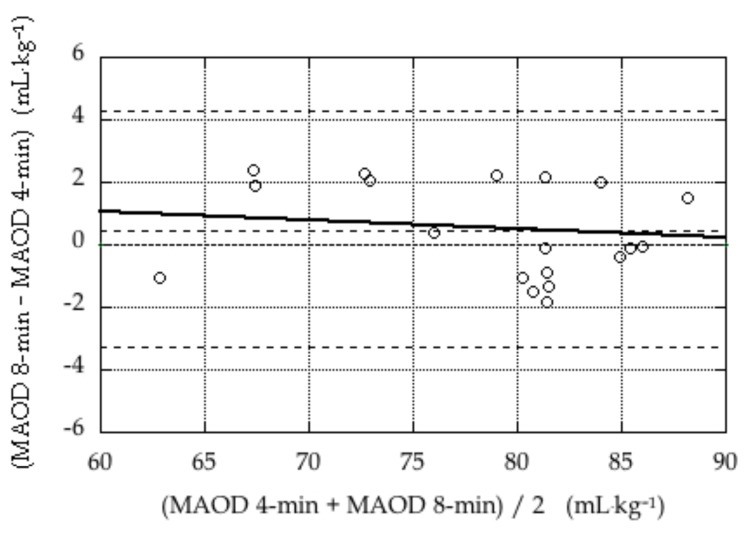
Results of the Shapiro-Wilk test confirmed that the data were normally distributed. Results of the two-way ANOVA revealed significant main effects for method (alternate vs traditional) and for test duration (4-min vs 8-min) and, most pertinent for the purpose of the study, a significant method by test duration interaction effect. Results of post hoc comparisons revealed no difference between AOD values from the 4-min and 8-min tests calculated using the alternate method (p = 0.14); the two values were highly correlated (r = 0.98, p < 0.01). Based on these results, a Bland-Altman plot (3) of the values obtained using the alternate method was produced; it is presented in Figure 2. In contrast, results of post hoc comparisons revealed a significant difference between AOD values from the 4-min and 8-min tests calculated using the traditional method (p < 0.01); the two values were not significantly correlated (r = 0.25, p = 0.23).

Figure 2.

The Bland-Altman plot of MAOD values obtained using the alternate method (which assumes that the oxygen demand increases over time during exhaustive severe intensity exercise) with the data from 4-min tests (MAOD 4-min) and 8-min tests (MAOD 8-min). The dashed lines in the figure indicate the mean difference (bias; 0.5 ± 1.5) and the mean ± 2 × SD. The solid line represents the linear regression of the difference against the mean (difference = 2.7 – 0.03 × mean), which was not statistically significant.

Results of t-tests revealed no differences in the RER, HR, or RPE values in the 4-min and 8-min tests. Results of an ANOVA revealed no differences among the VO_2max and two VO_2peak values. Data used to calculate AOD are presented in Table 1. In each exercise test, there was a quantifiable excess oxygen uptake attributable to the slow component; results of t-tests revealed that the magnitude of this excess oxygen uptake was almost 5-fold greater in the 8-min tests. Thus, for each test duration, the total oxygen cost was higher when calculated using the alternate method rather than the traditional method; the effect of including the excess oxygen cost in the total oxygen cost, in the alternate method, was greater in the 8-min tests.

Table 1.

Mean (± SD) values (with the 95% confidence intervals) for kinetics of the VO₂ responses during exhaustive severe intensity exercise.

	4-min test	8-min test
baseline VO2 (mL·kg−1·min−1)	4.0 ± 0.3	4.0 ± 0.3
(95% C.I.)	(3.9, 4.1)	(3.9, 4.1)
TDfast (s)	4 ± 2	5 ± 3
(95% C.I.)	(3, 5)	(4, 6)
SEE TDfast (s)	1 ± 1	2 ± 2
taufast (s)	23 ± 5	31 ± 6
(95% C.I.)	(21, 25)	(28, 34)
SEE taufast (s)	3 ± 1	3 ± 2
Afast (mL·kg−1·min−1)	34.2 ± 4.7	31.8 ± 4.9
(95% C.I.)	(32.1, 36.3)	(29.7, 33.9)
SEE Afast (mL·kg−1·min−1)	3.2 ± 1.7	2.8 ± 1.2
TDslow (s)	115 ± 15	124 ± 16
(95% C.I.)	(108, 122)	(117, 131)
SEE TDslow (s)	8 ± 3	6 ± 3
A′slow (mL·kg−1·min−1)	6.4 ± 2.1	9.9 ± 4.1
(95% C.I.)	(5.5, 7.3)	(8.1, 11.7)

Table 2.

Mean (± SD) values (with the 95% confidence intervals) for data used in calculation of MAOD.

	4-min test	8-min test
accumulated uptake (mL·kg−1)	148.8 ± 18.9	310.8 ± 31.8
(95% C.I.)	(140.5, 157.1)	(296.9, 324.7)
oxygen demand (mL·kg−1·min−1)	53.6 ± 2.5	43.3 ± 2.8
(95% C.I.)	(52.5, 54.7)	(42.1, 44.5)
total oxygen cost (mL·kg−1)	219.8 ± 17.1	353.3 ± 23.8
(95% C.I.)	(212.3, 227.3)	(342.9, 367.7)
traditional method, oxygen cost = oxygen demand × time
MAOD (mL·kg−1)	71.0 ± 7.9	42.5 ± 6.3
(95% C.I.)	(67.5, 74.5)	(39.7. 45.3)
traditional method, assumes oxygen demand is constant during exercise
excess oxygen cost (mL·kg−1)	8.1 ± 4.0	37.1 ± 8.0
(95% C.I.)	(6.3, 9.9)	(33.6, 40.6)
excess cost is assumed to equal excess oxygen uptake due to slow component
total oxygen cost (mL·kg−1)	227.9 ± 17.8	390.4 ± 21.9
(95% C.I.)	(220.1, 235.7)	(380.8, 400.0)
alternate method, oxygen cost = oxygen demand × time + excess cost
MAOD (mL·kg−1)	79.1 ± 7.6	79.6 ± 8.3
(95% C.I.)	(75.8, 82.4)	(76.0. 83.2)
alternate method, assumes oxygen demand increases during exercise

Note: Values were calculated assuming that the oxygen demand increases across the bout of exhaustive severe intensity exercise (alternate method) and they were calculated using the assumption that oxygen demand is constant across the bout of exhaustive exercise (traditional method).

DISCUSSION

The principle finding in the present study was that realistic and defensible (M)AOD values were obtained in the two exhaustive severe intensity exercise tests only when calculated using the alternate method, that is, only when the calculations presumed that oxygen demand was increasing over the course of the exercise, and specifically when the calculations presumed that the oxygen demand was increasing in concert with the expression of the slow component of the VO₂ response. The important outcome of the study is confirmation that the oxygen demand begins to increase (or exercise efficiency begins to decrease) less than two minutes into a bout of severe intensity exercise and that it is crucial to include this increase for accurate calculation of (M)AOD.

Fundamental to the interpretation of our results is the presumption that exhaustive severe intensity exercise engenders a MAOD. That is, a unique value for AOD (i.e., the maximal AOD) should be obtained from the results of exhaustive severe intensity exercise tests, regardless of where the intensity lies within the domain and regardless of the tolerable duration of that exercise. The intensities used in the 4-min and 8-min tests were indeed within the severe domain, as evidenced by the fact that VO_2peak values in these tests were not different from VO_2max: VO_2max can be achieved only during severe intensity exercise, defined as above critical power (5) but at or below the upper bound (9). However, in the present study, when calculated using the traditional method, AOD values from the two exhaustive severe intensity exercise tests were very different and poorly correlated. In contrast, including the excess oxygen cost in the total oxygen cost (alternate method) resulted in AOD values for the two exercise tests that were within 1%, highly correlated, and not significantly different. A Bland-Altman plot (3) demonstrated the similarity between the two measures.

Questions about the constancy of the oxygen demand during the severe exercise are often coupled with questions about the significance of the slow component of the VO₂ response. For example, it has been doubted that the excess oxygen uptake associated with the slow component should be included in the accumulated oxygen uptake, which is the measure of aerobic contribution (2). Rather than consider the excess VO₂ as simply ‘wasted’, it has been argued that it is more likely that the appearance and magnitude of the slow component occur simultaneously with increasing oxygen demand (decreasing efficiency) over the course of a bout of severe intensity exercise, as shown by Noordhof and colleagues (15, 18). We note that, mathematically, not including the excess oxygen uptake attributed to the slow component in the accumulated oxygen uptake (assuming it is ‘wasted’) generates the same value for AOD as including it in the measure of aerobic contribution and assuming that the oxygen cost is increased by an amount equal to it (alternate method). See Figure 1.

Indirect support for the alternate method is indicated when low or even negative (M)AOD values are obtained using the traditional method (21), suggesting that oxygen demand has been underestimated. Indeed, in the present study, during the 8-min tests, had we not assumed that the oxygen demand increased over the course of the exercise bout, then the demand (43.3 ± 2.8 mL·kg⁻¹·min⁻¹) would be lower than the VO_2peak that was achieved (45.7 ± 6.6 mL·kg⁻¹·min⁻¹).

We have reported results that directly demonstrate the validity of the alternate method, as it generated values for MAOD that were, as should be expected, greater in running than in cycling (8, 11, 12) and the same in exhaustive severe intensity bouts of 3-min, 5-min, and 7-min duration (8). In all cases (7, 8, 10, 11, 12), values approached the theoretical maximum of 100 mL·kg⁻¹ proposed by Saltin (22). Despite the redundant evidence of the validity of the alternate method, we can offer no explanation for the reduction in efficiency as early as one and a half to two minutes into a bout of exercise, nor for why there should be a tight linking between the change in exercise efficiency and emergence of the slow component of the VO₂. In addition, recent work (20) has provided strong evidence that the oxygen demand stays constant, that the anaerobic contribution is decreasing in concert with the increasing aerobic contribution, and thus that the traditional method is appropriate.

The values for AOD that were calculated in the present study using the traditional method were 71.0 mL·kg⁻¹ for exercise at 320 W and 42.5 mL·kg⁻¹ for exercise at 247 W. These values fall within the range of values typically reported for MAOD. Alone, neither value would signal an issue with methodology. However, exhaustive bouts of ~4 min and ~8 min duration elicit a maximal anaerobic contribution, meaning the AOD values should be the same (maximal). This result was obtained only when AOD was calculated using the alternate methods, that is, only when the oxygen demand was considered to increase over time.

The findings in the present study have significance for sport and exercise physiologists, for whom accurate determination of anaerobic contribution or anaerobic capacity is important. While traditional methods of calculating MAOD generally generate reasonable values, our results suggest that, to generate accurate values, calculations must include an increase in oxygen demand over the course of the exercise. Only with accurate measurement of MAOD can the metabolic demands of performance be accurately described and only with accurate measurement of MAOD can useful predictions of performance potential be made (i.e., in conjunction with measures of VO₂ kinetics, VO_{2 max,} and economy). Attention to methodology is crucial, because the impact of the increase in oxygen demand (i.e., the impact of correcting for the contribution of the slow component) is different at different intensities and, specifically, greater with longer exercise durations.

In conclusion, the results of the present study confirm that the oxygen demand increases during performance of severe intensity exercise, in concert with the expression of the slow component of the VO₂ response. In order to generate meaningful values for (M)AOD, the reduction in exercise efficiency during severe intensity exercise must be considered in the calculation of total oxygen cost.