Reply: The influence of sample size and arbitrary statistical thresholds in lesion-network mapping

Sir,

We thank Sperber and Dadashi (2020) for their interest in our recent paper (Cohen et al., 2019) and the techniques of lesion network mapping (Boes et al., 2015) and coordinate network mapping (Darby et al., 2019) more generally. In their letter, they highlight two methodological concerns: the size of the normative connectome and the threshold for defining a region as ‘functionally connected’ (Sperber and Dadashi, 2020). At present, both parameters represent ‘researcher degrees-of-freedom’ for which there is no accepted standard or single correct answer (Simmons et al., 2011; Wicherts et al., 2016). As such, these parameters have varied across our published studies, raising concern that they were chosen in an arbitrary manner. However, when organized chronologically, trends in this variability are apparent (Table 1). Over time, we have moved to a larger connectome, increased statistical power, and increased statistical rigor. Further, many of our papers have used multiple thresholds or even different normative connectomes to ensure our conclusions were robust to these parameter choices.

Table 1.

Chronological list of our lesion and coordinate network mapping studies

Study	Symptom of interest	Size of connectome	Sensitivity analysis			Specificity analysis
			Threshold P-level	Primary t-level threshold	Additional t-level thresholds reported	Were non-threshold dependent analyses performed?
Boes et al. (2015)	Multiple deficits	98	0.00005 (uncorrected)	4.25	Yes, multiple	No
Fischer et al. (2016)	Coma	98	0.00005 (uncorrected)	4.25	Yes, 9, 3.75, 2	Yes
Laganiere et al. (2016)	Hemichorea-hemiballismus	98	0.00005 (uncorrected)	4.25	Yes, multiple	Yes
Darby et al. (2017)	Capgras delusions	98	0.00005 (uncorrected)	4.25	Yes, multiple	Yes
Fasano et al. (2017)	Freezing gait	98	0.05 (uncorrected)	2	Yes, 4.25, 3	Yes
Darby et al. (2018a)	Criminal behaviour	98 and 1000	10−17 (uncorrected)	12	No	Yes
Darby et al. (2018b)	Free will	1000	10−6 (uncorrected)	5	No	Yes
Joutsa et al. (2018a)	Parkinson syndrome	1000	10 − 11 (uncorrected)	7	No	Yes
Joutsa et al. (2018b)	Tremor relief	1000	10 − 6 (FWE-corrected)	7	No	No
Joutsa et al. 2019	Holmes tremor	1000	0.05 (FWE-corrected)	5	No	Yes
Darby et al. (2019)	Neurogenerative disease	1000	0.05 (FWE-corrected)	5	Yes, 10, 7	Yes
Corp et al. (2019)	Cervical dystonia	1000	10−6 (FWE-corrected)	7	No	Yes
Weil et al. (2019)	Parkinson’s dementia	1000	10−6 (FWE-corrected)	7	No	Yes
Ferguson et al. (2019)	Amnesia	1000	10−6 (FWE-corrected)	7	No	Yes
Burke et al. (2020)	Migraine	1000	10−6 (FWE-corrected)	7	No	Yes
Kim et al. (2019)	Hallucinations	1000	10−6 (FWE-corrected)	7	Yes, 12, 5	Yes
Padmanabhan et al. (2019)	Depression	1000	Leave-one-dataset-out cross validation of unthresholded maps			Yes
Cohen et al. (2019)	Prosopagnosia	1000	10−11 (FWE-corrected)	9	Yes, multiple	Yes
Snider et al. (2020)	Consciousness	1000	Logistic regression of unthresholded maps			Yes

Studies are presented in order of when they were conducted, not necessarily when they were published. All studies that required a t-value threshold examined multiple thresholds, and many included these analyses in the final manuscript. All studies except one brief communication included analyses that were not dependent on a t-value threshold.

However, this variability raises good questions about which parameters investigators should choose if they seek to implement lesion network mapping in their own laboratories. As such, we thank Sperber and Dadashi for the opportunity to discuss these issues in greater detail.

Variability in normative connectome size

Our earliest lesion network mapping studies used resting state functional connectivity data from 98 healthy young controls to identify connectivity with each lesion location (Boes et al., 2015; Fischer et al., 2016; Laganiere et al., 2016; Darby et al., 2017; Fasano et al., 2017). We chose this connectome dataset for convenience, as it was high-quality, locally available, and part of a large ongoing data collection initiative (Holmes et al., 2015).

To combine connectivity measures for these 98 subjects, we used a random effects analysis to generate a ‘T map’ that reflected the statistical probability of connectivity with the lesion location, accounting for variance across subjects. An alternative we considered was to average connectivity maps across the 98 subjects, generating an average ‘r-map’ of Pearson’s correlation coefficients. This r-map would be consistent across connectomes with differing number of subjects, but it ignores the variability across subjects and does not allow one to easily assess the statistical significance of identified connections represented in the T map.

As this connectome dataset grew in size, we upgraded our network mapping pipeline to take advantage of an expanded 1000-subject connectome (Darby et al., 2018,a, b; Joutsa et al., 2018a, b, 2019; Cohen et al., 2019; Corp et al., 2019; Ferguson et al., 2019; Kim et al., 2019; Padmanabhan et al., 2019; Weil et al., 2019; Burke et al., 2020; Snider et al., 2020). Our first lesion network mapping paper using this expanded connectome compared results to those obtained using our original 98 subject cohort (Darby et al., 2018a). Lesion networks generated using both normative connectomes were very similar, with nearly identical spatial distributions of positive and negative connectivity (Darby et al., 2018a). Average r maps using the 98 and 1000 subject connectomes were also nearly identical, consistent with other work showing that group connectivity estimates stabilize above 150–200 subjects (Cremers et al., 2017; Dansereau et al., 2017; Cui and Gong, 2018; Turner et al., 2018; Varoquaux, 2018). However, t-values were much larger using our larger connectome, reflecting the increase in statistical power. When seeking to highlight only the most significant connections, a higher t-value threshold was required (Darby et al., 2018a).

Taking advantage of this increased statistical power, we found that a range of statistically significant t-value thresholds could be used, as has been done for years with functional MRI activation results, to focus on only the strongest findings or a broader network of slightly less significant findings (Darby et al., 2018a, b; Joutsa et al., 2018a, 2019; Cohen et al., 2019; Corp et al., 2019; Ferguson et al., 2019; Kim et al., 2019; Padmanabhan et al., 2019; Weil et al., 2019; Burke et al., 2020; Snider et al., 2020). We also began using improved statistical methods, including family-wise error rate (FWE) multiple comparison correction, non-threshold dependent specificity analyses, and non-parametric permutation testing for assessing statistical significance (Winkler et al., 2014; Eklund et al., 2016).

Now, efforts are underway to generate human connectomes from 100 000 subjects (Miller et al., 2016). Using this connectome for lesion network mapping would again result in increased t-values, to the point that almost every voxel would likely be considered ‘statistically significant’. As more and larger connectomes become available, it will be important to re-examine approaches for combining connectivity maps across large cohorts of subjects; and the notion of a ‘statistically significant’ connection may become irrelevant. Instead, metrics such as the ‘top 25%’ of connections may become more useful, an approach that has been used in graph theory analyses (Bullmore and Sporns, 2009; Power et al., 2011).

Variability in the t-value threshold

As noted above, we have used different t-value thresholds across different papers using the 1000 subject connectome to define a region as ‘connected’. This threshold variability is not unique to lesion network mapping, but is an issue for many types of functional connectivity analyses (Reijneveld et al., 2007; Stam and Reijneveld, 2007; Buckner et al., 2009; Bullmore and Sporns, 2009; Rubinov and Sporns, 2010; Wang et al., 2010; Power et al., 2011; Fornito et al., 2015).

Given the difficulty inherent in choosing a threshold, it is worth asking why we use a threshold at all. When we first introduced lesion network mapping (Boes et al., 2015), our primary goal was to show that the method added value compared to traditional lesion mapping. Using a threshold for lesion network maps (connected or not), facilitated comparison to traditional lesion mapping (lesioned or not). By binarizing lesion network maps, we were able to use the same statistical tools used in traditional lesion mapping and directly compare the two results (Boes et al., 2015).

A second motivation for using a threshold is that it can help simplify result interpretation, especially when presenting a new technique or concept. Concluding that ‘95% of lesion locations causing symptom X are connected to region Y’ is easy to understand. This result also means that connectivity with region Y (at the same threshold) defines a brain network that encompasses 95% of lesion locations causing symptom X. While this number is threshold-dependent and could change to 98% with a lower t-threshold or 90% with a higher t-threshold, choosing a threshold can help illustrate the lesion network mapping concept.

Finally, there are statistical advantages to binarizing a lesion network map. Because of the spatial autocorrelation inherent to seed-based connectivity analyses, a lesion network will have extremely high ‘connectivity’ at the lesion location itself. This results in high variance at each lesion location when a cohort of different lesion locations causing the same symptom is combined. As such, using a one-sample t-test to combine these maps, as suggested by Sperber and Dadashi (2020), is biased away from the lesion sites themselves, which are likely important locations within the affected network (Rorden and Karnath, 2004). By thresholding and binarizing lesion network maps prior to combining them, commonalities across a group of lesions can be identified without penalizing the lesion locations themselves.

Given that there is potential value in using a t-value threshold, yet multiple different thresholds could reasonably be used and values will change with the size of the connectome, how does one choose a threshold? Below we provide some recommendations:

Methodological recommendations for lesion network mapping

First, use normative connectomes large enough to provide stable group-level connectivity estimates, ideally larger than 150 subjects. If possible, we recommend trying to match the size of the connectome used in prior work, as this allows for more direct comparisons across studies.

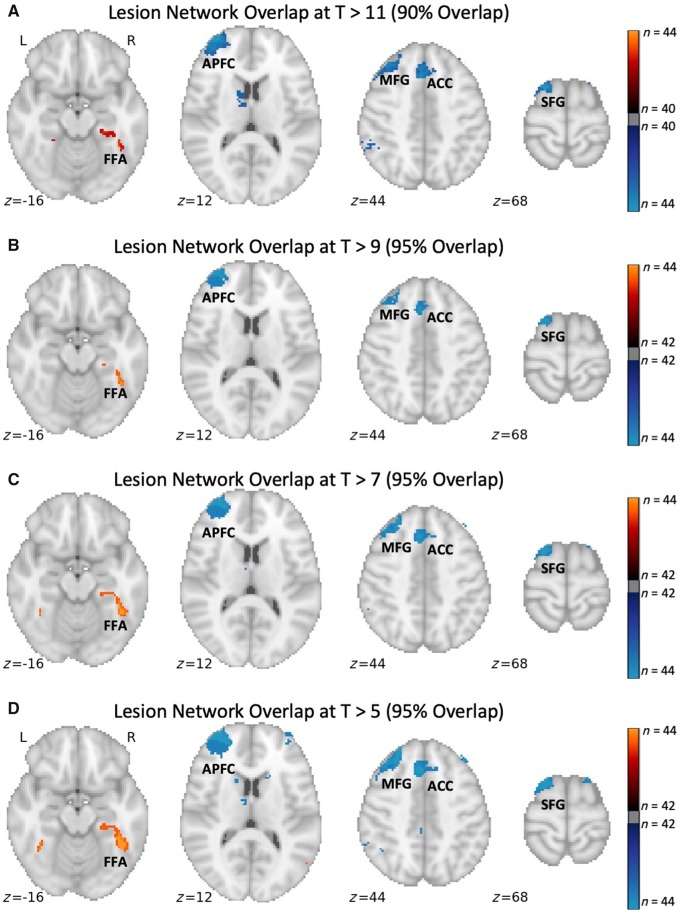
Second, ensure any conclusions based on threshold-dependent analyses hold true across a range of different thresholds. We have used this approach in almost all recent papers, including Cohen et al. (2019), which is demonstrated visually in Fig. 1. Consistent with this principle, results that do not hold true across different thresholds should be made explicit and de-emphasized relative to results that are more robust, an approach we have also used in prior papers (Fischer et al., 2016; Laganiere et al., 2016; Fasano et al., 2017).

Figure 1.

Lesion network mapping of prosopagnosia is consistent across a range of thresholds. Regions of peak lesion network overlap in the fusiform face area (FFA), anterior prefrontal cortex (APFC), middle frontal gyrus (MFG), anterior cingulate cortex (ACC), and superior frontal gyrus (SFG) are consistent across a range of t-value thresholds. At higher thresholds the percentage overlap decreases, but the topography of the lesion network and central findings remain unchanged. L = left; R = right.

Third, for simplicity, we often use a single threshold for presenting our ‘primary’ lesion network overlap results, and we include results at other thresholds as secondary analyses. When deciding which threshold to use for the ‘primary’ analysis, we choose the highest threshold that still demonstrates the relevant finding, as this will improve specificity. For example, in Cohen et al. (2019) we could have chosen a lower t-threshold that was still ‘statistically significant’ and obtained the same result (Fig. 1); however, the resulting prosopagnosia network would have been slightly less specific to prosopagnosia lesions. This principle is responsible for much of the variation in t-value threshold across our recent studies (Table 1).

Fourth, complement any threshold-dependent analysis with a threshold-independent analysis. In the vast majority of our papers we use unthresholded maps for assessing the specificity of lesion network mapping results (Table 1). For example, the conclusion that ‘95% of lesions causing symptom X are connected to region Y’ may be threshold dependent, but the conclusion that ‘lesions causing symptom X are significantly more connected to region Y then lesions not causing symptom X’ is not dependent on this parameter.

Fifth, whenever possible, analyse data from multiple independent cohorts to test whether lesion network mapping results, which may have used an arbitrary threshold, are reproducible across cohorts, independent of thresholds, e.g. Fig. 8 in Cohen et al. (2019).

Finally, if one is uncomfortable with choosing a threshold for lesion network analyses, one can avoid using a threshold at all, a choice we have made in some recent lesion network mapping reports (Padmanabhan et al., 2019; Snider et al., 2020). One study used logistic regression to identify connections that covaried with the severity of loss of consciousness (Snider et al., 2020) while another focused on connections that varied significantly with the presence or severity of depression (Padmanabhan et al., 2019). This latter study is also notable for confirming reproducibility across five independent datasets (Padmanabhan et al., 2019).

Future considerations

We anticipate that as the field of lesion network mapping and coordinate-based network mapping grows, there will be parallel growth in methodological studies seeking to identify the best approaches, similar to what has occurred for the field of functional connectivity in general (Ciric et al., 2017; Murphy and Fox, 2017; Parkes et al., 2018).

In summary, we thank Sperber and Dadashi for their interest in lesion network mapping and for the opportunity to discuss these methodological issues. There is no simple, or single, solution to the question of how ‘best’ to perform lesion network mapping. Presently, we feel that thresholding lesion connectivity maps provides some utility; however, we look forward to methodological advances that may circumvent this researcher degree of freedom.

Data availability

Data sharing is not applicable to this article as no new data were created or analysed in this work.

Funding

A.L.C. was supported by NIH T32MH112510 and the Child Neurology Foundation. M.D.F. was supported by the Sidney R. Baer, Jr. Foundation, NIH K23NS083741, the Dystonia Foundation, and the Nancy Lurie Marks Foundation.

Competing interests

The authors report no competing interests.