Opto-thermal diffusiophoresis of soft biological matter: from physical principle to molecular manipulation

Abstract

Transport of ions and molecules under external field gradients is fundamental phenomena relevant to many biological systems including molecular motors in nature. As inspired from such biological transport, novel optical manipulation by using local solute gradient and the creation of self-propulsive particles are being developed using this technology. In this review article, we describe the basic principles behind those transport phenomena under a temperature and a solute concentration gradient and discuss novel manipulation tools for soft biological materials. The control of such micron-scale transport will bring new insight in design principles of functional materials showing autonomous motion as seen in molecular motors.

Introduction

Cells are out of equilibrium systems that exchange molecules and energy with their surrounding. They uptake ions and small molecules from the outside through the cell membrane, and the proteins that are involved in this ion or molecular transport across cell membrane convert chemical energy from the hydrolysis of ATP to create concentration gradients of ions, e.g., Na⁺-K⁺ ion pump (Jorgensen et al. 2003). As shown in Fig. 1a, there are various molecular machines that operate with such an ion concentration gradient or the ATP hydrolysis (Vale and Milligan 2000; Kinosita et al. 2004). Although the structure of those molecular machines in cells has been elucidated, the underlying principle of their molecular engines are not yet fully understood.

Fig. 1.

Transport phenomena in biology and physics. a Ion channel and ion pump are proteins that are involved in many biological processes. (left) Cation such as Na⁺ and K⁺ is passively transported by ion channel and actively transported by ion pump coupled with the hydrolysis of ATP (Jorgensen et al. 2003). (middle) Transport of cargos by molecular motor proteins. A cargo binding onto a motor protein such as kinesin and dynein is transported along a filament of microtubule (Vale and Milligan 2000). (right) Unidirectional rotation of F₁ ATPase. This ATPase consisting of α, β, and γ subunits and the energy source of its rotational motion is the hydrolysis of ATP (Kinosita et al. 2004). b Physical transport phenomena. (left) Normal diffusion. The flux of solute J_d occurs in a gradient of concentration. (middle) Electrophoresis. Charged solute is transported along electric field and its solute flux J_Ep is proportional to the gradient of electric field (Viovy 2000). (right) Diffusiophoresis. Charged solute is transported along the concentration gradient of another electrolyte solute (Anderson 1989; Abecassis et al. 2008). The solute flux $J_{Dp}^{+}$ and $J_{Dp}^{-}$ are diffusiophoretic transport of positively and negatively charged solutes, respectively

In order to clarify the principle of transport phenomena out of equilibrium, it is effective not only to analyze complex biomolecules but also to understand simplified physical systems instead of complex biomolecules. According to Onsager’s theory of irreversible processes, the irreversibility of a state change of a system induces a temporal change in entropy, resulting in a flow in which thermodynamic variables (concentration and temperature) change in one direction (Piazza and Guarino 2002) (Fig. 1b). If this flow continues to occur constantly, the transport of heat, electrons, and even molecules occurs. There are many examples of such physical transport phenomena. One such example is electrophoresis in which charged polymers are transported in one direction under a electric potential gradient (Viovy 2000). Another example is diffusiophoresis (Anderson 1989; Abecassis et al. 2008) in which charged polymers are transported similarly along a concentration gradient of another solute. Rectified transport of molecules has been extensively studied, but the relationship between intracellular phenomena and physical transport has not been sufficiently explored yet despite its potential application for soft and biological materials. Hence, the important issue is how one can advance the understanding of relevant biological transport and what types of novel tools can be invented from understanding their physical mechanism.

The focus of this review article is to outline the recent developments in the understanding of physical transport phenomena, in particular, those which could be relevant for biological applications. We briefly introduce transport phenomena driven by the temperature and concentration gradients in an aqueous solution (Braun and Libchaber 2002; Duhr and Braun 2006). The interplay of temperature and concentration gradients demonstrates the pattern formation of colloidal particles and biological molecules such as DNA with little material dependence (Jiang et al. 2009; Maeda et al. 2011, 2012; Maeda 2013). This approach allows one to control soft biological materials for micro-scale analysis and molecular manipulation (Fukuyama et al. 2015; Weinert et al. 2008; Fukuyama et al. 2018). These understandings of physical transport phenomena may provide new insight in not only optical manipulation for intracellular fluid streaming but also autonomous motion driven by molecular engines.

Thermophoresis: solute flux in a temperature gradient

Charged ions and charged polyelectrolyte polymers such as DNA or RNA are transported under a gradient of electrical potential. This transport of molecules is driven by external force from electric field and this is known as electrophoresis (Viovy 2000). Electrophoresis of polymers in a gel is used in all biology laboratories in order to analyze the size of charged polymers of DNA or protein, but an external field in which solute molecules can be conveyed is not limited to electromagnetic ones. A possibly relevant but little explored thermodynamic field is temperature gradient.

Temperature gradient is ubiquitously present in nature and technology, and the resulting heat flux keeps systems out of equilibrium state. On the one hand, as seen in thermo-electric devices, temperature gradient induces the transport of electrons, which leads the generation of electric power in semiconductors. Because the control of electrons and spins can be possible by using electric potential gradient itself, the utilization of thermal heat transport is also advantageous for energy conversion from heat to reusable energy resource. On the other hand, not only for solid-state physics, temperature gradient in an aqueous solution also shows transport of solute species. It is known that transport of molecules under a temperature gradient, Ludwig-Soret effect (or simply, Soret effect), occurs in an aqueous solution (Soret 1879; Ludwig 1856). The control of molecular flux through use of a temperature gradient is a challenging enterprise, from both the perspective of achieving molecular manipulation as well as justifying possible relevance to biological phenomena.

Given that the stable heat spot is localized at the center r = 0, and the distance from the heat spot is defined as r. The temperature distribution in space is given by T(r) and the steady temperature gradient ∇T is created due to the heat conduction in a solution. The solute flux by temperature gradient at the position r is described by J_Tp = −cD_T∇T with thermal diffusion coefficient D_T and the concentration of solute c(r). This temperature driven flux creates inhomogeneity of solute concentration in a solution, while the gradient of solute concentration is smoothened by normal diffusion D∇c with diffusion constant of solute D. Those two distinct fluxes can balance at the steady state and in turn the spatial distribution of solute becomes stable. The net flux of solute J is given by the sum of thermophoretic transport and normal diffusion as (Braun and Libchaber 2002; Duhr and Braun 2006)

$$\mathit{J}=-D\nabla c-c{D}_T\nabla T\mathrm{.}$$ 1

When the solute fluxes are balanced everywhere with J = 0, the steady state distribution c(r) is given by $c_0\exp [-S_T(T\left(r\right)-T_0\left)\right]$ where c₀ is the solute concentration at infinity ($r\to \infty$), T₀ temperature at infinity, and S_T is the coefficient defined by S_T = D_T/D known as the Soret coefficient. This thermophoretic manipulation of solutes requires only a spatially inhomogeneous heat source (Braun and Libchaber 2002). The solute contrast can be controlled by local temperature difference ΔT = T(r) − T₀. Typical value of the Soret coefficient S_T for charged DNA or proteins is 10^− 2 to 10^− 1 [1/K]. Temperature difference of few Kelvin is sufficient to build roughly 10 percentile contrast of solute concentration. Notable application of thermophoresis is the sensitive detection of the solute size. As evident from its definition, S_T has size-dependence because D_T has weak size-dependence and D is inversely proportional to the hydrodynamic radius of solute. Because of the nature of exponential function in Eq. 1, the solute contrast c(r)/c₀ is highly sensitive to the change of the solute radius or ternary structure. Hence, quantitative measurement of micro-scale thermophoresis becomes novel biochemical analysis for structural change of proteins or direct association of proteins in aqueous solutions (Wienken et al. 2010).

Before going into further detail about molecular transport under a temperature gradient, it is worth noting that for the use of typical biological polymers such as DNA, RNA, charged proteins, and sugars, their thermally induced flux occurs from hot to cold, meaning a positive D_T. The typical hard colloids of polystyrene also show depletion from hot region due to positive D_T. However, silica particles of a similar size range are accumulated in the hot region, meaning that their D_T has opposite sign (i.e., a negative D_T). Controlling the direction of thermophoresis is a long-lasting challenge. The development of techniques for the thermal manipulation of solutes and fluids lies at the interdisciplinary area between soft matter physics and biology. How can one solve this technical difficulty for further applications of themophoresis?

Cross-effect of temperature and solute concentration gradients

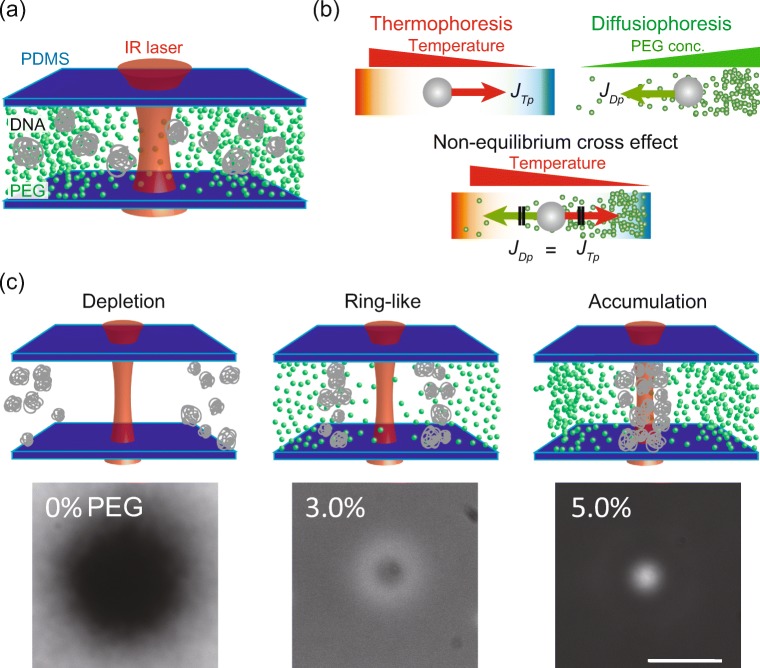
Jiang et al. (2009) have shown that one possible approach to overcome the above technical difficulty is to utilize an additional gradient of another solute. They built the local temperature gradient in a polymer solution (ternary solution), not in water (binary solution). For the solution of ternary mixtures (water, large solute, and smaller solute), a mixture of large solute such as colloidal particle $\sim$ 0.1 μ m in diameter and polyethylene glycol (PEG), $\sim$ 2 nm in diameter is made in water (Fig. 2a). A temperature gradient induces thermophoresis of two different solutes simultaneously, but the large solute of colloid is subject to both the temperature gradient and concentration gradient of PEG. This means that the large particles are driven by both thermophoresis, due to local temperature gradient and diffusiophoresis, due to the gradient of PEG solute (Fig. 2b). The diffusiophoretic velocity of the solute is given by u_Dp = (k_BT)/ηλ²∇c^p(r), where viscosity of polymer solution η, the thickness of depletion layer λ, and the concentration of polymer c^p(r), and the diffusiophoretic flux J_Dp = cu_Dp is proportional to the concentration gradient of polymer ∇c^p(r) (Jiang et al. 2009). The net flux of solute J is given by the sum of thermophoresis, diffusiophoresis, and normal diffusion as

$$\mathit{J}=-D\nabla c-c{D}_T\nabla T+c{\mathit{u}}_{Dp}\mathrm{.}$$ 2

By solving this equation at J = 0 and the boundary conditions where the concentration of DNA c(r) is equal to c₀ at infinity and similarly the concentration of PEG c^p(r) is equal to $c_0^p$ at infinity, the spatial profile of DNA at steady state c(r) is given by

$$c\left(r\right)=c_0\exp \left[-S_T\mathrm{\Delta }T\left(r\right)+(c_0^p-c^p(r\left)\right)V\right]$$ 3

S_T the Soret coefficient of DNA, and V = 2πaλ² with hydrodynamic radius of DNA a. The effect of diffusiophoretic trapping $\exp \left[\right(c_0^p-c^p\left(r\right)\left)V\right]$ can overcome thermal transport $\exp [-S_T\mathrm{\Delta }T(r\left)\right]$, either depletion (positive S_T) or accumulation (negative S_T), at larger concentration of polymer (Fig. 2c). Furthermore, the coexisted thermal and solute gradients allows one to handle many biological polymers from DNA, RNA, and proteins. This opto-thermal diffusiophoretic (OpTD) trapping also plays a role of size-dependent sorting: two different polymers of long DNA and short RNA are trapped by OpTD transport in a PEG solution, in which the larger DNA is accumulated at the hot region but smaller RNA is depleted from hot spot (Maeda et al. 2011, 2012). This size-dependent separation of DNA/RNA polymer is analogous to gel electrophoresis, indicting that light induced thermal gradient can trap, analyze, and sort biological molecules such as protein (Wienken et al. 2010; Maeda 2013). Moreover, this OpTD trapping is also applicable for living amoeba cells. The gradient of PEG concentration steers the direction of spontaneous cell motility to the center of hot spot (lower PEG concentration) (Fukuyama et al. 2015). Intriguingly, the speed of transport of cells becomes faster for non-adherent cells after depolymerization of actin cytoskeletons. This report indicates that OpTD trapping allows us to test mechanical property of cell motility in a non-invasive manner.

Fig. 2.

Opto-thermal diffusiophoretic manipulation. a Schematic illustration of experimental setup used in Maeda et al. (2011, 2012). A mixed solution of colloidal particles and polyethylene glycol (PEG) is enclosed in PDMS device. Focused infrared laser is focused in the solution and then a heat spot is built inside a microwell. b Schematic illustrations of themophoresis, diffusiophoresis and the competition of these two transport phenomena (non-equilibrium cross-effect). Colloidal particles are trapped at the position where thermophoretic flux J_Tp and diffusiophoretic flux J_Dp are balanced. c Spatial pattern of DNA solute (48.5 kbp) under temperature gradient (∇T = 5.0 kelvin in various PEG concentrations). White color indicates DNA in a solution (visualized by fluorescent intercalation dye) and heat spot is built at the center of images. (left) In the absence of PEG polymer in a solution (0% PEG), DNA is depleted from the heat spot due to thermophoresis. (middle) In the presence of few % of PEG solute, because of the competition of thermophoresis and diffusiophoresis, the spatial distribution of DNA changes from depletion pattern to ring-like localization (Maeda et al. 2011, 2012). (right) When the effect of diffusiophoresis driven by PEG concentration gradient overcomes thermophoresis, DNA accumulates at the heat spot. Scale bar, 35 μ m

Before closing this section, we raise possible relevance to the origin of life problem. In the experiment at the laboratory scale, huge temperature gradient 0.1 K μm^− 1 was built by infrared laser focusing, and such huge ∇T is rarely present in our daily life, except in the case of hydrothermal vents existing at the bottom of the sea. Hydrothermal vents where hot water stream out near volcanic active place have small pores at their surface, and the typical depth of this pore is millimeter. Not only possessing a huge thermal gradient, hydrothermal vents also possess mineral deposits able to act as chemical catalysts. These geochemical evidences imply that thermal gradient may trap and select chemical species at the hot region. This scenario is just one possibility suggested from laboratory scale experiments. However, if such physical mechanisms prove universal, then thermal transport of DNA, RNA, and proteins might be relevant to the route toward the complex polymers such as ribozyme at the early stage of life (Maeda et al. 2011; Braun et al. 2003; Kreysing et al. 2015; Mast et al. 2013).

Opto-thermal pumping of viscous fluids

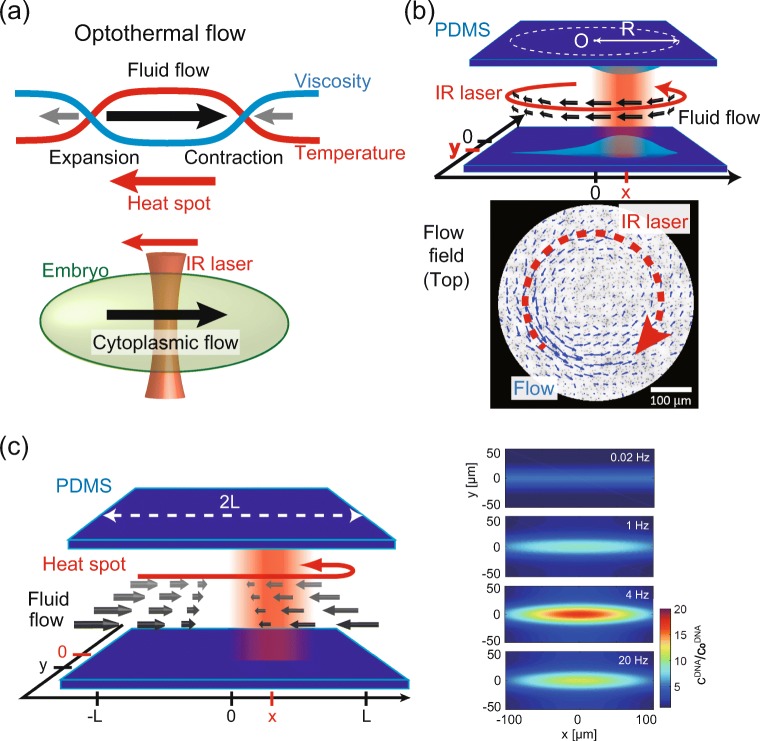
So far, we have discussed transport phenomena under static gradients of temperature and solute by stably fixed laser focusing. Stable light-induced thermal effect is advantageous for reproducible and reliable biochemical analysis in a test tube. However, another aspect of the optical setup is to move the laser spot with much freedom, e.g., sweep the laser spot back and forth at given speed. Such light scanning is found in every day life, e.g., barcode reader and projection mapping. What effects can be produced under such a moving temperature gradient? Weinert and Braun have found that a net flow of viscous fluids occurred when a heat spot moved in viscous glycerol solution (80 percentile wt/volume) by sweeping a focused infrared laser (Weinert et al. 2008; Weinert and Braun 2008) (Fig. 3a). Their finding indicates that a moving temperature gradient can be used as a non-invasive and miniaturized fluid pump at the micron-scale. This opto-thermal pumping was observed in a thin chamber (thickness ≈ 5 μ m) and a highly viscous and compressible fluid (90 percentile glycerol). Fukuyama et al. (2018) have reported that the opto-thermal pumping drives fluid streaming in a dilute polymer solution confined in a PDMS channel. This technical development allows one to pump viscous fluid by light-induced heating with a great deal of freedom in regard to experimental conditions. In addition, this opto-thermal viscous flow can trap and accumulate large DNA polymers under a heat spot oscillating in a back and forth manner (Fukuyama et al. 2018). For more biologically relevant study, Mittasch et al. (2018) have shown that the fluid streaming in a moving temperature gradient is feasible inside a zygote of C.elegans (Fig. 3a). They also provide evidence that fluid streaming driven by moving heat spot can overcome inherent cytoplasmic streaming and in turn build a concentration gradient of the PAR protein due to opto-thermal advection. Thus, a moving temperature gradient offers another type of OpTD manipulation for the control of viscous fluids.

Fig. 3.

Opto-thermal viscous flow in a moving heat spot in a polymer solution. a Schematic illustration of opto-thermal viscous flow. (top) Thermal expansion and contraction occurs in the front and rear of a moving heat spot, respectively. The temperature rise in the heat spot reduces the viscosity of the solution and in turn the net fluid flow in backward direction to the moving heat spot is enhanced (Weinert et al. 2008; Weinert and Braun 2008). (bottom) One example of this opto-thermal viscous flow to control cytoplasmic streaming in C.elegans egg (Mittasch et al. 2018). b Opto-thermal viscous flow in a 5% PEG solution. (top) Experimental setup and (bottom) fluid flow under a moving heat spot in a circular trajectory, Scale bar is 100 μ m (Fukuyama et al. 2018). The PEG solution is enclosed in a PDMS chamber with 25 μ m thickness. Because the PDMS substrate is a deformable elastomer, the local temperature increase by the laser focusing induces thermal expansion of the PDMS substrate at the top and bottom surfaces. c Opto-thermal hydrodynamic focusing in back and forth sweeping of a heat spot. (left) Schematic illustration of inward hydrodynamic flow in a 5% PEG solution along a straight line. (right) Opto-thermal hydrodynamic focusing of large solute in a PEG solution. Color map indicates the concentration of trapped large solute relative to the bulk concentration. The large solute is trapped at the center of the sweeping line by opto-thermal hydrodynamic focusing (Fukuyama et al. 2018). The speed of fluid flow shows frequency-dependence and the optimal sweeping speed exists. The number in color map indicates the frequency of periodic temperature rise

We now explain why the net flow is generated as a heat spot propagates in a viscous solution (Fig. 3b). The opto-thermal pumping of fluid flow is explained as follows: As a heat spot with finite size moves along one direction, the viscous fluid element at the front edge of the heat spot is exposed to heating and in turn its local density is decreased due to either thermal expansion of fluids or a thermally expanded boundary wall. On the other hand, the heated fluid element returns to the basal temperature after the heat spot pass through. Due to the conservation of volume, the drop of temperature leads local contraction of fluid elements and expanded volume becomes relaxed. Consequently, thermal expansion and contraction creates the source and sink of fluid flow across the moving heat spot. However, this fluid expansion and compression alone is not sufficient to generate net motion because the fluxes from the source and to the sink are balanced, as long as the viscosity profile is homogeneous.

To create the net flow, the multiplicative effect between fluid compression and viscosity reduction of a solution has to be taken into account. When viscous polymer solution is exposed to a time-varying temperature increase, the viscosity is reduced due to thermal viscous reduction and thermal depletion of polymer solute. By undergoing this viscosity reduction, the fluid velocity in the hot region is faster than that in the cold region far from hot spot. The coordination of thermal viscoelastic compression and viscosity reduction amplifies the fluid advection opposite to the movement of heat spot and in turn give rise to a net flow as seen in experiment (Fig. 3b).

Here we introduce a theoretical model of polymer solution under repeatedly moving heat spot. Coupling the effects of thermal viscoelastic expansion of boundary walls and viscosity reduction by thermal reduction of solvent and polymer depletion, we obtained flow velocity as following:

$$\mathit{u}=-{\mathit{u}}_l\frac{\mathrm{\beta }{\mathrm{\Gamma }}_{\tau }}{2}{\left(\mathrm{\Delta }T\right)}^2$$ 4

where the velocity of the heat spot u_l (Fukuyama et al. 2018). Heat-induced viscosity reduction is described by $\mathrm{\beta }=\partial ln\eta /\partial T$. Its sign is negative because viscosity η is known to decrease due to temperature rise and solute concentration reduction. Temperature dependence of thermal viscoelastic compression of solution can be written as ${\mathrm{\Gamma }}_{\tau }=\gamma (1-e^{-1/f_l\tau })$ with thermal compression rate at steady state given by $\gamma =\partial lnV/\partial T$, mechanical relaxation time τ, and frequency of periodic heat stimulus f_l (Fukuyama et al. 2018). When heat spot reaches at same position again, solution is locally squeezed by thermal expansion of walls and fluid volume decreases; thus, γ has a negative sign. As a result, the flow velocity (4) has the opposite sign of the velocity of the heat spot, meaning its direction is opposite to the sweeping of the heat spot.

When the heat spot repeatedly moves back and forth in a line, viscoelastic relaxation of wall strain drives microflows of spatially asymmetric velocities in opposite directions (Fig. 3c) (Fukuyama et al. 2018). A velocity of steady flow is derived by summing the asymmetric velocities as

$${\mathit{u}}_{hf}=-{\mathit{u}}_l\mathrm{\beta }(\gamma -{\mathrm{\Gamma }}_{\tau })sinh\left(\frac{2x}{u_l\tau }\right){\left(\mathrm{\Delta }T\right)}^2$$ 5

where the heat spot moves back and forth between x = − L and x = L. It creates a stagnation point in the middle of heat spot movement x = 0 and flow is inward as seen in ${\mathit{u}}_{hf}\propto -sinh\left(2x/u_l\tau \right)\propto -x$. Because the asymmetric relaxation effect (γ −Γ_τ) is necessary for this flow, this phenomenon is feasible as the driving force for viscoelastic fluid compression (e.g., thermal expansion of PDMS). Under this situation, the molecules or colloids are transported and accumulated at the middle point (Fig. 3c). This indicates that the thermal molecular focusing is an effective tool for the manipulation of various soft biological materials in a non-invasive manner.

Summary

We reviewed recent developments in the thermal transport of biopolymers in aqueous conditions. Micron-sized or submicron-sized objects are transported by applying either a thermal fiend or a concentration field (or both). The balance between thermophoresis and diffusiophoresis allows to control the direction and speed of molecular transport, which brings new possibilities for molecular separation with a simple mean of temperature gradient in a polymer solution (Braun and Libchaber 2002; Duhr and Braun 2006; Jiang et al. 2009; Maeda et al. 2011, 2012; Maeda 2013; Fukuyama et al. 2015). Moreover, a moving temperature gradient can pump fluids in a viscous polymer solution. This microflow is generated by changing the local compressibility and viscosity of polymer solution (Weinert et al. 2008; Fukuyama et al. 2018). This fluid pumping is non-invasive and has no limitation from electromagnetic material dependence. By taking these advantages, opto-thermal manipulation of cytoplasmic streaming is feasible in C. elegans zygote (Mittasch et al. 2018).

Based on the understanding of such transport phenomena, self-propulsive colloids known as active matter have been studied in the fields of physics and chemistry. This new class of colloidal particle spontaneously forms a concentration gradient of chemical species due to catalytic reactions on its surface and moves autonomously by using diffusiophoresis in a resulted solute gradient (Moran and Posner 2016). Controlling active matter that mimic the mechanism of molecular machines may advance the understanding of self-propulsion. Furthermore, the materials mentioned so far are limited to simple soft matters such as polymers and colloids. In recent years, there has been new developments in the transport phenomena of liquid crystal under out of equilibrium condition, from temperature gradient (Oswald and Dequidt 2008; Yoshioka and Araoka 2018) to light-induced polymerization (Hisano et al. 2017). Extensive study will further open this new field for the realization of functional devices as inspired by biological molecular motors in future.

Funding information

This work was financially supported by Grant-in-Aid for Scientific Research on Innovative Areas (JP16H00805, JP17H05234, JP18H05427 to YTM) and Grant-in-Aid for Scientific Research (B) JP17KT0025 from MEXT (to YTM).