Allosteric communication in molecular machines via information exchange: what can be learned from dynamical modeling

Abstract

Allosteric regulation is crucial for the operation of protein machines and molecular motors. A major challenge is to characterize and quantify the information exchange underlying allosteric communication between remote functional sites in a protein, and to identify the involved relevant pathways. We review applications of two topical approaches of dynamical protein modeling, a kinetic-based single-molecule stochastic model, which employs information thermodynamics to quantify allosteric interactions, and structure-based coarse-grained modeling to characterize intra-molecular couplings in terms of conformational motions and propagating mechanical strain. Both descriptions resolve the directionality of allosteric responses within a protein, emphasizing the concept of causality as the principal hallmark of protein allostery. We discuss the application of techniques from information thermodynamics to dynamic protein elastic networks and evolutionary designed model structures, and the ramifications for protein allostery.

Introduction

The activity of many proteins relies on the long-range communication between different functional regions. A specific event, often binding of a ligand, causes a time-delayed functional response at a remote site. This interaction scheme, referred to as allosteric coupling, provides a plethora of mechanisms to regulate protein operation: for example, to control the timing and speed of chemical reactions in enzymes (Lisi and Loria 2017), or to implement the chemo-mechanical coupling in molecular machines and motors (Lorimer et al. 2018).

The great availability of experimental data for proteins to date, as well as the opportunities to study conformational motions in computer simulations, has shifted the focus from traditional phenomenological models of protein allostery (Monod et al. 1965; Koshland et al. 1966) to models, which allow to study allosteric phenomena in proteins at a higher complexity level (see recent reviews (Wodak et al. 2019; Thirumalai et al. 2019; East et al. 2019)). Most nowadays studies address dynamical aspects of allostery, aiming, e.g., to quantify the transmission process underlying communication and to identify the network of critically involved amino acid residues.

In this short review, we present a summary of our recent contributions in which dynamical modeling was employed to characterize the exchange of information in allosteric systems in very different ways. The first approach was based on the construction and analysis of a single-molecule stochastic model of tryptophan synthase, an enzyme often referred to as an allosteric molecular factory. In this enzyme, the complex chemical reaction course could be reproduced by considering the dynamics of transitions on a Markov network of chemical states, allowing furthermore to probe the role of allosteric regulation on the operation mechanism (Loutchko et al. 2016, 2017). On the other side, the second approach resolves the conformational motions underlying the transmission of information between remote sites. The evolutionary design of elastic network structures which, inspired by protein allostery, encode optimized long-range communication has proposed a new class of simple model systems that allow to establish a link between functionality and the emergence of the underlying physical properties (Flechsig 2017; Flechsig and Togashi 2018).

We discuss the advantages of the two approaches. Using the phenomenological Markov network model, the link between allosteric interactions to flows of mutual information between the catalytic sites of the enzyme tryptophan synthase and the respective thermodynamics and energetics is elucidated. The structurally resolved elastic network models provide, through their evolutionary design, the possibility to identify general principles governing allosteric communication. As a natural union of the presented work, we outline how the concepts of information thermodynamics can be applied in new ways to dynamic protein elastic networks and their evolutionary designed model systems, and discuss possible ramifications.

Phenomenological kinetic models

Phenomenological models of protein dynamics provide a highly coarse-grained description of the protein kinetics. Thereby, the dynamics is modeled by transitions on the state space, which is given by metastable conformational and chemical states of the protein. The choice of the state space is made such that the transitions are memoryless and the respective rate constants are then deduced from experimental data. Using the channeling enzyme tryptophan synthase as an example, we illustrate how to extract quantitative information on allosteric communication from such phenomenological kinetic models.

The tryptophan synthase enzyme

The enzyme tryptophan synthase catalyzes the last two steps of the tryptophan biosynthesis. It converts the two substrates serine (ser) and indole glycerol phosphate (IGP) into tryptophan (trp) and the byproduct glycerol-3-phosphate (G3P). Tryptophan synthase consists of two subunits, termed α and β. Each subunit has its own catalytic site and the two sites are linked through an intra-molecular tunnel. The α-site catalyzes the cleavage of IGP into G3P and the intermediate indole. Indole is then channeled through the tunnel to the β-site, where it reacts with serine to form tryptophan. The prevention of indole release into the cytoplasm and the reaction kinetics at the catalytic sites are mediated trough a complex pattern of allosteric interactions.

Tryptophan synthase is known to adopt two different conformational states: the catalytically inactive state with unrestricted access to the catalytic sites (“open conformation”) and the state with enhanced catalytic activity and no exchange of matter between the catalytic sites and the cytoplasm (“closed conformation”). The conformation adopted by the enzyme is dictated by its chemical state (Ngo et al. 2007; Blumenstein et al. 2007). The switching between the two conformational states is mediated by the COMM subdomain at the β-subunit and the α L2 and α L6 loops at the α-subunit, which also serve as gates to the catalytic centers (Raboni et al. 2005).

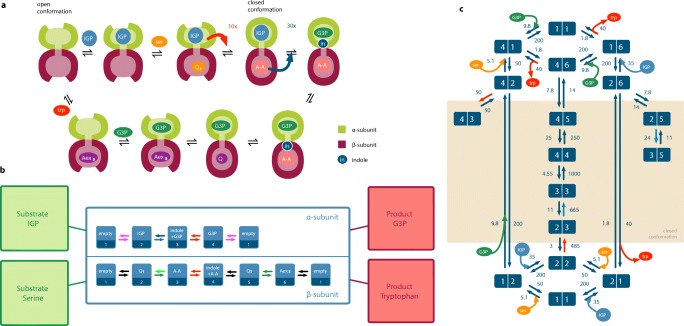
Figure 1a illustrates a catalytic cycle including allosteric regulations and conformational changes. The long-lived chemical states at the α- and β-sites as well as all known allosteric cross-regulations are presented in Fig. 1b. In particular, the rate of indole cleavage in the α-site is enhanced by a factor of 27.7 if the β-site is in the state A-A. The formation of A-A in the β-site is enhanced by a factor of 9.7 if the α-site has IGP bound. This creates an activation cascade and leads to a tight control of the catalytic processes occurring right before indole channeling.

Fig. 1.

Operations of the enzyme tryptophan synthase. a Schematic operation of tryptophan synthase. The catalytic cycle begins with the enzyme in the state where both sites are empty, and the catalytic subunits are accessible. The substrate IGP binds to the α-subunit and serine to the β-subunit, where it is quickly converted to the serine quinoline intermediate (Q₁). IGP activates the formation of the α-aminoacrylate (A-A) and the enzyme adopts the closed conformation. In the closed state (IGP,A-A), A-A activates the cleavage of IGP to produce G3P and indole. Indole is then channeled to the β-site where it reacts with A-A to give the tryptophan quinoline intermediate (Q₃), which is converted to tryptophan (Aex₂ is the external aldimine of tryptophan in the β-subunit). In the state (G3P,Aex₂), the enzyme opens and the products tryptophan and G3P are released. Thus, the enzyme returns to the initial conformation and is ready to start the next cycle. b Allosteric cross-regulation and channeling in tryptophan synthase. Magenta: transitions blocked in the states A-A, A-A + indole and Q₃ of the β-site. Green (light and dark): blocked in the state empty of the α-site. Light green: enhanced by a factor of 9.7 in the state IGP of the α-site. Blue (light and dark): blocked in the states empty, Q₁, Aex₂ of the β-site. Light blue: enhanced by a factor of 27.7 in the state A-A of the β-site. Red: channeling instantaneously changes the states of both sites. Numbers below the chemical notations will be used in the formulation of the kinetic model for the sake of clarity. c The kinetic Markov network of tryptophan synthase with numerical values of all transition rates, given as labels on the respective arrow, under physiological substrate and product concentrations in units of s^− 1. The states (a,b) are given by numerical values as introduced in b. The toned box corresponds to closed conformational states. All figures reprinted from Loutchko et al. (2017), with the permission of AIP Publishing

Several reviews devoted to tryptophan synthase are available (Barends et al. 2008; Dunn 2012). A single-enzyme kinetic model was constructed in Loutchko et al. (2016) and an information theoretic analysis was conducted in Loutchko et al. (2017).

A single-molecule kinetic model

The kinetics of a single molecule of tryptophan synthase can be modeled as a Markovian random walk on the sets of its internal states. Each internal state is given by a pair (a,b) with a = 1,...,4 and b = 1,...,6 representing a possible combination of the individual states a and b at the α- and the β-subunits (cf. Fig. 1b for the corresponding chemical states). The Markov network is shown in Fig. 1c. In Loutchko et al. (2016), the transition rates between the states have all been extracted from experimental data and thus the model does not require any free parameters.

Within the model, the dynamics of a single molecule of tryptophan synthase is governed by the master equation

$$\frac{d}{dt}p(a,b;t)=\sum _{a^{\prime },b^{\prime }}\left[w_{a,a^{\prime }}^{b,b^{\prime }}p\right(a^{\prime },b^{\prime };t)-w_{a^{\prime },a}^{b^{\prime },b}p(a,b;t\left)\right],$$ 1

which describes the time evolution of the probability p(a,b;t) to find the enzyme in the state (a,b) at time t (for the sake of clarity, the time dependence of p(a,b;t) will not be explicitly written out in the following). Thereby, $w_{a,a^{\prime }}^{b,b^{\prime }}$ denotes the transition rate from a state $(a^{\prime },b^{\prime })$ to the state (a,b) and the sum is taken over all states $a^{\prime }$ and $b^{\prime }$. The probability fluxes are defined as $J_{a,a^{\prime }}^{b,b^{\prime }}=w_{a,a^{\prime }}^{b,b^{\prime }}p(a^{\prime },b^{\prime })-w_{a^{\prime },a}^{b^{\prime },b}p(a,b)$. The master equation 1 is linear and can be solved explicitly for any initial probability distribution. Explicit realizations of the random walk on the Markov network obeying Eq. 1 can be generated with the Gillespie algorithm (Gillespie 1977).

The entropy of the system is given by $S=-{\sum }_{a,b}p(a,b)lnp(a,b)$ (in units of k_B and time dependence not explicitly written). Its time derivative can be split as dS/dt = σ − h, where $\sigma ={\sum }_{a>a^{\prime },b>b^{\prime }}{J}_{a,a^{\prime }}^{b,b^{\prime }}ln\left(w_{a,a^{\prime }}^{b,b^{\prime }}p(a^{\prime },b^{\prime })/w_{a^{\prime },a}^{b^{\prime },b}p(a,b)\right)$ is the entropy production and $h={\sum }_{a>a^{\prime },b>b^{\prime }}{J}_{a,a^{\prime }}^{b,b^{\prime }}ln\left(w_{a,a^{\prime }}^{b,b^{\prime }}/w_{a^{\prime },a}^{b^{\prime },b}\right)$ is the entropy flow into the environment (Seifert 2012). σ quantifies the irreversibility of the enzyme operation and h quantifies the heat exchanged with the environment.

Quantification of allostery using information thermodynamics

In Loutchko et al. (2016), for the first time, the intra-molecular correlations in tryptophan synthase have been numerically quantified. The Pearson correlation coefficients were used to detect correlations between the random variables given by the marginal probability distributions $p_{\alpha }\left(a\right)={\sum }_{b}p(a,b)$ and $p_{\mathrm{\beta }}\left(b\right)={\sum }_{a}p(a,b)$. Indeed, strong correlations were found for the states (2,3) and (3,3) leading up to indole channeling. The states corresponding to substrate binding and release in the open conformation are weakly correlated or even anticorrelated. This analysis successfully quantifies correlations between the two catalytic centers, yet the symmetry of the Pearson correlation coefficient does not allow to take into account causality or directed flows of information between the sites. The latter was achieved in Loutchko et al. (2017) using information thermodynamics.

The mutual information I(α,β) between the two tryprophan synthase subunits is defined as

$$I(\alpha ,\mathrm{\beta })=S\left(\alpha \right)-S\left(\alpha \right|\mathrm{\beta })=S(\mathrm{\beta })-S(\mathrm{\beta }\left|\alpha \right),$$ 2

where $S\left(\alpha \right)=-{\sum }_a{p}_{\alpha }\left(a\right)ln{p}_{\alpha }\left(a\right)$ is the marginal Shannon entropy of the α-system and $S\left(\alpha \right|\mathrm{\beta })=-{\sum }_b{p}_{\mathrm{\beta }}(b\left){\sum }_{a}p\right(a\left|b\right)lnp\left(a\right|b)$ is the respective conditional entropy; (p(a|b) is the conditional probability for b provided a; the entropies S(β) and S(β|α) are defined analogously). The mutual information can also be written as $I(\alpha ,\mathrm{\beta })={\sum }_{a,b}p(a,b)ln\left(p(a,b)/\left(p_{\alpha }\right(a\left)p_{\mathrm{\beta }}\right(b\left)\right)\right)$. It is symmetric in α and β and, similar to the Pearson correlation coefficient, quantifies the correlations between the α- and the β-subunits.

Information transfer in bipartite networks

If the master equation 1 does not contain cross-transitions, i.e., if the rate $w_{a,a^{\prime }}^{b,b^{\prime }}=0$ whenever $a\ne a^{\prime }$ and $b\ne b^{\prime }$, then the Markov network is called bipartite. Bipartite networks allow to relate the mutual information I(α,β) and its rate dI(α,β)/dt to the free energy and entropy production at the respective catalytic sites (Horowitz and Esposito 2014; Parrondo et al. 2015). Assume that, for a bipartite network, the rates $w_{a,a}^{b,b^{\prime }}$ only depend on b and $b^{\prime }$, but not on a. Then, the dynamics at the β-site is independent of the α-site. However, the α-site measures the β-site, i.e., the conditional probability p(b|a) is not equal to marginal probability p_β(b) for the states b. Thus, the knowledge of the current state of the α-site provides information on the current state of the β-site. For an ideal measurement device, the conditional probabilities p(b|a) would either be equal to 1 or 0 and thus one could unambiguously infer the current β-state from the α-state (however, due to thermal fluctuations, an ideal nanoscale measurement device does not exist). The measurement changes the free energy of the β-site from E(β) − TS(β) to E(β) − TS(β|α), i.e., by an amount of TI(α,β) (whereby E(β) denotes the internal energy of the β-site). The created correlations can be used to extract additional work from the measured system. However, resetting the measuring system, i.e., removing the correlations at the α-site that were created due to the coupling to the β-site, requires this exact amount of work (Parrondo et al. 2015). This provides an interpretation of protein allostery as an instance of Landauer’s principle (Landauer 1961).

If both subunits measure each other simultaneously, i.e., the rates $w_{a,a}^{b,b^{\prime }}$ (resp. $w_{a,a^{\prime }}^{b,b}$) depend on a (resp. b), the above interpretation still holds true as follows. The rate of mutual information dI(α,β)/dt in bipartite systems can be split as

$$\frac{d}{dt}I(\alpha ,\mathrm{\beta })=I^{\alpha }+I^{\mathrm{\beta }},$$ 3

where $I^{\alpha }={\sum }_{a>a^{\prime },b}{J}_{a,a^{\prime }}^{b,b}ln\left(p\left(b\right|a)/p(b\left|a^{\prime }\right)\right)$ and the analogous formula holds for I^β (Horowitz and Esposito 2014). Each transition between an α-state $a^{\prime }$ to a of the α-subunit contributes to I^α a term ${\sum }_b{J}_{a,a^{\prime }}^{b,b}ln\left(p\left(b\right|a)/p(b\left|a^{\prime }\right)\right)$ (note that it is symmetrical under exchange of a and $a^{\prime }$). If this term is positive, then the α-site acts as a measurement device for the β-site and the β-site can thus potentially perform additional work due to the coupling. If the term is negative, then information about the β-site at the α-site is erased during the transition between $a^{\prime }$ to a. Free energy from the β-site is thereby extracted and thus the β-site can potentially perform less work.

Application to tryptophan synthase

Using the above information theoretic framework, the allosteric coupling in tryptophan synthase has been analyzed (Loutchko et al. 2017). The Markov network model is bipartite except for the transition from (indole+G3P,A-A) to (G3P,indole+A-A), which corresponds to indole channeling. The theory for bipartite systems has been extended in Loutchko et al. (2017) to encompass such cross-transitions. Thereby, the splitting in Eq. 3 generalizes to dI(α,β)/dt = I^α + I^β + I^cross, where $I^{\text{cross}}=J_{4,3}^{4,3}ln\left(\left(p\right(3,3)/p(4,4)\right)$ is just the contribution to the change of Shannon entropy of the cross-transition. The summands in I^α and I^β retain their interpretation as discussed in the previous paragraph.

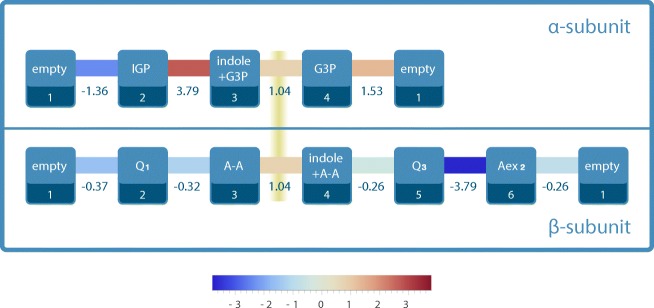
Figure 2 shows I^cross and the contributions to I^α and I^β of the individual transitions in units of bits per second. The numerical values were determined, using the above formalism, from the experimental kinetic data for the enzyme operating under physiological substrate and product concentrations, cf. Loutchko et al. (2017). It is remarkable that all transitions at the β-site have negative contributions to I^β. This means that the β-site is constantly being measured by the α-site and thus has the potential to perform a surplus of work resulting from the allosteric coupling. Equivalently, the information present in the β-site about the α-site is constantly being erased, which requires the extraction of work from the α-site. The analysis also identifies the α-transition from IGP to indole+G3P as the transition most strongly involved in the measurement of the β-site. Finally, the positivity of I^cross shows that the indole channeling leads to an information flow into both the α- and β-sites.

Fig. 2.

Information flows generated through the mutual measurement of the α- and β-sites in tryptophan synthase in bits per seconds. The figure shows the numerical values of ${\sum }_b{J}_{a,a^{\prime }}^{b,b}ln\left(p\left(b\right|a)/p(b\left|a^{\prime }\right)\right)$ for the α-site and of ${\sum }_a{J}_{a,a}^{b,b^{\prime }}ln\left(p\left(a\right|b)/p(a\left|b^{\prime }\right)\right)$ for the β-site. The cross term I^cross is shown on the yellow fuzzy line. Reprinted from Loutchko et al. (2017), with the permission of AIP Publishing

The schematic operation presented in Fig. 1a is symmetric in the allosteric interactions between α- and β-sites in the sense that the allosteric rate enhancement proceeds in both directions. However, the above analysis reveals, through the information theoretic structure of tryptophan synthase, a strong asymmetry in the enzyme operation. The information flows exclusively to the β-site, whereby the α-site acts as a measurement device. In other words, the catalytic action at the β-site is facilitated through the coupling to the α-site. This observation is consistent with the fact that the operation at the β-site consists of 9 elementary reaction steps and is thus substantially more complex than the cleavage reaction at the α-site.

Structurally resolved models

Allosteric regulation in a protein has an intuitive mechanical interpretation of propagating conformational motions. They originate from binding of a ligand to the allosteric pocket where specific interactions cause local deformations. Such deformations then propagate through the protein and eventually generate changes in the conformation of the remote site. It should be expected that functional intra-molecular communication in an allosteric protein, and the underlying physical properties, must have emerged during biological evolution, with the structure encoding the required information (see the recent review (Zhang et al. 2020)).

This information can be retrieved from structurally resolved modeling of protein dynamics. Functional collective conformational motions in protein machines and motors are typically too slow to be followed by atomistic molecular dynamics simulations. Hence, structure-based coarse-grained models are often employed to study allosteric communication in proteins with feasible computational expense (Takada et al. 2015; Pak and Voth 2018).

In particular, elastic network models (ENMs) (Tirion 1996; Bahar et al. 1997) which view a protein as a set of beads (typically amino acid residues) connected by elastic springs (effective interactions) have become very popular due to their simplicity and the efficient numerical computation of normal modes to predict fluctuations around the equilibrium conformation.

Protein elastic networks

The most common ENMs are anisotropic network models (Doruker et al. 2000; Atilgan et al. 2001) which resolve residue motions in all spatial directions. The potential energy of a network with N beads is

$$E=\frac{1}{2}\kappa \sum _{i,j>i}^N{A}_{ij}\cdot {\left(\right|{\mathbf{\text{R}}}_i-{\mathbf{\text{R}}}_j|-|{\mathbf{\text{R}}}_i^{\left(0\right)}-{\mathbf{\text{R}}}_j^{\left(0\right)}\left|\right)}^2\mathrm{.}$$ 4

Here, R_i is the position of bead i and ${\mathbf{\text{R}}}_i^{\left(0\right)}$ is the corresponding equilibrium value; κ is the same stiffness constant of all springs. The network adjacency matrix has elements A_ij = 1, if the distance between beads i and j in the equilibrium conformation $|{\mathbf{\text{R}}}_i^{\left(0\right)}-{\mathbf{\text{R}}}_j^{\left(0\right)}|$ is smaller than a given cutoff length, and A_ij = 0, otherwise. For motions near the equilibrium, energy contributions which are quadratic in the displacement of bead positions from equilibrium are dominant and the potential energy can be approximated as $U=\frac{1}{2}\mathrm{\Delta }{\mathbf{\text{R}}}^T\mathcal{H}\mathrm{\Delta }\mathbf{\text{R}}$, where displacements are collected in the 3N dimensional vector ΔR and $\mathcal{H}$ is the Hessian matrix with elements ${\mathcal{H}}_{kl}={\partial }^{2}E/\partial R_k\partial R_l{\left(\right|}_{\mathbf{\text{R}}={\mathbf{\text{R}}}^{\left(0\right)}}$. Using the eigenvalue decomposition, the Hessian matrix can be expressed in terms of the normal modes u_k which contribute to near-equilibrium fluctuations of network residues, i.e., $\mathcal{H}={\sum }_{{\lambda }_k\ne 0}{\lambda }_k{\mathbf{\text{u}}}_k{\mathbf{\text{u}}}_k^T$. Eigenvalues λ_k determine the mode frequencies.

Normal modes, correlations, and allostery

In a protein elastic network, allosteric coupling can be investigated by quantifying how motions of different residues are correlated. Computing the cross correlations of fluctuations in bead positions as the Boltzmann average over all possible configurations gives $<\mathrm{\Delta }{\mathbf{\text{R}}}_i\cdot \mathrm{\Delta }{\mathbf{\text{R}}}_j>=k_{B}T{\left[{\mathcal{H}}^{-1}\right]}_{ij}$, and hence

$$<\mathrm{\Delta }{\mathbf{\text{R}}}_i\cdot \mathrm{\Delta }{\mathbf{\text{R}}}_j>=k_{B}T\sum _{{\lambda }_k\ne 0}{\lambda }_k^{-1}{\left[{\mathbf{\text{u}}}_k{\mathbf{\text{u}}}_k^T\right]}_{ij}\mathrm{.}$$ 5

The slowest normal modes and their shapes are therefore the dominant contributions to correlations and should characterize important aspects of allosteric effects. It has been shown in a plethora of studies that ligand-induced collective conformational motions in enzymes and protein machines can be described well by a single or a few soft modes of their elastic networks (e.g., Tama and Sanejouand 2001; Zheng and Doniach 2003; Bahar et al. 2007, 2010).

The existence of soft modes in protein machines, often separated by a gap in the mode spectrum, has important functional implications. The dimensionality of conformational dynamics is effectively reduced, allowing proteins to robustly perform collective slow motions which enslave all faster conformational changes (Flechsig and Mikhailov 2019). Since slow modes reproduce well ligand-induced motions, their properties may already define the relevant communication pathways which allosterically couple different functional sites within a protein structure.

The automatized computation of elastic network normal modes and cross correlations is implemented in modeling packages (e.g., Bakan et al. 2011), allowing to efficiently search for possible allosteric couplings in proteins.

However, it is important to note that correlation functions of elastic networks with harmonic interactions are symmetric with respect to the interchange between sites i and j. This implies that in principle, no information about the directionality of allosteric responses can be inferred from analyzing them and the elastic network normal modes.

Nonetheless, by considering perturbations, directional effects can also be investigated within the linear response approximation of elastic network dynamics (Zheng and Brooks 2005; Ming and Wall 2005, 2006). The effect of specific local perturbations, mimicking, e.g., interactions with a ligand, on global conformational changes can thus be investigated and normal modes of the perturbed network can be compared with those of the free network.

There is an obvious drawback of elastic network normal modes. Normal mode analysis corresponds to the linear approximation of conformational motions around the equilibrium state of the network, considering only harmonic contributions to the elastic energy. This results in forces exerted by the springs to always act along their equilibrium orientations. Network motions of larger amplitude generally involve considerable displacements in bead positions from equilibrium and changes in the orientation of springs. In that case, anharmonicities appear and the network dynamics becomes different from NMA predictions (see our recent review (Togashi and Flechsig 2018)).

Previously, anharmonicities in elastic networks of protein machines have been addressed when attempting to improve predictions of large-amplitude conformational motions along the transition between two functional states (Miyashita et al. 2003; Maragakis and Karplus 2005). They arise from taking into account plastic deformations inside the protein network, which is not usually implemented in the standard description.

Dynamic elastic networks and causality of allostery

Generally, a protein elastic network is a nonlinear mechanical system since its energy (4) is a complex non-harmonic function of the spatial coordinates (Togashi and Mikhailov 2007; Togashi and Flechsig 2018; Flechsig and Mikhailov 2019). It has been shown in Togashi and Mikhailov (2007) that the behavior of protein elastic networks beyond the linear response regime, taking into account the full nonlinear elastic dynamics, can be explored by considering them as dynamical systems, with the time evolution described by overdamped Langevin equations for the motions of residues within the networks. The dynamical network equations are

$$\gamma \frac{d{\mathbf{\text{R}}}_i}{dt}=-\frac{\partial E}{\partial {\mathbf{\text{R}}}_i}+{\mathbf{\text{f}}}_i\left(t\right)+{\mathbf{\text{F}}}_i^{\text{ext}}\left(t\right),$$ 6

where γ is the common friction coefficient of network beads, ${\mathbf{\text{F}}}_i^{\text{ext}}$ is an external force which can be applied to bead i, and f_i is a random force representing thermal noise with correlations $<f_{\alpha ,i}\left(t\right)f_{\mathrm{\beta },j}\left(t^{\prime }\right)>=(2k_{B}T/\gamma ){\delta }_{\alpha \mathrm{\beta }}{\delta }_{ij}\delta (t-t^{\prime })$, where α,β indicate x,y,z components. Trajectories R_i(t) of residue motions are obtained by numerically integrating the set of equations.

Within this description, protein conformational dynamics is resolved as relaxation processes of the corresponding elastic network. Employing it, valuable insights into the functional activity of protein machines and motors can be obtained (see our recent reviews (Togashi and Flechsig 2018; Flechsig and Mikhailov 2019)). In dynamical simulations, the conformational responses of a protein to the application of external forces to individual residues (or groups of them) in specific parts of the structure can be systematically investigated. A sensitivity map of a protein can thus be obtained (e.g., Düttmann et al. 2012), allowing to quantify allosteric couplings between functionally important regions.

Interactions with ligands can be furthermore modeled and the resulting conformational motions monitored and analyzed (Flechsig and Mikhailov 2010; Flechsig et al. 2011; Flechsig 2016). In this way, it becomes possible to emulate binding (or the dissociation) of a ligand, which in the majority of cases is the event causing allosteric regulation in proteins. In the next section a demonstration will be provided.

An approach to study dynamical aspects of protein allostery in coarse-grained molecular dynamics simulations with feasible computational burden is therefore available; dynamical elastic network simulations can be typically carried out on conventional laptop computers. It allows to quantify allosteric effects and information exchange underlying intra-molecular communication based on propagating conformational motions.

Application to the myosin V motor

A demonstration of the applicability of the dynamic elastic network model to study allosteric communication was provided by studying the well-known rigor-to-postrigor transition in the motor domain of myosin V (myoV) (Flechsig 2017). In myoV, the nucleotide-binding pocket, where ATP-related chemical events take place, and the region where the motor interacts with actin and mechanical forces are exerted on the filament are spatially separated (Fig. 3d). Allosteric communication between the two sites is essential for the chemo-mechanical coupling and the motors’ functional activity: Binding of ATP to the pocket results in opening of the actin cleft, enabling the motor head to dissociate from the filament and eventually step along the filament. Employing the elastic network description, the conformational dynamics underlying this allosteric coupling were investigated. In the elastic network constructed for the nucleotide-free structure of myoV, binding of the ATP ligand was emulated by applying precise time-dependent external forces only locally to residues of the binding pocket. The effect of such forces was to dynamically steer the pocket to the experimentally known conformation bound with an ATP analog. By numerically integrating the equations of motion, the conformational dynamics subsequent to ligand binding was obtained and the propagation of motions from the nucleotide-binding pocket to the remote actin cleft was monitored. The model could remarkably well reproduce the expected opening of the actin cleft in response to binding of the ATP ligand. A time-resolved characterization of allosteric communication was provided in terms of propagating mechanical strain. Binding of ATP generated significant strain localized in the pocket, which then propagated through the structure towards the actin site where opening motions are activated (Fig. 3d). A main observation was that strain propagation proceeded through well-defined pathways which primarily coincided with structural motifs of conserved residues that are critical for chemo-mechanical coupling (Fig. 3d).

Fig. 3.

Allostery from structure-based modeling. a Evolutionary design of allosteric elastic networks. Starting from a random network (left) evolution gradually changed the network architecture by selecting favorable mutations, until a structure with optimized long-range communication between the ligand-binding pocket and the response site (blue beads) had emerged (right). b Allosteric communication in a designed network was characterized by the propagation of elastic strain. Upon ligand binding to the left pocket, contracting its size, neighboring links become strained first (left). Then, deformations propagate through the interface region and reach the right domain (middle), where eventually links around the response site are loaded with strain and the allosteric pocket opening is generated (right). Bond thickness indicates the strain magnitude and colors distinguish between stretched (blue) and compressed (red) links. c Communication pathways in two designed networks, constructed from the highly strained links. The structure on the left encoded symmetric allostery response (response site closed), while the other implemented asymmetric response (response site opened). d Allosteric communication during functional transition in the myosin V motor domain. By dynamically steering the ATP-binding site conformation from the free to the bound state, the allosterically regulated opening of the actin cleft was reproduced in elastic network simulations (left). The identified communication pathways involved during strain propagation (right) correspond to residue motifs important for chemo-mechanical coupling. All figures are adapted from the original publication (Flechsig 2017)

Evolutionary design of allosteric elastic networks

Protein elastic networks have been extensively studied to elucidate functional aspects of allostery. Can artificial elastic networks with protein-inspired allosteric responses be designed? What properties would such designed structures have? This topic has recently attracted a lot of attention and the idea has been put into practice using different approaches (Rocks et al. 2017; Yan et al. 2017; Flechsig 2017; Dutta et al. 2018).

We have developed an evolution model which allowed us to design special elastic networks whose structures encode optimized long-range communication between remote sites (Flechsig 2017; Flechsig and Togashi 2018). It was based on the dynamic elastic network description and the aim of optimization was that ligand binding at one site, changing its shape, should have produced pronounced conformational motions in a remote pocket. Through sequences of structural mutations, selecting only those which were favorable for the allosteric response, the networks gradually changed their architecture towards a structure that eventually performed best (Fig. 3a).

In the designed networks, allosteric communication results from the propagation of elastic strain from the ligand-binding site to the remote second site. Remarkably, only a minority of all network links get significantly strained during the transmission process (Fig. 3b), and the highly strained links form simple pathways connecting both sites (Fig. 3c). Hence, information exchange underlying allostery in the designed networks can be characterized in terms of strain flow which is channeled into the low-dimensional pathways. It is truly remarkable that the in-silico designed artificial structures, with the properties having emerged through a simple evolution scheme, have similar allosteric properties as those of biological molecular machines. As it turns out, the emergence of functionality in the designed networks during evolution is accompanied by the dimensionality reduction of conformational motions, manifested by the appearance of a single normal mode which sufficiently well describes the allosteric dynamics. Those observations were made in even simpler models of mechanical networks (Dutta et al. 2018; Yan et al. 2018).

The designed networks can be viewed as structurally resolved model systems of allostery in protein machines, resembling in their operation, e.g., the allosteric communication described in the previous section for myosin V. They can in principle be employed to refine the operation mechanism of a model molecular motor that was previously constructed (Sarkar et al. 2016) but was not sophisticated enough to include effects of allosteric control.

Summary and discussion

The two presented approaches provide different concepts for the modeling of allosteric communication in protein machines and the characterization of the underlying exchange of information between the involved functional regions.

Allosteric interactions between remote sites within the kinetic-based approach are quantified in terms of information transfer obtained from modeling the protein as an almost bipartite Markov network of chemical and conformational states. The use of information theory allows to quantify causality aspects of allosteric transitions in terms of information flows between remote sites and to assign magnitudes and directions of transferred information for each individual transition. Moreover, using information thermodynamics, the allostery in tryptophan synthase from the viewpoint of Landauer’s principle and Maxwell’s demon could be analyzed as the flows of mutual information are connected to changes of free energies and entropy production at the catalytic sites.

In contrast, structurally resolved elastic networks describe allosteric interactions in the (coarse-grained) space of conformational changes. Communication networks and pathways, which physically connect different sites, can be identified from dynamically probing the conformational space and analyzing flows of mechanical strain. Dynamic elastic network simulations play the role of coarse-grained molecular dynamics computation. Allosteric effects in proteins have been extensively studied from analyzing trajectories of atomistic molecular dynamics simulations. Several studies which employ concepts of information theory to quantify intra-molecular communication are available (Lange and Grubmüller 2006; LeVine and Weinstein 2014; Bowerman and Wereszczynski 2016).

Most protein machines perform slow conformational motions. The mean cycle time of the studied tryptophan synthase under physiological conditions for example is 0.75 s, which is more than six orders of magnitude longer than the timescales typically accessible in atomistic simulations.

Dynamic elastic networks provide the models of intermediate complexity, bridging the gap between highly coarse-grained phenomenological kinetic models and full-detailed atomistic descriptions. Their representation of protein dynamics presents the opportunity to investigate important aspects of causality behind allosteric effects in protein machines and to employ the methods of information theory to quantify them. Concepts of entropy transfer have already been recently applied to the harmonic dynamics of Gaussian network models to determine allosteric communication in example proteins (Hacisuleyman and Erman 2017a, b). Yet, the link to thermodynamics with the respective interpretations and consequences as presented here for the kinetic-based approach remains unexplored.

Of topical interest are evolutionary designed elastic networks which can reproduce the same allosteric properties found in real protein machines. They represent a platform to study the physical properties, which emerge during optimization of allosteric communication. Possible topics include the identification of structural features that lead to the maximization of information flows, the investigation of the connection between the information flows and the magnitude of structural changes, its proper thermodynamic and energetic interpretation, and the investigation of evolutionary designed elastic networks that act as Maxwell’s demons. This future research is important to further understand generic design principles of allosteric activity in protein machines.

Funding information

H.F. acknowledges support by the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan, through the World Premier International Research Center (WPI) Inititate and by JSPS Kakenhi grant no. JP16K05518. D.L. acknowledges financial support from MEXT Kakenhi Grant No. 15H05876.

Compliance with ethical standards

Conflict of interests

The authors declare that they have no conflict of interest.