Abstract
Here we review a new method for calculating a hydration free energy (HFE) of a solute and discuss its physical implication for biomolecular functions in aqueous environments. The solute hydration is decomposed into processes 1 and 2. A cavity matching the geometric characteristics of the solute at the atomic level is created in process 1. Solute-water van der Waals and electrostatic interaction potentials are incorporated in process 2. The angle-dependent integral equation theory combined with our morphometric approach is applied to process 1, and the three-dimensional reference interaction site model theory is employed for process 2. Molecular models are adopted for water. The new method is characterized by the following. Solutes with various sizes including proteins can be treated in the same manner. It is almost as accurate as the molecular dynamics simulation despite its far smaller computational burden. It enables us to handle a solute possessing a significantly large total charge without difficulty. The HFE can be decomposed into a variety of physically insightful, energetic, and entropic components. It is best suited to the elucidation of mechanisms of protein folding, pressure and cold denaturation of a protein, and different types of molecular recognition.
Keywords: Hydration free energy, Hydration energy, Hydration entropy, Biomolecule, Protein folding, Molecular recognition, Integral equation theory, Morphometric approach
Introduction
Hydration plays crucially important roles in a variety of physicochemical processes that take place in aqueous environments such as the dissolution of solutes, micelle formation, receptor-ligand binding, different types of molecular recognition, protein folding and denaturation, and association of proteins (Ball 2008). In particular, the hydration free energy (HFE) of a solute is one of the most essential quantities in analyses on these processes (Ratkova et al. 2015). The development of a reliable method for calculating the HFE is a central issue in modern science. Advantageous properties of any such developed method involve the following:
Calculation result is sufficiently accurate.
Calculation is computationally efficient/fast even for a large, polyatomic solute like a protein.
Method is versatile. For example, solutes with a wide range of sizes can be handled in the same manner. The calculation should not be overly dependent on the solute size.
Parameter training nor complex parameterization schemes should not be required.
Solute possessing significant total charge can be handled without difficulty.
The HFE can be decomposed into a variety of energetic and entropic components which are physically insightful. Often these components are required for elucidating the mechanism of a physicochemical process.
In principle, the free energy perturbation (FEP) (Jorgensen and Ravimohan 1985) and thermodynamic integration (TI) (Kirkwood 1935) methods using the molecular dynamics (MD) simulations (hereafter, these are referred to as the “FEP- and TI-MD methods”) can yield sufficiently accurate values of the HFE (Shirts et al. 2003). In these approaches, a number of intermediate states of solute insertion, which connects pure water and the solution system of interest, must be treated, necessitating a heavy computational burden. As a result these approaches are essentially not applicable to large solutes. Moreover, when a solute possessing a significantly large total charge is treated, the HFE obtained is strongly dependent on the unit cell size, and its value must be corrected through arduous routes (Ekimoto et al. 2015). In general it is difficult to decompose the HFE into its energetic and entropic components. Thus, the FEP- and TI-MD methods do not satisfy items (2), (5), and (6).
Matubayasi and Nakahara (2000, 2002, 2003a, b) developed a novel method based on solution theory in energy representation (ER) (hereafter, this is referred to as the “ER method”). In the ER method, the HFE is calculated using an approximate functional of the distribution function of solute-water interaction energy, which is obtained by only two MD simulations for pure water and for the solution system of interest, respectively. Hence, no intermediate states of solute insertion are to be considered. It was demonstrated that the ER method gives the HFE with high accuracy for a solute with zero total charge (Karino et al. 2010; Karino and Matubayasi 2013). However, it is not completely free from drawbacks. The computational burden is still not moderate. Moreover, for a solute whose total charge is significantly large, the effect of variation in the size of the unit cell is more cumbersome than for FEP-MD and TI-MD methods. It is important to understand that this problem has not been solved yet (Tokunaga et al. 2018). In summary, the ER method is not reliable in terms of item (5).
The integral equation theories (IETs) based on statistical mechanics (Hansen and McDonald 2006) are efficient tools in calculating the HFE. The three-dimensional reference interaction site model (3D-RISM) theory (Beglov and Roux 1995; Kovalenko and Hirata 1999) possesses the advantages that items (2) through (5) are all satisfied (item (6) is also satisfied to some extent). However, it always gives too high a value of the HFE. In particular, it completely fails when the hydrophobic effect plays a pivotal role (Hayashi et al. 2016). Improved versions of the 3D-RISM theory are available in the literature (Misin et al. 2015; Truchon et al. 2014), but they have been shown to be successful only for very small organic solutes. For larger solutes, additional considerations and alterations specific to the solutes of interest will be required. Hence, the reliability of these improved versions is questionable in respect of item (3). Moreover, in the method proposed by Truchon et al. (2014), item (4) is not satisfied, either. The angle-dependent integral equation (ADIE) theory (Cann and Patey 1997; Hayashi et al. 2016; Kinoshita 2008; Kusalik and Patey 1988a, b), another type of IET for molecular liquids, gives quite fairly accurate results for spherical solutes. However, mathematical and numerical difficulties are encountered when applied to complexly shaped solutes. The ADIE theory has been extended and illustrated for a small polyatomic solute, a dipeptide (Ishizuka and Yoshida 2013), but the computational burden required is unacceptably heavy: Hence, item (2) is not satisfied when employed for a significantly larger polyatomic solute.
Taken together, none of the previously developed methods does satisfy all the six items listed above. We have recently developed a new method (this is referred to as the “hybrid method”) overcoming this problem (Hikiri et al. 2019). It is almost as accurate as the ER method (and the FEP- and TI-MD methods) and as rapid as the 3D-RISM theory. The ER method allows us to decompose the HFE into several components. In the hybrid method, however, a much larger number of components can be obtained and discussed. A solute possessing a significantly large total charge can be handled without difficulty. In this article, the hybrid method, which satisfies all the six items, is outlined, and its two example applications are briefly reviewed. The subjects to be pursued in future studies are also described.
Outline of the Hikiri et al. (2019) method
The new method (Hikiri et al. 2019) is a hybrid of the ADIE theory (Cann and Patey 1997; Hayashi et al. 2016; Kinoshita 2008; Kusalik and Patey 1988a, b) combined with the morphometric approach (MA) of Roth et al. (2006) (hereafter, this is referred to as the “ADIE-MA theory”) and the 3D-RISM theory (Beglov and Roux 1995; Kovalenko and Hirata 1999). It judiciously utilizes only the advantageous aspects of the ADIE theory, MA, and 3D-RISM theory. Since the ADIE-MA theory is much more rapid than the 3D-RISM theory, the computation time required in the hybrid method is almost equal to that in the 3D-RISM theory.
Decomposition of solute hydration into two processes
The solute insertion into water is considered under the isochoric (constant-volume) condition. This condition undergoes neither expansion nor compression of bulk water with the result that the thermodynamic quantities of hydration calculated provide physical insights. Hereafter, μH, SVH, and εVH denote the hydration free energy, entropy, and energy, respectively. Since the hydration entropy S and the hydration energy ε are dependent on the insertion condition (isochoric or isobaric), the value under the isochoric condition is distinguished by the subscript “V.” On the other hand, the hydration free energy μ is independent of the insertion condition: it is written as μH without the subscript “V.” The subscript “H” denotes “hydration.”
Solute insertion into water is considered under the isochoric (constant-volume) condition.
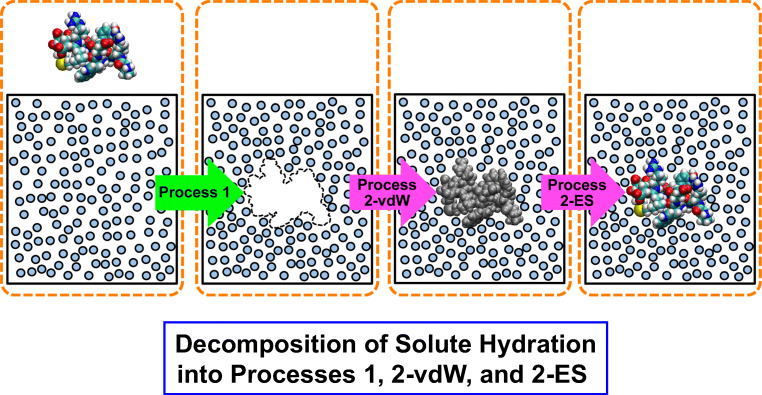
The solute hydration can be decomposed into two processes (Widom 1963; Dullens et al. 2005; Hikiri et al. 2019) as illustrated in Fig. 1.
Fig. 1.
Decomposition of solute hydration into two processes. In process 1, a cavity whose size and polyatomic structure correspond to those of the solute is created in water. In processes 2-vdW and 2-ES, respectively, solute-water van der Waals (vdW) and electrostatic (ES) interaction potentials are incorporated. Before process 2-ES, the partial charges of the solute atoms are all set at zero. After process 2-ES, the full partial charges are assigned to the solute atoms
Process 1: creation of a cavity matching the atomistic, geometric characteristics of the solute
A solute atom interacts with a water molecule through the hard-body potential. This process corresponds to the hydrophobic hydration.
Process 2: incorporation of solute-water interaction potentials
This general step can itself be further decomposed into two processes (processes 2-vdW and 2-ES) where solute-water van der Waals (vdW) and electrostatic (ES) interaction potentials are switched on, respectively. That is, the hard-body potential is replaced by the Lennard-Jones (LJ) potential in process 2-vdW, and the ES potential is incorporated in process 2-ES.
Hereafter, the subscripts “1” and “2” denote quantities in processes 1 and 2, respectively. The subscripts “vdW” and “ES” are used for signifying those in processes 2-vdW and 2-ES, respectively. The following equations hold (T is the absolute temperature):
| 1 |
| 2 |
| 3 |
| 4 |
Application of angle-dependent integral equation (ADIE) theory combined with morphometric approach (MA) to process 1
In the ADIE theory, the dependence of water-water and solute-water correlation functions on the molecular orientations is explicitly taken into account. A multipole model (Kusalik and Patey 1988a, b) is employed for water. For the hydration of a nonpolar, spherical solute, we showed that the results from the ADIE/HNC theory (the hypernetted-chain (HNC) approximation (Hansen and McDonald 2006)) are in very good accord with those from Monte Carlo (MC) and MD simulations using more popular water models such as TIP4P and SPC/E (Hayashi et al. 2016; Kinoshita 2008).
As mentioned above, the ADIE theory is not strictly applicable to a large, polyatomic solute. However, if solute-water vdW and electrostatic potentials are absent as in the case of the cavity considered in process 1, such a solute can readily be handled by combining the ADIE theory with the MA. The ADIE-MA combination was developed by us (Hikiri et al. 2019). Briefly the method involves performing the following.
First, a cavity is modeled as a set of fused, neutral hard spheres corresponding to the constituent atoms in a solute. The LJ potential parameters, σi and εi, are assigned to atom i. We proposed two methods (Methods 1 and 2) for determining the diameter of each neutral hard-sphere Di. In Method 1, Di is simply set at σi. A more sophisticated procedure is employed in Method 2, but it was shown that Methods 1 and 2 give almost the same results (Hikiri et al. 2019).
The MA (Roth et al. 2006) enables us to accurately account for the geometric characteristics of the cavity using only the four geometric measures, the excluded volume (EV) Vex, water-accessible surface (WAS) area A, and integrated mean and Gaussian curvatures of the accessible surface, Y and Z, respectively. A dimensionless thermodynamic quantity of hydration XH,1 (XH,1 = μH,1/(kBT), SVH,1/kB, or εVH,1/(kBT)) is expressed as the following linear combination of Vex, A, Y, and Z:
| 5 |
In Eq. (5), C1(XH,1)Vex and C2(XH,1)A + C3(XH,1)Y + C4(XH,1)Z are referred to as the “EV-dependent” and “WAS-dependent” terms, respectively. The water molecules near the cavity contribute to the WAS-dependent term, while those in the bulk contribute to the EV-dependent term. Hereafter, we use the subscripts “EV” and “WAS” for denoting the EV- and WAS-dependent terms, respectively. For example, SVH,1 = SVH,1,EV + SVH,1,WAS and εVH,1 = εVH,1,EV + εVH,1,WAS.
Since the four coefficients, Cj(XH,1) (j = 1, 2, 3, 4), are dependent only on the thermodynamic state of bulk water, they are determined beforehand using the thermodynamic quantities of hydration of isolated hard-sphere solutes with various diameters, which are calculated by the ADIE theory (Hayashi et al. 2016). μH,1IHSS (the superscript “IHSS” denotes that the quantity is calculated for an isolated hard-sphere solute) is first calculated, SVH,1IHSS is evaluated via the temperature derivative of μH,1IHSS with the system volume being fixed, and εVH,1IHSS is obtained as εVH,1IHSS = μH,1IHSS + TSVH,1IHSS (Hikiri et al. 2019).
Application of three-dimensional reference interaction site model (3D-RISM) theory to process 2
In the 3D-RISM theory, a water molecule is represented by atomic sites referred to as “interaction sites,” and the basic equations for bulk water are formulated using the site-site potentials and correlation functions which are dependent only on the distance between centers of two interaction sites. Thanks to this simplicity, in an analysis on the solute hydration, a polyatomic solute can readily be handled, in which case the correlation between the solute and a water interaction site is three-dimensional. A modified version of SPC/E, cSPC/E (Luchko et al. 2010), is adopted as the water model. Since the HNC closure may not converge to a solution, the Kovalenko-Hirata (KH) closure (Kovalenko and Hirata 1999) is employed instead.
Unfortunately, the 3D-RISM theory becomes quite problematic when applied to an analysis on the hydrophobic hydration (Hayashi et al. 2016). Curiously, for a nonpolar solute, even water based on a molecular model behaves like a hard-sphere solvent (i.e., a solvent formed by neutral hard spheres) whose particle diameter and number density are equal to those of water, respectively. However, the resulting HFE is too high. For a solvent whose particles interact through strongly attractive potential like water, the hydration energy of a nonpolar solute is negative and significantly large, which can correctly be reproduced by the ADIE theory. However, the hydration energy calculated by the 3D-RISM theory is positive (Hayashi et al. 2016).
When the hydration energy of a solute (not a cavity) is calculated solely by the 3D-RISM theory without decomposing the solute hydration into processes 1 and 2, the calculated value εVH3D-RISM should be equal to εVH,13D-RISM + εVH,23D-RISM (the superscript “3D-RISM” denotes a quantity which is calculated using the 3D-RISM theory but not necessarily adopted). However, on the basis of detailed analyses, we have found that unless solute-water vdW and electrostatic, attractive interaction potentials are weak, εVH3D-RISM~εVH,23D-RISM, which stems from the thermodynamic inconsistency of the 3D-RISM theory (Hikiri et al. 2019). (The thermodynamic inconsistency implies that εVH3D-RISM calculated is dependent on the way of decomposing the solute insertion into constituent processes (i.e., the path connecting the initial and final states of the system), and the dependency is influenced by the degree of the effect of solute-water attractive interaction potentials.) Therefore, the hydration energy in process 2 εVH,2 can be obtained as εVH3D-RISM: εVH3D-RISM~εVH,2. μH3D-RISM is first calculated, SVH3D-RISM is evaluated through the temperature derivative of μH3D-RISM, and εVH3D-RISM is obtained as εVH3D-RISM = μH3D-RISM + TSVH3D-RISM (Hikiri et al. 2019).
The partial charges of all the atoms constituting a solute are set at zero to shut off solute-water electrostatic interaction potential, and the hydration free energy, entropy, and energy of the resultant hypothetical solute are calculated as μ*H3D-RISM, S*VH3D-RISM, and εVH*3D-RISM, respectively. SVH,2,ES and εVH,2,ES are obtained as SVH,2,ES=SVH3D-RISM-SVH*3D-RISM and εVH,2,ES = εVH3D-RISM-εVH*3D-RISM, respectively. We note that εVH,2,vdW = εVH,2-εVH,2,ES~εVH3D-RISM-εVH,2,ES = εVH*3D-RISM. This approximate equation is more valid as the effect of solute-water attractive interaction potentials becomes larger. Since |SVH,2,vdW| < <|SVH,2,ES|, SVH,2,vdW is neglected: SVH,2,vdW~0.
Test calculations
We briefly summarize the result obtained. Our earlier publication (Hikiri et al. 2019) should be referred to for more details.
Comparison between results from our hybrid method and from molecular dynamics simulation based on solution theory in energy representation (ER method)
We tested the accuracy of our hybrid method (Methods 1 and 2) for solutes with a wide range of sizes, polypeptides possessing 2–123 residues. The solutes were categorized into “small,” “medium-sized,” and “large” solutes. They were “15 dipeptides”; “2 polypeptides with 20 residues, a miniprotein with 20 residues, and proteins with 52–60 residues”; and “proteins with 65–123 residues,” respectively. For most of the medium-sized and large solutes, multiple structures including the native and decoy structures were considered. We compared the HFEs calculated via the four routes: Methods 1 and 2, the ER method, and the 3D-RISM theory coupled with the KH closure (3D-RISM/KH). Via the last route, the HFE is calculated for a solute using the 3D-RISM theory alone without decomposing the solute hydration into processes 1 and 2. The water model adopted in the ER method was TIP3P. For all the solutes, the total charge is zero, because a solute with a nonzero total charge cannot be handled by the ER method with sufficient accuracy.
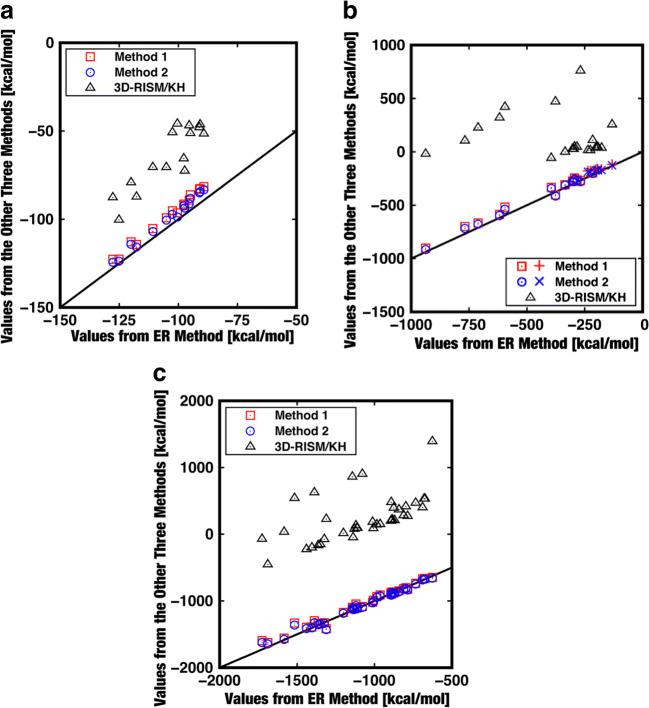
The HFEs calculated via the four routes are compared in Fig. 2 for the small (a), medium-sized (b), and large (c) solutes. The correlation coefficients for all the solutes considered are − 0.1192, 0.9973, and 0.9977 for the data combinations of (3D-RISM, ER method), (Method 1, ER method), and (Method 2, ER method), respectively. Only for the small solutes, the HFEs from Methods 1 and 2 are always slightly higher than those from the ER method. Here, we define the discrepancy DIS (%) by
| 6 |
where μΗ is the HFE from the 3D-RISM theory, Method 1, or Method 2 and μHER is that from the ER method. The average values of DIS for all the solutes considered are 115, 5.74, and 4.57% for the 3D-RISM theory, Method 1, and Method 2, respectively (when only the large solutes are considered, the average values of DIS are 2.70 and 2.30% for Methods 1 and 2, respectively). The very good agreement between the HFEs calculated using the ER method and Method 1 or 2 indicates that the following assumptions made in the hybrid method can be rationalized: εVH3D-RISM~εVH,2 and SVH,2,vdW~0. It is apparent that the results from the 3D-RISM theory are by far the worst. The HFEs calculated by the 3D-RISM are positive and very large for many of the peptides and proteins tested. This implies that these solutes are insoluble in water and leave water for the gas phase, which is highly unphysical.
Fig. 2.
Hydration free energies calculated by 3D-RISM/KH, Method 1, and Method 2 plotted against the hydration free energy calculated using the ER method. a Small solutes (15 dipeptides). On the straight line drawn, the values of the vertical and horizontal axes are equal. The correlation coefficients are 0.8823, 0.9950, and 0.9949 for the data combinations of (3D-RISM/KH, ER method), (Method 1, ER method), and (Method 2, ER method), respectively. b Medium-sized solutes (2 polypeptides with 20 residues, a miniprotein with 20 residues, and proteins with 52–60 residues). The data points for alanine 20 helix and leucine 20 helix are distinguished from those for the others using pluses (Method 1) and crosses (Method 2). On the straight line drawn, the values of the vertical and horizontal axes are equal. The correlation coefficients are − 0.0953, 0.9947, and 0.9952 for the data combinations of (3D-RISM/KH, ER method), (Method 1, ER method), and (Method 2, ER method), respectively. c Large solutes (proteins with 65–123 residues). On the straight line drawn, the values of the vertical and horizontal axes are equal. The correlation coefficients are 0.5618, 0.9, 91, and 0.9909 for the data combinations of (3D-RISM/KH, ER method), (Method 1, ER method), and (Method 2, ER method), respectively
A variety of components of hydration free energy
For three representative solutes, the components of the HFE are presented in Table 1. It is observed that SVH,1, εVH,1, SVH,2, and εVH,2 are negative, |SVH,2| is much smaller than |SVH,1|, and |εVH,2| and |εVH,1| are both significantly large. (We emphasize that εVH,1 is different from εVH,13D-RISM.) SVH,1,EV < 0, εVH,1,EV < 0, SVH,1,WAS > 0, and εVH,1,WAS > 0. The good agreement between μH and μHER manifests that the approximation, εVH3D-RISM~εVH,2, is justifiable. The effect of solute-water attractive interaction potentials should be large enough for the approximation to become valid when a large solute with large WAS area is considered. This explains the excellent agreement between the HFEs from the hybrid method and the ER method especially for the medium-sized and large solutes. On the other hand, for the small solutes considered in Fig. 2 c, it seems that μΗ is influenced by a remnant of positive εVH,13D-RISM. However, we emphatically remark that the hybrid method always gives remarkable improvement over the 3D-RISM theory. Even for alanine 20 helix and leucine 20 helix possessing only nonpolar residues, the good agreement between the HFEs from the hybrid method and the ER method observed in Fig. 2 b (see its caption) suggests that solute-water vdW interaction potential makes a significant contribution to the justification of εVH3D-RISM~εVH,2.
Table 1.
Components of hydration free energy (kcal/mol) for three representative solutes
| Quantity | Solute 1 | Solute 2 | Solute 3 |
|---|---|---|---|
| −TSVH,1,EV | 65.18 | 1416.52 | 2936.55 |
| −TSVH,1,WAS | − 18.50 | − 132.28 | − 246.75 |
| −TSVH,1 | 46.68 | 1284.23 | 2689.79 |
| εVH,1,EV | − 52.08 | − 1131.91 | − 2346.54 |
| εVH,1,WAS | 26.57 | 234.07 | 477.60 |
| εVH,1 | − 25.52 | − 897.84 | − 1868.94 |
| μΗ,1 | 21.16 | 386.39 | 820.85 |
| −TSVH,2,ES | 7.59 | 40.14 | 95.08 |
| εVH,2,vdW | − 7.70 | − 53.16 | − 116.37 |
| εVH,2,ES | − 143.64 | − 642.59 | − 1884.03 |
| εVH,2 | − 151.34 | − 695.75 | − 2000.40 |
| μΗ,2 | − 143.75 | − 655.61 | − 1905.33 |
| μΗ | − 122.58 | − 269.22 | − 1084.47 |
| μHER | − 125.08 | − 268.70 | − 1078.10 |
μHER is the hydration free energy calculated by the ER method. All the other quantities are calculated by Method 1. Solutes 1, 2, and 3 are diserine (a small solute), HPLC 1 in one of the two structures (a medium-sized solute), and profilin I in one of the five structures (a large solute), respectively
As performed in our earlier studies (Kinoshita 2013; Oshima and Kinoshita 2015), each of SVH,1,EV and SVH,1,WAS can further be decomposed into the cavity-water pair and many-body correlation terms: SVH,1 = SVH,1,EV,Pair + SVH,1,EV,Many-body + SVH,1,WAS,Pair + SVH,1,WAS,Many-body. The cavity-water “many-body correlation” represents the cavity-water triplet and higher-order correlation. Here, we explain SVH,1,EV,Many-body. The presence of a cavity generates an EV which is inaccessible to the centers of water molecules in the system. We note that the presence of a water molecule also generates an EV for the other water molecules and all the water molecules are entropically correlated. We refer to this entropic correlation as the “water crowding.” The water crowding is enhanced upon cavity creation, which is reflected upon negative SVH,1,EV,Many-body. The decomposition of SVH,1 into SVH,1,EV,Pair, SVH,1,EV,Many-body, SVH,1,WAS,Pair, and SVH,1,WAS,Many-body enables us to gain physical insights into a variety of processes in aqueous environments. (We note that |SVH,1,EV,Many-body| is much larger than |SVH,1,EV,Pair|.) As a paradigmatic example, |SVH,1,EV,Many-body| becomes smaller at low temperatures. This is responsible for the weakening of hydrophobicity at low temperatures and relevant to the cold denaturation of a protein (Kinoshita 2013; Oshima and Kinoshita 2015). (We note that the pair correlation terms of εVH,1,EV and εVH,1,WAS are zero for a hard-body cavity (Kinoshita 2008).)
For a protein with a significantly large total charge
In the MD simulation, the electrostatic energy is handled by the Ewald method in a periodic system. For a solute with a nonzero total charge, however, a problem of the effect of a finite unit cell size is raised. This problem becomes more serious as the total charge increases. Ekimoto et al. (2015) examined the effect of a finite unit cell size using the thermodynamic integration (TI) method. They analyzed the charging free energy (CFE) of ubiquitin with a total charge of +8e (e denotes the elementary charge) in explicit water and reported that the CFE varied by ~ 200 kcal/mol for the different unit cell sizes tested but could be corrected with an error of ~ 3 kcal/mol by taking account of the self-energy and the hydration effect. However, such corrections were quite tedious and time-consuming. Unfortunately, in the ER method, the assessment of such correction methods has not been achieved yet. This is why no solute with a nonzero total charge was considered in our test calculations described above.
We showed that the hybrid method (Method 1 or 2) can be applied to a solute possessing a significantly large total charge without any modification or correction (Hikiri et al. 2019). Using the 3D-RISM theory, we calculated the CFE (this is equivalent to “εVH,2,ES-TSVH,2,ES” in the hybrid method) of ubiquitin with a total charge of +8e. We note that the 3D-RISM theory does not employ the Ewald method. The structure of ubiquitin was the same as that considered in the test calculations, but the total charge was increased from zero to +8e. The buffer size Lmin in the 3D-RISM theory, which is defined as the minimum distance between the solute surface and the box edge, must be sufficiently large so that the structure and properties of water near the box edge are essentially the same as those of bulk water. The dependence of the CFE on Lmin is shown in Fig. 3 a, indicating that the CFE rapidly converges to − 1483.4 kcal/mol with increasing Lmin. In Fig. 3 b, the CFE calculated by the TI method in the MD simulation using the Ewald method is plotted against the number of layers of water molecules, a measure of the unit cell size. The convergence in Fig. 3 b is much slower than that in Fig. 3 a. The corrections for the self-energy and the hydration effect are absolutely required in the MD simulation. The corrected CFEs are also shown in Fig. 3 b. The corrected value in the system of 45 layers of water molecules, − 1484.6 kcal/mol, is in excellent agreement with that in the 3D-RISM theory. In conclusion, the hybrid method is applicable to a solute with a significantly large total charge without any modification or correction as long as Lmin is chosen to be sufficiently large.
Fig. 3.
a Dependence of charging free energy on buffer size observed for 3D-RISM/KH. The solute is ubiquitin with a total charge of +8e (e denotes the elementary charge). b Dependence of charging free energy (CFE) on number of layers of water molecules and unit cell size. The CFE is calculated using the molecular dynamics simulation and the thermodynamic integration method. The solute is ubiquitin with a total charge of +8e. Both of the uncorrected and corrected values are shown
Application of our hybrid method to analyses on biomolecular functions
In the hybrid method, the calculation of a thermodynamic quantity of hydration is performed for a fixed structure of the solute. However, this is not a problem because we can account for the structural fluctuation of the solute in water in accordance with the following steps: (I) An ensemble comprising sufficiently many solute structures is generated by the MD simulation in explicit aqueous solution and (II) the HFE and its components are calculated for all of these structures, and each of these quantities is evaluated as the average of the values calculated. In the MD simulation combined with our hybrid method, which is employed in (I), the generation of the structural ensemble is much easier and less time-consuming than that required for calculating the HFE solely by the MD simulation.
Only for small solutes, the HFE calculated by the hybrid method is not very accurate. This is not a problem because the calculation for small solutes can be conducted with sufficient accuracy using an improved version of the 3D-RISM theory developed by Misin et al. (2015). The hybrid method is best suited to the calculation of the HFE for sufficiently large biomolecules such as peptides and proteins. The remaining thermodynamic quantities to calculate are the intramolecular (conformational) energy and entropy of a solute itself. The former can readily be calculated once a force field is given, and the latter can be estimated using the Boltzmann-quasi-harmonic (BQH) method (Hikiri et al. 2016) combined with the aforementioned MD simulation. Thus, the hybrid method is expected to become a powerful tool in analyzing such subjects as the mechanisms of a variety of self-assembly processes for biomolecules and the temperature and pressure effects on the structures formed by biomolecules. We have already achieved successful results in the two example applications described below.
Example applications and physical implication for biomolecular functions
Mechanism of globule-to-coil transition of PNIPAM in water: relevance to cold denaturation of a protein
We briefly summarize the result obtained. Our earlier publication (Inoue et al. 2019) should be referred to for more details. In water, poly(N-isopropylacrylamide) (PNIPAM) is in a soluble coil state below the lower critical soluble temperature (LCST~305 K) but in an insoluble globule state above LCST. The coil state is significantly more extended than the globule state. This may be counterintuitive but similar to the cold denaturation of a protein when we take the view that PNIPAM exhibits a globule-to-coil transition upon temperature lowering.
We evaluated a variety of energetic and entropic components of thermodynamic quantities of the two states at the two temperatures, 273 and 323 K, which are below and above LCST, respectively. Molecular models were employed for water, and PNIPAM was modeled as a 30-mer (i.e., the model PNIPAM possesses 30 units). A thermodynamic quantity X (X is not the conformational entropy) of PNIPAM is calculated as a functional of the PNIPAM structure. First, sufficiently large ensembles of structures for the coil and globule states of the model PNIPAM are generated using the MD simulations at 273 K and 323 K, respectively. Some of the snapshot structures in the two states are shown in Fig. 4. Second, X is calculated for each structure. Third, X for the coil or globule state is obtained as the average of the values of X for all the structures generated (i.e., for the structural ensemble) in each state. Hereafter, X denotes this ensemble average. The HFE and its components are calculated using our hybrid method. We note that the conformational entropy is estimated by means of the BQH method.
Fig. 4.

Example snapshot structures of PNIPAM in the coil state (a) and in the globule state (b). The carbon atoms of the main chain are emphasized by the large spheres
In what follows, μH, EC, SC, and F = μH + EC − TSC denote the HFE, conformational energy and entropy of PNIPAM, and free energy of the water-PNIPAM system, respectively, and ΔX= “X of coil state” − “X of globule state.” − 23.4 ± 2.7 kcal/mol was obtained as −TΔSC at 273 K. As discussed in our earlier publication, however, it was difficult to avoid the underestimation of | − TΔSC|. Adopting −23.4 − 2.7 = −26.1 kcal/mol as −TΔSC at 273 K and assuming that ΔSC was independent of T, we obtained the following: ΔμH = − 26.4 and ΔF = − 0.7 < 0 at 273 K; ΔμH = − 16.5 and ΔF = 4.4 > 0 at 323 K (the unit is kcal/mol). (ΔEC = 51.8 kcal/mol and ΔSC = 95.6 (cal/(mol•K).) Thus, the coil state is more stable than the globule state at 273 K, whereas the opposite is true at 323 K. We were thus successful in reproducing the globule-to-coil transition. In the calculations, we take differences between two large quantities multiple times, giving rise to the inevitable cancellation of significant digits. Further, the force field used is more or less uncertain. Considering these matters, we can conclude that the success mentioned above is remarkable. We also calculated the change in enthalpy ΔH upon the globule-to-coil transition of the model PNIPAM and obtained approximately − 1.1 kcal/mol per PNIPAM unit. On the other hand, the value of ΔH experimentally measured is approximately − 1.3 kcal/mol. The agreement is very good.
A great advantage of our hybrid method is that the HFE can be decomposed into a variety of energetic and entropic components. We identified the components driving or opposing the globule-to-coil transition, evaluated their relative magnitudes, and analyzed their temperature dependences. An important result is as follows. The EV of the globule state is smaller than that of the coil state. Consequently, the globule state, for which the water crowding is less significant, is more favored in terms of the translational, configurational entropy of water. At low temperatures, however, this effect becomes significantly weaker, yielding to the factors favoring the coil state. As argued in our earlier works (Kinoshita 2013; Oshima and Kinoshita 2015), the mitigation of water crowding corresponds to the weakening of hydrophobicity, and this weakening at low temperatures is the cause of the globule-to-coil transition of PNIPAM as well as the cold denaturation of a protein. At lower T, the hydrogen bonding of water molecules is strengthened, the translational motion becomes less active, and the water crowding in the bulk is reduced. Consequently, |SVH,1,EV,Many-body| and |SVH,1,EV| decrease, giving rise to the weakening of the entropic power of driving PNIPAM to take a structure with smaller EV.
There is a claim in the literature (Tavagnacco et al. 2018) that the globule-to-coil transition of PNIPAM should be different from the cold denaturation of a protein in terms of the mechanism. The reasons for this claim are the following: The coil and globule states are soluble and insoluble in water for PNIPAM, whereas both of the denatured and native states are soluble in water for the protein. Very recently, we have demonstrated that this claim is irrelevant and the solubility differences among the two states of PNIPAM and those of the protein described above are all reproduced by our hybrid method. Still, the globule-to-coil transition of PNIPAM and the cold denaturation of a protein share physically the same mechanism. The result will be published in a future article.
Evaluation of binding affinities of three different peptides for an oncoprotein MDM2
We briefly summarize the result obtained. Our earlier publication (Yamada et al. 2019) should be referred to for more details. An oncoprotein MDM2 binds to the extreme N-terminal peptide region of a tumor suppressor protein p53 (p53NTD) and inhibits its anticancer activity. It is essential to design a peptide exhibiting a much higher binding affinity for MDM2 than p53NTD. To this end, we have to develop a theoretical method which enables us not only to calculate the MDM2-peptide binding free energy with quantitative accuracy but also to decompose the BFE into a variety of energetic and entropic components, evaluate their relative magnitudes, and identify the components driving or opposing the binding. The enhancement of one of the driving components can be useful to the peptide design mentioned above.
We calculated the BFEs for the three different peptides, p53NTD (ETFSDLWKLLPE), DI (LTFEHYWAQLTS), and MIP (PRFWEYWLRLME) (the letters within parentheses denote the amino acid sequence), using our hybrid method. MIP exhibits higher binding affinity for MDM2 than any other peptide currently known (Shiheido et al. 2011). A quantity X (X is not the conformational entropy of a biomolecule) of biomolecule J (J = MDM2, peptide, MDM2-peptide; peptide is p53NTD, DI, or MIP) whose structure fluctuates in aqueous solution, XJ, is calculated in the following manner: (a) Sufficiently many structures of biomolecule J are generated (i.e., a sufficiently large structural ensemble is constructed) using the MD simulation; (b) X is evaluated for each structure of biomolecule J; and (c) XJ is evaluated as the average of the values of X for all the structures generated (i.e., as the ensemble average). The starting structure of the MDM2-peptide complex in the MD simulation is the experimentally determined structure. The free energy of the system formed by water and biomolecule J, FJ, comprises the HFE and the intramolecular (conformational) energy and entropy of biomolecule J. The conformational entropy of a biomolecule is estimated using the BQH method. The BFE ΔFMDM2-peptide is obtained as FMDM2-peptide − (FMDM2 + Fpeptide) (peptide = p53NTD, DI, or MIP). It should be noted that MDM2 and each peptide change their structures upon binding. In particular, the change in the peptide structure is significantly large.
Here, we define ΔΔFMDM2-peptide as “ΔFMDM2-peptide − ΔFMDM2-p53NTD” (peptide = DI or MIP). The experimental value is denoted by the superscript “exp.”. The following data are available: ΔΔFMDM2-DIexpt.~ − 2.51 kcal/mol and ΔΔFMDM2-MIPexpt.~ − 3.95 kcal/mol. Since ΔF is not equivalent to ΔFexpt. in a strict sense, these two quantities cannot be compared quantitatively. As argued in our earlier publication (Yamada et al. 2019), however, a comparison can be made for ΔΔF and ΔΔFexpt. to examine the accuracy of the theory. Our theoretical results were as follows: ΔΔFMDM2-DI~ − 2.60 ± 0.68 kcal/mol, ΔΔFMDM2-MIP(FF1)~ − 4.80 ± 0.69 kcal/mol, and ΔΔFMDM2-MIP(FF2)~ − 8.38 ± 0.68 kcal/mol. The superscripts “(FF1)” and “(FF2)” represent that two different force fields, FF1 and FF2, were employed. We were thus successful in reproducing the order of binding affinity, MIP > DI > p53NTD, with quantitative accuracy. The difference, | − 8.38 − (−4.80)| = 3.58, arises from the uncertainty of the force field. The discrepancy between the theoretical and experimental values, | − 4.80 − (− 3.95)| = 0.85, is smaller. We can thus conclude that the discrepancy between the theoretical and experimental values is even smaller than the uncertainty of the force field.
We also discussed the reason for the order of binding affinity, MIP > p53NTD. Some of the significant results are recapitulated below. The change in energy originating from hydrophobic hydration (i.e., cavity creation in water) upon binding, ΔεVH,1, opposes the binding. This effect is larger for MDM2-MIP than for MDM2-p53NTD. The binding leads to a decrease in MDM2-peptide vdW and ES interaction energies, negative Δ(EvdW + EES). However, the binding accompanies an increase in the sum of MDM2-water, peptide-water, and water-water vdW and ES interaction energies, positive Δ(εVH,2,vdW + εVH,2,ES) (see Fig. 5a). Interestingly, Δ(EvdW + εVH,2,vdW) and Δ(EES + εVH,2,ES) are negative and positive, respectively. The change in total energy, Δ(εVH,1 + EvdW + εVH,2,vdW + EES + εVH,2,ES), is positive, and it is larger for MDM2-MIP than for MDM2-MIP. The loss of the conformational entropy defined for MDM2 and the peptide opposes the binding, but MDM2-MIP and MDM2-p53NTD share almost the same value of the loss. The binding leads to the overlap of the EVs generated by MDM2 and the peptide (see Fig. 5b), and the total volume available for the translational displacement of water molecules in the system increases by the overlapping volume. As a consequence, the water crowding is significantly mitigated, leading to a large gain of water entropy. This water-entropy gain is the pivotal driving force in the binding, and it is considerably larger for MDM2-MIP than for MDM2-p53NTD.
Fig. 5.
Changes in energetic (a) and entropic (b) components of thermodynamic quantities upon binding. The binding of MDM2 and MIP is illustrated as an example
For the development of a reliable anticancer drug, it is desired to modify the sequence of MIP so that the modified peptide can bind to MDM2 even more strongly than MIP. A further increase in the water-entropy gain upon binding primarily through larger ΔVex (the decrease in the total EV upon binding) is a simple but reliable approach, because ΔVex is closely related to geometric properties of the binding interface. As a matter of fact, using this approach, we have recently succeeded in designing a peptide which binds to MDM2 more strongly than MIP (the result will be published in a future article).
Concluding remarks
MD simulation has been used to elucidate the mechanism of the globule-to-coil transition of PNIPAM and the binding of two biomolecules. MD provides microscopic information on biomolecule-intramolecular and biomolecule-water hydrogen bonds, water structure near a biomolecule, and structural fluctuations of a biomolecule. However, the microscopic information alone is quite inadequate, and calculation of thermodynamic quantities is absolutely required. Even in the calculation of the HFE, use of MD simulation has been much more popular than a statistical-mechanical theory. There are two primary reasons for this situation. First, the MD simulation is usually more accurate than the statistical-mechanical theory despite the much heavier computational burden of the former (the accuracy is more important than the computational load). Second, significantly more knowledge of mathematics and numerical solution is required in the latter. The first situation does not apply for our statistical-mechanical theory, the hybrid method, reviewed in this article. Our approach is almost as accurate as the ER method which is applicable to a protein unlike the FEP- and TI-MD methods. Though the hybrid and ER methods are formulated on substantially different grounds, the agreement between the results from these two methods is surprisingly good, which indicates that they are both physically sound.
As described in the two example applications, thermodynamic quantities can be calculated using the hybrid method (Hikiri et al. 2019) and the BQH method (Hikiri et al. 2016) with quantitative accuracy: The agreement between theoretical and experimental values is quite good. By using the two methods in combination, we intend to investigate such subjects as cold, thermal, and pressure denaturations of a protein and different types of molecular recognition including a process where at least one of the two biomolecules exhibits a large structural change upon binding. The thermodynamic quantities reflecting hydration in processes 1 and 2 will be taken into consideration. The decomposition of SVH,1 into SVH,1,EV,Pair, SVH,1,EV,Many-body, SVH,1,WAS,Pair, and SVH,1,WAS,Many-body will also prove to be insightful. Application to the drug design is also an important task for the near future.
It is interesting and important to investigate the effects of salts (e.g., NaCl), cosolvents (e.g., sugar, alcohol, and urea), as well as those of temperature and pressure on the biological self-assembly processes. The addition of salts to water can be taken into account in the hybrid method (Kusalik and Patey 1988a; Kinoshita et al. 1996; Kinoshita and Harano 2005). However, the cosolvents cannot be handled by the hybrid method using elaborate, all-atom models. The ER method seems to be the only tool that enables us to investigate the cosolvent effects with quantitative accuracy (Masutani et al. 2019).
Acknowledgments
The author thanks all of the collaborators in the three references (Hikiri et al. 2019; Inoue et al. 2019; Yamada et al. 2019) reviewed in this article.
Funding information
This work was supported primarily by Grant-in-Aid for Scientific Research (No. 17H03663) from the Japan Society for the Promotion of Science (JSPS).
Compliance with ethical standards
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Ball P. Water--an enduring mystery. Nature. 2008;452:291–292. doi: 10.1038/452291a. [DOI] [PubMed] [Google Scholar]
- Beglov D, Roux B. Numerical solution of the hypernetted chain equation for a solute of arbitrary geometry in three dimensions. J Chem Phys. 1995;103:360–364. doi: 10.1603/1.469602. [DOI] [Google Scholar]
- Cann NM, Patey GN. An investigation of the influence of solute size and insertion conditions on solvation thermodynamics. J Chem Phys. 1997;106:8165–8195. doi: 10.1063/1.473822. [DOI] [Google Scholar]
- Dullens RPA, Aaarts DGAL, Kegel WK, Lekkerkerker HNW. The Widom insertion method and ordering in small hard-sphere systems. Mol Phys. 2005;103:3195–3200. doi: 10.1080/00268970500221925. [DOI] [Google Scholar]
- Ekimoto T, Matubayasi N, Ikeguchi M. Finite-size effect on the charging free energy of protein in explicit solvent. J Chem Theory Comput. 2015;11:215–223. doi: 10.1021/ct5008394. [DOI] [PubMed] [Google Scholar]
- Hansen J-P, McDonald LR. Theory of simple liquids. 3. London: Academic Press; 2006. [Google Scholar]
- Hayashi T, Oshima H, Harano Y, Kinoshita M. Water based on a molecular model behaves like a hard-sphere solvent for a nonpolar solute when the reference interaction site model and related theories are employed. J Phys Condens Matter. 2016;28:344003. doi: 10.1088/0953-8984/28/34/344003. [DOI] [PubMed] [Google Scholar]
- Hikiri S, Yoshidome T, Ikeguchi M. Computational methods for configurational entropy using internal and Cartesian coordinates. J Chem Theory Comput. 2016;12:5990–6000. doi: 10.1021/acs.jctc.6b00563. [DOI] [PubMed] [Google Scholar]
- Hikiri S, Hayashi T, Inoue M, Ekimoto T, Ikeguchi M, Kinoshita M. An accurate and rapid method for calculating solvation free energies of a variety of solutes including proteins. J Chem Phys. 2019;150:175101. doi: 10.1063/1.5093110. [DOI] [PubMed] [Google Scholar]
- Inoue M, Hayashi T, Hikiri S, Ikeguchi M, Kinoshita M. Mechanism of globule-to-coil transition of poly(N-isopropylacrylamide) in water: relevance to cold denaturation of a protein. J Mol Liq. 2019;292:111374. doi: 10.1016/j.molliq.2019.111374. [DOI] [Google Scholar]
- Ishizuka R, Yoshida N. Extended molecular Ornstein-Zernike integral equation for fully anisotropic solute molecules: formulation in a rectangular coordinate system. J Chem Phys. 2013;139:084119. doi: 10.1063/1.4819211. [DOI] [PubMed] [Google Scholar]
- Jorgensen WL, Ravimohan C. Monte Carlo simulation of differences in free energies of hydration. J Chem Phys. 1985;83:3050–3054. doi: 10.1063/1.449208. [DOI] [Google Scholar]
- Karino Y, Matubayasi N. Interaction-component analysis of the urea effect on amino acid analog. Phys Chem Chem Phys. 2013;15:4377–4391. doi: 10.1039/C3CP43346C. [DOI] [PubMed] [Google Scholar]
- Karino Y, Fedorov MV, Matubayasi N. End-point calculation of solvation free energy of amino-acid analogs by molecular theories of solution. Chem Phys Lett. 2010;496:351–355. doi: 10.1016/j.cplett.2010.07.054. [DOI] [Google Scholar]
- Kinoshita M. Molecular origin of the hydrophobic effect: analysis using the angle-dependent integral equation theory. J Chem Phys. 2008;128:024507. doi: 10.1063/1.2823733. [DOI] [PubMed] [Google Scholar]
- Kinoshita M. A new theoretical approach to biological self-assembly. Biophys Rev. 2013;5:283–293. doi: 10.1007/s12551-013-0100-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinoshita M, Harano Y. Potential of mean force between solute atoms in salt solution: effects due to salt species and relevance to conformational transition of biomolecules. Bull Chem Soc Jpn. 2005;78:1431–1441. doi: 10.1246/bcsj.78.1431. [DOI] [Google Scholar]
- Kinoshita M, Iba S, Harada M. Interaction between macroparticles in aqueous electrolytes. J Chem Phys. 1996;105:2487–2499. doi: 10.1063/1.472037. [DOI] [Google Scholar]
- Kirkwood JG. Statistical mechanics of fluid mixtures. J Chem Phys. 1935;3:300–3013. doi: 10.1063/1.1749657. [DOI] [Google Scholar]
- Kovalenko A, Hirata F. Self-consistent description of a metal-water interface by the Kohn-sham density functional theory and the three-dimensional reference interaction site model. J Chem Phys. 1999;110:10095–10112. doi: 10.1063/1.478883. [DOI] [Google Scholar]
- Kusalik PG, Patey GN. On the molecular theory of aqueous electrolyte solutions. I The solution of the RHNC approximation for models at finite concentration. J Chem Phys. 1988;88:7715–7738. doi: 10.1063/1.454286. [DOI] [Google Scholar]
- Kusalik PG, Patey GN. The solution of the reference hypernetted-chain approximation for water-like models. Mol Phys. 1988;65:1105–1119. doi: 10.1080/00268978800101631. [DOI] [Google Scholar]
- Luchko T, Gusarov S, Roe DR, Simmerling C, Case DA, Tuszynski J, Kovalenko A. Three-dimensional molecular theory of solvation coupled with molecular dynamics in Amber. J Chem Theory Comput. 2010;6:607–624. doi: 10.1021/ct900460m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masutani K, Yamamori Y, Kim K, Matubayasi N. Free-energy analysis of the hydration and cosolvent effects on the β-sheet aggregation through all-atom molecular dynamics simulation. J Chem Phys. 2019;150:145101. doi: 10.1063/1.5088395. [DOI] [PubMed] [Google Scholar]
- Matubayasi N, Nakahara M. Theory of solutions in the energetic representation. I Formulation. J Chem Phys. 2000;113:6070–6081. doi: 10.1063/1.1309013. [DOI] [Google Scholar]
- Matubayasi N, Nakahara M. Theory of solutions in the energy representation. II Functional for the chemical potential. J Chem Phys. 2002;117:3605–3616. doi: 10.1063/1.1495850. [DOI] [Google Scholar]
- Matubayasi N, Nakahara M. Erratum: “theory of solutions in the energy representation. II. Functional for the chemical potential” [J. Chem. Phys. 117, 3605 (2002)] J Chem Phys. 2003;118:2446. doi: 10.1063/1.1533752. [DOI] [Google Scholar]
- Matubayasi N, Nakahara M. Theory of solutions in the energy representation. III Treatment of the molecular flexibility. J Chem Phys. 2003;119:9686–9702. doi: 10.1063/1.1613938. [DOI] [Google Scholar]
- Misin M, Fedorov MV, Palmer DS. Communication: accurate hydration free energies at a wide range of temperatures from 3D-RISM. J Chem Phys. 2015;142:091105. doi: 10.1063/1.4914315. [DOI] [PubMed] [Google Scholar]
- Oshima H, Kinoshita M. Essential roles of protein-solvent many-body correlation in solvent-entropy effect on protein folding and denaturation: comparison between hard-sphere solvent and water. J Chem Phys. 2015;142:145103. doi: 10.1063/1.4917075. [DOI] [PubMed] [Google Scholar]
- Ratkova EL, Palmer DS, Fedorov MV. Solvation thermodynamics of organic molecules by the molecular integral equation theory: approaching chemical accuracy. Chem Rev. 2015;115:6312–6356. doi: 10.1021/cr5000283. [DOI] [PubMed] [Google Scholar]
- Roth R, Harano Y, Kinoshita M. Morphometric approach to the solvation free energy of complex molecules. Phys Rev Lett. 2006;97:078101. doi: 10.1103/PhysRevLett.97.078101. [DOI] [PubMed] [Google Scholar]
- Shiheido H, Takashima H, Doi N, Yanagawa H. mRNA display selection of an optimized MDM2-binding peptide that potently inhibits MDM2-p53 interaction. PLoS One. 2011;6:e17898. doi: 10.1371/journal.pone.0017898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirts MR, Pitera JW, Swope WC, Pande VS. Extremely precise free energy calculations of amino acid side chain analogs: comparison of common molecular mechanics force fields for proteins. J Chem Phys. 2003;119:5740–5761. doi: 10.1063/1.1587119. [DOI] [Google Scholar]
- Tavagnacco L, Zaccarelli E, Chiessi E. On the molecular origin of the cooperative coil-to-globule transition of poly(N-isopropylacrylamide) in water. Phys Chem Chem Phys. 2018;20:9997–10010. doi: 10.1039/c8cp00537k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tokunaga Y, Yamamori Y, Matubayasi N. Probabilistic analysis for identifying the driving force of protein folding. J Chem Phys. 2018;148:125101. doi: 10.1063/1.5019410. [DOI] [PubMed] [Google Scholar]
- Truchon J-F, Pettitt BM, Labute P. A cavity corrected 3D-RISM functional for accurate solvation free energies. J Chem Theory Comput. 2014;10:934–941. doi: 10.1021/ct4009359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Widom B. Some topics in the theory of fluids. J Chem Phys. 1963;39:2808–2812. doi: 10.1063/1.1734110. [DOI] [Google Scholar]
- Yamada T, Hayashi T, Hikiri S, Kobayashi N, Yanagawa H, Ikeguchi M, Katahira M, Nagata T, Kinoshita M. How does the recently discovered peptide MIP exhibit much higher binding affinity than an anticancer protein p53 for an oncoprotein MDM2? J Chem Inf Model. 2019;59:3533–3544. doi: 10.1021/acs.jcim.9b00226. [DOI] [PubMed] [Google Scholar]