Theoretical identification of thermostabilizing amino acid mutations for G-protein-coupled receptors

Abstract

Thermostabilization of a membrane proteins, especially G-protein-coupled receptors (GPCRs), is often necessary for biochemical applications and pharmaceutical studies involving structure-based drug design. Here we review our theoretical, physics-based method for identifying thermostabilizing amino acid mutations. Its novel aspects are the following: The entropic effect originating from the translational displacement of hydrocarbon groups within the lipid bilayer is treated as a pivotal factor; a reliable measure of thermostability is introduced and a mutation which enlarges the measure to a significant extent is chosen; and all the possible mutations can be examined with moderate computational effort. It was shown that mutating the residue at a position of N_BW = 3.39 (N_BW is the Ballesteros-Weinstein number) to Arg or Lys leads to the stabilization of significantly many different GPCRs of class A in the inactive state. Up to now, we have been successful in stabilizing several GPCRs and newly solving three-dimensional structures for the muscarinic acetylcholine receptor 2 (M2R), prostaglandin E receptor 4 (EP4), and serotonin 2A receptor (5-HT_2AR) using X-ray crystallography. The subjects to be pursued in future studies are also discussed.

Introduction

Membrane proteins play imperative roles in sustaining life (Boyd et al. 1998; Wallin and Heijne 1998). They represent a significantly large percentage of present drug targets (Hauser et al. 2017; Shimada et al. 2019). However, their intrinsic structural instability has been a major hindrance to biochemical and pharmaceutical studies. For instance, it is very difficult to solve the three-dimensional (3D) structure by X-ray crystallography. This difficulty must be overcome for efficient, structure-based drug design. It is known that amino acid mutations can enhance the thermostability of membrane proteins (Lau et al. 1999; Scott et al. 2013; Zhou and Bowie 2000). The thermostabilization usually leads to higher stability against various perturbations other than heat. Thermostabilizing mutations are currently identified by experiments on a trial-and-error basis. The prevailing approach is Ala scanning mutagenesis in which every residue is mutated to Ala and Ala is mutated to Leu (Magnani et al. 2008; Serrano-Vega et al. 2008; Shibata et al. 2009). This approach suffers drawbacks such as the quite limited mutational space explored and the unacceptably heavy experimental burden. The development of a reliable theoretical method is strongly desired for the identification of stabilizing mutations.

Four methods which do not rely on experiments were reported for the identification of thermostabilizing mutations for membrane proteins (Bhattacharya et al. 2014; Chen et al. 2012; Popov et al. 2018; Sauer et al. 2015). Three of them, which were reported by Chen et al., Sauer et al., and Popov et al., respectively, are knowledge-based methods. The method of Popov et al., which takes advantage of the structural and sequence conservation properties of the GPCRs and employs machine learning on accumulated mutation data, was quite successful in thermostabilizing the serotonin 5-HT_2C receptor. In these methods, however, the physicochemical origins of the stability changes arising from mutations are somewhat ambiguous. The method proposed by Bhattacharya et al. was claimed to be a physics-based one and uses an energetic score in which only van der Waals (vdW) and torsion energies are taken into account. However, its application is limited to a mutation from a nonpolar residue to Ala, primarily because protein intramolecular hydrogen bonds (HBs) are neglected in the score. We have been developing another physics-based method and applied it to G-protein-coupled receptors (GPCRs) (Kajiwara et al. 2016; Kajiwara et al. 2017; Yasuda et al. 2016; Yasuda et al. 2017), currently the most attractive targets for drug discovery, forming a large family of membrane proteins. In this article, we summarize the method, review the successful results which have been achieved so far, and describe the subjects to be pursued in future studies.

Crucial importance of thermodynamics

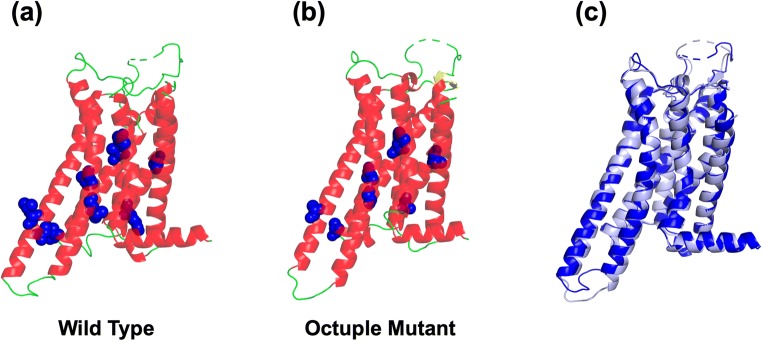
GPCRs are seven-transmembrane proteins (Pierce et al. 2002). The conformation of a GPCR with no ligand binding can be considered in terms of the two-state model: There are inactive and active states which are in equilibrium with each other (Kobilka and Deupi 2007; Latorraca et al. 2017; Vauquelin and Van Liefde 2005). In the solution of the 3D structure using X-ray crystallography, the structure either in the inactive state or in the active one is obtained, depending on the experimental condition. There are a number of cases where two membrane proteins, whose 3D backbone structures are almost indistinguishable, are quite different in terms of the thermostability. As a paradigmatic example, Fig. 1 compares the structures of the wild type and an octuple mutant (A54L, T88A, R107A, K122A, L202A, L235A, V239A, and S277A) for the human adenosine A_2A receptor (A_2AR), an important GPCR (Doré et al. 2011). They are quite similar to each other. Nevertheless, the apparent denaturation temperature T_m of the octuple mutant is higher than that of the wild type by ~ 20 °C.

Fig. 1.

Structures of (a) the wild type and (b) the octuple mutant of A_2AR in the inactive state. The residues before and after the octuple mutation are indicated by the blue sphere representation. (c) Backbone structure of the wild type (drawn in blue) superimposed on that of the octuple mutant (drawn in light blue)

It is impossible to predict which of the two structures is more thermostable by geometrically comparing their microscopic characteristics. A molecular dynamics (MD) simulation combined with an all-atom model, which provides atomistic details, is not capable of reproducing the stability difference, either. We emphasize that thermodynamics is indispensable. Correlating the microscopic structural information with thermodynamic properties through statistical mechanics is an indispensable tool for the elucidation of stability differences. Using our method developed in this direction, we were successful in reproducing for A_2AR that the octuple mutant is significantly more thermostable than the wild type and unveiling its physical origin (Kajiwara et al. 2016).

Folding mechanism of a water-soluble protein

Our theoretical method for membrane proteins has been developed on the basis of the progress made by Kinoshita and coworkers for water-soluble proteins (Harano and Kinoshita 2005; Hayashi et al. 2017; Hayashi et al. 2018; Kinoshita 2009a; Kinoshita 2009b; Kinoshita 2013; Murakami and Kinoshita 2016; Oshima and Kinoshita 2013; Oshima and Kinoshita 2015; Yasuda et al. 2012; Yasuda et al. 2010; Yoshidome et al. 2008). A water-soluble protein is immersed in water molecules which energetically move around. The translational displacement of water molecules due to this thermal motion plays essential roles in protein folding. The most important driving force in protein folding is the gain of translational, configurational entropy of water coexisting with the protein in the system. The backbone and side chains of a protein generate excluded volumes (EVs) for water molecules. An EV, the volume of the space inaccessible to the centers of water molecules, restricts the translational freedom of water molecules. A feature of protein folding is that the backbone and side chains are closely packed, which is accompanied by a decrease in the total EV, leading to a gain of water entropy. In particular, the close packing of side chains with a variety of geometric properties makes a dominant contribution to the water-entropy gain (see Fig. 2). Though the EV is emphasized in the above explanation, the water-entropy gain is also dependent on the changes in area and curvature of the water-accessible surface upon protein folding. In a conventional view, the water near a nonpolar group is entropically unfavorable due to the water structuring, and the reduction of the amount of such unfavorable water upon protein folding leads to a gain of water entropy. This effect is certainly present but much smaller than the EV effect described above. The water-entropy gain upon protein folding is quite large. For example, the folding of apoplastocyanin with 99 residues is accompanied by a gain of ~ 670k_B (k_B is the Boltzmann constant) (Yoshidome et al. 2008).

Fig. 2.

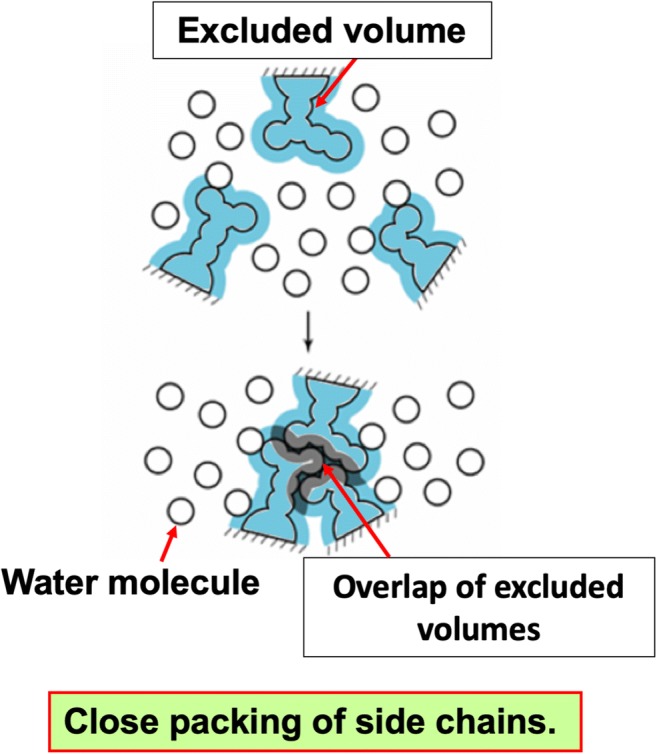
Close packing of side chains. The presence of a side chain generates an excluded volume (EV) to which the centers of water molecules are inaccessible, thus restricting the translational freedom of the water molecules. When side chains are closely packed, the EVs overlap, and the total volume available for water molecules increases by the overlapping volume, reducing the restriction

In the native state, the protein conformation exhibits only small fluctuation due to the close packing of the backbone and side chains. Hence, the number of accessible conformations is quite small. In the denatured state, by contrast, there is not a well-defined conformation with the result of a very large number of accessible conformations. Thus, protein folding is accompanied by a large loss of conformational entropy of the protein itself. A decrease in protein intramolecular energy, which arises primarily from the formation of intramolecular hydrogen bonds (HBs), is often pointed out as the factor surpassing the entropic loss. However, it is canceled out by an increase in the sum of protein-water and water-water interaction energies. Our analyses showed that the increase is larger than the decrease (we note that many of protein-water HBs are lost upon protein folding) (Hayashi et al. 2017; Hayashi et al. 2018; Yasuda et al. 2012; Yoshidome et al. 2008).

Folding mechanism of a membrane protein: similarity and difference in comparison with that for a water-soluble protein

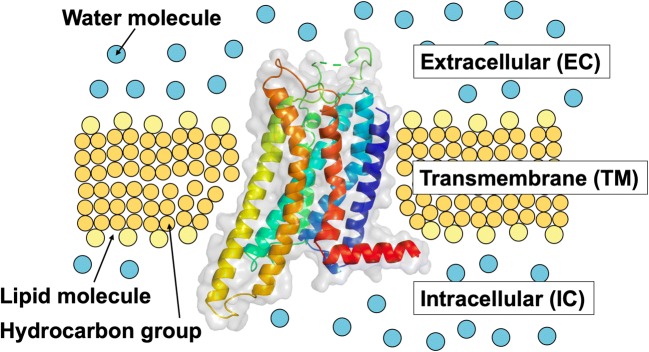
A membrane protein comprises transmembrane (TM), extracellular (EC), and intracellular (IC) portions (see Fig. 3). The EC and IC portions are exposed to aqueous solution. Since the stability of a GPCR is determined primarily by that of its TM portion as argued in the “Outline of our theoretical method”, our discussion is focused on the TM portion unless otherwise mentioned.

Fig. 3.

Transmembrane (TM), extracellular (EC), and intracellular (IC) portions of the human adenosine A_2A receptor (A_2AR)

A membrane protein is immersed in hydrocarbon groups within the lipid bilayer which energetically move around. The translational displacement of the hydrocarbon groups due to this thermal motion should play essential roles in protein folding, just as in the case of a water-soluble protein. A membrane protein is similar to a water-soluble one in this respect. Since the hydrocarbon groups are nonpolar, protein folding does not undergo an energetic penalty like the loss of protein-water HBs. A membrane protein is different from a water-soluble one in this respect. Taken together, protein folding is driven by the gain of translational, configurational entropy of the hydrocarbon groups and the decrease in protein intramolecular energy.

Our method for identification of thermostabilizing mutations for a membrane protein

Outline of our theoretical method

We calculate the change in free energy ΔF (< 0) upon protein folding. In general, all of the TM, EC, and IC portions must be considered for the seven-transmembrane proteins. For a GPCR, however, we can assume that ΔF is governed by the change in free energy for the TM portion for the following reason. The backbone and side chains in the EC and IC portions are not closely packed so that a ligand and a G protein can bind to the EC and IC portions, respectively. Hence, the changes in free energy for these two portions are significantly smaller (see a later section entitled “Entropic component”). It is worthwhile to add that we showed that all the three portions must be considered for the other seven-transmembrane proteins such as microbial rhodopsins (see Extension to microbial rhodopsins in the Successful results achieved).

Modeling the denatured state of a membrane protein is a difficult task. The TM portion in the folded state, which is abundant in hydrophobic residues, should remain within the TM region even in the denatured state. The EC and IC portions in the folded state, which consist of significantly many hydrophilic residues, should remain exposed to water even in the denatured state. That is, the folding process of the TM portion occurs in nonpolar environment while that of EC and IC portions occurs in aqueous environment, which was rationalized in our earlier work (Yasuda et al. 2019). We assume that the TM portion in the denatured state possesses neither the effective packing of side chains nor the intramolecular hydrogen bonding.

ΔF consists of an energetic component ΔU (< 0) and an entropic component ΔS (> 0): ΔF = ΔU−TΔS (T is the absolute temperature). A novel aspect of our method is the following: The hydrocarbon groups act as the solvent particles for a GPCR; and the entropic effect originating from the translational displacement of solvent particles must be taken into account as a pivotal factor. As argued in the “Physical picture of thermal denaturation”, ΔF calculated at T = T₀ = 298 K is a good measure of the thermostability. Hereafter, ΔF denotes the free-energy change at T = T₀. The lower ΔF is, the higher the thermostability is. Our concern is to identify a mutation which further lowers ΔF. Defining ΔΔF as ΔF_M−ΔF_W (the subscripts “M” and “W”, respectively, the values for a mutant and the wild type), we seek a mutation which makes ΔΔF lower as much as possible. Unless otherwise mentioned, we postulate that the 3D structure of the wild type is given as part of the input data. Since we wish to explore the whole mutational space (i.e., examine all the possible mutations), it is required that ΔF_M and ΔF_W be calculated quite rapidly. To this end, we account for only the fewest number of physicochemical factors that substantially influence the thermostability of a membrane protein and adopt as many simplifying treatments as possible with the physically essential factors being retained. As a consequence, ΔF_M or ΔF_W can be calculated only in ~ 1 s on a standard workstation.

Solvent for a membrane protein

Recent experimental studies showed that many membrane proteins fold and oligomerize quite efficiently in nonpolar environments which bear little similarity to a membrane (e.g., those provided by surfactant molecules and amphipols) (Popot and Engelman 2016). We interpret this result as follows. The essential factors required for membrane-protein folding are the thermal motion of surrounding solvent molecules (i.e., the presence of solvent-entropy effect) and the intramolecular hydrogen bonding without the energetic penalty, the loss of protein-solvent HBs. As long as these two factors are present, the details of specific characteristics of nonpolar chains of lipid molecules are not important.

Further, we note that a membrane is immersed in water. Lipid molecules forming the membrane generate the EVs for water molecules. When lipid molecules are closely packed, the EVs overlap, leading to an increase in the total volume available for the translational displacement of water molecules and to a corresponding gain in the water entropy. Thus, the EV of the membrane is determined by the packing efficiency of its lipid molecules. When a membrane protein takes a structure with a larger EV, the membrane generates a larger EV for water molecules. Thus, water indirectly acts as the solvent. Consequently, we should take the view that a membrane protein is immersed in bulk solvent. We showed that in a theoretical method focused on the entropic EV effect at ambient temperature and pressure, water can be modeled as a hard-sphere solvent whose diameter and packing fraction are set at those of water (Kinoshita 2009a; Oshima and Kinoshita 2013; Yasuda et al. 2010). Taken together, we can employ a simplified model for the bulk solvent mentioned above: an ensemble of neutral hard spheres whose diameter and packing fraction are set at those of water at ambient temperature and pressure. Refer to our earlier publications for more details (Kajiwara et al. 2016; Kajiwara et al. 2017; Yasuda et al. 2016; Yasuda et al. 2017; Yasuda et al. 2019).

Our method is pragmatic in the sense that it enables us to test all of the possible mutations with minor computational effort. The chemical properties and the connectivity of atoms of lipid molecules, which are neglected in our method, may influence the structural stability of a membrane protein. Taking account of these factors can lead to a higher success rate in the identification of stabilizing mutations, but the resultant method becomes much more sophisticated and the pragmatic aspect mentioned above will be vitiated. We emphasize that the success rate of the present version of our method is satisfactorily high.

Entropic component

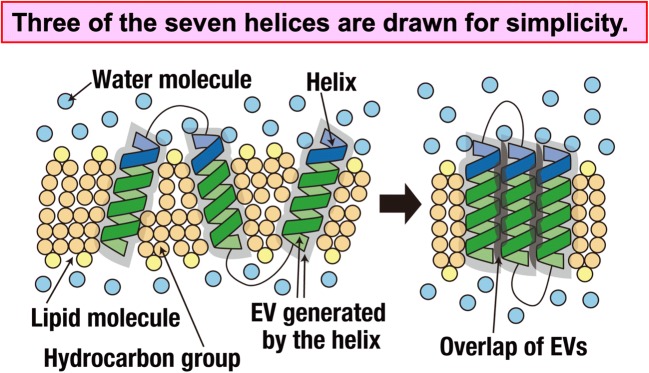
The effect of the solvent entropy, which corresponds to the number of accessible configurations of the solvent, is introduced in ΔS. In a molecular solvent, not only the translational entropy but also the rotational and vibrational entropies are present. However, as far as the solvation entropy of a solute is concerned, the contribution from the translational entropy is relatively much larger. This is why the solvent can be regarded as a hard-sphere solvent. For a membrane protein, the solvent-entropy gain upon protein folding is achieved primarily by the association of helices (the number of helices is seven in a GPCR) accompanying the close packing of side chains (see Fig. 4).

Fig. 4.

Association of helices of a membrane protein in a solvent formed by hydrocarbon (CH₂, CH₃, and CH) groups of lipid molecules and water molecules represented by the orange circles and the light-blue circles, respectively. Three of the seven helices are drawn for simplicity. The association is characterized by the close packing of side chains

ΔS=S_N−S_D (S is the solvation entropy and the subscripts “N” and “D” denote the native and denatured states, respectively) corresponds to the solvent-entropy gain upon protein folding represented by that achieved by the association of seven helices. It is not straightforward to calculate S_N or S_D using a statistical-mechanical theory because the solvent must be treated not as a continuum but as an ensemble of particles with finite sizes and the solute possesses a complex polyatomic structure. We have overcome this problem by combining the integral equation theory (Hansen and McDonald 2006) for solvation with the morphometric approach (MA) (Hayashi et al. 2017; Hayashi et al. 2018; Roth et al. 2006). The MA enables us to account for the polyatomic structure with quantitative accuracy and high speed. The idea of the MA is to express S by the linear combination of only four geometric measures of a solute molecule:

$$S/k_{\mathrm{B}}=C_1{V}_{\mathrm{ex}}+C_{2}A+C_{3}X+C_{4}Y.$$ 1

Here, Eq. 1 is referred to as the morphometric form, V_ex is the excluded volume generated by the solute molecule, A is the solvent-accessible surface (SAS) area, X and Y are the integrated mean and Gaussian curvatures of the SAS, respectively, and k_B is the Boltzmann constant. Hereafter, “C₁V_ex” and “C₂A + C₃X + C₄Y” are referred to as the “EV term” and the “SAS term”, respectively. The translational component of S is influenced by the EV and SAS terms. We note, however, that the EV term is significantly larger than the SAS term. On the other hand, the rotational and vibrational components of S are independent of the EV term and can reasonably be neglected. The four coefficients (C₁–C₄), which depend only on the solvent properties, can be determined in simple solute geometries: they are calculated from the values of S of isolated hard-sphere solutes with sufficiently many different diameters. Once the four coefficients are determined, ΔS is obtained simply by calculating the changes in these four geometric measures upon protein folding.

Energetic component

The effect of protein intramolecular electrostatic energy, which is represented primarily by hydrogen bonding, is incorporated in ΔU. Upon protein folding, protein intramolecular vdW or electrostatic interaction energy decreases, but the sum of protein-solvent and solvent-solvent vdW or electrostatic interaction energies increases. For the vdW term, it can be assumed that the decrease and the increase are compensating. For the electrostatic term, however, such compensation does not occur. Within the TM region, the formation of intramolecular HBs directly leads to energy lowering.

The formation of an intramolecular HB leads to an energy change of −E_NP (E_NP > 0). In principle, the interaction energy of a donor-acceptor pair is distance dependent. A quantum-chemical calculation showed that in vacuum the energy change −E* (E* > 0) accompanying the formation of an HB (i.e., the energy at the contact) is −10k_BT₀ (T₀ = 298 K) (Mitchell and Price 1991). However, the pair is in the environment where atoms possessing positive or negative partial charges are present. Therefore, it is physically more reasonable to regard the interaction energy as the potential of mean force (PMF). The PMF is weaker and shorter ranged than the direct interaction energy. We optimized E_NP to 5k_BT₀ for membrane proteins (Kajiwara et al. 2018; Yasuda et al. 2017; Yasuda et al. 2019). The PMF is a linear, short-ranged function of the distance. The minimum value of the PMF is −E_NP. We adopt a modified version of the criteria suggested by McDonald and Thornton (McDonald and Thornton 1994) for identifying a HB. The maximum distances between H and A (H is a hydrogen atom and an intramolecular hydrogen bond is expressed as DH· · · A where D is the donor and A is the acceptor) and between D and A are set at 3.0 and 4.4 Å, respectively. We assume that the denatured state possesses no intramolecular HBs. When an intramolecular HB is formed upon protein folding, we consider a decrease in energy expressed by −E_NP, which is linearly dependent on the distance between centers of H and A. We examine all of the donors and acceptors for intramolecular hydrogen bonds and calculate the net energy decrease. All of the backbone-backbone, backbone-side chain, and side chain–side chain intramolecular HBs are taken into consideration.

Physical picture of thermal denaturation

Protein denaturation leads to a significantly large gain of conformational entropy S_C measuring the number of accessible conformations of a protein. At low T, only the torsion angles with sufficiently low E_torsion (E_torsion is the torsion energy) are allowed. At high T, the angles possessing higher E_torsion become more allowable. Thus, the ranges of torsion angles allowed increase as T becomes higher. this effect is much larger in the denatured state than in the native one, due to the much weaker steric hindrance. For this reason, ΔS_C=S_C,D−S_C,N (ΔS_C > 0 is the conformational entropy gain upon protein denaturation, the subscripts “D” and “N” denote the values of the denatured and native states, respectively) is a strongly increasing function of T.

The effect of S_C, which is not incorporated in ΔF, is taken into account as explained in what follows. In any protein, all the 20 amino acid species are used rather impartially on the whole. Hence, not only S_C,D and S_C,N but also ΔS_C can be considered to be proportional to the number of residues N_r with the result that ΔS_C/(k_BN_r) is almost independent of the protein species. However, −ΔF/(k_BT₀N_r) (−ΔF > 0) is more sensitive to packing and hydrogen-bonding properties of the native state and dependent on the protein species. As illustrated in Fig. 5, the thermostability is determined by the competition between −ΔF/(k_BT₀N_r) and ΔS_C/(k_BN_r). The difference between the wild type and a mutant in ΔS_C can be neglected. The order of the denaturation temperature T_m is in accord with that of ΔF/(k_BT₀N_r) evaluated at T = T₀. Hence, ΔF/(k_BT₀N_r) = ΔU/(k_BT₀N_r)−ΔS/(k_BN_r) can be regarded as a measure of the thermostability (Yasuda et al. 2019). The lower the measure is, the higher the thermostability is. When the wild type and a mutant of the same protein are considered, there is no need to normalize ΔF/(k_BT₀) by N_r. ΔF/(k_BT₀) = ΔU/(k_BT₀)−ΔS/k_B is the measure (Kajiwara et al. 2016; Kajiwara et al. 2017; Yasuda et al. 2016; Yasuda et al. 2017).

Fig. 5.

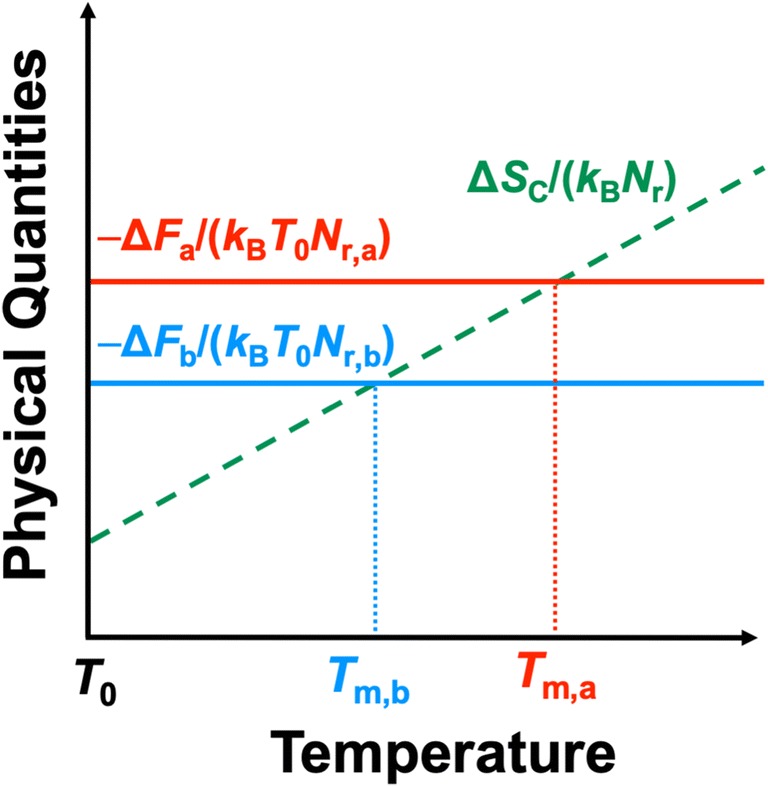
Physical picture of thermal denaturation of two membrane proteins. Subscripts “a” and “b” denote the values for proteins a and b, respectively. For example, ΔF_a/(k_BT₀N_r,a) and T_m,a, respectively, are the free-energy change upon protein folding and the denaturation temperature for protein a (N_r,a is the number of residues of protein a). ΔS_C is the conformational-entropy gain upon protein denaturation. −ΔF is almost independent of T. ΔS_C/(k_BN_r) do not necessarily increase in proportion to T. If −ΔF_a/(k_BT₀N_r,a) > −ΔF_b/(k_BT₀N_r,b), T_m,a > T_m,b. Thus, ΔF/(k_BT₀N_r) evaluated at a temperature T = T₀ is a good measure of the thermostability. The lower the measure, the higher the thermostability

Successful results achieved

Thermostabilization of A_2AR

We have achieved a number of successful results for GPCRs of class A in the inactive state. We first considered A_2AR (Yasuda et al. 2016). Using the wild-type structure experimentally solved and modeling the structure of a mutant by means of the MODELLER program, we identified several thermostabilizing mutations. It is found that T88 and S91 are key residues. Here, a key residue is the residue to be mutated in the sense that many of its mutations are highly stabilizing. For 19 mutations for each of T88 and S91, we calculated ΔΔF and chose those satisfying ΔΔF/(k_BT) < Φ (Φ is set at 0 or −5) as stabilizing mutations. For nine of the mutants chosen, we experimentally examined if they are actually more thermostable than the wild type. The double mutation, T88E−S91R, was also tested (T88E and S91R were theoretically predicted to be stabilizing). The measure of the thermostability was either the melting temperature T_m (a) or the half-life time τ at a moderately high temperature (b) (35 °C in the present study), which is defined as the time at which the percentage of folded protein decreased to 50%. The success rate was dependent on the value of Φ set and which of (a) and (b) was adopted, but it was in the range 6/8–7/7 which is quite high. Here, the success rate is defined as follows: When M₁ mutations are theoretically predicted to be stabilizing but only M₂ of them are actually stabilizing, the success rate is M₂/M₁. T_m of T88E or S91R was made higher than that of the wild type by ~ 7 °C and T_m of T88E−S91R by ~ 12 °C.

Success rate

When the 3D structures of the wild type and its mutant are both experimentally available, we have never failed to correctly guess which is more thermostable. For example, for the wild type and an octuple mutant of A_2A in the inactive state shown in Fig. 1 and the wild type and a quadruple mutant (L48A, A54L, T65A, and Q89A) of A_2A in the active state (Lebon et al. 2011), we could show that the mutant is more thermostable than the wild type (Kajiwara et al. 2016; Kajiwara et al. 2018). It follows that our method is capable of correlating the thermostability with the 3D structure. However, to put it the other way, our method is not successful if the 3D structure is not sufficiently accurate. A problem is that from a pragmatic point of view, the structure of the wild type as well as that of its mutant are usually unknown.

When the wild-type structure is unknown, we employ the homology modeling. In the homology modeling, the amino acid sequence of the target protein is aligned to that of another protein as a template protein, and the 3D-structure models of the target are constructed using the structural information of the template. It is required that a template possess sufficiently high TM region identity (TMI) with the target. Multiple structure models are thus generated, and the model with lowest ΔF is chosen. The success rate is remarkably dependent on the TMI. In the case of A_2AR, where the wild-type structure is intentionally not used and modeled as explained above, the best value of TMI found is 34% with the result of a success rate of 5/7 (i.e., it decreases from 7/7 to 5/7) (Kajiwara et al. 2017). For the prostaglandin E receptor 4 (EP4), however, the best value is only 17%, and the success rate is as low as 2/10. The improvement of how to model the wild-type structure is an urgent task.

Discovery of a hot-spot residue

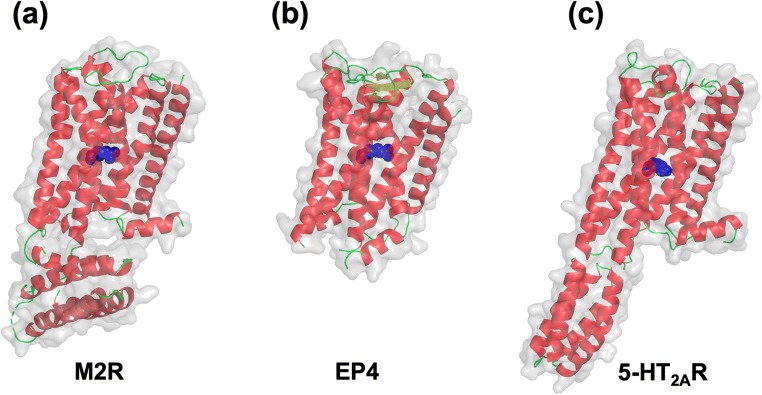
As one of the most important achievements, we discovered the existence of “key residues” and “hot-spot residues”. A key residue is the residue to be mutated in the sense that many of its mutations are highly thermostabilizing. A GPCR possesses multiple key residues. A hot-spot residue is the key residue designated by N_BW, which is common in different GPCRs. We have found that the residue with N_BW = 3.39 is a hot-spot residue for A2aR, M2R, EP4, and 5-HT_2AR in the inactive state. Here, N_BW is the Ballesteros-Weinstein (BW) number that is the enumeration of a GPCR transmembrane residue in the format, x.yz, where x is the helix number, and yz is the position of the residue relative to that of the most conserved residue designated as x.50 in the helix. The same BW number signifies the same position in the amino acid sequence. For example, “5.52” represents the second residue from the most conserved residue in helix 5 to the C-terminus side. By mutating the hot-spot residue to Arg or Lys, we were been successful in thermostabilizing several GPCRs including A_2AR, muscarinic acetylcholine receptor 2 (M2R), and EP4 (for A_2AR), the thermostabilizing mutations are S91R and S91K (Yasuda et al. 2017). In particular, new 3D structures for M2R and EP4 were solved using X-ray crystallography (Suno et al. 2018; Toyoda et al. 2019).

It is conjectured that a partially hydrated sodium ion Na⁺, which is bound to the surface of a pocket in the middle of the seven-transmembrane helical domain, plays important roles in stabilizing the inactive state for multiple GPCRs of class A including A_2AR (Katritch et al. 2014). There is a vacant space within the pocket and the net charge of its surface is negative. When Na⁺ is bound to the surface, the space is narrowed by surface-Na⁺ electrostatic attractive interaction. This brings not only energetic but also entropic stabilization. The narrower space results in a more compact protein structure and a smaller EV generated by the protein, leading to the entropic stabilization. S91 of A_2AR, S110 of M2R, or G106 of EP4 (the hot-spot residue) is on the pocket surface. Even in the absence of Na⁺, when the residue is mutated to the positively charged residue Arg or Lys, qualitatively the same effect comes into play, which stabilizes the inactive state. That is, S91R, S91K, S110R, S110K, G106R, or G106K mimics the allosteric modulation by Na⁺. Our method is capable of reproducing these features. We emphasize the following: For A_2AR, M2R, and EP4, our theoretical method predicts that the mutation of the hot-spot residues to Arg or Lys leads to exceptionally large, negative values of ΔΔU, −TΔΔS, and ΔΔF.

Of course, mutation of residues other than the hot-spot residue can possibly lead to considerably higher thermostabilization. We describe an example in what follows. Mutating the residue at a position of N_BW = 3.39 to Arg or Lys leads to significantly high thermostabilization for the serotonin 2A receptor (5-HT_2AR) in the inactive state (its 3D structure has newly been solved; the crystal structures of M2R, EP4, and 5-HT_2AR solved are shown in Fig. 6.) (Kimura et al. 2019; Suno et al. 2018; Toyoda et al. 2019). However, we found that another mutation for 5-HT_2AR in the inactive state, which is not relevant to the hot-spot residue, is even higher thermostabilizing (unpublished results). Further, we encountered a situation where the mutation of the hot-spot residue to Arg or Lys gives rise to instability (unpublished results). In such cases, our method should be very useful to the identification of thermostabilizing mutations.

Fig. 6.

Crystal structures of (a) M2R, (b) EP4, and (c) 5-HT_2AR. The mutated hot-spot residue at a position of N_BW = 3.39 (R110 in M2R, R106 in EP4, or K162 in 5-HT_2AR) is indicated by the blue sphere representation

Extension to microbial rhodopsins

The theoretical method reviewed in this article was developed for GPCRs. It has recently been extended to other seven-transmembrane proteins such as microbial rhodopsins. For GPCRs, we can assume that the stability is governed by the change in free energy for the TM portion because the backbone and side chains in the EC and IC portions are not closely packed so that a ligand and a G protein can bind to the EC and IC portions, respectively. However, we have shown that this is not always the case for general membrane proteins whose EC and IC portions are closely packed such as microbial rhodopsins. Therefore, the free-energy change upon protein folding is reformulated to consider the EC and IC portions. Refer to our recent publication for more details (Yasuda et al. 2019).

Concluding remarks

Some of the subjects to be pursued are as follows.

1. The free-energy change upon protein folding formulated and calculated in our theory is sensitive to the protein structure. This is quite reasonable because there are several cases where two proteins, whose 3D backbone structures are almost indistinguishable, are quite different in terms of the thermostability. Therefore, it is critical to develop reliable methods for modeling the wild-type and mutant structures.

2. For a GPCR, there are inactive and active states which are in equilibrium with each other in the absence of a ligand. Upon binding of a ligand to the GPCR in the active state form the outside of a cell, a change in the GPCR conformation takes place. The G protein bound to the GPCR is then activated by the exchange of the GDP to the GTP, and the activated G protein transmits signals to the cell interior. In general, the structural fluctuation in the active state is larger than that in the inactive state, and the active state is less stable than the inactive state. We wish to develop an efficient method enabling us to identify stabilizing mutations for GPCRs of class A in the active state, thus achieving results which are as successful as for those in the inactive state. We have already made a significant progress in this direction (unpublished results). A hot-spot residue for the active state needs to be discovered.

3. As mentioned above, the theoretical method has recently been extended to other seven-transmembrane proteins such as microbial rhodopsins. It is interesting to apply the extended version to GPCRs, because a mutation applied to the EC or IC portion could lead to significant thermostabilization. This type of stabilization may hinder the G-protein binding. However, if the structure of the TM portion is solved as a result, the solution should make a significant contribution to the structure-based drug design.

It is quite regrettable that people emphasize only the importance of solving the 3D structure of a protein with sufficiently high resolution and obtaining atomistic details of the structure, properties, and functions of a protein by means of the MD simulation. It is strongly desired to correlate microscopic, geometric characteristics with the thermodynamic quantities determining the thermostability through statistical mechanics, but studies on such a correlation are far behind those on the atomistic details mentioned above. Our study provides an important first step in this direction.

By further improving our theoretical method, a number of membrane proteins could be thermostabilized, making it possible to produce them in large amounts, facilitating functional analyses and biochemical applications, and increasing the efficiency in drug design.

Abbreviations

3D

Three-dimensional

5-HT_2AR

Serotonin 2A receptor

A_2AR

Human adenosine A_2A receptor

BW

Ballesteros-Weinstein

EC

Extracellular

EP4

Prostaglandin E receptor 4

EV

Excluded volume

GPCR

G-protein-coupled receptor

HB

Hydrogen bond

IC

Intracellular

M2R

Muscarinic acetylcholine receptor 2

MA

Morphometric approach

MD

Molecular dynamics

SAS

Solvent-accessible surface

TM

Transmembrane

TMI

Transmembrane region identity

vdW

van der Waals

Funding information

This work was supported by Grant-in-Aid for Scientific Research (No. 18H05425 to T. M., No. 17K15099 to S. Y., No. 19K14674 to T. H., and No. 17H03663 to M. K.) from Japan Society for the Promotion of Science (JSPS), by Research Grant from Koyanagi Foundation (to M. K.), by ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan), and by Basis for Supporting Innovative Drug Discovery and Life Science Research (BINDS) from Japan Agency for Medical Research and Development (AMED) under Grant Numbers JP18am0101083 and JP19am0101083 (to T. M.).

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.