Experimental and theoretical energetics of walking molecular motors under fluctuating environments

Abstract

Molecular motors are nonequilibrium open systems that convert chemical energy to mechanical work. Their energetics are essential for various dynamic processes in cells, but largely remain unknown because fluctuations typically arising in small systems prevent investigation of the nonequilibrium behavior of the motors in terms of thermodynamics. Recently, Harada and Sasa proposed a novel equality to measure the dissipation of nonequilibrium small systems. By utilizing this equality, we have investigated the nonequilibrium energetics of the single-molecule walking motor kinesin-1. The dissipation from kinesin movement was measured through the motion of an attached probe particle and its response to external forces, indicating that large hidden dissipation exists. In this short review, aiming to readers who are not familiar with nonequilibrium physics, we briefly introduce the theoretical basis of the dissipation measurement as well as our recent experimental results and mathematical model analysis and discuss the physiological implications of the hidden dissipation in kinesin. In addition, further perspectives on the efficiency of motors are added by considering their actual working environment: living cells.

Introduction

“Molecular motors work efficiently by using fluctuations.” You may have heard this phrase, but is it really true? Indeed, in the case of kinesin-1 (hereafter referred to as kinesin), one of the molecular motors that carry vesicles along microtubules in cells (Hirokawa et al. 2009; Vale 2003) (Fig. 1), its fluctuating movement was directly observed (Isojima et al. 2016). On the other hand, the efficiency remains undetermined due to the existence of the same fluctuations.

Fig. 1.

The molecular motor kinesin. Kinesin walks on a microtubule rail like a bipedal human, whereas the floating head fluctuates wildly (Isojima et al. 2016)

Kinesin is an energy transducer that converts chemical free energy into mechanical motion. Kinesin is a dimer protein about 50 nm long and composed of two catalytic sites (head), cargo binding sites (tail), and an elastic stalk region connecting the head and tail. The two heads cooperatively hydrolyze ATP by alternating the nucleotide binding states and binding to the microtubule rail (Mori et al. 2007). The kinetic mechanism of kinesin has been clarified through progressive single-molecule measurement technologies (Dogan et al. 2015; Isojima et al. 2016; Matsuzaki et al. 2019; Milic et al. 2014). However, the energetics, which are fundamental to understanding and improving the performance of energy transducers, are poorly understood for kinesin.

The problem on the energetics of kinesin stems from that they operate in nonequilibrium, small systems, whereas conventional thermodynamics typically focuses on macroscopic equilibrium systems. Recently, a novel nonequilibrium theory has been proposed that allows estimation of energy flows in such small systems; the Harada-Sasa equality (Harada and Sasa 2005). Using this theory, we have investigated the nonequilibrium energetics of kinesin both experimentally and analytically (Ariga et al. 2018). However, because these original papers were written for readers specialized in physics, understanding these works required a lot of knowledge in nonequilibrium statistical physics. Therefore, it was hard to access these studies for readers who specialize in biology, especially interested in molecular motors.

In this short review, we aim to introduce the published works for readers who are not familiar with physics. First, the problems in conventional energetics on kinesin are presented, and then we briefly explain the physical meaning of the novel equality that overcomes the problem (Harada and Sasa 2005). Then, we outline our recent work on kinesin’s energetics using this theory with experimental and analytical approaches (Ariga et al. 2018). Finally, we give further perspectives on the efficiency of motors by considering their working environment: living cells.

Conventional energetics of kinesin

The energetics of molecular motors have been discussed mainly through the measurement of the stall force (maximum traction force at zero velocity). Kinesin exerts a maximum force of about 7 pN, and its maximum work is estimated to be about 56 pNnm because the displacement per ATP is 8 nm. This value is about half that of the free energy change per ATP in vivo (Δμ = 80–100 pNnm). Thus, the efficiency is estimated to be around 50% (Howard 2001).

However, it is not appropriate to discuss the efficiency of kinesin in terms of the stall force for several reasons. First, under stall conditions, kinesin does not stop, but instead proceeds back and forth in 8 nm steps (Carter and Cross 2005; Nishiyama et al. 2002; Taniguchi et al. 2005). During the back steps, it can hydrolyze ATP, but not synthesize it. This means that, under the stall force condition, input chemical energy is continuously consumed without performing work, and the time-averaged efficiency becomes zero. Another point is that kinesin is a motor that transports vesicles within the cell, where the input free energy is fully dissipated through friction to the viscous fluid of the cytoplasm, rather than work in response to a conservative force such as optical tweezers. In the case of macroscopic motors, it may not be necessary to distinguish between work and viscous dissipation. However, in microscopic systems, the motion of motors is always agitated by thermal fluctuations and, in the case of kinesin, by kinesin’s own steps. Thus, to discuss the efficiency of kinesin, it is essential to separately measure the viscous dissipation consumed against viscous drag and the nonequilibrium dissipation generated by kinesin’s own stochastic steps. The Harada-Sasa equality enables the measurement of the two dissipations separately, which will be explained in the next section.

Theoretical basis of the nonequilibrium energetics: the Harada-Sasa equality

The Harada-Sasa equality has been proposed to evaluate energy dissipation in nonequilibrium small systems, as typified by molecular motors such as kinesin (Harada and Sasa 2005):

$$J_x=\gamma {〈v〉}^2+\gamma {\int }_{-\infty }^{\infty }\left[\tilde{C}\left(f\right)-2k_{B}T{\tilde{R}}^{\prime }\left(f\right)\right]\mathit{df}.$$ 1

Here, J_x is the dissipation per unit time through the degrees of freedom of the motion of interest (x), γ is the viscous drag, v is the velocity, and 〈〉 denotes average. C is the autocorrelation function of the velocity, indicating the velocity fluctuations, and R^′ is the real part (′) of the response function, which means the degree of change of the velocity when a tiny external force is applied. $\tilde{C}\left(f\right)$ and ${\tilde{R}}^{\prime }\left(f\right)$ are Fourier transformed (^~) to become functions of the frequency, f. This equality is complicated and requires knowledge of nonequilibrium physics to understand. In this section, for biological readers, we briefly describe the physical meaning of the Harada-Sasa equality by looking back at the history of its discovery.

Brownian motion and Einstein relation

Since the invention of early microscopes, it has been known that small objects in water move randomly. Robert Brown, a botanist in the early nineteenth century, observed the random motion of granules sprang out of pollens and initially believed that the motion was powered by the activity of life. However, he later discovered that small particles could cause the stochastic motion universally, even if not derived from living organisms. This motion has since been renamed Brownian motion. Because Brownian motion is due to the thermal motion of water molecules, it is also called thermal fluctuation. However, until the early twentieth century, the existence of molecules was still controversial.

Albert Einstein theoretically predicted the statistical properties of random motion without knowing that it had already been observed (Einstein 1905). Perrin used Einstein’s theory to demonstrate the existence of molecules by measuring Avogadro’s number (Perrin 1909). In the “Einstein relation,” the diffusion coefficient D of a particle is expressed with temperature T and its mobility μ:

$$D=\mu k_{B}T,$$ 2

where k_B is the Boltzmann constant. The mobility μ appearing on the right side is a coefficient proportional of the velocity change when a force is applied to the small particle. Thus, μ represents the response function of the particle. At the same time, Einstein also derived that the diffusion coefficient D on the left side is directly related to the magnitude of the fluctuation of the particle (〈x²〉 = 2Dt,where x is the particle displacement). That is, Eq. (2) represents the relationship between fluctuations and responses.

Fluctuation dissipation theorem

Ryogo Kubo extended this relationship to a more general medium that contains elastic elements but not a pure viscous fluid such as water. He showed that the following equation holds for the fluctuation of a system placed in equilibrium or where the response to a tiny external force does not change the state of the system (Kubo 1957):

$$\tilde{C}\left(f\right)=2k_{B}T{\tilde{R}}^{\prime }\left(f\right).$$ 3

Here, the left side corresponds to the power spectral density of the velocity fluctuation according to the Wiener–Khinchin theorem, meaning the magnitude of the fluctuation in the frequency domain. The response function on the right side is a complex quantity in a general medium. In a pure viscous fluid like water, it becomes a real quantity that corresponds to the mobility, μ. Because μ is the inverse of the viscous drag, γ, and is strongly coupled to the dissipation of energy through friction with the medium, this relationship between fluctuations and responses is termed the “fluctuation dissipation theorem.”

Note that Kubo’s original derivation for the general theorem (Eq. (3)) was starting from the basis of statistical physics. Einstein relation (Eq. (2)) can be derived by integrating Eq. (3). Readers interested in the derivations should refer to the textbook (Kubo et al. 1991).

Violation of the fluctuation dissipation theorem

The arguments so far are only valid at equilibrium or when just a tiny force is applied (linear response range). When the system is in a nonequilibrium state, far away from equilibrium, the right and left sides of Eq. (3) generally do not coincide with each other. The degree of this violation is considered a measure of the degree of nonequilibrium (Mizuno et al. 2007). In this case, besides thermal fluctuation (Brownian motion), an additional contribution such as active fluctuation or non-thermal fluctuation should consume energy. Harada and Sasa proposed that the dissipation from the system can be measured from the violation through Eq. (1), i.e., the Harada-Sasa equality (Harada and Sasa 2005).

Harada–Sasa equality

Let us now consider a small particle that is powered by a motor in water. The particle is driven by both the motor’s driving force and thermal fluctuations. All of the mechanical energy injected into the particle by the motor is dissipated into the water through the friction with water (viscous drag). However, the observed motion of the particle includes contributions from Brownian motion without dissipation. Therefore, to obtain the dissipation per unit time, J_x, it is necessary to remove the contribution of Brownian motion. Theoretically, by describing the motion of small particles in water with the Langevin equation, the total dissipation from the system can be determined as J_x ≡ 〈(γv − ξ) ∘ v〉, where ξ is the thermal fluctuating force that is assumed to be Gaussian white noise (Sekimoto 1997). Since ξ cannot be measured directly, J_x has not been experimentally obtained. However, it should be emphasized that all quantities on the right side of Eq. (1) can be measured experimentally. Thus, the Harada-Sasa equality is suitable for dissipation measurements in small stochastic systems such as molecular motors. A detailed derivation of Eq. (1) is given elsewhere (Deutsch and Narayan 2006).

The first term on the right side of Eq. (1) is the dissipative component of a particle moving at a constant velocity (viscous dissipation). The second term is a component in which the particles disturb the medium in a random way (nonequilibrium dissipation). For kinesin, the former dissipation can be regarded as the energy used to carry a cargo in the proper direction, whereas the latter seems to be wasteful energy dissipation. Thus, the components of each dissipation separately obtained by using Eq. (1) could be used as a new measure to describe the energy conversion efficiency of molecular motors such as kinesin. In fact, Harada’s first motivation to invent the equality was to elucidate the efficiency of kinesin molecules (Harada 2005; Harada and Sasa 2006), because he had been fascinated by the stochastic movement of kinesin motors (personal communications).

In the following sections, we review our recent works on the dissipation measurement of kinesin by utilizing the Harada-Sasa equality (Ariga et al. 2018). The obtained dissipation was a completely unexpected result, so that theoretical analysis with a mathematical model was also required to understand the energetics.

Measuring dissipation of kinesin

To measure the dissipation of kinesin, we developed a single-molecule manipulation microscope equipped with high-speed feedback-controlled optical tweezers. Optical tweezers are a tool in which a laser beam is focused at a certain point to add an attractive force toward the focal point to a micron-size small particle (Neuman and Block 2004). The 2018 Nobel Prize in Physics was awarded to Dr. Ashkin for his invention of optical tweezers. To manipulate kinesin movement, a small particle is attached to the end of the kinesin molecule with antibodies as a glue, and the intrinsic tail domain is truncated to eliminate autoinhibition (Aoki et al. 2013). The kinesin is allowed to walk on a microtubule rail while the probe particle is trapped with the optical tweezers (Fig. 2a). Since the trapping force is proportional to the distance between the particles and the focal point in the vicinity of the focal point, the force applied to the probe bead is changed by the kinesin walking. To overcome this effect, by recording the position of the particle with a quadrant photodiode (QPD) and making the focal point follow the movement of the particle through an acousto-optic deflector (AOD), it is possible to apply a constant external force (Force Clamp) (Fig. 2b).

Fig. 2.

Single-molecule dissipation measurements of kinesin. a Schematic diagram of the measurement system. A probe particle is attached to a single-molecule kinesin via an antibody. The image of the particle is projected to quadrant photodiodes (QPD). The position signals are processed in a field-programable gate array (FPGA) circuit and feedbacked to the focal point of the optical tweezers via an acousto-optic deflector (AOD). b A typical time-trace of the particle position and the focal point of the optical trap. When the kinesin does not interact with microtubules, the particle shows Brownian motion centered on the trap focus (Waiting). When it begins to interact with a microtubule, kinesin begins to walk. The motion is automatically detected, and feedback is initiated to keep the distance between the particle and the focal point constant (Force clamp). When the kinesin walks to the edge of the detectable range of the QPD, it is forcibly pulled back to the waiting position. c Relationship between kinesin’s fluctuation (red squares) and response (blue circles). The region of the difference between these two (green area) exhibits the violation of the fluctuation dissipation theorem (nonequilibrium dissipation)

We achieved high speed control of the focal point by using a field-programmable gate array (FPGA) for the feedback-loop circuit. By utilizing the property of the FPGA such that the electric circuit can be freely changed only by programming, arbitrarily external forces can be applied to the probe particle. To obtain the frequency spectrum of the response function, the change in velocity is measured by applying a tiny sinusoidal external force of various frequencies in addition to a constant external force. Velocity fluctuations can be determined from the power spectrum of the velocity under a constant external force. From the discrepancy between these two quantities, the total dissipation rate, J_x, can be obtained by using Eq. (1). Note that the focused degree of freedom, x, is not the position of the kinesin molecule, but of the probe particle.

Figure 2c shows the relationship between fluctuations and responses measured via the probe particle while the attached kinesin is walking on a microtubule. The input energy to the system sets the free energy change (Δμ~85 pNnm) associated with ATP hydrolysis under conditions close to the physiological environment. However, under conditions of high ATP concentration (~ 1 mM), which approximates the concentration in cells, it is difficult to measure the low frequency range because kinesin moving at high speed passes the detectable range of the QPD within 1 s. Thus, by reducing both the ATP and ADP concentrations without changing the ratio of the two (10 μM ATP, 1 μM ADP, 1 mM P_i), we reduced the velocity of kinesin without changing the input Δμ. In addition, a constant external force of F₀ = − 2 pN is constantly applied so that the output power is approximately maximized. The violation of the relationship between the velocity fluctuation and the response was clearly observed in the frequency range below about 20 Hz (Fig. 2c). From this area, the nonequilibrium dissipation per unit time was determined to be ~ 2.7 pNnm/s, and the viscous dissipation as ~ 1.4 pNnm/s. Both values are two orders of magnitude smaller than the power (~ 400 pNnm/s) for a constant external force.

The relationship between the free energy change input per unit time and the power and dissipation, J_x, is taken as follows:

$$\mathit{\Delta \mu }/\tau =-F_0〈v〉+J_x+J_{\mathit{All}\mathit{\text{others}}}.$$ 4

Here, the suffixes of J denote the degrees of freedom of interest, where x denotes the degree of freedom in the motion of the particle along the microtubule and All others denotes all other degrees of freedom. τ is the average time required for kinesin to hydrolyze one ATP molecule. The dissipation obtained in the experiment (J_x) was orders of magnitude smaller than the power (−F₀〈v〉), and when they were added together, the sum was only about 20% the rate of the input free energy change (Δμ/τ ~ 2200 pNnm/s). Similar results are obtained for 1 mM ATP, which is close to physiological conditions. These results suggest that ~ 80% of the input chemical energy is consumed as hidden dissipation (J_{All others}) through the other degrees of freedom, rather than dissipation through the motion of the particle being measured.

Mathematical model analysis

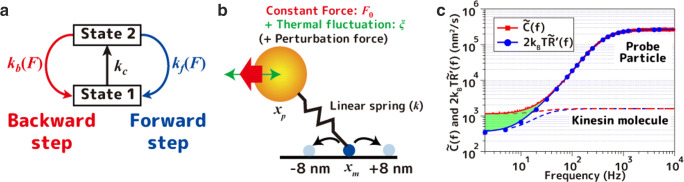
To investigate the origin of the hidden dissipation observed experimentally, we constructed a mathematical model of kinesin and performed numerical simulations and theoretical analysis. Although theoretical physicists have proposed a myriad of mathematical models for kinesin, we did not choose any of them for the following reasons. Most of the models assume a Brownian particle rolling over a one-dimensional potential, and as a result, the back step of kinesin is set to be the reverse path of the forward step. Experimentally, however, it is known that kinesin hydrolyzes ATP in the backward step (or by slippage without ATP hydrolysis), indicating that the back step is not the reverse path of the forward step (Hyeon et al. 2009). On the other hand, experimental biophysicists have proposed complex kinetic transition models by extracting the elementary transition rates mainly from single-molecule observations. However, the elementary process of the back step has not been clarified in detail (Clancy et al. 2011). Therefore, we adopted the most simple but branched model in which the intricate elementary processes of kinesin are degenerated into a transition between two states (Taniguchi et al. 2005) (Fig. 3a).

Fig. 3.

A mathematical model for kinesin. a A two-state transition model for kinesin. b Langevin dynamics including a particle. c Relation between the fluctuation and response of kinesin reproduced by the mathematical model. The dashed lines show fluctuations and responses derived from kinesin molecules

The transition between the two kinesin states is divided into transitions with and without steps, where the former is further divided into forward and backward steps. The rate constants for the transitions with steps k_f and k_b have a load dependency described as

$$k_{\left\{f,b\right\}}\left(F\right)=k_{\left\{f,b\right\}}^{0}exp\left(\frac{d_{\left\{f,b\right\}}F}{k_{B}T}\right),$$ 5

where F is the external force, k_f⁰ and k_b⁰ are the reaction rates when the external force is 0, and d_f and d_b are the response parameters to the external force having the dimension of distance. The five parameters, k_f⁰, k_b⁰, k_c, d_f, and d_b, required for the kinesin model can be obtained directly from the experiment (Taniguchi et al. 2005). To make the condition agree with the dissipation measurement, these parameters are obtained from fitting the force-velocity relationship of kinesin measured under the same conditions as the dissipation measurement with the theoretical equation in (Ariga et al. 2018).

The physical quantity measured in the experiment is the position of the particle pulled by kinesin. Thus, the motion of the particle is combined with the kinesin model described above (Fig. 3b). Assuming kinesin as a point (position: x_m) jumping back and forth with a step size d = 8 nm, the position of the particle (x_p) connected by a linear spring with a spring constant, k, can be described by the Langevin equation as

$$\gamma \frac{d}{\mathit{dt}}{x}_p=k\left(x_m-x_p\right)+F+\xi ,$$ 6

where the spring constant, k, and viscous drag, γ, are experimentally determined from the fluctuation analysis of kinesin-tethered particles immobilized on microtubules using ATP analogs (Gittes and Schmidt 1997).

Simulation results of the relationship between the fluctuation and the response of the kinesin model are shown in Fig. 3ccircles and squares. Despite the highly simplified model, the shape reproduced the experimental results very well, and quantitative agreement was also found for each physical quantity calculated from the mathematical model. This model can also be solved analytically (Fig. 3csolid lines), and it was confirmed that the Harada-Sasa equality (Eq. (1)) holds in this model (see Supplemental Material in (Ariga et al. 2018) for derivations). However, the origin of the ~ 80% hidden dissipation is still unknown.

What is hidden dissipation?

In the case of kinesin, the dissipation through the probe particle is more than two orders of magnitude smaller than the input Δμ and the work for a constant external force, indicating a hidden dissipation of ~ 80%. On the other hand, similar dissipation measurements have been carried out by Toyabe et al. for the rotary motor F₁-ATPase (Toyabe et al. 2010). They found that the sum of viscous dissipation and nonequilibrium dissipation from the rotation probe attached to F₁-ATPase is almost equal to the input Δμ, indicating that no hidden dissipation exists. To explain the different dissipations between the walking motor kinesin and rotary motor F₁-ATPase, we consider two candidate reasons: reversibility of the motor and softness of the linker.

First, we consider the reversibility of the motor. F₁-ATPase is a reversible motor that also acts as a power generator for ATP synthesis through the reverse reaction path when it is rotated backward by an external force. In contrast, the backward step of kinesin is not through the reverse path of the forward step, but rather through an alternative pathway that consumes ATP or through a state transition that does not involve ATP hydrolysis (slippage), meaning that kinesin is irreversible. However, in our measurement condition of physiologically high Δμ and low external force, the frequency of backsteps and slippage is estimated to be less than a few percentage points (Sumi 2017). Considering this point, wasteful ATP hydrolysis pathways cannot account for the ~ 80% hidden dissipation. Thus, the irreversibility of kinesin is not considered the main cause of the hidden dissipation.

The second candidate is the softness of the linker, which links the motor to the particle. In the experimental system of F₁-ATPase, the probe particles are attached directly to the rotation axis, so that the motion is totally transmitted. On the other hand, in the case of kinesin measurements, since the probe particle is connected via an elastic rod domain (stalk), it is possible that the motion of kinesin is not fully transmitted to the particles due to the softness of the stalk. However, by analyzing the violation of the fluctuation and response of the kinesin molecule with the mathematical model (Fig. 3cdotted lines), we found that the area almost agrees with the amount of the violation measured through the particle. This result indicates that the non-thermal motion of the kinesin molecule is properly transmitted to the particle. In other words, the softness of the linker has no artificial effect on the measurement of the nonequilibrium dissipation.

It should be noted that the dissipation discussed here is only from the degree of freedom, x, along the microtubule. We have performed the dissipation measurement for the y direction, but no difference between fluctuations and responses was observed within the error range. Although z-axis displacement cannot be measured with our equipment, we expected there to be almost no dissipation because no motion other than thermal fluctuation has been reported in that direction. Another degree of freedom is rotation. It has been reported that kinesin generates torque and spins cargo (Ramaiya et al. 2017). However, since we focus on the dissipation at low load condition with freely rotating probe particles, which is similar to the condition for vesicle transport, the dissipation associated with the rotation of the probe particle was estimated to be much smaller than the hidden dissipation due to the slow rotational velocity reported previously (Ramaiya et al. 2017).

Several other verifications have indicated that walking kinesin dissipates very little energy through the motion of the probe particle, meaning that as much as 80% of the input free energy is not used to transport the cargo. The experimental results of the dissipation measurements and the verification using a mathematical model suggest that the origin of the hidden dissipation is the internal dissipation that dissipates from inside the kinesin molecule (Ariga et al. 2018).

Efficiency in living cells

The above conclusion that most of the input free energy is dissipated from the interior of the kinesin molecule seems to be that kinesin is an inefficient motor (Hendricks 2018). However, this is unlikely when considering that kinesin has evolved over hundreds of millions of years. Instead, the above analysis may ignore the actual working environment of kinesin: living cells.

Unlike experimental conditions in vitro, the intracellular environment is extremely crowded with macromolecules and thereby has high viscosity (Ellis 2001; Goodsell 1991). It is easy to expect that higher viscosity increases the contribution of viscous dissipation (the first term in Eq. (1)) and thus the apparent efficiency of motors too. So, how crowded is the inside of a cell? Surprisingly, when cellular constituents are extracted from a cell, the cell extract shows remarkably high viscosity; as the extract approaches the intracellular concentration, the viscosity approximates divergence (Nishizawa et al. 2017b). If the viscosity diverges, the environment freezes, such that the motors cannot move. In living cells, however, molecular motors are always moving. Currently, this behavior is explained by the cell’s metabolic activity fluidizing the crowded intracellular environment (Parry et al. 2014).

The intracellular environment is not only crowded, but it is also actively (non-thermally) fluctuating (Guo et al. 2014; Nishizawa et al. 2017a). Generally, when colloidal particles in solution are highly crowded, they become a solid state by undergoing a glass transition (Hunter and Weeks 2012). It has been proposed that frozen (jammed) colloidal particles can be fluidized by applying a load or shaking (Liu and Nagel 1998). In fact, such systems under shear stress can fluidize through rearrangements of the particles (Petekidis et al. 2002). Similar fluidization has been observed in living cells (Nishizawa et al. 2017b; Parry et al. 2014), in which the cytosol was agitated by active fluctuations (Guo et al. 2014; Nishizawa et al. 2017a). Since fluidization and active fluctuations in cells exhibit a similar metabolism dependency, these results suggest that the intracellular environment is fluidized by active fluctuations.

On the other hand, it has long been proposed that molecular motors such as kinesin move by utilizing thermal fluctuations (Vale and Oosawa 1990), and recently fluctuating kinesin heads were directly visualized (Isojima et al. 2016). Molecular motors that operate with thermal fluctuations may also utilize non-thermal (active) fluctuations to optimize their performance in the intracellular environment. That vesicles transported by kinesin in cells move faster than in vitro is an example of “the dark matter of biology” (Ross 2016). More study of kinesin in living cells is necessary to evaluate its efficiency.

In addition to the kinesins reviewed here, various molecular motors, such as myosin and dynein, also operate in cells. These motors move many organelles not only directionally but also randomly. For example, the position of mitochondria in cells is always fluctuating (del Álamo et al. 2008), but the physiological role of this fluctuation is unclear. Active fluctuations in cells are unlikely to be noise, but have physiological significance for living beings (Oosawa 2007). Quantitative dissipation measurements of walking molecular motors and analytical methods with mathematical models will help clarify the energetics of these motors to understand how they operate efficiently in a fluctuating world.

Funding information

This work was supported by JSPS KAKENHI grant numbers JP18K03564 and JP19H05398.