Abstract
Exploiting the combination of latest microfabrication technologies and single cell measurement technologies, we can measure the interactions of single cells, and cell networks from “algebraic” and “geometric” perspectives under the full control of their environments and interactions. However, the experimental constructive single cell-based approach still remains the limitations regarding the quality and condition control of those cells. To overcome these limitations, mathematical modeling is one of the most powerful complementary approaches. In this review, we first explain our on-chip experimental methods for constructive approach, and we introduce the results of the “community effect” of beating cardiomyocyte networks as an example of this approach. On-chip analysis revealed that (1) synchronized interbeat intervals (IBIs) of cell networks were followed to the more stable beating cells even their IBIs were slower than the other cells, which is against the conventional faster firing regulation or “overdrive suppression,” and (2) fluctuation of IBIs of cardiomyocyte networks decreased according to the increase of the number of connected cells regardless of their geometry. The mathematical simulation of this synchronous behavior of cardiomyocyte networks also fitted well with the experimental results after incorporating the fluctuation-dissipation theorem into the oscillating stochastic phase model, in which the concept of spatially arranged cardiomyocyte networks was involved. The constructive experiments and mathematical modeling indicated the dominant rule of synchronization behavior of beating cardiomyocyte networks is a kind of stability-oriented synchronization phenomenon as the “community effect” or a fluctuation-dissipation phenomenon. Finally, as a practical application of this approach, the predictive cardiotoxicity is introduced.
Keywords: On-chip cell network assay, Constructive approach, Community effect, Cardiomyocyte, Synchronization, Fluctuation-dissipation phenomena
Introduction
From the late twentieth century, starting with determination of the way in which genetic information is stored, encoded, and transmitted, another challenge has arisen regarding epigenetic information. Epigenetic information is complementary to genetic information and essential to understand the entire landscape of living systems, such as how living cells can choose, reserve, share, and inherit acquired epigenetic information among neighboring cells and between generations through cell divisions. As we have moved into the post-genomic/proteomic era, such the complementary to genetic information should become more apparent. The cells in a group are individual entities, and differences arise even among cells with identical genetic information that have developed under the same conditions. These cells respond differently to perturbations (Spudich and Koshland 1976). Why and how do these differences arise? How are these differences of individual cells ironed out when they become groups, clusters, or tissues? We call this behavior the “community effect” of cells as induced uniformity. To understand the community effect, we need to understand the potential underlying differences of cells, and why and how their characteristics change when they form networks as epigenetic information.
If we are to obtain a comprehensive understanding of a living system, we need to analyze its epigenetic information, such as adaptation processes and community effect in a group of cells. As cells are minimal units of the system in terms of both genetic and epigenetic information, we must analyze their epigenetic information starting from the twin complementary perspectives of cell regulation being an “algebraic” system (with emphasis on temporal aspects; non-genetic adaptation in time) and a “geometric” system (with emphasis on spatial aspects; spatial pattern-dependent community effect) using identified single cells and their patterned groups. We thus commenced a series of studies to analyze the epigenetic information of single cells and the spatial geometric structures of cell networks to expand our understanding of how the fates of living systems are determined and how they can be changed.
The importance of understanding epigenetic information is expected to become apparent in cell-based biological and medical fields such as cell-based drug screening and the regeneration of organs from stem cells, fields in which phenomena cannot be interpreted without taking epigenetic factors into account. We thus started a series of studies focusing on developing a system that could be used to evaluate the epigenetic information in cells by continuously observing specific examples of cells and their interactions under fully controlled conditions as a constructive experimental method. However, the issues of limitations regarding the quality of cells and control of their conditions remained in the experimental constructive approaches. Mathematical modeling is one of the most powerful approaches to overcome these limitations of those experimental approaches.
Among the epigenetic information studies of cell network dynamics, synchronization of beating intervals of cardiomyocytes is one of the most attractive phenomena to understand how the cells acquire their synchronized “community information” from the mixture of different dynamical characteristics of component cells. Goshima explained this coordinated synchronous behavior as the faster firing regulation of heart beating (Goshima and Tonomura 1969) and is now called “overdrive suppression” (Vassalle 1977). This conduction regulation mechanism can also suppress the spontaneous beating of cells such as Purkinje fibers to follow to the contraction impulse from upstream sinoatrial (SA) node with its faster beating intervals. However, synchronization behavior of spontaneously beating single cardiomyocytes cannot be explained by one way upstream to downstream regulation mechanism. Especially the behavior of equal two-way network communication of cardiomyocytes in their small networks did not show the overdrive suppression phenomenon but followed unstable cardiomyocytes to more stable cardiomyocyte (Kojima et al. 2003; Kojima et al. 2006). And the tendency of entrainment of cardiomyocytes synchronization and synchronized beat intervals were depending on the number of cardiomyocytes in the network regardless of their geometry (Kaneko et al. 2007a). These experimental results of lower fluctuation regulation of synchronized heart beating have been examined in silico model simulations and successfully explained exploiting the “fluctuation-dissipation” theorem into the synchronization rule (Hayashi et al. 2017). Hence, our experimental and mathematical results on the community effect in the synchronization behavior of beating in cardiomyocyte networks indicated that the dominant rule of their synchronization is the stability-oriented synchronization phenomenon, which we call this “community effect,” as one of the fluctuation-dissipation phenomena.
In this review, we introduce the experimental and mathematical approach for analyzing the synchronization behavior of interbeat intervals (IBIs) of spontaneously beating cardiomyocytes as an example of on-chip cellomics study for epigenetic information analysis.
Experimental approach
On-chip cellomics technology: teconstructive understanding of the community effect in cardiomyocytes
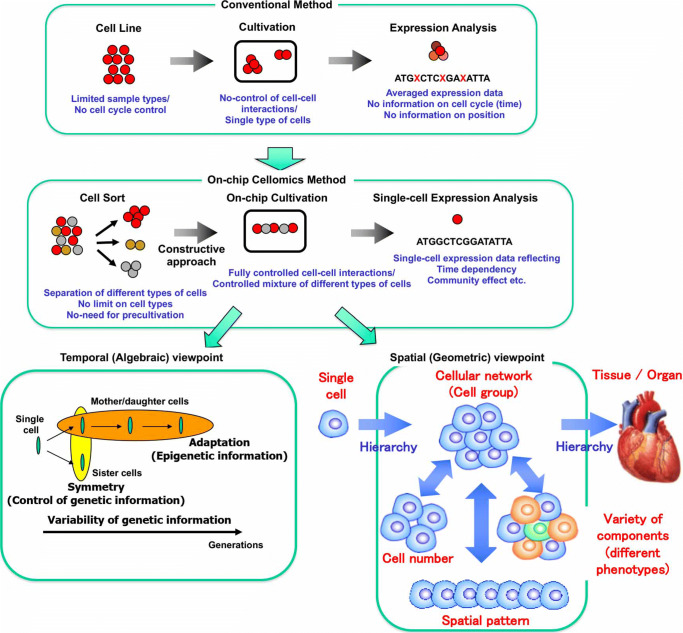
We have developed a constructive experimental approach both in temporal and spatial viewpoints for understanding epigenetic information exploiting latest microfabrication technologies and single cell handling-observation technologies. As shown in Fig. 1, the strategy behind our on-chip microfabrication methods, which we call “on-chip cellomics technologies” (Yasuda 2004), is constructed through three steps. First, we purify target cells from tissue individually in a nondestructive manner using several technologies, such as digestible DNA-aptamer labeling and cell collection (Anzai et al. 2007), ultra-high-speed camera-based real-time imaging cell sorting (Hayashi et al. 2011; Kim et al. 2014; Girault et al. 2017), or noninvasive handling of cells using an acoustic radiation force (Yasuda et al. 1996; Yasuda et al. 1996; Yasuda et al. 1997; Yasuda 2000). We then cultivate and observe the cells under fully controlled conditions (e.g., cell population, network patterns, or nutrient conditions) using an on-chip single-cell cultivation chip (Inoue et al. 2001; Inoue et al. 2004; Wakamoto et al. 2003; Wakamoto et al. 2005; Wakamoto and Yasuda 2006; Matsumura et al. 2003; Umehara et al. 2007; Umehara et al. 2007; Kawai-Noma et al. 2006) or an on-chip agarose microchamber system exploiting photo-thermal etching technology, which can control the microstructure of microchambers even during cell cultivation (Moriguchi et al. 2002; Kojima et al. 2003; Hattori et al. 2004; Sugio et al. 2004; Suzuki et al. 2004; Suzuki et al. 2005, 2004; Suzuki et al. 2007; Suzuki and Yasuda 2007a, ??; Kojima et al. 2003; Kojima et al. 2003; Kojima et al. 2004, 2005, 2006). Finally, we undertake single-cell-based genome/proteome analysis through a set of nanoprobes and adaptive electron microscopy (Kim et al. 2010), single-cell-based DNA/RNA release technology (Yasuda et al. 2000), or a 3-min ultra-high-speed polymerase chain reaction (PCR) measurement technology (Terazono et al. 2010).
Fig. 1.
On-chip cellomics analysis. Aim of single-cell-based analysis of multicellular systems: Temporal (algebraic) aspect and spatial (geometric) aspect
The advantage of the experimental on-chip cellomics approach is that, as it is a reconstructive approach of the simplified artificial minimum cell network model on a chip, it removes the complexity of the underlying physicochemical reactions that are not always completely understood and for which most of the necessary variables cannot be measured. Moreover, this approach shifts the view of cell regulatory processes from basic chemical grounds to a paradigm of the cell as an information-processing unit working as an intelligent machine capable of adapting to changing environmental and internal conditions. This is an alternative representation of the cell and can provide new insights into cellular processes. Thus, models derived from such a viewpoint can directly help in more conventional biochemical and molecular biological analyses that assist in our understanding of control in cells.
From the geometric perspective, two more detailed viewpoints of analysis should also be taken: one is on the population/community size dependence and the other is on the spatial (network) pattern dependence of groups of cells. In conventional cell-based studies, cell lines are usually used for acquiring the same type of cells, and are then cultivated in a cultivation dish without any control of their population or any formation of a community with other cell types. Finally, they are analyzed as a group regardless of any differences in their cell cycle regardless of their possible differences. In contrast, on-chip cellomics technology involves a new strategy with three steps: First, the cells are taken from a community using a nondestructive cell sorting procedure. Then, the cells are cultivated in a microchamber, in which cell network formation and medium environment are controlled. Finally, the genome/proteome measurement in each cell is measured (Fig. 1).
Photo-thermal etching on agarose layer for cell network formation control
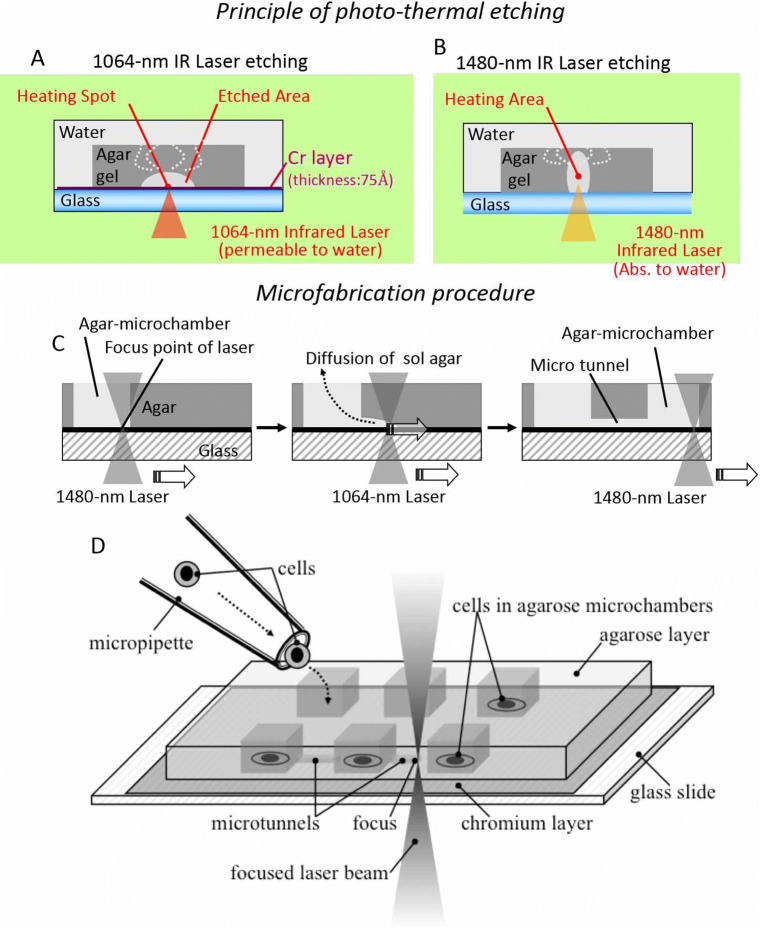
Flexible change of microstructures of cell-to-cell interactions or cell-network shapes on a chip during cultivation is necessary for the “temporal” and “geometric” constructive/reconstructive approach of cell-network studies. To accomplish this requirement, we have developed a photothermal etching method (Moriguchi et al. 2002; Hattori et al. 2004; Kojima et al. 2003; Kojima et al. 2004; Suzuki et al. 2005) with an agarose-microchamber cell-cultivation system (Fig. 2). This involves the area-specific melting of a portion of agarose of a whole light pathway by spot heating using a focused infrared laser beam of 1480 nm, which absorbs water; and of a portion of agarose close to a thin layer made of a light-absorbing material, such as chromium, with a laser beam of 1064 nm, which is permeable to water. When we combine infrared lasers with these two different wavelengths, we can fabricate microchambers and microtunnels flexibly for the noncontact three-dimensional photo-thermal etching of agarose. In other words, as the 1480-nm infrared beam is associated with the absorption of water and agarose gel, the agarose gel in the 1480-nm infrared light pathway was heated and completely melted. Moreover, as the 1064-nm infrared beam was not associated with this absorbance, the agarose melted just near the thin chromium layer, which absorbed the beam.
Fig. 2.
Photo-thermal etching method. Using focused infrared (IR) lasers of two different wavelengths, the thin layer of low-melting-point agarose on the chip was selectively melted in different manners. a A 1064-nm IRlaser etching. As the 1064-nm IR laser is not associated with the absorption of water, only a portion of the agarose near the thin absorption layer is heated and melted, changing its state from a gel to a sol. b A 1480-nm IR laser etching. In contrast, as the 1480-nm IR laser is associated with the absorption of water, all of the agarose in the light pathway is heated and melted. The agarose changed to a sol state is dispersed into the agarose gel and holes or tunnels are formed in the agarose layer. c Microfabrication procedure. Combining 1064-nm laser and 1480-nm laser, agarmicrochamber and micro tunnel were formed on the chip. d An example of stepwise cell network formation exploiting photothermal etching method
For phase-contrast microscopy and this μm-scale photo-thermal etching, lights of three different wavelengths (visible light for observation, and 1480-nm/1064-nm infrared lasers for spot heating to construct microchambers/microtunnels, respectively) were used simultaneously to observe the positions of the agarose chip surface and to melt a portion of the agarose in the area being heated. As described above, the advantage of this method is that we can apply this stepwise network formation (addition) approach even during cultivation, so we can change the network size and pattern of cardiomyocyte cells during cultivation by adding microchannels between two adjacent microchambers in a step-by-step fashion (Kojima et al. 2005, 2006); moreover, this approach is also applicable for neuronal networks (Sugio et al. 2004; Suzuki et al. 2004; Suzuki et al. 2005; Suzuki et al. 2007; Suzuki and Yasuda 2007b; 2007a).
Community effect of cells for their synchronization (1): two-cell model
As described in the previous subsection, the ability of photo-thermal etching of agarose microstructures to control the cell arrangement is beneficial for cardiomyocyte network studies. In this subsection, we introduce the application of this technology to reveal the involvement of the community effect in cardiomyocyte beating synchronization (Kojima et al.2003; Kojima et al. 2003; Kojima et al. 2004, 2005, 2006; Kaneko et al. 2007a, ; Kaneko et al. 2011; Kaneko et al.2014).
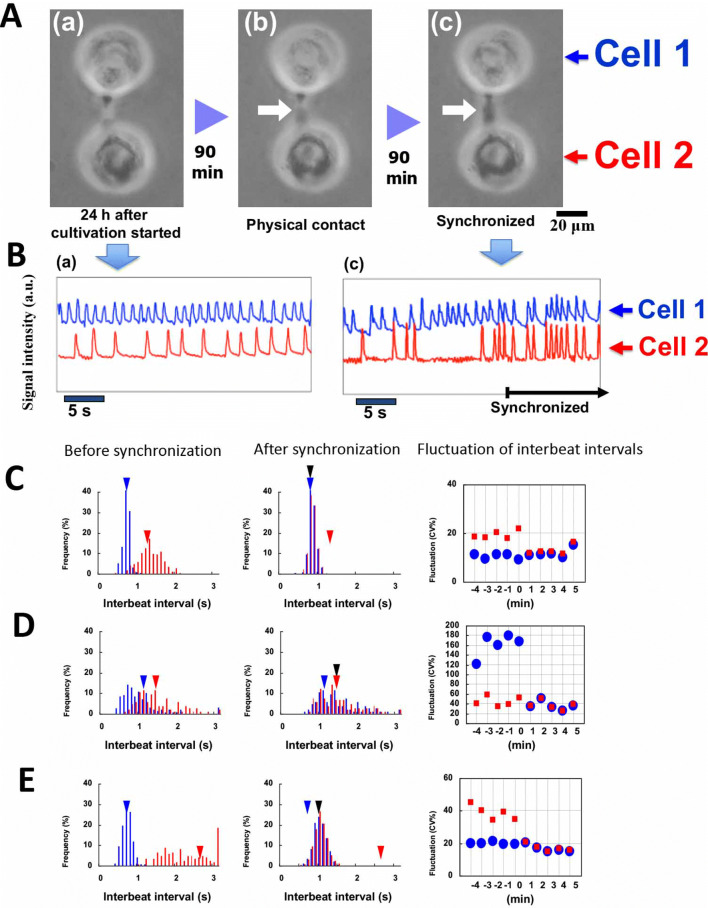
First, we investigated the roles of the beat rates (interbeat intervals, IBIs) and beat-rate fluctuation of isolated single cardiomyocytes in the reestablishment of synchronous beating by analyzing the changes of beating rates and their fluctuations before and after the synchronization of two cardiomyocytes through narrow channels with initially different rhythms (e.g., Fig. 3A, B) (Kojima et al. 2005; 2006). The results showed three types of synchronization of two cardiomyocyte networks: (1) the beating of the two cardiomyocytes synchronized at the faster of the two initial rates, but there was beating fluctuation at the lower of the two initial rates (Fig. 3C); and (2) the beating of the two cells synchronized at the lower of the two initial rates, but fluctuated at the lower of the two initial rates (Fig. 3D); and (3) the synchronization occurred at neither of the initial rates of single cardiomyocytes, with fluctuation of smaller of the initial fluctuations (Fig. 3E).
Fig. 3.
Synchronization of two cardiomyocytes. (A) Micrographs of two cardiomyocytes under isolated conditions (a), just after they were connected together (b), and just after synchronization started (c). (B) Beating waveforms at (a) and (c) in panel (A). (C)–(E) (left graph and center graph) Beating frequency spectrum before and after synchronization, respectively; distribution of interbeat intervals of two cardiomyocytes, and the change of the mean value of beating rhythm fluctuation at intervals of 1 min measured for 5 min before and after synchronization. Blue and red triangles show the mean values before synchronization, and black triangles show the mean value for the two cells after synchronization. (right graph) The change of the mean value of beating rhythm fluctuation [CV%: coefficient of variation (100 x standard deviation / mean beat rate)] at intervals of 1 min measured for 5 min before and after synchronization. Blue circles and red squares show the corresponding mean values of beating rhythm fluctuation for 1 min. Three types of synchronization tendencies were described: (C) synchronization to a faster beating cell, (D) synchronization to a slower beating cell, and (E) synchronization with a new beating frequency
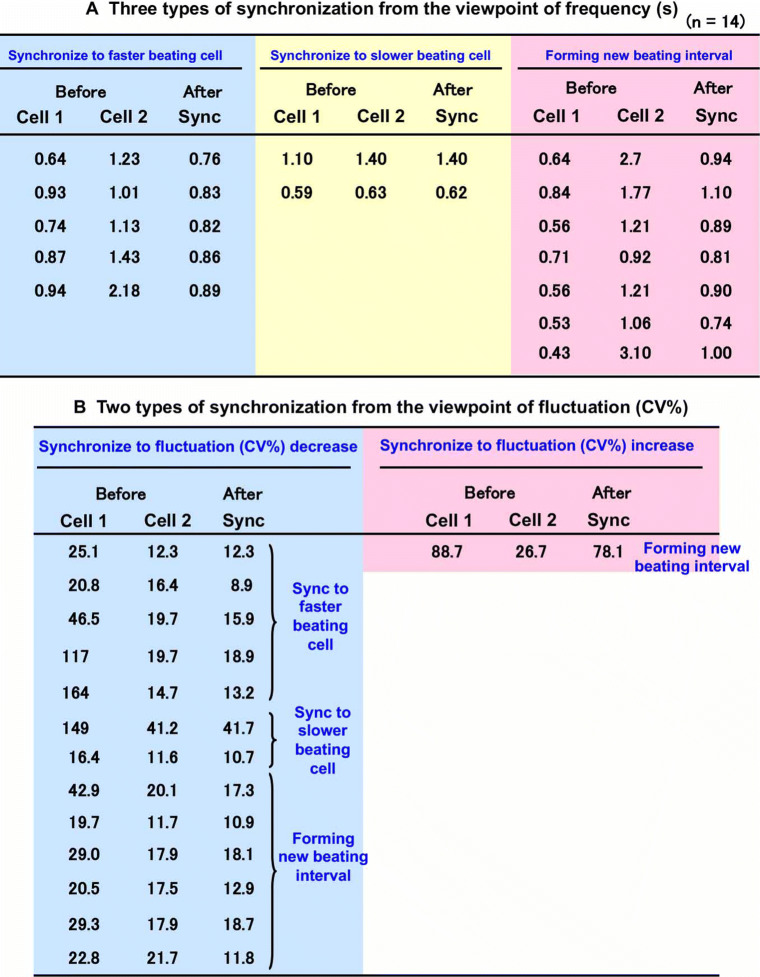
The IBIs of 14 two-cell pairs before and after synchronization are listed in Table A of Fig. 4. Five of the two-cell pairs synchronized at the initial rate of the faster cell, two of the pairs synchronized at the initial rate of the slower cell, and the other seven pairs synchronized at a rate other than one of the initial rates. In Table B of Fig. 4, the fluctuation data for the 14 cell pairs whose rate data are listed in Table A are grouped according to the change of the fluctuation before and after synchronization. Thirteen pairs synchronized with a fluctuation equal to or less than the initial fluctuation of the slower member of the pair, and one pair synchronized with a fluctuation larger than that of either of the two initial fluctuations.
Fig. 4.
Tendency of synchronization of two cardiomyocytes. (A) Three types of synchronization of two cardiomyocytes from the perspective of beating intervals. (B) Two types of synchronization from the perspective of beating stability (fluctuation of beating)
These results suggest that the fluctuation of reestablished synchronous beating by isolated cardiomyocytes is influenced more strongly by the fluctuation of the initial fluctuation of the beat rates of the isolated cardiomyocytes than the rate of the reestablished synchronous beating is influenced by the initial beat rates of the isolated cardiomyocytes. It is therefore possible that a cardiomyocyte whose beat rate fluctuates less than that of another cardiomyocyte entrains the beating rhythm of that cardiomyocyte, but we observed one pair of cells in which this did not happen. This indicates that the influence of a single cell is still not sufficiently strong to account for the process of entrainment in heart tissue.
Community effect of cells for their synchronization (2): cell number dependence
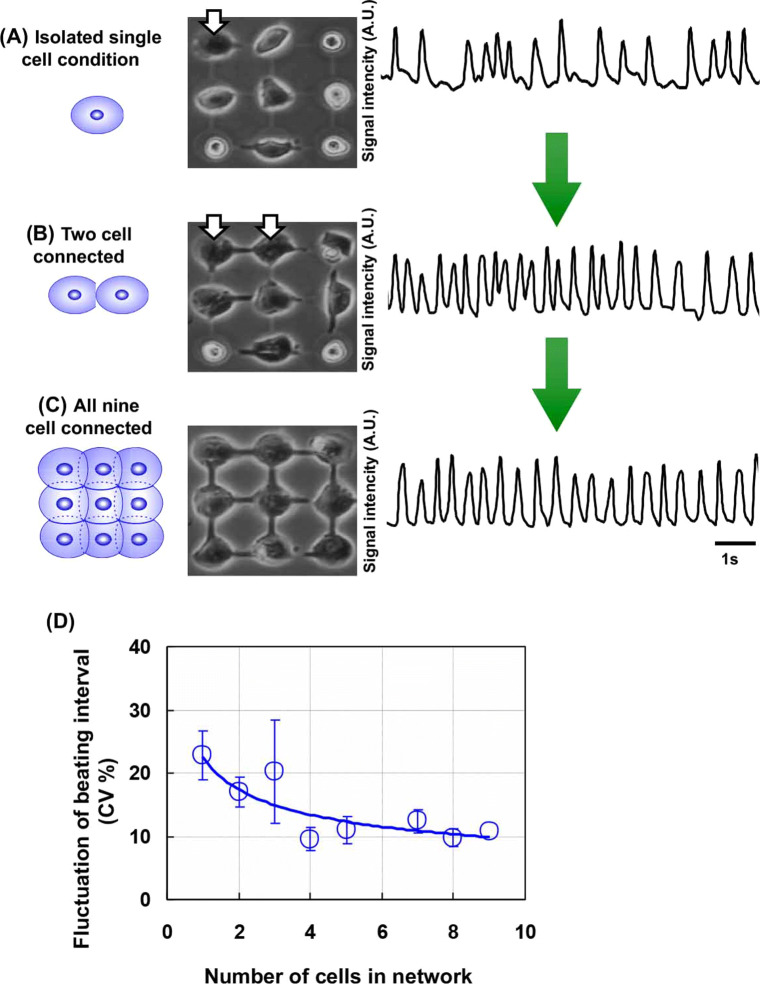
Figure 5 also describes the community size effect of a cardiomyocyte network on its beating stability. In this work, we explore the relationship between entrainment and community size by examining the synchronization process of a cardiomyocyte network formed by the interaction of single cardiomyocytes cultured in a 3 × 3 grid of agarose microchambers with connecting microchannels (Kojima et al. 2006). After nine isolated cells had been cultured in the nine-chamber agarose microcultivation chip for 24 h, we started to measure the synchronization process continuously and found that, when an isolated single cell came into contact with another cell and formed a two-cell network (Fig. 5 top and middle), these two cells synchronized at the initial rate of the first cell and the fluctuation decreased from the initial fluctuation of the first cell. When all nine cells came into contact and formed a nine-cell network (Fig. 5 bottom), it synchronized at a rate equal to the initial rate of the first cell, with a decrease of fluctuation.
Fig. 5.
Effect of increase in connected cell number on increase in beating stability. (A) Isolated single cell, (B) two-cell network, and (C) nine-cell network. (D) Dependence of beating interval fluctuation on cell number
These results suggest that the beating rhythm of a single cardiomyocyte tends to entrain the rhythm of the cell network and the strength of this tendency increases with the size of the network. Therefore, it is thought that the fluctuation of the rate at which a network of cardiomyocytes beats decreases as the size of the network increases. The tendency of the synchronization above was simply explained by asserting that the synchronization of two cardiomyocytes was caused by the more unstable cell (the one with the more variable beating intervals) following the more stable cell. Such tendency for reduced fluctuation was more pronounced when the number of cardiomyocytes in the network increased; we call this phenomenon the “community effect” of synchronization.
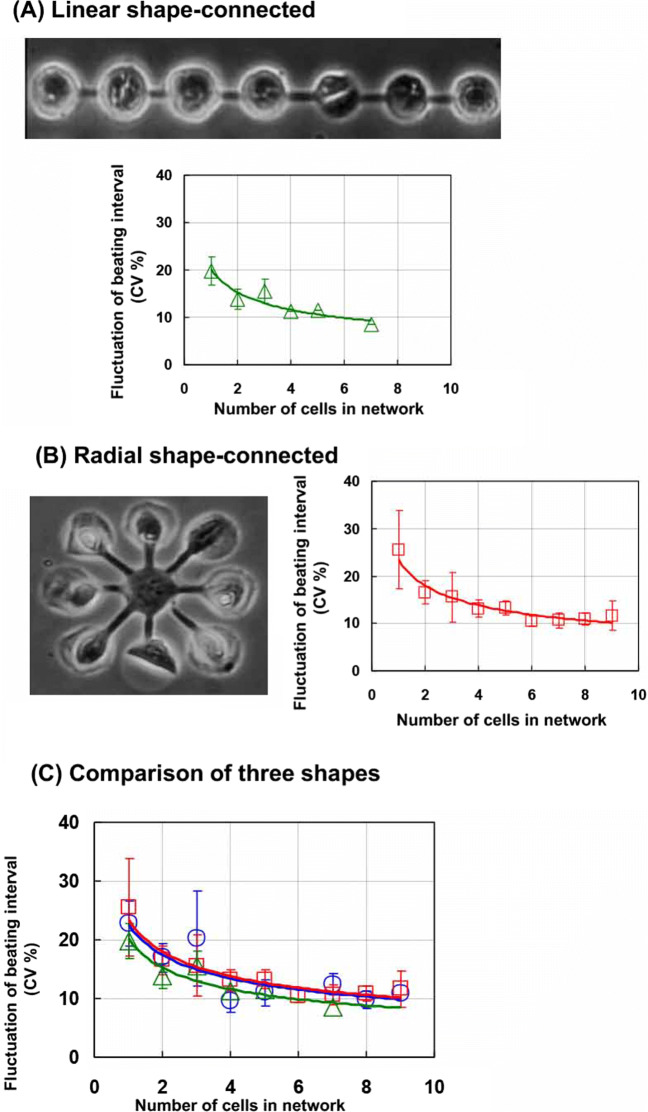
Using the agarose microchambers, we can examine the dependence on the spatial arrangement of the synchronization stability of cardiomyocyte networks (Kaneko et al. 2007a). As shown in Fig. 6, we can arrange the cardiomyocytes in three different shapes, a linearly lined-up shape, a radial spoke-like shape, and a lattice shape, and can compare their tendencies for beating stabilization relative to cell numbers. The results indicated that there was no apparent relationship between the number of cells and their shape, and that the most important index for the stabilization of cell beating is not the geometry of cells but their number.
Fig. 6.
Dependence of spatial arrangement of cardiomyocyte networks on cell number for beating stability. Three types of spatial arrangements (i.e., lattice shape, blue open circles and lines (Fig. 5); linear shape, green open triangles and lines (A); and radial shape, red open squares and lines (B)) were compared with investigate their contributions to the beating stability (C).
Community effect of cells on their synchronization (3): mixture of different types of cells
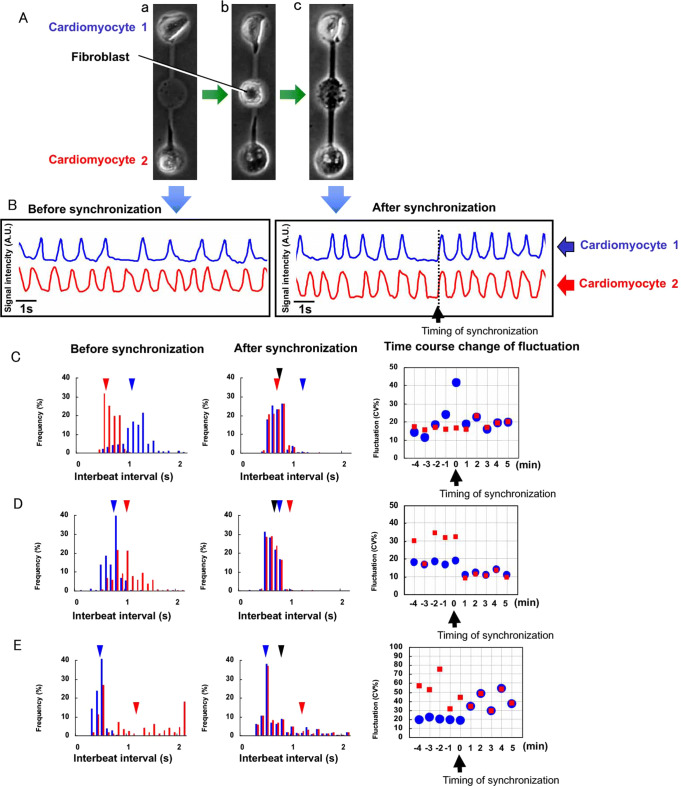
We also examined the contribution of fibroblasts to the synchronization of cardiomyocytes(Kaneko et al. 2011). We connected two cardiomyocytes through a single fibroblast and synchronized them, as shown in Fig. 7A and B, and then used this heterogeneous cardiomyocyte–fibroblast coupling to examine the tendency of the IBIs and beating rhythm fluctuation of two cardiomyocytes through a fibroblast before and after their synchronization.
Fig. 7.
Synchronization of two cardiomyocytes through a fibroblast. (A) Micrographs of two cardiomyocytes under isolated conditions (a), when a fibroblast was added between two cardiomyocytes (b), and when two cardiomyocytes were connected through a fibroblast and synchronization started (c). (B) Beating waveforms at (a) and (c) in panel (A). (C)–(E) Three types of synchronization tendencies. Beating frequency spectrum before (left graphs) and after (center graphs) synchronization, and their beating fluctuation (right graphs). (C) Synchronization to a cell beating faster and more stably. (D) Synchronization and creation of new beating intervals contributing to beating stability. (E) Synchronization with new beating frequency, but beating fluctuation increased
The first type of synchronization involved the tendency for the fluctuation to decrease due to synchronization, which is the same tendency as seen in a network formed by the direct connection of two cardiomyocytes. As shown in Fig. 7C and D, the two cardiomyocytes having different interbeat intervals before synchronization synchronized to achieve an interbeat interval of less than a second after synchronization (e.g., Fig. 7B). The fluctuation of the synchronized network became almost equal to or smaller than either of the two initial fluctuations.
In contrast, the second type involved the tendency for the fluctuation to increase due to synchronization, which did not occur in the pure cardiomyocyte networks (Fig. 7E). In this case, two cardiomyocytes having two different interbeat intervals before synchronization exhibit a higher mean interbeat interval after synchronization, and the fluctuation of the synchronized network is greater than that of the cell that had the lower fluctuation before the synchronization.
Our photo-thermal etching method with agarose microchambers allows us to regulate the cell type and community size of cultured cells at the single-cell level. This could not be done when using the conventional cell cultivation method, so the prolific growth of cardiac fibroblasts made it difficult to culture only cardiomyocytes and investigate the properties of a single cell within a group of cells. By using our on-chip single-cell-based cultivation, we were able to investigate how the fluctuation of the rates at which cardiomyocytes beat affects the reestablishment of synchronized beating.
Summary of experimental results
The results of the on-chip constructive cardiomyocyte network experiments are summarized as follows:
When two isolated, independently beating cardiomyocytes come into contact, they tend to beat synchronously at a rate that fluctuates no more than that of the cell whose beat rate fluctuated less than did that of the other cell.
When initially isolated cardiomyocytes form a network, its rhythm tends to entrain the beating rhythm of single cells whose beating rhythm fluctuated more than that of the network.
The entrainment activity of cell networks increases with their size, i.e., the fluctuation decreases.
Spatial arrangement does not affect the manner of synchronization of cardiomyocytes, and only the cell number of the network determines their tendency for synchronization.
The interbeat interval after the synchronization of two cardiomyocytes connected by a fibroblast is not the same as that after the synchronization of two cardiomyocytes directly connected to each other, and the tendency for the community effect to occur appears to be suppressed when the cardiomyocytes are heterogeneously coupled through a fibroblast.
They might indicate that unstable isolated cardiomyocytes reestablish a cell network that beats stably and synchronously. A novel finding of this study is that a cardiomyocyte network containing only a few cells acquires a stable rhythm. Moreover, once the cell or cell network achieves stable beating, an additionally attached unstable cell can synchronize to the stable cell or cell network and follow its stable beating intervals. This phenomenon also suggests that the factor of stability is very important in determining the fate of the beating frequency of the network after the connection of unstable cells.
Ability and limitation of constructive experimental approach
As described above, the on-chip constructive experimental approach is one of the potential solutions to solve the issue of quality control of cells. However, cells inherently display a variety of dynamic characteristics, even when cultivating cells in completely the same conditions and also when using those from the same single stem cells (López-Redondo et al. 2016). The results in this section clearly indicate the ability and limitation of the experimental approach of single cell-based assays. Each isolated single cell does not inherently show the same dynamics; however, once they formed a network, their diversity disappeared and stable shared characteristics appeared. We call this phenomenon the “community effect.” To understand the meaning of the community effect, we need to have a set of completely controlled single cells. However, this is beyond the scope of the experimental approach. Even using the on-chip cellomics technologies, this experimental approach has a limitation of not allowing full control of the condition of all of the cells, especially in a dynamic context such as beating of the heart.
Numerical approach to synchronization of cardiomyocytes
Mathematical models of cardiomyocyte beating
As the periodical oscillation behavior of cardiomyocytes is one of the most popular phenomena in living systems, massive mathematical models have been proposed to investigate the mechanism of their beatings. One approach is an elaborated mathematical model composed of a large number of equations, each of which is reflecting the complex electrophysiological processes causing cardiomyocyte beating (Hatano et al. 2011). Another approach is a simple mathematical model using just a few ordinary equations, which are representing the key phenomenon of the membrane currents and action potentials (Keener and Sneyd 2008), such as the famous Hodgkin-Huxley model, the FitzHugh-Nagumo model and the Van der Pol model.
For investigating the statistical behavior of beating and synchronization period of cardiomyocytes, we should remark the essence of beating intervals and their synchronization period from the idea that the cardiomyocytes as oscillators. From this viewpoint, starting from the phase model is one of the suitable ways for the construction of beating interval model (Kuramoto 1984; Kori et al. 2012). However, to capture the characteristic features of cardiomyocyte beating, we have to consider and incorporate the conventional stochastic phase models with three important ideas:(i) irreversible at firing, (ii) a refractory period after firing, and (iii) induced pulsation associated with firing of surrounding cells. A part of those ideas were considered in the well-known “integrate-and-fire” model as a spiking neuron model (Keener et al. 1981; Burkitt 2006; Sacerdote and T. 2013). We have investigated the mathematical phase models with stochastic differential equations for cardiomyocytes involving above three important ideas.
Simple phase model and stochastic differential equation
At first, we can describe a simple phase model of periodical oscillation behavior of cardiomyocytes as follows. Let ϕ be the phase of an oscillator with phase velocity (or drift) ω > 0 and initial state ϕ(0) = 0. The phase model is given by
| 1 |
Assuming that the phase returns to 0 when it reaches 2π, we see that T = 2π/ω is the period of the oscillator. We can also write (1) into an equivalent differential form:
| 2a |
| 2b |
When we adopt this oscillator for cardiomyocyte beating intervals, it beats when the phase reaches 2π and then returns to 0 immediately to start a next beating interval. Then, the phase equation (1) describes the beating intervals with period T. And it can satisfy two of the above three important ideas; irreversible at firing, and a refractory period after firing.
In general, one can consider the phase model with time-dependent and state-dependent drift, that is ω(t, ϕ(t)) is a function depending on t and ϕ. Then the phase model with initial value ϕ0 becomes
The above equation is equivalent to the following integration form
| 3 |
which is called as the “integrate-and-fire” model.
However, for a cardiomyocyte, as the beating process is usually affected by the fluctuation and noise of internal reaction process, surrounding cells and environments, the beating interval varies each time.
Incorporating the phase model (2a) with noise effect, we write the phase model in a formal way:
| 4a |
| 4b |
where ζ(t) denotes the “white noise” (which has been widely applied in many mathematical models), and σ is a constant representing the strength of the noise. Since the white noise can be regarded as the time derivative of Brownian motion (or called Winner process) denoted by W(t), (4a) becomes
| 5 |
which is a stochastic differential equation.
Mathematical modeling for synchronization of cardiomyocytes in network
The remaining issue of the three important ideas of stochastic phase model is the induced pulsation associated with firing of surrounding cells. We have examined synchronous behaviors of cardiomyocyte networks theoretically based on the integrate-and-fire phase equation model combining with fluctuation-dissipation theorem, in which community effect was simulated successfully (Hayashi et al. 2017).
In this model, we consider a network of N cardiomyocytes and call i th cardiomyocyte cell-i. The model was described with the phase variables ϕi(t) (0 ≤ ϕi(t) ≤ 2π, i = 1, 2, ... , N), which denote the state of cell-i at a time t. We assumed that the cell-i fires (depolarized) when ϕi(t) = 0 (= 2π).
In the network, the firing occurs by internal oscillation or by the influence of neighboring cells, that is, either at ϕi(t), reaches 2π, or the following conditions are satisfied: . Additionally, one of the cardiomyocytes connected to cell-i (e.g., cell-j) fired at a retardation time τ ago (i.e., ϕj(t − τ) = 0). Otherwise, we assumed that ϕi(t) is governed by the following interacting stochastic differential equation. Our mathematical modeling for cell-i is as follows:
| 6 |
where ωi is the average phase velocity of cell-i, dW(σ) is a stochastic process with standard deviation σ, and θi is a phase corresponding to the refractory period of cell-i(0 < θi < 2π). V (ϕi, ϕj) shows the weak interaction between cardiomyocytes through the membrane potential, which we assumed as the following form:
| 7 |
where μ is a positive constant. An important point is that the stochastic process and the cell-to-cell interaction are correlated through the fluctuation-dissipation theorem that gives the relation between fluctuations and linear response to external force (Kubo 1957). The positive constant μ is the only free parameter in our model that cannot be directly determined by experiments, while ωi, θi, σi can be determined by single-cell experiments for each cardiomyocyte.
In addition, we assumed that the boundary at ϕi(t) = 0 is the reflective boundary condition, which ensures that the phase fluctuation is irreversible after firing.
Numerical simulation method
The stochastic process in our simulation is described by an extended random walk. We used the following difference equations as a numerical approximation of equation (6). For almost all cardiomyocytes with a standard beating rhythm, we considered an ordinary random walk as follows:
| 8 |
| 9 |
where the standard deviation is defined by , Δt is the time difference interval, is the spatial difference determined by σi, and the delay time τ is set as Δt × k (k is a non-negative integer). However, we could not reproduce the same beating fluctuation by using an ordinary random walk for cardiomyocytes with a large fluctuation. This is because the coefficient variation (CV %), which is defined by 100 × standard deviation/mean beating rate, could be proved less than . As shown in Fig. 4, some cardiomyocytes with the CV % which exceed this value are observed. Therefore, we adopted the following extended random walk, which is a history-dependent stochastic process, when beating fluctuation was larger than 81.65 (CV %):
| 10 |
The noise term is defined as:
| 11 |
However,
| 12 |
The model could reproduce the large fluctuation observed in the experiments by setting appropriate values of q and r.
Comparison of the model with experimental results of two cardiomyocytes
In the experiments shown above, the mean beating rate and its fluctuation before and after synchronization were observed for 14 pairs of cardiomyocytes. We investigated whether our model could reproduce the results of these pairs of cardiomyocytes. We numbered these 14 pairs from Nos. 1 to 14 and distinguished the two cardiomyocytes in a pair by denoting “cell-1” and “cell-2.” For each pair, we defined ωi, σi, θi in equation (6) for cell-i (i = 1, 2), so that the model reproduced the same mean beating rate and fluctuation in beating rhythm. Since refractory periods of cardiomyocytes are almost the same as those for normal cardiomyocytes, we assumed that each cell had the common refractory period tref = 0.3 s. Therefore, θi is given by θi = trefωi.
We could regard the retardation time τ as almost 0 because it was estimated as of the mean beating rate. Therefore, we put τ = 0. We used μ = 6.5 in numerical simulations. The dependence of theoretical calculation on μ is shown later. We found that the simulated values accurately agree with the experimental values except for pair No. 14. The experimental result of pair No. 14 is exceptional because it is the only pair in which fluctuation increased after synchronization. Beating fluctuation of a pair of synchronized cardiomyocytes was equal to or less than that of less fluctuating cardiomyocytes, while the mean beating rate was widely distributed. Some pairs synchronized at faster rates of the two initial rates, some at slower rates of the two initial rates, and others at intermediate rates of the initial rates of the pair.
Comparison with the Kuramoto model
The two-oscillators phase model (the Kuramoto model (Kuramoto 1984)) with noise is as follows: for i, j = 1, 2, i ≠ j,
| 13 |
where and denote the drift and noise strength constants, respectively, Ai, j are non-negative constants, and {Wi}i= 1, 2 is independent standard Brownian motion. For two cases (Case (i) and Case (ii)), we applied the Kuramoto model (13) and our model (6) to synchronization of two coupled cardiomyocytes. The numerical simulation results were compared with in vitro experimental data (Kojima et al. 2006).
Case (i) A case of synchronization to a cardiomyocyte with a fast and stable beating rhythm. Two cardiomyocytes that we used in the Case (i) were cell-1 and cell-2 of pair No. 1, which have a mean beating rhythm of 0.64 s and fluctuation of 12.3 (CV%) and cell-2 with 1.23 s and 25.1 (CV%), respectively. When the two cardiomyocytes were coupled, we found that the bating rhythm after synchronization was tuned to cell-1 with a fast and stable beating rhythm. We investigated whether our model and the Kuramoto model could reproduce the experimental results. The mean beating rate and beating fluctuation for the experimental result, our model, and the Kuramoto model are shown in Table 1.
Table 1.
Comparison between the experimental result and the numerical results. The symbol Ti and Fi denote the mean beating rate and the beating fluctuation of the cell-i(i = 1, 2), respectively. The symbol T denotes the mean beating rate and F the beating fluctuation after synchronization
| Before synchronization | After synchronization | |||||
|---|---|---|---|---|---|---|
| T1(s) | F1 (CV%) | T2 (s) | F2 (CV%) | T (s) | F (CV%) | |
| Experiments | 0.64 | 12.3 | 1.23 | 25.1 | 0.76 | 12.3 |
| Our model | 0.64 | 12.3 | 1.23 | 25.1 | 0.74 | 11.4 |
| Kuramoto model | 0.64 | 12.3 | 1.23 | 25.1 | 0.85 | 12.7 |
Case (ii) A case of synchronization to a cardiomyocyte with a slow and stable beating rhythm. Two cardiomyocytes that we used in the Case (ii) were cell-1 and cell-2 of pair No. 6, which have a mean beating rhythm of 1.10 s and fluctuation of 149 (CV%) and cell-2 with 1.40 s and 41.2 (CV%), respectively. When the two cardiomyocytes were coupled, we found that the bating rhythm after synchronization was tuned to cell-2 with a slow and stable beating rhythm. When we compared the numerical result of our model with that of the Kuramoto model, we found that our model was closer to the experimental data than the Kuramoto model. Our model showed that the beating rhythm after synchronization was tuned to the rhythm of the slow and stable cardiomyocyte. However, the Kuramoto model showed that beating fluctuation of the slow and stable cardiomyocyte was increased after synchronization, which differed from the experimental results. The mean beating rate and beating fluctuation of the experimental result, those of our model and those of the Kuramoto model are shown in Table 2.
Table 2.
Comparison between the experimental result and the numerical results. The symbol Ti and Fi denote the mean beating rate and the beating fluctuation of the cell-i(i = 1, 2), respectively. The symbol T denotes the mean beating rate and F the beating fluctuation after synchronization
| Before synchronization | After synchronization | |||||
|---|---|---|---|---|---|---|
| T1 (s) | F1 (CV%) | T2 (s) | F2 (CV%) | T (s) | F (CV%) | |
| Experiments | 1.1 | 149 | 1.4 | 41.2 | 1.4 | 41.7 |
| Our model | 1.1 | 149 | 1.4 | 41.2 | 1.3 | 46.3 |
| Kuramoto model | 1.1 | 149 | 1.4 | 41.2 | 1.3 | 86.8 |
Therefore, our model showed that even though the mean beating rate of a cardiomyocyte was slow, a cardiomyocyte with more stable beating fluctuation dominated the beating rhythm after synchronization.
Size and configuration dependence on fluctuation of the system
We investigated the dependence of fluctuation in beating rhythm of cardiomyocytes on the size and configuration of the network. Network patterns in cardiomyocyte groups that we considered were radial spoke-like, 2D lattice and 1D linear lined-up networks as shown in Fig. 6.
We assumed that all the elements in cell networks have the same parameters and beating properties. We found that the beating fluctuation decreased as the size of the network increased irrespective of network pattern just same as the experimental results. Among the three configurations, a reduction in fluctuation tended to be most rapid in the 2D lattice network, and fluctuation in the 1D linear lined-up network tended to be always larger than that in the other two configurations. In addition, we considered the larger size (about 1000 cells) of the network in the 2D lattice network. The size dependence of fluctuation of the 2D lattice network where all the elements had the same beating properties. The numerical results suggested that the beating fluctuation decreased as the community size increased, but the CV value of the network approached to a constant value for large network size N. For an ordinary stochastic ensemble, such as an independently identical distributed ensemble, the dependence of standard deviation of fluctuation on system size N was proportional to N− 1/2. However, the features of beating fluctuation behave differently from that of ordinary stochastic ensembles.
Summary of numerical simulation results
As shown in above experimental results, IBIs of cell networks were slower than the fastest beating component cells, and hence were not regulated by the fastest beating component cardiomyocytes. For the confirmation of the dominant rule of the synchronized IBI formation in the networks, one of the best way is in silico experiment of cardiomyocyte network formation. Our in silico results showed the dominant rule of synchronized networks’ IBIs in the experimental results can be explained by the selection rule of more stable firing intervals, where stable IBI is dominance, were the same IBIs regardless of all connection manners. We also have discussed the limitation of conventional phase model like Kuramoto model for the estimation of cardiomyocyte network’s IBIs without consideration of fluctuation-dissipation theorem (Hayashi et al. 2017). That means, if the cardiomyocytes are well described only by phase equations of Kuramoto model, the network’s IBI equals to the average value of its components’ IBIs.
The reason why a cardiomyocyte with an unstable bating rhythm tends to follow a cardiomyocyte with a stable bating rhythm may be explained as follows. A cardiomyocyte with a stable bating rhythm has the property where its dynamics are only slightly affected by external or internal disturbance. Therefore, there is little effect of interactions from neighboring cardiomyocytes. While, a cardiomyocyte with an unstable beating rhythm has the opposite property and is strongly affected by its neighbors. A cardiomyocyte with a stable beating rhythm corresponds to a pendulum with a heavy mass in contrast to a cardiomyocyte with an unstable beating rhythm that corresponds to that with a light mass. When these pendulums are connected, the pendulum with a light mass tends to follow that with a heavy mass. This feature is a consequence of the fluctuation-dissipation theorem, which provides a universal relation between fluctuation and a linear response (Kubo 1957).
The fact reported in this review tells us the importance of community effect of cells, which cannot be explained simply by the expansion of the knowledge of single-cell studies (López-Redondo et al. 2016). Acquisition of those hidden rules in higher compleity of cell networks should lead to development of well designed quasi in vivo models.
Application of synchronization behavior for predictive cardiotoxicity
Recently, as a practical application of fluctuation measurement of cell-to-cell synchronization, quasi in vivo predictive cardiotoxicity measurement assay has been extensively examined and found that such conduction measurement can give us more precise prediction of cardiotoxicity than the conventional in vitro screening assays like hERG assay (Kaneko et al. 2014; Nozaki et al. 2016; Asahi et al. 2018; Asahi et al. 2019).
Lethal arrhythmias, including torsades de pointes (TdP) and ventricular tachycardia (VT), are the phenomenon of losing coordinated synchronous ability in neighboring cardiomyocytes and hence are critical safety issues in drug development. To exclude torsadogenic compounds in earlier stage of development, the International Council for Harmonisation of Technical Requirements for Pharmaceuticals for Human Use (ICH) has implemented the two essential assays, in vitro human ether-a-go-go-related gene (hERG) and in vivo QT assays, and additional in vitro action potential duration (APD) as a follow up under the ICH S7B guideline (Gintant 2011). However, in vitro hERG, in vitro APD and in vivo QT assays still have difficulty in fully predicting lethal arrhythmias, resulting in some compounds are judged as false negative or false positive (Gintant 2011; Ponti et al. 2002; Giorgi et al. 2010) in these assays.
One reason of the false negative or false positive problems was caused by the difference of species, i.e., animal model and human. Human pluripotent stem cell-derived cardiomyocytes (hPSC-CMs), which expresses physiologically functioning all of human’s ion channels, have been developed as a more appropriate cell source for assessing proarrhythmia risks. Although it still remains the problem of maturation or control of differentiation, once those problems can be solved, those cells should contribute for more precise prediction of cardiotoxicity risks. For example, combining with those human cells with the multi-electrode array (MEA) assay, extracellular recording of field potential duration (FPD) prolongation, which is equivalent to APD and QT interval prolongation, can predict clinical QT prolongation and arrhythmogenic liability more accurately than existing in vitro and ex vivo assays (Kaneko et al. 2014; Tanaka et al. 2009; Ando et al. 2017; Kitaguchi et al. 2016; Clements et al. 2015). In a typical waveform obtained from field potential recordings of hPSC-CMs, FPD is defined as the temporal interval from the first peak of the fast, sharp wave component to the second peak in the slow, broad wave component, and the duration is mostly reflected by IKr along with other cardiac ionic currents such as INa, ICa, and IKs. However, FPD prolongation also cannot fully predict lethal arrhythmia or QT prolongation, particularly for arrhythmias induced by multi-channel effects. Hence, to improve the clinical relevance, various efforts have been made in the MEA assay using hPSC-CMs. For example, it is possible to analyze waveform abnormalities, such as early after depolarization, triggered activity and ectopic beats, which are potent proarrhythmia markers for both IKr inhibitors and multi-channel blockers (Harris et al. 2013; Nozaki et al. 2014). Moreover, the combination with FPD in MEA assays and other types of assays, such as impedance, motion field imaging, Ca2+ transient, beating pattern assessment, and in silico simulation based on multi-ion channel activities, seemed to improve prediction of cardiac liabilities and provides insight into the mechanism-of-action of drugs (Sirenko et al. 2013; Takasuna et al. 2017; Clements et al. 2015; Kramer et al. 2013; Kaneko et al. 2007b; Sugio et al. 2004). Intracellular recording of APD in hESC-CMs also indicated overall pharmacological sensitivity and predictability of the cardiac risk of arrhythmogenic drugs (Peng et al. 2010). Besides those waveform analyses, the temporal fluctuation, that is, short-term variability (STV) of APD in hESC-CMs, has specificity that recognized moxifloxacin as a safe drug, although APD itself was prolonged (Nalos et al. 2012). The STV of APD or STV of QT has been shown to identify individuals at high risk of arrhythmia in vivo and in clinical (Abi-Gerges et al. 2010; Hinterseer et al. 2010; Varkevisser et al. 2012). Moreover, this approach was also proposed to be useful for precision medicine but not only for cardiotoxicity assessment by using patient-derived hPSC-CMs (Sala et al. 2016; Sala et al. 2017). These findings suggest that a surrogate arrhythmic marker such as STV, which is not exclusively dependent on hERG inhibition or QT prolongation, is needed for appropriate judgment of the risk of drugs. STV of the QT interval or APD, which represent a temporal fluctuation, has been well studied and known as a quantitative proarrhythmic marker in in vivo animal models, isolated primary cardiomyocytes, and retrospective analysis of clinical observation (Oosterhoff et al. 2011; Altomare et al. 2015; Floré and Willems 2012; Thomsen et al. 2007; Zareba and de Luna 2005). However, little was known about influence on temporal fluctuation of FPD in the MEA assay using hPSC-CMs (i.e., STVs of FPD).
The ion channel panel assay consisting of six ion channels (IKr, INa, ICa, IKs, Ito and IK1) has been proposed and those currents are important in repolarization and depolarization of the cardiac action potential (Fermini et al. 2016). From the viewpoint of cell-to-cell conduction of cardiomyocytes, sodium channel blockers have been well studied in both in vitro cardiomyocytes and in vivo animal models. It has been reported that quinidine and flecainide decelerate the electrical conduction, although lidocaine or mexiletine show no or a lower effect on conduction in isolated animal cardiomyocytes (Heath et al. 2011; Osadchii 2014). Clinically, proarrhythmia induced by sodium channel blockers is limited to class Ia (e.g., quinidine) and class Ic (e.g., flecainide) agents (Almroth et al. 2011; Morganroth and Goin 1991), whereas class Ib agents (e.g., lidocaine and mexiletine) appear to be safe (Wyman et al. 2004; Woosley et al. 1984). In addition, not only deceleration of conduction but also spatiotemporal fluctuation in both cell-to-cell conduction and APD can lead to VT and ventricular fibrillation (VF) (Wagner et al. 2015; Ogawa et al. 2008; Weiss et al. 2005). However, there are few reports focusing on the relationship between depolarization delay and slowing of cell-to-cell conduction.
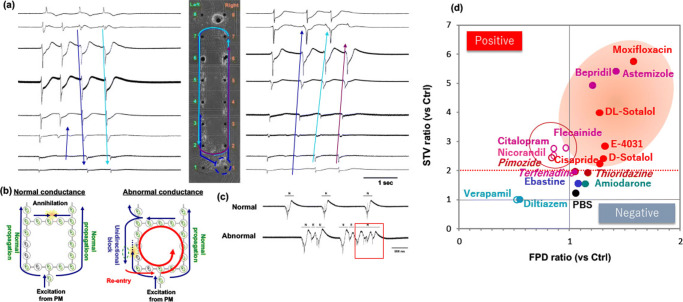
To overcome the limitation of conventional measurement assays, we need to consider the importance of the synchronous beating behavior of cardiomyocytes with an increase in their cell number of networks as a “community effect” (Yasuda 2004; Kaneko et al. 2007a). Using an on-chip constructive approach, IBIs of two neighboring isolated cardiomyocytes synchronize to the more stable cardiomyocyte (i.e., lower coefficient of variability (CV) of IBIs) regardless of their IBIs (Kojima et al. 2006). These results indicated that the importance of cell-to-cell connection and cell number in the in vitro cardiomyocyte screening assay because the response might be ruled by the most stable cardiomyocytes in the inhomogeneous cardiomyocyte clusters. As all those above conventional screening assays neglected those “community effect” of cardiomyocytes, and those differences caused the redundancy of the results. Hence, we have demonstrated the importance of cell number of networks as a “community effect” for the measurement of temporal fluctuation of FPD, short-term variability of FPD (STVFPD), of cardiomyocyte networks to predict the arrhythmic risk more precisely (Kaneko et al. 2014). And then we also have proposed the lined-up hESC-CMs in the MEA assay as a small scale quasi in vivo model to detect cell-to-cell conduction and its STV (spatiotemporal fluctuation) of the simultaneous combined spatiotemporal field potential duration (FPD) and cell-to-cell conduction time (CT) measurement, STVFPD and STVCT, to evaluate two origins of lethal arrhythmia, repolarization and depolarization, which is patented internationally and was reported (Asahi et al. 2018; Asahi et al. 2019). Effects of E-4031 and verapamil, well-known drugs with QT-prolongation and QT-shortening effect, respectively, on FPD, CT, and their STVs in lined-up hESC-CMs were examined and we found that E-4031 had a QT-prolonging effect and verapamil showed a QT-shortening effect in our assay. Furthermore, the effects of sodium channel blockers (flecainide and lidocaine; positive and negative control for cell-to-cell conduction, respectively) and two other arrhythmogenic drugs as multi-channel blockers (astemizole and terfenadine) on these four parameters were examined. The repolarization index, FPD, was prolonged by E-4031 and astemizole, and shortened by verapamil, flecainide and terfenadine at 10 times higher than therapeutic plasma concentrations of each drug, but it did not change after lidocaine treatment up to 100 μM. CT was increased by astemizol, flecainide, terfenadine, and lidocaine at equivalent concentrations of Nav1.5 IC50. Those results suggested that CT can be an index of cardiac depolarization because the increase in CT (i.e., decrease in cell-to-cell conduction speed) was relevant to Nav1.5 inhibition. Fluctuations (STV) of FPD and CT, STVFPD and STVCT also discriminated between torsadogenic and non-torsadogenic compounds with significant increases in their fluctuation values, enabling precise prediction of arrhythmogenic risk as potential new indices. As shown in Fig. 8, cell-to-cell conduction was evaluated geometrically by conduction time (CT) between two neighboring electrodes with 150-μm inter-electrode distance in the lined-up cell network using hESC-CMs, and their geometrical propagation manner was electrically measured and evaluated the arrhythmic risk directly and more precisely as their abnormality of propagation and the change of field potential waveforms simultaneously.
Fig. 8.
On-chip quasi in vivo assay for predictive cardiotoxicity screening. (a) Geometrically arranged cardiomyocyte lined-up closed network and the time course FPD waveforms of microelectrodes. As described in the waveforms, the propagation of conduction was visualized by comparing the neighboring FP signals. (b) Schematic illustration of conduction propagation in coordinated synchronous condition (left) and abnormal condition (right). (c) The 16 waveforms acquired from those electrodes can be added to be the electrocardiograph (ECG)-like waveform. Normal propagation (upper) and abnormal arrhythmic condition (lower). (d) Schematic diagram showing the contribution of fluctuation index (y-axis) adding to the conventional FPD recording (x-axis). As the conventional results were in the one-dimensional screening, false negative and false positive compounds were overlapped. However, when the second axis (y-axis) is added by the fluctuation evaluation (STV), all the compounds are spread two-dimensionally and hence can be distinguished precisely as positive/negative compounds
Quality and quantity control of cardiomyocyte network still remain a key issue for establishment of reproducible on-chip assays. Especially, as described above, the influence of fibroblasts has been examined in on-chip cell-network assay, indicating that fibroblasts reduce the ability of synchronization of cardiomyocytes (Kaneko et al. 2011; Nomura et al. 2011). Heterogeneity of cardiomyocytes also should be an issue for improvement of reliability. We have previously evaluated the single cells obtained from single hESC-CMCs visually and concluded that 73% of total cells beat spontaneously; however, their action potential analysis of APD20 − 40/APD50 − 70 and dV/dtmax revealed that they would have at least more than two major phenotypes, arbitrary “ventricular-like” and “atrial-like” cells (López-Redondo et al. 2016). To overcome those cell quality problems caused by the mixture of phenotypes, computational simulation might be one of the possible solutions. For example, the role of community effect of single phenotype cardiomyocyte network was simulated successfully with fluctuation-dissipation theorem as described in this review (Hayashi et al. 2017).
Summary
As described in this review, the community effect of cardiomyocyte synchronization behavior was explained using the following three viewpoints: First, we introduced the experimental results of the synchronous behavior of cardiomyocyte networks after a brief explanation of the experimental set-up of microfabrication techniques regarding how the constructed approach of step-wise synchronization of cardiomyocytes was accomplished. Next, the firing of cardiomyocytes as a mathematical oscillating phase model, and the oscillating stochastic phase model with the fluctuation-dissipation theorem, and revealed that the model of cardiomyocyte networks showed the same tendencies of the experimental results of synchronization behavior. Specifically, it revealed that the stability-oriented synchronization phenomenon and the fluctuation of beating intervals determine the cell-network synchronous behavior. Third and finally, an application of synchronous behavior of cardiomyocytes for drug screening was introduced and the importance of cell number and their geometry, which can cause the different results in conduction properties, was explained with our more precise prediction approach of quasi in vivo model beyond the conventional in vitro assay.
In this review, we also intended to speculate about the macroscopic behavior behind the synchronization of beating cardiomyocytes. Such a synchronized network of living organisms appears to be a macroscopic system in which part of its behavior is not just purely mechanical, but also exhibits statistical features that all systems tend to present. Hence, the community effect of cells should also be based on the statistical tendency of matter to become disordered as a part of the ordinary laws of physics.
At present, however, it is not clear whether and how this synchronization rule or community effect is regulated at the molecular ion channel level. In other words, no detailed information about the functioning of the community effect can emerge from a description of the genetic mechanism and its expression as general as that given above. In this regard, the next step for a mathematical approach to studying the community effect is to connect the macroscopic interpretation with the microscopic interpretation. For this, the in silico membrane potential model should become more precise (Hamada et al. 2013), and it can also be applied in practical applications for drug discovery or predictive toxicity screening as described in this review.
Finally, with regard to the community effect, living systems appear to maintain and perhaps encourage orderly and regulated behaviors, acting against the tendency for natural systems to progress from order to disorder, but based partly on some hidden existing order that is retained.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Abi-Gerges N, Valentin J-P, Pollard C-E. Dog left ventricular midmyocardial myocytes for assessment of drug-induced delayed repolarization: short-term variability and proarrhythmic potential. Br J Pharmacol. 2010;159(1):77–92. doi: 10.1111/j.1476-5381.2009.00338.xhttps://doi.org/10.1111/j.1476-5381.2009.00338.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almroth H, Andersson T, Fengsrud E, Friberg L, Linde P, Rosenqvist M, Englund A. The safety of flecainide treatment of atrial fibrillation: long-term incidence of sudden cardiac death and proarrhythmic events. J Intern Med. 2011;270(3):281–290. doi: 10.1111/j.1365-2796.2011.02395.xhttps://doi.org/10.1111/j.1365-2796.2011.02395.x. [DOI] [PubMed] [Google Scholar]
- Altomare C, Bartolucci C, Sala L, Bernardi J, Mostacciuolo G, Rocchetti M, Zaza A. IKr impact on repolarization and its variability assessed by dynamic clamp. Circ Arrhythm Electrophysiol. 2015;8(5):1265–75. doi: 10.1161/CIRCEP.114.002572. [DOI] [PubMed] [Google Scholar]
- Ando H, Yoshinaga T, Yamamoto W, Asakura K, Uda T, Taniguchi T, Sekino Y. A new paradigm for drug-induced torsadogenic risk assessment using human iPS cell-derived cardiomyocytes. J Pharmacol Toxicol Methods. 2017;84:111–127. doi: 10.1016/J.VASCN.2016.12.003https://doi.org/10.1016/J.VASCN.2016.12.003. [DOI] [PubMed] [Google Scholar]
- Anzai Y, Terazono H, Yasuda K. Simple non-invasive cell separation method using magnetic aptamer-conjugated microbeads and nuclease digestion. J Biol Phys Chem. 2007;7:83–86. doi: 10.4024/30701.jbpc.07.03. [DOI] [Google Scholar]
- Asahi Y, Hamada T, Hattori A, Matsuura K, Odaka M, Nomura F, Yasuda K. On-chip spatiotemporal electrophysiological analysis of human stem cell derived cardiomyocytes enables quantitative assessment of proarrhythmia in drug development. Sci Rep. 2018;8:14536. doi: 10.1038/s41598-018-32921-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asahi Y, Nomura F, Abe Y, Doi M, Sakakura T, Takasuna K, Yasuda K. Electrophysiological evaluation of pentamidine and 17-AAG in human stem cell-derived cardiomyocytes for safety assessment. Eur J Pharmacol. 2019;842:221–230. doi: 10.1016/j.ejphar.2018.10.046. [DOI] [PubMed] [Google Scholar]
- Burkitt AN. A review of the integrate-and-fire neuron model: I. Homogeneous synaptic input. Biol Cybern. 2006;95(1):1–19. doi: 10.1007/s00422-006-0068-6. [DOI] [PubMed] [Google Scholar]
- Clements M, Millar V, Williams AS, Kalinka S. Bridging functional and structural cardiotoxicity assays using human embryonic stem cell-derived cardiomyocytes for a more comprehensive risk assessment. Toxicol Sci. 2015;148(1):241–260. doi: 10.1093/toxsci/kfv180https://doi.org/10.1093/toxsci/kfv180. [DOI] [PubMed] [Google Scholar]
- Fermini B, Hancox JC, Abi-Gerges N, Bridgland-Taylor M, Chaudhary KW, Colatsky T, Vandenberg JI. A new perspective in the field of cardiac safety testing through the comprehensive in vitro proarrhythmia assay paradigm. J Biomol Screen. 2016;21(1):1–11. doi: 10.1177/1087057115594589. [DOI] [PubMed] [Google Scholar]
- Floré V, Willems R. T-wave alternans and beat-to-beat variability of repolarization: pathophysiological backgrounds and clinical relevance. Acta Cardiol. 2012;67(6):713–718. doi: 10.1080/AC.67.6.2184675. [DOI] [PubMed] [Google Scholar]
- Gintant G. An evaluation of hERG current assay performance: Translating preclinical safety studies to clinical QT prolongation. Pharmacol Ther. 2011;129(2):109–119. doi: 10.1016/J.PHARMTHERA.2010.08.008https://doi.org/10.1016/J.PHARMTHERA.2010.08.008. [DOI] [PubMed] [Google Scholar]
- Giorgi M, Bolanos R, Gonzalez C, Di Girolamo G. QT interval prolongation: Preclinical and clinical testing arrhythmogenesis in drugs and regulatory implications. Curr Drug Saf. 2010;5(1):54–57. doi: 10.2174/157488610789869148. [DOI] [PubMed] [Google Scholar]
- Girault M, Kim H, Arakawa H, Matsuura K, Odaka M, Hattori A, Yasuda K. An on-chip imaging droplet-sorting system: a real-time shape recognition method to screen target cells in droplets with single cell resolution. Sci Rep. 2017;7:40072. doi: 10.1038/srep40072https://doi.org/10.1038/srep40072. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goshima K, Tonomura Y. Synchronized beating of embryonic mouse myocardial cells mediated by FL cells in monolayer culture. Exp Cell Res. 1969;56(2-3):387–392. doi: 10.1016/0014-4827(69)90029-9. [DOI] [PubMed] [Google Scholar]
- Hamada H, Nomura F, Kaneko T, Yasuda K, Okamoto M. Exploring the implicit interlayer regulatory mechanism between cells and tissue: Stochastic mathematical analyses of the spontaneous ordering in beating synchronization. Biosystems. 2013;111(3):208–215. doi: 10.1016/j.biosystems.2013.02.007. [DOI] [PubMed] [Google Scholar]
- Harris K, Aylott M, Cui Y, Louttit JB, McMahon NC, Sridhar A. Comparison of electrophysiological data from human-induced pluripotent stem cell–derived cardiomyocytes to functional preclinical safety assays. Toxicol Sci. 2013;134(2):412–426. doi: 10.1093/toxsci/kft113. [DOI] [PubMed] [Google Scholar]
- Hatano A, Okada J, Washio T, Hisada T, Sugiura S. A three-dimensional simulation model of cardiomyocyte integrating excitation-contraction coupling and metabolism. Biophys J. 2011;101(11):2601–2610. doi: 10.1016/j.bpj.2011.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hattori A, Moriguchi H, Ishiwata S, Yasuda K. A 1480/1064 nm dual wavelength photo-thermal etching system for non-contact three-dimensional microstructure generation into agar microculture chip. Sens Actuators B Chem. 2004;100(3):455–462. doi: 10.1016/j.snb.2003.11.041. [DOI] [Google Scholar]
- Hayashi M, Hattori A, Kim H, Terazono H, Kaneko T, Yasuda K. Fully automated on-chip imaging flow cytometry system with disposable contamination-free plastic re-cultivation chip. Int J Mol Sci. 2011;12(6):3618–3634. doi: 10.3390/ijms12063618https://doi.org/10.3390/ijms12063618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi T, Tokihiro T, Kurihara H, Yasuda K. Community effect of cardiomyocytes in beating rhythms is determined by stable cells. Sci Rep. 2017;7:15450. doi: 10.1038/s41598-017-15727-5https://doi.org/10.1038/s41598-017-15727-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heath B, Cui Y, Worton S, Lawton B, Ward G, Ballini E, McMahon N. Translation of flecainide- and mexiletine-induced cardiac sodium channel inhibition and ventricular conduction slowing from nonclinical models to clinical. J Pharmacol Toxicol Methods. 2011;63(3):258–268. doi: 10.1016/J.VASCN.2010.12.004. [DOI] [PubMed] [Google Scholar]
- Hinterseer M, Beckmann B, Thomsen MB, et al. Usefulness of short-term variability of QT intervals as a predictor for electrical remodeling and proarrhythmia in patients with nonischemic heart failure. Am J Cardiol. 2010;106(2):216–220. doi: 10.1016/j.amjcard.2010.02.033. [DOI] [PubMed] [Google Scholar]
- Inoue I, Shiomi D, Kawagishi I, Yasuda K. Simultaneous measurement of sensor-protein dynamics and motility of a single cell by on-chip microcultivation system. J Nanobiotechnology. 2004;2(1):4. doi: 10.1186/1477-3155-2-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inoue I, Wakamoto Y, Yasuda K. Non-genetic variability of division cycle and growth of isolated individual cells in on-chip culture system. Proc Jpn Acad Ser B Phys Biol Sci. 2001;77(8):145–150. doi: 10.2183/pjab.77.145. [DOI] [Google Scholar]
- Kaneko T, Kojima K, Yasuda K. Dependence of the community effect of cultured cardiomyocytes on the cell network pattern. Biochem Biophys Res Commun. 2007;356(2):494–49. doi: 10.1016/j.bbrc.2007.03.005. [DOI] [PubMed] [Google Scholar]
- Kaneko T, Kojima K, Yasuda K. An on-chip cardiomyocyte cell network assay for stable drug screening regarding community effect of cell network size. Analyst. 2007;132(9):892–898. doi: 10.1039/b704961g. [DOI] [PubMed] [Google Scholar]
- Kaneko T, Nomura F, Hamada T, Abe Y, Takamori H, Sakakura T, Yasuda K. On-chip in vitro cell-network pre-clinical cardiac toxicity using spatiotemporal human cardiomyocyte measurement on a chip. Sci Rep. 2014;4:4670. doi: 10.1038/srep04670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaneko T, Nomura F, Yasuda K. On-chip constructive cell-network study (i): Contribution of cardiac fibroblasts to cardiomyocyte beating synchronization and community effect. J Nanobiotechnology. 2011;9(1):21. doi: 10.1186/1477-3155-9-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai-Noma S, Ayano S, Pack CG, Kinjo M, Yoshida M, Yasuda K, Taguchi H. Dynamics of yeast prion aggregates in single living cells. Genes Cells. 2006;11(9):1085–1096. doi: 10.1111/j.1365-2443.2006.01004.x. [DOI] [PubMed] [Google Scholar]
- Keener JP, Hoppensteadt FC, Rinzel J. Integrate-and-fire models of nerve membrane response to oscillatory input. SIAM J Appl Math. 1981;41(3):503–517. doi: 10.1137/0141042. [DOI] [Google Scholar]
- Keener JP, Sneyd J. Mathematical physiology. New York: Springer-Verlag; 2008. [Google Scholar]
- Kim H, Negishi T, Kudo M, Takei H, Yasuda K. Quantitative backscattered electron imaging of field emission scanning electron microscopy for discrimination of nano-scale elements with nm-order spatial resolution. J Electron Micros. 2010;59(5):379–385. doi: 10.1093/jmicro/dfq012. [DOI] [PubMed] [Google Scholar]
- Kim H, Terazono H, Nakamura Y, Sakai K, Hattori A, Odaka M, Yasuda K. Development of on-chip multi-imaging flow cytometry for identification of imaging biomarkers of clustered circulating tumor cells. PLoS One. 2014;9(8):e104372. doi: 10.1371/journal.pone.0104372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitaguchi T, Moriyama Y, Taniguchi T, Ojima A, Ando H, Uda T, Miyamoto N. CSAHi study: Evaluation of multi-electrode array in combination with human iPS cell-derived cardiomyocytes to predict drug-induced QT prolongation and arrhythmia — Effects of 7 reference compounds at 10 facilities. J Pharmacol Toxicol Methods. 2016;78:93–102. doi: 10.1016/J.VASCN.2015.12.002https://doi.org/10.1016/J.VASCN.2015.12.002. [DOI] [PubMed] [Google Scholar]
- Kojima K, Kaneko T, Yasuda K. A novel method of cultivating cardiac myocytes in agarose microchamber chips for studying cell synchronization. J Nanobiotechnology. 2004;2(1):9. doi: 10.1186/1477-3155-2-9https://doi.org/10.1186/1477-3155-2-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kojima K, Kaneko T, Yasuda K. Stability of beating frequency in cardiac myocytes by their community effect measured by agarose microchamber chip. J Nanobiotechnology. 2005;3(1):4. doi: 10.1186/1477-3155-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kojima K, Kaneko T, Yasuda K. Role of the community effect of cardiomyocyte in the entrainment and reestablishment of stable beating rhythms. Biochem Biophys Res Commun. 2006;351(1):209–215. doi: 10.1016/j.bbrc.2006.10.037. [DOI] [PubMed] [Google Scholar]
- Kojima K, Moriguchi H, Hattori A, Kaneko T, Yasuda K. Two-dimensional network formation of cardiac myocytes in agar microculture chip with 1480 nm infrared laser photo-thermal etching. Lab Chip. 2003;3(4):292–296. doi: 10.1039/b304652d. [DOI] [PubMed] [Google Scholar]
- Kojima K, Takahashi K, Kaneko T, Yasuda K. Flexible control of electrode pattern on cultivation chamber during cultivation of cells using nondestructive optical etching. Jpn J Appl Phys. 2003;42(Part 2, No. 8A):L980. doi: 10.1143/JJAP.42.L980. [DOI] [Google Scholar]
- Kori K, Kawamura Y, Masuda N. Structure of cell networks critically determines oscillation regularity. J Theor Biol. 2012;297:61–72. doi: 10.1016/j.jtbi.2011.12.007. [DOI] [PubMed] [Google Scholar]
- Kramer J, Obejero-Paz CA, Myatt G, Kuryshev YA, Bruening-Wright A, Verducci JS, Brown AM. MICE Models: Superior to the HERG model in predicting torsade de pointes. Sci Rep. 2013;3:2100. doi: 10.1038/srep02100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubo R. Statistical-mechanical theory of irreversuble processes. I. General theory and simple applications to magnetic and conduction problems. J Phys Soc Japan. 1957;12:570–586. doi: 10.1143/JPSJ.12.570. [DOI] [Google Scholar]
- Kuramoto Y. Chemical oscillations, waves and turbulence. New York: Springer-Verlag; 1984. [Google Scholar]
- López-Redondo F, Kurokawa J, Nomura F, Kaneko T, Hamada T, Furukawa T, Yasuda K. A distribution analysis of action potential parameters obtained from patch-clamped human stem cell-derived cardiomyocytes. J Pharmacol Sci. 2016;131(2):141–145. doi: 10.1016/j.jphs.2016.04.015. [DOI] [PubMed] [Google Scholar]
- Matsumura K, Yagi T, Yasuda K. Role of timer and sizer in regulation of Chlamydomonas cell cycle. Biochem Biophys Res Commun. 2003;306(4):1042–1049. doi: 10.1016/S0006-291X(03)01089-1. [DOI] [PubMed] [Google Scholar]
- Morganroth J, Goin JE. Quinidine-related mortality in the short-to-medium-term treatment of ventricular arrhythmias. A meta-analysis. Circulation. 1991;84(5):1977–83. doi: 10.1161/01.CIR.84.5.1977. [DOI] [PubMed] [Google Scholar]
- Moriguchi H, Wakamoto Y, Sugio Y, Takahashi K, Inoue I, Yasuda K. An agar-microchamber cell-cultivation system: flexible change of microchamber shapes during cultivation by photo-thermal etching. Lab Chip. 2002;2(2):125–132. doi: 10.1039/b202569h. [DOI] [PubMed] [Google Scholar]
- Nalos L, Varkevisser R, Jonsson M, Houtman M, Beekman J, van der Nagel R, Vos M. Comparison of the IKr blockers moxifloxacin, dofetilide and E-4031 in five screening models of pro-arrhythmia reveals lack of specificity of isolated cardiomyocytes. Br J Pharmacol. 2012;165(2):467–478. doi: 10.1111/j.1476-5381.2011.01558.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nomura F, Kaneko T, Hattori A, Yasuda K. On-chip constructive cell-network study (II): On-chip quasi-in vivo cardiac toxicity assay for ventricular tachycardia/fibrillation measurement using ring-shaped closed circuit microelectrode with lined-up cardiomyocyte cell network. J Nanobiotechnology. 2011;9:39. doi: 10.1186/1477-3155-9-39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nozaki Y, Honda Y, Tsujimoto S, Watanabe H, Kunimatsu T, Funabashi H. Availability of human induced pluripotent stem cell-derived cardiomyocytes in assessment of drug potential for QT prolongation. Toxicol Appl Pharmacol. 2014;278(1):72–77. doi: 10.1016/J.TAAP.2014.04.007. [DOI] [PubMed] [Google Scholar]
- Nozaki Y, Honda Y, Watanabe H, Saiki S, Koyabu K, Itoh T, Kunimatsu T. CSAHi study: Validation of multi-electrode array systems (MEA60/2100) for prediction of drug-induced proarrhythmia using human iPS cell-derived cardiomyocytes -assessment of inter-facility and cells lot-to-lot-variability- Regul Toxicol Pharmacol. 2016;77:75–86. doi: 10.1016/J.YRTPH.2016.02.007https://doi.org/10.1016/J.YRTPH.2016.02.007. [DOI] [PubMed] [Google Scholar]
- Ogawa M, Lin SF, Weiss JN, Chen PS, January C, Beaumont J, Jalife J. Calcium dynamics and ventricular fibrillation. Circ Res. 2008;102(5):e52–e52. doi: 10.1161/CIRCRESAHA.108.171538. [DOI] [PubMed] [Google Scholar]
- Oosterhoff P, Tereshchenko LG, van der Heyden MA, Ghanem RN, Fetics BJ, Berger RD, Vos MA. Short-term variability of repolarization predicts ventricular tachycardia and sudden cardiac death in patients with structural heart disease: A comparison with QT variability index. Heart Rhythm. 2011;8(10):1584–1590. doi: 10.1016/j.hrthm.2011.04.033. [DOI] [PubMed] [Google Scholar]
- Osadchii OE. Effects of Na+ channel blockers on extrasystolic stimulation-evoked changes in ventricular conduction and repolarization. J Cardiovasc Pharmacol. 2014;63(3):240–251. doi: 10.1097/FJC.0000000000000041https://doi.org/10.1097/FJC.0000000000000041. [DOI] [PubMed] [Google Scholar]
- Peng S, Lacerda AE, Kirsch GE, Brown AM, Bruening-Wright A. The action potential and comparative pharmacology of stem cell-derived human cardiomyocytes. J Pharmacol Toxicol Methods. 2010;61(3):277–286. doi: 10.1016/J.VASCN.2010.01.014https://doi.org/10.1016/J.VASCN.2010.01.014. [DOI] [PubMed] [Google Scholar]
- Ponti FD, Poluzzi E, Cavalli A, Recanatini M, Montanaro N, De Ponti F, Montanaro N. Safety of non-antiarrhythmic drugs that prolong the QT interval or induce torsade de pointes: an overview. Drug Saf. 2002;25(4):263–286. doi: 10.2165/00002018-200225040-00004https://doi.org/10.2165/00002018-200225040-00004. [DOI] [PubMed] [Google Scholar]
- Sacerdote L, T. GMwatnm (2013) Stochastic integrable and fire Mmodels: A review on mathematical methods and their applications. In: Bachar M, Batzel J, Ditlevsen S (eds) Berlin Heidelberg: Springer-Verlag
- Sala L, Bellin M, Mummery CL. Integrating cardiomyocytes from human pluripotent stem cells in safety pharmacology: has the time come? Br J Pharmacol. 2017;174(21):3749–3765. doi: 10.1111/bph.13577https://doi.org/10.1111/bph.13577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sala L, Yu Z, Ward-van Oostwaard D, van Veldhoven JPD, Moretti A, Laugwitz K, Bellin M. A new hERG allosteric modulator rescues genetic and drug-induced long-QT syndrome phenotypes in cardiomyocytes from isogenic pairs of patient induced pluripotent stem cells. EMBO Mol Med. 2016;8(9):1065–1081. doi: 10.15252/emmm.201606260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirenko O, Crittenden C, Callamaras N, Hesley J, Chen YWW, Funes C, Cromwell EF. Multiparameter in vitro assessment of compound effects on cardiomyocyte physiology using iPSC cells. J Biomol Screen. 2013;18(1):39–53. doi: 10.1177/1087057112457590https://doi.org/10.1177/1087057112457590. [DOI] [PubMed] [Google Scholar]
- Spudich JL, Koshland DE. Non-genetic individuality: chance in the single cell. Nature. 1976;262(5568):467–471. doi: 10.1038/262467a0. [DOI] [PubMed] [Google Scholar]
- Sugio Y, Kojima K, Moriguchi H, Takahashi K, Kaneko T, Yasuda K. An agar-based on-chip neural-cell-cultivation system for stepwise control of network pattern generation during cultivation. Sens Actuators B Chem. 2004;99(1):156–162. doi: 10.1016/S0925-4005(03)00550-1. [DOI] [Google Scholar]
- Suzuki I, Hattori A, Yasuda K. On-chip multichannel action potential recording system for electrical measurement of single neurites of neuronal network. Jpn J Appl Phys. 2007;46(42):L1028–L1031. doi: 10.1143/JJAP.46.L1028. [DOI] [Google Scholar]
- Suzuki I, Sugio Y, Jimbo Y, Yasuda K. Individual-cell-based electrophysiological measurement of a topographically controlled neuronal network pattern using agarose architecture with a multi-electrode array. Jpn J Appl Phys. 2004;43(3B):L403–L406. doi: 10.1143/JJAP.43.L403. [DOI] [Google Scholar]
- Suzuki I, Sugio Y, Jimbo Y, Yasuda K. Stepwise pattern modification of neuronal network in photo-thermally-etched agarose architecture on multi-electrode array chip for individual-cell-based electrophysiological measurement. Lab Chip. 2005;5(3):241–247. doi: 10.1039/b406885h. [DOI] [PubMed] [Google Scholar]
- Suzuki I, Sugio Y, Moriguchi H, Jimbo Y, Yasuda K. Modification of a neuronal network direction using stepwise photo-thermal etching of an agarose architecture. J Nanobiotechnology. 2004;2(1):7. doi: 10.1186/1477-3155-2-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki I, Yasuda K. Constructive formation and connection of aligned micropatterned neural networks by stepwise photothermal etching during cultivation. Jpn J Appl Phys. 2007;46(9B):6398–6403. doi: 10.1143/JJAP.46.6398. [DOI] [Google Scholar]
- Suzuki I, Yasuda K. Detection of tetanus-induced effects in linearly lined-up micropatterned neuronal networks: application of a multi-electrode array chip combined with agarose microstructures. Biochem Biophys Res Commun. 2007;356(2):470–475. doi: 10.1016/j.bbrc.2007.03.006. [DOI] [PubMed] [Google Scholar]
- Takasuna K, Asakura K, Araki S, Ando H, Kazusa K, Kitaguchi T, Miyamoto N. Comprehensive in vitro cardiac safety assessment using human stem cell technology: Overview of CSAHi HEART initiative. J Pharmacol Toxicol Methods. 2017;83:42–54. doi: 10.1016/j.vascn.2016.09.004. [DOI] [PubMed] [Google Scholar]
- Tanaka T, Tohyama S, Murata M, Nomura F, Kaneko T, Chen H, Fukuda K. In vitro pharmacologic testing using human induced pluripotent stem cell-derived cardiomyocytes. Biochem Biophys Res Commun. 2009;385(4):497–502. doi: 10.1016/j.bbrc.2009.05.073. [DOI] [PubMed] [Google Scholar]
- Terazono H, Takei H, Hattori A, Yasuda K. Development of a high-speed real-time polymerase chain reaction system using a circulating water-based rapid heat-exchange. Jpn J Appl Phys. 2010;49(6):06GM05. doi: 10.1143/JJAP.49.06GM05. [DOI] [Google Scholar]
- Thomsen MB, OROS A, Schoenmakers M, VANOPSTAL J, Maas JN, Beekman JDM, Vos MA. Proarrhythmic electrical remodelling is associated with increased beat-to-beat variability of repolarisation. Cardiovasc Res. 2007;73(3):521–530. doi: 10.1016/j.cardiores.2006.11.025. [DOI] [PubMed] [Google Scholar]
- Umehara S, Hattori A, Inoue I, Yasuda K. Asynchrony in the growth and motility responses to environmental changes by individual bacterial cells. Biochem Biophys Res Commun. 2007;356(2):464–469. doi: 10.1016/j.bbrc.2007.03.001. [DOI] [PubMed] [Google Scholar]
- Umehara S, Inoue I, Wakamoto Y, Yasuda K. Origin of individuality of two daughter cells during the division process examined by the simultaneous measurement of growth and swimming property using an on-chip single-cell cultivation system. Biophys J. 2007;93(3):1061–1067. doi: 10.1529/biophysj.106.098061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varkevisser R, Wijers SC, van der Heyden MA, Beekman JD, Meine M, Vos MA. Beat-to-beat variability of repolarization as a new biomarker for proarrhythmia in vivo. Heart Rhythm. 2012;9(10):1718–1726. doi: 10.1016/j.hrthm.2012.05.016. [DOI] [PubMed] [Google Scholar]
- Vassalle M. The relationship among cardiac pacemakers. Overdrive suppression. Circ Res. 1977;41(3):269–277. doi: 10.1161/01.RES.41.3.269https://doi.org/10.1161/01.RES.41.3.269. [DOI] [PubMed] [Google Scholar]
- Wagner S, Maier LS, Bers DM. Role of Sodium and Calcium Dysregulation in Tachyarrhythmias in Sudden Cardiac Death. Circ Res. 2015;116(12):1956–1970. doi: 10.1161/CIRCRESAHA.116.304678https://doi.org/10.1161/CIRCRESAHA.116.304678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wakamoto Y, Ramsden J, Yasuda K. Single-cell growth and division dynamics showing epigenetic correlations. Analyst. 2005;130(3):311–317. doi: 10.1039/b409860a. [DOI] [PubMed] [Google Scholar]
- Wakamoto Y, Umehara S, Matsumura K, Inoue I, Yasuda K. Development of non-destructive, non-contact single-cell based differential cell assay using on-chip microcultivation and optical tweezers. Sens Actuators B Chem. 2003;96(3):693–700. doi: 10.1016/S0925-4005(03)00549-5. [DOI] [Google Scholar]
- Wakamoto Y, Yasuda K. Quantitative evaluation of cell-to-cell communication effects in cell group class using on-chip individual-cell-based cultivation system. Biochem Biophys Res Commun. 2006;349(3):1130–1138. doi: 10.1016/j.bbrc.2006.08.149. [DOI] [PubMed] [Google Scholar]
- Weiss JN, Qu Z, Chen PS, Lin SF, Karagueuzian HS, Hayashi H, Karma A. The dynamics of cardiac fibrillation. Circulation. 2005;112(8):1232–1240. doi: 10.1161/CIRCULATIONAHA.104.529545https://doi.org/10.1161/CIRCULATIONAHA.104.529545. [DOI] [PubMed] [Google Scholar]
- Woosley R, Wang T, Stone W, Siddoway L, Thompson K, Duff H, Roden D. Pharmacology, electrophysiology, and pharmacokinetics of mexiletine. Am Heart J. 1984;107(5):1058–1065. doi: 10.1016/0002-8703(84)90175-3. [DOI] [PubMed] [Google Scholar]
- Wyman MG, Wyman R, Cannom DS, Criley J. Prevention of primary ventricular fibrillation in acute myocardial infarction with prophylactic lidocaine. Am J Cardiol. 2004;94(5):545–551. doi: 10.1016/J.AMJCARD.2004.05.014https://doi.org/10.1016/J.AMJCARD.2004.05.014. [DOI] [PubMed] [Google Scholar]
- Yasuda K. Non-destructive, non-contact handling method for biomaterials in micro-chamber by ultrasound. Sens Actuators B Chem. 2000;64(1-3):128–135. doi: 10.1016/S0925-4005(99)00495-5. [DOI] [Google Scholar]
- Yasuda Kenji. Lab-on-Chips for Cellomics. Dordrecht: Springer Netherlands; 2004. On-chip single-cell cultivation systems; pp. 225–256. [Google Scholar]
- Yasuda K, Haupt SS, Umemura S-i, Yagi T, Nishida M, Shibata Y. Using acoustic radiation force as a concentration method for erythrocytes. J Acoust Soc Am. 1997;102(1):642–645. doi: 10.1121/1.421009. [DOI] [PubMed] [Google Scholar]
- Yasuda K, Kiyama M, Umemura SS-i, Takeda K. Deoxyribonucleic acid concentration using acoustic radiation force. J Acoust Soc Am. 1996;99(2):1248–1251. doi: 10.1121/1.414635. [DOI] [Google Scholar]
- Yasuda K, Okano K, Ishiwata S. Focal extraction of surface-bound DNA from a microchip using photo-thermal denaturation. Biotechniques. 2000;28(5):1006–1011. doi: 10.2144/00285rr06. [DOI] [PubMed] [Google Scholar]
- Yasuda K, Umemura S-i, Takeda K. Particle separation using acoustic radiation force and electrostatic force. J Acoust Soc Am. 1996;99(4):1965–1970. doi: 10.1121/1.415382. [DOI] [Google Scholar]
- Zareba W, de Luna AB. QT Dynamics and Variability. Ann Noninvasive Electrocardiol. 2005;10(2):256–262. doi: 10.1111/j.1542-474X.2005.10205.xhttps://doi.org/10.1111/j.1542-474X.2005.10205.x. [DOI] [PMC free article] [PubMed] [Google Scholar]