Efficiencies of molecular motors: a comprehensible overview

Abstract

Many biological molecular motors can operate specifically and robustly at the highly fluctuating nano-scale. How these molecules achieve such remarkable functions is an intriguing question that requires various notions and quantifications of efficiency associated with the operations and energy transduction of these nano-machines. Here we give a short review of some important concepts of motor efficiencies, including the thermodynamic, Stokes, and generalized and transport efficiencies, as well as some implications provided by the thermodynamic uncertainty relations recently developed in nonequilibrium physics.

Energetics

Biological molecular motors are nano-sized chemical engines functioning in highly fluctuating environments. The understanding of how energies convert between different forms is essential to elucidate the motors’ operations and design principles. In a broader sense, energetics treats the relations between thermodynamic quantities such as work, heat, entropy, and free energy; they tells us what motors can do and cannot do. Similar to macroscopic motors, efficiency is one of the most important quantities to characterize the molecular motor’s energetics and quantifies how efficiently the input energy is exploited by the motor (Derėnyi et al.1999; Wang 2005, 2008; Zimmermann and Seifert 2012; Dechant and Sasa 2018; Hwang and Hyeon 2018; Brown and Sivak 2019). However, there exists various definitions and notions of motor efficiencies in the literatures and therefore, it may be confusing what aspects of the motor energetics different efficiencies characterize.

In this short article, we review some basic concepts of efficiencies, including the thermodynamic, Stokes, generalized and transport efficiencies, as well as some implications from the thermodynamic uncertainty relations, associated with the operations of molecular motors. Instead of giving a technical discussion, we aim to provide an intuitive overview of the physical meanings carried by these concepts. For more mathematical account of the corresponding subjects, we refer the readers to the references given below in the article.

Thermodynamic efficiency

One of the most commonly used motor efficiency is the thermodynamic efficiency. Most molecular motors derive the free energy input by hydrolyzing ATP molecules, thermodynamic efficiency quantifies how the free energy input is used to do work against a conservative force. For example, one can think of a kinesin motor walking on a microtubule rail against an external conservative force produced by optical trapping of a nano-probe attached to the motor. The kinesin hydrolyzes ATP and uses the free energy change Δμ from ATP to ADP + P_i for climbing up the free-energy potential of the optical trap. Here, in each reaction cycle, the kinesin does work against the conservative force by the optical tweezers to convert free energies of reactions Δμ > 0 to those of the optical trap (Fig. 1). It is noted that thermodynamic efficiency does not apply to setups when the motors undergo free rotation or translation.

Fig. 1.

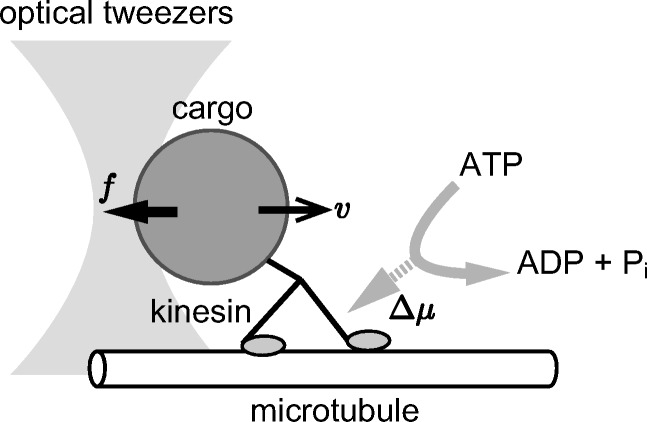
Kinesin motor walking on a microtubule. By using, e.g., optical tweezers, we can apply force on the motor to measure the response of the motor (Ariga et al. 2018). Such a response measurement enables us to estimate energetic quantities like the maximum work by the motor, which is the stalling force times the stepping size

The second law of thermodynamics says that the total free energy change of an isothermal isobaric reaction cycle is negative, i.e., −Δμ + W ≤ 0, implying the amount of work W from the motor to the external agent, e.g., the optical trap, cannot exceed Δμ. Therefore, the thermodynamic efficiency η_th defined by

$${\eta }_{\text{th}}=\frac{\dot{W}}{J\mathrm{\Delta }\mu }=\frac{f\langle v\rangle }{J\mathrm{\Delta }\mu }\le 1$$ 1

cannot exceed one, where f, 〈v〉, and J are the external force, average velocity, and the rate of reaction cycle rate of the motor, respectively.

η_th at the stalled state is determined by the extent of mechano-chemical coupling. Tightly coupled motors, e.g., the F₁-motor (Toyabe et al. 2011), have 1-to-1 correspondence between the mechanical steps and the reaction cycles (i.e., each free energy input Δμ generates a step with size l such that 〈v〉 = Jl holds that leads to the maximum value of η_th = fl/Δμ = 1. Note that J = 0 at the stalled state with 〈v〉 = 0 because the numbers of hydrolysis and synthesis reactions are balanced with no net progression of the reaction cycle. At the stalled state, the motor-generating force Δμ/l and the external force f are balanced. On the other hand, loosely coupled motors result in η_th = 0 at the stalled state. For instance, one can think of a motor which hydrolyzes ATP in all the forward steps but does not necessarily synthesize ATP in all the backward steps. This motor has a finite value of J at the stalled state due to the imbalance between the hydrolysis and synthesis rates. Therefore, η_th vanishes at the stalled state 〈v〉 = 0 and reaches its maximum at a finite velocity.

In summary, η_th is an well-defined efficiency characterizing the tightness of mechano-chemical coupling of the molecular motor; it is defined as a ratio of input and output energies resembling the efficiency of heat engines discussed in classical thermodynamics.

Stokes and generalized efficiencies

Since the thermodynamic efficiency compares the work against an external conservative force with the free energy input derived from chemical reactions, it does not apply to situations where the motor undergoes directed motions against viscous drag of the fluid medium. Viscous drags are non-conservative forces through which energies dissipated to the fluid medium cannot be retrieved later in contrast to the case of conservative forces. Many single molecule measurements, e.g., observing the free rotation and linear motions of rotary and linear motors by the attachment of nano-probes, fall into this case. For such cases, the Stokes efficiency has been proposed (Derėnyi et al. 1999; Wang and Oster 2002) to quantify motor efficiency which is defined as

$${\eta }_{\text{st}}=\frac{\gamma {\langle v\rangle }^2}{J\mathrm{\Delta }\mu }\le 1,$$ 2

where γ is the friction coefficient of the fluid medium. JΔμ corresponds to the rate of free energy input to the motor. Since γ〈v〉 is the viscous force acting on the mechanical motion, γ〈v〉² can be interpreted as the viscous dissipation rate via the average motion of the motor.

It is noted that the motor motion also dissipates energy as heat to the environment due to the rapid fluctuating Brownian forces acting by the solvent molecules (Sekimoto 2010; Harada and Sasa 2005; Toyabe et al. 2010; Ariga et al. 2018); therefore, γ〈v〉² alone cannot account for the rate of total work done on the fluid by the motor, i.e., the power output. As a result, the Stokes efficiency does not correspond to the ratio of energy output to energy input (Sekimoto 2010) in contrast to the thermodynamic efficiency.

Nevertheless, an energetic interpretation of the Stokes efficiency has been given by Derėnyi et al. (1999), where the Stokes efficiency was termed as the generalized efficiency. Accordingly, the Stokes efficiency (2) can be written as a ratio of energies, ${\eta }_{\text{st}}={Ė}_{\text{in}}^{\min }/{Ė}_{\text{in}}$, where ${Ė}_{\text{in}}$ is the actual power input ${Ė}_{\text{in}}=J\mathrm{\Delta }\mu$, and ${Ė}_{\text{in}}^{\min }$ is the minimum power input required for the motor to operate at the observed average velocity 〈v〉. In terms of coarse-grained modeling of the chemo-mechanical coupling of the molecular motors (Wang 2008), where the chemical and mechanical dynamics are described by stochastic jumps and Brownian dynamics, respectively, Wang and Oster (2002) have shown that the Stokes efficiency cannot exceed one. Moreover, they have shown that the minimum necessary power input to maintain a motor motion with the observed average velocity 〈v〉 is given by ${Ė}_{\text{in}}^{\min }=\gamma {\langle v\rangle }^2$, which gives rise to the form of Stokes efficiency in Eq. 2. The condition ${Ė}_{\text{in}}^{\min }=\gamma {\langle v\rangle }^2$ is achieved when all chemical reactions are much faster than the diffusion dynamics (i.e., fast reaction limit) and the driving potential profile is as smooth as possible (i.e., with constant slope, see Fig. 2a). Therefore, the Stokes efficiency is often used to characterize how close the machine driving force is to constant. Generally, molecular motors operate with finite reaction rates and nonlinear potential profiles, e.g., angular fluctuations in F₁-motors are usually modeled by harmonic or harmonic-like potentials (Wang 2008; Toyabe et al. 2012; Kawaguchi et al. 2014; Watanabe et al. 2013), this requires a bigger power input ${Ė}_{\text{in}}=J\mathrm{\Delta }\mu >\gamma {\langle v\rangle }^2$ to maintain the observed average velocity 〈v〉 (see Fig. 2b), implying η_st < 1.

Fig. 2.

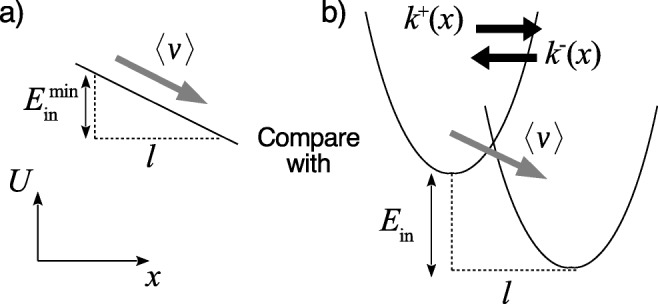
Intuition of Stokes efficiency for a simple motor example with stepsize l per reaction cycle and one state. a Given an observed average velocity 〈v〉, the required energy input per cycle reaches the minimum ($E_{\text{in}}^{\min }=\gamma \langle v\rangle l$) at fast reaction limit with linear potential profile. b Motor dynamics are generally governed by nonlinear potentials and finite reaction rates (k⁺(x) and k⁻(x)). To maintain the same 〈v〉, bigger energy input per cycle $E_{\text{in}}=\mathrm{\Delta }\mu >E_{\text{in}}^{\min }$ is required. The ratio $E_{\text{in}}^{\min }/E_{\text{in}}$ is the Stokes efficiency. Here, x and U denotes the mechanical coordinate and free energy, respectively

While the Stokes efficiency (a special case of generalized efficiency) focuses on the specific task of the motor as maintaining the average velocity 〈v〉, the generalized efficiency, ${\eta }_{\mathrm{g}}={Ė}_{\text{in}}^{\min }/{Ė}_{\text{in}}$, can be readily generalized to other tasks, such as maintaining the observed velocity variance Var(v) or displacement variance Var(x) per reaction cycle that relates to the precision of the motor motions. One can then ask what is the minimum power input ${Ė}_{\text{in}}^{\min }$ required to achieve Var(v) or Var(x) by varying the model parameters (e.g., potential profile, number of rotary steps, reaction rates), and again compare with the actual power input ${Ė}_{\text{in}}=J\mathrm{\Delta }\mu$. As the precision of motor steps has been considered for kinesin in some earlier works (Visscher et al. 1999; Block et al. 2003) in terms of the Fano factor, it will be interesting in future studies of motor energetics to see how such generalized efficiencies associated with various tasks relevant to the motor functions depend on the characteristics of chemo-mechanical couplings in various linear and rotary motors.

Thermodynamic uncertainty relations and motor efficiencies

The studies of motor efficiency can further benefit from the recently developed thermodynamic uncertainty relations (TURs) in statistical physics. The TUR was initially proposed by Barato and Seifert (2015) in the long time limit with proofs later given in Gingrich et al. (2016), which has also been shown to hold in finite time (Pietzonka et al. 2017; Horowitz and Gingrich 2017) (see Horowitz and Gingrich (2019) for a review of recent developments). The TUR highlights the tradeoff between the rate of entropy production rate σ (also equal to energy dissipation times temperature), the average of any fluctuating current 〈J_τ〉 integrated up to a time τ, and the corresponding current variance Var(J_τ) for systems operated in nonequilibrium steady states such as molecular motors. Specifically, the finite time TUR for stochastic jump processes with arbitrary reaction scheme reads (Pietzonka et al. 2017; Horowitz and Gingrich 2019)

$$\frac{\text{Var}\left(J_{\tau }\right)}{{\langle J_{\tau }\rangle }^2}\ge \frac{2k_{\mathrm{B}}}{\tau \sigma }\mathrm{.}$$ 3

Here, k_B is the Boltzmann constant. The fluctuating current $J_{\tau }={\sum }_{i<j}d(i,j)J_{\tau }(i,j)$ is a weighted sum over jumps between the states where J_τ(i,j) is the net number of transitions from state j to i during time τ. d(i,j) is the change of the physical quantity of interest when the system jumps from state j to i. In particular, if d(i,j) is the change of the motor mechanical coordinate Δx when jumping from state j to i, the TUR, Eq. 3, can be written as (Pietzonka et al. 2016)

$$\sigma D/{\langle v\rangle }^2\ge k_{\mathrm{B}}$$ 4

in terms of the average velocity 〈v〉 = 〈Δx(τ)〉/τ and the diffusion coefficient D ≡〈(Δx(τ) −〈Δx(τ)〉)²〉/2τ that can be estimated directly from single molecule trajectories.

An immediate consequence of the TUR in Eq. 4 is that it provides tighter bounds for both the thermodynamic and Stokes efficiencies (Pietzonka et al. 2016). From the first law of thermodynamics, the rate of energy dissipation Tσ = JΔμ − f〈v〉 = f〈v〉(1/η_th − 1), providing us with a relation between σ and η_th to express (4) as

$${\eta }_{\text{th}}\le \frac{1}{1+k_{\mathrm{B}}T\langle v\rangle /Df}\mathrm{.}$$ 5

Likewise, Tσ = JΔμ = γ〈v〉²/η_st when no external force is applied (f = 0) and after eliminating σ, Eq. 4 can be expressed as

$${\eta }_{\text{st}}\le \gamma D/k_{\mathrm{B}}T\mathrm{.}$$ 6

On the other hand, Dechant and Sasa have proposed the transport efficiency (Dechant and Sasa 2018),

$${\eta }_{\text{tr}}=\frac{k_{\mathrm{B}}{\langle v\rangle }^2}{\sigma D}\le 1,$$ 7

to assess how efficiently a molecular motor suppresses the uncertainty in displacement, D, and transports loads in high speed 〈v〉 by means of energy consumption σ. An efficient motor in performing the task of cargo transport is characterized by a large η_tr close to one. By comparing η_tr estimated from the ATP-driven motions of different linear and rotary motors in terms of simple discrete state models, Hwang and Hyeon (2018) concluded that some of the motors considered in their studies operate semi-optimally under cellular conditions, suggesting that evolutionary pressure has played a role in molding the molecular motors to their function.

Similar to the generalized efficiency, it remains an open question what are the general characteristics of the chemo-mechanical couplings and the corresponding nonequilibrium dynamics that can optimize the transport efficiency. In future studies, we suggest that more realistic models can be considered, such as the diffusion-jump model (Wang 2008; Watanabe et al. 2013; Li et al. 2015; Tamiya et al. 2018), that explicitly takes into account the modulation of the reaction rates by the mechanical motions of the motor.

Conclusion

Modern developments in nonequilibrium thermodynamics and statistical physics have provided us with a systematic theoretical framework to study molecular systems operating at the highly stochastic nano-scale. We believe that the application of these physical concepts to the understanding of the efficiency and the design principles of molecular motors related to their functions is only in its beginning stage. In particular, recent single molecule experiments have revealed that F-type and V-type motors from different species, such as the bacterial and mammalian mitochondrial ATPases (Adachi et al. 2007; Bilyard et al. 2013; Suzuki et al. 2014; Li et al. 2015; Iida et al. 2019; Kobayashi et al. 2020), demonstrate very different characteristics in rotary steps, chemo-mechanical pathways, and couplings. It is expected that these experimental findings will provide us with a rich set of model systems to evaluate, validate, compare, and generalize the existing notions of motor efficiencies.

Funding information

This work was financially supported by a Grant-in Aid for Scientific Research on Innovative Areas “Molecular Engine” (JSPS KAKENHI grant number JP18H05427) and the STINT initiation grant for internationalization.