Dynamic variations of the COVID-19 disease at different quarantine strategies in Wuhan and mainland China

Abstract

Background

The Coronavirus Disease 2019 (COVID-19) firstly announced in Wuhan of Hubei province, China is rapidly spreading to all the other 31 provinces of China and to more than 140 countries. Quarantine strategies play the key role on the disease controlling and public health in the world with this pandemic of the COVID-19 defined by the World Health Organization.

Methods

In this study, a SEIRQ epidemic model was developed to explore the dynamic changes of COVID-19 in Wuhan and mainland China, from January 27, 2020 to March 5, 2020. Moreover, to investigate the effects of the quarantine strategies, two perspectives are employed from the different quarantine magnitudes and quarantine time points.

Results

The major results suggest that the COVID-19 variations are well captured by the epidemic model with very high accuracy in the cumulative confirmed cases, confirmed cases, cumulative recovered cases and cumulative death cases. The quarantine magnitudes in the susceptible individuals play larger roles on the disease control than the impacts of the quarantines of the exposed individuals and infectious individuals. For the quarantine time points, it shows that the early quarantine strategy is significantly important for the disease controlling. The time delayed quarantining will seriously increase the COVID-19 disease patients and prolongs the days of the disease extinction.

Conclusions

Our model can simulate and predict the COVID-19 variations and the quarantine strategies are important for the disease controlling, especially at the early period of the disease outbreak. These conclusions provide important scientific information for the government policymaker in the disease control strategies.

1 Introduction

Since the Coronavirus Disease 2019 (COVID-19) (or NCP: Novel Coronavirus Pneumonia) was reported in Wuhan city, China, it has been spreading to all the provinces of China and to more than 20 countries (e.g. America, Japan, Singapore and Thailand) in the world with a high rapid speed. The number of the cumulative laboratory-confirmed cases is fast increasing from 27 on December 31, 2019 to 42638 on February 10, 2020 with only 41 days from the National Health Commission of the People's Republic of China (http://www.nhc.gov.cn/).

Strong evidences have been proved that COVID-19 has the person-to-person transmission in hospital and family settings [1]. The COVID-19 was declared a public health emergency of international concern by the World Health Organization (WHO) at January, 1, 2020. To fight against this serious COVID-19 virus, the Chinese government had been setting up extreme control strategies, such as the lockdown of Wuhan and initiating a top-level emergency response to rein in the outbreak of the epidemic associated with COVID-19 in the other provinces of China, which has made great contribution to the global human society.

Accurately assessing and predicting the COVID-19 spread plays the key role in the present disease control in China. Until now, some literatures has used the disease dynamic models to analyze the spread and outbreak of COVID-19 in China [2], [3], [4], [5], [6], [10], [7]. A SEIR epidemic model to estimate the spread in the major cities of China considering the international passengers [2]. However, with the present disease control strategies, the quarantine in different representative populations should be considered and the total population is constant. Therefore, in this study, considering the quarantine, we establish a SEIRQ epidemic model to explore the COVID-19 spread characteristics under the current control conditions.

The organization of this paper is as follows. In the next section, a SEIRQ model is established and illustrated, data and methodology are displayed. In Section 3, the simulation and forecast, and scenario analysis of the quarantine strategies effects on the COVID-19 variations are investigated which are our main results. A brief discussion is provided in Sections 4.

2 SEIRQ model, data and methodology

2.1 SEIRQ model

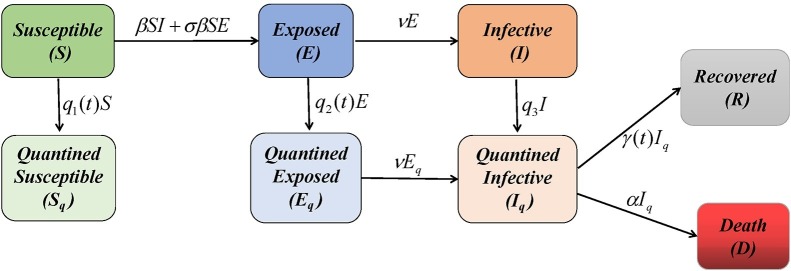
In this study, according to the characteristics of the COVID-19 transmission, the whole population at time t is divided into seven compartments which include the susceptible individuals S(t), exposed individuals E(t), infectious individuals I(t), removed individuals R(t), quarantined susceptible individuals S _q(t), quarantined exposed individuals E _q(t) and quarantined infectious individuals I _q(t). The COVID-19 disease is transmitted from I(t) to S(t) with the incidence rate of β, and from E(t) to S(t) with the incidence rate of σβ, respectively. The susceptible individuals S(t) is partly quarantined with the rate of q ₁(t). We assume that exposed individuals E(t) and quarantined exposed individuals E _q(t) are transmitted to infectious individuals I(t) and quarantined infectious individuals I _q(t) with the same transition rate of ν. The quarantined rates of exposed individuals E(t) and infectious individuals I(t) are q ₂(t) and q ₃. The death rate induced by the COVID-19 disease of quarantined infectious individuals I _q(t) is α. γ(t) is the recovery rate of quarantined infected individuals I _q(t) which is the mainly part of removed individuals R(t) (Fig. 1 ).

Fig. 1.

Flowchart of COVID-19 SEIRQ epidemic model.

According to the above analysis, the corresponding SEIRQ epidemic model can be described by the following system of ordinary differential equations

$$\left\{\begin{array}{c}{S}^{\prime }=-\beta \mathrm{SI}-\sigma \beta \mathrm{SE}-q_1(t)S,\hfill \\ E^{\prime }=\beta \mathrm{SI}+\sigma \beta \mathrm{SE}-\nu E-q_2(t)E,\hfill \\ I^{\prime }=\nu E-q_{3}I,\hfill \\ R^{\prime }=\gamma (t)I_q+\alpha I+\alpha I_q,\hfill \\ {S_q}^{\prime }=q_1(t)S,\hfill \\ {E_q}^{\prime }=q_2(t)E-\nu E_q,\hfill \\ {I_q}^{\prime }=q_{3}I+\nu E_q-\gamma (t)I_q-\alpha I_q.\hfill \end{array}\right)$$ (1)

Here parameters 0 <  β, σ, ν, γ, α  < 1 and the quarantine rates 0 ≤  q _i  ≤ 1, i  = 1, 2, 3. All the initial values of different individual groups: S(0), E(0), I(0), R(0), S _q(0), E _q(0), I _q(0) are non-negative.

2.2 Data and methodology

The COVID-19 cases of Wuhan and mainland China are obtained from the National Health Commission of the People's Republic of China (http://www.nhc.gov.cn/), and the Health Commission of Hubei Province (http://wjw.hubei.gov.cn/). The data of Wuhan and mainland China are from January 27, 2019 to March 5, 2020. The variables include the cumulative confirmed cases, confirmed cases and cumulative recovered cases and cumulative death cases.

To evaluate the accuracy of our model, five statistical indices are applied, including the absolute error (AE), relative error (RE), mean absolute percentage error (MAPE), determinant coefficient R  *  ² which is the square of correlation coefficient R* and distance between indices of simulation and observation (DISO) [8]. Assuming the observed COVID-19 cases are A  = (a ₁, a ₂, …, a _n) and the simulated data of SEIRQ model is B  = (b ₁, b ₂, …, b _n), we have

$$\mathrm{AE}=\frac{1}{n}\sum _{i=1}^{i=n}(b_i-a_i),$$

$$\mathrm{RE}=\frac{1}{n}\sum _{i=1}^{i=n}\frac{b_i-a_i}{a_i}\times 100\%,$$

$$\mathrm{MAPE}=\frac{1}{n}\sum _{i=1}^{i=n}\left|\frac{b_i-a_i}{a_i}\right|\times 100\%,$$

$${R*}^2={\left(\frac{{\sum }_{i=1}^{i=n}(a_i-\overline{a})(b_i-\overline{b})}{\sqrt{{\sum }_{i=1}^{i=n}{(a_i-\overline{a})}^2}\sqrt{{\sum }_{i=1}^{i=n}{(b_i-\overline{b})}^2}}\right)}^2,$$

$$\mathrm{DISO}=\sqrt{{(1-R*)}^2+{\mathrm{NAE}}^2+{\mathrm{NRMSE}}^2},$$

where $\overline{a}$ and $\overline{b}$ are the mean values of A and B, NAE is the ratio between AE and $\overline{a}$, and

$$\mathrm{NRMSE}=\frac{1}{\overline{a}}\sqrt{\frac{1}{n}\sum _{i=1}^{i=n}{(a_i-b_i)}^2}.$$

The bigger value of R  *  ² and the smaller values of AE, RE, MAPE and DISO mean the higher accuracy by the model simulated and predicted [5], [6].

In order to investigate the impacts of the different quarantine rates on the COVID-19 variations of Wuhan and mainland China, different scenarios of the quarantine rates q ₁(t), q ₂(t) and q ₃(t) on susceptible individuals, exposed individuals and infectious individuals are explored, respectively. Moreover, considering the latent periods of the COVID-19 disease, the effects of the quarantine strategies on the COVID-19 variations before with different time points are analyzed. The step time with 5 days are averaged from the latent periods of 3–7 days.

3 Result

3.1 Simulation and prediction of the COVID-19 variations

In this section, the variations of the COVID-19 in Wuhan and mainland China are simulated and predicted based on our SEIRQ model. The simulated cumulative confirmed COVID-19 data are from January 27, 2019 to March 2, 2020. The performance is evaluated by the data from March 3, 4, 5, 2020, and R  *², AE,RE, RMSE, MPAE and DISO are employed to quantify the accuracy.

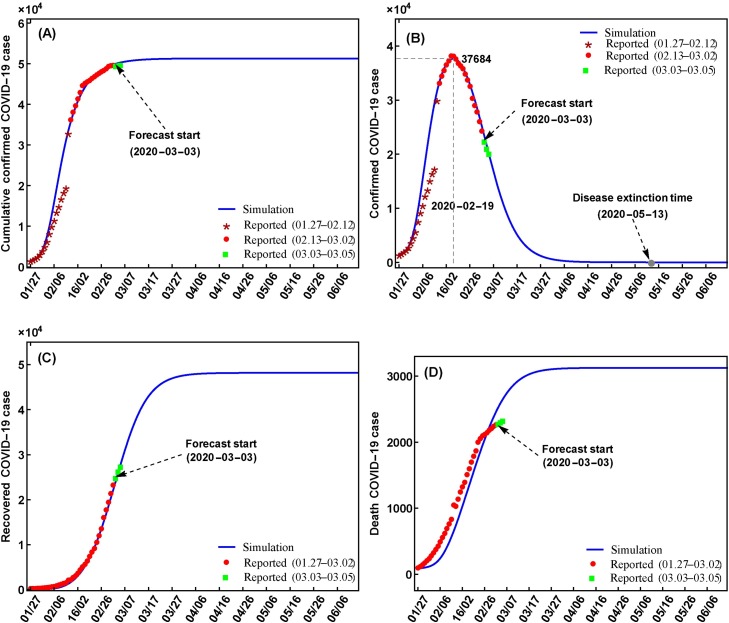
Fig. 2 displays the variations of the COVID-19 disease in Wuhan. For Wuhan, our model has high accuracy to capture the variations of the cumulative confirmed cases, the confirmed cases, the cumulative removed cases and the cumulative death cases with R  *² larger than 0.97, and DISO smaller than 0.25 (Fig. 2 and Table 1 ). For the prediction of the COVID-19 disease variations at March 3, March 4, and March 5, 2020, the values of RE are very close to zero which indicate our SEIRQ model has highly accuracy in the COVID-19 predictions.

Fig. 2.

Simulation and prediction of the COVID-19 in Wuhan. The initial values and parameters are S(0) = 10967505, E(0) = 220, I(0) = 130, R(0) = 45, S_q(0) = 110810, E_q(0) = 745, I_q(0) = 1460, q₁ = 0.12, q₂ = 0.55, q₃ = 0.78, β = 2.06 × 10⁻⁷, ν = 0.13, α = 0.002789, σ = 0.63, γ(t) = 0.001 + 0.16/(1 + exp(5.2088 − 0.13856t)).

Table 1.

Evaluation results of the simulation and prediction in Wuhan.

Study cases	Simulation			Prediction
				3/3	4/3	5/3
	R *2	MAPE(%)	DISO	RE(%)	RE(%)	RE(%)
Confirmed	0.9448	0.1433	0.1913	5.53	3.91	0.16
Cumulative	0.9729	0.1146	0.1300	0.91	0.96	0.92
Recovery	0.9981	0.2479	9.91	4.12	2.36	0.54
Death	0.9715	0.2534	0.2378	10.39	12.06	13.45

The maximum value of the cumulative confirmed cases in Wuhan is 51308 at May 12, 2020, which indicates that the disease will be extinct around May 12, 2020 (Fig. 2A). The peak value of the confirmed cases is 37684 at February 19, 2020 which means that the COVID-19 disease variations are controlled to the positive perspective (Fig. 2A and B). For the cumulative recovered cases and the cumulative death cases, they are also captured by our model with very high accuracy (Fig. 2C and D). The number of the cumulative recovered cases will reach 48182 and the cumulative death number will be 3206 in Wuhan (Fig. 2C and D).

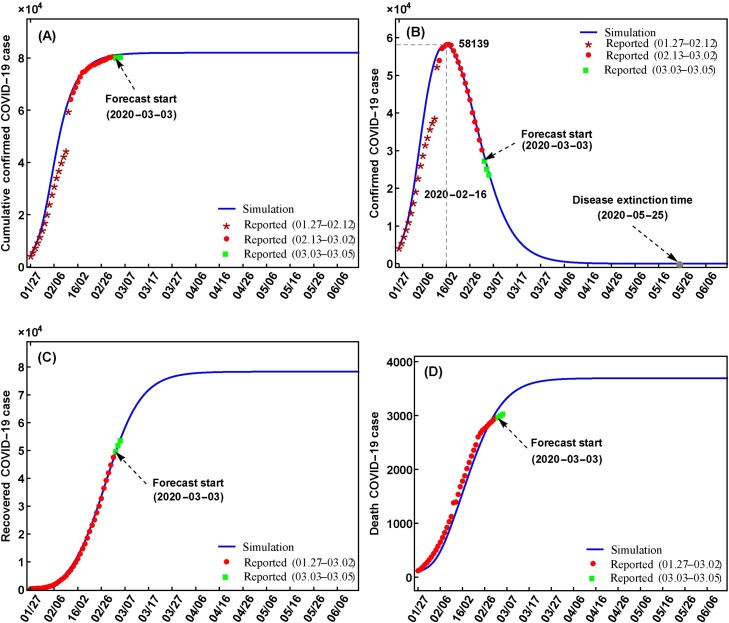
For mainland China, the COVID-19 variations are simulated and predicted with very high accuracy, such as the R  *² larger than 0.97, the RE values of the prediction nearly to zero (Fig. 3 , Table 2 ). It is also obtained that the cumulative removed cases and the cumulative death cases are simulated and predicted with much higher accuracy than the cumulative confirmed cases and confirmed cases as the results of Wuhan (Fig. 2, 3, Table 2). The maximum value of the cumulative confirmed cases in mainland China is 82005, and the peak value of the confirmed cases is 58139 at February 16, 2020 (Fig. 3A and B). The numbers of the cumulative recovered cases and the cumulative death cases will reach to 78290 and 3694 (Fig. 3C and D).

Fig. 3.

Simulation and prediction of the COVID-19 in mainland China. The initial values and parameters are S(0) = 1381411962, E(0) = 1720, I(0) = 1050, R(0) = 60, S_q(0) = 13953800, E_q(0) = 6973, I_q(0) = 4329, q₁ = 0.11, q₂ = 0.5, q₃ = 0.76, β = 1.14 × 10⁻⁹, ν = 0.15, α = 0.0021, σ = 0.63, γ(t) = 0.009 + 0.12/(1 + exp(4.7984 − 0.1448t)).

Table 2.

Evaluation results of the simulation and prediction in mainland China.

Study cases	Simulation			Prediction
				3/3	4/3	5/3
	R *2	MAPE(%)	DISO	RE(%)	RE(%)	RE(%)
Confirmed	0.9375	0.1000	0.1668	5.07	4.45	1.85
Cumulative	0.9748	0.0976	0.1265	1.02	1.00	0.96
Recovery	0.9987	0.2141	0.0761	1.46	0.97	0.23
Death	0.9916	0.1496	0.1352	4.66	5.51	6.21

3.2 Scenario analysis of the quarantine rates effects on the COVID-19 variations

To investigate the impacts of the different quarantine rates on the COVID-19 variations of Wuhan and mainland China, different scenarios of the quarantine rates on susceptible individuals, exposed individuals and infectious individuals are explored. The parameters and initial values obtained in the simulation and prediction of the Section 3.1 are noted as baseline values.

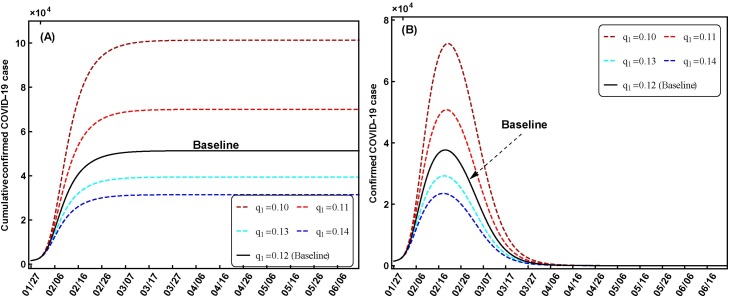
For the quarantining on the susceptible individuals of Wuhan, remarkable differences are obtained from the different effects of the quarantine strategies on the cumulative confirmed cases and the confirmed cases (Fig. 4 ). The peak values of the cumulative confirmed cases and the confirmed cases are seriously decreased with the increasing of the quarantine rates from 0.11 to 0.14 (Fig. 4A and B). These results indicate that the relax of the quarantine on the susceptible individuals may cause the serious of the COVID-19 disease variations, and the quarantine strategy on the susceptible plays a key role on the disease control.

Fig. 4.

Scenario results of the COVID-19 variations with different q₁ values in Wuhan. The other parameters and initial values are assumed as the baseline values.

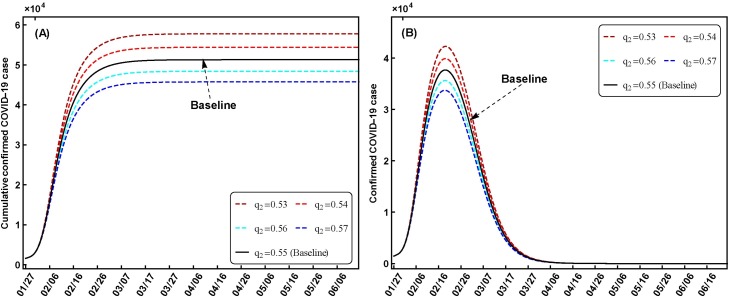
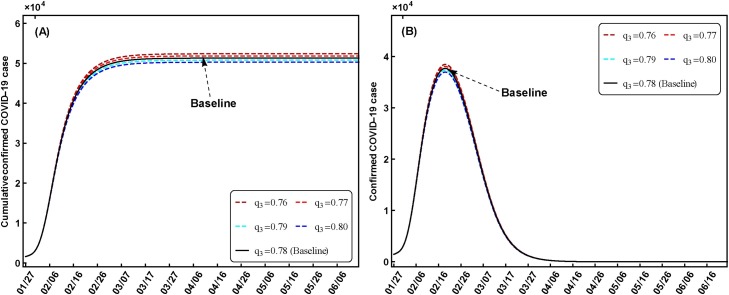
For the other quarantine rates of q ₂ and q ₃, the effects of the quarantine strategy on the exposed individuals are larger than the infectious individuals when these parameters are changed at small step value of 0.01 (Fig. 5, Fig. 6 ). In particularly, the numbers of the cumulative confirmed cases increased from 45753 to 57789 with the q ₂ value decreasing from q ₂  = 0.57 for q ₂  = 0.53, and the corresponding time days range from 92 days to 107 days (Fig. 5A). The peak values of the confirmed cases increased from 33720 to 42285, and the corresponding time days are 107 days and 109 days (Fig. 5B). For the quarantine strategy on the infectious individuals, it has not largely impacts on the COVID-19 disease variations when q ₃ is changed close to the baseline value, such as the peak values of the cumulative confirmed cases from 52393 to 51308 for q ₃  = 0.76, 0.78, respectively (Fig. 5A).

Fig. 5.

Scenario results of the COVID-19 variations with different q₂ values in Wuhan. The other parameters and initial values are assumed as the baseline values.

Fig. 6.

Scenario results of the COVID-19 variations with different q₃ values. The other parameters and initial values are assumed as the baseline values.

Moreover, we explored the variations of the disease extinction days and the maximum values of the cumulative death individuals induced by the COVID-19 disease. The disease extinction days are defined as the days with the zero value of the confirmed cases in this study. The disease extinction days are 114, 111, 108, 106 and 104 for q ₁  = 0.1, 0.11, 0.12, 0.13 and q ₁  = 0.14, respectively which shows that the strong quarantine on the susceptible individuals can shorten the disease extinction time. However, the disease extinction days with the q ₂ from 0.53 to 0.57 and q ₃ from 0.76 to 0.80 have small differences with the values of 0–2 days. For the maximum values of the cumulative death individuals, the numbers are decreased from 5736 for q ₁  = 0.1 to 2033 for q ₁  = 0.14, from 3478 for q ₂  = 0.53 to 2821 for q ₂  = 0.57, and from 3184 for q ₃  = 0.76 to 3070 for q ₃  = 0.80.

For mainland China, the peak values of the cumulative confirmed cases are decreased from 120731 for q ₁  = 0.09 to 62729 for q ₁  = 0.13, from 88997 for q ₂  = 0.53 to 75915 for q ₂  = 0.57, and from 83556 for q ₃  = 0.74 to 80536 for q ₃  = 0.78 indicating the stronger impacts of the quarantine on the susceptible individuals than the other two individuals. However, the disease extinction days have not large differences among the changes of the quarantine strategies of the susceptible individuals, exposed individuals and infectious individuals, respectively. For the maximum values of the cumulative death individuals, the numbers are decreased from 7135 for q ₁  = 0.09 to 3960 for q ₁  = 0.13, from 5451 for q ₂  = 0.53 to 4672 for q ₂  = 0.57, and from 5112 for q ₃  = 0.74 to 4938 for q ₃  = 0.78.

3.3 Effects of the quarantine rates on the COVID-19 variations with the time points changes

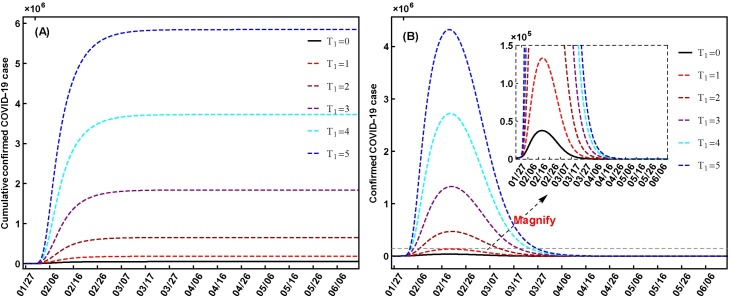
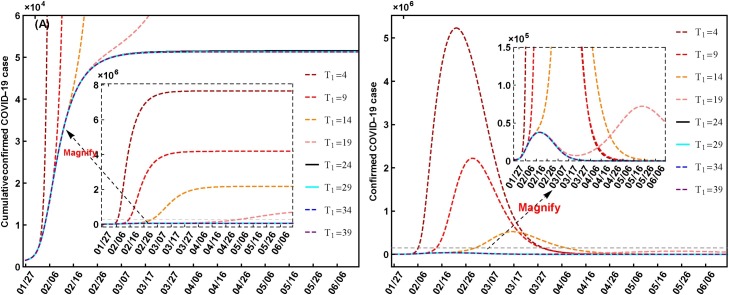
In this section, we focus on the effects of the quarantine rates on the COVID-19 variations with the time point changes. Based on the above results, only the COVID-19 variations in Wuhan are discussed. The first day January 27, 2020 is noted as t  = 0, and the second day January 28, 2020 is t  = 1. Flowing this rule, each day date have a t  =  T ₁ number. Then, two extreme aspects of the time point changes with the baseline quarantine rate values are considered. For the first aspect, we set the quarantine strategies as the baseline values with T ₁  = 0, 1, 2, 3, 4, 5 days time interval which means that the base line quarantine strategy is employed after 0, 1, 2, 3, 4, 5 days. For the second aspect, the date of the peak value of the confirmed cases is Feb 19, 2020 which is the 24 days (i.e. t  = 24). Because the averaged latent period of the COVID-19 is 5 days, the other time points are T ₁  = 4, 9, 14, 19, 29, 34 and T ₁  = 39 which are January 30, February 4, February 9, February 14, February 24, February 29 and March 5, 2020, respectively. The baseline quarantine values are employed before the eight time points (including the baseline), and after these time points there is no quarantine on the susceptible individuals and exposed individuals. It should be noted that the quarantine on the infectious individuals is always employed in all the days of the two aspects. The effect results of the two aspects are displayed in Fig. 7, Fig. 8.

Fig. 7.

Effects of the quarantine strategy on the COVID-19 variations after different time points. The other parameters and initial values are assumed as the baseline values.

Fig. 8.

Effects of the quarantine strategy on the COVID-19 variations before different time points. The other parameters and initial values are assumed as the baseline values.

For the first aspect, the quarantine time points at T ₁  = 0, 1, 2, 3, 4, 5 indicate the baseline quarantine strategy is applied with 0, 1, 2, 3, 4, 5 days time delay which result in the increasing peak values of the cumulative confirmed cases and the corresponding prolonged time days (Fig. 7 A). The peak values of the confirmed cases are increased, while the corresponding time days all around 25 days (Fig. 7B). The disease extinction days are increased from 108 at T ₁  = 1 to 142 at T ₁  = 5 with the cumulative death number dramatically increasing from 3125 to 334577.

For the second aspect, the peak values of the cumulative confirmed cases are decreased from the largest value of 7654573 at T ₁  = 4 to the smallest value of 51308 at T ₁  = 39, and the peak values of the confirmed cases are also rapidly decreased with the prolonged quarantine time (Fig. 8 A and B). It should be noted that there exists the second outbreak at T ₁  = 19 which prolonged the disease extinction days (Fig. 8B). For the cumulative death cases, their peak values are also rapidly decreased with the quarantine time variations.

4 Discussion

Until now, the latest numbers of the cumulative confirmed COVID-19 cases of Wuhan are highly to 49991 at March 12, 2020 from the government reports of Hubei Province. Thereby, for an epidemic with the human-to-human transmission characteristic, the reported case numbers are increasing exponentially at the early stage of outbreak, and the evaluation and prediction play a crucial importance role in the public health and disease control [2]. In this study, we established a SEIRQ epidemic model based on the present quarantine strategy to investigate the COVID-19 variations in Wuhan and mainland China employing the reported data from January 27, 2020 to March 5, 2020. Moreover, to explore the effects of different quarantine strategies, scenario discussions were employed from the perspectives of different quarantine magnitudes and quarantine time points.

For the simulation and prediction abilities of our model, it displayed that our model can well capture the COVID-19 variations with high accuracy. In general, it is very hard to capture the disease variations with high accuracy by the dynamical models. We have been compared our forecasting with the observed data prolonged 10 days from March 6, 2020 to March 15, 2020. The absolute values of RE (relative error) of the cumulative confirmed cases are smaller than 2.05% (Table 3 ).

Table 3.

Evaluation results of the prediction in cumulative confirmed cases.

RE(%)	6/3	7/3	8/3	9/3	10/3	11/3	12/3	13/3	14/3	15/3
mainland China	0.95	1.00	1.03	1.08	1.12	1.15	1.18	1.20	1.21	1.22
Wuhan	1.09	1.22	3.62	1.47	1.59	1.71	1.81	1.91	1.98	2.05

The results suggest that the COVID-19 variations are well captured by the epidemic model with very high correlation coefficients and very small biases in the cumulative confirmed cases, confirmed cases, cumulative recovered cases and cumulative death cases. The quarantine magnitudes in the susceptible individuals play larger roles on the disease control than the impacts of the quarantines of the exposed individuals and infectious individuals. For the different quarantine time points, it shows that the early quarantine strategy is significantly important for the disease controlling. The time delayed quarantining will seriously increases the COVID-19 disease patients and prolongs the days of the disease extinction. These results provide important scientific information for the government policymaker in the disease control strategies and public health.

Declarations

Ethics approval and consent to participate

Because no individual patient's data was employed, the ethical approval or individual consent was not applicable.

Availability of data and materials

All data are publicly available.

Funding

This research was supported by National Natural Science Foundation of PR China [11771373, 61662060], Natural Science Foundation of Ningxia University [ZR18011], Major Innovation Projects for Building First-class Universities in China's Western Region [ZKZD2017009].

Disclaimer

The funding agencies had no role in the design and conduct of the study; collection, management, analysis, and interpretation of the data; preparation, review, or approval of the manuscript; or decision to submit the manuscript for publication.

Conflict of interests

We declare that we have no financial and personal relationships with other people or organizations that can inappropriately influence our work.

Authors’ contributions

Study design: Zengyun Hu, Qianqian Cui, Jing Qian, Junmei Han and Zhidong Teng; Conceptualization: Zengyun Hu, Qianqian Cui.

Data collection: Junmei Han, Jing Qian, Zengyun Hu and Qianqian Cui.

Data analysis: Zengyun Hu, Qianqian Cui.

Visualization: Qianqian Cui, Junmei Han.

Writing: Zengyun Hu.

Review and editing: Zhidong Teng, Zengyun Hu.