Acoustic radiation force optical coherence elastography for evaluating mechanical properties of soft condensed matters and its biological applications

Abstract

Evaluating mechanical properties of biological soft tissues and viscous mucus is challenging because of complicated dynamic behaviors. Soft condensed matter models have been successfully used to explain a number of dynamical behaviors. Here we reported that optical coherence elastography (OCE) is capable of quantifying mechanical properties of soft condensed matters, micellar fluids. A 7.5 MHz focused transducer was utilized to generate acoustic radiation force exerted on the surface of soft condensed matters in order to produce Rayleigh waves. The waves were recorded by optical coherence tomography (OCT). The Kelvin-Voigt model was adopted to evaluate shear modulus and loss modulus of soft condensed matters. The results reported that various concentrations of micellar fluids can provide reasonable ranges of elasticity from 65.71 to 428.78 Pa and viscosity from 0.035 to 0.283 Pa⋅s, which are close to ranges for actual biological samples, like mucus. OCE might be a promising tool to differentiate pathologic mucus samples from healthy cases as advanced applications in the future.

Introduction

The deformable properties of soft tissues are complicated due to dynamical fluctuations of rheology caused by the activity of cells. Soft condensed matter has high similarity with characteristics of biological tissues; therefore, these have been exploited to investigate tissue mechanics and have been successful in explaining dynamical tissue behaviors such as surface tension, elasticity and viscosity ¹. Micelles have been identified to have representative complexity of soft matter systems ² and have attracted much attention in areas such as nano-carriers for drug delivery ^3–9, mechanical responses ^10–14, and cancer treatment ^{15, 16} due to the versatility of the rheological properties with small amphiphilic molecules and their spontaneous self-assembly in a simplicity of the design with surfactant, salt and water ^{10, 17–19}.

The combinations of amphiphilic molecules form diverse aggregation micro-structures of micelles including spherical micelles, wormlike micelles, vesicles, hexagonal liquid crystals and lamellar liquid crystals, which are associated with temperature, concentration and the ratio of surfactant to salt ^{2, 20, 21}. Hydrophilic heads pattern the shell of a sphere and hydrophobic tails are pointed inward so that water-insoluble drugs can be loaded into the hydrophobic cores to be good drug carriers^{9, 20, 22}. Besides, microscopic micelles with a tubular, called wormlike, topology are presented in a few ten to hundred mM concentrations ²¹, which have the capability to break and reform under shear stress so that they can be described as an “alive polymer” ^{17, 23}. Importantly, micelles have a unique property called “self-healing” or “self-assembly”; therefore, its dynamical behaviors are similar with tissue mechanics, such as spontaneous cell sorting and aggregate fusion ¹. On the other hand, its appearance and behavior is that of a semi-solid, like biological mucus, rather than fluids although it bears the name micellar fluid.

To quantify mechanical properties of model tissues, several experimental techniques have been well-developed including aggregation centrifugation, micropipette aspiration, parallel-plate compression and aggregate fracture ¹. Aggregation centrifugation was proposed by H. M. Phillips and M. S. Steinberg ²⁴ who placed tissues in a centrifugal field with a larger gravity to produce deformations, and tissue surface tension was found to be inversely associated with the degree of flattening. However, an extra analysis algorithm of the deformed aggregate shape and surface tension might be needed so that this technique could in principle be performed ¹. Micropipette aspiration was introduced by K. Guevorkian et al. who utilized a micropipette with a constant suction pressure to aspirate an aggregation and characterize tissue rheology by the deformation of length with a function of time ²⁵. The low throughput of experimental measurement is an intrinsic drawback of a micropipette aspiration system ^{26, 27}. G. Forgacs et al. utilized two nonadhering parallel plates to deform living embryonic tissues and determine their viscoelastic properties ²⁸. However, a typical time scale with exerted stresses is about an hour ¹. C. Wiebe al. measured mechanical properties of embryonic cells by using fine wires with cyanoacrylate glue to adhere live aggregated embryo and evaluated the fracture energy ²⁹. Adhesive materials can alter cell behavior and sophisticated equipment is required to fabricate micropatterns, such as micropillar ³⁰.

Optical coherence tomography (OCT) has become a popular technology used to investigate superficial tissues in biomedical applications over the last decade due to a number of advantages: noninvasive, high spatial resolution, fast, and sensitive to the topology of a surface ^31–33. An extended technology from OCT to evaluate elasticity, viscosity, and response of local small tissues by measuring tissue motion is called optical coherence elastography (OCE). The landmark paper of OCE was proposed by Schmitt in 1998 ³⁴. OCE can be performed with many variants of temporal and spatial variables of loading technologies, soft tissue viscoelastic models and computational methods so that it is able to broaden the field in elastography ³³. Previous studies have demonstrated that OCE has the capability to characterize mechanical properties of skin ³⁵, chicken breast ³⁶, rat tumor tissue ³⁷, prostate cancer ³⁸ and especially cornea and lens in the eye ^{31, 39–43}. Recently, B. F. Kennedy et al. reported that OCE has shown promise in the fields of oncology, cell mechanics and tissue engineering ⁴⁴. Furthermore, OCE is able to deal with biological mucus and tissues with thin thickness or transparent status for differentiating low viscosity of bile with colecystectomized patients from normal subjects sampled the via bile duct ⁴⁵. In contrast, it would be difficult for ultrasonic shear wave elastography (SWE) technology to investigate these materials because extra scatterers would be required and the materials are of limited thickness ¹⁰.

It is known that tissue mechanics can be represented by using soft condensed matters models ¹; however, to predict dynamic properties of biological soft samples is still challenging due to complicated deformable behaviors ²¹. Gonzalez-Rodriguez et al. mentioned that soft condensed matters have been successfully used to explain a number of dynamical tissue behaviors and has served as a basis for tissue engineering within medicine ¹. In this study, we used OCE to evaluate soft condensed matters, micellar fluids in the case, to investigate the mechanical response of the biological very soft samples, like mucus. Due to easily controlling various concentrations in fabrication, micellar fluids can exhibit various complexity of biological soft samples ². Four concentrations of micellar fluids were fabricated to cover a range of mechanical properties from biological mucus to very soft tissues ²¹. In this work, we reported that OCE is capable of evaluating mechanical properties of soft condensed matter, which can be used to interpret mechanical properties of actual biological cases such as mucus.

Materials and Methods

2.1. Fabrication of Tissue-mimicking Phantom-Micellar Fluids

The micellar fluids were fabricated using surfactant, hexadecyltrimethyl ammonium bromide (CTAB, O3042, Thermo Fisher Scientific, Hanover Park, IL, USA) and sodium salicylate (NaSal, S2679, Sigma-Aldrich, St. Louis, MO, USA). The molar concentration ratio of CTAB to NaSal was 5:3 to maximize micelle length ^{21, 46}. The molar mass of CTAB and NaSal are 364.45 g/mol and 160.11 g/mol, respectively. For the 100 mM CTAB in the 200 mL of desired final volume, the mass of CTAB needed is 7.29 g. On the other hand, the NaSal needs 60 mM molar concentration to match the 5:3 ratios. According the equation mass (g) = concentration (mol/L) * volume (L) * formula weight (g/mol), the mass of NaSal needed is 1.92 g. According to this ratio, four molar concentrations (100, 200, 300 and 400 mM) were shown in Table 1. Two types of scatterers with different diameters were used for optical and acoustical scattering in the phantoms. One gram of Sigmacell cellulose with the size of 50 μm (Sigma-Aldrich, St. Louis, MO, USA) and 1 g of titanium dioxide (TiO₂) particles were used for scatterers in ultrasound and in OCT, respectively.

Table 1.

The molar concentration ratio of CTAB to NaSal for micellar fluid is 5:3 in the total volume of 200 mL.

Molar concentration of CTAB to NaSal (mM)	Hexadecyltrimethyl ammonium bromide (CTAB) (g)	Sodium salicylate (NaSal) (g)
100:60	7.29	1.92
200:120	14.58	3.84
300:180	21.87	5.76
400:240	29.16	7.68

A total volume of 200 mL distilled water in each concentration was distributed in 80 mL for CTAB, 80 mL for NaSal, and 40 mL for scatterers in three individual beakers and heated to 70 °C. The CTAB and NaSal were added to the separate beakers while stirring taking approximately 30 minutes to homogenize the solutions. Once the solutions in both beakers became homogeneous, scatterers were first added to the beakers with CTAB and then mixed those with NaSal while stirring. The mixed solution was covered to avoid evaporation and stirred with the speed of 250 revolutions per minute (rpm) for 5 hours at 50 °C. The micellar fluids were transferred to Petri dishes for cooling to room temperature and the thickness of micellar fluids was approximately 5 mm in the OCE experiment.

2.2. Rayleigh Wave Measurement with OCE

The basic optical layout of the spectral domain optical coherence tomography (SD-OCT) scanner is illustrated in Figure 1. The low coherence broadband source is split into two beams: a reference beam directed towards a stationary reference mirror and a sample beam directed towards the tissue-mimicking phantom, which is the typical optical setup of a Michelson interferometer. The back-reflected and back-scattered light from samples and retroreflected light from the reference mirror are recombined and the spectrometers are utilized to form a spectral interferogram. A depth signal, an axial scan, can be calculated by taking an inverse Fourier transform of the spectral interferogram.

Fig. 1.

Schematic of the OCE system. A general optical layout of the SD-OCT scanner was displayed in the upper rectangle with a blue dashed line. The ultrasound system was illustrated in the lower rectangle with a blue dashed line. Rayleigh waves of micellar fluids with four different concentrations were induced by ARF. A 7.5 MHz highly focused transducer equipped with a 50 dB radio frequency (RF) amplifier was used to generate radiation force. Rayleigh wave motions were recorded by using SD-OCT scanner.

The system was composed of an optical scanner and an ultrasound excitation. For the optical scanner, a SD-OCT system (TEL320C1, Thorlabs Inc., Newton, NJ, USA) equipped with a low coherence broadband source of 1300 nm central wavelength and lens kit (OCT-LK3, Thorlabs Inc., Newton, NJ, USA) was employed to produce 13 μm lateral resolution and 3.6 mm of penetration depth within 10 mm x 10 mm field of view (FOV), so that it is capable of detecting the motion of particles on the surface. In this study, 76 kHz was used to have a balance of signal-to-noise ratio and fast scan rate.

To be able to capture the propagation of Rayleigh waves in soft matter, the M-B scan mode was used to facilitate high frame rates to track dynamic processes in the space-time domain⁴⁷. Briefly, the M-part is accomplished by acquiring successive A-lines (M-mode) at a certain location for one realization of the experiment, and then the process is repeated at subsequent locations to obtain the B-part or B-mode. The customized acquisition was set to obtain data at 50 lateral positions with 0.2 mm interval within a 10 mm FOV and 4000 axial scans per each lateral position; therefore, the scan time for each M-mode map and an entire data set takes 52.63 ms and 2.63 seconds, respectively. The SD-OCT with the customized acquisitions was programmed using C++ with a SpectralRadar software development kit (SDK) 4.4 version provided by Thorlabs in Microsoft Visual Studio 2019 development environment (Microsoft, Redmond, WA).

A single element focused transducer at a center frequency of 7.5 MHz (ISO703HR, Valpey-Fisher, Hopkinton, MA, USA) was used to generate the acoustic radiation force exerted on the surface of the micellar fluids by placing ultrasound gel between the bottom of the Petri dish holding the micellar fluid and the transducer to account for distance such that the focus coincided with the air/fluid interface. The focal distance was determined to be 11.84 mm by pulse-echo response. The f-number of 1.07 (highly focused transducer) was obtained by the definition of the focal distance divided by the aperture size (11 mm). The lateral resolution is defined as the f-number multiplied by wavelength and was 211 μm in this study assuming a speed of 1480 m/s. The lateral focal size can be calculated by the equation: 2.44 × f# × λ and is 514.84 μm in the study ⁴⁸. The burst sinusoid signals of 30,000 cycles were provided by a function generator (33250A, Agilent, Santa Clara, CA, USA) in the external mode and was amplified in 50 dB by a radiofrequency power amplifier (240L, Electronics and Innovation, LTD, Rochester, NY, USA) to drive the transducer. The second function generator (33500B, Keysight, Santa Rosa, CA, USA) was set as a 19 Hz square wave as a master trigger so that the repeated rate of the excitation can be synchronized with each M-mode map in OCT. In our experiment, the necessary time to complete a whole scan at each location was 4000*1/(76 kHz) = 52.63 ms, which is a 19 Hz measurement rate. A 4 ms excitation signal repeated every 52.63 ms was transmitted to excite the samples, and the OCT would start to free scan in 76 kHz at any moment. The timing between OCT and excitation was corrected by a time shifting method. Ten Rayleigh wave measurements were collected for each of the phantoms.

The local particle displacement on the surface of micellar fluids was detected by the autocorrelation. A median filter was employed to remove noise from a two-dimensional wave motion image before autocorrelation was performed. The data in each column of the wave motion image was upsampled by five times, by spline interpolation. After the autocorrelation calculation, the OCE data were averaged over depth to make the base line of wave motions to be zero, and two-dimensional wave motion images with time factor in the x axis and propagation distance in the y axis were reconstructed. At each spatial location, the maximum of the motion signal was found and the time of that peak was recorded. The group velocities for Rayleigh (C_gR) and shear waves (C_gS) were estimated in micellar fluids based on a lateral time to peak displacement algorithm (lateral TTP algorithm) proposed by M. L. Palmeri et al. ⁴⁹. The group velocity was determined by a least-squares linear fitting to the spatial locations and peak times.

A polyvinylidene fluoride (PVDF) membrane hydrophone (IP054, GEC-Marconi, Chelmsford, England) was used to measure the pressure of the transducer and calculate the intensity. The spatial peak, temporal average intensity (I_spta) and spatial peak pulse average intensity (I_sppa) under the conditions of a 4 ms pulse duration and 19 Hz pulse repetition frequency (PRF) were measured. In the study, I_spta and I_sppa were 6.76 mW/cm² and 88.97 W/cm², respectively.

2.3. Viscoelastic Parameter Estimation using OCE

In soft tissues with viscoelastic properties, the shear modulus is frequency dependent and can be characterized with the complex shear modulus, G^*(ω), defined as

$$G^{*}(\omega )=G_S(\omega )+i{G}_L(\omega )$$ (1)

where ω is the angular frequency, G_S(ω) is storage modulus and G_𝐿(ω) is loss modulus ^{39, 50}. The complex shear modulus can also be written as

$$G^{*}(\omega )=\frac{\rho {\omega }^2}{k^2(\omega )}$$ (2)

where 𝜌 is the mass density of the medium and usually assumed to be 1000 kg/m³ for the soft tissue. k is the complex wave number and can be written as k(ω) = k₁(ω) + ik₂(ω). The shear wave phase velocity, 𝐶_𝑝, can be written as

$$C_p(\omega )=\frac{\omega }{Re[k(\omega )]}=\frac{\omega }{k_1(\omega )}$$ (3)

In order to thoroughly describe the viscoelastic properties of materials, a well-known rheological model, the Kelvin-Voigt model, was adopted to analyze dispersion curves of micellar fluids in k-space created by a two-dimensional Fourier transform (2D-FT) of a spatiotemporal particle motion with the wavenumber-frequency pairs ^{51, 52}. The Kelvin-Voigt model consists of a viscous damper in parallel to an elastic spring. The elastic spring contributes the property of shear modulus (𝜇_𝑒) and the viscous damper provides viscosity (𝜇_𝑣). To apply this model, the medium is assumed to be isotropic and locally homogeneous, and then (ω) = 𝜇_𝑒 and G(ω) = ω𝜇_𝑣.

The frequency range from 50 to 100 Hz in the dispersion curves was selected to calculate storage and loss moduli because the measured surface waves have their main frequency content localized in this frequency range. This frequency range corresponds to the region where the normalized magnitude spectrum was greater than 0.30~0.40 measured from the k-space. Rayleigh waves at higher frequencies typically undergo higher attenuation for very soft materials. Therefore, the frequency of 50–100 Hz is an acceptable range for the four different concentrations for the curve fitting procedure. A nonlinear least-squares fit method (lsqcurvefit in MATLAB R2019a) was utilized to estimate the (ω) and G(ω). The complete viscoelastic shear modulus of the Kelvin-Voigt model, (ω)^*, can be written as

$${\mu }^{*}(\omega )={\mu }_e+i\omega {\mu }_v$$ (4)

Substituting equation (4) into (2) and working through equation (3), the shear wave phase velocity (C_p) can be written as

$$C_p(\omega )=\sqrt{\frac{2({\mu }_e^2+{\omega }^2{\mu }_v^2)}{\rho ({\mu }_e+\sqrt{{\mu }_e^2+{\omega }^2{\mu }_v^2})}}$$ (5)

The full details of the phase velocity derivation can be found in our previous papers ^{50, 53, 54} and the articles published by M. A. Kirby et al. ^{39, 50}. Although the Rayleigh wave will have wave fronts with different motion shapes, our previous works have demonstrated that equations for the wave propagation in a viscoelastic material can still be governed by the equation (5) in the study ^{53, 55}. The velocities are modified by a factor related to the boundary conditions. In our case, the Rayleigh wave velocity is a factor of 0.955 lower than the shear wave velocity as the micellar fluid is assumed to be incompressible with a Poisson’s ratio very close to 0.5 ^{33, 56}. Phase velocities of Rayleigh (C_pR) and shear waves (C_pS) were evaluated by transforming the spatiotemporal representation of the propagating wave to the dispersion curves from the k-space calculated by 2D-FT ⁵¹. To obtain the dispersion curve, we located the maximum of the magnitude spectrum at each frequency in the k-space. The dominant mode or highest energy mode can identify the maximum amplitude for each value of frequency and its corresponding wave number (k).

2.4. Acoustic Radiation Force Shear Wave Elastography for Validation

Five measurements using shear wave elastography (SWE) of micellar fluids were captured in each concentration for references using a Verasonics V1 ultrasound system (Verasonics, Inc., Kirkland, WA, USA) equipped with a 128-element linear array transducer (L7–4, Philips Healthcare, Andover, MA) with 4.09 MHz of center frequency and 200 μs pulse duration. In the SWE experiment, the transducer was directly coupled to a mixture of 200 mL of the micellar fluid in a plastic container and the thickness was around 30 mm. The focal distance was set as 15 mm and 40 elements were used to generate the ARF push. Shear wave propagation was measured using a plane wave compounding imaging technique ⁵⁷. Plane wave compounding with three angles was emitted at 10 kHz pulse repetition frequency and produced a frame rate of 3.33 kHz for the compound images. The spatial resolution both in x and z directions was 0.154 mm. Usually, the assumption of incompressibility for soft matter is a reasonable approximation ⁵⁸ so that the Poisson’s ratio v can be assumed to be 0.5. In this case, with an air-sample interface, the C_gR is approximately 0.955 of C_gS ^{39, 56}. Group and phase velocities were estimated in similar manners as described in the sections above for the OCE data.

Results

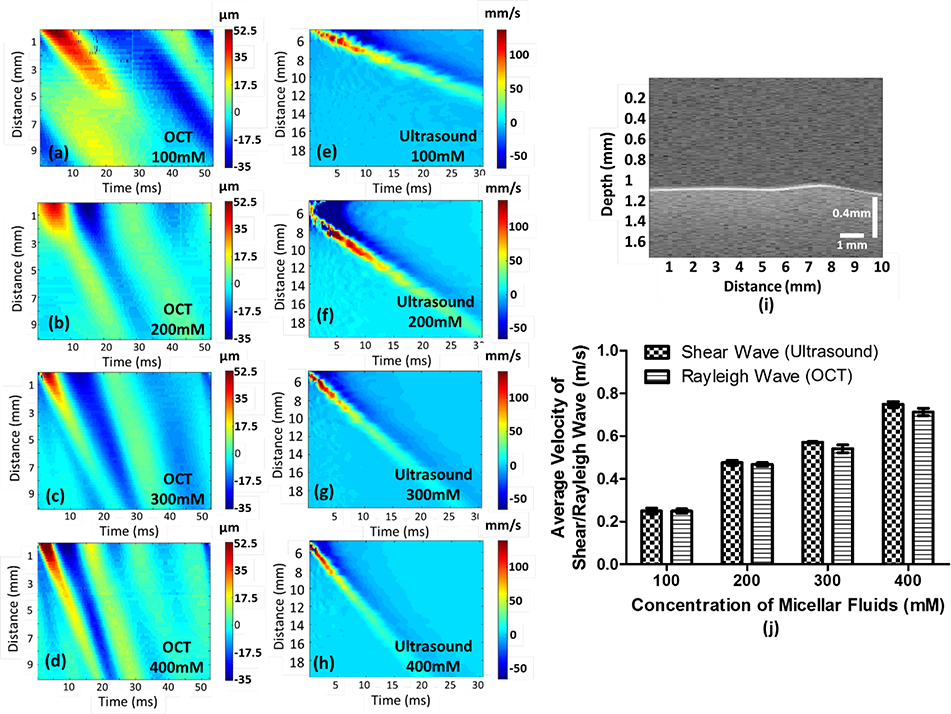
The Rayleigh waves in the micellar fluids in four concentrations were generated using ARF. The Rayleigh wave displacements were recorded with the OCT, and the group velocities were illustrated in Figures 2(a–d) as a function of time (ms) and lateral distance (mm) in each concentration. The C_gS in micellar fluids using a Verasonics ultrasound system was obtained to be a reference dataset, presented in Figures 2(e–h). A Rayleigh wave image was illustrated in Figure 2(i), and its displacement was measured by using an autocorrelation algorithm. In the study, each concentration includes ten cases for Rayleigh waves and five cases for shear waves, and their average values with standard deviation (SD) were exhibited in Figure 2(j). The average C_gR in concentrations of 100, 200, 300 and 400 mM micellar fluids are 0.249 ± 0.01 m/s, 0.468 ± 0.008, 0.541 ± 0.019 m/s and 0.713 ± 0.017, respectively. The average C_gS in four concentrations are 0.250 ± 0.013 m/s, 0.476 ± 0.011 m/s, 0.571 ± 0.002 m/s and 0.748 ± 0.014 m/s, respectively. In the OCE experiments, the thickness of the fluids was approximately 5 mm. From a further analysis of the data, the motion did not penetrate more than 1~2 mm into the sample (supplementary figure and video), which indicates that the boundary condition of the Petri dish was not relevant. Therefore, in this case, we can consider this to be a half-space where Rayleigh waves are present. In the SWE experiment, we were directly coupling to a mixture of 200 mL of the micellar fluid in a plastic container such that the thickness is around 30 mm. In this case, we can consider the medium to be homogeneous and isotropic and shear waves are propagating.

Fig. 2.

Illustration of group velocity measurements in micellar fluids with four concentrations. Figure (a-d) shows the group velocities of Rayleigh waves in micellar fluids measured by ARF in each concentration, as reference dataset, and figure (e-h) demonstrate the group velocities of shear waves generated by the Verasonics ultrasound system. A Rayleigh wave with 300 mM concentration as an example was displayed in figure (i) to express a Rayleigh wave propagating on the surface of a soft matter (see Visualization 1). Ten cases of each concentration have been measured by OCE to obtain the average Rayleigh wave velocity with standard deviation (SD), and five cases have been evaluated by the Verasonics ultrasound system to acquire the average shear-wave velocity with SD as reference dataset, presented in (j). The velocity of Rayleigh waves is approximately 95.5% of the velocity of shear waves.

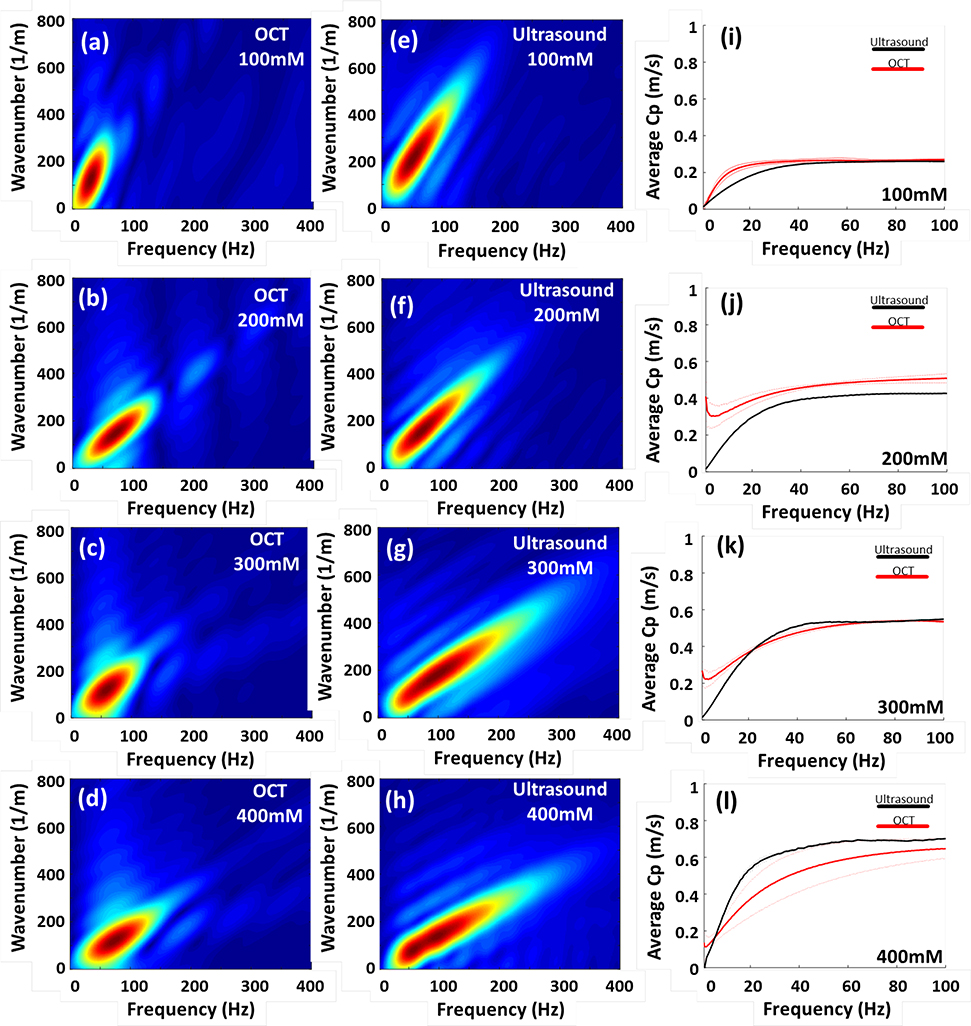
The Rayleigh waves and shear waves in the micellar fluids in k-space were illustrated in Figures 3(a–d) and Figures 3(e–h), respectively, as a function of frequency (Hz) and wavenumber (1/m). Based on the information of k-space, average wave dispersion curves were calculated and displayed in Figures 3(i–l). The thick lines and thin lines indicate the average phase velocities and the corresponding standard deviation (SD) in four concentrations, respectively. The red and black colors represent the phase velocities of Rayleigh waves from OCE and shear waves from SWE, respectively. The results demonstrated that the average C_pR are highly comparable with those in C_pS, and a relative small SD was observed in average C_pR, which means OCE is capable of measuring viscoelasticity of soft matter, shown in Figures 3(i–j).

Fig. 3.

Illustration of k-space and phase velocity measurement in soft condensed matters-micellar fluids in the four concentrations. Figure (a-d) demonstrate that OCE is capable of measuring viscosities of Rayleigh waves of micellar fluids with the four concentrations. Figure (e-h) shows the phase velocities of shear waves, obtained by SWE, in the k-space in each concentration. The average dispersion curves with the standard deviation (SD) in each concentration were displayed in figure (i-l). The thick and thin lines represented average phase velocities and SD, respectively.

In order to estimate viscoelasticity properties 𝜇^*(ω) of the soft condensed matters, the Kelvin-Voigt model was used to obtain shear modulus (𝜇_𝑒) and viscosity (𝜇_𝑣). Figures 4(a–d) exhibit storage modulus (ω) and loss modulus G(ω) in fluids with four concentrations by using the Kelvin-Voigt model. The solid and dotted lines represent viscoelastic properties of micellar fluids by using OCE and SWE, respectively. The blue and red colors depict the (ω) and G(ω), respectively. Table 2 shows the estimated shear elasticity and viscosity properties with standard deviations of micellar fluids in the four concentrations. The dispersion for each acquisition was fit for individual storage and modulus estimates. The 𝜇_𝑒 and 𝜇_𝑣 of micellar fluids of four concentrations by OCE were in good agreement with those measured using ultrasound-based SWE. The viscoelastic properties are positively correlated with the concentration of micellar fluids.

Fig. 4.

The shear complex modulus, storage modulus and loss modulus, of Rayleigh waves and shear wave in four concentrations. Figure (a-d) showed the storage modulus and loss modulus in the four concentrations estimated using the Kelvin-Voigt model. The solid lines and dotted lines represent the shear complex modulus obtained by OCE and SWE, respectively. The red and blue colors indicate complex modulus from SWE and OCE, respectively. The symbol “x” and ‘-’ represent the storage modulus and loss modulus, respectively. The thick lines and thin lines denote the average storage modulus and average loss modulus and the corresponding standard deviation, respectively.

Table 2.

Elasticity and viscosity of the four concentrations of micellar fluids measured by OCE and ultrasound.

Modalities	OCT (n=10)		Ultrasound (n=5)
CTAB Molar Concentration	Elasticity ± SD (Pa)	Viscosity ± SD (Pa·s)	Elasticity ± SD (Pa)	Viscosity ± SD (Pa·s)
100 mM	65.71 ± 6.98	0.035 ± 0.013	64.32 ± 0.92	0.031 ± 0.003
200 mM	217.33 ± 10.57	0.174 ± 0.061	166.02 ± 0.39	0.150 ± 0.005
300 mM	249.43 ± 14.21	0.211 ± 0.026	274.24 ± 1.86	0.105 ± 0.001
400 mM	428.78 ± 10.75	0.283 ± 0.022	460.24 ± 2.94	0.210 ± 0.015

^*The abbreviation SD and n are standard deviation and case number, respectively.

Discussion

The group velocity of Rayleigh waves can be precisely quantified by using OCE. It was observed that the C_gR was slightly slower than C_gS, presented in Figure 2. For example, C_gR in 400 mM was 0.713 ± 0.017 and C_gS in 400 mM was 0.748 ± 0.014; therefore, the ratio of C_gR to C_gS was 0.953 in the study. The average ratio of C_gR to C_gS in four concentrations was 0.970. The relationship between shear waves and Rayleigh waves has been well-defined and demonstrated in previous literatures: that Rayleigh wave velocity is approximately 95.5% of shear wave velocity under the circumstance of a solid-air interface ^{39, 59}. On the other hand, the elasticity and viscosity of micellar fluids were measured by classical mechanical test methods in previous papers reported by Gladden et al. ²¹ and Amador, et al. ¹⁰. In Gladden et al., the shear wave speeds in micellar fluids with concentrations of 100, 200, 300 and 400 mM were 0.25, 0.45, 0.54 and 0.65 m/s by using a mechanical shaker and measurements of the motion with a camera operating at 2000 frames/sec ²¹. Amador et al. reported that the group velocity in 100, 200, 300 and 400 mM were 0.24, 0.44, 0.56 and 0.71 m/s by using SWE, respectively ¹⁰. Our results are comparable (figures 2a–d) with both reported studies and OCE has ability to measure Rayleigh wave behaviors in the soft condensed matters.

It is important to note in applications using OCE whether surface, shear, or guided waves are present based on the boundary conditions and the wave propagation. Lamb waves are a type of guided wave generated in plates and shell components ⁶⁰. The thickness of the micellar fluids is adjustable. In the study, we kept the thickness of the micellar fluids approximately 5 mm for all OCT experiments. For soft material with 5 mm thickness such as those tested in this study, the motion did not penetrate more than 1~2 mm into the samples and elastic waves attenuate very fast in these types of materials. Therefore, it would be very difficult to generate Lamb waves. Elastic waves propagating in thin plates undergo multiple reflections from structural boundaries, where longitudinal (L) and shear (S) bulk wave components are converted into further L and S waves that interfere, forming Lamb waves ⁶⁰. In our case, the shortest total distance for incident and reflected wave propagation in vertical direction is 10 mm which is too long to generate Lamb waves, due to high attenuation of the examined soft matter materials.

Moreover, the wave motion generated on the top surface of the samples did not reach the bottom of the 5 mm layer of micellar fluids. The particle motion in micellar fluids with concentrations 100 mM and 400 mM was illustrated as a supplementary figure and a supplementary video shows the particle motions in micellar fluid with concentration 100 mM. The penetration depth can be observed to be approximately 0.5 mm (supplementary figure and video). In our study, the tightly ultrasound beam was focused at the surface of the samples. With the combination of the tightly focused beam and the air/fluid interface, a high reflectivity coefficient will be generated⁴⁰, which is the location of the strongest acoustic radiation force. Therefore, the Rayleigh waves are generated at the surface and the shear waves can also be existed within the medium due to absorption of the ultrasound and production of acoustic radiation force⁶¹. However, it would be difficult to monitor the shear wave movement with the OCT because of the high attenuation of lights in the micellar fluids. In our case, we only detect the surface motions of the samples. According to above reasons, the measured waves might be considered as Rayleigh waves.

This implementation of OCE was capable of producing a k-space with good energy distribution over a wide frequency range compared with those from SWE measurements (Figures 3e–h), but the range of frequency was slightly narrower, which is largely due to the different excitation signals. Broadband mechanical waves were produced in the SWE measurements. For our OCE system, a 7.5 MHz highly focused transducer with 4 ms of pulse duration was considered to generate broadband excitation combined with 19 Hz repeated rate (harmonic excitation) for fitting each M-mode map. Therefore, the dynamic loading in the study was considered to be impulsive combined with harmonic in temporal characteristics. The major reason that we used this special dynamic loading, a 4 ms transient signal with 19 Hz repeating measurement rate, is to obtain a reasonable frequency response of phase velocity in low frequency range (usually less than 50 Hz) as very soft samples were measured ^{1, 62}. For example, the peak magnitude in the k-space of micellar fluid with 100 mM concentration is around 25 Hz presented in figures 3(a) and (e). However, measuring phase velocities of 0–50 Hz range are not typically reliable. According to the magnitude distributions in k-space, frequencies of 50–100 Hz represent an acceptable range for being able to cover the data for the four different concentrations during the curve fitting procedure. In addition, a 4 ms excitation was needed to provide pushes from the single-element transducer that yielded adequate surface wave motion. The linear array transducer driven by the Verasonics system for the SWE experiments could produce larger motion amplitudes with a shorter ultrasound tone burst due to the electronic focusing and larger surface area of the transducer compared to the single element transducer. The study demonstrated that the results from the OCE system are highly comparable to those from ultrasound-based SWE for the purpose of biological viscous fluids or mucus.

The shear modulus and viscosity of micellar fluids for both methods were obtained by using the Kelvin-Voigt model and presented in Figure 4(a–d) and Table 2. The four concentrations of micellar fluids provided reasonable ranges of elasticity 𝜇_𝑒 from 65.71 to 428.78 Pa and viscosity 𝜇_𝑣 from 0.035 to 0.283 Pa⋅s using OCE, and those are highly comparable to the data obtained using ultrasound shear wave elastography, from 64.31 to 460.23 Pa for elasticity and from 0.031 to 0.21 Pa⋅s for viscosity, presented in Table 2. The two most common rheological models used in the elastography field are the Kelvin-Voigt and Maxwell models ³⁹. In our experiments, the two models were used for fitting, and we obtained good consistency of results between OCE and SWE by using the Kelvin-Voigt model, but discrepant results using the Maxwell model. The Maxwell model describes materials as a Newtonian fluid ³⁹. In fact, the appearance and macroscopic behavior of the micellar fluids is that of a semi-solid, like biological mucus rather than fluids although it bears the name micellar fluid. Two similar studies reported the viscosity in micellar 200 mM using Maxwell models and the results are not in the good agreement, 0.48 Pa⋅s versus 0.12 Pa⋅s ^{10, 21}. On the contrary, the Kelvin-Voigt model is more reliable to be used especially as storage modulus is significantly larger than loss modulus ³⁹, which can be reasonably associated with our experimental cases illustrated in figure 4. According to our experiments, the Kelvin-Voigt model is able to provide consistent results between OCE and SWE presented in Table 2.

J. R. Curt and R. Pringle reported that the viscosity of healthy gastric mucus is approximately 0.085 Pa⋅s and increases significantly during duodenal ulceration ⁶³. Normal mucus is 97% water and 3% solids which include mucins, non-mucin proteins, salts, lipids, and cellular debris and represent a gel property with low viscosity and elasticity that is easily transported by ciliary action, whereas pathologic mucus has higher viscosity and elasticity and is less easily cleared ⁶⁴. Normally, the shear modulus of mucus is usually between 0.1 to 160 Pa and the viscosity of human mucus ranges from 0.001 to a few hundred Pa⋅s depending on a type of mucus and animals ⁶². The healthy soft tissues ranges from 160 Pa to 20 kPa ⁶⁵. For tissue mimicking phantoms, fabricating stiff phantoms are easy to achieve using agar ⁶⁶ or gelatin phantoms ⁶⁷. The Young’s modulus in phantoms with low agar concentrations (1% and 2%) was reported as 10 kPa and 60 kPa. In addition, X. Liang et al. described that the shear modulus of gelatin phantoms in low concentration (3% and 4%) is over 200 Pa and 500 Pa. It is noted that a small concentration change produces a large increase in stiffness. However, fabricating ultra-soft human biological mucus or biological fluid phantoms are challenging. For regular biological mucus or fluids (~Pa to hundred Pa), micellar fluids might be a suitable material for fabricating biological mucus or fluids mimicking phantom.

We reported that OCE is a promising tool to evaluate the viscoelastic properties of soft condensed matters. OCE has an advantage to address the biological samples with transparent property and small size samples, which is difficult to achieve by using ultrasonic SWE. The OCE method is also nondestructive and noncontact other than coupling the transducer to the bottom of the Petri dish in this work. Additionally, an advantage that should be noted in the study is a unique property of micellar fluids, “self-healing” or “self-assembly”, which is similar to biological samples. Therefore, it can be used to exhibit mechanical properties of very soft tissues or mucus. OCE might be a promising tool to differentiate pathologic mucus, gastric mucus for example ⁶², from healthy mucus as advanced applications in the future study, based on viscosity. On the other hand, two factors will affect the results to be inaccurate: improper boundary detection of Rayleigh wave motions and inappropriate region-of-interest (ROI) on wave motion images. To obtain precise Rayleigh wave motions, a robust autocorrelation algorithm is needed. A ROI with a reasonable size and location on motion images will dominate the accuracy of storage modulus and loss modulus due to high sensitivity of Fourier transform. Generally speaking, a precise phase velocity is more challenging to obtain than a group velocity due to background noise on wave motion images. An ultra-short pulse duration as an ARF excitation signal might be able to address this issue.

Conclusion

We reported that OCE could be a promising tool to evaluate mechanical properties of soft condensed matter, micellar fluids in this case. Based on analysis of dispersion curves, the storage modulus and loss modulus of micellar fluids were determined by using the Kelvin-Voigt model. Four concentrations of micellar fluids provided ranges of storage modulus from 65.71 to 428.78 Pa and viscosity ranges from 0.035 to 0.283 Pa⋅s, which can mimic the mechanical properties of actual soft biological samples and might potentially be biological mucus phantoms. OCE is a promising tool to evaluate mechanical properties of biological samples with transparent and small sizes. It can be used to differentiate actual pathologic mucus or blood, like hyperviscosity syndrome from healthy cases in the future.