Abstract
The problem of backscattering of light by a discrete random medium illuminated by an obliquely incident plane electromagnetic wave is considered. The analysis is performed in a linear-polarization basis and includes (i) a complete derivation of the cross reflection matrix for a layer with densely and sparsely distributed particles, (ii) the design of an approximate method for computing the ladder and cross reflection matrices in the case of a semi-infinite medium with a sparse distribution of particles, (iii) the derivation of the relations between the elements of the ladder and cross reflection matrices in the exact backscattering direction for dense and sparse media, and (iv) the development of practical algorithms for solving the underlying integral equations by the method of Picard iterations and the discrete ordinate method. Simulation results for particles with large size parameters are also presented.
1. Introduction
In this paper we continue the analysis initiated in Refs. [1, 2, 3] by focusing on the coherent backscattering of light by discrete random media.
Scattering characteristics of discrete random media are primarily determined by the so-called ladder and cyclical diagrams [4, 5, 6]. The sum of all ladder diagrams characterizes the incoherent part of the scattered radiation and reduces to the vector radiative transfer equation, while the sum of the cyclical (cross) diagrams characterizes the coherent part of the scattered radiation and reflects the interference of pairs of conjugate waves propagating along the same self-avoiding path but in opposite directions [7]. Constructive interference of the scattered waves manifests itself as a narrow interference peak of intensity centered at exactly the backscattering direction, which is why this phenomenon is known as the coherent backscattering effect. The coherent backscattering effect was first predicted theoretically in studies of backscattering of electromagnetic waves by turbulent plasmas [8], and then observed and analyzed in numerous experimental and theoretical studies (see, e.g., Refs. [7, 9, 10, 11] and references therein).
The exact numerical solution of the equation for the coherent part of the scattered radiation is an extremely complicated problem. In Refs. [12, 13, 14, 15], it was addressed by using the double-scattering approximation, which allows one to analyze coherent backscattering as a function of the medium properties. A complete analytical solution for a semi-infinite medium composed of nonabsorbing Rayleigh scatterers and illuminated by an external radiation propagating perpendicularly to the boundary of the medium has been established in Refs. [16, 17, 18]. In a more general framework, a rigorous equation describing the coherent backscattering for a plane-parallel medium consisting of arbitrary randomly oriented and randomly positioned scatterers has been obtained in the cases of normal and oblique incidences in Refs. [19] and [20], respectively, while in Ref. [21], a simple approximate method for the numerical solution of the equation for the coherent part of the scattered radiation in the case of a semi-infinite medium at normal incidence was described. A comprehensive review of these results was given in Ref. [22].
The analysis described in Refs. [19, 20, 21, 22, 23] is performed in a circular-polarization basis, and relies on the following idea: to sum up the cyclical diagrams, one of the series in each diagram is transformed in such a way that the wave propagation direction is reversed, i.e., the reciprocity principle is applied to one of the series. In this review, we follow closely the derivation of Refs. [19, 20, 21, 22], but we conduct our analysis in a linear-polarization basis and for an obliquely incident plane electromagnetic wave. For this reason, the final integral equations describing coherent backscattering are different.
2. Reflection and transmission matrices
We consider the problem of electromagnetic scattering by a discrete random medium. More specifically, we consider a group of N identical spherical particles of radius a centered at quasi-random positions R1, R2, ..., RN ∈ D, where the domain D is a laterally infinite plane-parallel layer with imaginary (non-scattering) boundaries z = 0 and z = H. The wavenumbers of the non-absorbing, non-magnetic background medium and the particles are k1 and k2 = mk1, respectively, where m is the relative refractive index. We denote by f = n0V0 the particle volume concentration, where n0 = N/V is their number concentration, V is the cumulative volume occupied by the particles, and V0 = (4/3)πa3 is the volume of each particle. The particulate medium is illuminated from below by a plane electromagnetic wave with the propagation direction given by the unit vector , 0 ≤ θ0 < π/2, and the amplitude , that is,
| (1) |
| (2) |
where , r is the position vector connecting the origin of the laboratory coordinate system and the observation point, θ and φ hereinafter denote the corresponding spherical-coordinate angles, and and are the transverse polarization components of the amplitude vector.
If the observation point r is outside any particle, the total field sums the contributions of the incident field and all individual scattered fields contributed by the N particles,, i.e.,
| (3) |
where with ri = r − Ri is the field scattered by particle i, X3(k1ri) is the column vector of the vector spherical wave functions, is the particle-centered transition matrix of a spherical particle, and ei is the vector of the exciting field coefficients. If moreover, the observation point is assumed to be in the far-field region of the entire particulate medium, the representation for the field scattered by particle i is used along with the far-field approximation for the radiating vector spherical wave functions
| (4) |
| (5) |
where is the column vector of the vector spherical harmonics in the direction . The far-field pattern of the field scattered by particle i, defined by , is
| (6) |
and for , we have
| (7) |
| (8) |
In the far-field region, the scattering by particle i can be described through the elements of the amplitude matrix which relates the amplitudes of the far-field pattern to that of the incident field:
| (9) |
From Eqs. (8) and (9), and the relation , we obtain the representation
| (10) |
Note that for the incident field coefficients , eiξ satisfies the ξ-polarized equation
| (11) |
where , is the translation matrix relating the radiating and the regular vector spherical wave functions X3(k1rj) and X1(k1ri), respectively, and the summation runs implicitly from 1 to N. The far-field pattern of the total scattered field Esct(r) = ∑i Escti(r), defined by , is . Consequently, we get
| (12) |
| (13) |
and further (cf. Eq. (9))
| (14) |
| (15) |
Similarly, the far-field pattern of the total diffuse scattered field , defined by , is
| (16) |
so that for
| (17) |
we find (cf. Eqs. (12), (14), and (16))
| (18) |
| (19) |
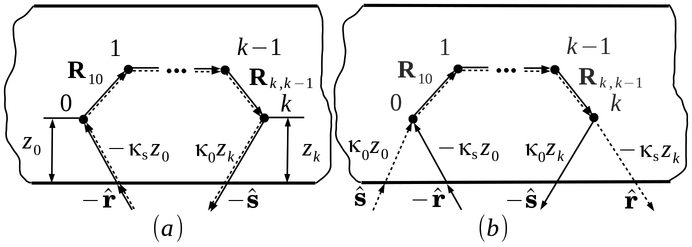
The next step is to introduce the diffuse specific coherency dyadic at the lower boundary of the layer, and relate this quantity to the configuration-averaged products of the amplitude matrix elements. For this purpose, we define the (elementary) diffuse reflection coherency dyadic in an elementary solid angle ΔΩ around the direction , by (Fig. 1a)
| (20) |
and the diffuse specific coherency dyadic at the lower boundary z = 0 in the direction , by
| (21) |
where the asterisk denotes complex conjugation and ⊗ is the dyadic product sign. Using the relation ΔΩ = A∣ cos θs∣/r2, where A is the area of the illuminated surface, we deduce from Eqs. (20) and (21) that the diffuse specific coherency dyadic is given by
| (22) |
or, equivalently, that its components,
| (23) |
are (cf. Eq. (18))
| (24) |
where
| (25) |
Figure 1:
Geometries for defining (a) the reflection and (b) the transmission matrices.
Considering the decomposition
| (26) |
we find the representations
| (27) |
| (28) |
where the ladder and cross components of , defined by
| (29) |
are (cf. Eqs. (15), (19), and (25))
| (30) |
and
| (31) |
respectively. In Eqs. (30) and (31), the domain D is a cylinder with the base area A, and g(Rij) is the pair correlation function.
We are now in a position to introduce the reflection and transmission matrices of the particulate layer. We stipulate that at the lower boundary z = 0, the diffuse specific coherency column vector with elements
| (32) |
is related to the coherency column vector of the incident field with elements
| (33) |
through the relation
| (34) |
where is the reflection matrix of the layer. In Eqs. (32) and (33), the multi-index ν = (η, ξ) is such that ν takes the values ν = 1, 2, 3, 4 for (η, ξ) = (θ, θ), (θ, φ), (φ, θ), (φ, φ), respectively. For sparse media, it is known that at the lower boundary z = 0, the coherent field is equal to the incident field. Therefore, we have , and Eq. (34) states that
| (35) |
From Eq. (24) along with Eqs. (32)–(34), we infer that the elements of the reflection matrix
are
| (36) |
In view of the decomposition (29), we write
| (37) |
where the ladder and cross components of , or simply, the ladder and cross reflection matrices, are given, respectively, by
| (38) |
| (39) |
To introduce the transmission matrices of the layer we define the (elementary) diffuse transmission coherency dyadic in an elementary solid angle ΔΩ around the direction , by (Fig. 1b)
and the diffuse specific coherency dyadic at the upper boundary z = H in the direction , by
| (40) |
In this case, the elements of the amplitude matrix are (compare with Eq. (10))
| (41) |
while the transmission matrix of the layer (not to be confused with the no-argument notation for the single-particle transition matrix), defined through the relation
| (42) |
where
is computed as in Eq. (36) in conjunction with Eqs. (15), (19), (25), and (41).
3. Discrete random layer
In the following, we compute the ladder and cross quantities and by means of Eqs. (30) and (31), respectively. Apart from a normalization factor, these quantities are the elements of the ladder and cross reflection matrices and , respectively.
Consistent with Ref. [3], we make a series of simplifications.
-
For a ξ-polarized incidence, the conditional configuration average is computed by using the sparse-medium approximation (cf. Eq. (40) of Ref. [3])
where and(43)
is the effective incident wave vector. For a medium with densely distributed particles, the effective wave number K is computed from the generalized Lorentz–Lorenz law for a semi-infinite discrete random medium at normal incidence, while for a medium with sparsely distributed particles, we use the relation(44)
where(45) (46) Observe that in Eq. (43), the dependency of eiξ and e0ξ on the incidence direction is indicated explicitly.
- To describe the propagation of the scattered waves in an effective medium, we make the following replacements:
(47) (48) (49)
(50)
According to the change (49), the elements of the amplitude matrix for particle i defined by Eq. (10) become
| (51) |
Recalling the notation (59) of Ref. [3], i.e.,
| (52) |
we introduce, as a counterpart of the attenuation coefficient along the incident direction κ0, the attenuation coefficient along the scattering direction κs by
| (53) |
3.1. Incoherent part of the scattered radiation
For the incoherent scattered radiation we adapt the results established in Ref. [3] to the case of an external observation point.
3.1.1. Dense medium
For a ξ-polarized incidence, we consider the series representation for eiξ (cf. Eq. (47) of Ref. [1])
| (54) |
in which, (k1Rij) and are replaced by (KRij) and , respectively, that is,
| (55) |
multiply it by its complex conjugate transpose , and retain in the matrix product only the terms corresponding to the ladder diagrams. We obtain
| (56) |
which is equivalent to the following system of equations:
| (57) |
In Eqs. (56)–(57), the symbol † stands for complex conjugate transpose, while the brackets indicate the self-contained paths corresponding to and .
By means of Eq. (51), we find
| (58) |
Inserting Eq. (56) in Eq. (58) yields
| (59) |
where
| (60) |
is the single-scattering contribution, and
| (61) |
is the multiple-scattering contribution. The term corresponds to all self-contained paths starting at particle j and ending at particle i. A diagramatic illustration of the product is

where
and
The first diagram corresponds to the single-scattering term , while the rest of them corresponds to the multiple-scattering term .
Taking the configuration average of Eq. (58) we find that the ladder quantity given by Eq. (30) is (note that in the backscattering direction, κs = κ/ cos θs < 0)
| (62) |
where the ladder correlation matrix Lξξ′ (zi), defined by
| (63) |
satisfies the integral equation (compare with Eqs. (61) and (137) of Ref. [3])
| (64) |
with
| (65) |
Recall that in Eq. (64), the domain D is a cylinder with the base area A.
If we let A → ∞, the integral equation (64) can be simplified by using the technique described in Ref. [3]. In this approach, the integral in Eq. (64) is split into two integrals according to the decomposition g(Rji) = [g(Rji) − 1] + 1. The first integral containing the term g(Rji) − 1 is typical of dense media and is computed by making use of the approximation
| (66) |
while the second integral is typical of sparse media and is computed by employing the sparse-medium approximation for the integration domain, as well as the far-field representation for the radiating spherical wave functions. Note that because the function g(Rji) − 1 tends to zero after a distance of several particle radii, the approximation (66) is local in the sense that it is valid in the vicinity of particle i (more precisely, inside a ball around particle i whose radius R0 is determined by the interval [2a, R0] in which the function g(Rji) − 1 is not negligible, e.g., R0 ≈ 8a).
In summary, the ladder reflection matrix for a layer with densely distributed particles is computed as follows:
solve the integral equation (64) for the ladder correlation matrix Lξξ′ (zi);
compute from Eq. (62); and
compute the ladder reflection matrix from Eq. (38), that is,
| (67) |
From Eqs. (62) and (67) it is apparent that does not depend on the illuminated area A.
Some comments can be made here.
-
In the case of transmission, the approximation (49) implies that the elements of the amplitude matrix for particle i defined by Eq. (41), are given by (compare with Eq. (51))
(68) Consequently, we get (compare with Eq. (62) and take note that in the forward scattering direction, κs = κ/ cos θs > 0)
while the elements of the ladder transmission matrix(69)
are(70) The expressions for the reflection matrix given by Eqs. (62) and (67), and for the transmission matrix given by Eqs. (69) and (70), coincide with those derived in Ref. [3]. The difference is that in the present derivation, the observation point is outside the discrete random layer.
| (74) |
3.1.2. Sparse medium
For sparse media, the complexity of the problem can be reduced by means of the following approach. Using the far-field representation for the matrix (−k1Rji),
| (75) |
| (76) |
the relation , and the approximation g(Rji) ≈ 1, we find that the ladder correlation matrix Lξξ′ (zi) obeys the integral equation
| (77) |
where Ω+ and Ω− are the upper and the lower unit hemispheres and δb,sgn(zi−zj) is the indicator function
| (78) |
Defining the 4 × 4 ladder matrix
| (79) |
by
| (80) |
and using Eq. (77) along with the relations
| (81) |
and
| (82) |
where are the elements of the single-particle amplitude matrix in the particle-centered coordinate system and
| (83) |
is the ladder coherency phase matrix, we obtain the following integral equation for xsxs:
| (84) |
The ladder reflection matrix and its single-scattering component are then computed as
| (85) |
and
| (86) |
respectively.
The integral equation (84) is similar to the integral equation (116) of Ref. [3] for the diffuse ladder specific coherency dyadic . In view of this analogy, Eq. (84) can be solved by employing the solution methods of the radiative transfer theory, e.g., Picard iterations in conjunction with the discrete ordinate method.
3.2. Coherent part of the scattered radiation
A method for summing up the cyclical diagrams in the case of an external observation point has been given in Refs. [19, 20]. The idea is to consider the matrix product of the exciting field coefficients and apply the reciprocity principle to the series for ; in other words, to consider a series which corresponds to a reversed propagation direction . Essentially, by using the reciprocity principle, the cyclical diagrams are transformed into ladder diagrams involving only pair correlation functions.
3.2.1. Dense medium
The cross quantity , which determines the cross reflection matrix, is associated with the interference of two waves propagating along the same self-contained path connecting particles i and j, but in opposite directions. From Eq (31), we have
| (87) |
with (cf. Eq. (10))
| (88) |
For the time being, in Eq. (88) and in what follows, we use the free-space quantities , , and (k1·) instead of K0, Ks, and (K·), respectively; they will be replaced with the effective-medium quantities just before taking the configuration average. The derivation involves the following steps.
Step 1. Using the series representations for and as given by Eq. (54) with , and retaining in the matrix product only the terms corresponding to the cyclical diagrams, we obtain
| (89) |
Inserting Eq. (89) in Eq. (88), we find (compare with Eq. (59))
| (90) |
with
| (91) |
and
| (92) |
In a diagramatic representation, the product is illustrated as

where
and
Step 2. Consider the single-scattering term given by Eq. (91). Replacing and by K0 and Ks, respectively, taking the configuration average, and combining the resulting expression with the coherent term gives the following contribution to in Eq. (87) (Rji = Rj − Ri):
| (93) |
For sparse media, we have g(Rji) = 1, implying
Thus, when taking the configuration average, the contribution of the single-scattering term is canceled by the contribution of the coherent term . Adopting this sparse-medium simplification in Eqs. (87) and (90), we compute by means of the relation
| (94) |
with as in Eq. (92).
Step 3. Using the symmetry relation for the ξ-polarized vector of spherical harmonics (cf. Eq. (12) of Ref. [1])
where hξ is the indicator function
as well as the symmetry relation for the translation matrix (cf. Eq. (23) of Ref. [1])
we transform the series for in Eq. (92) according to the reciprocity principle. Specifically, each term in the series for is transformed by using the basic result
which follows from the representation , the relation , the identity (note that for spherical particles, is a diagonal matrix)
and the symmetry relation
Summing over j in Eq. (92) yields an expansion in which the wave propagation direction in the series for is reversed; the result is
| (95) |
Step 4. On the other hand, using Eq. (10) we form the product
| (96) |
By taking into account the series representations for and given by Eq. (54), we retain in the matrix product only the terms corresponding to the ladder diagrams, that is,
| (97) |
By analogy with Eq. (57), the above series representation implies that the matrix satisfies the system of equations
| (98) |
Substituting Eq. (97) in Eq. (96) gives
| (99) |
with (compare with Eq. (60))
| (100) |
and (compare with Eq. (61))
| (101) |
A diagramatic illustration of the product is
Where
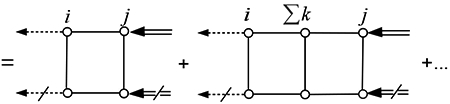
and
Comparing Eq. (95) with Eq. (101) and recalling Eq. (99), we obtain
| (102) |
From Eq. (102) it is clear that when switching from to , we do not reverse only the incident and the scattering directions but also the polarization state.
Step 5. Replacing by K0, by Ks, and (k1·) by (K·), summing over i, taking the configuration average of Eq. (102), and using Eq. (94), we are led to the following representation for :
| (103) |
In the above equation, the single-scattering term is (compare with Eq. (73))
| (104) |
For the multiple-scattering term we proceed as follows. Taking the configuration average of Eq. (96), where the matrix obeys the system of equations (98), we get
| (105) |
Apart from that, averaging Eq. (98) under the quasi-crystalline approximation, we deduce that the matrix , which enters the above equation, satisfies the integral equation
| (106) |
Defining the cross correlation matrix of the exciting field coefficients by
| (107) |
we infer from Eq. (106) that Cξη′ (zi) satisfies the integral equation
| (108) |
where
and
| (109) |
Note that the specific form of the integral equation (108) implies that Cξη′ depends only on zi. Finally, substituting Eq. (107) in Eq. (105), we obtain
| (110) |
The integral equations (108) and (64) are similar; however, the kernel of Eq. (108) is highly oscillating due to the exponential term .
In conclusion, the cross reflection matrix for a layer with densely distributed particles is computed as follows:
solve the integral equation (108) for the cross correlation matrix Cξη′ (zi);
compute from Eq. (103); and
compute the cross reflection matrix from Eq. (39), i.e.,
| (111) |
From Eq. (103) along with Eqs. (104) and (110), we see that in Eq. (111) does not depend on the illuminated area A.
In the limit A → ∞, the technique described in Ref. [3] can also be used to simplify the integral equation (108). This approach is presented in Appendix 1.
A backward Monte Carlo method for computing the ladder and cross reflection matrices in the case of a dense medium is discussed in Appendix 2. This model relies on the solutions of the integral equations (64) and (108), and employs essentially the same assumptions as those used in Ref. [3] and Appendix 1.
3.2.2. Sparse medium
Using the far-field representation for the matrix (−k1Rji) as given by Eqs. (75)–(76), the approximation g(Rji) ≈ 1, and the spherical wave expansion of the plane wave
| (112) |
where are the regular spherical wave functions, jl (x) are the spherical Bessel functions, are the spherical harmonics for the direction , and
| (113) |
we find that the cross correlation matrix Cξη′ (zi) satisfies the integral equation (compare with Eq. (77))
| (114) |
Defining the 4 × 4 cross matrix
| (115) |
according to
| (116) |
and the so-called cross coherency phase matrix
| (117) |
by
| (118) |
we are led to the following integral equation for in the case :
| (119) |
where
| (120) |
The elements of the cross reflection matrix are then computed as
| (121) |
where
| (122) |
and
| (123) |
Practical algorithms for computing the ladder and cross reflection matrices for a layer with sparsely distributed particles by means of the method of Picard iterations and the discrete ordinate method are discussed in Appendix 3.
In Figs. 2 and 3 we illustrate the interference peak, defined by
where for and with φ0 = 0°, Θ is the phase angle between the scattering direction and the exact backscattering direction , and is the (1, 1) element of the reflection matrix corresponding to the specific intensity column vector . This matrix, which is defined through the relation , is calculated as , where
| (124) |
and (cf. Eq. (37)) . In these simulations,
Figure 2:
Interference peak versus the phase angle for three values of the volume concentration: f = 7 × 10−4, 14 × 10−4, and 28 × 10−4. For these values of the volume concentration, the relative errors in κ are εκ = 9 × 10−4, 1.8 × 10−3, and 3.6 × 10−3, respectively. The parameters of the calculations are indicated in the plots.
Figure 3:
Left: interference peak versus the phase angle for three value of the layer thickness: H = 600a (τ ≈ 0.7), 1200a (τ ≈ 1.4), and 2400a (τ ≈ 2.8). Right: interference peak versus the phase angle for two values of the incidence angle: θ0 = 30° and 60°. The parameters of the calculations are indicated in the plots.
the volume concentration f is chosen such that relative error between the values of κ = 2K″, computed on the one hand from Eq. (45) and on the other hand from the generalized Lorentz–Lorenz law for a semi-infinite discrete random medium at normal incidence, is smaller than 10−2;
the layer is discretized in Nlay = τ/Δτ sublayers, where τ = κH = n0CextH is the optical thickness of the layer, Cext is the the extinction cross section of the particles, and Δτ is chosen as Δτ = 0.1;
to ensure that the Picard iterations method converges, weakly absorbing particles with the relative refractive index m = 1.33+0.01j are considered.
It is evident that the half-width of the interference intensity peak decreases with increasing the concentration, the geometrical thickness of the layer, and the incidence angle. Note that the first two traits are consistent with the numerically-exact superposition T-matrix computations in Ref. [24].
4. Semi-infinite discrete random medium
To simplify our analysis, we restrict ourselves to the case of a semi-infinite medium with a sparse distribution of particles. In the following we consider the integral equations (77) and (114) in the limit H → ∞, and reformulate them in terms of the altitude-independent ladder correlation matrix
| (125) |
and the altitude-independent cross correlation matrix
| (126) |
respectively.
4.1. Incoherent part of the scattered radiation
For the incident and scattering directions and with μs > 0, respectively, the ladder reflection matrix satisfies the Ambartsumian’s integral equation:
| (127) |
The solution of the nonlinear integral equation (127) by using the method of Picard iterations is discussed in Ref. [25]. Note that simple iterations can diverge if the particles are nonabsorbing or weekly absorbing, in which case additional constraints on the solution must be invoked [26, 27, 28, 29]. In the following we present an approximate method for computing the ladder reflection matrix. This approach is particularly relevant because the same type of approximation will be used to compute the cross reflection matrix.
Multiplying Eq. (77) by exp(κszi) and integrating over zi, we are faced with the computation of the integrals (note that in the backscattering direction, we have cos θs < 0 implying κ0 − κs > 0)
and
| (128) |
that is
| (129) |
| (130) |
To compute L+, we change the order of integration according to the rule
| (131) |
and obtain
| (132) |
while for IL−, we use the approximation
| (133) |
and obtain
| (134) |
A simple representation for the function fL(·) is [21, 22]
| (135) |
where w = [w1] and for very large optical depths the parameter w1 is close to one. More general representations are
| (136) |
with w = [w1, . . . , wNw]T and
| (137) |
with w = [w1, w2]T, whereby the vector of parameters w is the solution of a least squares problem which will be formulated below. Note that the approximation (133), stating that the ladder correlation matrix Lξξ′ (zj) decreases with respect to Lξξ′ (zi) as zj increases, is a global approximation in the sense that it is valid for all zj > zi. This is in contrast to the local approximation (66) which is assumed to be valid for zj in the proximity of zi.
Taking these results into account and introducing the ladder matrix
| (138) |
by
| (139) |
where is defined by Eq. (125), we find that obeys the integral equation
| (140) |
Then, using the relation (cf. Eq. (62))
| (141) |
we compute the ladder reflection matrices and as (compare with Eqs. (85) and (86))
| (142) |
and
| (143) |
respectively.
We now come to the problem of computing the vector of parameters w. For macroscopically isotropic and mirror-symmetric media and in the exact backscattering direction, the ladder reflection matrix is of the form [30]
| (144) |
with
| (145) |
The (1, 1) element of the ladder reflection matrix , corresponding to the ladder specific intensity column vector, is
| (146) |
In this regard, we determine the vector of parameters as
| (147) |
where now, adopting a more precise notation, is the (1, 1) element of the reflection matrix in the exact backscattering direction computed by using the approximation (133), and is the corresponding element of the “exact” reflection matrix (which satisfies the Ambartsumian’s integral equation).
Two comments can be made here.
-
The integral IL+(∣ cos θij ∣) given by Eq. (129) has been computed by using the integration rule (131). Denoting μ1 = cos θij and μ = − cos θs > 0, this result can be written as
where is defined by(148) (149) To compute the integral IL−(∣μ1∣) given by Eq. (130) we do not employ the approximation (133). Instead, we use the integration rule
and obtain the exact result(150) (151) Note that IL−(∣μ1∣) is not singular at ∣μ1∣ = μ; in the limit ∣μ1∣ → μ, IL−(∣μ1∣) is proportional to the derivative of at μ. Then, by means of Eqs. (148) and (151), we come to the following findings: (i) the ladder matrix
defined by(152)
for μ > 0 and any , obeys the integral equation(153)
and (ii) in the scattering direction , the ladder reflection matrix is(154) (155) Note again that the integrand of the second integral in Eq. (154) is regular and hence can be integrated using Gaussian quadratures. The integral equation (154) can be considered an alternative to the Ambartsumian’s nonlinear integral equation (127). Although this equation is linear, the numerical computation of the second integral in Eq. (154) should be handled carefully.
In general, the vector of parameters w can be determined by matching the exact and the approximate (1, 1) elements of the reflection matrices and , respectively, at a set of scattering angles. More specifically, if is a set of Nr scattering angles including the exact backscattering direction, that is, for some p0, w is computed as
| (156) |
4.2. Coherent part of the scattered radiation
The cross correlation matrix defined by Eq. (126) is computed by employing an approximation which is similar to that used in Eq. (133). The integral of interest is
| (157) |
that is
| (158) |
| (159) |
For b = +, the integral is computed by changing the order of integration as in Eq. (131), while for b = −, the integral is computed by using the approximation (compare with Eq. (133))
| (160) |
The function fC(·) is of the form
| (161) |
| (162) |
| (163) |
where the vector of parameters w in Eqs. (161)–(163) coincides with the vector of parameters w in Eqs. (135)–(137). We get
| (164) |
| (165) |
and
| (166) |
| (167) |
Furthermore, defining the cross matrix
| (168) |
by
| (169) |
we find that in the case obeys the integral equation
| (170) |
where
| (171) |
Taking into account the representation of the cross quantity as given by Eq. (103) with (cf. Eq. (110))
| (172) |
we compute the elements of the cross reflection matrix according to (compare with Eqs. (121)–(123))
| (173) |
where
| (174) |
and
| (175) |
The computation of the ladder and cross reflection matrices for a semi-infinite medium with sparsely distributed particles is organized as follows:
compute the ladder reflection matrix by solving the exact Ambartsumian’s integral equation (127);
compute the vector of parameters w by solving the least squares problem (147), that is, by matching the exact and the approximate (1, 1) elements of the ladder reflection matrices in the exact backscattering direction; and
compute the approximate cross reflection matrix from Eq. (173).
Detailed descriptions of the corresponding algorithms relying on the method of Picard iterations and the discrete ordinate method are provided in Appendix 4.
An important observation should be made here. As already mentioned, the vector of parameters w in Eqs. (161)–(163) is the same as the vector of parameters w in Eqs. (135)–(137). Because of this choice, in the exact backscattering direction when , the functions fL(·) and fC(·) are identical. As will be shown in the next section, this result implies that in the exact backscattering direction, the elements of the approximate ladder and cross reflection matrices satisfy some equations which are the result of the reciprocity relation for the single-particle amplitude scattering matrix.
5. Exact backscattering direction
In the exact backscattering direction, when the coherent intensity is maximal and is comparable to the incoherent intensity, the elements of the ladder and cross reflection matrices are related through remarkably simple relations. In Ref. [30], these relations were derived for a discrete random medium with a sparse distribution of particles by employing the Saxon’s reciprocity relation for the amplitude scattering matrix [31]. In this section they will be obtained by making use of the results established so far and which are valid for a macroscopically isotropic and mirror-symmetric discrete random medium with a dense distribution of (spherical) particles. A more general derivation is given in Appendix 5. Note that in the exact backscattering direction , i.e., cos θs = − cos θ0; hence ks0 = 0, κs = −κ0, and Ks0 = −jκ0.
First, we consider a discrete random layer with densely packed particles. For , Eq. (103) becomes
| (176) |
where (cf. Eq. (110))
| (177) |
and the matrix satisfies the ladder-type integral equation (cf. Eq. (108))
| (178) |
From Eqs. (64) and (178), we deduce that
| (179) |
so that by using this result in Eq. (62) with and accounting of Eq. (177), we obtain
| (180) |
Then, from Eqs. (73) and (104) we get
| (181) |
so that from Eqs. (72) and (180), the relation
| (182) |
readily follows. Because both and are as in Eq. (144), the above relation can be written explicitly as ()
| (183) |
where with and is the multiple-scattering component of the ladder reflection matrix. This result shows that the (total) reflection matrix at the exact backscattering direction can be calculated from the ladder reflection matrix.
Let us now prove that for a semi-infinite discrete random medium with sparsely distributed particles, the equality
| (184) |
implies that the relation (183) is valid for the elements of the approximate ladder and cross reflection matrices. From Eqs. (165), (167), and (184) in conjunction with the relations
we find
| (185) |
| (186) |
Consequently, making use of the special value of the (normalized) Legendre polynomial in Eq. (171), we obtain
| (187) |
while from Eqs. (140) and (170), and the identity
we get
| (188) |
Finally, Eqs. (142) and (173) with , Eq. (188) with , and the relation
which follows from Eqs. (143) and (175), yield the relation (182) for the approximate ladder and cross reflection matrices.
We conclude our analysis with some comments regarding the computation of the vector of parameters w.
-
From Eq. (183), we find that the (1, 1) element of the cross reflection matrix , corresponding to the cross specific intensity column vector, is
(189) In this regard, an alternative approach for computing the vector of parameters w relies on the solution of the least squares problem
where is calculated as(190) (191) -
Taking into account that the minimizer (147), matching and , is the least squares solution of the equation
we deduce from Eq. (192) that the minimizer (147) is also the least squares solution of the equation(193) (194) This equation was used in Ref. [22] to determine the vector of parameters w. Although Eqs. (193) and (194) are equivalent, it is apparent that the algorithm based on Eq. (193) involves the approximate ladder matrix , while the algorithm based on Eq. (194) involves the approximate cross matrix . Because the computation of is faster than that of (the problem decouples over the azimuthal modes), the former algorithm is more efficient.
In order to check the accuracy of the approximate method, we compare the enhancement factor for a discrete random layer with a “large” optical thickness and a semi-infinite discrete random medium. For a discrete random layer, the enhancement factor is defined by , where as before, the incident and scattering directions are and with φ0 = 0°, respectively, while for a semi-infinite discrete random medium, ξ(Θ) is computed as
The results shown in Fig. 4 correspond to a large volume concentration (f = 10−2) which makes possible to keep the number of layers manageable (Nlay ≈ 100 for Δτ = 0.1). The vector of parameters w is the solution of the least squares problem (147), the function fL(·) is as in Eq. (137), and at the solution, the relative residual
is smaller than 2 × 10−4. The agreement between the curves is quite acceptable.
Figure 4:
Enhancement factor versus the phase angle for a discrete random layer and a semi-infinite discrete random medium. For the volume concentration f = 10−2 , the relative error in κ is εκ = 1.2 × 10−2. The computational parameters are indicated in the plots.
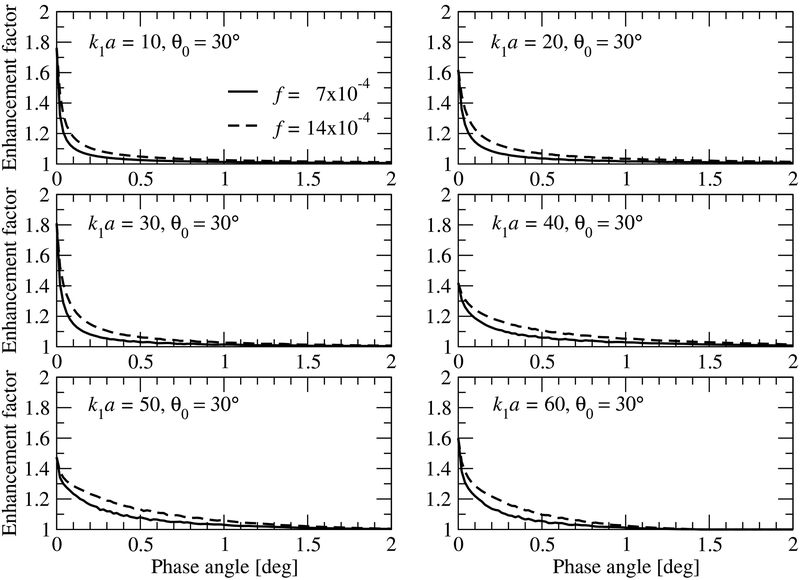
Finally, in Figs. 5 and 6 we show simulation results for a semi-infinite discrete random medium consisting of particles with large size parameters. It is interesting to note that in contrast to a finite discrete random layer, the half-width of the interference intensity peak increases with increasing the concentration, while its dependency on the incidence angle is rather weak.
Figure 5:
Enhancement factor versus the phase angle for two values of the volume concentration: f = 7 × 10−4 and 14 × 10−4. The number of discrete ordinates per hemisphere Nμ (see Appendix 4) is 16 for k1a = 10, 24 for k1a = 20, 32 for k1a = 30, 36 for k1a = 40, 42 for k1a = 50, and 48 for k1a = 60. The computational parameters are indicated in the plots.
Figure 6:
Enhancement factor versus the phase angle for two values of the incidence angle: θ0 = 30° and 60°. The computational parameters are indicated in the plots.
6. Conclusions
Following closely the approach described in Refs. [19, 20, 21, 22], we have analyzed the coherent backscattering in a linear-polarization basis and for an obliquely incident plane electromagnetic wave. The main results of our analysis can be summarized as follows.
In Section 3 we have provided a complete derivation of the ladder and cross reflection matrices for a layer with densely and sparsely distributed particles. For a dense medium, the reflection matrices are expressed in terms of the ladder correlation matrix Lξξ′ (zi) satisfying the integral equation (64), and the cross correlation matrix Cξη′ (zi) satisfying the integral equation (108). The integral equation (108) is the result of transforming the cyclical diagrams into ladder diagrams by means of the reciprocity principle. These integral equations, which are the starting point for our analysis, are similar; however, the kernel of the integral equation (108) is highly oscillating due to the phase term . The integral equation (64) can be simplified into a form that is suitable for a numerical analysis by using an approach described in Ref. [3]; the same approach, described in Appendix 1, is used here to simplify the integral equation (108). For reasons of completeness, a backward Monte Carlo method employing essentially the same simplifications (assumptions) is presented in Appendix 2. For a sparse medium, the reflection matrices are expressed in terms of the ladder matrix satisfying the integral equation (84), and the cross matrix satisfying the integral equation (119) in the case . Roughly speaking, both integral equations have the same kernel, i.e., the ladder coherency phase matrix defined by Eq. (83). However, the source term of the integral equation (84) depends on the ladder coherency phase matrix, while the source term of the integral equation (119) depends on the so-called cross coherency phase matrix defined by Eq. (117). Algorithms for computing the ladder and cross reflection matrices for a layer with sparsely distributed particles by means of the method of Picard iterations and the discrete ordinate method are discussed in Appendix 3.
In Section 4 we have described an approximate method for computing the ladder and cross reflection matrices in the case of a semi-infinite medium with a sparse distribution of particles. The key quantities are the ladder matrix satisfying the integral equation (140), and the cross matrix satisfying the integral equation (170) in the case . Analytical representations for the kernels of these integral equations are obtained under the approximations (133) and (160), i.e.,Lξξ′ (zj) ≈ exp[−fL(κ0 (zj−zi); w)]Lξξ′ (zi) and for some vector of parameters w. These approximations are global in the sense that they are valid for all zj > zi. The vector of parameters w is computed by matching the exact and approximate (1, 1) elements of the ladder reflection matrices in the exact backscattering direction, whereby the exact ladder reflection matrix is the solution of the Ambartsumian’s integral equation (127). Strictly speaking, the approximate ladder reflection matrix is used only for computing the vector of parameters w, and consequently, the approximate cross reflection matrix. In fact, we have adopted an approximate method for computing the cross reflection matrix of a semi-infinite discrete random medium because our efforts to design an approach similar to that given by Eqs. (152)–(155) and relying on the integration rule (150) have failed. Nevertheless, our numerical analysis has shown that the approximate method is fairly accurate. Algorithms for solving the Ambartsumian’s integral equation and for computing the approximate ladder and cross reflection matrices by means of the method of Picard iterations and the discrete ordinate method are provided in Appendix 4.
In Section 5 we have established the relations between the elements of the ladder and cross reflection matrices in the exact backscattering direction for dense and sparse media. These relations are first derived for a layer of macroscopically isotropic and mirror-symmetric discrete random medium with a dense distribution of particles, and then, by taking into account that in the exact backscattering direction, the functions fL(·) and fC(·) are identical, for a semi-infinite discrete random medium with sparsely distributed particles. A more general derivation using the Saxon’s reciprocity relation for the amplitude matrix is given in Appendix 5.
For sparse media, the final integral equations are different from those of Refs. [19, 20, 21, 22]; in the present approach the unknowns are the matrix functions , , , and depending on direction, while in Refs. [19, 20, 21, 22], the unknowns are roughly similar to the expansion coefficients of these matrix functions in terms of spherical harmonics. Actually, these integral equations which can be solved by employing the solution methods of the radiative transfer theory are the main findings of our analysis.
The numerical results presented in this study are intended to demonstrate that the algorithms can be applied to particles with large size parameters and not to draw (pertinent) conclusions regarding the dependence of coherent backscattering on the properties of the particles, concentration, and incidence angle. For this purpose, a more systematic numerical analysis should be performed.
We conclude our presentation by mentioning that the developed algorithms can be used for computing the reflection matrix of a (finite) inhomogeneous atmosphere by means of the matrix operator method. To explain this technique, let us express the interaction principle equation for a discrete random layer with the geometrical thickness H in a simplified form as (we omit the cosine of the incident direction)
| (195) |
Furthermore, let us approximate
| (196) |
where for the given scattering direction , is a (small) solid angle around the incident direction , in which does not vanish, i.e., is non-zero for all incident directions . Consequently, if is a set of quadrature nodes and weights on the upper unit hemisphere, the discrete form of the interaction principle equation is
| (197) |
where
| (198) |
The reflection matrix of the entire atmosphere can then be obtained by applying the doubling/adding algorithm. Obviously, this approach enables us to estimate the amplitude of the interference intensity peak, but not its angular shape.
Acknowledgements
The authors are indebted to Gerhard Kristensson and Victor Tishkovets for their helpful comments and criticism during the course of this work. Adrian Doicu acknowledges the financial support from DLR programmatic (S5P KTR 2 472 046) for the S5P algorithm development. Michael I. Mishchenko was supported by the NASA Radiation Science Program and the NASA Remote Sensing Theory Program.
Appendix 1
In this appendix we apply the technique described in Ref. [3] to simplify the integral equation (108). We write this equation as
| (199) |
where and are integral operators defined by
| (200) |
and
| (201) |
respectively, and (cf. Eq. (113)) . Putting
| (202) |
we obtain the component form representation of the integral equation (199):
| (203) |
where are the block-matrix components ofC0ξη′,
| (204) |
and
| (205) |
In Eqs. (204) and (205), are the radiating spherical wave functions, the coefficients are given by Eq. (76) of Ref. [3], and the sum should be understood as
| (206) |
where Nrank is the maximum expansion order.
Computation of the matrix. For the integral
| (207) |
we use the approximation
| (208) |
and, by taking into account the representation for the source term in Eq. (199), we assume that (zj = zi + Rji cos θji):
| (209) |
Obviously, as in Eq. (66) and in contrast to Eq. (160), the approximation (209) is local. Using the spherical wave expansion of a plane wave as given by Eq. (112), i.e.,
| (210) |
where are the regular spherical wave functions, jl (x) are the spherical Bessel functions, and are the spherical harmonics for the direction , we then obtain
| (211) |
where
| (212) |
hn(x) are the spherical Hankel functions of argument x, and are the associated Legendre functions of degree n and order m. In Eq. (212), the integral over θji can be computed analytically. Using the expansion
| (213) |
and the spherical harmonic expansion theorem
| (214) |
we obtain
| (215) |
with
| (216) |
Thus, the elements of the matrix are
| (217) |
Computation of the matrix . For the integral
| (218) |
we employ the sparse-medium approximation for the integration domain
| (219) |
and the far-field representation for the radiating spherical wave functions
| (220) |
Then, using again the expansion (112), we get
| (221) |
where Θ+ and Θ− are the intervals [0, π/2) and (π/2, π], respectively. Thus, the elements of the matrix are
| (222) |
It should be pointed out that for dense media, the integral equation (199) can be solved by the iteration method (see Eq. (99) of Ref. [3])
| (223) |
Appendix 2
In this appendix we present a backward Monte Carlo method for computing the ladder and cross reflection matrices in the case of a dense medium. The analysis is similar to that used in Ref. [32] in the case of a sparse medium. Taking into account that these matrices are given respectively, by (cf. Eqs. (38) and (39))
| (224) |
| (225) |
we focus on the estimation of the ladder and cross quantities and .
Ladder reflection matrix For the incoherent part of the scattered radiation, we rewrite Eq. (62) for as
| (226) |
and the integral equation (64) for Lξξ′ (R0) as
| (227) |
where R01 = R0 − R1. Inserting the iterated solution of Eq. (227) in Eq. (226), and using the reciprocity relations
| (228) |
where Rk,k−1 = Rk − Rk−1 = −Rk−1,k, we obtain
| (229) |
where
| (230) |
and
| (231) |
with tL0 = 1 and 0 =. For k ≥ 1, the quantities tLk(·) and k(·) in Eq. (231) are computed recursively as
| (232) |
and
| (233) |
respectively, where, as before, tL0 = 1 and 0 = .
Cross reflection matrix For the coherent part of the scattered radiation, we use Eq. (103) to compute . In this equation, we use the representation (cf. Eq. (105))
| (234) |
where Cξη′ (R0) satisfies the integral equation (cf. Eq. (108))
| (235) |
Inserting the iterated solution of Eq. (235) in Eq. (234) and the result in Eq. (103), and making use on the reciprocity relations (228) and
| (236) |
we end up with
| (237) |
where
| (238) |
In Eq. (238), FCkηξη′ξ′ (·) is given by
| (239) |
where tCk(·) and k(·) are computed by means of the relation
| (240) |
and Eq. (233), respectively.
From a physical point of view, FLkηξη′ξ′ (·) corresponds to the interference of the waves scattered by the particles chain {R0:k} = {R0, . . . , Rk} illuminated by the same plane electromagnetic wave propagating in the direction , while FCkηξη′ξ′(·) corresponds to the interference of the waves scattered by the particles chain illuminated by two plane electromagnetic wave propagating in the directions and (Fig. 7). In addition, from Eq. (240) we see that tCk(·) and tLk(·) differ by a phase term depending on the relative positions of the particles in the chain.
Figure 7:
Scattering by the particles chain {R0:k} illuminated by (a) the same plane electromagnetic wave propagating in the direction , and (b) two plane electromagnetic wave propagating in the directions and .
Monte Carlo method Consider L independent Markov chain paths of lengths K(l), l = 1, . . . , L, i.e.,
| (241) |
with the initial probability density function on D, a transition function , and the absorbing state ⊘ ∉ D. An unbiased estimate for is
| (242) |
with
| (243) |
while an unbiased estimate for is
| (244) |
with
| (245) |
The initial probability density p(R0) and the probability transition function p(Rk-1 → Rk) are chosen as follows.
- For the probability densities pL(R0) and pC(R0), satisfying the normalization condition
we adopt the representations(246)
and(247)
respectively, where R0 = (x0, y0, z0). The above probability densities show that the horizontal variables x0 and y0 do not play any role in the simulations. Moreover, the area of the illuminated surface A in the expressions of pL(R0) and pC(R0), and the same area in the expressions of and given by Eqs. (224) and (225), respectively, cancel out. Note that in the exact backscattering direction, κs = −κ0 and so, both probability densities coincide.(248) -
The transition function p(Rk−1 → Rk) is represented in the form
where ω is the single-scattering albedo of the particle. For p(Rk,k−1), we assume the probability density function(249) (250) To construct the probability density function with we consider the scattering by the particles chain {R0:K} placed in free space and illuminated by the η-polarized plane electromagnetic wave propagating in the direction (Fig. 8(a)),In this case,
are the the expansion coefficients of the field exciting particle k − 1,(251)
are the amplitudes of the far-field pattern in the direction , and is the differential scattering cross section. Taking these results into account, we construct the probability density function as(252)
and sample the polar angle from the marginal probability density , and the azimuth angle from the conditional probability . As in Ref. [32], the probability density function pC(Θ, Φ) can be chosen as pC(Θ, Φ) = pL(Θ, Φ). Another possible choice which relies on the observation that for the coherent part of the scattered radiation, the particles chain is illuminated by two plane electromagnetic waves propagating in the directions and (Fig. 8(b)), is(253)
Figure 8:
Scattering geometries for constructing the probability density functions (a) pL(Θ, Φ) and (b) pC(Θ, Φ).
| (254) |
It remains an open question if these choices of the probability density functions reduce the variance in the contribution of each photon, thus reducing the number of photons and hence the CPU time required to obtain a prescribed accuracy.
We conclude this appendix with some comments.
To construct the probability density functions we considered a chain of particles placed in free space whose positions are uncorrelated, and assumed that particle k is situated in the far zone of particle k − 1. Thus, the probability density functions are typical for a sparse medium. On the other hand, the probability density function p(r) including the pair correlation functions g(r) is a characteristic of a dense medium.
-
For a sparse medium, we use the far-field approximation (cf. Eqs. (75) and (76))
the representation of the elements of the single-particle amplitude matrix in the particle-centered coordinate system(255)
and the relation giving the components of the ladder coherency phase matrix(256)
to obtain(257)
and(258) (259) Similarly, under the additional assumption K′ ≈ k1 yielding
we get(260) (261) It should be pointed out that if we insert the iterated solution of Eq. (119), i.e.,
in Eq. (122), i.e.,(262)
and the result in Eq. (121), and furthermore, take into account the reciprocity relations(263)
and(264)
we are led to the same series representation for RC(ηη′)(ξ,ξ′) (,) as that obtained from Eqs. (225), (237), (238), and (261). Furthermore, because for sparse media, g(r) = 1 and , the probability density function p(r) given by Eq. (250) simplifies to(265) (266) The probability density functions pL(Θ, Φ) and pC(Θ, Φ) become
and(267)
respectively, where, for example, is the phase function for the incident and scattering directions and , corresponding to a η-polarized plane electromagnetic wave illuminating the first particle of the chain in the direction . Thus, pL(Θ, Φ) is the sum of the normalized phase functions for the two polarization states of the incident wave propagating in the direction , while pC(Θ, Φ) is the sum of the normalized phase functions for the two polarization states of the incident waves propagating in the directions and . Note that in the exact backscattering direction, pL(Θ, Φ) and pC(Θ, Φ) coincide. Also note that in Eqs. (243) and (245), the product in the expressions of FLkηξη′ξ′ (·) and FCkηξη′ξ′ (·), and the same product in the expressions of and (resulting from Eq. (249)) cancel out.(268)
Appendix 3
In this appendix we present algorithms for computing the ladder and cross reflection matrices for a layer with a sparse distribution of particles.
Let be an incident direction and with μs > 0 be a scattering direction. Consider a discrete set of points in the altitude interval [0, H] , and let be a set of Nμ Gauss–Legendre quadrature nodes and weights in the interval [0, 1]. For the directions and , assume the azimuthal expansions
| (269) |
and
| (270) |
where Mrank is the maximum azimuthal order.
Ladder reflection matrix. The algorithm for computing the ladder reflection matrix for a given incident direction involves the following steps:
- for each azimuthal mode m, solve the system of integral equations (cf. Eq. (84))
for with i = 1, . . . , Nz and k = 1 , . . . , Nμ, by the method of Picard iterations;(271) - for each azimuthal mode m and the scattering direction −μs, compute
(272) compute the ladder reflection matrix as (cf. Eq. (85))
| (273) |
| (274) |
Cross reflection matrix. For the specified incident and scattering directions and , assume the azimuthal expansions
| (275) |
and
| (276) |
| (277) |
Furthermore, for , express the function (cf. Eq. (120))
| (278) |
with a sufficiently large truncation index N, as the Fourier series
| (279) |
where
| (280) |
The algorithm for computing the cross reflection matrix for given incident and scattering directions and , respectively, involves the following steps:
- solve the system of integral equations (cf. Eq. (119))
for (sign +) and (sign −) with i = 1, . . . , Nz, k = 1, . . . , Nμ, and m = −Mrank, . . . , Mrank, by the method of Picard iterations;(281) - compute (cf. Eq. (122))
(282) - compute the elements of the cross reflection matrix as (cf. Eq. (121))
(283)
Note that the system of integral equations (271) is solved separately for each azimuthal mode, while the system of integral equations (281) is solved simultaneously for all azimuthal modes. Also note that the integrals over zj in Eqs. (271) and (281) are calculated by using the quadrature scheme described in Appendix 4 of Ref. [3].
Appendix 4
In this appendix we present algorithms for computing the exact and the approximate ladder reflection matrices, as well as the approximate cross reflection matrix for a semi-infinite discrete random medium with a sparse distribution of particles.
Exact ladder reflection matrix. Consider the azimuthal expansions
| (284) |
| (285) |
and assume that the incident direction μ0 coincides with the discrete ordinate direction μj0.
The algorithm for computing the exact ladder reflection matrix satisfying the Ambartsumian’s integral equation (127) is organized as follows:
- for each azimuthal mode m, solve the system of equations
for Lm(−μi, μj) with i, j = 1, . . . , Nμ, by the method of Picard iterations;(286) - for each azimuthal mode m and the scattering direction −μs, solve the system of equations
for Lm(−μs, μj) with j = 1, . . . , Nμ, by the method of Picard iterations;(287) compute the exact ladder reflection matrix L(−μs, μ0, φs − φ0) from Eq. (284) with μ0 = μj0.
Approximate ladder reflection matrix. With the same notation as in Appendix 2, consider the azimuthal expansion
| (288) |
The algorithm for computing the approximate ladder reflection matrix for given incident and scattering directions and , respectively, is organized as follows:
- for each azimuthal mode m, solve the system of equations (cf. Eq. (140))
for with k = 1, . . . , Nμ, by the method of Picard iterations, where(289) (290) (291) - for each azimuthal mode m and the scattering direction −μs, compute
(292)
Approximate cross reflection matrix. For , consider the azimuthal expansion
| (295) |
and, for , express the function (cf. Eq. (171))
| (296) |
with a sufficiently large truncation index N, as the Fourier series
| (297) |
where
| (298) |
and
| (299) |
| (300) |
The algorithm for computing the approximate cross reflection matrix for given incident and scattering directions and , respectively, is organized as follows:
- solve the system of equations (cf. Eq. (170))
for (sign +) and (sign −) with k = 1, . . . , Nμ and m = −Mrank, . . . , Mrank, by the method of Picard iterations;(301) - compute (cf. Eq. (174))
(302) - compute the elements of the cross reflection matrix as (cf. Eq. (173))
(303)
Remark that in contrast to the system of equations (289), the system of equations (301) involves all azimuthal modes.
Appendix 5
In this appendix we derive the relations between the elements of the ladder and cross reflection matrices by using the reciprocity relation (cf. Eq. (102))
| (304) |
We begin by considering the decomposition of the reflection matrix into a ladder and a cross component as in Eq. (37), and the decomposition of the ladder reflection matrix into a single- and a multiple-scattering component as in Eq. (71), i.e.,
| (305) |
The single-scattering reflection matrix is determined by (cf. Eq. (72))
the multiple-scattering reflection matrix is determined by (cf. Eqs. (74) and (304))
| (306) |
and the cross reflection matrix is determined by (cf. Eqs. (103), (111), and (304))
| (307) |
In the backscattering direction, Eqs. (306) and (307) become
| (308) |
and
| (309) |
respectively. Using Eqs. (308) and (309), we express the reflection matrices and in terms of the matrix elements
as
| (310) |
and
| (311) |
respectively. From Eqs. (310) and (311) we find that the cross reflection matrix C can be expressed in terms of the matrix elements of the multiple-scattering reflection matrix as
| (312) |
For a macroscopically isotropic and mirror symmetric medium with a dense distribution of particles, the representation (144) is also valid for , and so, Eq. (312) simplifies to Eq. (183).
References
- [1].Doicu A Mishchenko MI. Electromagnetic scattering by discrete random media. I: The dispersion equation and the configuration-averaged exciting field. J Quant Spectrosc Radiat Transfer 2019;230:282–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Doicu A Mishchenko MI. Electromagnetic scattering by discrete random media. II: The coherent field. J Quant Spectrosc Radiat Transfer 2019;230:86–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Doicu A Mishchenko MI. Electromagnetic scattering by discrete random media. III: The vector radiative transfer equation (submitted to J Quant Spectrosc Radiat Transfer). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Tsang L, Kong JA. Scattering of electromagnetic waves Advanced topics. New York: Wiley; 2001. [Google Scholar]
- [5].Mishchenko MI, Travis LD, Lacis AA. Multiple scattering of light by particles Radiative transfer and coherent backscattering. Cambridge, UK: Cambridge University Press; 2006. [Google Scholar]
- [6].Mishchenko MI. Multiple scattering, radiative transfer, and weak localization in discrete random media: the unified microphysical approach. Rev Geophys 2007;46:RG2003. [Google Scholar]
- [7].Barabanenkov YuN, Kravtsov YuA, Ozrin VD, Saichev AI. Enhanced backscattering in optics. Prog Opt 1991;29:65–197. [Google Scholar]
- [8].Ruffine RS, DeWolf DA. Cross-polarized electromagnetic backscatter from turbulent plasmas. J Geophys Res 1965;70:4313–4321. [Google Scholar]
- [9].Kuz’min VL, Romanov VP. Coherent phenomena in light scattering from disordered systems. Phys Usp 1996;39:231–260. [Google Scholar]
- [10].Mishchenko MI. Electromagnetic scattering by particles and particle groups: an introduction. Cambridge, UK: Cambridge University Press; 2014. [Google Scholar]
- [11].Muinonen K, Mishchenko MI, Dlugach JM, Zubko E, Penttila A, Videen G. Coherent backscattering verified numerically for a finite volume of spherical particles. Astrophys J 2012;760:118. [Google Scholar]
- [12].Mishchenko MI, Tishkovets VP, Litvinov PV. Exact results of the vector theory of coherent backscattering from discrete random media: an overview In: Videen G, Kocifaj M, editors. Optics of cosmic dust. Dordrecht: Kluwer; 2002. p. 239–260. [Google Scholar]
- [13].Tishkovets VP, Litvinov PV, Lyubchenko MV. Coherent opposition effect for semi-infinite discrete random medium in the double-scattering approximation. J Quant Spectrosc Radiat Transfer 2002;72:803–811. [Google Scholar]
- [14].Tishkovets VP, Litvinov PV, Tishkovets SV. Interference effects in backscattering of light by a layer of a discrete random medium. Opt Spectrosc 2002;93:899–907. [Google Scholar]
- [15].Litvinov P, Tishkovets V, Ziegler K. Coherent backscattering effects for discrete random media. J Quant Spectrosc Radiat Transfer 2007;103:131–145. [Google Scholar]
- [16].Ozrin VD. Exact solution for coherent backscattering of polarized light from a random medium of Rayleigh scatterers. Waves Random Media 1992;2:141–164. [Google Scholar]
- [17].Amic E, Luck JM, Nieuwenhuizen ThM. Multiple Rayleigh scattering of electromagnetic waves. J Phys I (France) 1997;7:445–483. [Google Scholar]
- [18].Mishchenko MI, Luck JM, Nieuwenhuizen ThM. Full angular profile of the coherent polarization opposition effect. J Opt Soc Am A 2000;17:888–891. [DOI] [PubMed] [Google Scholar]
- [19].Tishkovets VP. Multiple scattering of light by a layer of discrete random medium: backscattering. J Quant Spectrosc Radiat Transfer 2002;72:123–137. [Google Scholar]
- [20].Tishkovets VP, Mishchenko MI. Coherent backscattering of light by a layer of discrete random medium. J Quant Spectrosc Radiat Transfer 2004;86:161–180. [Google Scholar]
- [21].Tishkovets VP, Mishchenko MI. Approximate calculation of coherent backscattering for semi-infinite discrete random media. J Quant Spectrosc Radiat Transfer 2009;110:139–145. [Google Scholar]
- [22].Tishkovets VP, Petrova EV, Mishchenko MI. Scattering of electromagnetic waves by ensembles of particles and discrete random media. J Quant Spectrosc Radiat Transfer 2011;112:2095–2127. [Google Scholar]
- [23].Tishkovets VP, Petrova EV. Light scattering by densely packed systems of particles: near-field effects. Light Scattering Rev 2013;7:3–36. [Google Scholar]
- [24].Mishchenko MI, Dlugach JM, Liu L, Rosenbush VK, Kiselev NN, Shkuratov YuG. Direct solutions of the Maxwell equations explain opposition phenomena observed for high-albedo solar system objects. Astrophys J Lett 2009;705:L118–L122. [Google Scholar]
- [25].Mishchenko MI, Dlugach JM, Chowdhary J, Zakharova NT. Polarized bidirectional reflectance of optically thick sparse particulate layers: an efficient numerically exact radiative-transfer solution. J Quant Spectrosc Radiat Transfer 2015;156:97–108. [Google Scholar]
- [26].Dlugach JM, Yanovitskij EG. The optical properties of Venus and the Jovian planets. II. Methods and results of calculations of the intensity of radiation diffusely reflected from semi-infinite homogeneous atmospheres. Icarus 1974;22:66–81. [Google Scholar]
- [27].de Rooij WA, Domke H. On the nonuniqueness of solutions for nonlinear integral equations in radiative transfer theory. J Quant Spectrosc Radiat Transfer 1984;31:285–99. [Google Scholar]
- [28].de Rooij WA. Reflection and transmission of polarized light by planetary atmospheres. Amsterdam: Free University; 1985. [Google Scholar]
- [29].Mishchenko MI, Dlugach JM, Yanovitskij EG, Zakharova NT. Bidirectional reflectance of flat, optically thick particulate layers: an efficient radiative transfer solution and applications to snow and soil surfaces. J Quant Spectrosc Radiat Transfer 1999:63:409–32. [Google Scholar]
- [30].Mishchenko MI. Enhanced backscattering of polarized light from discrete random media: calculations in exactly the backscattering direction. J Opt Soc Am A 1992;9:978–982. [Google Scholar]
- [31].Saxon DS. Tensor scattering matrix for the electromagnetic field. Phys Rev 1955;100:1771–1775. [Google Scholar]
- [32].Muinonen K Coherent backscattering of light by complex random media of spherical scatterers: numerical solution. Waves Random Media 2004;14:365–368. [Google Scholar]