Are We Approaching a Biological Limit to Human Longevity?

Abstract

Until recently human longevity records continued to grow in history, with no indication of approaching a hypothetical longevity limit. Also, earlier studies found that age-specific death rates cease to increase at advanced ages (mortality plateau) suggesting the absence of fixed limit to longevity too. In this study, we reexamine both claims with more recent and reliable data on supercentenarians (persons aged 110 years and older). We found that despite a dramatic historical increase in the number of supercentenarians, further growth of human longevity records in subsequent birth cohorts slowed down significantly and almost stopped for those born after 1879. We also found an exponential acceleration of age-specific death rates for persons older than 113 years in more recent data. Slowing down the historical progress in maximum reported age at death and accelerated growth of age-specific death rates after age 113 years in recent birth cohorts may indicate the need for more conservative estimates for future longevity records unless a scientific breakthrough in delaying aging would happen. The hypothesis of approaching a biological limit to human longevity has received some empirical support and it deserves further study and testing.

The topic of the limit to human life span received a lot of attention from gerontologists and biodemographers after 2016 publication in Nature, suggesting that the limit to human life span does exist and is equal to 115 years (1). This publication was followed by a flurry of published comments and a subsequent publication in Science on Italian semi-supercentenarians aged 105 years and older (2) that rejected the conclusion about human life-span limit. It should be noted that the idea of no fixed limit to human life span was discussed in the field of gerontology and biodemography for a long time. This topic got a particular attention when the hypothesis of human life-span limit has been tested by analyzing mortality trajectories at advanced ages (3). It was hypothesized that mortality rate should rise to infinity when approaching the limit to life span and hence accelerate compared with the typical exponential growth with age (the Gompertz law). After finding out that the observed mortality slows down rather than accelerates compared with the Gompertz law, it was concluded that there is no evidence for human life-span limit (3). Wilmoth elaborated on this topic further and analyzed trends in the maximum reported age at death (MRAD) both by year of death and by year of birth (4). He suggested that there should be no steady increase in MRAD if life-span limit hypothesis is correct. At the time of his study, MRAD demonstrated very strong growing trend both for the year of death and for the year of birth (4,5), suggesting that there is no fixed limit to human life span. This conclusion was reinforced further by studies of mortality trajectories that showed mortality deceleration rather than mortality acceleration at advanced ages for many countries (6–8). Thus, earlier studies demonstrated the so-called “old-age mortality deceleration,” “mortality leveling-off,” and “mortality plateaus” when death rates at extreme old ages do not grow as fast as at younger ages.

Later, some new developments in the study of old-age mortality questioned this common view. Study of more recent and more reliable data on the U.S. mortality demonstrated that mortality continues to grow exponentially with age even at extreme old ages (9,10). This finding cannot be explained by lower quality of U.S. data, because age misreporting is associated with lower rather than higher estimates of mortality and hence with more expressed mortality deceleration (9,11,12). In another study, exponentially growing Gompertz-like mortality trajectories were found for old-age mortality in females of Australia, Canada, and the United States (13). This means that the chances of exceptional survival are much smaller than it was assumed earlier. Another recent observation is that mortality of centenarians does not decrease noticeably in the recent decade, despite a significant decline in mortality of younger age groups (14–16). Thus, the projected estimates of old-age survival are expected to be lower than it was formerly believed.

These new developments in the study of old-age mortality suggest the need of revisiting the limit to human life-span concept. Supercentenarians (persons surviving to age 110 years) may be a useful model for testing the life-span limit hypothesis. Although mortality of supercentenarians was analyzed earlier (17), the conclusions about mortality trajectories were based on visual inspection of graphs rather than quantitative analysis. Previous studies of supercentenarians analyzed longevity records by year of death and did not account for the truncation bias in non-extinct birth cohorts (1,18). In this study, we test the limit to life-span hypothesis by analyzing the pace of historical increase of maximum age at death in historical birth cohorts (4) and by evaluating the shape of age-specific mortality trajectories at extreme old ages (3,4). We suggest that accelerating trend of mortality trajectory at advanced ages and asymptotic decelerating growth of maximum life span across subsequent birth cohorts should be expected when approaching the biological limit to human longevity.

Methods

Data

International Database on Longevity

We used records of supercentenarians available in the International Database on Longevity (IDL) (www.supercentenarians.org). This database contains validated records of persons aged 110 years and older from 15 countries with good quality of vital statistics (19). Database contains information on 4 living supercentenarians and age at death of 668 supercentenarians. The database was last updated in March 2010 and the last deaths in IDL were observed in 2007. IDL is considered to be an official data source and is claimed by its developers to be a gold standard of data for persons aged 110 years and older (2).

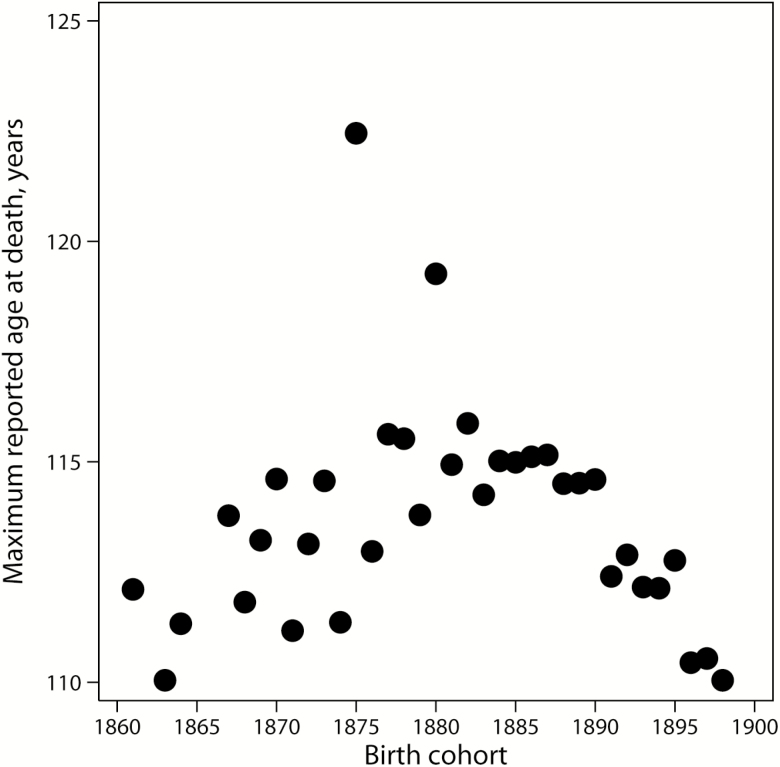
However, we found that IDL contains many truncated records. Figure 1 shows MRAD across subsequent birth cohorts in IDL. Note that longevity records rapidly decline for cohorts born after 1889, indicating that these cohorts are not extinct and data for these cohorts are truncated. Truncation occurs when individuals belonging to non-extinct birth cohorts are still alive but are not accounted for. This observation is in agreement with reports that data collection for IDL was finished in different years for different countries (20). Thus, we deal here with incomplete data when part of the relevant subjects are not present because of data truncation. The changing point when longevity records start declining in IDL corresponds to 1886 birth cohort (95% CI: 1883, 1888). To avoid bias caused by data truncation, IDL records in our study were analyzed only for cohorts born before 1885.

Figure 1.

Maximum reported age at death, by year of birth in the International Database on Longevity.

Gerontology Research Group database on supercentenarians

One of the continuing interests of the Gerontology Research Group (GRG; cofounded in 1990 by Drs. Steven Kaye and Stephen Coles) is to authenticate cases of the oldest humans in history, the population of supercentenarians. GRG publishes the most current validated list of living and deceased supercentenarians on a regular basis in the journal Rejuvenation Research (21). The GRG also maintains database on supercentenarians on their website http://www.grg.org. In order to be included in the GRG official database, a person needs to have at least three independent sources of documentation: a Birth Certificate, Baptismal Certificate, or Marriage Certificate; consistent U.S. Census records dating back to 1900; and some other photo identification, such as an old driver’s license. GRG database is being updated on a regular basis and is publicly available; the last reported deaths in this database occurred in 2018. In this study, GRG data for validated supercentenarians were downloaded from the following URL: http://gerontology.wikia.com/wiki/Category:Lists_of_supercentenarians_by_year_of_birth (Accessed February 15, 2019). This source of information is based on validated records from the GRG database (list A). Unlike IDL, longevity records in GRG database continue to grow across subsequent birth cohorts up to the 1900 birth cohort (Supplementary Figure 1). Thus, cohorts born before 1900 in GRG database are extinct and not subject to truncation bias.

Outliers

It follows from Figure 1 that IDL has two obvious outliers: Jeanne Calment who died at age 122 years and Sarah Knauss who died at age 119 years. The age at death of Jeanne Calment lies outside the upper threshold of so-called Tukey’s fence equal to 120 years. Tukey’s fence is measured as upper quartile in a series of maximum life span across birth cohorts plus interquartile range multiplied by 1.5 (22). The age of death of Sarah Knauss is below the upper threshold of Tukey’s fence so that her case is not considered to be an outlier according to this criterion. However, another method of outlier detection based on blocked adaptive computationally efficient outlier nominators algorithm (23) implemented in Stata package detects both Jeanne Calment and Sarah Knauss as outliers. Both outliers were removed in the analysis of MRAD trends to eliminate irregularities in the trend line. Addition of these two outliers to the trend line does not change the conclusions about the trend of longevity records across subsequent birth cohorts. In the study of old-age mortality trajectories, both outliers were included in the analyses of 1860–1884 birth cohort.

Comparison of IDL and GRG databases

As we already noted, IDL is often claimed to be the most reliable source of data on supercentenarians. In the case of GRG database, there were concerns that this database is skewed in favor of more famous cases with record high longevity whereas cases with lower age at death (110–112 years) may be underrepresented. We compared age distributions of death in IDL and GRG databases for 1860–1888 extinct birth cohorts (comparable extinct birth cohorts in both databases). It turns out that age distributions of death in IDL and GRG databases do not differ significantly according to the chi-squared test (p = .994; see also Supplementary Figure 2). Proportion of deaths for the youngest age group (110 years) is similar in both databases: 51.57% (95% CI: 46.99, 56.12) in IDL and 50.34% (95% CI: 46.21, 54.47) in GRG database. Proportion of deaths for the 110 age group in later birth cohort (1889–1898) in GRG database is equal to 45.88% (95% CI: 42.92, 48.86), which is slightly lower (but not statistically significantly lower) than the same proportion for earlier birth cohort (see also Supplementary Figure 3). We do not have a comparable sample of supercentenarians in IDL for later birth cohort to make a direct comparison. These comparisons suggest that the life-span distribution in GRG database is not skewed in favor of individuals with longer life, so we used the GRG database in this study as the main and more up-to-date source of information about supercentenarians.

Earlier study of mortality at advanced ages based on the U.S. Social Security Administration Death Master File found that data for earlier birth cohorts demonstrate more expressed mortality deceleration (9). This difference is most likely caused by age misreporting by the members of earlier birth cohorts (12). Indeed, further study of U.S. birth cohorts found that for earlier cohorts (born before 1885), the old-age mortality shows deceleration whereas mortality of later birth cohorts follows the Gompertz law (24). To capture possible effects of different birth cohorts on mortality, supercentenarian data were split into earlier (born before 1885) and later (born in 1885–1898) birth cohorts. The same split into earlier and later birth cohorts was made in the previous study of mortality after age 110 years (17) and ensures approximately equal split by the number of records in IDL. Taking into account very small number of male records, data for both sexes combined were used in the analyses keeping in mind that mortality difference between males and females is not significant after age 110 years (17).

Statistical Methods

Hazard rate was estimated using standard statistical package Stata (procedure ltable). Procedure ltable calculates hazard rate for discrete data in the following way. Let f_j= d_j/n_j is within-interval failure rate (where d_j is number of deaths within interval j and n_j is number alive at the beginning of interval j). Then, the maximum likelihood estimate of the hazard rate for interval j is as follows:

$${\displaystyle \begin{array}{l}{\displaystyle {\mu }_j=\frac{1}{\mathrm{\Delta }x}\frac{f_j}{1-\frac{f_j}{2}}}\end{array}}$$ (1)

where ∆x is the length of age interval j.

This empirical estimate of hazard rate is less biased at older ages compared to 1-year probability of dying, which has a theoretical upper boundary equal to one (9). Hazard rates were calculated using semiannual (6 months) age intervals and expressed in yearly units (year^–1). It was shown that estimates of hazard rates for more narrow age intervals are less biased at older ages compared with yearly estimates (9). We used semiannual age intervals in our analyses keeping in mind relatively small samples of supercentenarians. Analyses of mortality were conducted in the age interval of 110–114.5 years for earlier birth cohort (1860–1884) and 110–115 years for later birth cohort (1885–1898) to avoid discontinuity in hazard rate estimation and to ensure that the number of survivors in the last age interval is higher than 20.

Hazard rates were fitted by two competing models of mortality: the Gompertz model (3,25,26), and the exponential model or flat mortality model (2,17).

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{G}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{z}:{\mu }_x=a{e}^{bx}}\end{array}}$$ (2)

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{E}\mathrm{x}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{m}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}:{\mu }_x=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}}\end{array}}$$ (3)

where x corresponds to age and α and b are parameters.

Parameters of Gompertz and exponential models were calculated using weighted nonlinear regression (Stata nlin command). Age-specific exposure values (person-years) were used as weights (27). Goodness of fit for the competing models was evaluated using the Akaike’s information criterion (AIC) (28). This criterion is calculated using the following formula:

$${\displaystyle \begin{array}{l}{\displaystyle AIC=2k-2\ln (L)}\end{array}}$$ (4)

where k is the number of parameters in the statistical model, and L is the maximized value of the likelihood function for the estimated model. AIC is widely used as a measure of the goodness of fit of an estimated statistical model, and the best model demonstrates minimal value of AIC (29). In the case of model selection, it is important to calculate AIC difference (∆ _i) for compared models, which is more important than absolute AIC values. Model with higher AIC and ∆ _i less than 10 has essentially no support and with ∆ _i is equal to 4–7, it has considerably less support compared with model with minimal AIC. AIC difference less than 3 does not allow researchers to distinguish between two models (29).

Changing points for trends were estimated using a system of linear equations by Stata nlin command.

All calculations were conducted using Stata statistical software, release 14.

Results

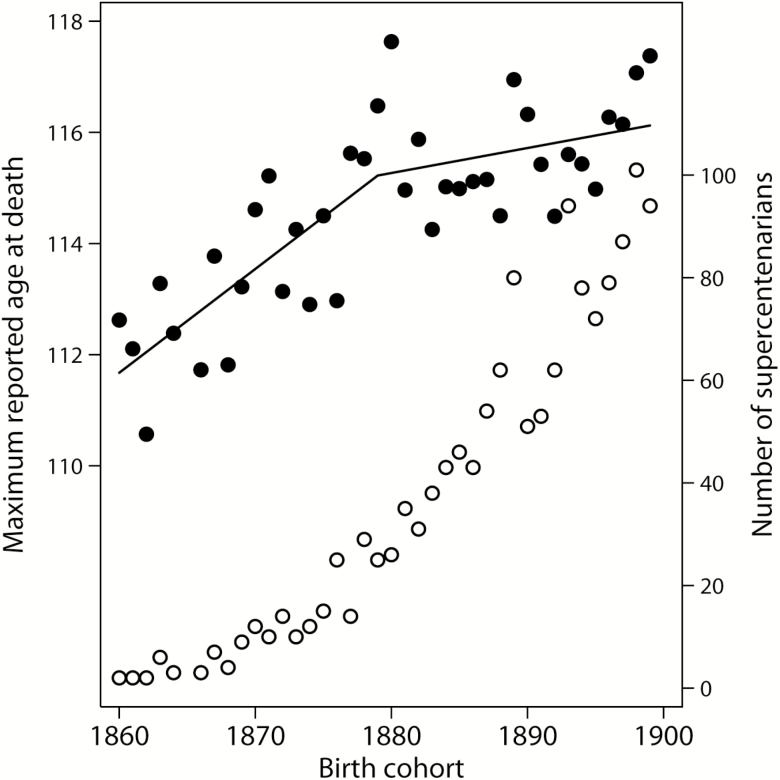
Figure 2 shows MRAD as a function of birth year (black circles, left axis). Note that the pace of MRAD growth is slower for later birth cohorts. Changing point for the slope of linear dependence is equal to birth year 1879 (95% CI: 1869, 1889). Table 1 presents results of linear regression for MRAD as a function of birth cohort and shows that for earlier birth cohorts MRAD grows faster across subsequent cohorts compared with the later birth cohorts. In later birth cohorts, the slope coefficient of linear regression becomes not significantly different from zero, indicating that there may be practically no further growth of longevity records. These results demonstrate that the pace of MRAD growth slows down in more recent birth cohorts as if approaching the biological limit to human longevity. Slowing down in the pace of MRAD increase cannot be explained by decreasing number of supercentenarians in more recent birth cohorts. As demonstrated by Figure 2, there is an accelerated growth of the number of supercentenarians in subsequent birth cohorts (white circles, right axis). This observation means that MRAD virtually does not grow despite increasing number of people surviving to age 110 years in each subsequent birth cohort.

Figure 2.

Maximum reported age at death (black circles, left axis) and number of supercentenarians (white circles, right axis), by year of birth. Lines correspond to linear fit before and after 1879 birth year. On the basis of GRG data.

Table 1.

Results of Ordinary Least Squares (OLS) Regression for Maximum Reported Age at Death as a Function of Year of Birth^a

Regression coefficient	Birth year range
	1860–1878	1879–1898
Slope	0.171*** (0.077, 0.265)	0.033 (–0.041, 0.108)
Intercept	115.17*** (114.04, 116.29)	115.41*** (114.60, 116.23)
Observations	18	21
Number of studied supercentenarians in the birth year range	179	1,254
R-squared	0.4830	0.0440

Note: GRG data. 95% confidence intervals shown in parentheses; *** p < .001.

^aYear of birth was mean-centered around the overall sample mean equal to 1,879.87 to avoid negative values for intercept parameter.

Another approach to test the limit to life-span hypothesis is to analyze the shape of age-specific mortality trajectories for supercentenarians. Table 2 compares two competing mortality models (Gompertz model and constant mortality model) for earlier and later birth cohorts using AIC as a goodness-of-fit measure. In the case of later birth cohorts, the Gompertz model demonstrates better fit than the “flat mortality” exponential model for all studied groups. In the case of earlier birth cohorts, exponential (constant mortality) model shows the best fit for all studied groups (Table 2) regardless of inclusion or exclusion of outliers. The latter result is in agreement with the previous reports (17,30). Better mortality fit by exponential model in the case of earlier birth cohort is observed for both IDL and GRG data. Note that for the later birth cohort, the Gompertz model has substantially better support compared with the exponential model. In the case of earlier birth cohort, the exponential (flat mortality) model has only slightly better support according to the AIC difference values (Table 2).

Table 2.

Testing Competing Mortality Models for Supercentenarian Data (110+ Years). Akaike Information Criterion (AIC) for the Gompertz and the “Flat Mortality” Exponential Model of Hazard Rate^a

Group	N	AIC, Gompertz model (1)	Gompertz slope parameter (95% CI)	AIC, exponential model (2)	Constant hazard rate parameter (95% CI)	AIC difference, ∆ i ((2)–(1))
Earlier birth cohort (born in 1860–1884)b
IDL, All records	297	–11.52	–0.034 (–0.151, 0.083)	–13.01	0.70 (0.62, 0.79)	–1.49
IDL, outlier aged 122 years excluded	296	–10.18	–0.021 (–0.143, 0.102)	–12.01	0.71 (0.62, 0.80)	–1.83
GRG, All records	379	–16.04	–0.013 (–0.108, 0.081)	–17.92	0.68 (0.61, 0.75)	–1.88
GRG, outlier aged 122 years excluded	378	–15.02	–0.003 (–0.101, 0.095)	–17.01	0.69 (0.62, 0.76)	–1.99
GRG, two outliers aged over 118 years excluded	377	–13.90	0.007 (–0.095, 0.109)	–15.87	0.69 (0.62, 0.77)	–1.97
Later birth cohort (born in 1885–1898)
Age interval: 110–115
GRG, All records	962	–16.65	0.101 (0.020, 0.183)	–12.98	0.68 (0.59, 0.76)	3.67
GRG, women	873	–14.75	0.108 (0.019, 0.197)	–11.35	0.67 (0.58, 0.76)	3.40
Age interval: 113–115
GRG, All records	130	–22.54	0.468 (0.407, 0.529)	3.41	0.88 (0.49, 1.27)	25.95
GRG, women	120	–23.54	0.469 (0.415, 0.523)	3.53	0.89 (0.50, 1.28)	27.07
Age interval: 110–113
GRG, All records	832	–18.70	0.008 (–0.088, 0.103)	–20.65	0.65 (0.60, 0.70)	–1.95
GRG, women	753	–15.37	0.010 (–0.112, 0.131)	–17.31	0.65 (0.58, 0.71)	–1.94

Note: Data on supercentenarians are taken from the International Database on Longevity (IDL) and Gerontology Research Group (GRG) databases. IDL = International Database on Longevity; GRG = Gerontology Research Group; 95% CI = 95% confidence intervals.

^aHazard rates were estimated using semiannual age intervals.

^bFor earlier birth cohort, mortality models were compared in the age interval 110–114.5 years.

Comparison of actuarial aging rate (slope parameter b in the Gompertz model) for earlier and later birth cohorts demonstrates marked difference. For earlier birth cohort (1860–1884), the actuarial aging rate is not significantly different from zero: –0.034 year^–1 (95% CI: –0.143, 0.102). For later birth cohort (1885–1898), the actuarial aging rate is much higher: 0.101 year^–1 (95% CI: 0.020, 0.183). These results suggest that mortality is flat for earlier birth cohort only.

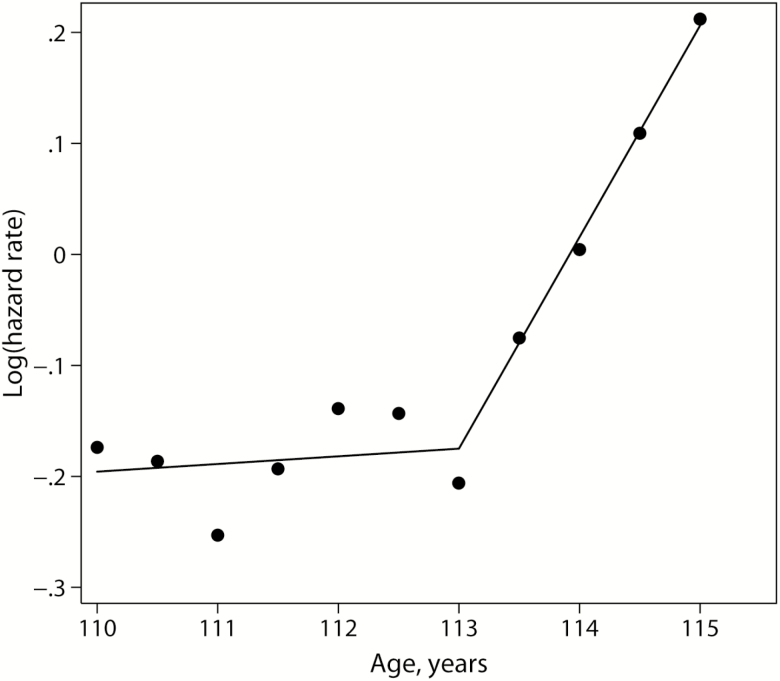
Further analysis of mortality for later birth cohort revealed that mortality trajectory is not uniform in the studied age interval (110–115 years). It turns out that mortality is practically flat for ages 110–113 years, which is reflected in the Gompertz slope coefficient not significantly different from zero (Table 2). At the same time, mortality after age 113 years demonstrates very steep growth with very high actuarial aging rate (0.468 year^–1) that is much higher than typical actuarial aging rate of 0.1 year^–1 observed in human populations (3). Figure 3 demonstrates the shape of mortality trajectory for 1885–1898 birth cohort, which consists of two different parts: very slow and insignificant growth of mortality at the beginning and very rapid growth after age 113 years. This pattern may suggest a possibility of accelerating trend in mortality for more recent birth cohort of supercentenarians, although presented data are not a sufficient proof for the fixed limit to human life span. At least we observe very rapid Gompertz-like growth of mortality after age 113 years. Note that the Gompertz model itself does not suggest an existence of fixed deterministic life-span limit.

Figure 3.

Mortality of later (1885–1898) birth cohort as a function of age. Hazard rates are estimated for semiannual age units. Lines correspond to linear fit of the logarithm of hazard rate before and after 113 years of age. On the basis of GRG data.

Discussion

We tested two predictions of the biological limit to human life-span hypothesis: asymptotic deceleration of historical growth of maximum age at death across birth cohorts (4) and accelerating age-specific mortality pattern at extreme ages (3) in the case of limit existence. We found that rapid growth of MRAD was replaced by negligible growth for more recent cohorts born in 1879 and later. It is important to emphasize that this observation was found using data containing only extinct birth cohorts without truncation bias. Earlier study suggesting the evidence of human life-span limit analyzed MRAD trend by calendar year of death with IDL data and found increasing trend for MRAD until 2000 and declining trend thereafter (1). This declining trend is most likely a result of data contamination by non-extinct birth cohorts and this problem of data truncation bias was already identified in the article rebuttal (20). In our study, we analyzed MRAD trend in extinct birth cohorts that produce unbiased trend and found out that MRAD growth decelerates as if approaching the biological limit to human longevity. Recent study of Japanese centenarians is consistent with our findings: it was found that MRAD of Japanese centenarians ceased to grow for cohorts born after 1894 (31).

Study of mortality trajectories at extreme old ages revealed that mortality continues to grow after age 113 years in the case of more recent birth cohort in contrast to earlier birth cohort demonstrating mortality plateau. We found that the slope parameter of Gompertz function after age 113 years is steeper than the slope parameter estimated for earlier ages (3). This finding does not agree with the idea of mortality plateau at extreme old ages (2,3).

We also found that mortality of earlier cohort of supercentenarians demonstrates a constant mortality. This is in line with earlier studies, which found no increase in mortality with age after 110 years (17,30). On the other hand, Gampe (17) reported that mortality is flat for both earlier (<1885) and later (1885+) birth cohorts. However, the author’s conclusion about the shape of mortality trajectories was based on visual inspection of mortality curves rather than quantitative measures. Study of Japanese centenarians found that the growth of mortality from age 100 to 110 years is observed for more recent birth cohorts in contrast to earlier birth cohorts (31). Similar observation of Gompertz-like trajectories for later birth cohorts compared with mortality deceleration pattern for earlier birth cohorts was also reported for the U.S. data (9,24). One possible explanation for this observation is low quality of age reporting in earlier birth cohorts resulting in mortality underestimation (12,32). Another explanation of steeper mortality in more recent birth cohorts is genuine more rapid mortality growth with age in later birth cohorts as we observed in the case of supercentenarians whose age is carefully validated.

For a long time, the idea of fixed limit to human life span was not particularly popular among biodemographers and some gerontologists. After the first study testing the limit to life-span hypothesis (3), more data were accumulated that showed mortality deceleration at advanced ages and hence no indication of possible fixed limit to life span (6,7). In addition to that, studies of trends in maximum life span demonstrated continuous growth of longevity records both over time and by birth cohort, so that the idea of fixed limit to human life span was generally discredited (4,5,33). Some researchers, however, considered possibility of limit to life span on the basis of physiological constraints and warned against extrapolation approaches in predicting the future of human longevity (34–36). Others attempted to determine the limit to human life span using theoretical models of aging and longevity (37,38).

Study by Finch and Pike is of particular interest here (37). These researchers did not suggest that the fixed limit to life span really exists but rather made an attempt to estimate the maximum age in a finite population dying out according to the Gompertz law. According to their calculations, the maximum life span is equal to 117 years for population size of 1 billion (37). Further calculations for 10 billion population resulted in maximum life span estimation of 120 years for women and 113 years for men (39). These estimates are in agreement with existing longevity records if we exclude one outlier (Jeanne Calment). Estimations by Finch and Pike are of particular interest in view of the Gompertz-like mortality observed now for more recent birth cohort after age 113 years. If mortality grows according to the Gompertz law then longevity in a finite population still would be capped, although the Gompertz distribution has no theoretical fixed upper limit for maximum life span. For example, it was estimated that survival beyond age 120 years is not plausible if mortality grows according to the Gompertz law (40,41). However, it was later pointed out that maximum age at death may be subject to stochastic variation and that the longevity record of Jeanne Calment (122 years) is “indeed plausible” (42).

Many gerontologists became now more conservative regarding the future growth of longevity citing environmental problems, climate change, social inequality, and evolutionary reasoning (18,43,44). Our results confirm that further growth of maximum life span for humans becomes an increasingly difficult task. Still, there are reasons for cautious optimism here. Systematic analysis of human mortality throughout the 20th century revealed that, once a particular cause of death is accounted for, there is a proportional increase in both median age of death and maximum life span (45). So the authors of this study believe that application of aging-focused interventions could result in a continued increase not only in the median, but in maximal life span in humans as well. Further research is needed to overcome obvious limitations of our study by addressing remaining concerns about data quality and representativeness, as well as increasing sample sizes. Still, the data used in our study are the best available data so far, and their analysis suggests that there may be a provisional limit to human life in our current state of biomedical knowledge.

Conclusion

We applied two methods of testing the limit to human life-span hypothesis: an analysis of historical trends in maximum life span across birth cohorts and a study of the shape of age-specific mortality trajectories after age 110 years. We found that growing trend of longevity records across subsequent birth cohorts is followed by negligible increase of the MRAD for more recent cohorts born after 1879. In addition to that, mortality of supercentenarians born after 1884 increases after age 113 years in contrast to constant mortality observed for earlier birth cohorts. Moreover, mortality of 1885+ cohort of supercentenarians demonstrates very steep mortality increase for ages older than 113 years. Thus, both methods point to the changes in mortality patterns at extreme old ages, which limit further rapid growth of maximum life span in more recent birth cohorts. Despite these findings suggesting possible provisional limits to human longevity, there is still no conclusive evidence for inevitable fixed biological limit to human life span.

Funding

This work was supported by the National Institute on Aging at the National Institutes of Health under Award Number R21AG054849 (to N.G.). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Conflict of Interest

None declared.