Summary
When individuals learn from observing the behavior of others, they deploy at least two distinct strategies. Choice imitation involves repeating other agents’ previous actions, while emulation proceeds from inferring their goals and intentions. Despite the prevalence of observational learning in humans and other social animals, a fundamental question remains unaddressed: how does the brain decide which strategy to use in a given situation? In two fMRI studies (the second a pre-registered replication of the first), we identify a neuro-computational mechanism underlying arbitration between choice imitation and goal emulation. Computational modelling, combined with a behavioral task that dissociated the two strategies, revealed that control over behavior was adaptively and dynamically weighted toward the most reliable strategy. Emulation reliability, the model’s arbitration signal, was represented in the ventrolateral prefrontal cortex, temporoparietal junction and rostral cingulate cortex. Our replicated findings illuminate the computations by which the brain decides to imitate or emulate others.
Keywords: observational learning, decision-making, arbitration, social neuroscience, computational model, imitation, emulation, fMRI, replication
eTOC Blurb
Charpentier et al. show in two independent studies that people learn from observing others by flexibly deploying one of two strategies, imitation or emulation, depending on the conditions of the environment. By tracking changes in the reliability of emulation, fronto-parietal brain regions assign control to the most reliable strategy.
Introduction
Whether learning a new skill by observing an expert perform it, learning to seek rewards and avoid punishments, or making complex strategic decisions, observational learning (OL) is prevalent in our daily lives; and allows individuals to learn the consequences of actions without being exposed to the risks from directly sampling them.
Two distinct strategies for reward OL have been proposed (Heyes and Saggerson, 2002; Huang et al., 2006; Whiten et al., 2009): imitation and emulation. In imitation, individuals choose actions most frequently selected by another agent in the past; and in emulation, individuals infer the other agent’s goals, beliefs, intentions or hidden mental states (Charpentier and O’Doherty, 2018; Dunne and O’Doherty, 2013). Notably, the term “imitation” refers to a broad range of cognitive and behavioral phenomena: from wholesale mimicking of motor movements (Carcea and Froemke, 2019) to the more abstract process of copying another agent’s choices (Burke et al., 2010; Najar et al., 2019; Suzuki et al., 2012). Here we focus on the latter, “choice” imitation, in line with the economics, decision neuroscience and reinforcement learning literature (Abbeel and Ng, 2004; Eyster and Rabin, 2014; Le et al., 2018; Mossel et al., 2018). Emulation can also describe an array of cognitive processes (Huang and Charman, 2005). Here we focus on inferences about another agent’s goal: “goal” emulation.
Computationally, choice imitation can be described in a reinforcement learning (RL) framework: the other agent’s chosen action is reinforced by an action prediction error (APE) – the difference between the other agent’s selected action and how expected this action was. APEs have been reported in dorsomedial and dorsolateral prefrontal cortex (dmPFC, dlPFC) and inferior parietal cortex (Burke et al., 2010; Suzuki et al., 2012). Although choice imitation is agnostic about specific motoric components of actions, the mirror neuron system – active when an action is observed and performed (Catmur et al., 2009; Cook et al., 2014; Lametti and Watkins, 2016; Rizzolatti and Craighero, 2004; Rizzolatti et al., 1996) – has been implicated. In contrast, goal emulation consists of a more complex and flexible inference process. Several computational accounts have been provided (Collette et al., 2017; Devaine et al., 2014; Diaconescu et al., 2014), often as a form of Bayesian inference: prior beliefs about the other agents are combined with the evidence received from observation to produce posterior updated beliefs. These inference processes recruit regions of the mentalizing network (Frith and Frith, 2006), specifically dmPFC, temporoparietal junction (TPJ) and posterior superior temporal sulcus (pSTS) (Behrens et al., 2008; Boorman et al., 2013; Collette et al., 2017; Hampton et al., 2008; Hill et al., 2017; Yoshida et al., 2010).
If these two distinct OL strategies exist alongside each other, fundamental questions remain: how does the brain decide which strategy should be deployed in a given situation, and under what conditions does one or other strategy guide behavior? We hypothesized that the brain deploys an arbitration process whereby the influence of these strategies is dynamically modulated depending on which strategy is most suitable to guide behavior at a given time. To understand this process, we developed a computational model of arbitration between choice imitation and goal emulation, and tested it with human behavioral and neural data.
In experiential learning, behavior is controlled by multiple competing systems, such as habits versus goal-directed actions (Balleine and Dickinson, 1998; Balleine and O’Doherty, 2010) or model-free (MF) versus model-based (MB) learning (Daw et al., 2011; Glascher et al., 2010). To ensure that the control of these systems over behavior is adaptive, an arbitration mechanism has been proposed (Daw et al., 2005). In a specific implementation (Lee et al., 2014), the reliability of each system’s predictions is dynamically computed by leveraging their respective prediction errors. In the brain, the ventrolateral prefrontal cortex (vlPFC) and frontopolar cortex (FPC) were found to encode the output of a comparison between the reliability of the two systems. This suggests that the brain allocates control over behavior to the most reliable experiential learning strategy at a given time point.
Whether a similar arbitration mechanism exists in OL remains unknown. Using similar principles to those found in the experiential domain, we hypothesized that the allocation of control in OL between goal emulation and choice imitation is related to the relative uncertainty in each system’s predictions. Concretely, choice imitation tracks predictions about actions selected by an observed agent. Thus, if the agent’s choices become more stochastic, uncertainty in the imitation model predictions should increase, resulting in emulation being favored. Conversely, if choices based on goal inference become more uncertain (and more difficult), the predictions of the emulation system should also become more uncertain (and less reliable), thereby favoring the imitation system.
To test this hypothesis, we designed a novel OL task (Fig. 1), in which changing experimental conditions allowed us to distinguish engagement of the two strategies, as prescribed by our model. Two groups of 30 participants, referred to as Study 1 (initial sample) and Study 2 (replication sample) completed the task while undergoing fMRI. The methods, computational modelling, behavioral analyses, fMRI pipeline, and results of Study 1 were pre-registered before Study 2 data collection. This allowed us to reduce both modeler and experimenter degrees of freedom markedly, thus reducing the risk of overfitting and improving generalizability and reproducibility.
Figure 1. Task design.
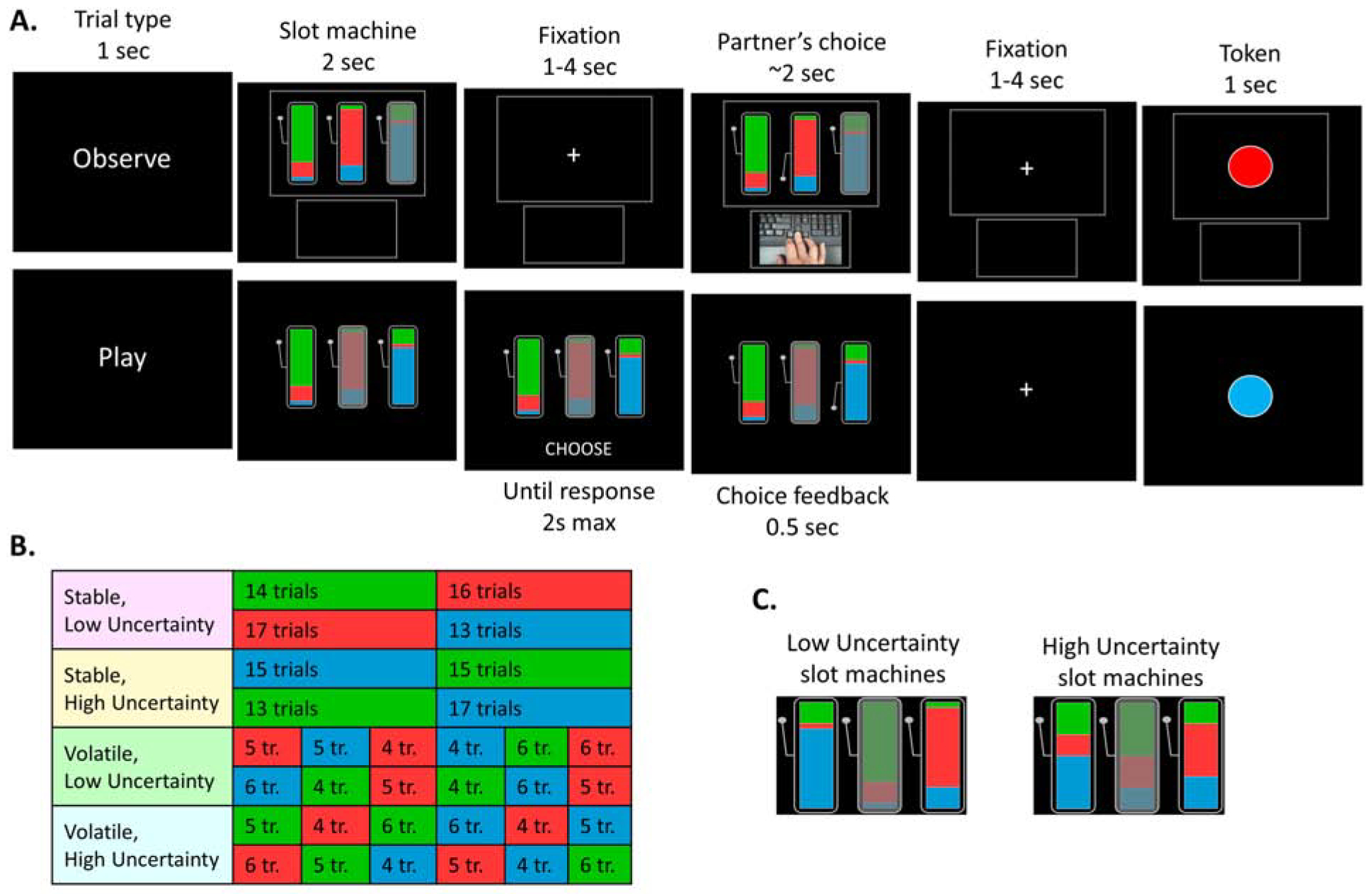
(A) In observe trials (top), participants see the agent’s slot machine choices. The colors on each machine indicate the relative probability that a particular token will be delivered to the agent if that machine is chosen. One of the three slot machines is unavailable (greyed out) on each trial but the associated token probabilities remain visible. Participants know that one token is valuable (but not which one) and that the agent has full information and is performing optimally. The agent’s choice is indicated by a video and by the arm of the chosen slot machine being depressed. (B) The task contained 8 blocks of 30 trials, in a 2 (stable/volatile) by 2 (low/high uncertainty) design. The background color in the table depicts which token (green, red or blue) is currently valuable (unknown to the participant). Block order was counterbalanced across subjects. Stable blocks had one switch in the valuable token occurred; volatile blocks had 5 switches. (C) In low uncertainty blocks, the token probability distribution was [0.75, 0.2, 0.05], making slot machine value computation less difficult than for high uncertainty slot machines, for which the distribution was [0.5, 0.3, 0.2].
We predicted that participants’ behavior would be best explained by a mix of goal emulation and choice imitation, and that engagement of one strategy over the other would depend on volatility and uncertainty. We also hypothesized distinct neural signatures for the two strategies. Choice imitation was expected to recruit fronto-parietal regions of the mirror-neuron system, namely pre-motor cortex, inferior parietal cortex, and dlPFC (Catmur et al., 2009; Cook et al., 2014; Gazzola and Keysers, 2009; Rizzolatti and Craighero, 2004); and emulation was predicted to recruit regions of the mentalizing system, involved in goal inference (Fletcher et al., 1995; Frith and Frith, 2006; Van Overwalle and Baetens, 2009). Finally, we hypothesized overlapping neural arbitration mechanisms to those in the experiential domain: vlPFC and FPC driving trial-by-trial variations in the arbitration controller (Lee et al., 2014), with possible involvement of regions of the social brain, such as the TPJ.
Results
In the task (Fig. 1A), participants see another agent choose between slot machines. The color proportions on each machine explicitly represent the probability of obtaining one of three tokens (red, green, blue) if that machine is chosen. Participants were instructed that only one of the tokens is valuable at each moment in time and that the valuable token switches many times throughout the task, but were not told which token is valuable nor when the switches occurred. On 2/3 of trials (‘observe’ trials), they observed another agent play through video, knew that this other agent had full information about the valuable token and was performing optimally. On 1/3 of trials (‘play’ trials), participants played for themselves. On each trial, one slot machine was unavailable and could not be chosen. Crucially, participants can learn by inferring which token is currently valuable and compute the relative values of slot machines based on the observable color distributions (goal emulation). Alternatively, they can simply imitate the agent’s prior behavior by choosing the action most frequently selected by the agent on recent trials (choice imitation). By varying the position of the unavailable machine across trials, we could separate the two strategies.
Importantly, the outcome monetary value was not revealed. While participants observed the outcome tokens, they could not tell their value just from observing their color. This ensured that they had to utilize inference within their emulation system to work this out, and that they could not rely on vicarious reward-learning, a third potential OL strategy in which one learns from another agent’s rewards as if experiencing them directly (Burke et al., 2010; Charpentier and O’Doherty, 2018; Cooper et al., 2012; Dunne and O’Doherty, 2013).
Study 1
Behavioral signatures of imitation and emulation
A logistic regression was run to test for the two strategies. Choice of left versus right slot machine on each ‘play’ trial was predicted by an action learning regressor (signature of imitation: past left versus right actions performed by the partner) and a token learning regressor (signature of emulation: probability to choose left over right slot machine given inferred token information; see Methods – Behavioral analysis for details). Both regressors significantly predicted choice (action learning β=0.865 ±0.80 (SD), T29=5.94; token learning β=1.174 ±1.00, T29=6.42; all Ps<0.0001; Fig. 2A), suggesting that behavior on the task is a combination of the two strategies.
Figure 2. Behavioral signatures of OL strategies.
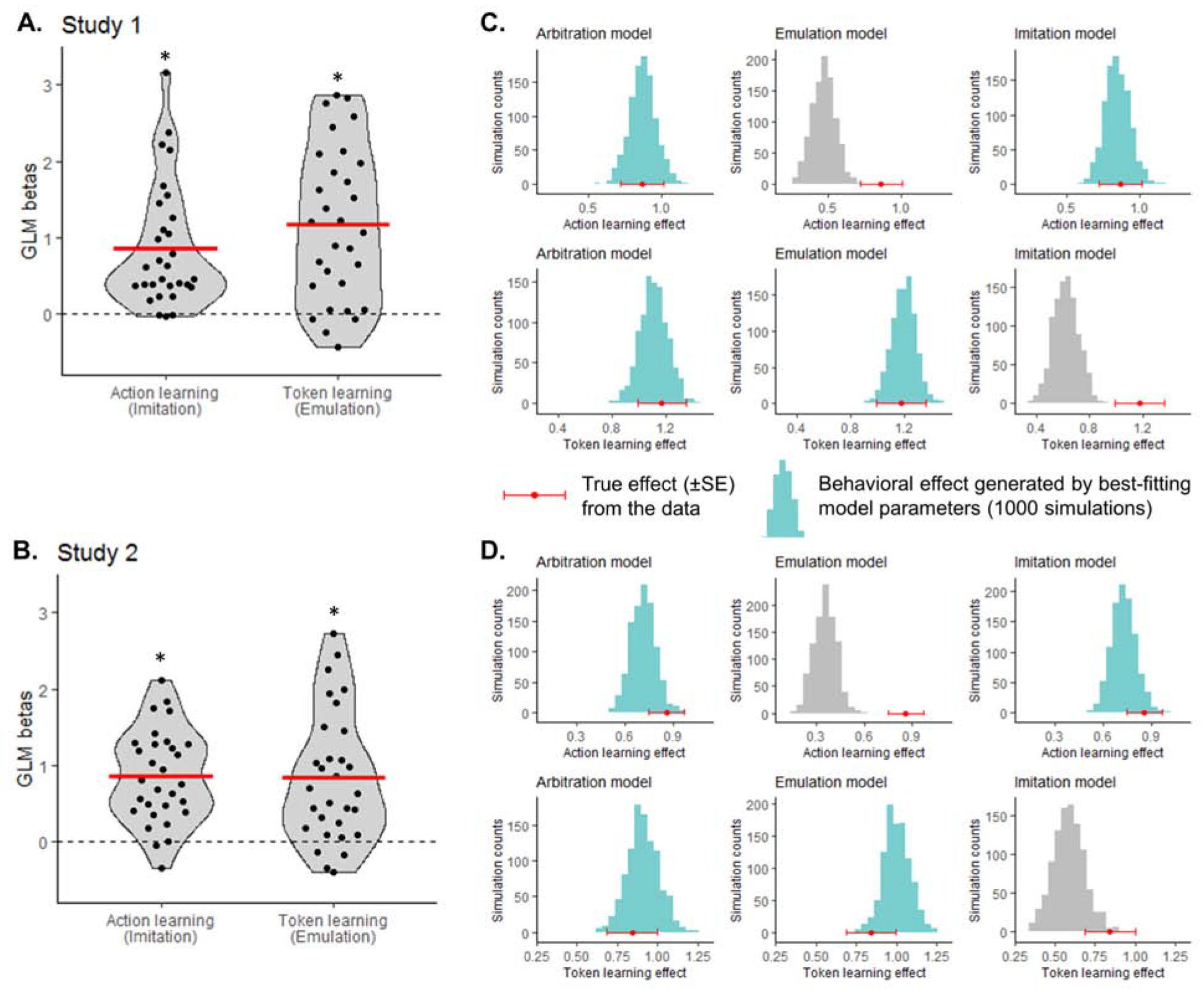
(A–B) Choice predicted by regressors capturing past actions and of past token inference. In Study 1 (A) and Study 2 (B), both effects were significant, suggesting hybrid behavior between imitation and emulation. Dots represent individual subjects; the red bar represents the mean β value. T-test: * P<0.0001. (C–D) Test of how well the winning model (Arbitration Model 7), as well as simple emulation (Model 2) and choice imitation (Model 3), capture the action learning (top) and token learning effects (bottom). Red data points depict the true effect from the data; histograms show the distribution of recovered effects from the model-generated data. Effects well recovered are shown in light blue; effects not well recovered in grey. In Study 1 (C) and Study 2 (D), the arbitration model (left) effectively captured both learning effects. Data generated by the emulation model (middle) only captured token-based learning; data generated by the imitation model (right) only captured action-based learning.
Computational model of arbitration between choice imitation and goal emulation
To test for an arbitration mechanism, we compared 9 computational models, split into 5 classes (see Methods – Computational models of behavior for details). Emulation-only models (Models 1–2) rely on multiplicative inference over token values. Imitation-only models (Models 3–4) use RL to learn about the other agent’s past actions. Emulation RL models (Models 5–6) implement an RL mechanism rather than multiplicative inference. In arbitration models (Models 7–8), the likelihood of relying on one strategy over the other varies as a function of their relative reliabilities. An outcome RL model (Model 9) tests whether participants mistakenly learn from the token presented at the end of the trial. Model comparison was implemented via between subjects out-of-sample predictive accuracy and group-level integrated Bayesian Information Criteria (iBIC) (Huys et al., 2011; Iigaya et al., 2016). Arbitration models were found to perform best (Table 1), with Model 7 exhibiting the highest out-of-sample accuracy and lowest iBIC, suggesting that an arbitration mechanism between imitation and emulation explained behavior better than each strategy individually. Finally, we tested whether the arbitration model could reliably recover behavioral signatures of imitation and emulation (Fig. 2A). To do so, we generated behavioral data for each subject using the winning model (Model 7), emulation Model 2 and imitation Model 3. Running the same logistic regression on the model-generated data, we found that the arbitration model reliably predicted both learning effects (Fig. 2C left). In contrast, the emulation model only predicted token learning (Fig. 2C middle) and the imitation model only predicted action learning (Fig. 2C right). Showing that the winning model is able to generate the behavioral effects of interest (Palminteri et al., 2017) confirms its validity and specificity.
Table 1. Computational model comparison.
Out-of-sample (OOS) accuracy was calculated in a 5-fold cross-validation analysis by estimating mean parameters in 4 groups of 6 subjects and calculating the accuracy of predicted behavior in the remaining group. Group-level integrated Bayesian Information Criteria (iBIC) values were calculated following hierarchical model fitting. See Methods for details. Numbers in bold: winning model out of preregistered models (1–9). Numbers in bold and italics: winning model across all 10 models.
| Class | Model # | Parameters | OOS accuracy (%) | Group-level iBIC | |||
|---|---|---|---|---|---|---|---|
| Study 1 | Study 2 | Study 1 | Study 2 | ||||
| Preregistered models | Emulation inference | 1 | β | 67.8 | 66.1 | 2416 | 2458 |
| 2 | β, λ | 68.3 | 67.9 | 2384 | 2368 | ||
| Imitation RL | 3 | β, α | 71.3 | 71.6 | 2448 | 2455 | |
| 4 | β, η, α0 | 70.5 | 69.8 | 2493 | 2472 | ||
| Emulation RL | 5 | β, α | 67.1 | 67.4 | 2610 | 2537 | |
| 6 | β, η, α0 | 65.4 | 64.8 | 2724 | 2597 | ||
| Arbitration | 7 | βem, βim, δ, α | 76.5 | 74.9 | 2296 | 2321 | |
| 8 | βem, βim, δ, α, λ | 73.9 | 72.1 | 2367 | 2291 | ||
| Outcome RL | 9 | β, α | 58.7 | 58.5 | 3046 | 3052 | |
| Exploratory model | Arbitration with 1-step IM | 10 | βem, βim, δ | 76.5 | 76.2 | 2236 | 2241 |
Arbitration is influenced by uncertainty and volatility
Two factors were manipulated: volatility (frequency of switches in valuable token; Fig. 1B) and uncertainty (token color distribution associated with the slot machines; Fig. 1C). In volatile blocks, the partner’s actions become less consistent, predominantly taxing choice imitation and indirectly favoring emulation. Uncertainty in the token color distribution makes it more difficult to infer the best decision given the valuable token, while having no effect on the consistency of the partner’s actions. This should tax the emulation system and indirectly favor choice imitation. To test this, we extracted the model’s arbitration weight ω(t) values for each subject and each condition, representing the probability of emulation (over imitation). These are computed as a softmax of the reliability difference between the two strategies, added to a bias parameter δ (Eq. 14), characterizing each individual’s propensity to emulate (δ>0) or imitate (δ<0). As predicted, the arbitration weight was higher in volatile, low uncertainty (VL) trials (ω=0.604 ±0.26) than on stable, high uncertainty (SH) trials (ω=0.474 ±0.25; T29=15.22, P<0.0001; Fig. 3A). Across all 4 conditions (2-by-2 repeated-measures ANOVA), there was a main effect of volatility (F1,29=61.2, P<0.0001) and a main effect of uncertainty (F1,29=267.3, P<0.0001), suggesting a moderating effect of both manipulations. Second, we compared the performance of imitation Model 3 and emulation Model 2, by calculating the mean likelihood (LL) of each model separately for each condition (Fig. 3C). Participants favor emulation when uncertainty in the token color distribution is low (emulation LL – imitation LL for SL trials = 0.051 ±0.047, T29=5.88; for VL trials = 0.059 ±0.061, T29=5.27; all Ps<0.0001). Choice imitation is favored when the partner’s actions are stable and uncertainty in the token color distribution is high (emulation LL - imitation LL for SL trials = −0.053 ±0.053, T29=−5.49, P<0.0001). There was no difference between strategies in volatile, high uncertainty trials (LL difference = 0.007 ±0.048, T29=0.74, P=0.46).
Figure 3. Modulation of arbitration by volatility and uncertainty.
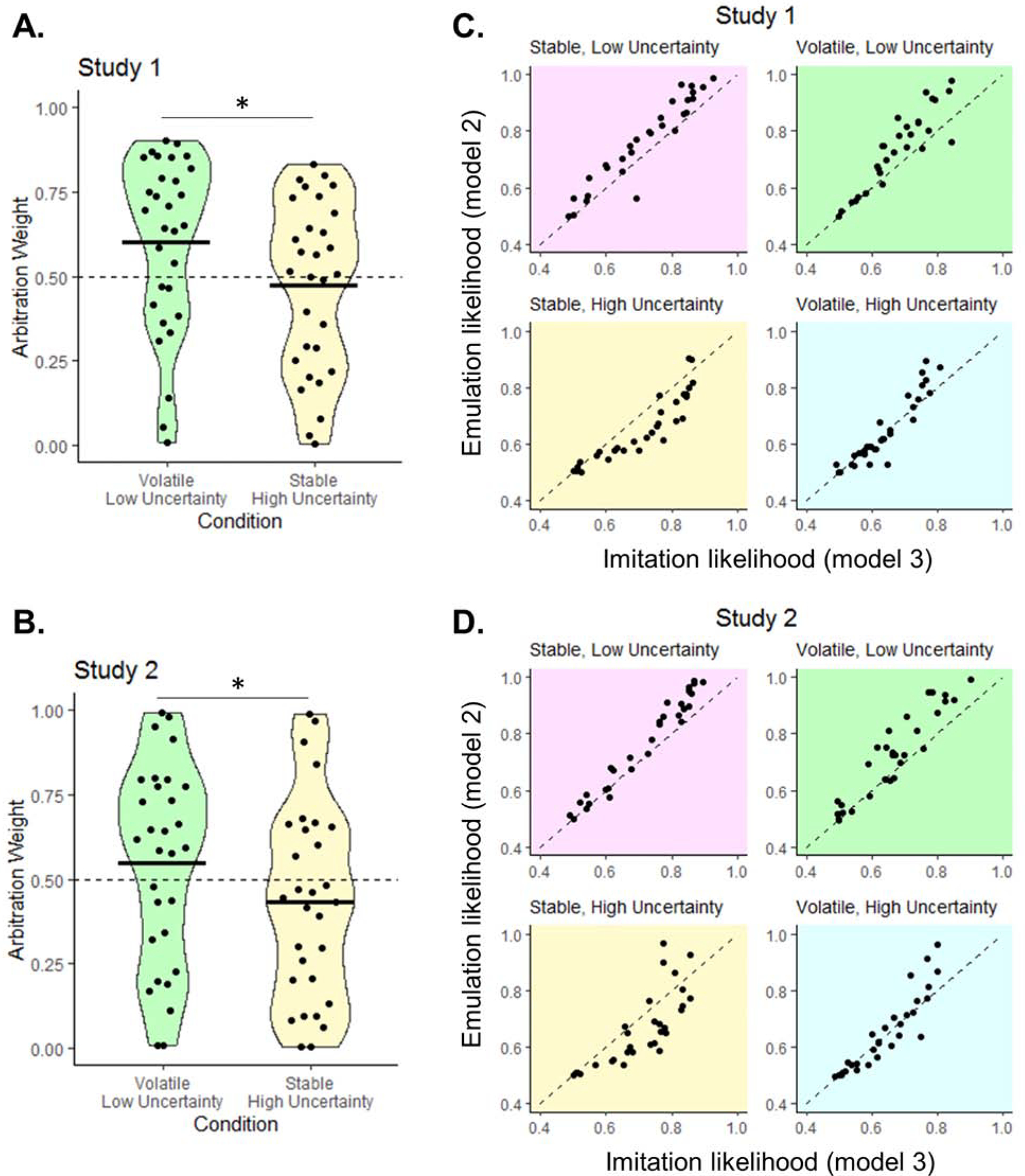
(A–B) Arbitration weight values ω (probability of relying on emulation over imitation), were extracted from the winning arbitration model for each trial and averaged for each subject and condition. The plots show, for Study 1 (A) and Study 2 (B), mean and distribution of ω for two conditions of interest: volatile/low uncertainty trials (green), and stable/high uncertainty trials (yellow). Dots represent individual subjects; the black bar the mean. T-test: *P<0.0001. (C-D) Mean per-trial emulation (Model 2) and imitation (Model 3) likelihood, plotted against each other separately for the 4 task conditions. In both Study 1 (C) and Study 2 (D), most participants favor emulation (dots above the diagonal) when uncertainty is low (green & pink plots) but favor choice imitation (dots below the diagonal) when the environment is stable and uncertainty is high (yellow plot).
fMRI analyses of Study 1
Two fMRI models were used for Study 1 fMRI analysis: SPM GLM1 and GLM2 (see Methods – fMRI data modelling - preregistered). We tested for emulation-related (emulation reliability, update of token values, entropy over token values), imitation-related (imitation reliability, imitation action value difference), and arbitration-related signals (emulation – imitation reliability difference, chosen action value). A region of interest (ROI) analysis was performed (see Methods – Regions of interest) to generate hypotheses for Study 2 (Table S1). Whole-brain group-level T-maps were also evaluated, and uploaded on NeuroVault, before Study 2 data collection. Significant activation clusters for Study 1 (Table S2), were identified and saved as functional regions of interest for Study 2. Results from both analyses are presented in Fig. 4 (arbitration signals), Fig. 5 (emulation and imitation signals).
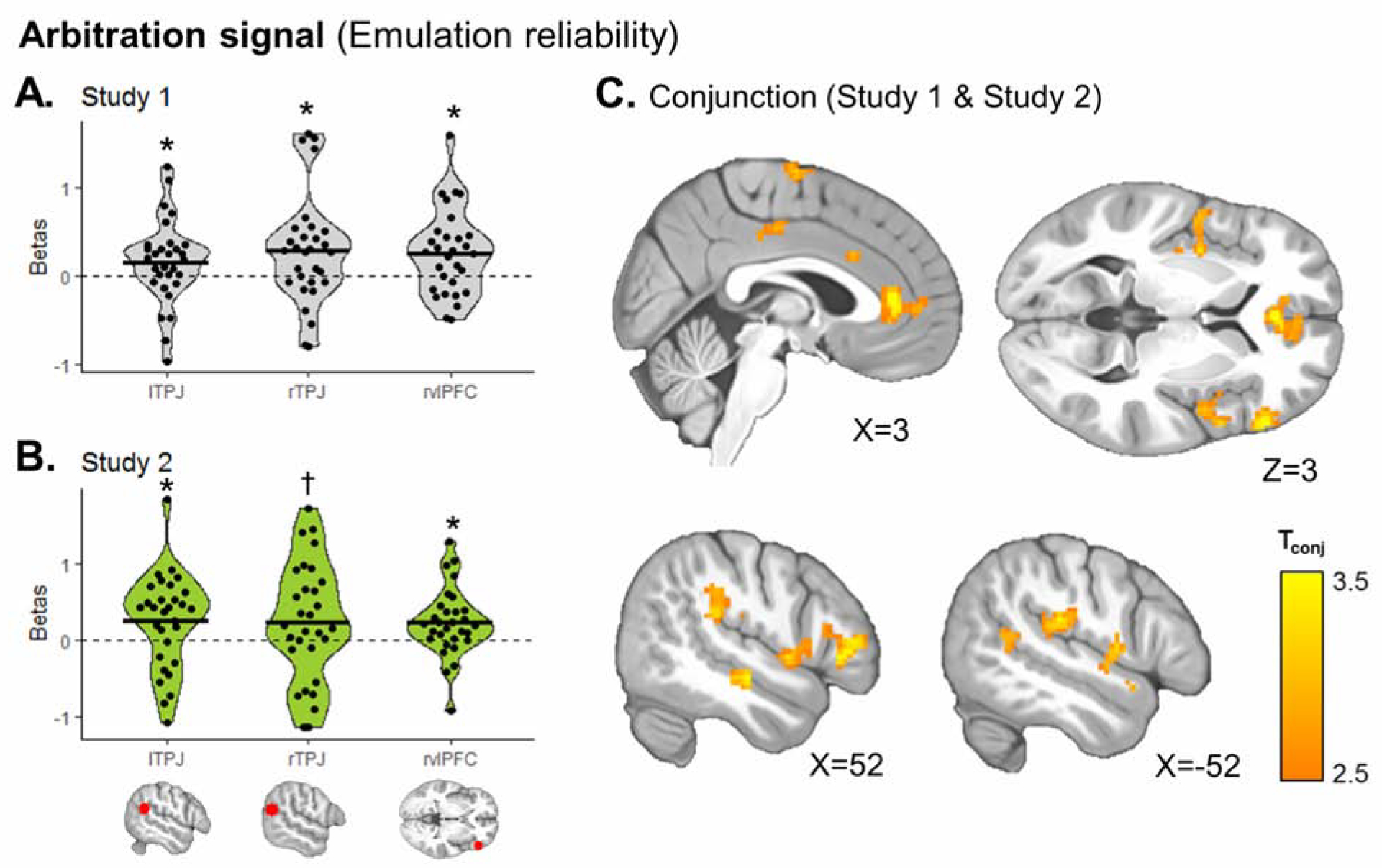
Figure 4. Arbitration signals, pre-registered analyses.
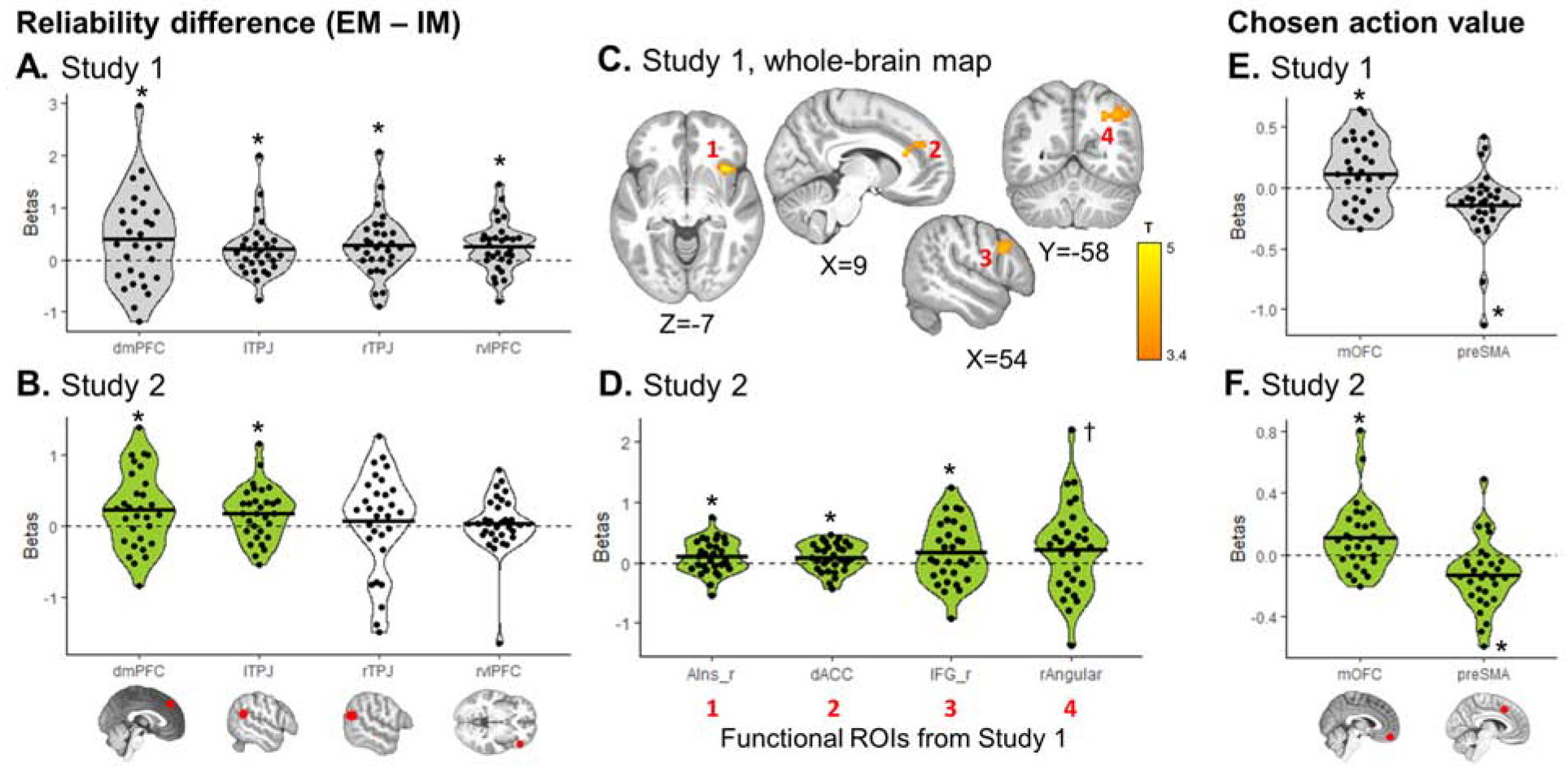
Reliability difference (A–D) and chosen action value (E–F) signals were extracted from each pre-registered ROI. (A, E) Regions with significant signals in Study 1 (grey) were selected as hypotheses for Study 2. (C) Whole-brain map for the reliability difference signal was also examined in Study 1, with a cluster-forming threshold of P<0.001 uncorrected, followed by cluster-level FWE correction at P<0.05. Significant clusters were saved as functional ROIs to be examined in Study 2. No cluster survived correction for chosen value. (B, D, F) Green plots represent significant effects in Study 2, confirming a priori hypothesis from Study 1. White plots represent hypotheses not confirmed in Study 2. Dots represent individual subjects; the black bar the mean beta estimate. T-tests: * P<0.05, † P=0.052.
Figure 5. Emulation and imitation signals, pre-registered analyses.
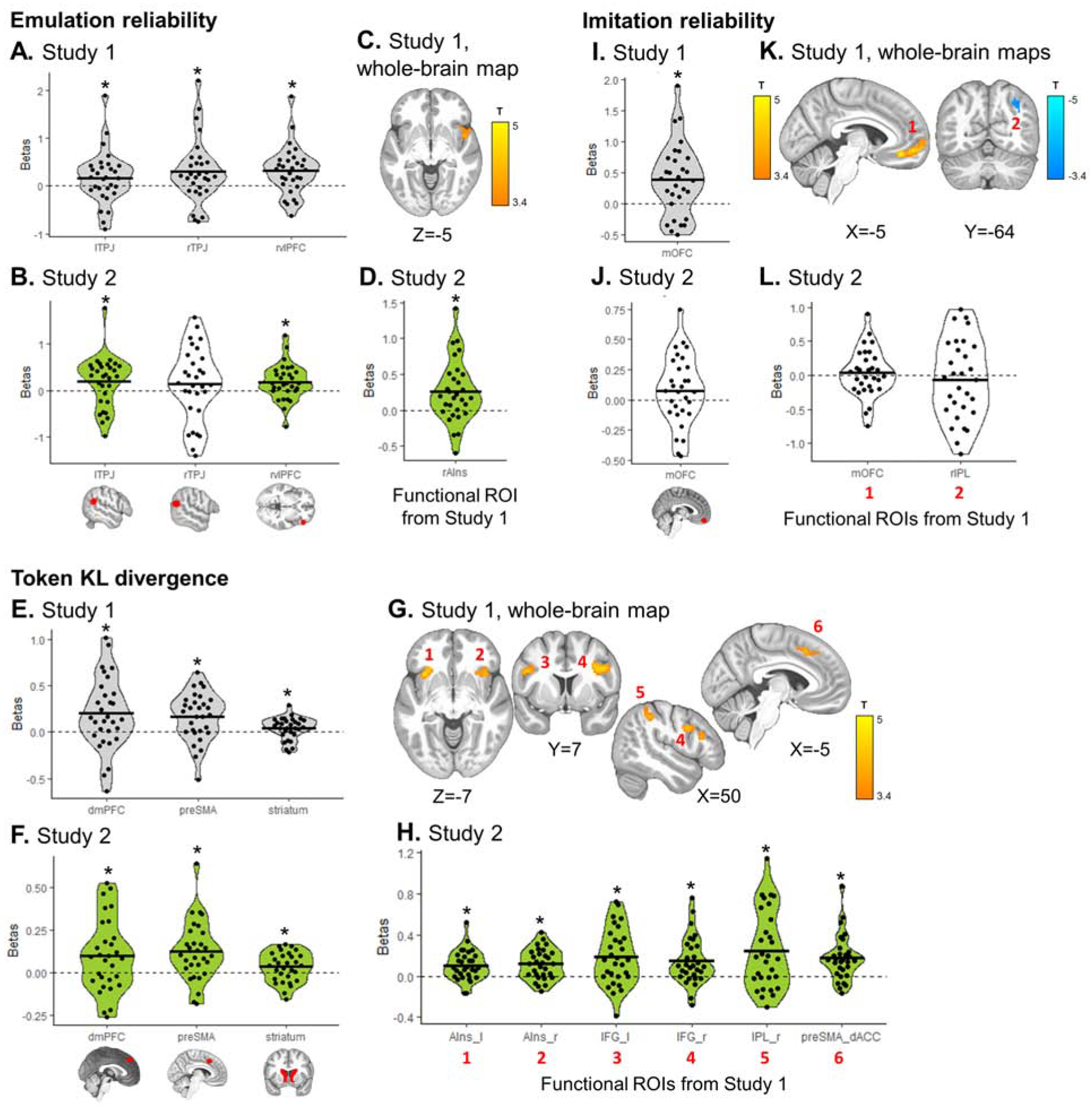
Emulation reliability (A–D), update in token values (E–H), and choice imitation reliability (I–L) signals extracted from each pre-registered ROI. (A, E, I) Regions with significant signals in Study 1 (grey) were selected as hypotheses and a priori ROIs for Study 2. (C, G, K) Whole-brain maps were examined in Study 1, with a cluster-forming threshold of P<0.001 uncorrected, followed by cluster-level FWE correction at P<0.05. Significant clusters were saved as functional ROIs to be examined in Study 2. (B, D, F, H, J, L) Green plots represent significant effects in Study 2, confirming the a priori hypothesis from Study 1. White plots represent hypotheses that were not confirmed in Study 2. Dots represent individual subjects; the black bar the mean beta estimate. T-tests: * P<0.05.
The difference in reliability between choice imitation and goal emulation, predictive of trial-by-trial arbitration, was tracked in four ROIs (Fig. 4A): dmPFC (β=0.383 ±0.89, T29= 2.37, P=0.012), bilateral TPJ (left: β=0.201 ±0.53, T29=2.10, P=0.022; right: β=0.277 ±0.59, T29=2.56, P=0.008) and right vlPFC (β=0.250 ±0.48, T29=2.86, P=0.004). Using whole-brain group analyses, four significant clusters were found (all PFWE<0.05; Fig. 4C): right anterior insula, dorsal ACC, (partially overlapping with the dmPFC ROI), right IFG, and right angular gyrus (Table S2). At the time of choice, the chosen slot machine expected value was coded positively in the mOFC (β=0.110 ±0.28, T29=2.16, P=0.019) and negatively in the pre-supplementary motor area (preSMA; β=−0.144 ±0.29, T29=−2.74, P=0.005; Fig. 4E). There was no cluster surviving correction for chosen action value in the whole-brain analysis.
Emulation reliability was represented in bilateral TPJ (left: β=0.172 ±0.55, T29=1.72, P=0.048; right: β=0.299 ±0.66, T29=2.46, P=0.010) and right vlPFC (β=0.320 ±0.50, T29=3.50, P=0.0008; Fig. 5A). In the whole-brain analysis, an additional cluster was identified encoding emulation reliability in the right anterior insula (Fig. 5C; Table S2). The KL divergence between prior and posterior token values, a key signature of emulation learning, was found during observation of the partner’s action in three regions (Fig. 5E): dmPFC (β=0.201 ±0.39, T29=2.84, P=0.004), preSMA (β=0.170 ±0.26, T29=3.62, P=0.0006) and dorsal striatum (β=0.043 ±0.12, T29=1.99, P=0.028). Whole-brain analyses revealed KL divergence of token values in the bilateral anterior insula, bilateral IFG, right supramarginal and inferior parietal cortex and preSMA extending into the dorsal ACC (Fig. 5G; Table S2). Finally, imitation reliability was tracked in the mOFC ROI (β=0.387 ±0.58, T29=3.67, P=0.0005, Fig. 5I) and in a significant cluster spanning mOFC and vmPFC (Fig. 5K; Table S2). Imitation reliability negatively correlated with a right inferior parietal cluster (Fig. 5K; Table S2).
For completeness, all pre-registered ROI results are reported in Table S1 and Figure S1, and whole-brain analyses in Table S2. The statistical significance of all ROI results for both Study 1 and Study 2 remained unchanged when using non-parametric permutation tests. Pre-registration of computational models, model-fitting procedures, fMRI pre-processing pipeline and fMRI statistical models was conducted in advance of Study 2 data collection (https://osf.io/37xyq). We focused specifically on testing the replicability of Study 1 findings in both the behavioral and neuroimaging data.
Study 2
Replication of behavioral and computational modelling results
Logistic regression testing for token learning and action learning strategies yielded the same results as in Study 1. Both regressors were found to significantly predict choice (action learning β=0.857 ±0.60, T29=7.78; token learning β=0.843 ±0.85, T29=5.42; both Ps<0.0001; Fig. 2B).
Computational modelling revealed that the arbitration Model 7 also had the highest out-of-sample accuracy of all pre-registered models (Table 1). While Model 7 had the lowest iBIC in Study 1, Model 8 had the lowest iBIC in Study 2. Models 7 and 8 are very similar; the only difference is the presence of a free parameter λ in Model 8, which represents trust in current token values and captures a tendency to overestimate volatility in the environment (see Methods). Given that Model 7 is a more parsimonious model, we kept it as our winning model in both studies to maintain consistency. Data generated using arbitration Model 7 in Study 2 can, similarly to Study 1, reliably predict both action learning and token learning effects (Fig. 2D). We also find a very similar pattern of results when using arbitration Model 8 to generate data (Fig. S2A–B).
Finally, arbitration was influenced by uncertainty and volatility in the same way as in Study 1. Action volatility increased the arbitration weight, while uncertainty in the token color distribution decreased it (high volatility & low uncertainty: ω=0.550 ±0.29; low volatility & high uncertainty: ω=0.434 ±0.29; difference: T29=10.97, P<0.0001; Fig. 3B). Across all 4 conditions, there was a main effect of volatility (F1,29=47.3, P<0.0001) and a main effect of uncertainty (F1,29=124.8, P<0.0001), confirming the combined effect of both manipulations. Emulation was also favored when uncertainty was low, as shown by significantly positive emulation-imitation likelihood difference (SL condition = 0.050 ±0.043, T29=6.31; VL condition = 0.061 ±0.061, T29=5.49; all Ps<0.0001; Fig. 3D). Choice imitation was favored when uncertainty was high and partner’s actions stable, as shown by significantly negative emulation-imitation likelihood difference (mean = −0.045 ±0.081, T29=−3.04, P=0.0025). There was also no difference between imitation and emulation in volatile, high uncertainty trials (mean = 0.009 ±0.059, T29=0.90, P=0.37). These findings confirm that behavior is best explained by an arbitration model in which observers flexibly allocate control between two learning strategies depending on the environment.
Replication of emulation and decision value signals, but not imitation signals
BOLD responses related to emulation were largely replicated in Study 2. Specifically, emulation reliability was significant in two of the three ROIs identified in Study 1 (Fig. 5B) – the left TPJ (β=0.195 ±0.55, T29=1.96, P=0.030) and the right vlPFC (β=0.186 ±0.39, T29=2.62, P=0.0069), but not in the right TPJ (β=0.137 ±0.78, T29=0.96, P=0.17). Emulation reliability was also significant in the right anterior insula functional ROI saved from Study 1’s whole-brain map (Fig. 5D; Table S2). KL divergence over token values was tracked in the same three ROIs (Fig. 5F): dmPFC (β=0.098 ±0.21, T29= 2.52, P=0.0087), preSMA (β=0.123 ±0.17, T29=3.91, P=0.00025) and dorsal striatum (β=0.033 ±0.085, T29=2.15, P=0.020). Examining functional clusters saved from Study 1, all six regions showed significant emulation update signals in Study 2 (Fig. 5H; Table S2): bilateral anterior insula, bilateral IFG, right inferior parietal extending into supramarginal cortex, and preSMA/dorsal ACC. Entropy over token values, at the time of initial slot machine presentation on observe trials, was negatively represented in the mOFC (Study 1: β=−0.080 ±0.25, T29=−1.73, P=0.047; Study 2: β=−0.107 ±0.19, T29=−3.08, P=0.0023; Fig. S1A–B), suggesting the mOFC is more active when token values are more certain.
Decision values signals (expected value of the chosen slot machine on play trials) recruited the same ROIs in Study 2 (Fig. 4F), with positive value coding in mOFC (β=0.109 ±0.22, T29=2.70, P=0.0057) and negative value coding in preSMA (β=−0.135 ±0.22, T29=−3.38, P=0.0011). The reliability difference between the two strategies was found to replicate in two of the four ROIs identified in Study 1 (Fig. 4B) – left TPJ (β=0.182 ±0.38, T29=2.63, P=0.0068) and dmPFC (β=0.228 ±0.54, T29=2.31, P=0.014) – as well as in functional clusters in the dorsal ACC, right anterior insula, IFG and angular gyrus (Fig. 4D; Table S2).
However, when examining whether this signal was a true difference signal, by separately extracting emulation and imitation reliabilities from the ROIs, we did not find evidence for negative tracking of imitation reliability or representation of the two reliability signals in opposite directions in either study (Fig. S3). Instead, reliability difference signals were mainly driven by positive encoding of emulation reliability, suggesting that arbitration in the brain might rely more on emulation reliability than on imitation reliability. In addition, all signals pertaining to choice imitation did not replicate well in Study 2 – imitation reliability (all T29<1.49, all Ps>0.15; Fig. 5J and 5L) and the difference in imitation action values (Fig. S1D; Table S2).
Exploratory analyses: arbitration between emulation and simpler (1-step) choice imitation
Behavioral evidence
The lack of replicability of neural imitation signals led us to revise our model of arbitration and choice imitation. Specifically, our pre-registered imitation model did not account well for the experimental data, necessitating an alternative framework. Similarly, arbitration may rely less on imitation reliability than originally hypothesized and instead be exclusively driven by variations in emulation reliability. We tested these possibilities in a revised model. A simpler form of choice imitation (“1-step imitation”) was defined, such that out of the two available options on a given play trial, the slot machine most recently selected by the partner is chosen. Furthermore, arbitration was assumed to be driven solely by emulation reliability, such that if emulation reliability is high, participants will more likely rely on emulation, whereas if it is low, they will more likely default to choice imitation. While exploratory, we tested our new model on both independent datasets to confirm the robustness of our findings.
In both studies, this new arbitration model (Model 10) performed better than the pre-registered winning model (Model 7), with higher out-of-sample accuracy (Study 1: 76.5%, Study 2: 76.2%) and lower iBIC (Table 1). Given that this simpler imitation strategy does not require a learning rate parameter, Model 10 is more parsimonious than Model 7, in part accounting for lower iBIC values. However, the improved accuracy suggests better out-of-sample generalization in Model 10 than Model 7, possibly because Model 7 was overfitting, or Model 10 offers a more accurate account of the OL mechanism. Using data generated by this more parsimonious model, we recovered both action learning and token learning from a simple logistic regression analysis (Fig. S2C–F), confirming the model validity. This suggests an arbitration process between inferring the valuable token and repeating the partner’s most recent choice, rather than integrating over recent choice history. In both studies, the bias parameter δ was not different from 0 (Study 1: mean δ=0.267 ±1.78, T29=0.82; Study 2: mean δ =0.0004 ±2.15, T29=0.001; P>0.4), suggesting that both strategies were overall equally relied upon.
Neuroimaging evidence
This revised arbitration process predicts trial-by-trial emulation reliability signals in the brain, as a driver of arbitration. Learning signals specific to each strategy should be observed at feedback, when the partner’s action is shown. For goal emulation, update was defined as the KL divergence over token values. For choice imitation, an update should occur when the most recently selected action is available on the current trial, but the partner chooses a different option. To test these predictions, we defined an additional fMRI model, SPM GLM3 (see Methods – fMRI data modelling - exploratory). Using Bayesian model selection (BMS), we confirmed that this new model performed better than the pre-registered model testing for neural signatures of imitation as an RL mechanism (SPM GLM2). In both studies, GLM3 was associated with the highest exceedance probability averaged across all grey matter voxels (Study 1: 0.861; Study 2: 0.946; Fig. S4), and in all but one of the pre-registered ROIs (Table S3). Thus, this new SPM GLM, based on the best performing model of behavior, also explained variations in BOLD signal best.
Variations in emulation reliability, calculated as in the pre-registered models, were represented in the same three ROIs: the right vlPFC (Study 1: β=0.253 ±0.48, T29=2.90, P=0.0035; Study 2: β=0.232 ±0.45, T29=2.84, P=0.0041), the left TPJ (Study 1: β=0.154 ±0.47, T29=1.80, P=0.041; Study 2: β=0.252 ±0.62, T29=2.23, P=0.017), and the right TPJ, albeit only at trend level in Study 2 (Study 1: β=0.284 ±0.62, T29=2.52, P=0.0088; Study 2: β=0.234 ±0.78, T29=1.65, P=0.055; Fig. 6A–B). Exploratory conjunction analysis also revealed significant clusters in the ACC, bilateral insula, and supramarginal gyrus (Fig. 6C; Table S4).
Figure 6. Neural representation of emulation reliability as an arbitration signal.
Trial-by-trial emulation reliability values from the winning arbitration Model 10, were added as a parametric modulator of the BOLD signal during both observe and play trials. (A–B) Using our preregistered ROIs, we found in Study 1 (A) and Study 2 (B) that this signal was represented in bilateral TPJ and right vlPFC. T-tests: * P<0.05, † P=0.055. (C) Exploratory whole-brain conjunction analysis between the second-level T-maps of Study 1 and Study 2 shows additional clusters, including the ACC and bilateral insula (Table S4). Threshold at Pconjunction<0.0001 uncorrected, followed by whole-brain cluster-level FWE correction at P<0.05.
We found neural signatures of emulation update similar to the pre-registered results (Fig. 7A–B), with significant effects in the dmPFC (Study 1: β=0.164 ±0.34, T29=2.63, P=0.0067; Study 2: β=0.112 ±0.23, T29=2.72, P=0.0054), preSMA (Study 1: β=0.135 ±0.24, T29=3.09, P=0.0022; Study 2: β=0.093 ±0.17, T29=2.96, P=0.0031), right TPJ, albeit only at trend in Study 2 (Study 1: β=0.062 ±0.18, T29=1.84, P=0.038; Study 2: β=0.073 ±0.24, T29=1.66, P=0.054), and dorsal striatum (Study 1: β=0.043 ±0.12, T29=2.00, P=0.027; Study 2: β=0.028 ±0.075, T29=2.07, P=0.024). Exploratory conjunction analysis confirmed this, and showed additional clusters in the bilateral insula, inferior frontal gyrus, and other frontoparietal regions (Fig. 7C; Table S4), overlapping with Neurosynth “mentalizing” map (Fig. 7D).
Figure 7. Emulation and imitation update signals during observation.
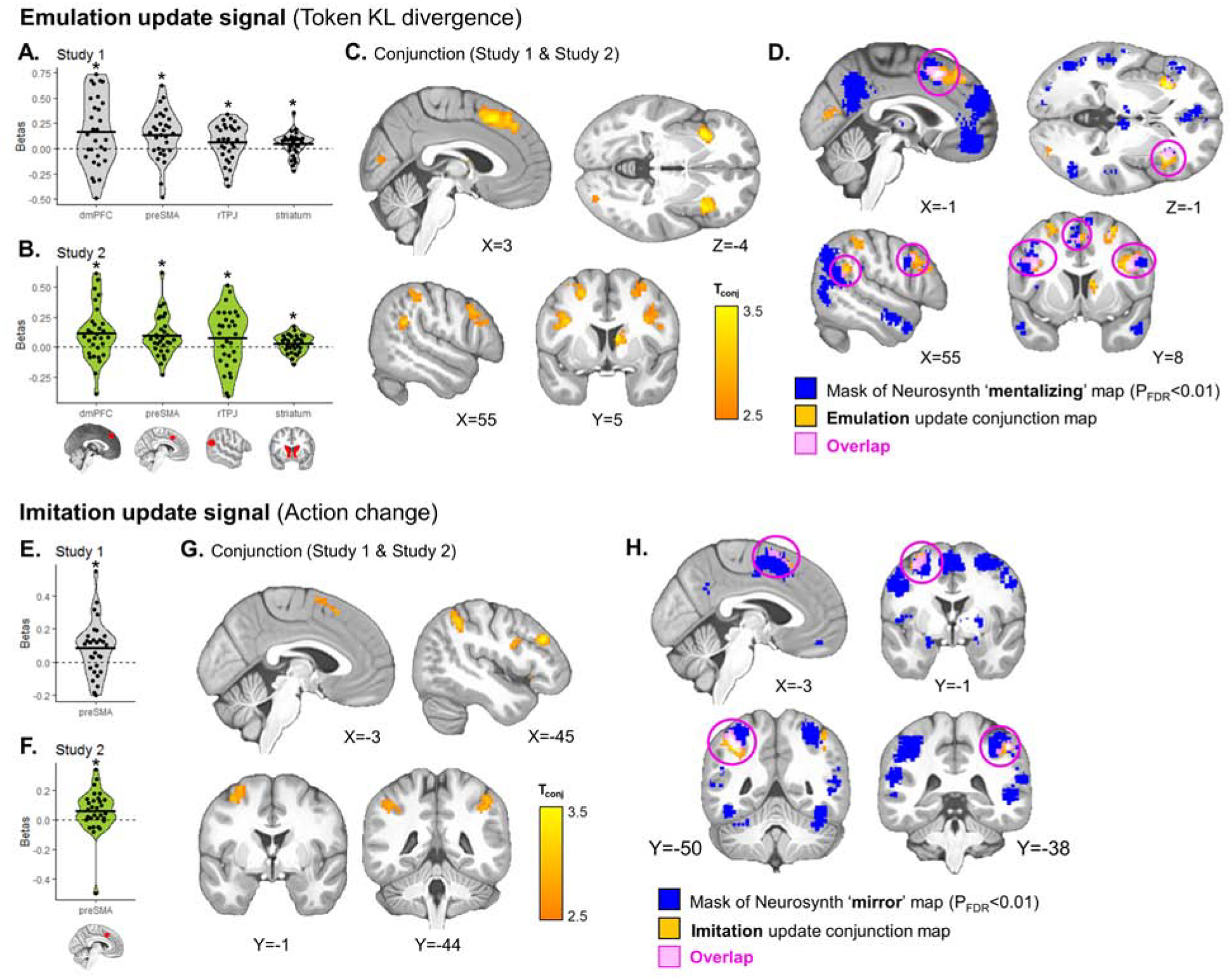
KL divergence over token values (emulation update) and changes in the partner’s action relative to the previous trial (imitation update) were added as parametric modulators of the BOLD signal at feedback, competing for variance within the same model. (A, B, E, F) In both studies, we found significant emulation update signals in the dmPFC, preSMA, right TPJ and dorsal striatum ROIs (A–B) and significant imitation update signals in the preSMA ROI (E–F). T-tests: * P<0.05, † P=0.054. (C, G) Exploratory whole-brain conjunction analysis between the second-level T-maps of Study 1 and Study 2 shows additional clusters tracking emulation (C) or imitation (G) update (Table S4). Threshold at Pconjunction<0.0001 uncorrected, followed by whole-brain cluster-level FWE correction at P<0.05. (D, H) Overlap of emulation and imitation signals with Neurosynth mentalizing (D) and mirror (H) maps, respectively.
However, contrary to the pre-registered findings in which imitation signals were not replicated, here we find robust responses to when the partner’s current action marks a change from the previous action, consistent with the 1-step imitation strategy. This signal was found in the preSMA ROI (Study 1: β=0.083 ±0.16, T29=2.78, P=0.0047; Study 2: β=0.057 ±0.15, T29=2.14, P=0.021; Fig. 7E–F), consistent with a motor component of action imitation. The conjunction analysis revealed regions involved in action observation and action preparation, preSMA, SMA, bilateral inferior parietal lobule (IPL), left motor cortex, and left dlPFC (Fig. 7G; see Table S4 for details), overlapping substantially with the Neurosynth “mirror” map (Fig. 7H).
Despite some overlap between the two update signals (preSMA ROI, bilateral IPL, left precentral gyrus), follow-up analyses (Fig. S5) suggest that activity in these regions uniquely contributes to each update process, consistent with a functional dissociation between the two strategies. Finally, other signals in this new SPM GLM3 were also significant across studies, such as responses to the partner’s last action being no longer available, representation of the propensity to choose according to emulation or to imitation during play trials, and token value coding (Fig. S6; Table S4).
Individual bias towards emulation is reflected in the strength of the emulation update signal
Examining individual brain-behavior differences revealed that the strength of the emulation update signal in four brain regions (dmPFC, bilateral IFG and right anterior insula) correlated with the value of the bias parameter (Fig. S7), suggesting those individuals with stronger emulation update signals are more biased towards emulation. There was no correlation between the bias parameter and imitation update signals, indicating that choice imitation in this task may be more of a default strategy that individuals rely on when they fail to engage emulation learning.
Discussion
Across two independent fMRI studies, we provide evidence for an arbitration process between two observational learning strategies: choice imitation and goal emulation. Behavior was best explained by a computational model in which choice is a hybrid of the two strategies, weighted by a controller driven by the reliability of emulation. Using model comparison, we show that this arbitration model performed better than models solely implementing one strategy. Despite imitation and emulation often making similar behavioral predictions, the present computational framework allowed us to adequately separate the two strategies. Nonetheless, we note that future optimizations of the task design could make the two strategies more distinguishable by increasing the proportion of trials in which behavior is consistent with one strategy, but not the other.
Our fMRI results show that learning signals associated with each strategy are represented in the brain during action observation. When the selected action differed from the previous trial, activity in premotor and inferior parietal cortex increased, possibly reflecting an update in the now-preferred action according to choice imitation. This activity substantially overlaps with regions of the human mirror neuron system (Catmur et al., 2009; Cook et al., 2014; Rizzolatti and Craighero, 2004; see Fig. 7H), implying that imitation learning relies on observing an action and repeating that same action in the future. Emulation learning related to updating in token values was represented in a network of regions including the dmPFC, bilateral insula, right TPJ, IFG and dorsal striatum. The dmPFC and right TPJ likely implement mentalizing, by representing the agent’s goal (Frith and Frith, 2006; see Fig. 7D). Additional regions such as the dorsal striatum and IFG are implicated during social learning, namely inverse RL (Collette et al., 2017), expertise learning (Boorman et al., 2013), or tracking vicarious reward prediction errors (Cooper et al., 2012). The IFG and anterior insula play a role in attentional and executive control (Cieslik et al., 2015; Hampshire et al., 2010), possibly reflecting that emulation requires increased cognitive and attentional resources. These distinct signals suggest that the brain tracks decision values associated with each strategy in parallel, allowing individuals to deploy either strategy when needed.
We found that arbitration depends on trial-by-trial variations emulation reliability, monitored in a continuous fashion, leading to increased engagement of emulation when it is most reliable, rather than when the two strategies are difficult to distinguish. This could suggest that imitation is a default strategy, deployed when emulation becomes too difficult or uncertain. Arbitration regions may act as hubs whereby information relevant to imitation (e.g. from premotor or inferior parietal cortex) and emulation (e.g. from dmPFC or IFG) are dynamically integrated. While anatomical connectivity exists between these regions (Fan et al., 2016; Fig. S8), functional connectivity analyses may add insight into how the arbitration process is implemented at the network level. Furthermore, brain stimulation methods could help establish causal effects on behavioral markers of emulation and imitation. Notably, the right vlPFC region was also found to track reliability signals related to arbitration between MB and MF RL (Lee et al., 2014). However, here we found evidence for additional brain regions associated with OL arbitration not implicated in experiential arbitration, including the bilateral TPJ.
The finding that vlPFC tracks emulation reliability in the present study and MB/MF reliability in a past study (Lee et al., 2014), suggests partial overlap in the neural mechanisms of arbitration between OL and experiential learning. This could indicate a general role for the vlPFC in arbitrating between strategies, both across and within cognitive domains. An interesting question is whether the addition of outcome information, enabling vicarious RL, would shift the balance between other strategies. At the neural level, such three-way interactions may be mediated by the same arbitration circuitry.
It could be argued that emulation and imitation are mere implementations of MB and MF RL in an OL situation. However, by design, we excluded the possibility that a simple extension of MF RL into the observational domain – vicarious RL (Burke et al., 2010; Cooper et al., 2012) – can explain the findings. The tokens’ reward values are not revealed, thus a vicarious RL strategy, learning from rewards experienced by another agent, cannot succeed. Instead, choice imitation involves copying the choice last selected by the agent. Distinct to MF RL, it involves learning about actions rather than rewards, and does not include value computation. Second, MB RL does not typically involve the capacity for reverse inference – inferring the hidden goals of an agent based on observing that agent’s behavior (Collette et al., 2017). Instead, this type of inference, described as “inverse” RL (Ng and Russell, 2000), constitutes a distinct class of algorithms to that of MB RL. Third, at the neural level, mentalizing regions, such as the TPJ (Boorman et al., 2013; Collette et al., 2017; Hampton et al., 2008; Hill et al., 2017), tracked both emulation and arbitration. These regions are not typically recruited in MB RL, suggesting a distinction between underlying neural circuits. Finally, brain regions implicated in choice imitation (premotor and inferior parietal cortex) also do not cleanly map onto the areas involved in previous studies of MF or MB RL.
Our study focuses on specific forms of imitation and emulation. Imitation is concerned with copying another agent’s choice, rather than implementing the exact same sequence of finger movements. Our imitation framework is thus applied to the study of decision-making (Burke et al., 2010; Najar et al., 2019; Suzuki et al., 2012), and does not address the operationalization of imitation in which specific motor actions are reproduced from a demonstrator and relevant movement features are learned (Carcea and Froemke, 2019). Similarly, emulation in our task involves inferring which of three possible goals is pursued by another agent. While they may all rely on similar mechanisms, other implementations of emulation have focused on different types of social inference, such as inverse RL, trust learning, recursive belief inference, or strategic behavior (Collette et al., 2017; Devaine et al., 2014; Lee and Seo, 2016; Xiang et al., 2012). Several open questions remain for future work: How do specific implementations of imitation or emulation differ mechanistically? How adaptable is the proposed arbitration framework to these various operationalizations? Can it be generalized to explain complex, real-world learning situations?
Beyond shedding light on arbitration in OL, the present study is noteworthy for methodological reasons. Although replication is often recognized as the bed-rock for validation of scientific claims (Open Science Collaboration, 2012, 2015; Poldrack et al., 2017), within-paper replications of fMRI studies are rare. Furthermore, in both computational modelling and fMRI, large datasets combined with high flexibility in analysis pipelines increase the risk that reported findings are invalidated by modeler and/or experimenter degrees of freedom (Carp, 2012; Daw, 2011; Simmons et al., 2011). We addressed this by implementing a replication study in which we pre-registered analysis pipelines for both behavioral and fMRI data, before obtaining a fully independent out-of-sample test of our findings. Our computational model results and a substantial subset of our fMRI results were closely replicated even when analytical flexibility was virtually eliminated. Our MRI scanner was also upgraded from a Siemens Trio to Prisma between studies. Despite this, brain activity patterns for most contrasts were highly similar. Once flexibility in analyses is minimized, the replicability of fMRI studies can be established, even across platforms.
Those results that did not replicate pertained to the choice imitation system, as implemented via a choice history RL model. This motivated us to revisit our imitation model for a much simpler implementation, tracking which option the agent chose when that option was last available. Our fMRI results also suggested a modified arbitration process as imitation reliability did not feature in the arbitration signal. Thus, we implemented a new arbitration scheme that assigns control to emulation or imitation based on emulation reliability only. This revised model was found to clearly outperform the original in terms of fits to both behavior and BOLD responses; and neural signals pertaining to imitation and arbitration were well replicated across studies. Using knowledge about the quality of fMRI evidence to revisit our original hypotheses, we demonstrate how evidence from neural data can be used to inform computational and psychological theory. While exploratory, we suspect these additional analyses reveal robust mechanisms. Not only do they generalize across two separate datasets, but there is also a direct link between the robustness of the behavioral model fits and of the fMRI results.
Imitation and emulation have been studied at length in psychology (Horner and Whiten, 2005; Nielsen, 2006; Thompson and Russell, 2004; Whiten et al., 2009) and are of significance for many fields, from education to evolutionary psychology. Here we developed a novel paradigm and associated neuro-computational modelling approach to separate the mechanisms of imitation and emulation as OL strategies. We illuminate how these two strategies compete for control over behavior in a reliability-driven arbitration process.
STAR Methods
LEAD CONTACT AND MATERIALS AVAILABILITY
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Caroline Charpentier (ccharpen@caltech.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Thirty healthy participants (12 females, 18 males, mean age = 31.67 ± 4.94 (SD)) took part in Study 1 between November 2017 and January 2018. For the replication study (Study 2), 33 healthy participants were recruited between October 2018 and January 2019. Three participants were excluded for excessive head motion in the scanner (N=1), incidental finding (N=1) and missing more than 20% of responses on the task (N=1). As preregistered, our final sample for Study 2 included 30 participants (12 females, 18 males, mean age = 31.2 ± 8.15 (SD)). There was no age (t58=0.27, p=0.79) or gender difference across studies. All participants met MRI safety criteria, had normal or corrected-to-normal vision, no psychiatric/neurological conditions, and were free of drugs for 7 days prior to the scan that might potentially interfere with the BOLD response (cannabis, hallucinogenic drugs). They were paid $20 per hour, in addition to bonus money earned during the task ($5 to $8) depending on their performance. The research was approved by the Caltech Institutional Review Board, and all participants provided informed consent prior to their participation.
METHOD DETAILS
Experimental design.
Participants performed a task in which they have to choose between slot machines in order to maximize their chances of winning a valuable token (worth $0.10). They were instructed that there are 3 tokens available in the game (green, red, or blue) and that at any given time, only one token is valuable and the other two are worth nothing. When arriving to the lab, participants first completed an experiential version of the task (~5 minutes) in which the computer told them at the beginning of each trials which token is valuable. They were then presented with the 3 slot machines and instructed that the proportion of green, blue and red colors on each slot machine corresponds to the probability of obtaining each token upon choosing that slot machine. In addition, on each trial one of the slot machines was greyed out an unavailable; therefore, participants had to choose between the remaining two active slot machines.
During the main task (observational learning, Fig. 1A), participants were instructed that the valuable token would switch many times during the task, but they would not be told when the switches occur anymore. Instead, they would have to rely on observing the performance of another agent playing the task. On 2/3 of trials (‘observe’ trials), participants observed that other agent play and knew that this agent had full information about the valuable token and was therefore performing 100% correctly. On 1/3 of trials (‘play’ trials), participants played for themselves and the sum of all play trial outcomes was added to their final bonus payment.
Participants completed a practice of the observational learning task before scanning (2 blocks of 30 trials), followed by 8 blocks of 30 trials of the task while undergoing fMRI scanning. Each block of 30 trials contained 20 observe trials and 10 play trials. The sequence of trials within each block was pre-determined with simulation in order to maximize learning. Block order was counterbalanced across subjects.
Four conditions were implemented in a 2 (stable vs volatile) by 2 (low vs high slot machine uncertainty) design across blocks. Volatility was manipulated by changing the frequency of token switches (Fig. 1B): there was one switch in the valuable token during stable blocks, and 5 switches during volatile blocks. Uncertainty associated with the slot machines was experimentally manipulated by changing the token probability distribution associated with each slot machine (Fig. 1C): [0.75, 0.2, 0.05] in low uncertainty blocks and [0.5, 0.3, 0.2] in high uncertainty blocks.
Trial timings are depicted in Fig. 1A. Trial type (“Observe” or “Play” printed on the screen) was displayed for 1s, immediately followed by the presentation of the slot machine for 2s. On observe trials, there was then a jittered fixation cross (1–4s), followed by the video showing the choice of the partner (around 2s). After another jittered fixation cross (1–4s), the token obtained by the partner was shown on screen for 1s. On play trials, the slot machine presentation was immediately followed by the onset of the word “CHOOSE” indicating participants they had 2s to make their choice. The chosen slot machine was highlighted for 0.5s, followed by a jittered fixation cross (1–4s) and the presentation of the token obtained by the participant. Finally, there was a jittered inter-trial interval of 1–5s. The procedure and task were exactly the same between Study 1 and Study 2.
Software.
The task was coded and presented using PsychoPy (Peirce, 2007) version 1.85 under Windows. Behavioral analyses, including computational models, were run on Matlab (R2018a). MRI data was analyzed using FSL, ANTs and SPM12).
fMRI data acquisition.
For Study 1, fMRI data was acquired on a Siemens Magneto TrioTim 3T scanner at the Caltech Brain Imaging Center (Pasadena, CA), which was later upgraded to a Siemens Prisma 3T scanner before Study 2. The same 32-channel radio frequency coil was used for both studies. MRI acquisition protocols and sequences were also kept as similar as possible. For functional runs, 8 scans of 410 volumes each were collected using a multi-band echo-planar imaging (EPI) sequence with the following parameters: 56 axial slices (whole-brain), A-P phase encoding, −30 degrees slice orientation from AC-PC line, echo time (TE) of 30ms, multi-band acceleration of 4, repetition time (TR) of 1000ms, 60-degree flip angle, 2.5mm isotropic resolution, 200mm × 200mm field of view, EPI factor of 80, echo spacing of 0.54ms. Positive and negative polarity EPI-based fieldmaps were collected before each block with very similar factors as the functional sequence described above (same acquisition box, number of slices, resolution, echo spacing, bandwidtch and EPI factor), single band, TE of 50ms, TR of 4800ms (Study 1)/4810ms (Study 2), 90-degree flip angle. T1-weighted and T2-weighted scans were also acquired either at the end of the session or halfway through, both with sagittal orientation, field of view of 256mm × 256mm, and 1mm (Study 1)/0.9mm (Study 2) isotropic resolution.
QUANTIFICATION AND STATISTICAL ANALYSIS
Behavioral analysis.
To test for the presence of the two learning strategies (choice imitation, based on learning from previous partner’s actions, versus emulation, based on learning from previous evidence about valuable token), a general linear model (GLM) was run using the glmfit function on Matlab. Specifically, the dependent variable was choice of left (coded as 1) or right (coded as 0) slot machine, and the two independent variables (regressors) were constructed as follows:
Effect of past actions: for each previous observe trial between last switch in valuable token and current play trial, the other agent’s action was coded as +1 if the current left-most slot machine was chosen, −1 if it was unchosen or 0 if it was unavailable. The value of the regressor at each play trial was calculated as the sum of these past actions scores, which represents the accumulated evidence for the left slot machine given past actions chosen by the other agent.
Effect of past tokens: for each previous observe trial between last switch in valuable token and current play trial, token information can be inferred (e.g. “green is the valuable token for sure”, or “the valuable token could be green or blue”). From this, the probability that the left (vs right) slot machine results in the valuable token was calculated based on token color distribution associated with each slot machine. The value of the regressor at each play trial was calculated as the sum of these probability differences, which represents accumulated evidence for the left slot machine given past token information.
We ran this GLM for each participant, averaged the resulting beta values across all participants and tested their significance with permutation tests (10,000 permutations), since data were usually not normally distributed across the sample.
Computational models of behavior.
As reported in the preregistration, a total of 9 computational models of behavior were tested, split into 5 classes of models.
1). Approximate Bayesian Emulation Models:
In these models, emulation learning is based on a multiplicative update of the probability of each token being valuable, Vg, Vr, and Vb, for green, red, and blue tokens respectively. At t=0, all values are initialized at 1/3. The update occurs after observing the partner’s action (example for green token):
| (Eq. 1) |
where PPA|g (t) is the probability of observing the partner’s action given that green is the valuable token on trial t. Given that the partner is always correct, PPA|g (t) equals either 1 or 0.
The prior value is calculated as follows:
| (Eq. 2) |
The parameter λ represents trust in current estimates of token values and allows for switches to happen by resetting reward probability of each token to a non-zero value on each trial. Our simulations showed that the value of this parameter that maximizes model’s inference performance changes when volatility is high (token switch frequency higher than 0.2, i.e. more than one switch every 5 trials). However, in our task, token switch frequency is 0.067 per trial for stable blocks and 0.167 per trial for volatile blocks. In these conditions, the value of λ that maximizes performance is as close as possible to 1, but with a small leak to allow the values to be updated on the next trials. Therefore, we used λ=0.99. However, if participants overestimate volatility in the environment, a model with a smaller λ could capture behavior of such participants better. We thus tested two models: one with a fixed λ of 0.99 (Model 1) and one allowing the λ parameter to vary for each participant (Model 2).
Token values Vg, Vr, and Vb are then normalized so that they sum to 1 (Louie et al., 2013). Then the value of choosing each slot machine i () is computed through a linear combination of token values and token probabilities (pg, pr, pb) given by the slot machine:
| (Eq. 3) |
Finally, decision value is calculated as a soft-max function of the difference in value between the two available slot machines on the current play trial.
| (Eq. 4) |
where β is an inverse temperature parameter, estimated for each subject.
2). Choice Imitation RL Models:
These models were implemented as reinforcement learning (RL) models in which the value of each action (left, middle or right) is updated after every observation depending on whether it was chosen by the partner or not. On the first trial, action values (AV) are initialized at 0. Actions chosen by the other agent are updated positively, while unchosen actions are updated negatively, both according to a learning rate α:
| (Eq. 5) |
| (Eq. 6) |
The learning rate α was either estimated as a fixed parameter for each subject (Model 3) or varied over time depending on recency-weighted accumulation of unsigned prediction errors with weight parameter η and initial learning rate α0 (Model 4) (Li et al., 2011; Pearce and Hall, 1980):
| (Eq. 7) |
Decision rule is implemented using Eq. 4.
3). Emulation RL Models:
Two additional models were defined to test the possibility that emulation is implemented as an RL process, rather than as a multiplicative update as described in Models 1 and 2. The value of each token (example below for the green token g) is initialized as 0, and updated based on a token prediction error (TPE) and a learning rate α:
| (Eq. 8) |
| (Eq. 9) |
Similarly to the imitation models above, the learning rate α was either estimated as a fixed parameter for each subject (Model 5) or varied over time depending on recency-weighted accumulation of unsigned prediction errors (|TPE|) with weight parameter η and initial learning rate α0 (Model 6).
Action values are then calculated from token values using Eq. 3, and decision rule is implemented using Eq. 4.
4). Arbitration Models:
Arbitration was governed by the relative reliability of emulation (REM) and imitation (RIM) strategies. REM is driven by the min-max normalized Shannon entropy of emulation action values (i.e. the slot machines action values AVi predicted by the Approximate Bayesian Emulation Models described above):
| (Eq. 10) |
| (Eq. 11) |
RIM is driven by the min-max normalized unsigned action prediction error (APE):
| (Eq. 12) |
| (Eq. 13) |
Minimum and maximum entropy and |APE| values were obtained from practice trial data, by fitting the emulation-only and imitation-only model to that practice data and extracting the minimum and maximum values from the two variables.
This definition of reliability suggests that when entropy between slot machines is high (driven both by uncertainty about which token is valuable and by the uncertainty manipulation depicted in Fig. 1C), emulation becomes unreliable. When action prediction errors are high (driven by unexpected partner’s actions), imitation becomes unreliable.
Arbitration is then governed by an arbitration weight ω, implemented as a soft-max function of the reliability difference, with the addition of a bias parameter δ (δ>0 reflects a bias towards emulation, δ<0 reflects a bias towards imitation):
| (Eq. 14) |
The probability of choosing the slot machine on the left is computed separately for each strategy:
using Eqs. 1–4 for emulation (), with either an optimal λ of 0.99 (Model 7) or an estimated λ parameter for each subject (Model 8), and with inverse temperature parameter βEM
using Eqs. 5, 6 and 4 for imitation ), with fixed learning rate α and with inverse temperature parameter βIM
Then the two decision values and are combined using the arbitration weight ω:
| (Eq. 15) |
5). Outcome RL Model:
One last model we tested (Model 9) is the possibility that participants mistakenly learn from the token that is presented as an outcome at the end of the trial, instead of learning from the partner’s actions. This was implemented similarly to other RL models. The value of each token was updated positively every time that token was obtained as an outcome, either by the partner or by the participant, and negatively if that token was not obtained. Action values and decision value were then calculated using Eqs. 3 and 4.
6). Exploratory Arbitration Model:
This model (Model 10) was defined to test the possibility that imitation is implemented as a simpler 1-step learning strategy in which the most recent partner’s action is repeated on the current trial. Specifically, the probability of choosing the left slot machine on each play trials according to imitation is calculated as follows:
The probability of choosing left according to emulation was defined as above (Eqs. 1–4). Arbitration in this model was driven exclusively by the reliability of the emulation strategy (Eq. 11), with the arbitration weight ω calculated as a soft-max function of the emulation reliability, with the addition of a bias parameter δ. Then the two decision values and are then combined with arbitration weight ω like above (Eq. 15).
Model fitting and comparison.
As preregistered, model fitting and comparison were performed in two different ways to assess robustness of model-fitting results:
1) Using maximum likelihood estimation in Matlab with the fminunc function to estimate parameter estimated for each subject, followed by an out-of-sample predictive accuracy calculation to compare models. Specifically, for the accuracy calculation, subjects were split into 5 groups of 6 subjects, mean parameters were estimated for 4 groups (24 subjects) and tested on the remaining group (6 subjects). This was repeated for all groups, as well as for 100 different groupings of subjects. Mean predictive accuracy (proportion of subjects’ choices correctly predicted by the model) for each model is reported in Table 1.
2) Using hierarchical Bayesian random effects analysis. Following (Huys et al., 2011; Iigaya et al., 2016), the (suitably transformed) parameters of each participant are treated as a random sample from a Gaussian distribution characterizing the population. We estimated the mean and variance of the distribution by an Expectation-Maximization method with a Laplace approximation. We estimated each model’s parameters using this procedure, and then compared the goodness of fit for the different models according to their group-level integrated Bayesian Information Criteria (iBIC, see Table 1). The iBIC was computed by integrating out individual subjects’ parameters through sampling. The full method is described in e.g. (Huys et al., 2011; Iigaya et al., 2016).
Posterior predictive analysis.
We tested that the winning model could reliably predict the behavioral effects obtained by simple GLM (see “Behavioral analysis” paragraph above), namely the effects of past actions and past tokens on current choice. To do so, we used individual subject’s parameters from the winning model (Model 7), as well as individual subject’s parameters from the simple emulation (Model 2) and imitation (Model 3) models, to generate hypothetical choice data for each participant using that participant’s trial sequence. We then ran the same GLM on the model-generated data for each participant, calculated the mean GLM betas across participants and repeated the process (data generation + GLM fitting) 1000 times. The GLM betas from these 1000 iterations are plotted as histograms on Fig. 2C–D, together with the true effect on participants’ actual behavioral data (red point ± standard error).
We also examined our prediction that the use of imitation versus emulation strategies is modulated by volatility and uncertainty. To do so, we extracted the arbitration weight ω(t) from Model 7 for each trial and each participant, and averaged it for each of the 4 conditions (Fig. 3A–B): stable/low uncertainty, volatile/low uncertainty, stable/high uncertainty, volatile/high uncertainty. Differences in arbitration weight across conditions were tested in a 2-by-2 repeated-measures ANOVA. In a separate analysis, we compared the mean likelihood per trial of imitation (Model 3) and emulation (Model 2) for each of the 4 conditions (Fig. 3C–D).
fMRI data preprocessing.
The same preprocessing pipeline was used in both studies. First, reorientation and rough brain extraction of all scans were performed using fslreorient2std and bet FSL commands, respectively. Fieldmaps were extracted using FSL topup. Following alignment of the T2 to the T1 (FSL flirt command), T1 and T2 were co-registered into standard space using ANTs (CIT168 high resolution T1 and T2 templates(Tyszka and Pauli, 2016)). Then an independent component analysis (ICA) was performed on all functional scans using FSL MELODIC; components were classified as signal or noise using a classifier that was trained on previous datasets from the lab; and noise components were removed from the signal using FSL fix. De-noised functional scans were then unwarped with fieldmaps using FSL fugue, co-registered into standard space using ANTs and skull-stripped using SPM imcalc. Finally, 6mm full-width at half maximum Gaussian smoothing was performed using SPM.
fMRI data modelling - preregistered.
Two separate GLMs were used to model the BOLD signal, incorporating an AR(1) model of serial correlations and a high-pass filter at 128Hz. Regressors were derived from each subject’s best fitting parameters from the winning arbitration Model 7.
SPM GLM1: The first GLM was built to examine the neural correlates of arbitration and included the following regressors:
Slot machine onset – observe trials (1), parametrically modulated by (2) the difference in reliability (REM − RIM), (3) the difference in available action values as predicted by the imitation strategy (), and (4) the entropy over the 3 token values as predicted by the emulation strategy (−∑token V · log2 V).
Slot machine onset – play trials (5), parametrically modulated by (6) the difference in reliability (REM − RIM), and (7) the chosen action value (expected reward probability) as predicted by the arbitration model.
Partner’s action onset – observe trials (8), parametrically modulated by (9) the difference in reliability (REM − RIM), and (10) the reduction in entropy over token values calculated as the KL divergence between prior and posterior token values predicted by the arbitration model.
Token onset – observe trials (11), parametrically modulated by (12) the difference in reliability (REM − RIM), and (13) an observational reward prediction error (oRPE), calculated as the difference between the initial expected reward value given the chosen slot machine, and the posterior value of the token shown on screen (as predicted by the model).
Token onset – play trials (14), parametrically modulated by (15) an experiential reward prediction error (eRPE), calculated as described above. We hypothesized that the difference in reliability would not occur at this onset given that it is not associated with any learning (occurring only during observe trials) or choice (occurring earlier during play trials).
SPM GLM2: The second GLM was identical to the first except that each arbitration-related regressor was separated into its emulation (REM) and imitation (RIM) components. In addition, the chosen action value regressor used during play trials slot machine onset was replaced by two action value difference (chosen vs unchosen) regressors predicted by the imitation and emulation strategy separately. This model allowed looking for a neural signature of each strategy.
For both GLMs, trials from all 8 blocks were collapsed into one session in the design matrix. Regressors of no interest included missed choice onsets (if any) as well as 7 regressors modelling the transitions between blocks. All onsets were modeled as stick functions (duration = 0 s). All parametric modulators associated with the same onset regressors were allowed to compete for variance (no serial orthogonalization). GLMs were estimated using SPM’s canonical HRF only (no derivatives) and SPM’s classical method (restricted maximum likelihood).
First-level contrast images were created through a linear combination of the resulting beta images. For the reliability difference signal (SPM GLM1) and for individual reliability signals (SPM GLM2), first-level contrasts were defined as the sum of the corresponding beta images across all onsets where the parametric modulator was added. A global RPE signal was also examined by summing over the oRPE and eRPE contrasts.
fMRI data modelling - exploratory.
A third fMRI model, SPM GLM3, was defined to test the neural implementation of the behavioral arbitration Model 10, in which imitation is implemented as a simpler 1-step learning strategy of repeating the partner’s most recent action. The regressors were as follows:
Slot machine onset – observe trials (1), parametrically modulated by (2) the reliability of emulation (REM), and (3) whether the partner’s previous action is available or not.
Slot machine onset – play trials (4), parametrically modulated by (5) the reliability of emulation (REM), (6) whether the partner’s previous action is available or not, and the propensity to choose according to imitation (7) or according to emulation (8), as predicted by the arbitration model.
Partner’s action onset – observe trials (9), parametrically modulated by (10) the reliability of emulation (REM), (11) the KL divergence between prior and posterior token values predicted by the arbitration model, and (12) whether the partner’s most recent action is repeated, not repeated or unavailable on the current trial, coded as 1, −1 and 0 respectively. Note that the two update regressors (KL divergence (11) and action change (12)) were only moderately correlated (mean R=0.348, corresponding to a shared variance R2=0.121), thus making the dissociation between emulation and imitation update signals possible.
Token onset – observe trials (13), parametrically modulated by (14) the reliability of emulation (REM), and (15) the value of the token shown on screen (as predicted by the model).
Token onset – play trials (16), parametrically modulated by (17) the value of the token shown on screen (as predicted by the model).
Regions of interest.
Based on previous literature on observational learning (Collette et al., 2017) and arbitration processes between learning strategies (Lee et al., 2014), as well as the Neurosynth (http://neurosynth.org/) “Theory of Mind” meta-analysis map, the following 8 ROIs were defined and pre-registered:
Left and right TPJ/pSTS: two 8-mm radius spheres around peaks of the Neurosynth map: (−54,−53,22) and (58, −58,20) for left and right, respectively.
Medial OFC: 8-mm radius sphere around peak of the Neurosynth map (2,49, −20).
dmPFC: 8-mm radius sphere around peak activation tracking expected value in other-referential space(Collette et al., 2017): (0,40,40).
Pre-SMA/dACC: 8-mm radius sphere around peak activation tracking entropy reduction (KL divergence(Collette et al., 2017): (−6,18,44).
Left and right vlPFC: two 8-mm radius spheres around peak activations tracking maximum reliability of model-free and model-based learning(Lee et al., 2014): (−54,38,3) and (48,35, −2) for left and right, respectively.
Dorsal striatum: anatomical bilateral caudate mask from AAL atlas(Tzourio-Mazoyer et al., 2002).
Parameter estimates from the different contrasts in each ROI by extracting the mean signal across all voxels in the ROI for each subject, then averaging across subjects (Table S1). T-tests were performed to establish significance, and were confirmed with non-parametric permutation tests (with 10,000 permutations) in all ROI analyses, since data were not always normally distributed across the samples. Because the goal of the ROI analysis in Study 1 was to generate hypotheses prior to Study 2 data collection, we did not correct for multiple comparisons across the different ROIs. Instead, in our subsequent pre-registration for Study 2, we selected significant ROIs in Study 1 to restrict the space of regions to examine in Study 2.
fMRI model comparison.
Model comparison and selection between SPM GLMs was performed using the MACS (Model Assessment, Comparison and Selection) toolbox for SPM (Soch and Allefeld, 2018) and included the following steps. For each subject and each model, cross-validated log model evidence (cvLME) maps were estimated. cvLME maps rely on Bayesian estimations of the models and Bayesian marginal likelihood to calculate, for each voxel, a voxel-wise cross-validated log model evidence for that model. Then, cross-validated Bayesian model selection(Soch et al., 2016) (cvBMS) was performed to compare GLMs. In cvBMS, second-level model inference is performed using random-effects Bayesian model selection, leading to voxel-wise model selection via exceedance probability maps. For each voxel in a grey matter mask, the exceedance probability was calculated as the posterior probability that a model is more frequent than any other model in the model space (Fig. S4). Exceedance probability was also averaged across voxels in the different ROIs (Table S3).
Group-level inference and conjunction analysis.
Second-level T-maps were constructed separately for each study by combining each subject’s first level contrasts with the standard summary statistics approach to random-effects analysis implemented in SPM. To assess the evidence for consistent effects across studies, conjunction maps were calculated with the minimum T-statistic approach (Friston et al., 2005) for each contrast of interest in the winning SPM GLM (Table S4), combining the second-level T-maps of each study. We thresholded conjunction maps at a conjunction P-value of Pconjunction<0.0001 uncorrected, and minimum cluster size of 30 voxels, corresponding to a whole-brain cluster-level family-wise error corrected P-value of PFWE<0.05. To examine the overlap of emulation and imitation signals with mentalizing and mirror-neuron networks, respectively, we used Neurosynth (Yarkoni et al., 2011) to extract uniformity test maps associated with the term ‘mentalizing’ (meta-analysis of 151 studies) and with the term ‘mirror’ (meta-analysis of 240 studies). These maps reflect the degree to which each voxel is consistently activated in the corresponding studies. We then overlapped the emulation update map with the ‘mentalizing’ map (Fig. 7D) and the imitation update map with the ‘mirror’ map (Fig. 7H).
Individual brain-behavior difference analysis.
Two second-level models were defined in SPM to examine whether individual variability in the bias parameter δ is correlated with emulation update or imitation update signals. The models combined data from both studies (N=60), included values of δ as a covariate of either the emulation update signal or the imitation update signal, and controlled for study group. Two maps were then examined, thresholded at P<0.001 uncorrected and minimum cluster size of 10 voxels: positive correlation between emulation update signal and δ (masked by the emulation update conjunction map; Fig. S7); negative correlation between imitation update signal and δ (masked by the imitation update conjunction map).
Supplementary Material
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| Behavioral data | This paper | https://osf.io/49ws3/ |
| fMRI data (2nd level T-maps) | This paper | https://neurovault.org/collections/UBXVWSMN/ |
| Software and Algorithms | ||
| PsychoPy v.1.85 | (Peirce, 2007) | https://www.psychopy.org/ |
| MatlabR2018a | MathWorks | https://www.mathworks.com/ |
| FSLv.5.0 | (Smith et al, 2004) | https://fsl.fmrib.ox.ac.uk/fsl/fslwiki |
| Advanced Normalization Tools | (Avants et al., 2009) | http://stnava.github.io/ANTs/ |
| (ANTs) | ||
| SPM12 | (Penny et al, 2011) | https://www.fil.ion.ucl.ac.uk/spm/software/spml2/ |
| MACS | (Soch and Allefeld, 2018) | https://github.com/JoramSoch/MACS |
| Neurosynth | (Yarkoni et al., 2011) | http://neurosvnth.org/ |
| R Studio (with Rv. 3.6.1) | RStudio Team | https://rstudio.com/ |
| ggplot2 | (Wickham, 2016) | https://ggplot2.tidyverse.org/ |
| Brainnetome Atlas | (Fan etal, 2016) | http://atlas.brainnetome.org/index.html |
| Custom code (to run experiment and analyses) | This paper | https://github.com/ccharpen/ObsLearnarbitration |
Highlights.
Replicable evidence for arbitration between choice imitation and goal emulation
Control over behavior is adaptively weighted towards the most reliable strategy
Distinct brain networks implement each strategy’s learning signals in parallel
Arbitration is driven by variations in emulation reliability in rvlPFC, ACC and TPJ
Acknowledgements
This work was funded by the Caltech Conte Center for the Neurobiology of Social DecisionMaking. K.I. is supported by the Japan Society for the Promotion of Science and the Swartz Foundation.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests
The authors declare no competing interests.
DATA AND CODE AVAILABILITY
OSF project (behavioral data): https://osf.io/49ws3/
OSF pre-registration: https://osf.io/37xyq
Code (to run experiment and analyses): https://github.com/ccharpen/ObsLearn_arbitration
Group-level T-maps and conjunction maps: https://neurovault.org/collections/UBXVWSMN/
References
- Abbeel P, and Ng AY (2004). Apprenticeship Learning via Inverse Reinforcement Learning In Proceedings of the 21st International Conference on Machine Learning, (ACM; ), p. [Google Scholar]
- Avants BB, Tustison N, and Song G (2009). Advanced normalization tools (ANTS). Insight J 2, 1–35. [Google Scholar]
- Balleine BW, and Dickinson A (1998). Goal-directed instrumental action: Contingency and incentive learning and their cortical substrates. Neuropharmacology 37, 407–419. [DOI] [PubMed] [Google Scholar]
- Balleine BW, and O’Doherty JP (2010). Human and rodent homologies in action control: Corticostriatal determinants of goal-directed and habitual action. Neuropsychopharmacology 35, 48–69. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens TEJ, Hunt LT, Woolrich MW, and Rushworth MFS (2008). Associative learning of social value. Nature 456, 24524–24529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boorman ED, O’Doherty JP, Adolphs R, and Rangel A (2013). The behavioral and neural mechanisms underlying the tracking of expertise. Neuron 80, 1558–1571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burke CJ, Tobler PN, Baddeley M, and Schultz W (2010). Neural mechanisms of observational learning. Proc. Natl. Acad. Sci 107, 14431–14436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carcea I, and Froemke RC (2019). Biological mechanisms for observational learning. Curr. Opin. Neurobiol 54, 178–185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carp J (2012). On the plurality of (methodological) worlds: estimating the analytic flexibility of fMRI experiments. Front. Neurosci 6, 149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catmur C, Walsh V, and Heyes C (2009). Associative sequence learning: The role of experience in the development of imitation and the mirror system. Philos. Trans. R. Soc. Biol. Sci 364, 2369–2380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charpentier CJ, and O’Doherty JP (2018). The application of computational models to social neuroscience: promises and pitfalls. Soc. Neurosci 13, 637–647. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cieslik EC, Mueller VI, Eickhoff CR, Langner R, and Eickhoff SB (2015). Three key regions for supervisory attentional control: Evidence from neuroimaging meta-analyses. Neurosci. Biobehav. Rev 48, 22–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collette S, Pauli WM, Bossaerts P, and O’Doherty JP (2017). Neural computations underlying inverse reinforcement learning in the human brain. Elife 6, e29718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cook R, Bird G, Catmur C, Press C, and Heyes C (2014). Mirror neurons: From origin to function. Behav. Brain Sci 37, 177–192. [DOI] [PubMed] [Google Scholar]
- Cooper JC, Dunne S, Furey T, and O’Doherty JP (2012). Human dorsal striatum encodes prediction errors during observational learning of instrumental actions. J. Cogn. Neurosci 24, 106–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daw ND (2011). Trial-by-trial data analysis using computational models In Decision Making, Affect, and Learning: Attention and Performance XXIII, Delgado MR, Phelps EA, and Robbins TW, eds. (Oxford University Press; ), pp. 3–38. [Google Scholar]
- Daw ND, Niv Y, and Dayan P (2005). Uncertainty-based competition between prefrontal and dorsolateral striatal systems for behavioral control. Nat. Neurosci 8, 1704–1711. [DOI] [PubMed] [Google Scholar]
- Daw ND, Gershman SJ, Seymour B, Dayan P, and Dolan RJ (2011). Model-based influences on humans’ choices and striatal prediction errors. Neuron 69, 1204–1215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devaine M, Hollard G, and Daunizeau J (2014). The social Bayesian brain: Does mentalizing make a difference when we learn? PLoS Comput. Biol 10, e1003992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diaconescu AO, Mathys C, Weber LAE, Daunizeau J, Kasper L, Lomakina EI, Fehr E, and Stephan KE (2014). Inferring on the intentions of others by hierarchical Bayesian learning. PLoS Comput. Biol 10, e1003810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunne S, and O’Doherty JP (2013). Insights from the application of computational neuroimaging to social neuroscience. Curr. Opin. Neurobiol 23, 387–392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eyster E, and Rabin M (2014). Extensive Imitation is Irrational and Harmful. Q. J. Econ 1861–1898. [Google Scholar]
- Fan L, Li H, Zhuo J, Zhang Y, Wang J, Chen L, Yang Z, Chu C, Xie S, Laird AR, et al. (2016). The Human Brainnetome Atlas: A New Brain Atlas Based on Connectional Architecture. Cereb. Cortex 26, 3508–3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher PC, Happé F, Frith U, Baker SC, Dolan RJ, Frackowiak RSJ, and Frith CD (1995). Other minds in the brain: A functional imaging study of “theory of mind” in story comprehension. Cognition 57, 109–128. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Penny WD, and Glaser DE (2005). Conjunction revisited. Neuroimage 25, 661–667. [DOI] [PubMed] [Google Scholar]
- Frith CD, and Frith U (2006). The neural basis of mentalizing. Neuron 50, 531–534. [DOI] [PubMed] [Google Scholar]
- Gazzola V, and Keysers C (2009). The observation and execution of actions share motor and somatosensory voxels in all tested subjects: Single-subject analyses of unsmoothed fMRI data. Cereb. Cortex 19, 1239–1255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glascher J, Daw N, Dayan P, and O’Doherty JP (2010). States versus rewards: dissociable neural prediction error signals underlying model-based and model-free reinforcement learning. Neuron 66, 585–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampshire A, Chamberlain SR, Monti MM, Duncan J, and Owen AM (2010). The role of the right inferior frontal gyrus: inhibition and attentional control. Neuroimage 50, 1313–1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hampton AN, Bossaerts P, and O’Doherty JP (2008). Neural correlates of mentalizing-related computations during strategic interactions in humans. Proc. Natl. Acad. Sci 105, 6741–6746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heyes C, and Saggerson A (2002). Testing for imitative and nonimitative social learning in the budgerigar using a two-object/two-action test. Anim. Behav 64, 851–859. [Google Scholar]
- Hill CA, Suzuki S, Polania R, Moisa M, O’Doherty JP, and Ruff CC (2017). A causal account of the brain network computations underlying strategic social behavior. Nat. Neurosci 20, 1142–1149. [DOI] [PubMed] [Google Scholar]
- Horner V, and Whiten A (2005). Causal knowledge and imitation/emulation switching in chimpanzees (Pan troglodytes) and children (Homo sapiens). Anim. Cogn 8, 164–181. [DOI] [PubMed] [Google Scholar]
- Huang CT, and Charman T (2005). Gradations of emulation learning in infants’ imitation of actions on objects. J. Exp. Child Psychol 92, 276–302. [DOI] [PubMed] [Google Scholar]
- Huang CT, Heyes C, and Charman T (2006). Preschoolers’ behavioural reenactment of “failed attempts”: The roles of intention-reading, emulation and mimicry. Cogn. Dev 21, 36–45. [Google Scholar]
- Huys QJM, Cools R, Gölzer M, Friedel E, Heinz A, Dolan RJ, and Dayan P (2011). Disentangling the roles of approach, activation and valence in instrumental and pavlovian responding. PLoS Comput. Biol 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iigaya K, Story GW, Kurth-Nelson Z, Dolan RJ, and Dayan P (2016). The modulation of savouring by prediction error and its effects on choice. Elife 5, e13747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lametti DR, and Watkins KE (2016). Cognitive neuroscience: The neural basis of motor learning by observing. Curr. Biol 26, R288–R290. [DOI] [PubMed] [Google Scholar]
- Le HM, Jiang N, Agarwal A, Dudík M, Yue Y, and Daumé H (2018). Hierarchical imitation and reinforcement learning. 35th Int. Conf. Mach. Learn. ICML 2018 7, 4560–4573. [Google Scholar]
- Lee D, and Seo H (2016). Neural basis of strategic decision making. Trends Neurosci. 39, 40–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SW, Shimojo S, and O’Doherty JP (2014). Neural computations underlying arbitration between model-based and model-free learning. Neuron 81, 687–699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Schiller D, Schoenbaum G, Phelps EA, and Daw ND (2011). Differential roles of human striatum and amygdala in associative learning. Nat. Neurosci 14, 1250–1252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Louie K, Khaw MW, and Glimcher PW (2013). Normalization is a general neural mechanism for context-dependent decision making. Proc. Natl. Acad. Sci. U. S. A 1217854110-. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossel E, Mueller-Frank M, Sly A, and Tamuz O (2018). Social Learning Equilibria. SSRN Electron. J [Google Scholar]
- Najar A, Bonnet E, Bahrami B, and Palminteri S (2019). Imitation as a model-free process in human reinforcement learning. BioRxiv 797407. [Google Scholar]
- Ng A, and Russell S (2000). Algorithms for inverse reinforcement learning In Proceedings of the Seventeenth International Conference on Machine Learning, Vol. 67, De Sousa JP, ed. (Morgan Kaufmann Publishers Inc; ), pp. 663–670. [Google Scholar]
- Nielsen M (2006). Copying actions and copying outcomes: Social learning through the second year. Dev. Psychol 42, 555–565. [DOI] [PubMed] [Google Scholar]
- Open Science Collaboration (2012). An open, large-scale, collaborative effort to estimate the reproducibility of psychological science. Perspect. Psychol. Sci 7, 657–660. [DOI] [PubMed] [Google Scholar]
- Open Science Collaboration (2015). Estimating the reproducibility of psychological science. Science (80-. ). 349, aac4716. [DOI] [PubMed] [Google Scholar]
- Van Overwalle F, and Baetens K (2009). Understanding others’ actions and goals by mirror and mentalizing systems: A meta-analysis. Neuroimage 48, 564–584. [DOI] [PubMed] [Google Scholar]
- Palminteri S, Wyart V, and Koechlin E (2017). The Importance of Falsification in Computational Cognitive Modeling. Trends Cogn. Sci 21, 425–433. [DOI] [PubMed] [Google Scholar]
- Pearce JM, and Hall G (1980). A model for Pavlovian learning: variations in the effectiveness of conditioned but not of unconditioned stimuli. Psychol. Rev 87, 532. [PubMed] [Google Scholar]
- Peirce JW (2007). PsychoPy - Psychophysics software in Python. J Neurosci Methods 162, 8–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny WD, Friston KJ, Ashburner J, Kiebel S, and Nichols TE (2011). Statistical parametric mapping: the analysis of functional brain images (Elsevier; ). [Google Scholar]
- Poldrack R, Baker C, Durnez J, Gorgolewski K, Matthews P, Munafò M, Nichols T, Poline J, Vul E, and Yarkoni T (2017). Scanning the horizon: towards transparent and reproducible neuroimaging research. Nat Rev Neurosci 18, 115–126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rizzolatti G, and Craighero L (2004). The mirror-neuron system. Annu. Rev. Neurosci 27, 169–192. [DOI] [PubMed] [Google Scholar]
- Rizzolatti G, Fadiga L, Gallese V, and Fogassi L (1996). Premotor cortex and the recognition of motor actions. Cogn. Brain Res 3, 131–141. [DOI] [PubMed] [Google Scholar]
- Simmons JP, Nelson LD, and Simonsohn U (2011). False-positive psychology: Undisclosed flexibility in data collection and analysis allows presenting anything as significant. Psychol. Sci 22, 1359–1366. [DOI] [PubMed] [Google Scholar]
- Smith SM, Jenkinson M, Woolrich MW, Beckmann CF, Behrens TEJ, Johansen-Berg H, Bannister PR, De Luca M, Drobnjak I, Flitney DE, et al. (2004). Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 23, 208–219. [DOI] [PubMed] [Google Scholar]
- Soch J, and Allefeld C (2018). MACS – a new SPM toolbox for model assessment, comparison and selection. J. Neurosci. Methods 306, 19–31. [DOI] [PubMed] [Google Scholar]
- Soch J, Haynes J, and Allefeld C (2016). How to avoid mismodelling in GLM-based fMRI data analysis: cross-validated Bayesian model selection. Neuroimage 141, 469–489. [DOI] [PubMed] [Google Scholar]
- Suzuki S, Harasawa N, Ueno K, Gardner JL, Ichinohe N, Haruno M, Cheng K, and Nakahara H (2012). Learning to simulate others’ decisions. Neuron 74, 1125–1137. [DOI] [PubMed] [Google Scholar]
- Thompson DE, and Russell J (2004). The ghost condition: Imitation versus emulation in young children’s observational learning. Dev. Psychol 40, 882–889. [DOI] [PubMed] [Google Scholar]
- Tyszka JM, and Pauli WM (2016). In vivo delineation of subdivisions of the human amygdaloid complex in a high-resolution group template. Hum. Brain Mapp 37, 3979–3998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, and Joliot M (2002). Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 15, 273–289. [DOI] [PubMed] [Google Scholar]
- Whiten A, McGuigan N, Marshall-Pescini S, and Hopper LM (2009). Emulation, imitation, over-imitation and the scope of culture for child and chimpanzee. Philos. Trans. R. Soc. Biol. Sci 364, 2417–2428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickham H (2016). ggplot2: Elegant Graphics for Data Analysis.
- Xiang T, Ray D, Lohrenz T, Dayan P, and Montague PR (2012). Computational phenotyping of two-person interactions reveals differential neural response to depth-of-thought. PLoS Comput. Biol 8, e1002841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T, Poldrack RA, Nichols TE, Van Essen DC, and Wager TD (2011). Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods 8, 665–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida W, Seymour B, Friston KJ, and Dolan RJ (2010). Neural mechanisms of belief inference during cooperative games. J. Neurosci 30, 10744–10751. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


