Constructing and Forgetting Temporal Context in the Human Cerebral Cortex

Summary

How does information from seconds earlier affect neocortical responses to new input? We found that when two groups of participants heard the same sentence in a narrative, preceded by different contexts, the neural responses of each group were initially different, but gradually fell into alignment. We observed a hierarchical gradient: sensory cortices aligned most quickly, followed by mid-level regions, while some higher-order cortical regions took more than 10 seconds to align. What computations explain this hierarchical temporal organization? Linear integration models predict that regions which are slower to integrate new information should also be slower to forget old information. However, we found that higher order regions could rapidly forget prior context. The data from the cortical hierarchy were instead captured by a model in which each region maintains a temporal context representation that is nonlinearly integrated with input at each moment, and this integration is gated by local prediction error.

In Brief

Chien and Honey measured how information in a spoken narrative is integrated and separated in the human cerebral cortex. They observed a hierarchical representation of temporal context, distributed across the cortex. Computational modeling suggests the distributed context is flexibly updated or reset based on surprise.

Introduction

Events such as gestures, melodies, speech, and actions unfold over time, so we can only perceive and understand information in the present by integrating it with information from the past (Buonomano and Maass, 2009; Fuster, 1997; Kiebel et al., 2008). This process is complex because the world contains meaningful structure on scales ranging from milliseconds to minutes (Gibson et al., 1982; Poeppel, 2003; Zacks and Tversky, 2001): a series of phonemes makes up a word, a series of words forms a sentence, a series of sentences expresses an idea. How is the human brain organized to integrate information across multiple timescales in parallel?

We and others have argued that the human brain employs a distributed and hierarchical architecture for integrating information over time (Baldassano et al., 2017; Fuster, 1997; Hasson et al., 2015; Honey et al., 2012; Lerner et al., 2011; Runyan et al., 2017). The architecture is distributed because almost all regions of the human cerebral cortex exhibit temporal context dependence in their responses. The architecture is hierarchical because early sensory regions integrate over short timescales (milliseconds to seconds), while higher-order regions integrate information over longer timescales (seconds to minutes).

The timescale hierarchy is a highly reliable phenomenon with functional implications across the brain (Baldassano et al., 2017; Burt et al., 2018; Chaudhuri et al., 2015; Cocchi et al., 2016; Demirtaş et al., 2019; Watanabe et al., 2019), yet our models of the underlying information processing have remained phenomenological. What are the computations that integrate past and present information within the hierarchical networks of our brains? How are past and present information represented within each stage of processing, and then passed on to higher stages? We set out to answer these questions using a combined empirical and modeling approach.

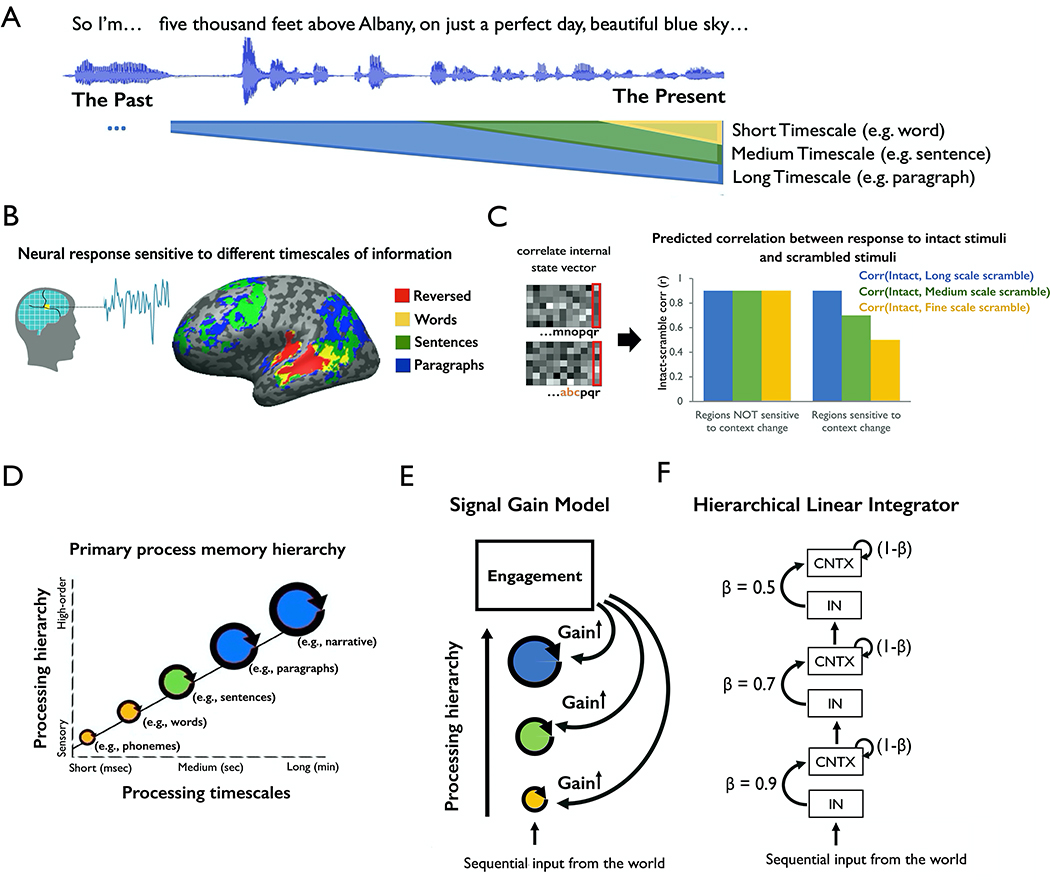
To investigate how information is integrated over time, prior studies have measured the “processing timescales” of different brain regions. Processing timescales were quantified by comparing a brain region’s response to a stimulus at time t across various contexts, where the stimulus properties at time (t-τ) were altered. For example, Lerner et al., (2011) used functional magnetic resonance imaging (fMRI) to measure the neural responses to temporally manipulated versions of an auditory narrative (Figure 1A). They compared the responses during the original intact clip against the response during versions of the stimulus in which the ordering of words, sentences or paragraphs was scrambled. The authors observed that early sensory regions exhibited similar responses to the intact and scrambled audio; these early regions were said to have a short processing timescale, because their responses at each moment were largely independent of prior context. Moving toward higher-order cortices, such as temporoparietal junction, precuneus, and lateral prefrontal cortex, Lerner et al. (2011) observed different responses to the intact and scrambled input. In these higher-order regions, the response at one moment could depend on stimulus properties from more than 30 seconds earlier (Figure 1B). Overall, higher stages of cortical processing were said to have longer processing timescales, because their responses at time t were affected by properties of the stimulus from many seconds earlier (Figure 1C).

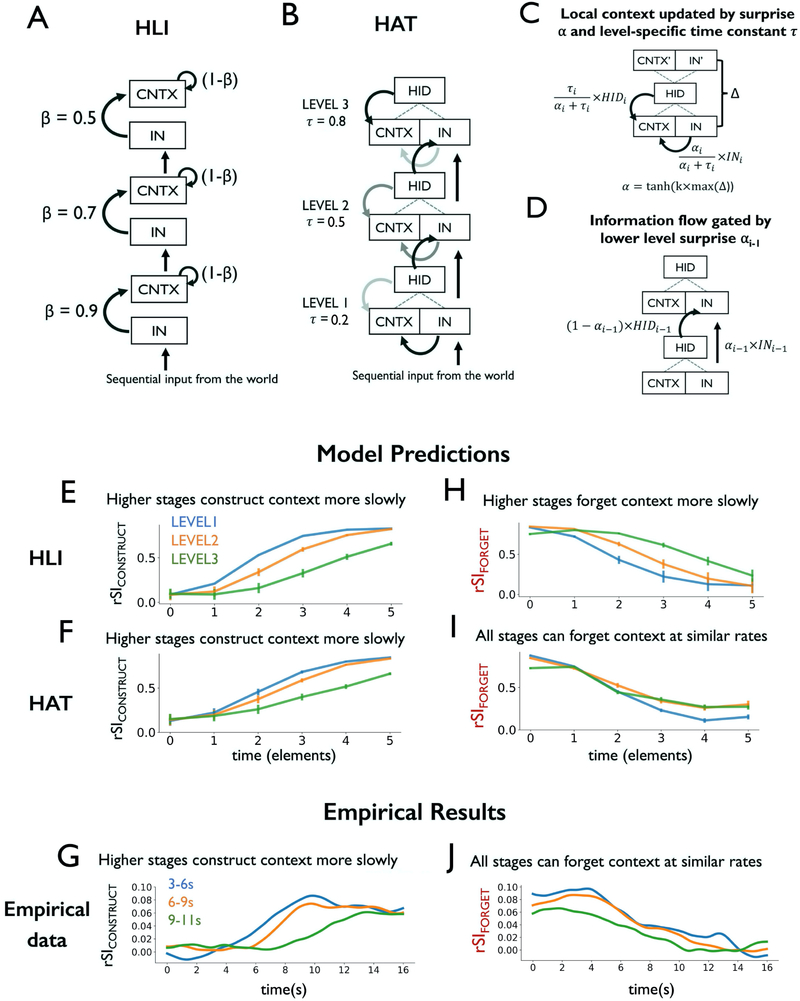
Figure 1. Computational models of distributed and hierarchical process memory.

(A) Schematic of experiment and results from Lerner et al. (2011). fMRI participants listened to an intact auditory narrative as well as versions scrambled at the scales of words, sentences and paragraphs. (B) Lower-level regions (e.g. auditory cortex) exhibited responses that were reliable across all stimuli, with little dependence on prior temporal context. By contrast, higher-level regions (e.g. precuneus) exhibited responses that depended at each moment on tens of seconds of prior context in the stimuli. (C) Schematic of the “process memory hierarchy”. Lower-level regions (e.g. sensory regions) exhibit shorter integration timescales, integrating over entities such as phonemes and words. Higher-level regions (e.g. lateral and medial parietal regions) exhibited longer integration timescales, combining information on the scale of entire events (e.g. paragraphs of text). (D) Schematic of predicted data when comparing the representations of brain regions sensitive to temporal context on different scales. The dependent variable is the “intact-scramble correlation”, quantifying the similarity of neural response to the same input in different contexts. (E) Schematic of a signal gain model for explaining the pattern of brain responses shown in panel D. (F) Schematic of hierarchical linear integrator model, HLI. LSS = long scale scramble, MSS = medium scale scramble, FSS = fine scale scramble. HLI = hierarchical linear integrator model.

In this study, we first developed computational models that could explain the key empirical phenomena from prior studies (e.g. Lerner et al., 2011). If we have measured the neural responses to temporally “intact” and “scrambled” versions of the stimulus, then we can quantify the similarity of responses to the same segment presented in the intact and scrambled order as the “intact-vs-scramble correlation” (Figure 1D). The two key phenomena of hierarchical context dependence are then:

(P1) lower processing stages are largely insensitive to temporal context (Figure 1D, left bars);

(P2) progressively higher processing stages are increasingly sensitive to temporal context extending further into the past (Figure 1D, right bars).

We found that P1 and P2 could be explained by a model that does not invoke explicit integration of past and present information (the “signal gain model”, Figure 1E) and also by a model that does employ temporal integration (the “hierarchical linear integrator” model, HLI, Figure 1F). To distinguish between these two models, we empirically tested a distinctive prediction of hierarchical integration models: when two people with distinct neural states are presented with a common input, their neural responses should gradually align over time as the common input continues, and this alignment should occur more slowly in higher order regions.

Our empirical measurements revealed new evidence that cortical circuits hierarchically integrate input with prior context. We measured moment-by-moment changes in fMRI responses as two groups of participants heard the same natural auditory speech segments preceded by different contexts. We found that the fMRI responses gradually aligned over time across the two groups, when each group heard the same input preceded by a different context. The responses aligned earliest in sensory regions, but later and later in regions at consecutive stages of processing. This finding is consistent with the predictions of the hierarchical linear integrator, but could not be explained by the signal gain model. Thus, the topography of these alignment patterns provides new evidence for a distributed and hierarchical representation of temporal context in the human brain.

If temporal integration is linear in the brain, then regions which are slower to integrate new information should also be slower to forget old information – but is this observed? To measure forgetting, we examined the rate at which fMRI states “separate” when two groups of participants begin with a common context, but are then exposed to distinct input. We found that, although higher order regions aligned across contexts more gradually than sensory regions, they did not separate more gradually. This decoupling of alignment times and separation times rules out standard linear integrator models, and seems to require a mechanism for flexibly varying how new and old information are combined.

Finally, to account for the decoupling between alignment times and separation times in cortical dynamics, we proposed a hierarchical nonlinear integrator model – the hierarchical autoencoders in time (HAT) model. By combining non-linear integration and context gating mechanisms, HAT generated learning-dependent representations that account for the existing empirical phenomena (P1 and P2, above), while also exhibiting hierarchical alignment times, and a distinct set of timescales for alignment and separation. In the HAT model, integration is flexible: at appropriate moments, such as the start of a new event, the model can generate a response that depends less on the prior context.

We conclude that each stage of cortical hierarchy maintains a temporal context representation, which is continually updated as a simplified combination of past and present information, and which can also be reset following surprising input.

Results

We considered two computational models to account for the empirical phenomena P1 and P2: a model based on engagement with the stimulus (signal gain model, Figure 1E), and a model employing hierarchical temporal integration (the hierarchical linear integrator, HLI, Figure 1F).

The signal gain model

It is possible to account for the hierarchical context dependence phenomena (P1 and P2, Figure 1D) without invoking distributed temporal integration. Instead, one can offer an explanation based on “signal gain” combined with a qualitative notion of “engagement”. This model makes three assumptions: (i) when participants engage more deeply with a stimulus, the gain of their response to that stimulus increases relative to the noise level, and they produce more reliable neural responses to that stimulus (Cohen et al., 2018; Dmochowski et al., 2012), (ii) participants are less “engaged” with temporally scrambled stimuli than with intact stimuli, and (iii) the effects of engagement on neural reliability are larger in higher-order cortical regions. Under these assumptions, the existing empirical data can be explained: first, sensory neocortex would be largely unaffected by engagement (and thus unaffected by scrambling prior context); second, higher order regions would respond less reliably to scrambled stimuli, and so their intact-vs-scramble correlations would also be decreased (Figure 1E, see STAR Methods). Thus, the signal gain model could explain data from the scrambling experiment, without recourse to any neural representation of temporal context, and it provides an important null model.

The hierarchical linear integrator (HLI) model

It is also possible to account for the hierarchical context dependence phenomena (P1 and P2, Figure 1D) using a model that explicitly represents and integrates temporal context. We used a linear integration approach, inspired by neural integrators in systems neuroscience and mathematical psychology (Huk and Shadlen, 2005; Koulakov et al., 2002; Mazurek et al., 2003; Townsend and Ashby, 1983) and in particular by the seminal “temporal context model” (TCM) in memory research (Howard and Kahana, 2002). In TCM, the arrival of each new stimulus generates linear “drift” of an internal context variable. In particular, if we define the current context as CNTX(t) and the current input as IN(t), a simple form of the update equation for TCM is:

$$\mathit{CNTX}(\text{t}+1)={\rho }_i\mathit{CNTX}(\text{t})+{\beta }_i\mathit{IN}(\text{t})$$

where ρ_i and β_i are parameters that determine the proportion of new and old information in the updated context.

To generate a hierarchical linear integrator, we stacked these linear integrator units in stages, and we increased ρ (and decreased β) at higher levels of processing. In this way, we increased the proportion of prior information retained at higher stages of the simulated hierarchy. The input to the higher-level integrators was the updated CNTX vector from the lower-level integrator, generating a cascade of temporal integration (Figure 1F; see STAR Methods).

Testing computational models of hierarchical context dependence

We quantitatively confirmed that both the signal gain model and the hierarchical linear integrator (HLI) could capture the previously described phenomena (P1 and P2) of hierarchical context dependence (Figure 1D, Figure S2 and STAR Methods). Therefore, to provide direct evidence for hierarchical temporal integration (and to rule out the signal gain model) it was necessary to collect more fine-grained measurements of the neural processing of temporally extended sequences.

Measuring the Moment-by-Moment Construction of Temporal Context

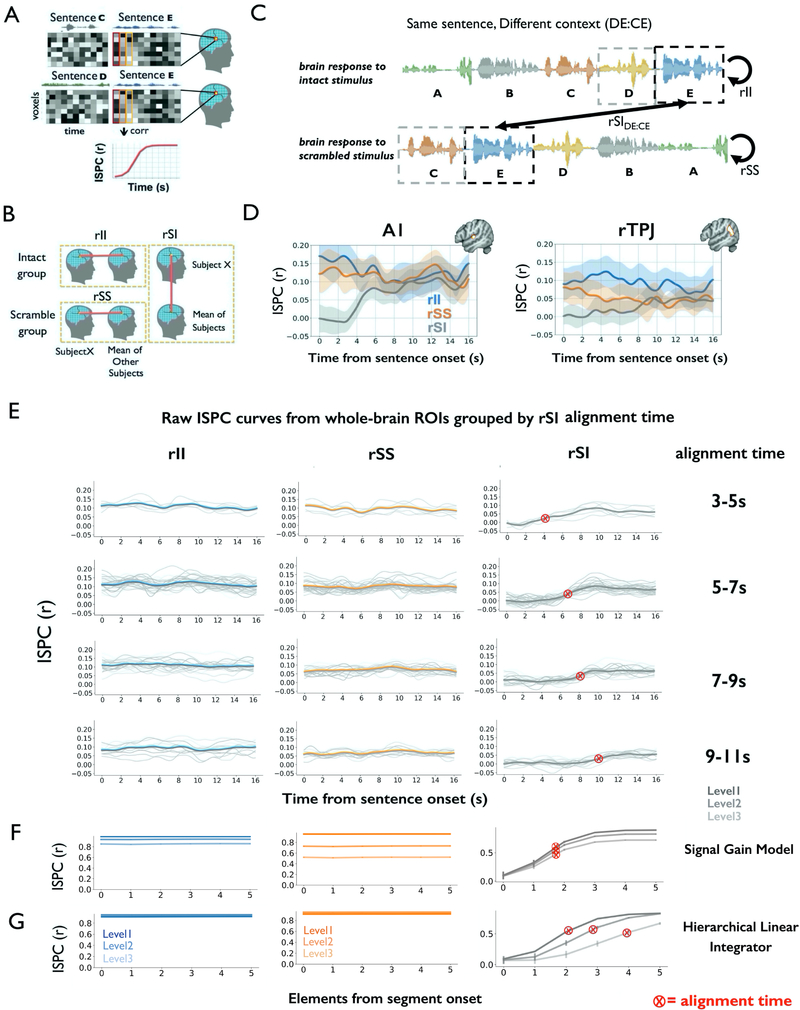
We developed a time-resolved fMRI pattern analysis approach for measuring context-dependent responses to auditory narratives. To understand the time-resolved analysis, consider a case in which two groups of subjects are exposed to the same ~20 s segment of natural speech (e.g. sentence E), but this shared segment is preceded by different speech segments across the two groups (e.g. sentence C or sentence D, Figure 2A). In this setting we can ask: how similar are the neural responses within and across these groups, second by second, as they process the shared segment from start to end? At the start of the sentence, the two groups share none of their prior context, but by the end of the sentence they share much greater amounts of prior context.

Figure 2. Gradual alignment of responses to a common stimulus preceded by different context.

(A) For each sentence, inter-subject pattern correlation (ISPC) was measured by correlating the spatial pattern of activation at each time point across the two groups. (B) ISPC was calculated between one subject and the average of the rest of the subjects within the intact group (rII); or between one subject and the rest of the scrambled group (rSS); or across the intact and scrambled groups (rSI). (C) ISPC analysis for the same sentence preceded by different contexts (DE:CE). Here, sentence E followed sentence D for the Intact group, but it followed sentence C for the Scrambled group. (D) Average ISPC for all sentences in ROIs within an auditory (A1+) region and a right TPJ region. Shaded area indicates a 95% confidence interval on individual rSI estimates. (E) The rII, rSS, and rSI_DE:CE curves are shown for individual regions, grouped by “alignment time”. The individual region curves are pale gray, while mean curves for each group of regions is in thick blue (rII), orange (rSS), and gray (rSI_DE:CE). Note that the rII and rSS curves do not ramp, neither for the mean curve, nor for individual regions, while the rSI curves show ramping in almost all regions. (F) Simulation of rII, rSS and rSI for the signal gain model. The rSI curves exhibit ramping, but the alignment times are stable across levels. (G) Simulation of, rSS and rSI for the HLI model. The alignment time is greater in higher levels of the HLI model. A1 = primary auditory cortex, rTPJ = right temporal-parietal junction.

To quantify neural similarity within and across groups, we calculated the inter-subject pattern correlation (ISPC) at each time point. Three kinds of ISPC were calculated (STAR methods): similarity within the intact group (i.e. intact-intact correlation, rII), similarity within the scramble group (i.e. scramble-scramble correlation, rSS) and similarity across the intact and the scramble groups (i.e. intact-scramble correlation, rSI) (Figure 2B, 2C).

We first examined the curves of rII, rSS and rSI within one lower-order region (near A1+, Figure 2D left) and one higher-order region (near the TPJ, Figure 2D right). In both regions we observed that (i) the rII and rSS curves were essentially constant from the beginning to the end of a segment; and (ii) the rSI curve ramped upward over time, as the intact and scrambled groups were exposed to more and more shared input. These patterns (flat rII; flat rSS; ramping rSI) are preserved across the cerebral cortex (Figure 2E, Figure S4A) when we broaden our analysis to a cortex wide atlas or ROIs (Schaefer et al., 2018).

We next examined how the temporal integration profile (rII, rSS and rSI) differed across regions. To illustrate the basic phenomenon, we examined the rII and rSS curves (within-group correlation) for one sensory region (A1+) and one higher-order region (right TPJ). In A1+, we found that rII and rSS were similar to each other across the whole segments, suggesting that A1 showed highly reliable responses to the same segments in the two conditions in which the contexts are different (Figure 2D left). In rTPJ, on the other hand, the rII curve was significantly higher than the rSS (t(21)=2.83, p=0.007, t-test of mean rII and rSS values per segment, Figure 2D right). The increased response reliability in the TPJ for the intact condition could reflect greater engagement, or the fact that the intact stimulus is more familiar. However, the rII and rSS curves do not provide a time-resolved measurement of shared context representation, which can instead be obtained via the across-group correlation (rSI).

The across-group correlation (rSI) ramped upward over time within each story segment, and this ramping occurred later in the higher order cortex (TPJ) than in sensory cortex (A1+). In A1+, the rSI timecourse begins to achieve alignment at 4 s after the segment-onset, while in TPJ the rSI timecourse begins to achieve alignment more than 7 s post-onset (Figure 2D). Importantly, the fact that rSI = 0 at the onset of the segment does not necessarily reflect a neural context: the hemodynamics introduce temporal smoothing, carrying signal from the previous segment into the start of the current segment, even if the underlying neural response is unaffected by context. This hemodynamic artifact makes it difficult to use BOLD imaging to estimate the shortest possible time at which temporal context effects operate. However, the hemodynamics cannot account for the ramping in TPJ occurring more than 3 seconds later than in A1+. Instead, the later alignment time in TPJ points to a neural context effect, with a longer timescale in higher order regions. Thus, we tested the generality of this hierarchical pattern by mapping the timescales of context construction across the cerebral cortex.

Moment-by-moment context analysis reveals a hierarchical organization

The alignment of response across the intact and scramble groups (rSI) increased over time in almost every ROI, and the latency of this ramping differed across brain regions. Because the shape of the rSI curve is not meaningful when the response in the scrambled condition is unreliable, we restricted our analysis of the rSI ramping to the 83 ROIs in which there was a reliable response to the scrambled stimulus (i.e. mean rSS > 0.06, see STAR Methods, Figure S3A). After confirming that a logistic function could accurately summarize the rSI curves (Figure S3C), we used logistic fitting to quantify the timescale of rSI ramping in each ROI. We defined the “alignment time” as the time at which the logistic curve reaches its half maximum. We excluded 4 ROIs that were not well-fit by a logistic function (Figure S3B), and 9 ROIs for which alignment times were unreliable (assessed by bootstrapping, Figure S3D, see STAR Methods). We thus entered 70 ROIs into further analysis. A direct visualization of the raw rSI timecourses in each ROI reveals that the logistic fitting accurately captured the profile of the rSI curves and that alignment times differ across areas (Figure 2E, Figure S4).

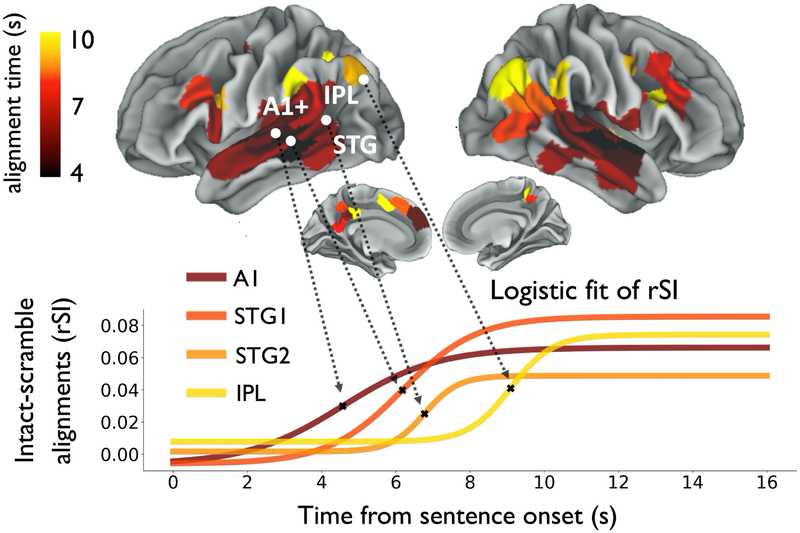
Mapping the alignment times across the lateral and medial cortical surface, we observed a “hierarchy of context construction” in the human brain. Early auditory regions first arrive at a shared context-dependent response, followed by consecutive stages of the cortical hierarchy. Alignment times of rSI curves gradually increased from sensory cortex (alignment times ~ 4 s) toward higher order regions (alignment times of 10 s or longer, Figure 3, top). Plotting rSI curves along the auditory processing pathway confirmed the hierarchical organization (Figure 3, bottom): lower-level regions (e.g. A1) quickly arrived at a shared response between intact and scrambled groups, while regions in inferior parietal and medial parietal cortex took longer to align across the intact and scrambled groups.

Figure 3. Hierarchical timescales of context construction across the human cerebral cortex.

(top) Cortical map of the timescale at which neural responses align to a common input preceded by different contexts. Alignment time is quantified as the time for each rSI_DE:CE curve to reach half its maximum value. (bottom) Fitted logistic curves for four representative ROIs along the cortical hierarchy. A1 = primary auditory cortex, IPL = inferior parietal lobe, STG = superior temporal gyrus, rSI = intact-scramble inter-subject pattern correlation.

Hierarchical integrator model predicts hierarchical context construction

The results of hierarchical context construction rule out the signal gain model, because it could not account for different rates of context construction at different levels of the cortex (Figure 2F). On the other hand, the HLI model could account for these inter-regional, because its higher-level integrators have longer time constants: the rSI curves in the HLI model ramp upward later for higher-level linear integrators (Figure 2G, t=−104, p<0.0001), and this effect is magnified by the fact that the integrators are stacked in a hierarchy (Figure S5C, Table S1). Because the signal gain model can capture variations in the mean level of the rII and rSS curves, and the asymptotic height of each rSI curve (which may reflect variation in engagement across the intact and scrambled stimuli) (Figure 2F), the signal gain mechanisms should still be considered as a component of future models. However, the dominant pattern in our data – the hierarchical variation in alignment times – requires a model that maintains temporal context to varying degrees across regions.

Time-resolved analysis of context forgetting

The time-resolved pattern analysis indicates that information is temporally integrated second-by-second throughout the cortex – but is integrating information from the past always desirable? For example, if the subject of a new sentence is unrelated to the verb of the previous sentence, then perhaps we might want to separate these pieces of information, rather than integrate them. Therefore, in addition to the process of integrating information over time, we also measured the neural process of separating information from distinct events.

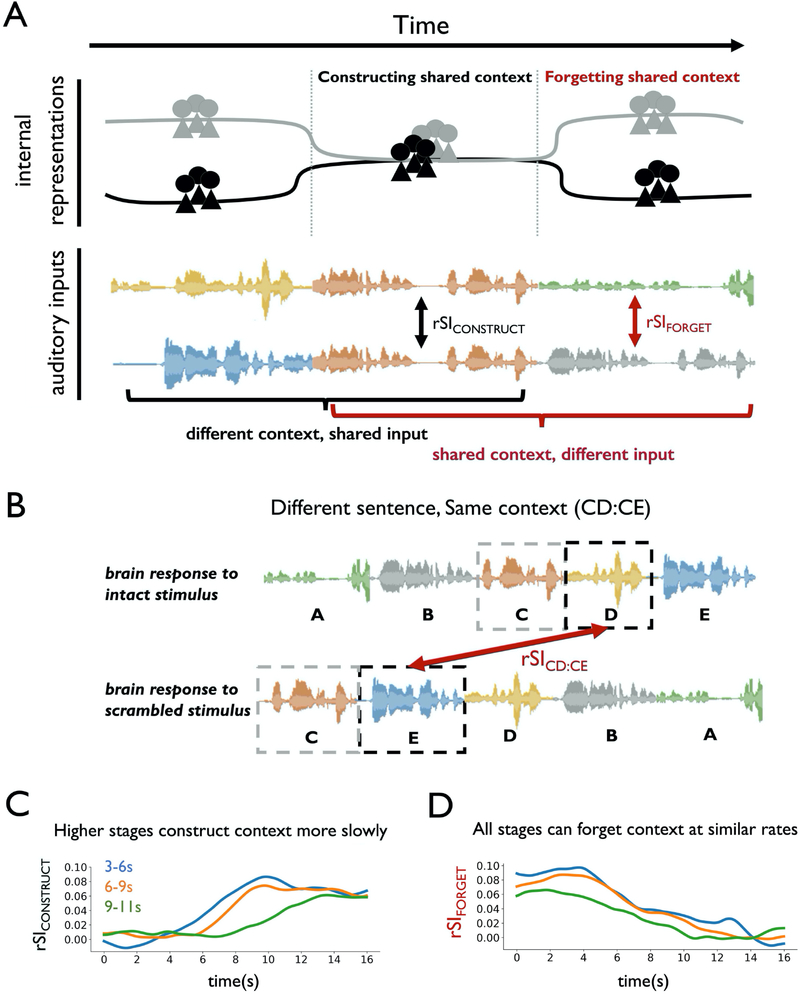
We have already shown that the two groups will gradually construct an aligned mental context and will begin to respond in the same way to common input (Figure 4A, middle), but what happens when the common input ends? At this moment, the two groups begin to hear different inputs, and yet these different inputs are preceded by the shared context. We expect that the two groups should gradually “forget” the previously shared mental context, but its influence may persist for some time (Figure 4A, right).

Figure 4. Distinct timescales of alignment and separation in cortical dynamics.

(A) Schematic of internal representations falling into and out of alignment as common and distinct inputs are presented. Two groups gradually construct a shared context when they listen to the same input preceded by different contexts, and thus their neural responses fall into alignment. When common input ends, the two groups begin to process a distinct input preceded by a shared context, and participants forget this shared context over time. (B) Schematic of inter-subject pattern correlation (ISPC) analysis, when different speech segments are preceded by the same context. Here, segment D in the intact group and segment E in the scramble group were both preceded by segment C (CD:CE). (C) Empirical rSI_DE:CE results grouped by alignment time of 3–6 seconds, 6–9 seconds and 9–11 seconds. (D) Empirical rSI_CD:CE results, using the same region groupings from the rSI_DE:CE results in Panel C. Regions at different levels of cortical hierarchy can forget context at similar rates. rSI = intact-scramble ISPC.

How quickly will individual brain regions “forget” the previous shared context? In a linear integrator model, such as HLI, information is integrated with a fixed time constant, and so the rate of accumulating new information is strongly correlated with the rate of forgetting old information (See STAR Methods). This leads to a testable prediction: if temporal integration within each region has a fixed time constant, then regions which integrate information more slowly (i.e. higher-order regions) should also forget prior information more slowly. Thus, we can test the class of linear integrator models by testing whether rates of contextual alignment and separation are correlated across regions.

Contrary to the predictions of linear integrator models, rates of alignment and separation were uncorrelated in the human cerebral cortex. We operationalized the “forgetting” of shared context as the “separation time” of neural responses that begin with a common context. The separation time was measured analogously to alignment time: how quickly neural responses diverge when participants processed different input preceded by a shared prior context. To visualize the relationship between context construction and forgetting, we grouped brain regions according to their alignment time (rSI_CONSTRUCT or rSI_DE:CE) and then visualized the rate at which they forgot prior information (rSI_FORGET or rSI_CD:CE). The rSI_FORGET curves decreased at a similar rate, regardless of whether the corresponding rSI_CONSTRUCT curve had a fast or a slow alignment time (Figure 4D). Moreover, we observed no correlation between alignment time and separation time across ROIs (r = −0.13, p=0.33, Figure S5B). This decoupling of alignment times and separation times cannot be explained by fixed-rate linear integrator models, such as HLI, in which the correlation between alignment times and separation times is strong (r = 0.99, Figure S5B).

Gated integration using hierarchical autoencoders in time (HAT)

The mismatch of alignment and separation times in cortical dynamics indicates that the integration rate is variable, consistent with the notion that temporal sequences are grouped into events, and that prior context is more rapidly forgotten at event boundaries (Reynolds et al., 2007; Zacks and Tversky, 2001). Therefore, we set out to develop a model which can account for the existing data on hierarchical temporal processing, while also providing mechanisms for grouping temporal sequences. We developed the hierarchical autoencoders in time (HAT) model, which employs a nonlinear and gated approach to temporal integration. The HAT model was inspired by TRACX2, a recurrent network model of human sequence learning (French et al., 2011; Mareschal and French, 2017).

The HAT model is composed of a stack of “autoencoder in time” (AT) units (Figure 5B, details in STAR Methods). At each time step, each AT unit attempts to generate a simplified, or compressed, joint representation (hidden representation, HID) of its current input (IN) and its prior context (CNTX, Figure S1). The higher order AT units possess longer intrinsic timescale τ, so their context is less influenced by their input at each moment (Figure 5C). Also, the proportion of present input that is combined with prior context (and transmitted from a lower AT unit to a higher AT unit) depends on a reconstruction error (or “surprise”), α, which is computed locally within each AT unit (Figure 5D). In sum, the HAT model performs a nonlinear (compressive) integration of its context representation with each input, and this integration is gated by surprise.

Figure 5. Modeling context construction and context forgetting.

(A) HLI model schematic: the new state of each unit is a linear weighted sum of its old state and its new input. (B) HAT model schematic: each region maintains a representation of temporal context, which is combined with new input to form a simplified joint representation. (C) An AT unit, in which local context CNTX is updated via hidden representation HID and current input IN, modulated by time constant τ and “surprise” α. α is computed via auto-associative error Δ and a scaling parameter k. (D) In HAT, the input to level i is gated by surprise α from level (i-1). (E) HLI simulation of rSI_DE:CE predicts longer alignment time at higher stages of processing. (F) HAT simulation of rSI_DE:CE predicts longer alignment time at higher stages of processing. (G) Empirical rSI_DE:CE results grouped by alignment time, consistent with predictions of both HLI and HAT. (H) HLI simulation of rSI_CD:CE predicts that regions that construct context slowly will also forget context slowly. (I) HAT simulations predict that the timescale of context separation (rSI_CD:CE) need not be slower in levels of the model with longer alignment times (rSI_DE:CE). (J) Empirical rSI_CD:CE results grouped by alignment time. HLI = hierarchical linear integrator, HAT = hierarchical autoencoders in time, AT = autoencoder in time, rSI = intact-scramble ISPC.

HAT captures empirical patterns of context construction and forgetting

The HAT model successfully captured the hierarchical context dependence phenomenon (Figure S2G). Moreover, HAT exhibited an important advantage over the signal gain model and HLI model: its ability to integrate over time was more selective for previously learned sequences (STAR Methods; Figure S2C, E, G; Model by Training Interaction η² = 0.37). In fact, integration in the full HAT model was more learning-dependent than any other model tested, including linear integrator variants and HAT variants (Figure S5C, Table S1). We analyze the HAT model further in Supplemental Information (Figure S2 and S5; Table S1).

The HAT model also captured the empirical result that higher-level regions construct new context more slowly than sensory regions (delayed ramping in rSI_DE:CE or rSI_CONSTRUCT, Figure 5F). Moreover, because the HAT model can prevent the integration of prior context with new information (using its context gating mechanism) the influence of prior context could be reduced at moments of high surprise (Figure 5D, E, Figure S2K, L). Therefore, while the HLI model predicts that regions which slowly integrate input must also slowly forget prior context (Figure 5H), the HAT model predicts that higher-level regions need not forget prior information more slowly (Figure 5I). Thus, HAT provided predictions most consistent with all of our empirical results (see also Figure S5C, Table S1).

We have shown that HAT model can account for two new empirical phenomena: hierarchical variation in the “alignment time” during processing of a shared input (Figures 2, 3) and the decoupling of alignment-timescales and separation-timescales (Figure 4, 5). But what are the essential computational elements required to account for these data? Although it is difficult to determine necessity in general, we tested an ensemble of model variants and found that the gating of integration was a necessary component, within this ensemble, to explain the data. Moreover, both hierarchical architecture and nonlinearity of integration increased the sensitivity of all models to prior temporal context (Table S1; Figure S5; and STAR Methods).

Discussion

The theory of hierarchical timescales in the cerebral cortex is influential across cognitive, systems and clinical neuroscience (Baldassano et al., 2017; Burt et al., 2018; Chaudhuri et al., 2015; Chen et al., 2016; Cocchi et al., 2016; Demirtaş et al., 2019; Fuster, 1997; Hasson et al., 2008, 2015; Himberger et al., 2018; Kiebel et al., 2008; Murray et al., 2014; Runyan et al., 2017; Scott et al., 2017; Simony et al., 2016; Watanabe et al., 2019; Yeshurun et al., 2017; He, 2011; Spitmaan et al., 2020; Wasmuht et al., 2018; and Zuo et al., 2020). The intrinsic timescale of brain dynamics are longer in higher order areas, as shown by single unit data in macaques (Murray et al., 2014; Ogawa and Komatsu, 2010), optical imaging in mice (Runyan et al., 2017) and neuroimaging and intracranial measures in humans (Honey et al., 2012; Stephens et al., 2013). The hierarchical gradients of timescales in brain dynamics are correlated with gradients of myelin density (Glasser and Van Essen, 2011), gene transcription (Burt et al., 2018) and anatomical connectivity (Margulies et al., 2016). Moreover, accounting for regional variation in timescales improves the prediction of human functional connectivity (Demirtaş et al., 2019), and individual differences in timescales predict clinical behavioral symptoms (Watanabe et al., 2019).

Despite these advances in our understanding of hierarchical cortical dynamics, our models of the associated information processing have remained phenomenological. What are the computations that integrate past and present information within the hierarchical networks of our brains? Here, we used a new approach to measure the construction and forgetting of temporal context in the human brain, and we used these data to constrain computational models of hierarchical temporal integration.

Our inter-subject pattern correlation (ISPC) analysis revealed a phenomenon of “hierarchical context construction”: when two participants heard the same sentence preceded by different contexts, their neural responses gradually align. The responses aligned earliest in early sensory cortices, followed by secondary cortices, and some higher order regions did not align until participants shared 10 seconds of continuous common input. This phenomenon of hierarchical context construction suggests the existence of a distributed and multi-scale representation of prior context, which affects the neural response to input at each moment. The existence of a distributed context representation is consistent with the finding that recurrent neural networks provide a better prediction of visual pathway responses than feedforward models (Shi et al., 2018; Kietzmann et al., 2019), especially for the later component of the neural response (Kar et al., 2019).

Regional variations in hemodynamic peaks (about ~1–2 seconds between sensory and higher order cortices (Belin et al., 1999; Handwerker et al., 2004)) cannot account for the 8 s inter-regional variation we observed in alignment time (Figure S4B). Additionally, if a hemodynamic delay increased the alignment time in a particular region, this should also delay its separation time, leading to a positive correlation between alignment and separation times, but this was not observed (Figure S5B).

Regions do not “forget” the context at the same rate as they “construct” context (Figure 5E, H). This implies the existence of a mechanism for flexibly altering how the past influences present responses. Linear integrator models lack such flexibility: the rate of contextual alignment and the rate of separation are both inversely related to a fixed parameter, ρ, and so the past and present information are linearly mixed in the same way regardless of their content. By contrast, models such as HAT can flexibly modulate how prior context is integrated with new input. In HAT, if prior context can be successfully compressed with new input, then information about context is preserved, but if prior context and new input are incompatible (leading to prediction error), then the context is overwritten (Mareschal and French, 2017). A distributed and surprise-driven “context gating” mechanism is consistent with evidence for pattern violations being signaled at multiple levels of cortical processing (Bekinschtein et al., 2009; Himberger et al., 2018; Wacongne et al., 2011).

Context gating is important for clearing out irrelevant prior information at the boundaries between chunks or events (DuBrow et al., 2017; Ezzyat and Davachi, 2011; Reynolds et al., 2007). Baldassano et al. (2017) revealed that almost all stages of cortical processing are sensitive to event structure, with sensory regions changing rapidly at the boundaries between shorter events (e.g. eating a piece of food) and higher order regions changing at the boundaries between longer events (e.g. having an entire meal). However, because the immediate stimulus and its preceding context always covaried, it was uncertain whether rapid cortical state changes reflected rapid changes in input, rapid changes in contextual influence, or both. Here, by separately controlling current input and prior context, we demonstrated that with the sharp event boundaries introduced in our stimuli, the local context could be gated at those boundaries. The gating of context may be driven by an immediate prediction error, as in the HAT model, or via a more diffuse breakdown of temporal associations (Schapiro et al., 2013)

At a computational level, context gating is widely used in processing information sequences and in easing learning. Gated neural networks are applied to capture long-range temporal dependencies in sequence learning (Hochreiter and Schmidhuber, 1997). Combining gated neural networks with structured probabilistic inference can generate human-like event segmentation of natural video input (Franklin et al., 2019). Moreover, gating is a broadly useful process in biological models of working memory, both for preventing sensory interference with maintained information and for flexible updating and integration (Carpenter and Grossberg, 1987; Heeger and Mackey, 2018; O’Reilly and Frank, 2006), and disturbances in gating mechanisms may manifest in severe cognitive deficits (Braver et al., 1999).

Our computational approach was inspired by the neurocognitive models of Botvinick, (2007) and Kiebel et al. (2008), in which higher stages of cortical processing learned or controlled temporal structure at longer timescales. More generally, multi-scale machine-learning architectures have been proposed for reducing the complexity of the learning problem at each scale, and for representing multi-scale environments (Chung et al., 2016; Jaderberg et al., 2019; Mozer, 1992; Mujika et al., 2017; Schmidhuber, 1992; Quax et al., (2019)). In neuroscience, multiple timescale representations have been proposed for learning value functions (Sutton, 1995), for tracking reward (Bernacchia et al., 2011), and for perceiving and controlling action (Botvinick, 2007; Paine and Tani, 2005). Moreover, the concept of temporal “grain” is influential in theories of hippocampal organization (Brunec et al., 2018; Momennejad and Howard, 2018; Poppenk et al., 2013; Shankar et al., 2016) and cortical organization (Baldassano et al., 2017; Fuster, 1997; Hasson et al., 2015; Lü et al., 1992; Wacongne et al., 2011). Consistent with hierarchical timescale models, we find that more temporally extended representations are learned in higher stages of cortical processing, where dynamics change more slowly. These data constrain future models by revealing the moment-by-moment time-course of context construction in the cerebral cortex, and by demonstrating that slowly-evolving context representations can be rapidly updated at event boundaries.

Limitation and Future Directions

For parsimony, we modeled temporal integration using only within-layer recurrence (i.e. without inter-regional recurrence), but there is rich anatomical reciprocity in the brain (Bastos et al., 2012; Markov et al., 2013; Sporns et al., 2007) and many models of cortical function emphasize the importance of feedback and prediction (Friston and Kiebel, 2009; Heeger, 2017; Heeger and Mackey, 2018; Rao and Ballard, 1999; Kietzmann et al. (2019)). It is not clear which expectation effects in temporal processing rely on top-down predictions from high-level representations, as opposed to more local recurrent integration or facilitation (e.g. Ferreira and Chantavarin, 2018). Long-range feedback is essential for some brain functions (e.g. attentional control and imagery), and models with (weak) long-range feedback could account for our data. Still, the local recurrence of the HAT model was sufficient to account for the integration processes we measured during narrative comprehension. Also, feedforward signaling in the HAT model does depends on the magnitude of layer-local surprise, which is a feature in common with predictive coding models.

The gating and learning in the HAT model are much less flexible than in many machine learning architectures (e.g. long-short-term-memory networks, LSTMs, and gated recurrent units, GRUs). Gates in neural networks (such as forget gates in LSTMs or update gates in GRUs) can be triggered by arbitrary states elsewhere in the network, but the gating in HAT is determined entirely by a local prediction error. Additionally, learning in HAT is layer-local, rather than end-to-end. The locality of the HAT model adds to its biological plausibility, but future work should test the necessity of more powerful forms of gating and event-learning, for capturing human sequence processing.

In future work we will train HAT variants on linguistic corpora, and use these to generate context-aware encoding models of the neural response to complex language (e.g. Jain and Huth, 2018; Jain et al., 2019). Encoding models quantitatively predict the neural response at each moment, providing a comparison against the full richness of the data; at the same time, powerful encoding models may also be more difficult to mechanistically interpret. More generally, three important questions for future work will be (i) whether gating of past context is binary or graded, depending on the magnitude of local prediction error; (ii) whether context gating can occur entirely independently across distinct levels of processing; and (iii) how the context gradient we observed relates to local neuronal processes on the sub-second scale (Demirtaş et al., 2019; Norman-Haignere et al., 2019; Goris et al., 2014 and Zhou et al., 2018).

To recap, we showed that brain regions align, second-by-second, in a hierarchical gradient, when they are exposed to a common input preceded by distinct contexts. We ruled out explanations of this phenomenon based on stimulus engagement or fixed-rate integration processes. Our models and data provide concrete constraints for models of brain function in which memory is inherent to perceptual and cognitive function (Buonomano and Maass, 2009; Frost et al., 2015; Fuster, 1997; Hasson et al., 2015; McClelland and Rumelhart, 1985; Shi et al., 2018), and we suggest general principles – active integration and gating – that are used in temporal information processing across the cortical hierarchy.

STAR Methods

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Christopher J. Honey (chris.honey@jhu.edu).

Neuroimaging data and stimuli are available at https://openneuro.org/datasets/ds002345 (DOI: 10.18112/openneuro.ds002345.v1.0.1; alias: notthefall).

Python model implementations are available at https://github.com/HLab/ContextConstruction.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Subjects

Forty-three subjects (all native English speakers) were recruited from the Princeton community (20 male, 23 female, ages 18–29). Out of the 43 subjects, 21 subjects participated only in the intact condition, 21 subjects participated only in the scramble condition, and one subject participated in both conditions. Nine subjects (all native English speakers) were recruited from the Johns Hopkins community (5 male, 4 female, ages 19–41), and all 9 subjects participated in both intact and scramble conditions. All subjects had normal hearing and provided informed written consent prior to the start of the study in accordance with experimental procedures approved by the Princeton University Institutional Review Board (Princeton data) and the Johns Hopkins Medical Institute Institutional Review Board (Johns Hopkins data). Conditions in which the head motion were >1 mm or where the signal was corrupted were discarded from the analysis. Overall, 31 subjects participated in the intact condition, and 31 subjects participated in the scramble condition.

Acquiring and Preprocessing of Neuroimaging Data Princeton Dataset

Imaging data were acquired from Princeton Neuroscience Institute (Nastase et al.), on a 3T full-body scanner (Siemens Skyra) with a 20-channel head coil using a T2*-weighted echo planar imaging (EPI) pulse sequence (TR 1500 ms, TE 28 ms, flip angle 64 °, whole-brain coverage 27 slices of 4 mm thickness, in-plane resolution 3 by 3 mm, FOV 192 by 192 mm). Preprocessing was performed in FSL, including slice time correction, motion correction, linear detrending, high-pass filtering (140 s cutoff), coregistration and affine transformation of the functional volumes to a template brain (MNI). Functional images were resampled to 3 mm isotropic voxels for all analyses.

Johns Hopkins Dataset

Imaging data were acquired on a 3T full-body scanner (Phillips Elition) with a 20-channel head coil using a T2*-weighted echo planar imaging (EPI) pulse sequence (TR 1500 ms, TE 30 ms, flip angle 70 °, whole-brain coverage 28 slices of 3 mm thickness, in-plane resolution 3 by 3 mm, FOV 240 by 205.71 mm). Preprocessing was performed in FSL, including slice time correction, motion correction, linear detrending, high-pass filtering (140 s cutoff), and coregistration and affine transformation of the functional volumes to a template brain (MNI). Functional images were resampled to 3 mm isotropic voxels for all analyses.

METHOD DETAILS

Linear Integrator Models

The linear integrator model was adapted and modified from the classical temporal context model (TCM). TCM successfully accounts for human sequence encoding and retrieval behavior, using the concept of a drifting internal context (Howard and Kahana, 2002). The linear integrator model employs two buffers, each of which is represented as a real-valued vector: the feature buffer which contains the features of items processed in the sequence stream; the context buffer (CNTX) composed of a “temporal context vector”. A weight matrix M^FT, which is trained by Hebbian learning mechanism, maps stimulus features to their corresponding representation in the context space; this transformation results in an “input vector”, IN. At each time step, the temporal context at the next time point CNTX(t + 1) is updated by adding the mapped input IN(t) to the prior context CNTX(t):

$$\mathit{CNTX}(\text{t}+1)={\rho }_i\mathit{CNTX}(\text{t})+{\beta }_i\mathit{IN}(\text{t})$$ (1)

where ρ_i determines the rate of temporal integration, and we choose ${\rho }_i\approx \sqrt{1-{{\beta }_i}^2}$ in order to prevent the CNTX vector from changing its length.

Parallel Linear Integrator Model: PLI

In order to simulate a very multi-scale temporal integration process, we built a parallel linear integration model (PLI), in which we set the β_i parameter in Equation (1) to 0.9, 0.7 and 0.5 for Level 1, Level 2 and Level 3 of the model, respectively. Thus, in the PLI model, all levels receive the same input IN, but the higher levels of the model will preserve more context (via their larger ρ_i parameters).

Hierarchical Linear Integrator Model: HLI

In order to approximate a sequence of processing stages in a cortical hierarchy, we implemented a hierarchical linear integrator (HLI) model in which the output of lower stages serves as the input to the next stage of processing. In particular, we stacked the three linear integrator units (Equation 1), with time constants set just as for the PLI model. However, the input vector IN for stage N+1 of the model was taken to be equal to the CNTX vector from stage N.

The Signal Gain Model

We implemented a simple signal gain model whose architecture is similar to the PLI model, but where the signal, X(t), is unaffected by its previous state. In particular, we set ρ_i = 0 in Equation (1). The signal gain model assumes that (i) scrambling the stimulus decreases the relative magnitude the stimulus representation and (ii) this effect is larger in higher-order brain regions. Thus, to simulate scrambling effects, we decreased the signal-to-noise ratio in the model for higher processing stages or finer scrambling conditions. In particular, we decreased signal-to-noise ratio by increasing the noise amplitude, σ, as follows:

$$X(t)=IN(t)+{ϵ}_{layer}(t){ϵ}_{scramble}(t)$$ (2)

where ϵ_layer(t) and ϵ_scramble are independent random variables, sampled independently at each time step from a Normal distribution with 0 mean and standard deviations σ_layer and σ_scramble, respectively. Implementing the assumptions of the signal gain model, we set σ_layer = 0 in Layer 1, σ_layer = 0.05 in Layer 2, and σ_layer = 0.09 in Layer 3 to simulate hierarchical temporal integration; and we set σ_scramble= 0.1, 0.5 or 0.9 for the paragraph-level, sentence-level, and word-level scrambling conditions.

Hierarchical Autoencoders in Time: HAT Model

Local processing unit: the AT module

Each local processing stage in HAT is an “autoencoder in time” (AT) module. This AT module was adapted from the influential TRACX2 model for modeling human statistical learning and sequence learning behavior (Mareschal and French, 2017). Each AT module consists of three layers. There is an input layer (consisting of a concatenated input unit, IN, and a context unit, CNTX); there is a hidden layer (HID) which stores the compressed representation of the input layer; and there is an output layer storing the reconstruction of the input layer from the compressed HID representation (Figure S1). During training, the model will learn good internal (i.e. HID) representations of the [CNTX, IN] pairings that frequently co-occur. At the end of training, it should be able to accurately reconstruct “chunks” of input-and-context from the compressed (i.e. lower-dimensional) internal representation, HID.

In the AT module, information from the world is presented as a stream of symbols, one symbol at a time. For every time step of the model, the current input symbol, S_t, from the sensory environment is represented as a 1-by-N one-hot vector, where one scalar value is 1 and all others are −1. This new input vector is mapped to the IN bank at each time step. The prior context stored in the model is represented as another 1-by-N vector, which is stored in the CNTX bank.

Each time-step of the model proceeds as follows (please refer to Figure S1)

A. For the very first timestep, the model it is initialized with two consecutive stimuli (S_t-1, S_t) in the CNTX and IN banks (CNTX₁ = S₀, IN₁ = S₁). For all subsequent timesteps, the CNTX vector is updated according to Equation 7 (below), while IN_t = S_t.

B. Activity is propagated forward from the input and context banks (jointly of length 1-by-2N) to the hidden bank (1-by-N) via an affine transformation followed by a hyperbolic nonlinearity.

$$HI{D}_{1\times N}=\tanh \left({[CNTX,IN]}_{1\times 2N}\times V_{2N\times N}\right)$$ (3)

Thus, a compressive transformation is implemented via the mapping from the input and context (1-by-2N) to the hidden units, HID_t (1-by-N). A weight matrix V (of size 2N x N) contains the synaptic weights that transform the input layer to the hidden layer in this compression stage. After the hidden units in the model are updated in this way, another linear-nonlinear transformation is used to update the output nodes. A second weight matrix, W (of size N x 2N), is then right-multiplied with the hidden layer vector, HID_t, generating an output bank that is meant to approximately reconstruct the input bank of the model:

$${\left[CNT{X}^{\prime },I{N}^{\prime }\right]}_{1\times 2N}=\tanh \left(HI{D}_{1\times N}\times W_{N\times 2N}\right)$$ (4)

C. The objective is to make the “reconstruction” in the output banks, [CNTX′,IN′], as similar as possible to the actual input [CNTX,IN]. Therefore, an auto-associative error Δ is generated as the absolute difference of the input and output layer (the difference of the veridical and reconstructed representations):

$$\mathrm{\Delta }=\left|\left[CNT{X}^{\prime },I{N}^{\prime }\right]-[CNTX,IN]\right|$$ (5)

D. The “surprise” parameter, α, is calculated as the maximum value of Δ, multiplicatively scaled by a parameter k:

$$\alpha =\tanh (k\max (\mathrm{\Delta }))$$ (6)

Here, α is taken to indicate the “surprise” or “familiarity” that the model experiences in response to the combination of the current context, CNTX, and the current input, IN. When k is larger, the average amount of surprise (magnitude of α) is increased, and IN makes a larger contribution to the CNTX variable at the next time step.

The CNTX bank is updated as a linear mixture of IN(t) and HID(t), weighted by the surprise parameter, α:

$$CNTX(t+1)=(1-\alpha )HID(t)+\alpha IN(t)$$ (7)

If α is large, the model has not learned a good HID representation for accurately reconstructing IN_t and CNTX_t, and so the CNTX_t+1 bank will be overwritten by the input IN_t. If α is small, the model has learned a good compressed joint representation, HID_t, and this compressed representation becomes the context that is used for associating with the next sequential input IN_t+1.

The steps from A-D complete one iteration of the model, and the cycle continues with step A

When the model is brain trained, the transformation matrices (matrix V mapping from input layer to hidden layer, and matrix W mapping from hidden to output layer, Figure S1) are adjusted via backpropagation. The loss function is the norm of the auto-associative error vector Δ. The backpropagation weight updates are performed incrementally, one training exemplar at a time. Backpropagation is entirely local to each processing unit (it is not performed end-to-end across the entire network, even when AT units are stacked).

As the model is exposed to the sequential regularities of the input stream, it gradually learns good internal representations of [CNTX, IN] sequences, and so the auto-associative error gradually decreases. The model can also detect the event boundaries occuring in the sequence. At event boundaries, the model will be unable to generate an accurate compressed representation of [CNTX, IN], and will generate a large error α. This large error will then bias the model to overwrite its prior context (from the old event) with its current input (from the new event).

In summary, the AT module exhibits three important features: (1) prior context is preserved in the CNTX bank; (2) the updating / overwriting of prior context is gated by an auto-associative error Δ which is summarized in the “surprise” parameter, α; and (3) the model minimizes its auto-associative error Δ by learning the statistical relationships between prior context and new input.

We hypothesize that each stage of processing in the cortical hierarchy exhibits these three functional properties. Therefore, the HAT model is thus composed of a stack of AT modules, each with these functional properties.

Stacked AT Modules: Hierarchy of Autoencoders

We employed a HAT model with three levels (Figure 5B). Each level is an AT module. The information flow in HAT is globally feedforward with local feedback: each AT module receives recurrent input from its own past state, but there is no backward information flow from AT module i+1 to AT module i.

Information processing in the HAT architecture possess two key features: first, the context update depends on a local timescale and is gated by surprise; second, the information flow between levels is gated by surprise.

Context update via timescale and surprise

Figure 5C illustrates the structure of each AT module in HAT. As described above, the AT module transforms the input and context [CNTX, IN] into a compressed internal representation, HID, and the model then attempts to reconstruct the [CNTX, IN] pairing from this lower-dimensional internal representation. The local context in each level unit is updated by a combination of HID and IN, modulated by a level-specific time constant τ and local surprise α, respectively (Figure 5C). If τ is larger than α, the model tends to preserve more context from HID; if α is larger than τ, the model tends to overwrite the context using the current input IN, as the equation illustrates:

$$CNT{X}_i(t+1)=\frac{{\tau }_i}{{\tau }_i+{\alpha }_i}\times HI{D}_i(t)+\frac{{\alpha }_i}{{\tau }_i+{\alpha }_i}\times I{N}_i(t)$$ (8)

Note that in the full HAT model implementation reported in the main text, we employed Equation (8) rather than the simpler Equation (7) which describes a single AT module.

To capture the assumption that higher-level regions process information over longer timescales while lower-level regions process information over shorter timescales, we set τ equal to 0.8 for the top level, 0.5 for the middle level and 0.2 for the bottom level of the 3-level HAT model. Thus, relative to the lower levels of the model, the CNTX variable in higher levels of the model will preserve more information about the context in prior timesteps. Of course, in addition to this fixed parameter τ which determines how much context is typically preserved in each level, the context updating is also influenced by the surprise parameter, α, which can transiently increase the influence of the input IN as the context is updated.

Information flow in HAT is gated by surprise

We designed the feedforward information flow in HAT based on the notion that temporal integration is a distributed process, assuming that higher-level circuit perform a similar operation as lower-level circuits (i.e. linking input to prior context) but the higher levels may learn to associate chunks instead of single elements in the sequence. Our goal was that, for a multi-level compound like the word airplane, the first level of the model might learn to chunk the phonemes within air and plane, and the second level might learn to chunk air and plane to represent the larger word airplane. Thus, the input to the higher levels of the HAT model should be the compressed (chunked) representations from the lower levels. However, this process should also be modulated by surprise, as higher levels should only accept “successful” chunks from the layer below.

Therefore, the input to the higher levels of HAT is a linear mixture of HID and IN from the level below, modulated by the surprise α:

$$I{N}_{i+1}(t)=\left(1-{\alpha }_i\right)\times HI{D}_i(t)+{\alpha }_i\times I{N}_i(t)$$ (9)

If the lower-level unit detects a large surprise (if α is near 1), more of the lower-level’s input would be passed on as input to the upper level. On the other hand, if the lower-level unit detects small surprise (if α is near 0), then the “temporal chunk” representation from the lower level would be transmitted as input to the upper level (Figure 5D).

Nonlinearity

In the HAT model, the representation of the word is a nonlinear combination of the letters, which depends on those letters having been seen before in similar sequences. This is in contrast to the HLI model, where the representation is simply an exponentially weighted sum of each item; the relationship of new input and prior context (e.g. whether they are related or unrelated) does not affect the magnitude or form of the context update in HLI.

HAT variants

Parallel AT model

To examine whether a hierarchical stage-by-stage processing architecture is required to reproduce the empirical phenomena reported here, we implemented a Parallel AT (PAT) model which consists of three AT units with different τ parameters (i.e. 0, 0.4 and 0.8 for level 1, 2 and 3, analogous to the hierarchical models). In contrast to HAT, each AT unit in the PAT model directly receives the same sequence of inputs from the environment. The inputs are processed in parallel, without any interaction between the AT units.

HAT variants with limited gating

To examine whether context gating is a necessary mechanism for the HAT model to be able to reproduce the empirical phenomena of hierarchical temporal integration, we generated a set of HAT models with variations their gating mechanisms. Specifically, we turned off the surprise-modulated context gating mechanism, either locally (i.e. the context gating within each AT module) or globally (i.e. the gating of transmission between levels of the model), or we turned off all gating effects.

HAT-Local Gating: HAT-LG

HAT-LG is a HAT model with only local gating (within each AT module) but no transmission gating mechanism (between AT modules). Thus, the input to the higher levels of the model is simply a copy of the HID from the lower level, regardless of the α parameter (as in Equation 10).

$$I{N}_{i+1}\left(t\right)=HI{D}_i\left(t\right)$$ (10)

However, the within-level CNTX update is still gated by surprise (Equation 8).

HAT-Transmission Gating: HAT-TG

HAT-TG is a HAT model with only transmission gating but no local gating mechanism. That is, the local context is reset by a fixed amount of input based on the level-specific τ (Equation 2) without the modulation of surprise ⍺.

$$CNT{X}_i(t+1)={\tau }_i\times HI{D}_i(t)+\left(1-{\tau }_i\right)\times I{N}_i(t)$$ (11)

However, the between-level transmission is still gated by surprise α from level below, as in Equation (9).

HAT-No Gating: HAT-NG

HAT-No Gating or HAT-NG, is a HAT model with neither local nor transmission gating mechanism. There is no surprise or α modulated gating mechanism; instead, the local context is reset by a fixed amount of input based on the level-specific τ (Equation 11). There is no transmission gating in this model: the input of the upper level is a copy of the HID vector from the lower level, as described in Equation (10).

Model Simulations and Predictions

Simulations of Hierarchical Context Dependence

To test for the phenomenon of hierarchical context dependence in each model (Figure 1D), we employed a strategy analogous to the original human experiments. We presented the model with intact and scrambled versions of a time-varying stream of input. We then measured the context effects by comparing the model responses (internal representations) of the same input preceded by different contexts.

As described in the main text, for a model to account for the hierarchy of context dependence it should capture two key phenomena

(P1) lower processing stages of the model should be insensitive to context change (analogous to sensory cortical regions, Figure 1D, left bars);

(P2) increasingly higher processing stages of the model should be increasingly sensitive to temporal context further in the past (analogous to the higher stages of cortical processing, Figure 1D, right bars).

We trained and tested six different models, including the signal gain model, the parallel linear integrator model (PLI), the HLI model, the parallel autoencoders in time model (PAT), as well as the HAT model, and the no-gating variant of the HAT model. In addition, we tested (for each model) whether the context dependence effect was selective for previously trained sequences. In other words, we measured the “learning effect” (Table S1, see below).

Training Procedure

To examine whether each of our models exhibit a hierarchy of context dependence, we simulated an approximation of the experimental paradigm in Lerner et al. (2011). We trained the models with a 30-element long “intact” sequence. The intact sequence was presented 600 times. Each element of the input was encoded as a one-hot vector of length 30. We also added uniformly distributed noise to each scalar value of each input sequence. The noise samples were independently drawn from a uniform distribution on [−0.3, 0.3]. The purpose of the noise was to improve the model’s generalizability, and to approximate the fact that real-world sequence learning occurs in the presence of noise. To prevent the model from learning a spurious relationship between the end of the intact sequence and the beginning of the next presentation of the intact sequence, we added “random filler” sequences (length=5 symbols) between intact segments. Each of the random filler symbols was an independently generated random vector, with elements uniformly distributed in the range [−1, 1] for the HAT model and its variants, and in the range [0,1] for other models. (Figure S2A, depicted as an ‘x’ between intact segments).

Testing Procedure

After training, the weights in each model were fixed; no further weight change was allowed during test. We then compared the models’ representations of intact and scrambled sequences. The three scrambled sequences were designed to preserve the intact structure at three different scales: the long-scale (6 element subsequences were preserved), medium-scale (3 element subsequences were preserved) and fine-scale (2 element subsequences were preserved). Each testing ensemble (e.g. “medium scale scramble”) was composed of 10 “test sequences”. Each test sequence was a length-30 sequence which was a randomly scrambled version of the intact sequence. All test sequences within an ensemble were scrambled at the same scale, but with different permutations. Therefore, each test sequence exhibited preserved structure on the relevant scale. As during training, fillers were again inserted between each of the 10 sequences that composed a testing ensemble (Figure S2A, the ‘x’ between the length-30 test sequences). We then defined the “context dependence” (CD) effect as the difference in intact-scramble correlation across the long-scramble and short-scramble conditions: CD = corr(intact, LSS) – corr(intact, FSS) (see Figure S2).

Testing the Learning Effect

To assess whether models captured the temporal structure of the intact sequences due to sequence-specific learning (rather than due to an intrinsic ability to maintain prior context of any kind of sequence), we additionally trained models with random sequences, that were generated by shuffling the intact structured sequences. We then tested these shuffle-trained models with the same (non-random) testing sequences that were used to test the normal structure-trained models. In this way, we could compare the CD effects for the models trained with structured sequences against the CD effect for models trained with randomly shuffled sequences (Figure S5C). We defined the “learning effect” as the difference in CD values between a model trained with structured sequences and the same model trained with shuffled sequences.

Simulations of context construction and forgetting

We set out to model the context construction results (Figure 2,3) using the signal gain model, the linear integrator models and the HAT model and its variants. The training sequences and procedure were the same as for modeling of the Lerner et al. (2011) data. For testing, we only simulated the models with the intact and the paragraph-level scrambled sequences, as we took these levels to correspond to the intact and scramble conditions in the empirical data.

Timescales of alignment and separation were analyzed in the model in an analogous manner to how they were assessed in the empirical data. For clarity, we introduce notation that discriminates the cross-group similarity measure rSI for the alignment and separation analyses. Specifically, we use rSI_CONSTRUCT = rSI_DE:CE for the rSI in the context alignment (“construction”) analysis, and rSI_FORGET = rSI_CD:CE for the rSI in the context separation (“forgetting”) analysis. The context alignment curve, rSI_DE:CE, was estimated by computing ISPC on the internal representations of each model. Internal representations were measures as the same six-element segments were presented as input, preceded by different segments in the intact and scramble group. Similarly, for the separation curve, rSI_CD:CE, the correlations were measured in the model simulation by performing ISPC on the hidden representations across two different “groups” of model runs.

To simulate different “participants”, we added noise to the inputs of each model, so that there would be some variation across runs in the generated responses. In particular, for the HAT model we added independent random sample from a Normal distribution $\sim \mathcal{N}(0,0.5)$ and for the HLI model we added independent random noise $\sim \mathcal{N}(0,2)$ (the HLI model noise was larger, in order to generate more variance between “subjects” and better approximate the empirical data pattern). These noise samples were added independently to each element of the input vector on each timestep. In this way, by running 200 simulations, each with unique noise structure, we generated 100 simulated “subjects” for the intact and the scramble group, respectively.

Each model run was treated in the same way as the neural response of a single participant. Thus, we measured the responses across two groups of model runs, where responses were correlated across different segments (e.g. segment D in Group 1 and segment E in Group 2) which were preceded by the same segment (e.g. segment C was the preceding segment in both Group 1 and Group 2).

To compare the patterns of model predictions against empirical data, we also approximated the effect of “hemodynamics” in our model, by convolving the timecourse of each model’s internal representation with a temporal smoothing function. This convolution was performed only on the model output, and did not affect the internal dynamics of the simulation. The temporal smoothing function in the model consisted of two gamma functions to approximate the hemodynamic response (HRF). The probability density function of the gamma function is:

$$f(x,a)=\frac{x^{a-1}\exp (-x)}{\mathrm{\Gamma }(a)}$$

Here we set a = 2.5 for one gamma function to set the peak value, and a = 2 for the other gamma function for the undershoot value of our HRF.

Analysis of Linear Integrators

We analytically confirmed that the “alignment time” and the “separation time” of a linear integrator model are closely related. In particular, in limiting cases of simple linear integrators, the alignment time and separation are expected to be identical.

We consider two integrators, A and B, each of which is treated as a model of one participant. We will measure the correlation of the state of these integrators as a function of time.

At each time, t, the state of each integrator is an n-dimensional vector:

$$\begin{gathered} A_i(t)=\mathrm{scalar}\mathrm{value}\mathrm{of}\mathrm{voxel}i\mathrm{in}\mathrm{participant}A\mathrm{at}\mathrm{time}t \\ {B}_i(t)=\mathrm{scalar}\mathrm{value}\mathrm{of}\mathrm{voxel}i\mathrm{in}\mathrm{participant}B\mathrm{at}\mathrm{time}t \end{gathered}$$

Then we can define the vector of initial states of each integrator:

$$\begin{gathered} \mathit{A}(0)=\mathrm{initial}\mathrm{state}\mathrm{of}\mathrm{vector}\mathit{A} \\ \mathit{B}(0)=\mathrm{initial}\mathrm{state}\mathrm{of}\mathrm{vector}\mathit{B} \end{gathered}$$

and we can define the vector of time-varying input that each integrator receives:

$$\begin{gathered} {\mathit{I}}_{\mathit{A}}(t)=\text{input}\text{to}\mathit{A}\text{at}\text{time}t \\ {\mathit{I}}_{\mathit{B}}(t)=\text{input}\text{to}\mathit{B}\text{at}\text{time}t \end{gathered}$$

The alignment time is the time for two integrators to produce a similar response after receiving a series of identical input. Thus, to measure the alignment time, we assume that A(0) and B(0) are random initial starting points (eqch A_i(0) ~ N(0,1), each B_i(0) ~ N(0,1)) but the input is identical, so that I_A(t) = I_B(t) for all t. Under these conditions, we write A(t) = A_align(t), B(t) = B_align (t), and we define the “alignment similarity” using the Pearson correlation:

$$r_{align}(t)=corr\left({\mathit{A}}_{align}(t),{\mathit{B}}_{align}(t)\right)$$

Suppose the alignment time is the smallest t for which r_ALIGN(t) > K where 0 < K < 1 is an arbitrary threshold.

The separation time is the time for two integrators to produce a dissimilar response after receiving independent input. Thus, to measure the separation time, we assume that A(0) = B(0) while the inputs, I_A(t) and I_B(t), are statistically independent draws from N(0,1). Under these conditions, we write A(t) = A_sep(t), B(t) = B_sep(t), and we now define the separation similarity using the Pearson correlation:

$$r_{sep}(t)=corr\left({\mathit{A}}_{sep}(t),{\mathit{B}}_{sep}(t)\right)<1-K$$

Suppose that the separation time is the smallest t for which r_SEP(t) < 1 − K where 0 < K < 1 is the same threshold as chosen for the alignment time.

To show that alignment times and separation times are tightly related, we will show that

$$r_{align}(t)+r_{sep}(t)=1$$

so that r_align must increase at the same rate as r_sep decreases. Thus, for any choice of threshold, K, the time to align and the time to separate are equal.

For the update of our discrete-time linear integrator, we take:

$$A_i(t+1)=\rho A(t)+\lambda I_A(t)$$

where $\lambda =\sqrt{\left(1-{\rho }^2\right)}$.

By definition,

$$A_i(1)=\rho A(0)+\lambda I_A(0)$$

and

$$\begin{gathered} A_i(2)=\rho A(1)+\lambda I_{A,i}(1) \\ =\rho \left[\rho A(0)+\lambda I_A(0)\right]+\lambda I_{A,i}(1) \\ ={\rho }^{2}A(0)+\sum _{m=0}^1{\rho }^{1-m}\lambda I_{A,i}(m) \end{gathered}$$

We can iterate this equation to derive the form of A_i(t):

$$A_i(t)={\rho }^t{A}_i(0)+\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{A,i}(m)$$

and similarly

$$B_i(t)={\rho }^t{B}_i(0)+\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{B,i}(m)$$

We assume that each of the scalar values within the inputs, I_A,i and I_B,i, are independent draws from a Normal distribution with zero mean and unit variance. In conjunction with the choice of $\lambda =\sqrt{\left(1-{\rho }^2\right)}$, which scales the relative amplitudes of prior states of the integrator and its new input, this guarantees that $E\left[A_i(t)\right]=E\left[B_i(t)\right]=0$ and $\mathit{VAR}\left[A_i(t)\right]=\mathit{VAR}\left[B_i(t)\right]=1$.

Now suppose we consider the expression for the sample Pearson product-moment correlation between A(t) and B(t). This is a correlation computed across voxels (i.e. the vector A(t) correlated with the vector B(t). If we assume that each vector is composed of n voxels, then the correlation takes the following form:

$$\begin{gathered} r_{AB}(t)=corr(\mathit{A}(t),\mathit{B}(t)) \\ =\frac{{\sum }_{i=1}^n{A}_i(t)B_i(t)-n{\mu }_{A(t)}{\mu }_{B(t)}}{(n-1)s_{A(t)}{s}_{B(t)}} \end{gathered}$$

where μ_A(t) and μ_B(t) are the sample means of the vectors, and S_A(t) and S_B(t) are their sample standard deviations.

By the construction, the individual linear integrator units maintain a mean value of zero, and so μ_A(t), μ_B(t) → 0 as n →∞. Moreover, because of the choice $\lambda =\sqrt{\left(1-{\rho }^2\right)}$, which preserves the variance of the individual elements of the vector, the sample standard deviations, S_A(t) and S_B(t) are approximately constant over time.

Therefore, the variation in r_AB over time arises from changes in the inner product of the vectors describing each integrator:

$$\begin{gathered} \sum _{i=1}^n{A}_i(t)B_i(t)=\sum _{i=1}^n\left[{\rho }^t{A}_i(0)+\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{A,i}(m)\right]\left[{\rho }^t{B}_{i(0)}+\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{B,i}(m)\right] \\ =\sum _{i=1}^n[{\rho }^t{A}_i(0){\rho }^t{B}_i(0)+\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{A,i}(m){\rho }^t{B}_i(0) \\ +\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{B,i}(m){\rho }^t{A}_i(0)+\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{B,i}(m)\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{A,i}(m)] \\ \cong \sum _{i=1}^n\left[{\rho }^{2t}{A}_i(0)B_i(0)+\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{B,i}(m)\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{A,i}(m)\right] \end{gathered}$$

This last simplification occurs because the input to the integrators (I_A and I_B) are zero-mean vectors that are statistically independent of the initial states (A(0) and B(0));thus the cross-terms that multiply these factors have an expectation of zero, and their contribution to r_AB will tend to zero as n → ∞.

Now, if we consider the formula for ${\sum }_{i=1}^n{A}_i(t)B_i(t)$ above, the first term is a sum over products of the initial states (A(0) and B(0)) of the two integrators, while the second term is a sum over products of the inputs to the integrators (I_A and I_B). Thus, the variation in the correlation over time can be decomposed into two terms: one term is a contribution from the decaying memory of the initial conditions (A(0) and B(0)) while the other term is the contribution from the correlation in the input (I_A and I_B) to each linear integrator.

Finally, we can show that the quantity r_align(t) measures the time-varying contribution from shared input, while the quantity r_sep(t) measures the time-varying contribution from the shared initial conditions.

Recall that when we are measuring r_align(t), we assume that initial states of the two integrators are statistically independent but the inputs are identical. In this case $E[\left({\rho }^t{\mathit{A}}_i(0){\rho }^t{\mathit{B}}_i(0)\right]=0$, so that:

$$r_{align}(t)\cong \sum _{i=1}^n\left[\sum _{m=0}^{t-1}{\rho }^{t-1-m}\lambda I_{B,i}(m)\sum _{m=0}^{t-1}{\rho }^{t-m}\lambda I_{A,i}(m)\right]/K$$

where $\text{K}=(n-1)s_{A(t)}{s}_{B(t)}$ summarizes the length of the vector and the sample standard deviations, which are essentially constant over time and invariant to the initial conditions.

On the other hand, recall that when we are measuring r_SEP(t), the initial states of the two integrators are identical, but their inputs are statistically independent. In this case, $E\left[{\sum }_{m=1}^t{\rho }^{t-m}\lambda I_{B,i}(m){\sum }_{m=1}^t{\rho }^{t-m}\lambda I_{A,i}(m)\right)]=0$, so that

$$r_{sep}(t)\cong \sum _{i=1}^n{\rho }^{2t}{A}_i(0)B_i(0)/K$$

where again $K=(n-1)s_{A(t)}{s}_{B(t)}$.

Now suppose we have two linear integrators, and we set them to an identical initial state, and we provide them with identical input. In this case, both the initial state and the input are identical, and thus the correlation of the states of these two linear integrators will remain r_identical(t) = 1 for all values of t. But recall that we have shown that the correlation between the states of two linear integrators at time t, can be expressed as a sum of two values: the correlation that would have been measured if they had independent initial conditions (and identical input) and the correlation that would have been measured if they had identical initial conditions (and independent input). Thus, we can decompose the “identical” correlation into these two parts, writing:

$$r_{identical}(t)=r_{align}(t)+r_{sep}(t)=1$$

This identity implies that a linear integrator that generates a rapidly increasing alignment (with a short alignment time) must equally generate a rapidly decreasing separation (with an equally short separation time).

Empirical Measurements of Context Dependence

We time-shifted the neural response in each participant so as to minimize inter-subject variation in the hemodynamic response (Handwerker et al., 2004). First, we upsampled all BOLD timecourses to a 50 Hz timebase. Second, we aligned the neural response timecourses across subjects by shifting each subject to maximize the temporal cross-correlation with the mean timecourse of all other subjects within the A1 region. This shifting process was performed for each subject, iterating until no further shifting occurred. Having mitigated hemodynamic differences in this way, it was then necessary to align all participants to the timebase of the acoustic stimulus. A reference timecourse was generated by convolving the acoustic envelope of the auditory stimulus with a hemodynamic response function. The mean (across subjects) response timecourse in A1 was then shifted to maximize the correlation with this stimulus reference timecourse. These operations were performed separately for data from the intact condition and the scramble condition. Finally, we confirmed that the procedure was accurate by showing that the unscrambling procedure was accurate within A1. First, we checked that the intact and scrambled data exhibited the same ramping BOLD time-course in A1, locked to the onset of each sentence within each stimulus. Second, we confirmed that the unscrambled data (dependent on accurate segment onset timing) correlated with the auditory amplitude of the intact stimulus: r (intact neural response in A1, intact audio stimulus) = 0.53; r (unscrambled neural response in A1, intact audio stimuli) = 0.50.

We next partitioned the neural responses into distinct segments, based on the segment onset timing within the intact stimulus and scrambled stimulus, and unscrambled the data based on which segments corresponded. With this done, we first evaluated rSI in the primary auditory cortex (A1) and the right temporal parietal junction (rTPJ) to ensure that the unscrambling procedure was successful.

Inter-subject pattern correlation (ISPC)

The ISPC analysis quantifies the similarity of spatial patterns of neural responses at a moment in time. We quantify the similarity by correlating the pattern of voxel activation at each time point (Figure 2A). Similar to the inter-subject correlation (ISC) analysis which provides a measure of the temporal reliability of the responses to complex stimuli (Hasson et al. 2004), the ISPC analysis provides a measure of the spatial reliability of the response to the stimuli at each time point (see also Zuo et al., 2020). The ISPC method differs from conventional fMRI data analysis methods in that it circumvents the need to specify a model for the neuronal processes in any given brain region during story listening. Instead, the ISPC method uses one subject’s neural responses to a stimulus as a model to predict the neural responses within other subjects.

Using ISPC, we quantified the changes in the neural responses over time within each segment of the auditory stimulus. We computed similarity within the group of subjects listening to the intact story (the intact condition, rII), similarity within the group listening to the scrambled story (the scramble condition, rSS), and similarity across the intact and scrambled groups (rSI) (Figure 2B). The rII and rSS analyses provide an indication of how reliably a given region is responding to the stimulus (Intact or Scrambled) at a particular moment. Conversely, the rSI analysis across the two groups indicates the similarity across two groups, which may be experiencing the same input (but different contexts) or experiencing different input (but with the same prior context). For example, the main analysis (Figure 2C) examines the similarity across intact and scrambled groups when subjects process the same segments preceded by different contexts: we correlated responses to segment E, which was preceded by segment D in the intact group but preceded by segment C in the scrambled group). That is, when the context is disrupted in the scramble group, we measure how subjects re-construct the temporal context in order to align with the intact group.

Methodologically, the pattern-correlation method used here provides several practical advantages for measuring integration timescales. First, we showed that it can be used to measure timescales of context forgetting in addition to context construction. Second, the method is efficient: if reference data exists for the responses to the intact stimulus, then an rSI curve can be computed in a single participant using one presentation of one scrambled stimulus. Third, the rSI curve provides a profile of how context influence varies over time. We focused on alignment times in this study, but future studies could use the asymptote and slope of the rSI curve to constrain quantitative models of temporal integration.

Measuring similarity within and between groups

To calculate rII, we segmented the neural response according to the segments used to make the scrambled stimuli. For each segmentation, we analyzed the neural response of the first 16 seconds. We performed ISPC by correlating the neural response pattern of one subject in the intact group to the average neural responses of the remaining subjects in the intact group for each time point. This calculation of spatial patterns was performed separately for each timepoint in each segment. We generated an ISPC time course within each long segment for each subject. The rII was calculated by averaging the ISPC time course across all segments and subjects. The rSS was calculated using the same method, within the scramble group. To calculate rSI, for each long segment, we performed ISPC by correlating the neural response pattern of one subject in the scramble group to the average neural response of all subjects in the intact group. The rSI time-course was calculated by averaging the ISPC time-course across all segments and all subjects.

QUANTIFICATION AND STATISTICAL ANALYSIS

We used a combination of resampling methods and parametric tests to statistically evaluate all empirical and modeling results, as described below under each heading.

Quantifying context dependence in models

We measured the similarity of the representations generated by different levels of the model as a function of the amount of shared context. To quantify similarity, we correlated the hidden representation that was generated when the models were processing the intact and the scrambled sequences (Figure S2A). Specifically, we correlated the hidden representations of the last elements of the subsequences (e.g. the “r” in “qr”) in each scrambled sequence with the hidden representations of the same elements (the “r” in “qr”) in the intact sequences (see red symbols in Figure S2A). In this way, we measured how the representation of the identical stimulus was altered as a function of the context change.

We then defined the “context dependence” (CD) effect as the difference in intact-scramble correlation across the long-scramble and short-scramble conditions: CD = corr(intact, LSS) – corr(intact, FSS) (see Figure S2). To compare the CD in two models, we computed the distribution of CD values for each network and computed: (i) a parametric t-test of the difference in means and (ii) Cohen’s d to quantify the separation of the distributions. Training the HAT model on shuffled sequences produced a large and highly statistically significant decrease in sensitivity to temporal context. Comparing the original HAT model against the shuffle-trained variant, we obtained a large and highly statistically significant difference in context dependence: mean CD original = 0.50, mean CD shuffle-trained = 0.10; Cohen’s d = 5.42; t(98) = 27.1, p < 0.001. The results for other models are shown in Figure S5C.

Validating neural responses reliability

To examine whether there is a hierarchy of context construction in the cerebral cortex, we conducted the ISPC analysis for 400 ROIs across the whole brain, based on the parcellation of the cerebral cortex provided by (Schaefer et al., 2018). To determine the ROIs that showed reliable responses when people were processing the naturalistic narratives, we first identified brain regions that responded somewhat reliably to both the intact and scrambled stimuli. In particular, we chose an arbitrary threshold for rSS = 0.06 which produced a set of ROIs which are visually similar to the set of narrative-responsive regions reported by (Lerner et al., 2011).

We further validated the threshold by conducting a permutation test of the rII in primary auditory cortex, in which we compared the true rII with the “shuffled rII” calculated after shuffling the order of the segments: We first generated 10,000 shuffled orders of the segments. For each of these shuffled orders, we reordered the neural responses of one subject according to the shuffled order, and calculate the rII between the shuffled neural response of this one subjects with the mean neural responses of the rest of the subjects in the intact group (For the other subjects, the order was preserved). We repeated this procedure to all the 31 subjects in the intact group using the same 10,000 shuffled orders, and calculated the average rII for each shuffled order, generating a null distribution of the rII. We found that 0.06 is significantly higher than the null distribution (p<0.0001, Figure S3A), confirming that this is a valid threshold for determining ROIs showing reliable responses when people are processing naturalistic stimuli.

Using this validation criterion, we identified 83 ROIs out of 400 ROIs for further analyses. The raw curves of rII and rSS showed that the 83 ROIs showed reliable responses from the beginning to the end of the segments (Figure 2E), further indicating that rSS=0.06 is a valid threshold to determine ROIs showing meaningful responses when people were processing the intact and the scrambled stimuli.

Quantifying alignment time

To quantify the alignment time as an index for context construction of different regions, we fit the rSI_DE:CE curves with the logistic function

$$y=\frac{a}{1+e^{-b(t-c)}}+d$$

by using least-square regression to minimize error. Here, y is the dependent variable which is the rSI value and t is the time in seconds since the segment onset. The parameter a is the curve’s maximum value, b is the steepness of the curve, c is the time when the logistic curve reaches its half maximum value, and d is an offset term to adjust the initial value of the curve. Here we use the parameter c as the alignment time measurement for each ROI. Among the 83 ROIs which exhibited reliable responses to the scrambled stimuli, 4 ROIs were excluded because the logistic fitting procedure did not reliably converge; the rSI curves for these ROIs are shown in (Figure S3B).

We used a cross-validation approach to confirm that the logistic function is a good model for fitting rSI curves and evaluating the alignment time. In particular, we tested whether the logistic model fit (and associated alignment time) in a given ROI will generalize to predict similar values when the same fitting is preserved for that ROI in a separate group of participants. In each of the 100 folds of the cross-validation procedure, we randomly split the data into two subsets of participants (N=15 and N=16). We then used the training group (N=16) to estimate model parameters and the second half (N=15) as a test group for measuring out-of-sample error. In the in-sample data, we measured (i) the shape of the rSI curve; and (ii) the best-fit parameters for the logistic fit to that curve. We then measured the shape of the rSI curve in the out-of-sample data. In order to compute test error, we measured the mean squared error (MSE) in two ways. First, we computed MSE-data: we measured the error when predicting the out-of-sample rSI curve using the in-sample rSI curve. Second, we computed MSE-logistic: we measured the error when predicting the out-of-sample rSI curve using the logistic fit to the in-sample curve. After averaging MSE-data and MSE-logistic across all folds, we compared MSE-data and MSE-logistic for each ROI (Figure S3C). If the MSE for the logistic fit is comparable to that for the rSI curve itself, then we concluded that the logistic fit accurately captures the shape of the rSI curve in that ROI. As shown in the figure, the logistic model was not only comparable to the in-sample data in predicting the out-of-sample data, it was often even better, producing a more accurate prediction than the in-sample curve. This cross-validation performance suggests that logistic model (which correctly assumes a ramping profile) is a valid model for approximating the rSI curve and quantifying the alignment time of the data. The quality of the logistic model can also be confirmed by visually inspecting the curve fits (Figure S4A).

Having confirmed that logistic curves provide a good overall model fit, we used bootstrapping to estimate the uncertainty in the alignment time estimates derived from the logistic fits. In each ROI, the alignment time was derived from the c parameter in the logistic equation above. For each of 1,000 bootstrap iterations, we resampled 31 subjects with replacement from the subject pool, and then recomputed the rSI curve, the logistic fit, and the c parameters. This generated a distribution of 1,000 c values for each ROI. We then excluded ROIs in which fewer than 90% of the bootstrap values were within 3-seconds of the originally estimated c parameter. Using this method, we identified and excluded 9 ROIs out of the 79 ROIs. These ROIs were mostly higher order regions whose ISPC curves had lower values and lower signal-to-noise compared to other ROIs (Figure S3D). Thus, 70 ROIs proceeded to context construction analysis. Finally, the alignment time of the individual ROIs were mapped from MNI space to a cortical space, and visualized on a cortical surface map using Workbench Viewer (https://www.humanconnectome.org/software/connectome-workbench).

ROI analysis: Quantifying separation time

To test the predictions of the HAT and HLI models regarding context forgetting, we performed another ISPC analysis. We operationalized context forgetting by measuring the separation rate of neural dynamics initialized from a common context. In particular, we examined the similarity of neural responses over time across two groups of “subjects” (i.e. model simulations) processing the different segments preceded by the same context. For example, in the rSI_FORGET (= rSI_CD:CE ) analysis, we correlated the responses between segment D in the intact group and segment E in the scramble group, when both were preceded by segment C (Figure 4B). The procedure for calculating procedure of rSI_FORGET (= rSI_CD:CE ) was directly analogous to the calculation of rSI_CONSTRUCT (as illustrated in Figure 2) except that we paired non-matching segments with matching contexts (CD:CE), rather than pairing matching segments with non-matching contexts (DE:CE). To quantify the rate of context forgetting (i.e. the “separation time”) we used a procedure analogous to that used for measuring alignment times. We fit the rSI_FORGET curves with the logistic function, and again used the half-maximum value (the c parameter) as our estimate of separation time. The measurement of ISPC to generate rSI_FORGET curves was more variable here than for the rSI_CONSTRUCT analysis, because here we measured the correlation of responses to distinct stimuli, rather than the correlation to identical stimuli. Therefore, it was only possible to successfully fit the rSI_FORGET curves in 60 of the 70 ROIs from the previous procedure (Figure 4C, D), and the ROIs which could not be well-fit were: LH_SomMotB_Aud_8; LH_TempPar_3; LH_TempPar_4; LH_TempPar_6; RH_SomMotB_S2_2; RH_SomMotB_S2_6; RH_SomMotB_S2_10; RH_ContA_PFCl_2; RH_TempPar_2; RH_TempPar_4.

The rate of separation in the HAT model was more variable across simulation runs than for the HLI model. The variability in the HAT model arises because its performance depends on a nonlinear learning process: the network weight initialization and the specific randomization order for the scrambled stimulus affect the hidden representations that are learned across different runs, and this induces variability in the strength of the gating at sentence boundaries. We plot a representative rSI_FORGET simulation in Figure 5I, but variability across model runs can be observed in the simulations shown in Figure S5B. Despite this variability, the HAT model was consistently different from the HLI model, which always predicted that regions with slower changes in rSI_CONSTRUCT would also exhibit slower changes in rSI_FORGET (Figure 5H, Figure S5B).

Simulating alignment time and separation time

To obtain a quantitative comparison of model performance and empirical results, we examined the relationship between the alignment time and separation time measured from the ISPC curves generated by the model. For each model we simulated, we computed rSI_CONSTRUCT and an rSI_FORGET curves at each level of the model. We then fit these curves with logistic function to get the alignment time and separation time (i.e. the half maximum value of the logistic curve). We repeated this procedure for the PLI, HLI, HAT-NG and HAT model, respectively, until we obtained at least 50 data points for each model (in a small portion of simulations, the curves could not be well-fit by the logistic function, and the simulation was repeated). To summarize the predictions of each model, we plotted the pairs of alignment-separation values across all three levels and all simulations (Figure S5B). Finally, we calculated the Pearson correlation between the alignment time and separation times for each model, as well as associated parametric p-values.

DATA AND CODE AVAILABILITY

The Princeton datasets used and generated during this study are available at Open Neuro (https://openneuro.org/datasets/ds002345; DOI: 10.18112/openneuro.ds002345.v1.0.1; alias: notthefall) under the “notthefall” alias. Python model implementations are available at https://github.com/HLab/ContextConstruction.

Highlights.

• When the same input is preceded by different contexts, cortical responses differ

• Responses align as common input continues: sensory and then higher-order cortex

• Cortical regions maintain a distributed and hierarchical representation of context

• Distributed cortical memory is gated: prior context can be flexibly forgotten