Searching for safe-haven assets during the COVID-19 pandemic

Abstract

The ongoing COVID-19 pandemic has shaken the global financial system and caused great turmoil. Facing unprecedented risks in the markets, people have increasing needs to find a safe haven for their investments. Given that the nature of this crisis is a combination of multiple problems, it is substantially different from all other financial crises known to us. It is therefore urgent to re-evaluate the safe-haven role of some traditional asset types, namely, gold, cryptocurrency, foreign exchange and commodities. This paper introduces a sequential monitoring procedure to detect changes in the left-quantiles of asset returns, and to assess whether a tail change in the equity index can be offset by introducing a safe-haven asset into a simple mean-variance portfolio. The sample studied covers a training period between August–December 2019 and a testing period of December 2019–March 2020. Furthermore, we calculate the cross-quantilogram between pair-wise asset returns and compare their directional predictability on left-quantiles in both normal market conditions and the COVID-19 period. The main results show that the role of safe haven becomes less effective for most of the assets considered in this paper, while gold and soybean commodity futures remain robust as safe-haven assets during this pandemic.

Highlights

• •We evaluate the safe-haven role of assets in the current COVID-19 pandemic.
• •A sequential monitoring procedure is applied to detect left-quantile changes.
• •Gold and soybean futures are found to have strong safe-haven role in the current crisis.
• •Safe-haven property is found to be changing over time and sensible to the choice of markets.

1. Introduction

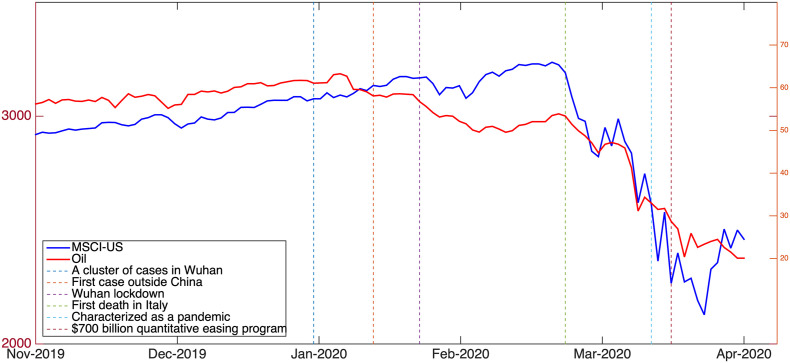
Global financial markets have faced enormous risks during the recent outbreak of COVID-19. Stock markets in the US, for example, hit four circuit breakers in two weeks. Crude oil prices plunged to lower than $20 per barrel, a historic low since the start of the new century. More astonishing, on April 20, 2020, crude oil futures for the West Texas Intermediate (WTI), the US oil benchmark, closed at -$37.63 per barrel, an unprecedented event that will have a profound impact on practitioners and policymakers. Due to the global spread of COVID-19, stock markets all over the world have responded in terms of growing risks and changing inter-market linkages (Zhang, Hu, & Ji, 2020). Fig. 1 plots the daily closing price of MSCI-US index and WTI crude oil commodity futures from November 01, 2019 to March 31, 2020. Both assets have experienced disastrous losses since February 2020 and been moving at a very similar trend during this period.

Fig. 1.

Trajectories of daily closing price of MSCI-US and crude oil prices.

Unlike previous financial crises, the underlying forces behind the current crisis are more complicated than ever. The outbreak of COVID-19 has been considered a “once-in-a-century” pandemic (Gates, 2020). To contain this extremely contagious virus, countries across the world have implemented extensive measures, including the lockdown of cities and the closing of borders, which has caused a temporary economic suspension in many places. In 2003, the severe acute respiratory syndrome, better known as SARS, was estimated to cost the world between $30–100 billion (Smith, 2006). A much larger impact on the global economy is expected from the COVID-19 outbreak. Fernandes (2020), for example, estimated that the outbreak could cause a median economic slowdown of 2.8%, while the extreme case, such as Spain, could fall by more than 15%. With the great uncertainty on when the virus might be fully contained, financial markets are expected to see more troubles and many related issues call for further investigation (Goodwell, 2020). Facing great losses, the need to search for safe-haven assets has resurfaced for both practitioners and researchers.

Traditionally, gold (Baur & Lucey, 2010; Baur & McDermott, 2010), bitcoin (Bouri, Molnár, Azzi, Roubaud, & Hagfors, 2017; Urquhart & Zhang, 2019), and foreign exchange currencies (Forex, in short) (Grisse & Nitschka, 2015) are all considered safe-haven investments during times of financial turmoil. The question is whether their ability to protect investments remains true in the current crisis. It is therefore urgent to re-evaluate the role of traditional safe-haven assets during this pandemic period.

Due to the lack of a theoretical model, the definition of safe-haven assets can be controversial. A major perception is that safe-haven assets are uncorrelated or negatively correlated with other assets or portfolios during times of market turmoil (Baur & Lucey, 2010; Bouri, Shahzad, Roubaud, Kristoufek, & Lucey, 2020). This definition makes sense as safe haven-assets can help investors build a portfolio that mitigates the downside market risk. From an econometric modeling point of view, we thereby need to assess the dependence between assets on left-quantiles of the return distribution. However, many of the conventional methods hardly deliver precise results simply because the task is timely demanding and sufficient observations are not available. This challenge can be addressed, however, if we only focus on the stability of left-quantiles from safe-haven assets. The idea is that the tail-quantiles should maintain a stable level for an effective safe-haven asset during the market stress period. If a safe-haven asset experiences a tail change like other assets experience, it is more likely to correlate with those assets and will lose its effectiveness.

In this paper we consider a few potential safe-haven assets that are usually discussed in the literature, and then empirically examine their effectiveness toward equity index under the current market conditions due to the COVID-19 distress. We use a sequential surveillance test to monitor the stability of the tail behaviour of potential safe-have assets. Moreover, taking the idea that practitioners hope to use safe-haven assets to offset market risk, we construct mean-variance optimised portfolios between equity indices and safe-haven assets, and we test the tail behaviour of portfolio returns during the COVID-19 period. As a robustness check, we also apply the cross-quantilogram method to identify the safe-haven property toward equity indices for each asset in both a normal market and a market during turbulent phase. Our results indicate the validity of a safe haven becomes weak when it comes to bitcoin, forex currencies and the crude oil commodity futures, while gold and the soybean commodity futures remain robust safe-haven assets during the pandemic.

The paper is structured as follows: Section 2 reviews the related literature on studying safe-haven assets. Section 3 discusses the main econometric methods applied, including the sequential approach to detect changes in the tails of asset returns, and the cross-quantilogram approach. Empirical results are presented in Section 4. The conclusion to our findings is given in Section 5.

2. Related literature

The first thing to note is that the concept of a safe-haven asset (Baur & McDermott, 2016) is clearly different from that of a safe asset (Gorton, Lewellen, & Metrick, 2012). While the need to hedge or diversify an investment portfolio applies at all times, safe-haven assets are mainly relevant during times of market crash or crisis (Baur & Lucey, 2010; Baur & McDermott, 2010). To qualify as a safe-haven asset, a candidate must be able to retain or increase in value in case of market downturns. Statistically, the returns from a safe-haven asset should be uncorrelated or negatively correlated with the returns of other assets during a crisis period (Baur & Lucey, 2010).

Under such a notion, gold has naturally been considered a safe-haven asset given its historical role as natural money or a store of value (Bouri et al., 2020). A large volume of literature empirically investigates whether gold can act as a safe-haven asset, but the results are mixed. For example, Baur and McDermott (2010) use 30 years of data from major emerging and developing countries to test the safe-haven asset hypothesis of gold. They confirm this property of gold for the US and major European stock markets but not for other markets. Reboredo (2013) finds that gold can have both the role of a hedge and an effective safe haven. Similar results are found also in Beckmann, Berger, and Czudaj (2015). Meanwhile, Hood and Malik (2013) suggest that gold is a hedge for the US stock market, but its role as a safe haven is weak relative to the volatility index (VIX). Lucey and Li (2015) study the role of precious metals as safe havens in a time-varying framework and they find the strength of gold being a safe haven changes over time. Li and Lucey (2017) extend their earlier study (Lucey and Li (2015)) to eleven countries. They find that economic and political determinants can affect the choice of safe-haven assets among precious metals.

Cryptocurrency is another popular candidate for a safe-haven asset. Bitcoin, for example, was introduced by Nakamoto (2008) as a decentralised digital currency. Its special nature makes bitcoins independent of any particular government or central banks. Statistical analysis by Baur, Hong, and Lee (2018) suggests that bitcoin is uncorrelated with other financial assets. Bouri, Lucey, and Roubaud (2019) find cryptocurrencies can be used as hedges against downside risk in equity investment. This property applies to normal times and crisis periods, which makes bitcoin consistent with the concept of a safe-haven asset. Opinions on the role of bitcoin, however, are often on opposite side. Klein, Thu, and Walther (2018) analyse the statistical properties of bitcoin with other asset classes, and their portfolio analysis suggests that bitcoin is not a safe-haven asset and cannot hedge against risk, even for developed markets. Smales (2019) suggests that bitcoin should not even be considered as a potential safe asset. Shahzad, Bouri, Roubaud, and Kristoufek (2019) find that gold has an “indisputable” safe-haven property over that of bitcoin. While gold is an effective safe-haven asset for all G7 stock indices, bitcoin only offers a safe-haven role for the Canadian stock index.

Supporting evidence to the safe-haven role of bitcoin can also be found in the recent literature. Bouri et al. (2017) use a dynamic conditional correlation (DCC) approach to support that bitcoin can act as a safe haven for stock markets in the Asia Pacific area. Urquhart and Zhang (2019) study intraday data and find evidence that bitcoin is safe haven for several currencies. Shahzad, Bouri, Roubaud, Kristoufek, and Lucey (2019) propose the concept of weak/strong safe haven and examine the role of bitcoin, gold and commodities for stock market indices. They use cross-quantilogram of Han, Linton, Oka, and Whang (2016) for the data between 2010 and 2018. Their main results suggest that bitcoin has weak safe-haven properties to certain indices but its role changes over time.

In addition to the two popular candidates, currencies and commodities can also potentially offer a safe-haven role in financial markets. Ranaldo and Söderlind (2010), for example, suggest that the Swiss franc and the Japanese yen demonstrate safe-haven properties during a crisis period. Grisse and Nitschka (2015) add further evidence that the Swiss franc exchange rate can act as a safe-haven currency in some cases. Shahzad, Bouri, Roubaud, Kristoufek, and Lucey (2019) show that the commodity index is a weak safe haven for some stock indices. For other commodities, Creti, Joëts, and Mignon (2013) include oil, coffee and cocoa together with gold to examine their links with stocks between 2001 and 2011. Gold is found to have the safe-haven properties, whereas other commodities' correlation with stock prices changes according to market conditions. The role of commodities in hedging and as safe-haven assets are affected by the recent trend of financialization (Bouri et al., 2020; Zhang, 2017; Zhang & Broadstock, 2018). In other words, commodities such as crude oil (Xia, Ji, Zhang, & Han, 2019) and food commodities (e.g., soybeans) behave quite differently since the 2008 global financial crisis (Wu, Zhao, Ji, & Zhang, 2020). Their role as safe-haven assets related to the current health crisis is therefore worthy of further exploration. In general, what can be considered safe-haven assets remains a controversial topic. Even with gold, the most popular candidate, its role as a safe haven is not entirely secure.

From the literature, a few characteristics stand out. First, the value of an asset as a safe haven may not be universal. The effectiveness of a safe-haven asset is subject to the particular asset class or market studied. Second, safe-haven property may change over time or depend on the fundamental characteristics of the market turmoil. In this sense, we would expect that safe-haven assets under the COVID-19 pandemic are different from those in the 2008 global financial crisis. Third, the controversies in the current literature may be due to the methodology used. For example, the DCC approach only looks at correlations and do not allow for asymmetric responses. In terms of risk management in financial markets, it is often important to look at the tails of return distribution (Shahzad, Bouri, Roubaud, Kristoufek, & Lucey, 2019).

3. Methodology

Investors tend to endow the downside risk with more attention than the profitability during times of crisis and market disorder. Successfully monitoring the downside risk, i.e., the left-tail of the return distribution, would prevent losses and help procure strategic advice for future investment. Therefore, safe-haven assets draw more attention as they are expected to offset the downside risk when the market draws equity indices into a situation of risk while traditional portfolio management tools fail.

Following this logic, and to check the effectiveness of safe-haven assets, we use a sequential test (Hoga & Wied, 2017) to monitor the tail stability of return sequences and to investigate whether the tail instability of a stock index could be offset by safe-haven assets by constructing an optimised portfolio. In addition, Baur and Lucey (2010) and Shahzad, Bouri, Roubaud, Kristoufek, and Lucey (2019) point out that a safe-haven asset has a lead-lag effect for left-low quantiles with a stock index (strong version), or no predictability for left-low quantiles with stock index (weak version). Thus, we also use the cross-quantilogram approach (Han et al., 2016) to confirm the validity of safe-haven assets for each stock index. The details of these approaches are briefly discussed below.

3.1. The sequential monitoring test on the tails

A crucial step for monitoring the effectiveness of safe-haven assets is to assess the tail stability to a return sequence. Detecting changes in the quantile regression was studied by Qu (2008) as well as Oka and Qu (2011). However, their methods are not applicable in the current context because limited observations could be made from the period studied. Particularly, our focus is on studying asset behaviour during the global outbreak of COVID-19 in March 2020, i.e., at the end of the sample. This renders many conventional econometric methods impotent. We, therefore, apply a sequential surveillance test (Hoga & Wied, 2017) to monitor the tail behaviour of the return series. The sequential test accords more with the current situation as its statistics can converge to an asymptotic limit with less data so that the test successfully detects a tail change in a responsible period with the help of real-time observations. More importantly, to add more practical values, along with time-series observations during the pandemic, the results are easy to update.

Let us consider a financial time series y _t, t = {1, 2, …,  n,  n + 1, …}, which is defined with the conditional distribution function F _t and the survivor function ${\overline{F}}_t\left(y\right)=1-F_t\left(y\right)=\mathrm{\mathbb{P}}\left(y_t>y\right)$. Embedding this to the extreme value theory, the conditional quantile τ at time t is expressed as q _t(τ) = U _t(1/τ), where $U_t\left(u\right)=F_t^{-1}\left(1-\frac{1}{u}\right)$, and F _t ⁻¹ is the left-continuous inverse of F _t. To set a surveillance procedure, the sample from t = 1 to t = n is considered as a training sample, and observations since t = n + 1 are imported into a sequential testing sample. We are interested in testing the hypotheses ℋ₀ : q ₁(τ) = ⋯ = q _n(τ) = q _n+1(τ) = …, vs ℋ₁ : q ₁(τ) = ⋯ = q _n(τ) = ⋯ = q _⌊ns^∗⌋(τ) ≠ q _{⌊ns^∗⌋+1}(τ) = q _{⌊ns^∗⌋+2}(τ) = … for s ^∗ > 1.

Under the null hypothesis ℋ₀, the conditional quantile remains stable across the training and testing samples, and alternatively, a tail change occurs at some point in the testing sample. The basic idea is that, based on the information revealed from the training sample, we can foresee the tail behaviour of the time series beyond the training period. To adapt this to our context, we form a training sample and a testing sample with data collected from normal market condition and the COVID-19 outbreak period, respectively, and we expect that the tail behaviour of a safe-haven asset learned from the normal market phase could remain the same over the market crisis period.

To distinguish ℋ₁ from ℋ₀, Hoga and Wied (2017) propose two self-normalised statistics V _n(s) and W _n(s). Here, we focus on the latter as it requires fewer observations to detect a change, according to the simulation in Hoga and Wied (2017). The training sample [1,n] is normalised into the interval [0,1] for simplifying the notations. Then, the detector W _n ^τ(s) is specified as,

$$W_n^{\tau }\left(s\right)=\frac{{\left[s_{0}log\left(\frac{{\widehat{x}}_{\tau }\left(s-s_0,s\right)}{{\widehat{x}}_{\tau }\left(01\right)}\right)\right]}^2}{{\int }_{s_0}^1{\left[s_{0}log\left(\frac{{\widehat{x}}_{\tau }\left(v-s_0,v\right)}{{\widehat{x}}_{\tau }\left(01\right)}\right)\right]}^2\mathit{dv}},s\ge 1+s_0$$ (1)

where 0 < s ₀ < 1 separates a fraction of n from the testing sample for the preparation of monitoring. The quantile measurement ${\widehat{x}}_{\tau }\left(v,s\right)=Y_k\left(v,s\right){\left(\frac{n}{\mathit{k\tau }}\right)}^{-\widehat{\gamma }\left(v,s\right)}$, where Y _k(v,s) is the (⌊k(s − v)⌋ + 1)-th largest value of {y _⌊nv⌋+1, …,  y _⌊ns⌋}, for some k ≤ n − 1 and k/n → 0. The tail index estimator $\widehat{\gamma }\left(01\right)=\frac{1}{k}{\sum }_{i=0}^{k-1}log\left(\frac{Y_{n-i:n}}{Y_{n-k:n}}\right)$, for Y _n:n ≥ Y _n−1:n ≥ … ≥ Y _1:n denoting the order statistics of the training sample {y ₁, …,  y _n}. In the application we choose s ₀ = 0.2 and k/n = 0.2 as suggested by Hoga and Wied (2017). Then, the stopping time is determined by,

$$s^{\ast }=inf\left\{s\in \left[1+s_0,\mathfrak{T}\right]:W_n^{\tau }\left(s\right)>{\mathcal{C}}_{\tau }\right\}$$

where ${\mathcal{C}}_{\tau }>0$ is a threshold derived from the limit distribution, and $\mathfrak{T}>1$ is the normalised close end. Close-end approaches are commonly used in sequential change-point tests, such as in Aue, Hörmann, Horváth, Hušková, and Steinebach (2012), for monitoring portfolio betas, and in Aschersleben, Wagner, and Wied (2015), for monitoring cointegration relationships. Our dataset assures that the training sample contains as many observations as the testing sample, i.e., $\mathfrak{T}=2$.

Under the null hypothesis, the asymptotic limit of W _n ^τ(s) is provided by Hoga and Wied (2017) that,

$$W_n^{\tau }\left(s\right)\equiv \frac{\underset{s\in \left[1+s_0,\mathfrak{T}\right]}{sup}{\left[\omega \left(s\right)-\mathrm{W}\left(s-s_0\right)-s_0\mathrm{W}\left(1\right)\right]}^2}{{\int }_{s_0}^1{\left[\mathrm{W}\left(v\right)-\mathrm{W}\left(v-s_0\right)-s_0\mathrm{W}\left(1\right)\right]}^2\mathit{dv}},$$

where ${\left\{\mathrm{W}\left(s\right)\right\}}_{s\in \left[1,\mathfrak{T}\right]}$ is a standard Brownian motion. We thereby can simulate the threshold ${\mathcal{C}}_{\tau }$ given the suggestion from the size of empirical dataset.

In practice, safe-haven assets can be included in portfolios to avoid downside risk during a crisis period. A safe-haven asset is considered to add value if its pairwise optimised portfolio with an equity index does not experience a tail-behaviour change when a tail risk occurs in the equity index itself. In other words, if a stock index experienced a tail change during the crisis, this tail change could be offset by constructing a simple mean-variance portfolio with a potential safe-haven asset. To examine this, we build pair-wise portfolios and re-apply the sequential test to monitor the tail behaviour of these portfolio returns.

3.2. The cross-quantilogram approach

In addition, other than monitoring the tail behaviour of safe-haven portfolio returns, another popular method, the cross-quantilogram approach (Han et al., 2016) for evaluating a safe-haven role is implemented for a robustness check. We calculate the pair-wise cross-quantilograms between equity indices and potential safe-haven assets, and compare their lead-lag effects over the training and testing samples. The basic idea of this approach is briefly explained below.

Given a specific sample of data, we denote a stationary bivariate vector {y _t = [y _{1, t},  y _{2, t}]}, t ∈ [1,  T], where in our context y _{2, t} is a potential safe-haven asset to the equity index y _{1, t}. The unconditional τth quantile of the return {y _{i, t}}, i = 1, 2, is defined as q _i(τ) = inf {u : F _i(u) ≥ τ}, for τ ∈ [0, 1], where F _i(⋅) is the distribution function of y _{i, t} and that is equipped with the density function f _i(⋅).

To measure and test for the directional predictability between [y _{1, t},  y _{2, t}] for different quantiles, Han et al. (2016) propose the cross-quantilogram for τ-quantile with lag h as,

$${\rho }_{\tau }\left(h\right)\equiv {\rho }_{{\tau }_1,{\tau }_2}\left(h\right)=\frac{\mathbb{E}\left[{\psi }_{{\tau }_1}\left(y_{1,t}-q_1\left({\tau }_1\right)\right){\psi }_{{\tau }_2}\left(y_{2,t}-q_2\left({\tau }_2\right)\right)\right]}{\sqrt{\mathbb{E}\left[{\psi }_{{\tau }_1}^2\left(y_{1,t}-q_1\left({\tau }_1\right)\right)\right]}\sqrt{\mathbb{E}\left[{\psi }_{{\tau }_2}^2\left(y_{2,t}-q_2\left({\tau }_2\right)\right)\right]}},$$ (2)

where ${\psi }_{\tau }\left(u\right)\equiv \mathbb{I}\left(u<0\right)$, for an indicator function $\mathbb{I}$, so that ψ _τi(y _{i, t} − q ₁(τ _i)) describes the violation or “hit” process. According to the formula, the cross-quantilogram measures the serial correlation between a pair of variables at different quantiles. When h = 1, ρ _τ(1) indicates the cross-dependence between the quantile q ₁(τ ₁) of a stock index y _{1, t} at time t and the quantile q ₂(τ ₂) of a potential safe-haven asset y _{2, t} at time t + 1. This therefore measures the one-day lead-lag effect between y _{1, t} and y _{2, t}, and there is no predictability from the quantile τ ₁ of stock index to the quantile τ ₂ of safe-haven asset if ρ _τ(1) = 0, i.e., y _{2, t} is a weak safe-haven asset. Alternatively, for ρ _τ(1) ≠ 0, y _{2, t} is a strong safe-haven asset when the sign is negative. For a sample estimator, Han et al. (2016) suggest the cross-quantilogram ρ _τ(h) as,

$${\widehat{\rho }}_{\tau }\left(h\right)=\frac{\mathbb{E}\left[{\psi }_{{\tau }_1}\left(y_{1,t}-{\widehat{q}}_1\left({\tau }_1\right)\right){\psi }_{{\tau }_2}\left(y_{2,t}-{\widehat{q}}_2\left({\tau }_2\right)\right)\right]}{\sqrt{\mathbb{E}\left[{\psi }_{{\tau }_1}^2\left(y_{1,t}-{\widehat{q}}_1\left({\tau }_1\right)\right)\right]}\sqrt{\mathbb{E}\left[{\psi }_{{\tau }_2}^2\left(y_{2,t}-{\widehat{q}}_2\left({\tau }_2\right)\right)\right]}},$$

where ${\widehat{q}}_i\left({\tau }_i\right)$ is the unconditional sample quantile. Furthermore, in order to test the null hypothesis of no cross-dependence, ${\mathrm{\mathscr{H}}}_0:{\widehat{\rho }}_{\tau }\left(h\right)=0$, for all h ∈ [1,  H], vs ${\mathrm{\mathscr{H}}}_1:{\widehat{\rho }}_{\tau }\left(h\right)\ne 0$, for some h ∈ [1,  H], a portmanteau-typed statistics is proposed (Han et al., 2016) to detect the null,

$${\widehat{Q}}_{\tau }^H=\frac{T\left(T+2\right){\sum }_{h=1}^H{\widehat{\rho }}_{\tau }^2\left(h\right)}{T-H},$$ (3)

The pivotal distribution under ℋ₀ is not explicitly given due to the noise contained. Han et al. (2016) thus advise using the stationary bootstrap method in Politis and Romano (1994) to approximate the distribution under the null hypothesis, and derive critical values as well as confidence intervals. This method can be combined with a rolling window approach to track the time-varying cross-quantilogram and observe the evolution of the safe-haven role during the crisis period.

4. Empirical results

4.1. Data

Three regions that had been catastrophically impacted by COVID-19: China, Europe (EU), and the United States are studied in this paper. For each market, we collect the daily closing price of the MSCI equity index. Following the review of existing literature, cryptocurrency, gold, forex, and the commodity futures market are considered the candidates of safe-haven assets. We use the daily closing/spot price of bitcoin (CoinDesk price index), gold (ounce of gold-LBMA), forex rates (EUR-USD and CNY-USD), the WTI crude oil (rolling front-month futures contract), and soybeans commodity futures. The three-month Treasury bill rate is used as the risk-free rate. All data are collected from a publicly accessible database (see Table 1 for the source of all variables).

Table 1.

Summary statistics and stationary tests.

	Average	S.D.	Skewness	Kurtosis	S.R.training	S.R.covid	PADF	PKPSS
MSCIUS	−0.08%	2.26%	−1.0554	13.5176	0.0667	−0.0707	0.00	0.64
MSCIEU	−0.12%	1.81%	−2.5971	26.2536	0.0454	−0.1130	0.00	0.71
MSCICN	−0.01%	1.43%	−0.7272	6.2763	0.0255	−0.0184	0.00	0.44
Bitcoin	−0.27%	4.78%	−0.7750	17.2506	−0.0985	−0.0264	0.00	0.55
Gold	0.08%	1.09%	−0.4359	10.0930	0.0542	0.0846	0.00	0.45
EUR-USD	−0.01%	0.44%	−1.0511	12.8541	−0.0185	0.0021	0.00	0.15
CNY-USD	−0.01%	0.30%	−1.5145	8.7359	−0.0783	−0.0231	0.00	0.19
Oil	−0.57%	4.56%	−1.6792	22.1491	0.0167	−0.2009	0.00	0.49
Soybean	0.01%	0.90%	0.1766	4.8432	0.0079	0.0170	0.00	0.36
T-Bill	0.58%	0.20%	−1.9455	5.9809	–	–	0.01	0.10

Note: Equity indices are available from the MSCI website, bitcoin data is available from Coindesk, Forex and T-Bill are from Yahoo Finance, and Gold and commodity futures are available from Reuters. S.R. refers to the sharp ratio, which is calculated by dividing the standard deviation from the average of returns. The sharp ratio of T-Bill is not computed as it is considered as a risk-free asset. P_ADF and P_KPSS are p-values of the ADF and KPSS unit root tests, respectively.

Since the early cluster of confirmed cases of COVID-19 were reported in December 2019, we deem the testing/monitoring sample from 1 December 2019, to 31 March 2020, as the COVID-19 period. To meet the condition of $\mathfrak{T}>1$ (as discussed in Section 3.2), we set $\mathfrak{T}$ = 2 so that the training sample ranged from 1 August 2019 to 30 November 2020, having the same number of observations as the testing sample. Next, for stationarity, we take the log return transformation for each asset.

Table 1 presents key descriptive statistics of the return series. Not surprisingly, apart from the Treasure bill, gold and soybean commodity futures are the only assets that obtained positive average returns during the sample period. Similar patterns can also be spotted in the skewness, and the excess kurtosis shows assets were non-normally distributed, with fat tails. By comparing their Sharpe ratios across training and testing samples, we can see that except for bitcoin and forex rates, most of the assets achieved positive Sharpe ratios in the training sample. In contrast, only gold and soybean commodity futures retain positive Sharpe ratios during the COVID-19 pandemic. ADF unit root tests and KPSS stationary tests consistently indicate a stationary return sequence for each asset.

4.2. Monitoring the tails of safe-haven assets

Prior to studying the effectiveness of safe-haven roles toward stock indices, we investigate the tail behaviour of individual assets. Investors tend to focus on the tail of asset distribution as they explore statistic tools for risk control. Value-at-risk (VaR) is the most pervasive risk management tool implemented in the financial services industry, we thus apply the standard approach to calculate VaR at quantile τ and assess the performances in both the training and COVID-19 periods.

Specifically, for each time series y _{i, t}, we calculate VaR through ${\mathrm{VaR}}_{i,t}={\widehat{\sigma }}_{i,t}{\epsilon }_i^{\tau }$, where the conditional variance ${\widehat{\sigma }}_{i,t}$ is fitted through a GARCH(1,1) model, and the sample quantile ε _i ^τ is obtained from a bootstrapped distribution by resampling residuals 1000 times. Since our focus is not on evaluating VaR estimation, we do not go to back-test these estimators and only compute the ratio of violation/hit in both samples. Here we examine τ = 0.05 and do not study extreme quantiles considering the limited observations available at this stage.

Table 2 shows descriptive statistics of the VaR sequence on each of asset. We find that the VaR estimators are relatively high volatile for bitcoin, crude oil commodity futures, and equity indices in US and EU, indicating that these assets have fluctuations on the left-tail during the sample period. The columns Hit_{whole,training,covid} indicate the violation ratios in the entire, training, and testing sample, respectively. Against the nominal level τ = 0.05, we find that despite the violation ratio being close to the nominal quantile in the entire sample, the VaR cannot carry out its duty during the pandemic period, given that the overall violation ratios are significantly higher than the nominal level, especially for equity indices in the US, Chinese markets, as well as the WTI crude oil commodity futures. On the contrary, the violation ratios maintain an acceptable level over the COVID-19 period for MSCI_EU, Bitcoin, gold, and soybean commodity futures.

Table 2.

Descriptive statistics of VaR and detected changes (τ = 5%).

	Average	Median	S.D.	Min	Max	Hitwhole	Hittraining	Hitcovid	Change date
MSCIUS	−0.0296	−0.0145	0.0359	−0.2099	−0.0082	5.17%	2.30%	8.05%	09-Mar
MSCIEU	−0.0231	−0.0145	0.0226	−0.1462	−0.0092	4.60%	4.60%	4.60%	24-Mar
MSCICN	−0.0241	−0.0206	0.0092	−0.0590	−0.0158	4.60%	1.15%	8.05%	23-Mar
Bitcoin	−0.0566	−0.0501	0.0190	−0.1750	−0.0441	5.75%	5.75%	5.75%	–
Gold	−0.0155	−0.0126	0.0090	−0.0504	−0.0074	5.75%	4.60%	6.90%	–
EUR-USD	−0.0058	−0.0049	0.0026	−0.0180	−0.0035	5.75%	6.90%	4.60%	25-Mar
CNY-USD	−0.0042	−0.0040	0.0008	−0.0087	−0.0038	5.17%	3.45%	6.90%	–
Oil	−0.0485	−0.0324	0.0463	−0.2806	−0.0217	5.75%	3.45%	8.05%	18-Mar
Soybean	−0.0162	−0.0154	0.0024	−0.0253	−0.0132	5.17%	3.45%	6.90%	–
T-Bill	0.0041	0.0042	0.0013	0.0001	0.0055	5.75%	0	11.49%	23-Mar

Note: VaR estimators for asset i at quantile τ are calculated through ${\mathrm{VaR}}_{i,t}^{\tau }={\widehat{\sigma }}_{i,t}{\epsilon }_i^{\tau }$. The conditional volatility ${\widehat{\sigma }}_{i,t}$ is obtained by fitting a GARCH(1,1) model given a general presence of the conditional heteroscedasticity. The unconditional quantile for the error ε_i^τ is obtained from a bootstrapped distribution by re-sampling the historical residuals for 1000 times. The violations/hits are identified by the indicator function $\mathbb{I}\left(r_{i,t}<{\mathrm{VaR}}_{i,t}^{\tau }\right)$. All change dates are in the year 2020.

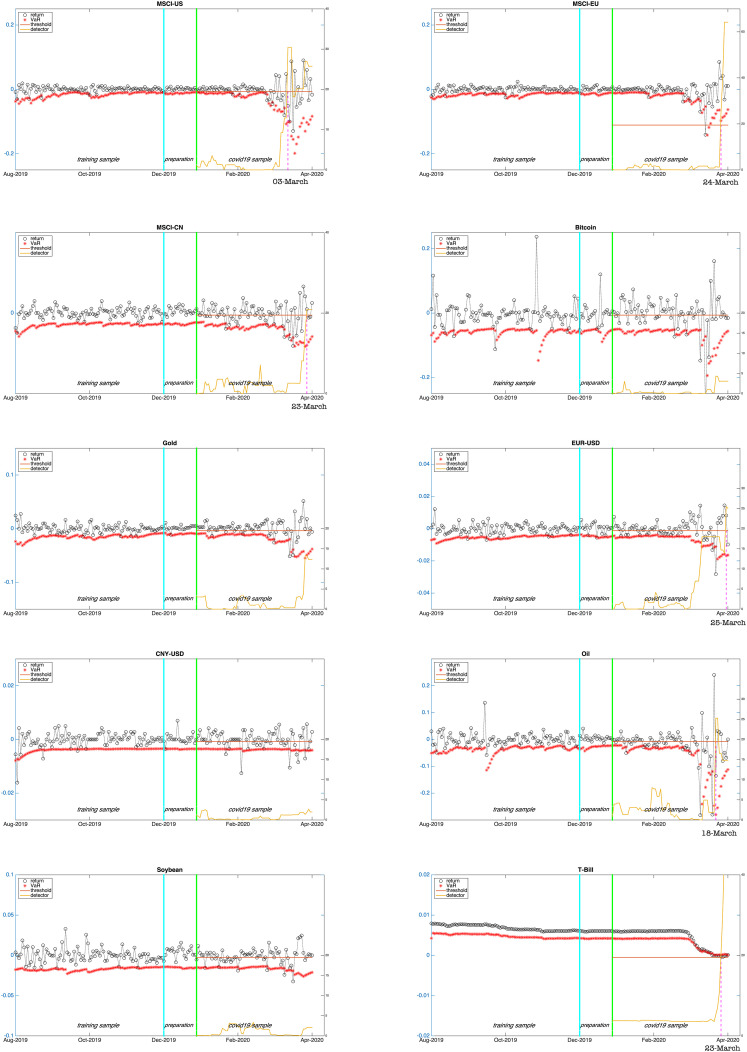
To speculate what causes the failure of VaR estimation, we closely monitor the tail stability of each asset for quantile τ = 0.05 by using the sequential W _n ^τ detector. Recall that k/n = 0.2, this leads to the surveillance procedure beginning from 25 December 2019, as a fraction of the testing sample is used for preparation. The detector W _n ^τ is then computed day by day in the testing sample, but the detection stops once there is the detector that exceeds the threshold ${\mathcal{C}}_{\tau }$.

Fig. 2 illustrates the sequential surveillance procedure for each of the assets, as well as the VaR estimators. Combined with the last column in Table 2, the results show that the equity indices in all three markets suffer from a tail change in March 2020. In particular, note that major market indices in the US fell more than 7% on March 9. Another remarkable case is the crude oil commodity future that experiences a tail change on March 18. This comes with a collapse of oil price, which dropped by 24% and was recorded as one of the worst days in the history. This partially explains why a breakdown found in the VaR estimation for the corresponding assets. On the other hand, four safe-haven candidates (bitcoin, gold, CNY-USD exchange rate, and soybean commodity futures), do not incur a tail change over the testing period (for a robustness checking, we also perform detections when τ = 0.10, 0.15, 0.20, and obtain similar results). These results bring us the hope that potential safe-haven assets to be effective during the crisis.

Fig. 2.

Plots of VaR estimators and sequential detections on tail behaviour of each of the asset when τ = 0.05.

Next, for the purpose of evaluating the role of safe-haven asset to investment strategies, we construct pairwise mean-variance portfolios between equity indices and potential safe-haven assets. Treasury bill is used as a risk free rate for calculating the portfolio weights. Panel A in Table 3 displays the Sharpe ratio of each portfolio return. Notably, only portfolios built with gold and soybean commodity futures obtained positive Sharpe ratios. Among the portfolios built with three stock market indices, those with the MSC-US and the MSCI-EU share some similarities, whereas those with the Chinese market index are different. This is consistent with the development of COVID-19 pandemic over time (Zhang et al., 2020).

Table 3.

Sharp ratio of optimised portfolios during the COVID-19 and detected change dates.

	Bitcoin	Gold	EUR-USD	CNY-USD	Oil	Soybean
Panel A: Sharp ratios
MSCI-US	−0.0347	0.0711	−0.0049	−0.0494	−0.0347	0.0125
MSCI-EU	−0.0652	0.0711	−0.0050	−0.0494	−0.0652	0.0120
MSCI-CN	−0.0023	0.0719	−0.0050	−0.0023	−0.0023	0.0125
Panel B: Break dates when τ = 0.05
MSCI-US	09-Mar	–	–	–	09-Mar	–
MSCI-EU	–	–	26-Mar	–	24-Mar	–
MSCI-CN	24-Mar	–	26-Mar	24-Mar	24-Mar	–
τ = 0.10
MSCI-US	23-Mar	–	06-Mar	–	12-Mar	–
MSCI-EU	–	–	06-Mar	–	24-Mar	–
MSCI-CN	–	–	06-Mar	24-Mar	–	–
τ = 0.15
MSCI-US	–	–	06-Mar	–	12-Mar	–
MSCI-EU	–	–	06-Mar	–	25-Mar	–
MSCI-CN	–	–	06-Mar	–	–	–
τ = 0.20
MSCI-US	12-Mar	–	06-Mar	–	12-Mar	–
MSCI-EU	–	–	06-Mar	–	–	–
MSCI-CN	–	–	06-Mar	–	–	–

Note: The sharp ratio from Panel A is calculated by dividing the standard deviation from the average of portfolio returns. In Panel B, the detection is performed for left-quantiles when τ = 0.05, 0.10, 0.15, 0.20. All change dates in Panel B are in the year 2020.

Let us now concentrate on the tail behaviour of portfolio returns. From the results shown in Table 2, we find that all of three equity indices experience tail changes during the pandemic period, while many safe-haven candidates keep a stable tail behaviour. To keep assessing the practical value of safe-haven candidates, we therefore sequentially monitor the stability of the tail behaviour of portfolio returns over the market crisis period through the detector W _n. The results are reported as the left-quantile τ varying from a set {0.05,0.10,0.15,0.20}. Panel B of Table 3 reports the detection results.

Among six asset candidates, again, only the portfolios constructed with gold and soybean commodity futures do not experience a change on the left-quantiles considered. Conversely, bringing bitcoin, forex currencies, and crude oil commodity futures into the portfolio cannot avoid changes on the left-tails. A few exceptional cases can be identified, some portfolios built with bitcoin and CNY-USD offset the tail instability in three equity indices, although the Sharp ratios show non-profitability for these portfolios. These results are generally in line with the existing literature that certain safe-haven assets are market specific.

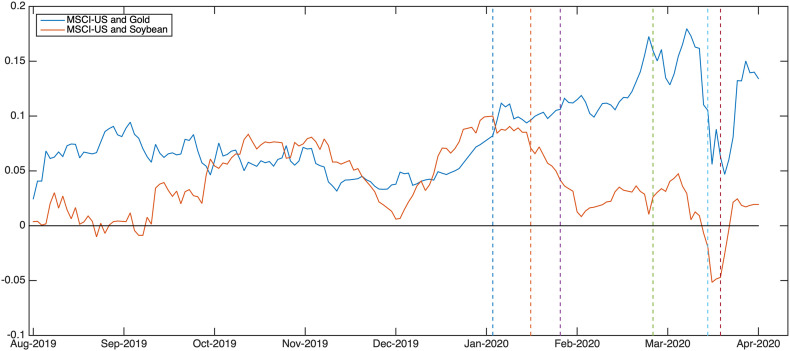
Among all candidates, gold and soybean commodity futures are found to be robust safe haven assets during the outbreak of COVID-19. Fig. 3 shows the cumulative returns of the portfolios that using gold and soybean commodity futures as safe-haven assets for the MSCI-US index, where the vertical lines indicate important dates related to COVID-19 mentioned in Fig. 1. We can see that except for a short-lived and small negative value shown for the portfolio of soybean commodity futures in the middle of March 2020, the overall cumulative returns are positive during the sample considered. Similar patterns are found for the other two stock market indices.

Fig. 3.

Cumulative returns of the pairwise optimised portfolio between MSCI-US, gold and soybean commodity futures.

4.3. A cross-quantilograms analysis for safe-haven assets

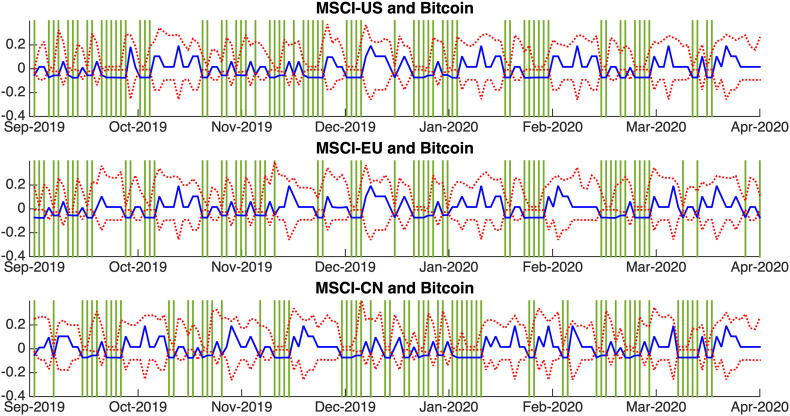
To further confirm our findings above, we implement the cross-quantilograms approach as used in Shahzad, Bouri, Roubaud, Kristoufek, and Lucey (2019) to evaluate the validity of safe-haven assets over the normal market and COVID-19 periods. First, to understand a dynamic effect of COVID-19 on the lead-lag effect between equity indices and safe-haven assets, we estimate the time varying cross-quantilograms with lag h = 1 and τ = 0.05 by using a one-day rolling window approach, where the window length is fixed with 21 trading days. Fig. 4 shows example plots of the time varying cross-quantilogram between equity indices and bitcoin, for the solid blue and dot red lines standing for time varying cross-quantilogram and bootstrapped 95% confidence interval, respectively. The vertical green lines indicate that bitcoin can be used as a strong version of safe-haven asset for that particular window, which is evidenced by the blue line across the lower bound of red lines. From the plots we observe that the role of bitcoin, as a potential safe-haven asset to equity indices, becomes less effective during the pandemic period. This is particularly manifest to MSCI-US and MSCI-EU, given that the patterns of a lead-lag effect are less often significant.

Fig. 4.

Time varying cross-quantilogram from equity indices to bitcoin when τ = 0.05 (the vertical green lines indicating significant negative cross-quantilogram on 95% confidence intervals.) (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Table 4 reports the shares of no and negative predictability indicated by the time varying cross-quantilograms for each asset pairs in both the training and COVID-19 samples. In general, the shares of no-predictability increased for almost all assets during the COVID-19 period, whereas most of assets has lower share of negative predictability during the crisis. This overall trend is not entirely surprising as we know that it is hard to find a perfect safe-haven in such a complicated crisis. Nonetheless, a few exceptions can be seen for bitcoin, gold and soybean commodity futures paired with MSCI-CN, CNY-USD paired with MSCI-US and MSCI-EU. In addition, we also need to note that the worst scenarios of this crisis happened in the very end of COVID-19 sample, which may further change the role of safe-haven assets.

Table 4.

Percentage of none and negative predictability over the training and COVID-19 periods (τ = 0.05).

		Training sample			COVID-19 sample
		MSCIUS	MSCIEU	MSCICN	MSCIUS	MSCIEU	MSCICN
Weak safe-haven (no predictability)	Bitcoin	0.44	0.57	0.62	0.61	0.62	0.53
	Gold	0.54	0.60	0.60	0.69	0.69	0.63
	EUR-USD	0.40	0.42	0.50	0.53	0.48	0.51
	CNY-USD	0.57	0.54	0.54	0.46	0.46	0.59
	Oil	0.57	0.65	0.68	0.70	0.69	0.65
	Soybean	0.48	0.51	0.65	0.65	0.66	0.51
Strong safe-haven (Negative)	Bitcoin	0.56	0.42	0.37	0.38	0.37	0.46
	Gold	0.45	0.39	0.39	0.31	0.31	0.36
	EUR-USD	0.59	0.56	0.48	0.46	0.50	0.46
	CNY-USD	0.41	0.45	0.45	0.51	0.52	0.40
	Oil	0.42	0.34	0.32	0.29	0.31	0.34
	Soybean	0.51	0.48	0.34	0.34	0.33	0.48

Note: By using a rolling window approach with the window length of 21 trading days, the time varying cross-quantilograms for lag h = 1 and τ = 0.05 are calculated at a daily frequency. The number of windows in the training sample is 66 as 21 observations are burned from the first window, the total number of windows in the testing sample remains 87. These ratios stand for the percentage of windows with no predictability or negative predictability indicated by the time varying cross-quantilograms.

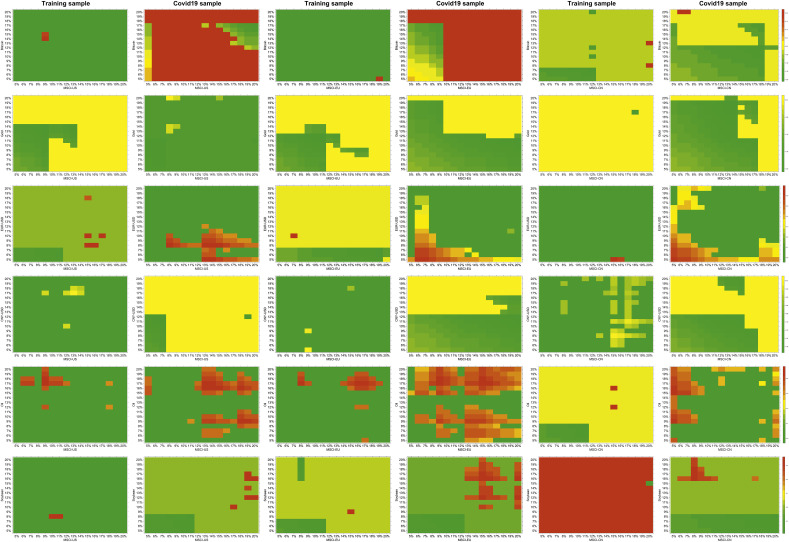
Following Shahzad, Bouri, Roubaud, Kristoufek, and Lucey (2019), we also report pair-wise cross-quantilograms with lag h = 1, but on left-quantiles τ = {0.05,0.06, …,0.20} in both the training and testing samples. Fig. 5 illustrates the results of cross-quantilograms, in which the green color on the heatmap represents negative lead-lag effect, meaning the candidate asset can be considered as a strong safe-haven asset. Red color represents a positive spillover effect between equity indices and candidate asset, while yellow color stands for no predictability on their left-quantiles, i.e., a weak version of safe-haven asset. An independence test is performed to test the significance of the cross-quantilogram under the stationary bootstrapping procedure (see Eq. (3)). We therefore assign a zero value to the cross-quantilogram if the null or no predictability cannot be rejected.

Fig. 5.

Cross-quantilogram across left-tail quantiles in training and COVID-19 periods. (The green and red blocks on heatmaps representing negative and positive values, respectively, whereas the yellow blocks represent no predictability.) (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The results of the pair-wise assets in training and testing samples are quite mixed (as seen in Fig. 5). We have the following three observations: first, some assets (bitcoin, CNY-USD, and the crude oil commodity futures) play a role of a safe-haven to equity indices in the period with normal market status, while their roles degenerate during the COVID-19 period. Second, the rest of the safe haven candidates (gold, EUR-USD, and the soybean commodity futures) either keep the same status of being safe-haven assets, or they act as a better safe-haven during the COVID-19 sample. And the third, with no conflict with the first two points, the directional predictive patterns between asset candidates and equity indices are quite similar in US and EU market, and patterns regarding China are slightly different in some cases, for example, there are positive spillover effects between MSCI-CN and gold and soybean in the training sample. These results in general are consistent with our findings from monitoring the tail behaviour of safe-haven portfolios in the previous section.

5. Conclusion

Searching for safe-haven assets is a timely and important issue under the current COVID-19 pandemic. The profound impact of this health crisis has caused investors all over the world to suffer great losses, and thus the demand for safe-haven assets has become even more urgent. Traditional candidates for a safe haven such as gold, cryptocurrency, forex currencies and commodities may loss some effectiveness given the nature of the current crisis. Their role as safe-haven assets must, therefore, be re-evaluated.

Extending the rich literature in this area, we introduce a sequential monitoring procedure to detect changes in the left-quantiles of asset returns. This approach allows us to assess whether a tail change in the equity index can be offset by adding a safe-haven asset into the simple mean-variance portfolio. Using data from August 2019 to December 2019 as a training period for the model, and then taking the outbreak between December 2019 and March 2020 as the testing period, our empirical results suggest that gold and soybean commodity futures can be used as safe-haven assets during the outbreak of COVID-19. We also used the cross-quantilogram approach (Shahzad, Bouri, Roubaud, Kristoufek, & Lucey, 2019) to check the robustness of our empirical findings. The results are generally consistent.

Overall, we confirm that gold has an irreplaceable role in preserving the value of an investment. The strong and robust role of soybean futures is slightly surprising as it is not normally considered a strong candidate. The logic behind this once again links to the nature of the current crisis. The financial turmoil is essentially driven by the health crisis. By implementing measures to contain the virus, both the industrial and consumer sector are affected, leading to an over-supply of crude oil and also ruling out its relevance as a safe-haven asset. The locking down of cities and borders also affect international trade, and thus put the foreign exchange market into great uncertainty. The crisis, however, raises the need for agricultural products. Food security, for example, has become a major issue for many countries (e.g., Deaton & Deaton, 2020), which makes agricultural commodities a strong hold under the current crisis. Our findings are also in line with the literature that safe-haven assets can change over time and across countries. In addition, when searching for safe-haven assets, investors cannot ignore the underlying characteristics/driving forces of the market turmoil.

Author statement

Qiang Ji: Conceptualization, supervision, reviewing and editing. Dayong Zhang: Conceptualization, writing-original draft preparation, reviewing and editing, validation. Yuqian Zhao: Methodology, software, writing-original draft preparation, investigation.