Insights from the study of complex systems for the ecology and evolution of animal populations

Abstract

Populations of animals comprise many individuals, interacting in multiple contexts, and displaying heterogeneous behaviors. The interactions among individuals can often create population dynamics that are fundamentally deterministic yet display unpredictable dynamics. Animal populations can, therefore, be thought of as complex systems. Complex systems display properties such as nonlinearity and uncertainty and show emergent properties that cannot be explained by a simple sum of the interacting components. Any system where entities compete, cooperate, or interfere with one another may possess such qualities, making animal populations similar on many levels to complex systems. Some fields are already embracing elements of complexity to help understand the dynamics of animal populations, but a wider application of complexity science in ecology and evolution has not occurred. We review here how approaches from complexity science could be applied to the study of the interactions and behavior of individuals within animal populations and highlight how this way of thinking can enhance our understanding of population dynamics in animals. We focus on 8 key characteristics of complex systems: hierarchy, heterogeneity, self-organization, openness, adaptation, memory, nonlinearity, and uncertainty. For each topic we discuss how concepts from complexity theory are applicable in animal populations and emphasize the unique insights they provide. We finish by outlining outstanding questions or predictions to be evaluated using behavioral and ecological data. Our goal throughout this article is to familiarize animal ecologists with the basics of each of these concepts and highlight the new perspectives that they could bring to variety of subfields.

Introduction

Animal populations are inherently complex. Animal populations can change in many ways, exhibiting sudden crashes, startling growth, or stability (Bjørnstad and Grenfell 2001). Furthermore, animal populations can be more diverse than would be expected under directional selection, displaying great diversity in life-history or behavioral traits. For instance, some individuals may grow faster or take more risks across different contexts than others, despite these different individuals experiencing similar environmental conditions (Dall et al. 2004). Some animal populations may further display “culture” (e.g., Whitehead et al. 2004; Gero et al. 2016) in that groups of individuals show socially learnt traits that differ from other groups for reasons separate from environmental differences and fitness consequences in the different groups (Laland and Hoppitt 2003). Animal populations therefore regularly show exceptionally noisy, even apparently unpredictable, patterns. Apparently unpredictable systems are however still comprehensible, as such dynamics can often be driven by underlying deterministic processes (e.g., chaos; May 1974; May and Oster 1976). This means that even “random-appearing” (in the colloquial sense) ecological patterns may in fact possess a degree of predictability.

Systems showing difficult to predict patterns underpinned by deterministic rules are often described as “complex,” and animal populations are not alone in being described in this manner. Complex systems are a class of system comprising interacting units that are characterized by nonlinear dynamics (Bradbury and Vehrencamp 2014b). For example, complex systems can possess bifurcation points, where a simple increase in a single parameter of the system causes it to shift from one state (e.g., a stable equilibrium) to another, qualitatively different state (e.g., cycles between 2 points; May and Oster 1976). Complex systems can be comprised of linear interactions among units that create a nonlinear outcome, nonlinear interactions among units giving a linear outcome, or nonlinear interactions and a nonlinear outcome (Bradbury and Vehrencamp 2014a). Mathematical, physical, and chemical systems can be characterized as complex systems. Within biology, interacting neurons, individuals within populations, and species within an ecosystem have all been modeled as complex systems (May 1975; Solé and Goodwin 2000; Solé and Montoya 2001).

Although complexity theory has been embraced to a small degree by ecosystem ecologists, the framework may be even more fitting for application at the level of population biology. When applying complexity science to ecology, the majority of workers (Levin 1998, 2005; Solé and Montoya 2001; Burkett et al. 2005; Proulx 2007; Filotas et al. 2014; Messier et al. 2015; Dakos and Soler-Toscano 2016) have considered entire ecosystems as complex systems, where species are involved in a network of trophic interactions. This approach has provided key insights into ecosystem dynamics and the stability of communities (Hastings et al. 1993; Levin 1998, 2005; Solé and Montoya 2001; Burkett et al. 2005; Proulx 2007), such as how changes in population size can show chaotic dynamics (May 1974, 1975, 1976; May and Oster 1976). Levin (1998) described complex systems as large networks characterized by sustained diversity of their underlying units as well as some form of autonomous selection acting on these units. Given that selection does not act on species, this definition seems to more closely match the case where individual animals represent the most fitting units within a system. If this is so, then considering populations of interacting individuals as a focal complex system is likely to be particularly fruitful (Whitehead 2008; e.g., Pruitt et al. 2018). Despite the expanding influence of complexity theory within ecology, Bradbury and Vehrencamp (2014b) observed how many current behavioral ecologists either were not aware of complex system theory, or never consider incorporating it into their work. Therefore, while many of the ideas surrounding complex systems may not be entirely new to ecology, they may be new to many ecologists. In this review, we hope to introduce various concepts from complexity theory to animal population ecologists and advocate viewing animal populations through the lens of complexity science (Whitehead 2008; Bradbury and Vehrencamp 2014b).

This review aims to highlight the insights that can be gained from viewing animal populations as complex systems, where individual animals are the interacting units of interest. We will focus on the (social) interactions among individuals, in particular, as well as the differences in behaviors (e.g., in dominance or leadership) among individuals that characterize animal populations (Frank 2007; Bell et al. 2009), as these properties are essential to the dynamics of complex systems. As a framework, we consider the same 8 characteristics of complex systems (hierarchy, heterogeneity, self-organization, openness, adaptation, memory, uncertainty, and nonlinearity) adopted by a review on viewing forest ecosystems as complex systems (Filotas et al. 2014). Focusing on the same 8 characteristics gives a very useful degree of cross-field consistency, facilitating interactions between forest and animal ecologists. Other authors give different criteria (e.g., Levin 1998), meaning there is no one agreed-upon definition of a complex system. We will therefore not focus on a dichotomy of “can animal populations be viewed as complex systems or not” or the nuanced difficulty of defining “complexity” (see also, Poisot and Gravel 2014).

For each of the 8 characteristics, we first outline how it might be understood in terms of the behaviors of interacting individuals within populations, and second, how insights gained in the study of complex systems could be applied to the ecological and evolutionary processes occurring in animal populations. A glossary of terms is provided in Table 1. Third, we close the review by providing a set of outstanding questions, and in some cases predictions, that can be tested with ecological data from any number of animal systems. While the noisiness of ecological systems may sometimes prevent ecologists from using analytical tools from complexity theory directly, a rigorous consideration of complexity characteristics promises to expand our understanding of a variety of ecological processes and issues. We highlight some of these issues here.

Table 1.

Glossary of terms from complexity theory used throughout this review

Term	Meaning
Adaptation	The ability of a system and its components to change behavior in the face of events such as perturbations
Bifurcation point	Where a simple increase in a single parameter of a system causes a qualitatively change in behavior
Chaos	System dynamics that, despite being based on deterministic laws, are inherently unpredictable, especially in the long-term
Deterministic	A process that is completely predictable, without randomness
Emergence	Properties of a system that are more than the sum of the individual components, and are often difficult to predict in advance
Fractal	A pattern apparent in a system that does not change depending on the scale the system is viewed at
Heterogeneity	The units of a system differ in their location, history, behavior, or other properties
Hierarchy	The systems possess structural properties at multiple organizational levels, nested within one-another
Hysteresis	When a system’s paths between 2 states follow different trajectories depending on its history
Memory	A property of a system such that the future states cannot be predicted on the current state alone
Nonlinearity	System outputs are disproportionate to system inputs
Openness	The system is open to external perturbations, and mass and energy can be transferred in and out of the system
Percolation threshold	The point at which the connectedness of a system is so great, any information or change can propagate across the entire system
Scale-free	In networks of interactions, when the slope of the relationship between the number of connections per individual and the frequency of that number is a straight line when plotted on log–log axes
Self-organizing	Interactions among individual units of the system spontaneously give rise to apparent order and emergent properties at higher levels of organization, without any top-down or central control
State	A property of the system that in some way characterizes it
Stochastic	Unpredictable, genuinely random
Uncertainty	Aspects of system state or behavior that are difficult to predict

Eight Characteristics

Hierarchy

Hierarchy refers to cases where systems exhibit structural properties at multiple organizational levels. More specifically, a complex system can be arranged in a series of nested groups, where connections are more frequent within than between neighboring groups, and that nestedness can extend to multiple levels (Figure 1). Interactions between the different levels of the hierarchy create a structure that characterizes the system. Importantly, this property is not necessarily related to the “hierarchies” of dominance familiar to animal ecologists. For instance, metabolic networks, formed by linking interacting molecules in cellular processes, are often considered to be complex systems, and have been shown to possess hierarchical structure in a range of organisms (Ravasz et al. 2002). Most molecules interact with others in a specific reaction chain, with a few linking these chains together into larger groups, which are in turn grouped into larger functional groups (Ravasz et al. 2002). This is assumed to allow rapid interactions among molecules within the lowest level of organization, whilst allowing different groups to be dynamically integrated.

Figure 1.

A hierarchically structured network, where each of the nodes is embedded within a local network of 5 (i.e., the 5 local square-shaped networks), as well as a wider network connecting these smaller local networks. Note how all nodes are linked to the central node, hence this is an example of a network produced by a model similar to that of Ravasz and Barabási (2003). Source: Rudolf.rajczi via Wikimedia Commons, accessed 24 April 2019.

Many animal populations exhibit hierarchical structuring. In some mammal and bird populations, a hierarchical population structure has been shown to be quite common (Hegner et al. 1982; Hill et al. 2008; Wiszniewski et al. 2009; de Silva and Wittemyer 2012). Mothers associate with offspring, and are then often grouped with related females and with 1 or several related males, which can then be associated into larger bands or clans (Hill et al. 2008). Of course, eusocial insect societies are also hierarchically structured, with workers grouped by task, to promote efficiency (Ratnieks and Anderson 1999; Anderson and Ratnieks 2000; Fewell 2003). The rise of social network analysis has led to a rapid increase in the investigation of different species’ social structures (Krause et al. 2014); however, there remains limited information as to whether reptiles, fish, or non-eusocial insect or other invertebrate groups possess such hierarchical population structuring. However, we have reason to believe such taxa should also exhibit hierarchical structuring because such structuring has been detected whenever and wherever it has been examined, suggesting that hierarchical structuring is inherent property of animal populations.

Hierarchical patterns of interactions can emerge from simple interaction rules. For example, Ravasz and Barabasi (2002) noted that hierarchically structured networks possess features of real-world networks such as a high degree of clustering, and a scale-free degree distribution (see also section “Self-organization”). They went on to show a model for network growth where each step involved recreating the existing network 4 times, and connecting the new nodes to the central node of the original network (Figure 1), which gave a hierarchical structure and other properties of real-world networks (Ravasz and Barabasi 2002). The result was a pattern of hierarchical interactions that emerged with a high degree of parallelism across simulations. Whether the development of animal interaction networks exhibit a similar repeatability is unknown, but such models emphasize that relatively simple rules can result in the seemingly complex characteristics of animal social groups.

If we are to understand why animal populations are hierarchically structured, we require simple mechanistic models, such as those outlined above, to re-create animal social structures. Random networks, which can be viewed as a kind of null model, have consistently been shown to be poor fits to any real-world network (Krause et al. 2014). Ilany and Akçay (2016) built a relatively simple model for the development of social networks, where offspring preferentially associated with their mother’s social associates. Thanks to a small set of tuning parameters, they demonstrated that this model could accurately re-create the structure of several mammal social networks (e.g., their degree of modularity; Ilany and Akçay 2016). Determining whether this model goes on to produce hierarchically structured populations, with the same number of levels as those found in nature, would be a logical next step. Furthermore, the Ilany and Akçay (2016) model requires mother–offspring contact, otherwise it creates random networks, yet mother–offspring contact is absent in many species. Clauset et al. (2008) also provide a simple model that generates networks that are hierarchically structured, and found that it re-created other properties of metabolic networks, networks of terrorists, and networks among different grassland species. This result conveys that simply re-creating a hierarchical structure can capture many aspects of network properties. However, Clauset et al.’s model is based on probabilities of nodes being linked, with no mechanism for how this might arise, and they did not give interactions among-groups, which is an unrealistic assumption in animal populations. Therefore, the literature requires additional simple models for the formation of animal social networks, which can then be compared with data collected by empiricists. Basing such models on a mixture of cooperation and conflict among individuals should be a good start, as these processes are ubiquitous in populations and represent the facilitation and interference that are often key to the dynamics of complex systems (Newman 2009). Once we have determined how general hierarchical structuring of animal groups is and what the rules are that could lead to it, we can move on to considering the functional consequences of this group structure.

Hierarchical group-structuring has the potential to create conditions for multilevel selection. Multilevel selection occurs when individuals interact more closely with some individuals than others, forming group or aggregations, and traits of these groups or aggregations influence the fitness of individuals within them (Goodnight et al. 1992). For example, the brooding behavior of a pair (Björklund and Gustafsson 2013) or the level of aggression of a whole social group (Eldakar et al. 2010; Pruitt and Goodnight 2014) can influence an individual’s fitness. Multilevel selection can have profound impacts on the direction and rate of evolutionary change (Queller 1992; Goodnight et al. 1992; Bijma et al. 2007; Bijma and Wade 2008; Fisher and Pruitt 2019). Hierarchical group structure creates many levels for multilevel selection to act on. Thus, understanding whether animal groups generally tend to become hierarchically structured is fundamental to our understanding of how they are likely to respond to selection (Fisher and McAdam 2017). If multilevel selection influences social interactions in a manner that favors hierarchically structured networks, it may then select for its own presence; a curious possibility that deserves investigation.

Heterogeneity

Complex systems can be made up of interacting components which are heterogeneous, in that they differ in their behavior, location, history, or other properties. Such heterogeneity, in turn, can have far-reaching impacts on the functioning of the system. For example, different species within an ecosystem will have been in the ecosystem for different lengths of time, possess different functional traits, and occupy different niches. These functional differences can knit together across the community to create complex dynamics (Levin 1998, 2005; Williams and Martinez 2000; Solé and Montoya 2001; Proulx 2007; Montoya et al. 2009).

When the animal population is the complex system, these interacting components are the individual animals, and so the heterogeneity is within- or among individuals. Within-population differences in reproductive or life history strategies, roles as a leader or a follower, positions in dominance hierarchies, and of course differences in individual fitness have long been considered more than just “noise” around a population mean (Beekman and Jordan 2017). Furthermore, greater interest has been burgeoning recently in integrating this study of within- and among-individual differences across contexts. Animal “personality” (i.e., consistent differences in behavior among individuals over time and contexts; Wilson 1998; Koolhaas et al. 1999; Dall et al. 2004; Sih et al. 2004), is now considered to be widely distributed (Bell et al. 2009), and related to various ecological and evolutionary processes (Wolf and Weissing 2012). Understanding and accounting for this heterogeneity is necessary, as the dynamics of populations can change depending on whether among-individual differences are present or not (Coulson et al. 2001; Benton et al. 2006; Sih et al. 2012; Gangloff et al. 2018; Hamel et al. 2018a, 2018b, 2018c; Jouvet et al. 2018; Smallegange et al. 2018; Vedder and Bouwhuis 2018).

The patterns of heterogeneity we see in nature can often arise from nonlinear processes such as feedback through interactions (Bradbury and Vehrencamp 2014a, 2014b). For instance, stable linear dominance hierarchies are ubiquitous in nature, yet the probability of a linear structure emerging purely by chance is low (Chase et al. 2002). Chase et al. (2002) found that in cichlid fish, although pre-existing differences among individuals contributed to position in a dominance hierarchy, social interactions reinforcing position and accentuating among-individual differences were fundamental to their formation (see also, Lindquist and Chase 2009). Likewise, the task specialization among individuals demonstrated by many social arthropod colonies (Ratnieks and Anderson 1999; Anderson and Ratnieks 2000) may arise from reinforcing feedback during the learning process, which can improve efficiency at 1 task while reducing it for another (Chittka and Muller 2009). Reinforcement of behavior is also thought to contribute to reduce within-individual variation, which then magnifies among-individual differences (Roberts and Del Vecchio 2000). At the community level, the evolution of differentiation among-species is thought to be increased by closer interaction amongst those species (Agrawal 2001; Martin et al. 2010; Grossenbacher and Whittall 2011; Laaksonen et al. 2015), and there is some evidence that this applies to changes among individuals as well (Laskowski and Pruitt 2014; Laskowski et al. 2016). The heterogeneity shown in animal populations may, therefore, depend on feedback among interacting units, which is common to complex systems.

In the particular case of animal personality, there are currently a multitude of different models for the evolution and maintenance of among-individual differences in behavior (Dingemanse and Wolf 2010; Sih et al. 2015). Some of these rely on interactions between individuals (e.g., Bergmüller and Taborsky 2010; Montiglio et al. 2013), whereas others do not. A general assessment of which class of models better fits existing data on behavioral variation within populations is vital. What would also be useful is if models for these processes could make their assumptions and predictions in units that empiricists typically measure. For instance, if a particular model leads to among-individual differences in behavior, or requires a certain degree of among-individual differences in more stable traits such as life-history strategy, then the expected or required differences among individuals should be expressed as a repeatability score (intra-class correlation coefficient; Nakagawa and Schielzeth 2010), allowing existing data sets to be compared with the model’s predictions.

In terms of social interactions, heterogeneity in the frequency, strength, and type of social interaction is common in animal populations. Animal social networks commonly show a skewed distribution in the number of unique connections an individual possesses (its “degree”), such that a few individuals have a great number of connections, whereas most individuals have only a few (Lusseau 2003; Kasper and Voelkl 2009; Pinter-Wollman 2011). This pattern is commonly seen in other classes of real-world networks, such as the Internet, and can stem from a network-growth model, where new individuals preferentially associate with already-influential individuals (Barabási and Albert 1999; see also the model of Ravasz and Barabási 2003, introduced above). Such a model could appear appropriate for animal populations, with immigrants tending to preferentially associate with the most well-connected and influential group members when arriving. Ilany et al. (2015) demonstrated that spotted hyenas Crocuta crocuta preferentially associate with the most well-connected individuals, and Ilany and Akçay (2016, see above) demonstrated that a type of preferential attachment model can create networks that possess structures similar to those observed in many mammal populations. Unfortunately, temporal analysis of animal social networks is relatively rare (Pinter-Wollman et al. 2013), and so we lack the data needed to assess whether this model of group joining is realistic. There are other types of network growth models (e.g., Krapivsky and Redner 2005; Fortunato et al. 2006), which might differ in their resemblance to animal networks. Assessing whether these models are good fits to the patterns of heterogeneous social interaction patterns observed within animal populations remains a question worth investigating.

Self-organization

Self-organization is a property of many kinds of systems, both living and non-living, including animal populations. If a system is self-organized, then interactions between individual units of the system (at the lowest level of the hierarchy) combine to give emergent properties at higher levels of organization. Emergence is defined as coherent patterns that are more than the sum of the individual components. For example, consider a stream of sand particles falling onto a flat surface. Over time these particles will build up on their own to create a pile of sand. The pile of sand was self-organized in that there was no top-down control to build upwards, just individual sand particles interacting with each other to form a structure (Bak et al. 1987, 1988; Creutz 2004). Such systems typically contain fractal patterns, which are patterns that are similar at whatever scale the data are viewed (Mandelbrot 1967). For instance, after a time the sand pile may partially collapse. The size of these collapses will be distributed according to a power-law, where the frequency of the events is proportional to their size raised to an exponent. When the frequency of the collapses is plotted against their size on log-log axes, a single straight line fits the data across its entire range; a pattern consistent at all scales. Fractal patterns occur when the exponent is negative but not necessarily an integer. Fractals are commonly associated with complex systems (Bradbury and Vehrencamp 2014b), and are intimately linked to the self-organizing principles that form them.

Within ecological networks, simple interaction rules are thought to give rise to complex structure (Williams and Martinez 2000). Within animal populations, for example, Sumpter (2006) identifies several aspects of animal collective action that can be explained through self-organizational phenomena. Migrations of fish, aggregations of cockroaches, and ant pheromone trails can be described in terms of individuals following simple rules (Sumpter 2006). Other aspects of ant and presumably other eusocial insect ecology, such as the construction of nests, may also be based on simple individual rules that nevertheless result in patterned and apparently complex end products (Bonabeau et al. 1997; Buhl et al. 2004; Annagiri et al. 2017).

Given that we are happy to invoke ideas of self-organization when studying these large, collectively moving and acting groups, the question becomes whether we can apply these ideas to our understanding of other kinds of animals. Detecting fractal patterns in animal populations may go some way to demonstrating that self-organization is at work, because, as outlined above, fractal patterns are typically associated with systems driven by self-organizing principles. For instance, there is considerable interest in whether social networks follow a fractal or “scale-free” pattern in the distribution of the degree of each individual. For this to be true, the slope of the relationship between the frequency of a given degree and the number of those connections should be invariant to the scale when plotted on log–log axes (i.e., it should follow a straight line). Lusseau (2003) concluded that bottlenose dolphin Tursiops spp. social networks possess scale-free properties only at high degree values (≥7). Manno (2008) found that ground squirrel Spermophilus columbianus networks showed a scale-free distribution over the entire range of degrees. However, various Macaque networks have been shown to be more random than fractal/scale-free, with a linear rather than power-law distribution (Sueur et al. 2011). In general, strong evidence for fractal/scale-free properties in animal social networks will be problematic, as degrees across many orders of magnitude are required to determine if a fractal/scale free pattern is present (Avnir et al. 1998). This is something that is absent from nearly all animal social networks, as they tend to be limited to a few hundred individuals at most. Both Clauset et al. (2009) and Fox Keller (2005) raised a number of further issues with the search for scale-free networks, including that many different network structures can have scale-free relationships: the tail of power-law distributions tend to fluctuate greatly, and many different processes can lead to these structures. A scale-free degree distribution may therefore not be a critical metric for detecting self-organization.

For animal populations to be self-organized, one would expect the structure to be consistent whenever it is re-created, assuming there had been no changes in the environment or in the rules governing the interactions. For example, Shizuka et al. (2014) found that a population of golden-crowned sparrows Zonotrichia atricapilla re-form the same 3 communities every winter in California after summering in Alaska, despite large turnover of individuals. In addition, field cricket Gryllus campestris networks have also been shown to have the same general structures across non-overlapping generations (Fisher et al. 2016). As individual animals presumably have some control of their actions, self-organization into the population structure typical of any given species is probably assumed to be the norm, rather than social structures emerging because of constraining external conditions or central or top-down control.

Many animals do not possess obvious “group” structure, but still live in aggregations governed by social interactions (e.g., territorial animals). To what degree to such populations structure themselves via self-organization? Because territory boundaries are determined by internal forces such as competition, which may be independent of or interact with external forces, the structuring of territories would appear to be a type of self-organization. However, since these forces are antagonistic rather than cooperative, the rules for the formation of such aggregations compared to the formation of more cooperative animal groups may well be different. Quantifying how self-organization and external forces jointly contribute (i.e., the mechanisms and relative importance of each) to the structure of a wide range of animal populations will allow us to evaluate the importance of self-organization as a general force, and when its importance varies. The most straightforward test would be to reset populations multiple times in order to determine the consistency with which populations converge on similar structures again and again (e.g., Formica et al. 2016). This could be accomplished in controlled laboratory studies or leveraging “natural experiments” of various kinds (e.g., seasonal migration; Shizuka et al. 2014).

Additional properties of populations indicate that their structures are likely to be self-organized. Perry (1995) noted that ecosystems are often 1) organized by positive feedback processes, 2) reside far from equilibrium, and 3) are thermodynamically open (where the transfer of matter, as well as energy, between the system and its surroundings is possible). Such characteristics are typically found in systems regulated by self-organization, although they are not entirely sufficient to identify a system as self-organizing (Perry 1995). Positive feedback processes have many influences on animal populations too, such as aggregations at mating sites and reciprocal helping behavior, however negative feedback processes are also prominent (e.g., Sinervo and Lively 1996). Whether or not populations are typically at equilibrium or not it is debated, in part, because equilibria can exhibit a variety of properties (e.g., stable vs. unstable; Cuddington 2001). Finally, whether populations can be defined as thermodynamically open remains to be assessed. Birth and death processes are deemed here to be internal processes within the population, however immigration and emigration of individuals in and out of the population are deemed to be a kind of “openness” by our definition, because individuals move in and out of the focal system. We discuss this further in the next section.

Openness

Energy, information, and disturbances can alter complex systems from beyond the system boundaries. This in contrast to closed systems, where there are no external inputs. Ecosystems, networks of neurones, electrical networks such as the Internet and weather systems are all influenced by external inputs, for example, climatic variation, sensory inputs, human entered commands and energy from the sun respectively. Animal populations too exhibit a high degree of openness, but their degree of openness may vary situationally or across species.

Animal populations are clearly influenced by external factors that emerge from processes occurring beyond the focal system (i.e., the population), such as varied environmental conditions, natural predation from other species, and anthropogenic pressures like hunting, and there is no shortage of interest in such topics. For instance, understanding savanna ecosystems requires data on climatic variation and frequency of fires; they cannot be understood without these external factors (Bodini and Clerici 2016). Although some questions exist about how to define the boundary of an animal population, there appears little doubt that animal populations are open. Openness may actually be necessary to avoid population collapse, as openness permits the release of energy and the movement of individuals, helping to stabilize the system (e.g., via rescue effects; Green and Sadedin 2005). As outlined above, whether animal populations can be thought of as specifically thermodynamically open may contribute to our understanding of the process that organize them. In particular, openness means that in order to understand the dynamics of a focal system, one must simultaneously consider the inputs from forces beyond the system’s “boundaries.” While many ecologists might convey that this is intuitively all obvious, the observation indicates that the thematic forces governing animal populations bear much resemblance to the phenomena explored by scientists ranging from neuroscientists to astrophysicists. Complexity theory therefore provides a common language for communication between ecology and these fields.

Memory

Information about the past may be retained in a complex system, which can influence how the complex system behaves in the future. This is often referred to as system’s “memory.” For example, the first pioneer species that colonizes an area can modify the habitat and influence later successional species in forests (Filotas et al. 2014; Messier et al. 2015). This “ecological memory” can also stem from seed banks, eggs in diapause, or the presence of unusual species within a community due to historical quirks (Anand et al. 2010). The presence of memory in the interacting units of a system can be fundamental for the formation of observed ecological patterns (e.g., spatial clumping of organisms; Hendry and McGlade 1995).

The term “hysteresis” is typically used for systems that show dynamics with an aspect of memory and conveys that a system’s tendency to pass between states depends highly on its history. Hysteresis is of interest to ecologists because it shows that the future state of the system depends on its past states, rather than solely on the current state (Figure 2). This commonly means that there exist (at least) 2 values of a response variable for a given input variable. An example of this would by the classic lynx–snowshoe hare cycles in the boreal forests of Canada. For a given number of snowshoe hares there are theoretically 2 likely numbers of lynx: a small number if the population has recently crashed and is on the increase, or a larger number if the population was at a peak and is now declining (Boutin et al. 1995). Predicting the number of lynx, therefore, is not possible based solely on the number of hares. Predictability based solely on the current state is an explicit assumption of Markov chain models (Brooks et al. 2011). Yet, if hysteresis, and thus system memory, is common in animal populations, Markov chains approaches may not be effective. Hysteresis can also be seen if a system is perturbed and then the perturbation is removed. Hysteresis is evidenced if the trajectory of the system from the original state to the perturbed state follows a different state path to that of the return from the perturbed state to the original one (Figure 2; Beisner et al. 2003). This too indicates that, for the same values of a set of parameters, there exist multiple possible states where the system may reside.

Figure 2.

A system showing memory or hysteresis. For a range of x-values, 2 possible y-values exist, which value the system takes depends on the previous values; for example, the direction the system has approached the current point. Therefore, knowledge of the current state alone is not sufficient to predict the future state. Source:http://www.enterpriseintegrationpatterns.com/ramblings/06_hysteresis.html, accessed 24 April 2019.

The presence of hysteresis can limit a system’s ability to return to past, stable states (Beisner et al. 2003; Folke et al. 2004), which raises concerns for conservation and remediation efforts. Blonder et al. (2017) developed a multi-species model for community dynamics that possessed hysteresis for certain parameter values. They used this to model the matching of species niches to available environmental niches. They demonstrated that unstable communities may not return to past states at all, even when modeled environmental variables return to previous values (Blonder et al. 2017).

Hysteresis can also occur at the level of individuals in the case of phenotypic plasticity. If organisms possess plastic traits, then we might expect them to alter their traits to best match the current environment. However, it is plausible that hysteresis may be present in these trait-environment relationships, so that how animals change their behavior along an increasing environmental gradient may not mirror how the behavior changes along a symmetrical but decreasing environmental gradient. For instance, it could be expected that cooperative breeding would be more common in harsher or more variable environmental conditions (Covas et al. 2004; Jetz et al. 2011). However, hysteresis would mean that the observed prevalence of the strategies depends on whether conditions are harsh and are becoming more benign (in which case cooperative breeding strategies might maintain dominance) or were benign and have become harsh (in which case individual-breeding strategies might be more common). Couzin et al. (2002)’s model for group-movement indeed demonstrated something of this sort, where changes in movement types along a gradient of changing model parameters are not symmetrical. Whether hysteresis exists in trait–environment relationships is completely unexplored in animal populations, but should prove an interesting avenue for future research. Pruitt et al. (2018) recently argued that hysteresis may well be present in many animal social groups, and provide a detailed example of hysteresis in group infighting in response to heating and cooling cycles in social spiders (Doering et al. 2018). Much more work is needed, however, to determine how common hysteresis truly is within animal populations and the population structures and species traits that reduce or magnify these system characteristics.

Phylogenetic inertia and parental effects are other forces through which past states can influence future system behavior. In phylogenetic inertia, traits that a species possess may principally depend on the fact that their ancestors possessed them, rather than contemporary selection pressures (Blomberg and Garland 2002). For example, the pharyngeal slits and post-anal tail in primate fetuses are not related to contemporary function but exist as they are present in all chordates. Therefore, considering a species’ evolutionary history is often important for understanding why contemporary traits appear as they are. Knowledge of the evolutionary history of a species can furthermore be important when predicting the response of populations to selection, as demonstrated in experimental cultures of bacteria (Travisano et al. 1995; Blount et al. 2008). This could be of particular importance as global climates change. Sih et al. (2011) noted that aspects of animals’ evolutionary histories, such as the variability of their ancestral environments, will likely influence a population’s response to environmental change.

Parental effects bring about memory effects because they alter populations’ expected response to selection depending on the mean trait value and selection strength on the current and previous generation (Kirkpatrick and Lande 1989). Parental effects are defined as influences that a parent (typically the mother) has on the traits of the offspring, beyond direct genetic inheritance. These parental effects exist in many forms: for instance, the rate at which a mother feeds her offspring may influence their growth rate. Such effects are expected to be common when any kind of parental care occurs (Mousseau and Fox 1998), and indeed have been shown in a range of wild and captive animal populations (McAdam and Boutin 2004; McAdam et al. 2014). Therefore, animal populations regularly show a response to selection that depends on traits and selection pressures in the previous generation, which is a form of memory. Fisher et al. (2019) showed that a red squirrel’s (Tamiasciurus hudsonicus) food cache, date of spring breeding, and even life time reproductive success are influenced by the sex and lifespan of the previous territory occupants, relatives or otherwise. This conveys that extended phenotypes can facilitate indirect effects between individuals. If such changes to the environment are at least semi-permanent, then they too can produce memory effects with the potential to alter population dynamics. For instance, robust caches created by prior generations may buffer current generations from short-term fluctuations in resource availability. Furthermore, red squirrel caches influence the abundance of other species (Posthumus et al. 2015). Therefore, memory effects in a system can have important within- and across-species impacts.

Nonlinearity

A key aspect of complex systems is that changes often show nonlinear trends, so that outputs from the system are disproportionate to inputs (see also, “non-monotonicity,” reviewed in: Zhang et al. 2015). For example, if trees in a regular grid catch fire if their neighbor is burning, then the total number of trees burnt across different starting densities of trees shows a clear departure from linearity (Bak et al. 1990; Chen et al. 1990; Drossel and Schwabl 1992; Clar et al. 1996). At low densities, increasing density does not result in many more trees burnt. However, there is a critical window where increasing the density causes the fraction of burnt trees to increase rapidly, before reaching a plateau for high densities, where most trees tend to be burnt regardless of the starting density. This is an example of a percolation threshold, a point above which a change can propagate throughout the entire group, and below which it cannot. Such critical thresholds are a hallmark of complex systems. Critical thresholds in complex systems can also exist as bifurcation points, where smooth changes in the parameters of a system (e.g., intrinsic growth rate) can lead to sudden, qualitative shifts in the system behavior (e.g., shifts from stable to unstable cycles; May and Oster 1976; Dennis et al. 1997). Therefore, nonlinearities can result from changes in internal parameters as well as environmental parameters (Pruitt et al. 2018).

Population biologists have long studied nonlinear dynamics in animals. Growth curves of populations, captured by the differential equations of Verhulst (1838, 1845), are a classic example. As each individual in the population contributes to population growth through reproduction, the larger the population becomes the faster the growth rate it exhibits, which begets exponential growth. Assuming that, as the population nears its carrying capacity growth rate is reduced, and that either reproduction is synchronized or counts are taken once a generation, different intrinsic growth rates produce different population dynamics. Populations can show stable equilibria, stable cycles around 2 or 4 point attractors, or chaotic dynamics restricted within the limits of the system (see Figure 1.2, p. 7 of Solé and Goodwin 2000). Such bifurcation points have been demonstrated in laboratory cultures of flour beetles (Tribolium sp.), by experimentally altering adult mortality rates (Dennis et al. 1997). Doing this caused shifts between equilibrium, periodic cycles and aperiodic cycles (Dennis et al. 1997); qualitative changes in system behavior. Therefore, not only is the growth itself nonlinear, but changing a single parameter in the system gives qualitatively different population dynamics, that is, its effect is nonlinear.

Nonlinearities such as percolation thresholds have been observed in animal populations too (termed “social tipping points” by Pruitt et al. 2018). Manipulations to networks via simulation or targeted removals are one means of testing for nonlinear responses in global network properties (e.g., information transfer). This question has been directly investigated in both mammals and social insects. Williams and Lusseau (2006), Manno (2008), Naug (2009), and Chaverri (2010) have all simulated the random removal of a small number of individuals from their real-word animal networks and found that this did not influence the connectedness of the entire network, which is analogous to the forest fire model, where at high densities changing the starting density still leads to all trees catching fire. Both Williams and Lusseau (2006) and Manno (2008) went on to show that targeting well-connected individuals much more quickly led to fragmentation of the network into small clusters. In a real population, Flack et al. (2006) demonstrated that the actual removal of keystone pigtailed macaques Macaca nemestrina destabilizes the entire group, leading to more isolated clusters of individuals. Indeed, when considering networks, and “small-world” networks (networks defined by a higher degree of clustering and short path lengths compared with random networks) in particular, selective removal of well-connected or pivotal individuals within a network generally has significant impacts on its global structure (Albert et al. 2000; Albert and Barabási 2002). Therefore, any function linked to the cohesiveness of a group of interacting individuals may show some form of percolation threshold during the loss or gain of individuals (see: Pruitt et al. 2018 for a review) particularly if those individuals assume keystone roles (Modlmeier et al. 2014).

Thresholds are also apparent in the behavior of individual animals. Animals can show nonlinear responses to various factors such as in habitat use when responding to human-induced disturbances (Frair et al. 2008; Beyer et al. 2013), whereas predators can show nonlinear responses to prey availability when making foraging decisions (Hines et al. 1997). Thresholds can also be observed in mating behavior, for instance when females sometimes accept a male when his “quality” is above a certain level (Thornhill 1976; Moore and Moore 1988), indicating that a male’s phenotype has a nonlinear effect on his mating success. Finally, and as suggested by the above research on social networks, collective decision-making, can also show “quorum” responses, whereby all individuals rapidly “agree” on a decision once a large enough number of other individuals have made it (Seeley and Visscher 2003, 2004; Ame et al. 2004; reviewed in: Sumpter and Pratt 2009). In some fields, there is therefore a strong appreciation of nonlinear processes in animals. However, these fields are often biased toward studies of highly social organisms and thus the generality of such properties remains largely unknown.

For further integration of this aspect of complexity into the study of animal populations, we advocate that researchers in disciplines where relationships are typically assumed to be linear consider nonlinear relationships. For instance, when estimating selection coefficients, a linear model is typically used to estimate the additive contribution of different traits to proxies for an individual’s fitness (e.g., lifetime reproductive success; Lande and Arnold 1983). This may not be reasonable in all situations. For example, it may be that a trait linked to some aspect of “quality” (e.g., body condition) is assumed to positively influence fitness, whereas lifespan is also positively associated with fitness (e.g., Hoogland and Brown 2016). Therefore, a simple additive combination of these 2 traits may be insufficient to predict fitness, as presumably the quality-linked trait counts for every breeding season, or every day of adulthood (depending on the species) that the organism is alive. This therefore suggests a multiplicative effect of lifespan and quality-linked traits on fitness (fitness = trait × lifespan), rather than an additive effect (fitness = trait + lifespan). Yet, the latter is what is represented in a linear model unless an interaction between the trait and lifespan is explicitly fitted. Fitness in wild organisms is nearly always highly skewed, in both group-living and solitary species (Keller and Reeve 1994; Clutton-Brock et al. 1997; Engh 2002; Frentiu and Chenoweth 2008; Ryder et al. 2009; Rodríguez-Muñoz et al. 2010; Thompson et al. 2011). This suggests a nonlinear function leading to fitness, hence associated models of selection should consider nonlinear relationships (see also “aster” models; Shaw et al. 2008; Shaw and Shaw 2014).

Adaptation

Adaptation refers to changes in the behavior of a complex system in response to changes in outside influence. Beisner et al. (2003) discuss how ecosystems can be moved to alternate stable states (e.g., stationary vs. cycling population sizes) through either changes in the internal variables of the system (e.g., the reproductive rate of individuals; May 1975), or to changes in the external parameters (e.g., the nutrient level of a lake; Scheffer et al. 1993). The latter case gives us the possibility to see adaptation, if the changes in external parameters cause a shift in system state that nevertheless does not drive the system to extinction. This is related to but a separate concept from a system’s resilience, which is its ability to stay in the same state despite perturbations (Beisner et al. 2003), which could be enhanced by the system’s ability to adapt in the complexity sense.

In animal populations, many authors have considered how perturbations, both human induced or otherwise, lead to the changes in animal population structure. Note that evolutionary change in animal populations (what is often thought of when the word “adaptation” is used) to not be a form of adaptation in the sense of a complex system, as it involves the replacement of individual units in a system. Adaptation in this context instead considers cases where the population exhibits change in labile traits in response to alterations to the environmental conditions in which it operates.

Factors external to an animal population that can be subject to change include environmental conditions and the composition of the ecosystem community in which that species resides. In the case of environmental conditions, human-induced climate change is projected to lead to widespread extinctions in marine fish and invertebrates (Cheung et al. 2009), mammals (McDonald and Brown 1992; Cardillo et al. 2005), and birds (Jetz et al. 2007) and is already linked to dramatic extinctions in amphibians (Stuart et al. 2004; Pounds et al. 2006). This environmental change is also expected to be accompanied by change in species distributions (Easterling et al. 2000; Hughes 2000; McCarty 2001; Parmesan and Yohe 2003; Robinet and Roques 2010; Schloss et al. 2012), which will result in changes to community composition, species interactions, and biodiversity (Vitousek 1994; Vitousek et al. 1997). Such intense selection pressure is expected to lead to behavioral change in animals (Tuomainen and Candolin 2010; Sih et al. 2011), which would be an “adaptation” in the sense that the system is acting differently as a result of external changes. However, extinctions imply that animal populations sometimes fail to adapt to external changes. Pushing any living system far outside of its usual operating window risks endanger it. However, even if the population does not go extinct, they may enter alternative states from which they resist return (they have entered alternate “basins of attraction,” e.g., Folke et al. 2004). Ultimately, the evidence for extinctions in the face of external change is myriad, but examples of animal populations adapting their structure or function to external change are required to demonstrate adaptation.

Behavior is well known to be plastic, and hence we will not discuss evidence for that here. Instead, we focus more narrowly on how animal social structures respond to change in external conditions. Spotted hyena C. crocuta social networks, for instance, respond to reduced rainfall by being denser (more of the total possible connections are present), presumably as their prey are more tightly clustered, but return to normal density when rainfall increases (Ilany et al. 2015). Forked fungus beetle Bolitotherus cornutus possess social networks that gradually change over time, unless they are disturbed by placing all individuals in temporary isolation (Formica et al. 2016). This perturbation appears to move the system back to its original state, thus “resetting” the social process, after which the beetles re-start the dynamic process they were previously engaged in (Formica et al. 2016). Leu et al. (2016) observed that sleepy lizard Tiliqua rugosa social networks were more stable and denser when barriers were inserted into their environment, although other patterns (e.g., the skewed interaction strengths) were unaffected. In fish, conflicting results exist, with no influence of habitat complexity on network structure found in some cases (Edenbrow et al. 2011), but less open environments leading to denser networks in others (Webster et al. 2013). Sloman et al. (2001, 2002) found that steady water flow facilitates the emergence of stable, linear dominance hierarchies in brown trout Salmo trutta that benefit the most dominant individuals. However, if drought or spate conditions are re-created, the stable hierarchies break down, and previously dominant fish no longer gain the same benefits (Sloman et al. 2001, 2002). This finding suggests that the population structure in terms of the dominance hierarchy does not exhibit compensatory adaptation that enables the persistence (resilience) in the face of changing conditions. These results demonstrate that, whereas it is certainly possible that animal social structures adapt to external changes, whether or not they will and the direction of any changes may be hard to predict. Furthermore, some of the above studies have demonstrated that populations can return to equivalent states (e.g., the perturbations appeared to have transitory effects in the forked fungus beetles and the hyenas), but not all. A complex system may not necessarily return to exactly its state before the perturbation, see the section on “hysteresis” above. Given the frequency of environmental changes, understanding whether animal populations can continue to function in the face of these varying perturbations is important. Thus, more studies are sorely needed to determine the kinds of system traits and external forces that cause adaptation versus collapse in animal populations.

Note that we have not discussed some kinds of human-induced perturbations, such as hunting, that involve directly removing individuals from the population. Although there are many such examples (e.g., Coltman et al. 2003; Donnelly et al. 2006; Smith et al. 2013; Elliser and Herzing 2014; Kubitza et al. 2015), these also conflate external perturbations with internal changes to the composition of the system, and so the influence of the “external” force is hard to separate.

Uncertainty

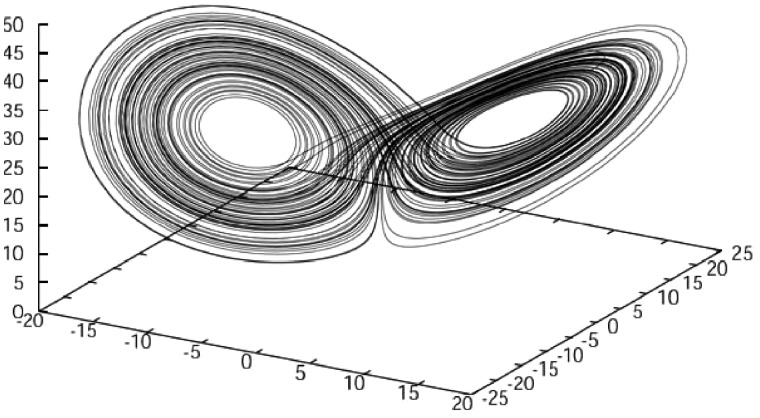
Complex systems are often characterized by low predictability. This low predictability can be caused by systems’ sensitivity to initial conditions or through the difficulty of predicting emergent phenomena. An example of sensitivity to initial conditions are the Lorenz equations, which comprise a set of 3 differential equations that produce a chaotic, non-periodic, but highly deterministic system moving through 3-dimensional state-space (Figure 3). The result is that, although the rules governing the state trajectories of the system are entirely deterministic, even very small measurement error in the system’s initial conditions (which, in the real world, always occurs), cause predicting the long-term behavior of the system to be impossible (Lorenz 1963).

Figure 3.

A Lorenz attractor in 3 dimensions. Note how 2 initially adjacent trajectories can rapidly diverge. Source:http://www.mizuno.org/c/la/img/lorenz_web.jpg, accessed 24 April 2019.

If uncertainty were not present in animal populations, ecology would not need to persist long as a discipline. Given that the science of ecology is alive and well, there exists much uncertainty about the dynamics of myriad ecological systems (Boyce 1992), including population responses to stress (Schindler and Hilborn 2015). Having discussed emergent phenomena in terms of percolation thresholds and bifurcation point above, we will examine ideas surrounding sensitivity to initial conditions in this section.

Animal populations are often governed by multiplicative processes, so that small variations in input variables can have a large influence on subsequent system trajectories and end points (Boyce 1992). This sensitivity to initial conditions is a hallmark of chaotic dynamics. Considering fluctuations in population size, Lotka–Volterra models with only 1 species are unlikely to be chaotic (Hassell et al. 1976), but models with 3 or more species often show chaotic dynamics (Hastings et al. 1993). The Lotka–Volterra model has been considered to be unrealistic because small changes in starting values lead to large changes in dynamics (Odenbaugh 2005), yet this may actually be a realistic property. To determine whether a system is sensitive to initial conditions, one can calculate Lyapunov exponents. Lyapunov exponents are measures of how quickly 2 nearby initial conditions diverge (Hastings et al. 1993). A positive Lyapunov exponent indicates that dynamics are chaotic (i.e., hard to predict in the long-term), whereas a negative Lyapunov exponent indicates the system will converge to an equilibrium. Benincà et al. (2008) showed chaotic dynamics, via positive Lyapunov exponents, in mesocosms of plankton. This led the authors to suggest that long term predictions of species abundance may therefore be impossible. If this were a common trend, then predictive ecology would appear to be a tautology. Medvinsky et al. (2015) reviewed efforts by ecologists to find chaotic population dynamics, and concluded that positive Lyapunov exponents were typically rarely observed. In most systems the dominant Lyapunov exponent is around zero, although this can change over time, giving periods of chaos (Medvinsky et al. 2015). For example, Becks and Arndt (2008) found transitions to chaos and back again through the manipulation of only 1 experimental parameter (concentration of a chemical) in a multi-species food web of 2 bacteria and a bacterivorous ciliate. This shift happens quickly, so it may be missed in field studies over short time periods or with intermittent sampling (Becks and Arndt 2008).

As a general rule, this form of unpredictability is distinct from stochasticity and measurement error. Stochasticity and measurement error may also cause us to be uncertain about any of our predictions, even in a system lacking chaotic dynamics. In a system governed by stochasticity, accurate predictions of any kind, either short- or long-range, are impossible, whereas in a chaotic but deterministic system short-term predictions are possible. Okamoto et al. (2016) fitted both stochastic and deterministic processes to a reef fish population, allowing them to separate said processes and then demonstrate how both contribute to population fluctuations. This approach could profitably be extended to aspects of behavioral ecology, such as whether a time-series of individual or group behaviors shows 1 of or both stochastic and deterministic properties (Fisher et al. 2018; Honegger and de Bivort 2018). A caveat to this is that chaos and stochasticity are not necessarily independent. For instance, Ottermanns et al. (2014) found increased stochastic disturbance lead to a reduction in the chaotic dynamics of Daphnia magna populations.

Most of the published examples separating chaos and stochasticity are limited to changes in population sizes over time. However, we do not see an obvious reason to limit the separation of chaos and stochasticity there, or to not apply it to longitudinal life history or behavioral data of individuals (Cole 1994). Researchers can often assume erratic data stems from stochastic noise or measurement error, but a third possibility is that it results from chaotic dynamics (May and Oster 1976). For example, studies are increasingly quantifying behavior variation over the life time of individuals (Biro and Stamps 2015). Fisher et al. (2015) found that individual crickets diverged in behavior over time, a pattern consistent with (although not sufficient to indicate) sensitivity to starting values. As Cole (1994) notes, chaotic dynamics of behavior due to sensitivity to initial conditions can give the impression of essentially random behavior. This implies no repeatability of individual behavior, and no genetic basis to behavior. As Fisher et al. (2018) describe, a period of chaotic behavioral change during development, followed by deterministic change, for example, due to age, can give among-individual variation in behavior, even in otherwise identical organisms (as observed by Polverino et al. 2016; Bierbach et al. 2017; see also, Honegger and de Bivort 2018). Such a mechanism remains to be tested however.

A key outstanding empirical question is, to what degree is behavioral variation deterministic (and possibly chaotic), and to what degree is it stochastic? There are theoretical reasons (stochastic unpredictability makes a prey animal harder to catch) and empirical lines of evidence for why animal behavior may be adaptively stochastic (Maye et al. 2007; Brembs 2011; Honegger and de Bivort 2018), but fitting both stochastic and deterministic process to behavioral data is required to assess their relative contributions to variation. We hypothesize that it is likely easier for selection to produce genetic, physiological, and behavioral outputs that are unpredictable but deterministic (i.e., chaotic) than to produce outputs that are truly stochastic.

Conclusions

We have argued that animal populations and the social interactions that structure them can be useful understood using insights from within complexity theory. Yet, there are also numerous avenues that need to be explored before a wider embracing of concepts from complex systems science can occur in population biology. We close here by outlining just some of the conceptual questions raised by considering animal populations through the lens of complexity theory.

Does heterogeneity interact with self-organization?

Models for self-organization typically assuming homogeneity among individuals. Yet given the heterogeneous within natural populations, such assumptions may be unrealistic. Do models for self-organization give more or less accurate predictions when the system components are heterogeneous? As mentioned above, reinforcement among individual workers during the self-organization process can lead to greater heterogeneity in task performance in social systems (Chittka and Muller 2009). Furthermore, the establishment of stable dominance hierarchies may be facilitated by pre-existing among-individual differences (Chase et al. 2002). Further work is required to determine whether heterogeneity contributes to other self-organizing processes, such as the formation of stable territorial boundaries.

Does uncertainty conflict with self-organization?

If complex systems possess chaotic dynamics, then the final state of the system predicted to be uncertain as it is expected to depend on initial conditions. Yet if the complex system is highly self-organized, then one would expect the same state to be reached from a range of starting conditions. This is also relevant for adaptation, for if initial conditions matter, then the dynamics following the perturbation of a developed system should be different to the dynamics of a new, growing system (i.e., hysteresis). This conflict is perhaps rescued by the fact that long term dynamics in chaotic systems do show convergence to attractors, if not stable equilibria (e.g., the saddle points of the Lorenz attractor, or the boundaries the population fluctuates within). So, while one cannot predict the route that a system will take, one might be able to predict the general form it will take. Taken together, animal populations, and chaotic systems in general, are predicted to show short-term predictability (change is deterministic) mid-term unpredictability (sensitivity to initial conditions) and long-term predictability (due to attractors keeping the system within certain bounds).

Are mathematical models for complex systems broadly applicable to animal populations?

To further cement the analogy between animal populations and complex systems, we need to evaluate whether mathematical equivalencies can be drawn between fields. For instance, do simulation models that give complex, hierarchically structured networks match the data for animal social networks collected in the wild? Creating such models will require accounting for key features of complexity, such as considering nonlinear interactions rather than defaulting to linear ones. Ecological systems may contain more uncertainty than mathematical (or physical and chemical) systems, suggesting that the transfer of some models might be inappropriate (Petrovskii and Petrovskaya 2012). However, even when not entirely appropriate, models that are overly simple can still be useful, as they can help us to explore the possible behaviors of ecosystems and the manner in which more complicated systems differ from simple models (Odenbaugh 2005). This therefore renders their application valuable.

Is animal behavior stochastic or chaotic?

Finally, a better understanding of the importance of stochasticity and chaos is required. Genuinely stochastic systems can appear regular, whereas deterministic systems can appear random due to chaotic dynamics (Lenormand et al. 2009). Appreciating “messy” data can arise from stochastic noise, measurement error, or chaotic dynamics (May and Oster 1976) should increase the range of questions that we ask with existing datasets. Animal behavior may well be inherently stochastic (Maye et al. 2007). In which case, models for this behavior and the consequences for population dynamics should reflect this. Generally, complexity and generalizability within a model are thought to trade off (but see: Evans et al. 2013). But, if animal behavior is inherently stochastic, then a model would become more generalizable to other species if stochasticity were added. Exploring this in a range of disciplines beyond where it is typically implemented would be greatly beneficial.