The maleness of larger angiosperm flowers

Significance

Understanding the selective pressures shaping flower strategies can unveil how angiosperms thrived for the last 150 Mya on Earth. Here, we show that heavier hermaphrodite flowers tend to be male-biased and invest strongly in petals to export their pollen, while lighter flowers tend to be female-biased and invest more in sepals to ensure the success of their own ovules. Strong male–male competition, represented by the ecological contest among pollen donors, helps to explain why flower biomass varies several orders of magnitude across the angiosperms and many aspects of their pollination biology.

Abstract

Flower biomass varies widely across the angiosperms. Each plant species invests a given amount of biomass to construct its sex organs. A comparative understanding of how this limited resource is partitioned among primary (male and female structures) and secondary (petals and sepals) sexual organs on hermaphrodite species can shed light on general evolutionary processes behind flower evolution. Here, we use allometries relating different flower biomass components across species to test the existence of broad allocation patterns across the angiosperms. Based on a global dataset with flower biomass spanning five orders of magnitude, we show that heavier angiosperm flowers tend to be male-biased and invest strongly in petals to promote pollen export, while lighter flowers tend to be female-biased and invest more in sepals to insure their own seed set. This result demonstrates that larger flowers are not simple carbon copies of small ones, indicating that sexual selection via male–male competition is an important driver of flower biomass evolution and sex allocation strategies across angiosperms.

Flowers are sexual organs that exhibit astonishing interspecific variation in color, structure, shape, and biomass (1, 2). Flower biomass captures the construction costs of a flower, being a species-specific functional trait bound to the flower biomass vs. number trade-off which modulates plant reproductive success. Flower biomass correlates with pollinator number, type, and size, influencing pollen dispersal distance and outcrossing rates (3, 4). In hermaphrodite flowers, this limited resource is partitioned between male (androecium) and female (gynoecium) primary sexual organs, producing pollen and ovules, respectively, but also between petals (corolla) and sepals (calyx), considered secondary sexual organs. How flower resources are partitioned between primary and secondary sexual organs can shed light on the selective forces behind the evolution of sex strategies across the angiosperms (2, 5).

Sex allocation theory predicts that relative investment into flower organs is governed by trade-offs due to resource limitation (5–8). In plants with hermaphrodite flowers, individual fitness will be the sum of male and female genetic contributions to the next generation. The relative investment into competing primary sexual organs should depend on the shape of the two fitness return curves describing how male-line and female-line reproductive success respond to investment. If biomass is reallocated from one sex to the other, the optimum is where marginal gains in fitness in one sex are balanced against marginal losses through the opposite sex. In line with Bateman’s principle, male-biased allocation can emerge when fitness return through the female function saturates due to resource limitation (considering also the requirements for seed and fruit production), while fitness return through male function continues to increase with investment in reproductive structures (9). Female-biased allocation is likely to emerge in evolutionary contexts where investment in self-fertilized seeds brings higher fitness gains than investment in pollen export (7).

The secondary sexual organs of flowers also contribute to reproductive success. Petals send long-distance signals to attract pollinators and promote outcrossing. However, observational and experimental studies indicate that investments in petals confer more impact on male than on female fitness (10–12). In contrast, sepals protect the inner flower organs against environmental hazards, herbivores, and pathogens of ovaries, ovules, and eventually seeds, thus with a higher impact on female fitness (13, 14). Therefore, allocation between petals and sepals is also expected to be determined by the shapes of male and female fitness returns on investment.

Evolutionary trade-offs have been successfully analyzed by cross-species allometry in both animals and plants (15, 16). When resources are limiting, distinct selective pressures will lead species to allocate their resources into alternative components. The biomass of a single flower (X), for instance, is simply the sum of the biomass of its i components (Y_i). Across species, the relationship between a given component and the whole flower can be described by the allometric equation Y = αX^β, the slope β_i being the rate at which Y_i changes with X, and α_i being the intercept. Thus, β_i = 1 indicates that biomass of the component increases proportionally to the flower biomass, while β_i higher or lower than 1 indicates steeper or shallower increase of the component in relation to the whole flower.

Several plant reproductive traits are thought to be influenced by sexual selection (17-19). Female choice plays a strong role in evolution and maintenance of heterostyly, autoincompatibility systems, style length, and selective seed abortion. Male–male competition has been implicated in the emergence of flower dimorphism among monoecious species, pollen:ovule ratio, and pollen tube growth rates. We hypothesize that male–male competition will have a strong role in the evolution of flower biomass and associated allocation trade-offs. Stronger male–male competition should favor heavier, male-biased flowers, and a higher allocation to petals to promote pollen export and outcrossing. In contrast, weaker male–male competition should favor lighter female-biased flowers, and a higher relative allocation to sepals to promote female fitness. Thus, we expect a steeper allometric slope for the male than for the female organs (β_male > β_female) and for petals than for sepals (β_petals> β_sepals).

Results and Discussion

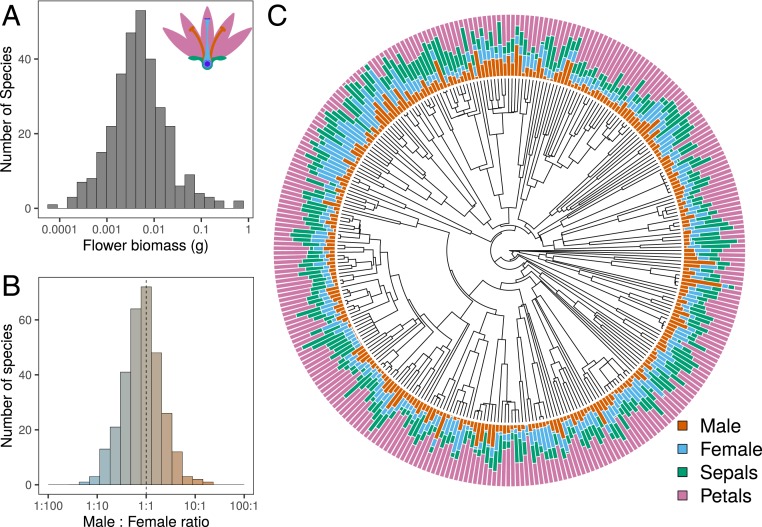
In our global dataset (20) encompassing 307 angiosperm species from 75 families and 32 orders (see Dataset S1 for the species list), flower biomass varied five orders of magnitude, from 0.000083 (Lepidium virginicum, Brassicaceae) to 0.73 g (Nymphaea alba, Nymphaeaceae, Fig. 1A and see SI Appendix, Table S2). The male:female biomass ratio (Fig. 1B) was centered around 1:1, but varied widely and continuously from 22.6 (male-biased, Epidendrum fulgens, Orchidaceae) to 0.07 (female-biased, Gentiana bavarica, Gentianaceae). Indeed, the allocation into the four main flower components (androecium, gynoecium, corolla, and calyx) varied considerably across angiosperm lineages reflecting an impressive diversity of flower allocation strategies (Fig. 1C and SI Appendix, Figs. S4–S6 and Table S1). In other words, a continuous spectrum of sex allocation strategies is found in nature.

Fig. 1.

Flower biomass and its partitioning across 307 hermaphrodite species from 75 families and 32 orders of angiosperms. (A) Flower biomass distribution across species, (B) distribution of male:female allocation ratio (log₁₀-transformed) across species, and (C) phylogenetic distribution of the percentage of biomass allocated to primary and secondary sexual organs. Male:female ratio was calculated dividing the biomass of androecium by the biomass of gynoecium. Colors represent different flower components.

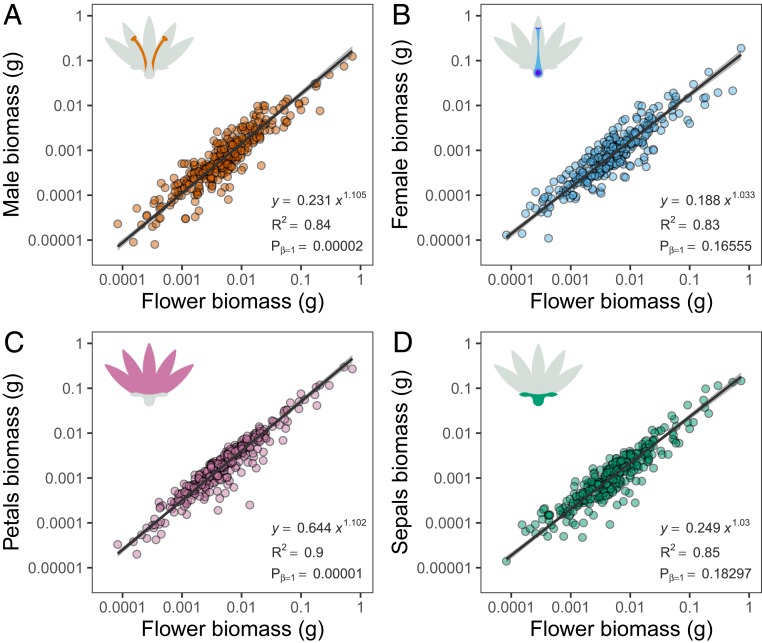
In terms of biomass allocation, large flowers are not simply enlarged copies of small ones; instead, flower organs scale at different rates with flower biomass (Figs. 2 and 3 and SI Appendix, Table S3). Standardized major axis (SMA) analyses revealed that the male organs scaled more steeply than one with total flower biomass (β = 1.10, CI_95% = 1.056–1.156, P_β=1 = 0.00002, r² = 0.84, Fig. 2A) while the female organs showed an isometric relationship (β = 1.03, CI_95% = 0.986–1.082, P_β=1 = 0.16555, r² = 0.83, Fig. 2B), the slopes being statistically different [LR = 4.12, degrees of freedom (d.f.) = 1, P = 0.042304]. The masculinization of heavier flowers (β_male > β_female) was further supported by phylogenetic SMA regressions, also showing positive allometry for the male organs (β = 1.11, P_β=1 < 0.00001, r² = 0.86) and isometry for the female organs (β = 0.99, P_β=1 = 0.69380, r² = 0.83); the difference being statistically significant (dif = 0.13, P = 0.0341) (see SI Appendix, section 5 for details).

Fig. 2.

Across-species flower allometries of 307 angiosperm species. Standardized major-axis relationship between flower biomass and the biomass allocated to (A) male organs, (B) female organs, (C) group of petals (corolla), and (D) group of sepals (calyx). All axes are log₁₀-transformed. The black lines are standardized major-axis line fits and the gray shadow their 95% CI. Allometric equations (Y = αX^β) and R² are provided. P_β=1 indicates the probability of rejecting the isometric hypothesis (β = 1). See SI Appendix for sensitivity analysis details.

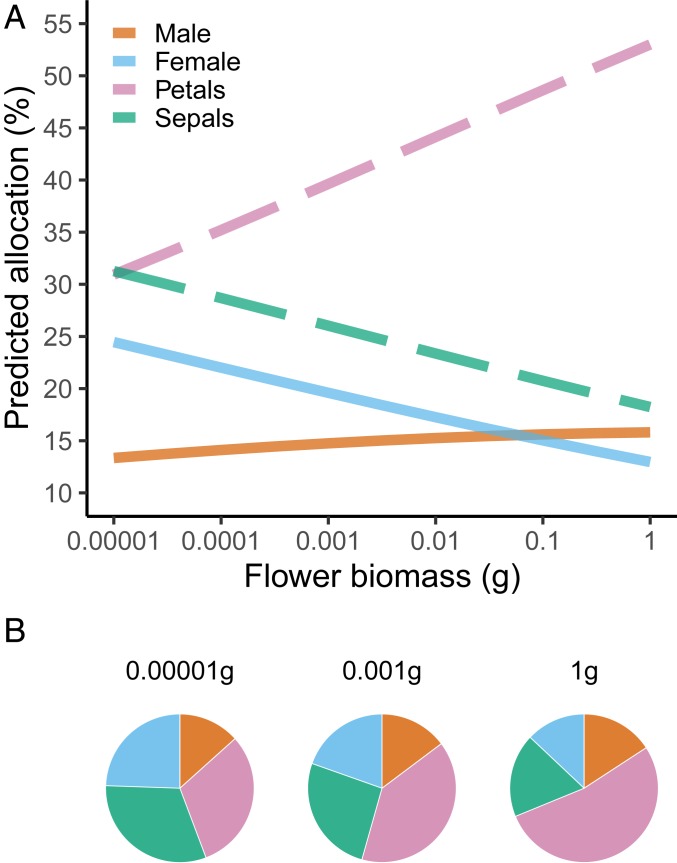
Fig. 3.

Relative biomass allocation in primary (male and female) and secondary (petals and sepals) sexual organs along the flower biomass gradient. (A) Predicted allocation (%) calculated from mean unbiased estimates for each component at a given total flower mass according to the OLS allometric regression models (Methods and SI Appendix), and then converted into percentages. (B) Visual representation of biomass partitioning between lighter (0.00001 g), medium (0.001 g), and heavier (1.0 g) flowers.

Biomass allocation to petals also scaled steeper than one with total flower biomass (SMA, β = 1.10, CI_95% = 1.063–1.143, P_β=1 < 0.00001, r² = 0.90; Fig. 2C) while biomass allocation to sepals showed an isometric relationship (SMA, β = 1.03, CI_95% = 0.986–1.076, P_β=1 < 0.18297, r² = 0.85; Fig. 2D). As expected, the slope for petals was significantly higher than for sepals [likelihood ratio (LR) = 5.49, d.f. = 1, P = 0.019145]. The results remained qualitatively similar when phylogenetic distance was taken into consideration. The slope for petals (phylogenetic SMA, β = 1.218, P_β=1 < 0.00001, r² = 0.85; Fig. 2C) was higher than for sepals (phylogenetic SMA, β = 0.960, P_β=1 = 0.11124, r² = 0.80; Fig. 2D), the difference being statistically significant (dif = 0.26, P = 0.0013, see SI Appendix, section 5 for details).

Sensitivity analyses showed that the allometric line fits presented above were robust to different types of uncertainties, such as sampling effort, taxonomic influence, and phylogenetic uncertainty (SI Appendix, Figs. S7–S15). The results also remained the same when each component was related to the sum of the others rather than to the total, for both phylogenetic and nonphylogenetic SMA fits (SI Appendix, Figs. S14 and S15).

Using ordinary least-square (OLS) regressions to predict how each flower component changes with total flower biomass (Fig. 3), one can estimate that the mean share allocated to female organs is predicted to decline from 24% to 13% across the studied range of total flower mass (∼0.0001–1.0 g), while the share allocated to male organs increases slightly, from 13% to 16%. More drastic changes are predicted for secondary sexual organs. While small flowers are expected to allocate similar biomass to both petals and sepals (around 31%), heavier flowers allocate most biomass to petals (53%) and relatively less to sepals (18%). Estimates from phylogenetic generalized least-squares (PGLS) fits (21) provided similar results (SI Appendix, Figs. S19 and S20).

Thus, larger angiosperm flowers were not simply enlarged carbon copies of smaller ones. Smaller flowers tended to be female-biased and to invest relatively more in sepals, while larger flowers were more male-biased and invested relatively more in petals. This indicates male–male competition is less important among small flowers and becomes an increasingly important driver as flowers get larger. These results are consistent with a previous suggestion based on a small number of North American species (22).

Male–male competition in angiosperms is frequently expressed by plant–plant competition for pollinators (19, 23). Investment with positive impact on the amount of pollen effectively exported is expected to increase male fitness. Within species, plants producing more and larger flowers, with large showy petals, and more reward for pollinators will have a higher male fitness. Larger flowers can be detected by pollinators from longer distances and are good indicators of nectar and pollen resource rewards (24). In pursuing their own interest, pollinators reward plants with heavier flowers. Across species, flower biomass has a good correlation with pollinator size and type. Larger flowers generally attract vertebrate or larger insect pollinators which have higher pollen-carrying capacity and capability to export pollen to longer distances, promoting outcrossing. Some traits associated with female choice also demand biomass allocation, such as long style tubes (25). However, several female choice mechanisms take place without substantial allocation of biomass (18, 19). For instance, the histochemical control over pistil receptivity, pollen germination, pollen tube growth, and selective seed abortion are female-choice mechanisms that assure the selection of high-quality pollen donors (19, 25, 26).

At the lower end of the flower biomass spectrum, female function tends to predominate over male fitness. Small flowers (0.00001 g) have the highest relative biomass investment in female organs but the lowest in male organs, suggesting a shift in the relevance of seed set over pollen export. They also have the highest relative investment in sepals and lowest in petals, indicating that ovule and seed defense is important for fitness when compared to pollinator attraction. Small flowers tend to be self-compatible and self-fertilized, to have low pollen–ovule ratios, and to commonly attract only tiny insects which promote short-distance pollination (27). Besides low levels of male–male competition, other forces are known to promote selfing. Under pollinator limitation, for instance, self-fertilization promotes reproductive assurance (28). The high fitness of locally adapted genomes can also promote selfing (29). Plant species associated with a lower diversity of pathogenic fungi have lower outcrossing rates, as predicted by the Red Queen hypothesis (30).

The higher relative allocation to sepals in smaller flowers supports the idea that they have a larger effect on female fitness (31). Being the outermost whorls, tougher, and hairier than petals, possessing secondary compounds, and often persisting after flower opening into fruit maturation, all these characteristics indicate sepals serve to defend ovaries, ovules, and developing seeds against insect herbivores and other natural enemies (13, 14). The higher investment in petals in larger flowers corroborates their predominantly male function, as has been well documented. For instance, in dioecious species, male flowers have larger petals than female flowers (10, 32). In hermaphrodite species, larger petals are positively correlated with pollen export but not necessarily with seed production. Experimental reduction of petal size has a more negative effect on pollen export than on fruit and seed set (10, 33). The higher relative biomass allocation into petals relative to male organs suggests continuing marginal gains to male fitness from allocation to petals more so than from investments made directly into stamens and pollen grains.

The flower allometries described here express general patterns across angiosperms. The fit of the relationships was fairly high (r² = 0.83–0.90), considering that species data were collected from different phylogenetic lineages (75 families), continents, latitudes, habitats, soil types, light environments, life forms, and pollination syndromes. Still, for a given total flower size, the biomass allocated to specific structures often varied considerably (Fig. 2). In some orchids, for example, sepals are as large and colorful as petals, and in many Proteaceae and Myrtaceae stamens are showy, suggesting that they are also being selected by male–male competition. In others, scents probably modulate the investment in petals. Still, some of the scatter can be explained by the effect of flower number and arrangement on pollination attraction (3, 4). Additional sensitivity analyses, however, indicates that our conclusions are robust to such species variation in showiness strategy (SI Appendix, Fig. S12 and Table S6). Important taxa which have been excluded from our sampling, such as Asteraceae and Poaceae, represent additional variation across the angiosperms. In Asteraceae, pollinators are attracted primarily by specialized, enlarged ligules (fusion product of all petals of a flower) of the ray flowers, and not by the small petals of the core flowers, while bracts around the inflorescence take over the protective function of the sepals. In Poaceae, which are wind-pollinated, petals are present as lodicules with different function than attraction since they are not needed for pollination. In such systems, the intensity of male–male competition is better expressed by pollen–ovule ratios (27).

A longstanding quest in ecology is to summarize plant ecological strategies via a small number of easy-to-measure, but meaningful, traits. Maximum plant height, specific leaf area, and seed size, for instance, are simple measurements that express important trade-offs (34). We propose that flower biomass has the potential to be such a key trait. Flower biomass captures the construction costs of a flower and, as shown here, it is strongly correlated with petal biomass that expresses pollen-export effort. It is a species-specific functional trait bounded to the flower biomass vs. number trade-off which modulates plant fitness. Nevertheless, flower biomass is poorly represented in most plant trait databases, perhaps due to the long botanical tradition of describing flower structures by counting and linear dimensions. Yet it is easy to measure and captures a fair amount of sex strategy variation across the angiosperms.

Angiosperm flowers are flamboyant adornments that have enchanted poets and artists across the globe. At first glance their elaborate and showy structures seem to be as nonsensical as the tail of a peacock. Under close investigation, however, both structures arose as complex products of sexual selection. Our comparative results indicate that increasing male–male competition across the spectrum of flower size is an important driver behind the evolution of sex allocation partitioning. The comparative patterns here described represent a predictable backbone behind the ravishing variation in flower size, structure, shape, color, and sex strategy across the angiosperms. We believe it can help to order our knowledge of all aspects of flower biology.

Methods

We collected data on flower biomass of hermaphrodite species for four different continents: South America (Brazil), Europe (Germany), Oceania (Australia), and North America (USA). While for North America the data came from the literature, most data for the remaining continents were collected in the field.

Field Sampling.

Species sampling was dependent on flower availability but we consciously maximized 1) phylogenetic diversity, by searching for species from a wide taxonomic range, 2) habitat diversity, by sampling species from contrasting ecosystem types (e.g., forests, shrublands, grasslands, alpine); 3) life-form diversity (e.g., herbaceous, shrubs, trees, lianas, aquatic), and 4) flower size range, by searching for species with distinct flower sizes, from tiny to very large. Because we were interested in the relative allocation of biomass among the four flower components in perfect flowers, we refrained from collecting: dioecious species; species whose individual flowers could not be confidently isolated; species with flowerheads containing different types of flowers (e.g., Asteraceae with enlarged peripheral flowers and reduced core flowers); and species lacking petals and sepals, such as many wind-pollinated taxa (e.g., Poaceae). Thus, we are mostly restricted to animal-pollinated species. Despite the wide spatial scale of our sampling, tropical species and trees were underrepresented.

In the field, species with flowering individuals were selected, and 10 spatially separated plants were selected from a population. From each individual plant, we sampled a single intact, fully opened and functional flower (preferably just after flower opening). Flowers with signs of developmental stress, physical damage, or herbivory were excluded. Each flower was individually placed in sealed tubes and stored inside a cooling bag with ice for tissue preservation.

In the laboratory, each individual flower was divided into four components: 1) male, including stamens with anthers (i.e., androecium); 2) female, including ovary, style, and stigma (i.e., gynoecium); 3) petals (i.e., corolla); and 4) sepals (i.e., calyx). For species with tepals, we used a functional approach to partition flower biomass. Tepal biomass was allocated into petals or sepals based on their positioning, color, and morphology, where inner, larger, and colorful tepals were considered petals. All flowers were dissected, while the tissues were still fresh. The material from each component was then oven dried at 70 °C for at least 48 h, and the dry biomass determined with 1-µg precision. For species with very small flowers, samples were pooled between individuals to calculate average values. In the following analyses, species traits were characterized by means across individuals.

Literature Data.

Data on flower biomass partition are scarce in the literature, but a pioneer study was available with data on several North American species (4). Besides that, a search was made in Web of Science looking for other papers with flower biomass data (keywords: flower AND plant AND flower biomass OR male biomass OR androecium biomass OR female biomass OR gynoecium biomass OR petal biomass OR corolla biomass OR sepal biomass OR calyx biomass). Few articles had the required information (35, 36), but such data were added to our database. Literature data represented 13% of the study dataset.

The Allometric Approach.

Allometric relationships can be described by (15)

$$\text{y}\hspace{0.17em}=\hspace{0.17em}{\mathrm{\gamma }\text{x}}^{\text{β}}.$$

If variables are log transformed, then the formula can be rewritten as

$$\text{log}\left(\text{y}\right)\hspace{0.17em}=\hspace{0.17em}\text{log}\left(\text{γ}\right)\hspace{0.17em}+\hspace{0.17em}\mathrm{\beta }\text{X}.$$

Then by substituting the log terms, the equation is described by a simple linear regression:

$$\text{Y}\hspace{0.17em}=\hspace{0.17em}\alpha \hspace{0.17em}+\hspace{0.17em}\beta \text{X}.$$

In this study, we want to understand how the biomass of the four flower components i (Y_i) scale with the total flower biomass (X). β_i represents the scaling coefficient of the component i and can be used to test if the relative resource allocation to any flower organ increases, decreases, or remains constant with increasing total flower biomass. In other words, one can ask if the estimated β_i statistically differs from 1. When β_i > 1, the relative allocation to a flower component increases with total flower biomass, representing a positive allometric relationship. When β_i < 1, the relative allocation to a flower component decreases with increasing flower biomass, representing a negative allometric relationship. Finally, if β_i = 1, the relative allocation to a flower component remains constant with increasing flower total biomass, indicating an isometric relationship where allocation to a flower organ increases proportionally with total floral biomass.

Statistical Analysis.

Several bivariate line-fitting methods have been used in allometric comparative studies, each one with its own assumptions, weaknesses, and strengths. It is now clear that model selection depends on the question at hand and the data under scrutiny. Here in the main text we present SMA line fits to describe how each flower component (y) scales with total flower biomass (x). Because there is continuing debate about line-fitting methods (e.g., ref. 37, 38), we present also OLS equivalents in SI Appendix, Supplementary Materials, and these show similar outcomes. Briefly, where OLS minimizes the sum of squares of the residual vertically, in respect to the y variable alone, SMA minimizes the sum of squares for both y- and x variables. SMA slopes have the same meaning regardless of which variable is treated as X and which as Y (37), an important property for measuring coordination between traits.

In recognition of the longstanding discussion about the meanings of allometric slopes for phylogenetically structured data (39, 40), we also performed phylogenetic reduced major axis line fits (phySMA), assuming the Brownian motion mode of evolution for the error structure (41). This analysis adjusts the expected covariances in the variance–covariance matrix according to phylogenetic structure.

Using SMA and phySMA line fits, we tested the isometric hypothesis that the regression slope (β_i) of each flower component was significantly different from 1 with a one-sample test of the SMA slope (37). We also tested differences in slope for the male (β_male) compared to the female organs (β_female), and for petals (β_petals) compared to sepals (β_sepals) using a likelihood ratio test for common SMA slope (37). SMA analyses were performed in the R packages “smatr” (42). For the phySMA fits, the isometric hypothesis for each flower component was tested using the R package “phytools” (43). Because a test for common SMA slope is not available for phySMA fits, we used a randomization procedure to test for differences in slope between the male (β_male) and female organs (β_female), and between petals (β_petals) and sepals (β_sepals). The difference in phySMA slopes between flower organs was tested with a permutation test using a null distribution generated from 10,000 permutations (shuffling the raw data) (SI Appendix).

In order to predict how flower biomass is partitioned between the four flower components, we used OLS regressions. For prediction purposes, OLS is the preferable line-fitting method while SMA performs poorly (37). Because the data have phylogenetic structure, we repeated such analyses using PGLS (21). PGLS analyses were performed using the R package “phylolm” (44). The working phylogeny for our species was pruned from the most recent calibrated supertree of the angiosperms (45).

An additional statistical concern emerges when allometric studies aim to understand how two or more parts are changing in respect to a whole: the problem of axis nonindependence. In our study, for instance, when one analyzes the biomass of petals against flower biomass, the component petal is present in both axes because flower biomass is simply the sum of the four flower components. This axis nonindependence can potentially generate bias in the estimates. To deal with this concern we also fitted regressions using flower component on the y axis and total flower biomass minus the flower component on the x axis (SI Appendix). Additionally, we performed 1) pairwise SMA regressions between flower organs (e.g., male ∼ female, male ∼ petals, male ∼ sepals), 2) between primary and secondary sexual organs against flower biomass, and 3) between primary against secondary sexual organs (SI Appendix).

Sensitivity Analysis.

Comparative results can be sensitive to several uncertainty causes (46). Here, we performed multiple sensitivity analyses to test the robustness of our conclusions (SI Appendix):

• (1)Sampling effort and species set: allometric models were reanalyzed after removing between 5–50% of the species at random. This procedure was repeated 1,000 times for each percentage of species removal. Model estimates fitted with reduced data were then compared with the estimates from the full data model. Additionally, in some species, stamens or sepals are showy, with a role in pollinator attraction while, in others, sepals and petals are alike (i.e., tepals). To test the robustness of our results, we reran the models after removing these species from the dataset.
• (2)Taxonomic influence: to account for possible effects of species-rich taxonomic groups driving model estimates. We reanalyzed all fitted regressions after removing species belonging to each of the top five species-rich families and orders from the dataset and compared the slopes and confidence intervals with full dataset estimates.
• (3)Phylogenetic uncertainty: to account for uncertainty in the variance–covariance matrix which describes the phylogenetic structure. In our study, 53 species were not present in the most recent calibrated supertree of the angiosperms (45). To overcome this problem, missing species were replaced by a random close relative (from the same taxonomic genus) available in the phylogeny, providing a good estimate of the phylogenetic placement of each missing species. This procedure was repeated 300 times, with unique solutions for the placement of each missing species, therefore producing 300 alternative phylogenetic hypotheses including all study species. One of these trees was selected at random for the main analysis and to represent the study phylogeny (working tree). PGLS and phylogenetic SMA regressions were repeated across all alternative trees to test if phylogenetic uncertainty affected the main results. All sensitivity analyses were performed following approaches proposed in the R package “sensiPhy” (46).

Data Availability.

Data and code supporting all findings of this study are available in the GitHub repository: https://github.com/paternogbc/ms_global_flower_allometry and Zenodo: https://doi.org/10.5281/zenodo.3746453.