Cavitation in lipid bilayers poses strict negative pressure stability limit in biological liquids

Significance

Numerous biological systems contain metastable liquids at considerable negative pressures. As a prominent example, plants use negative pressures to suck water from the soil into their leaves. A long-debated mystery is why the maximal negative pressures are approximately $-$100 bar. A ubiquitous ingredient of biological liquids is lipids. Combining atomistic simulations and kinetic modeling, we show that lipid bilayers lead to cavitation at negative pressures of about $-$100 bar over timescales of hours to days, whereas water with added salt or nonpolar gas stays stable over many years. Our findings show that the presence of lipid aggregates imposes an upper stability limit for the magnitude of negative pressures in biological liquids.

Abstract

Biological and technological processes that involve liquids under negative pressure are vulnerable to the formation of cavities. Maximal negative pressures found in plants are around $-$100 bar, even though cavitation in pure bulk water only occurs at much more negative pressures on the relevant timescales. Here, we investigate the influence of small solutes and lipid bilayers, both constituents of all biological liquids, on the formation of cavities under negative pressures. By combining molecular dynamics simulations with kinetic modeling, we quantify cavitation rates on biologically relevant length scales and timescales. We find that lipid bilayers, in contrast to small solutes, increase the rate of cavitation, which remains unproblematically low at the pressures found in most plants. Only when the negative pressures approach $-$100 bar does cavitation occur on biologically relevant timescales. Our results suggest that bilayer-based cavitation is what generally limits the magnitude of negative pressures in liquids that contain lipid bilayers.

Metastable water under negative pressures is encountered in various biological and technological processes. Examples include lithotripsy and sonoporation of cell membranes and other biological matter (1, 2), drying stresses in unsaturated porous materials (3–6), catapulting mechanisms of fern spores (7, 8), octopus suckers (9), and the most widespread example, the hydraulic system in plants (3, 10, 11). In the latter, negative pressures are generated through evaporation of water from leaf cell walls, with resistance in the hydraulic system (the xylem) causing negative pressure in the liquid (xylem sap), which serves to suck water out of the soil up to the leaves. Negative pressures in plants are typically around several −10 bar but can reach −80 bar in certain desert species (3). Under these conditions, the vascular system is vulnerable to cavitation (i.e., the spontaneous formation of rapidly expanding voids or gas bubbles), which can spread and result in fatal embolic crisis (12, 13).

Although pure bulk water is stable against cavitation at pressures less negative than −1 kbar over astronomically long times (14–17), the empirical limit that plants can sustain over the relevant timescales of hours to days is about −100 bar (3). Heterogeneous cavitation at the inner vascular surfaces has been speculated to be a reason for this as well as the preexistence of gas bubbles (18–24). Moreover, sap is far from being pure water. It not only contains small solutes, such as dissolved gases, ions, sugars, free amino acids, and proteins (25, 26), but also lipids (27) at an average concentration of the order of 1 $\mathrm{\mu }$M (28), far above the lipid critical micelle concentration. Recently, analysis of the chemical composition of sap lipids by electrospray ionization tandem mass spectrometry revealed a high relative abundance of phospholipids with neutral (phosphatidylcholine [PC], phosphatidylethanolamine [PE]) and negatively charged (phosphatidic acid [PA], phosphatidylserine [PS], phosphatidylinositol [PI]) headgroups as well as galactolipids with mono- and disaccharide headgroups (29). These headgroup chemistries are typically associated with packing parameters preferentially leading to lipid aggregates in the form of bilayers (30) in aqueous solution and on surfaces.

In this study, we investigate the influence of small hydrophobic and charged solutes as well as lipid bilayers on the formation of cavities in water under negative pressure conditions. For this purpose, we combine atomistic molecular dynamics (MD) simulation approaches with kinetic modeling. Applying increasingly negative pressures over time in the MD simulations allows us to predict cavitation at the biologically relevant length scales and timescales. This further enables us to determine the most negative pressures that biological systems can tolerate in the presence of lipid bilayer aggregates. We find that small solutes only weakly affect the cavitation rate of water. The presence of lipid bilayers, on the other hand, dramatically reduces the magnitude of the maximal sustainable negative pressures from more than 1,000 bar in pure water to less than 100 bar on the biologically relevant timescales of hours to days. This value is in excellent quantitative agreement with the most negative pressures measured in plants, suggesting that bilayer-based cavitation is what practically limits biologically sustainable negative pressure. In fact, we show that heterogeneous cavitation at surfaces, which is a commonly debated mechanism for negative pressure instabilities, is less relevant compared with cavitation within lipid bilayers.

Results

Cavitation in Pure Water.

We introduce our approach by first treating the well-studied case of pure water under constant negative pressure $p<0$ (14–17). Within the framework of classical nucleation theory (CNT) (31), the free energy of a spherical cavity in water can be written as

$$\mathrm{\Delta }{G}_{\mathrm{w}}=4\pi r^2\gamma +\frac{4}{3}\pi r^{3}p,$$ [1]

where the first term is the free energy of creating the bubble interface and the second term is the work performed by the volume expansion. A rigorous thermodynamic derivation of this relation is in SI Appendix, section 1. The growth of the bubble is initially opposed by the free energy barrier $\mathrm{\Delta }{G}_{\mathrm{w}}^{*}$ (Fig. 1A) reached at the critical bubble radius $r^{*}$. Both follow from $\mathrm{d}\mathrm{\Delta }{G}_{\mathrm{w}}/\mathrm{d}r=0$ as

$$r^{*}=-\frac{2\gamma }{p}\hspace{0.17em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{1em}\mathrm{\Delta }{G}_{\mathrm{w}}^{*}=\frac{16\pi }{3}\frac{{\gamma }^3}{p^2}.$$ [2]

As we will discuss later, curvature corrections of the surface tension $\gamma$ marginally modify these results but do not alter any of the following conclusions. In a simple Arrhenius description, the cavitation rate $k$ (i.e., the number of cavitation events per time for a given volume) is

$$k=k_0\hspace{0.17em}{\mathrm{e}}^{-\beta \mathrm{\Delta }{G}_{\mathrm{w}}^{*}},$$ [3]

where $\beta =1/k_{\mathrm{B}}T$ is the inverse thermal energy, $k_{\mathrm{B}}$ is the Boltzmann constant, and $k_0$ denotes the kinetic prefactor, representing the transition attempt frequency. The survival probability $f\left(t\right)$ that the system is still in the metastable state (i.e., that it has not yet cavitated) obeys the first-order rate equation $\stackrel{\cdot }{f}\left(t\right)=-kf\left(t\right)$, where the dot represents the time derivative, with the solution

$$f\left(t\right)={\mathrm{e}}^{-kt}$$ [4]

for the initial condition $f\left(0\right)=1$. That is, the probability for a critical bubble not to have formed decays exponentially with time, with a mean cavitation time ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}=k^{-1}$. While CNT provides an estimate for the free energy barrier $\mathrm{\Delta }{G}_{\mathrm{w}}^{*}$, it does not provide the kinetic prefactor $k_0$ for cavitation, which we determine from MD simulations. In principle, $k_0$ can be obtained from the mean cavitation time ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}$ at constant negative pressure $p$ and an estimate for the value of $\mathrm{\Delta }{G}_{\mathrm{w}}^{*}$ according to Eq. 3. However, this approach is computationally unsuitable because of the strong dependence of ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}$ on the value of the negative pressure.

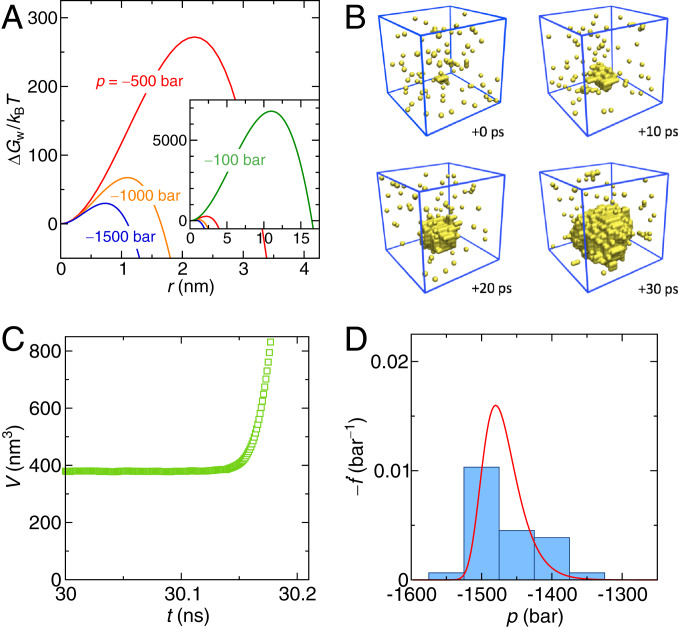
Fig. 1.

(A) Free energy of a bubble in pure SPC/E water under negative pressures as obtained from Eq. 1. Inset shows the result including $p=-$100 bar at increased scale. (B) Consecutive snapshots (in steps of 10 ps) of a cavity that forms in a constant rate simulation with $\stackrel{\cdot }{p}=-50$ bar/ns (occurring at $t\simeq 30$ ns and $p\simeq -1500$ bar). The yellow spheres indicate unoccupied grid points (voxels) of size 0.4 nm; water molecules are not shown. (C) Time-dependent box volume of the same simulation as in B, clearly indicating the cavitation event. (D) Distribution of cavitation pressures obtained from 30 independent simulation runs for $\stackrel{\cdot }{p}=-50$ bar/ns (blue bars) and the theoretical prediction $-\stackrel{\cdot }{f}\left(t\right){|}_{t=p/\stackrel{\cdot }{p}}$ (red curve).

Instead, we impose a time-dependent pressure $p\left(t\right)$ that decreases linearly with time

$$p\left(t\right)=\stackrel{\cdot }{p}t,$$ [5]

with $\stackrel{\cdot }{p}<0$ being the pressure rate. In our constant rate simulations, the free energy barrier (determined by Eq. 2) decreases inversely with the square of time as

$$\beta \mathrm{\Delta }{G}_{\mathrm{w}}^{*}\left(t\right)={\left(\frac{{\tau }_0}{t}\right)}^2,$$ [6]

where the time constant ${\tau }_0$ is given as

$${{\tau }_0}^2=\frac{16\pi }{3}\frac{{\gamma }^3}{k_{\mathrm{B}}T{\stackrel{\cdot }{p}}^2}.$$ [7]

Within this simulation protocol, the free energy barrier eventually becomes low enough for a cavitation event to occur within the simulation time. The probability $f\left(t\right)$ in this case follows from solving a modified rate equation (Methods). A typical cavitation event in a constant rate simulation is shown in Fig. 1B by a series of snapshots, where the yellow spheres indicate voids (bubbles) of more than 0.4 nm in size. Most of them are isolated and short lived, and they represent “unsuccessful” cavitation attempts. However, the large void in the center of the box successfully surpasses the critical cavitation radius and then, rapidly increases in volume. This is demonstrated in Fig. 1C, which shows the sudden divergence of the simulation box volume on cavitation. For each pressure rate $\stackrel{\cdot }{p}$, we analyze 10 to 30 independent simulation runs, which yield cavitation pressure distributions such as shown in Fig. 1D for $\stackrel{\cdot }{p}=-$50 bar/ns. The red line in Fig. 1D indicates the theoretical prediction of the distribution obtained as $-\stackrel{\cdot }{f}\left(t\right){|}_{t=p/\stackrel{\cdot }{p}}$ (computed a posteriori from the extracted value of $k_0$). The mean cavitation pressure, $p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}$, is then obtained by averaging the individual cavitation pressure values. The mean cavitation time in the constant rate protocol follows as ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}={\int }_0^{\infty }f\left(t\right)\mathrm{d}t$, which can be converted into the mean cavitation pressure as $p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}=\stackrel{\cdot }{p}\hspace{0.17em}{\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}$. Using the mathematical expression for $f\left(t\right)$ in Eq. 15 (Methods), we obtain

$$p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}=\stackrel{\cdot }{p}{\int }_0^{\infty }{\mathrm{e}}^{-k_{0}I\left(t\right)}\mathrm{d}t,$$ [8]

where $I\left(t\right)$ is defined in Eq. 16. Eq. 8 provides the crucial connection between the MD simulations and kinetic theory.

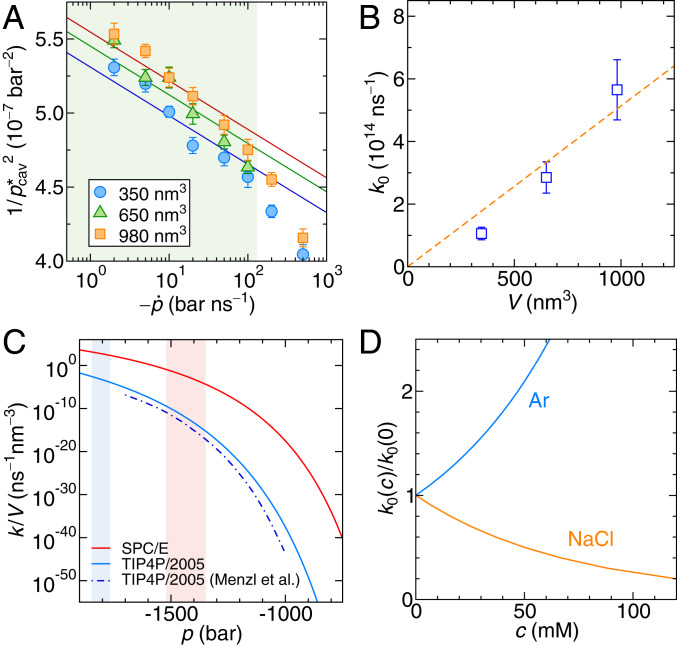
Fig. 2A shows the simulation results for pure water in terms of the inverse square of the mean cavitation pressure, ${1/p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}}^2$, vs. the pressure rate $-\stackrel{\cdot }{p}$ in logarithmic scale for three different simulation box sizes. In this presentation, Eq. 8 (solid lines in Fig. 2A) is virtually linear (SI Appendix, section 2 has a derivation of the asymptotic relation). By fitting Eq. 8 to the MD data for small pressure rates (shaded in green in Fig. 2A), where linear kinetic theory is expected to hold, and using the independently obtained simulation values for the surface tension $\gamma$ of water (SI Appendix, section 3), we obtain $k_0$ and its uncertainty from the least squares method (SI Appendix, section 4). In the limit of low $\stackrel{\cdot }{p}$, the slopes of the curves are determined by $\gamma$, whereas $k_0$ only controls their offsets (SI Appendix, Eq. S14). As shown in Fig. 2B, $k_0$ scales linearly with the simulation box volume $V$ as expected since cavitation can occur anywhere in the system. This allows us to extract the cavitation attempt frequency density for pure SPC/E (extended simple point charge model) water as ${\kappa }_0=k_0/V=5\times 10^{11}\hspace{0.17em}{\mathrm{n}\mathrm{s}}^{-1}{\mathrm{n}\mathrm{m}}^{-3}$.

Fig. 2.

(A) Simulation results for the inverse squared mean cavitation pressure vs. the pressure rate for three different simulation box volumes. The lines are fits of Eq. 8 to the data in the green-shaded region, where the kinetic prefactor $k_0$ is the only fitting parameter. (B) Results for $k_0$ from A as a function of the simulation volume. The orange line is a fit according to $k_0={\kappa }_{0}V$. (C) Cavitation rate density $k/V$ from Eq. 3 for the constant pressure protocol for the SPC/E (red line) and TIP4P/2005 (blue solid line) water models. The blue dashed–dotted line is the result for TIP4P/2005 by Menzl et al. (16). The pale red and blue shaded areas mark the intervals of cavitation pressures $p_{\mathrm{c}\mathrm{a}\mathrm{v}}*$ observed in the constant rate simulations with the SPC/E and TIP4P/2005 water models, respectively. (D) Dependence of the kinetic prefactor $k_0\left(c\right)$ on the concentration $c$ of argon and NaCl.

Knowing the free energy barrier $\mathrm{\Delta }{G}_{\mathrm{w}}^{*}$ and the kinetic prefactor $k_0$, we can now straightforwardly predict the cavitation rate $k$ at constant negative pressure from Eq. 3. In Fig. 2C, we show the cavitation rate density $k/V$ for the SPC/E water model (Fig. 2C, red solid line) and the TIP4P/2005 (transferable intermolecular potential with 3 points/2005) water model (32) (Fig. 2C, blue solid line), which compares well with previous results for the same water model by Menzl et al. (16) (Fig. 2C, blue dashed–dotted line), who used MD with a hybrid Monte Carlo scheme. The minor differences in the cavitation rate density for TIP4P/2005 water are attributed to the slightly different simulation methods used. The significant difference, especially at lower negative pressures, between the two water models comes almost entirely from their different surface tensions, which are $\gamma =55$ mN/m for SPC/E and $\gamma =65$ mN/m for TIP4P/2005 (obtained in independent simulations) (SI Appendix, section 3), while their kinetic prefactors are very similar, being ${\kappa }_0=5\times 10^{11}\hspace{0.17em}{\mathrm{n}\mathrm{s}}^{-1}{\mathrm{n}\mathrm{m}}^{-3}$ for SPC/E and ${\kappa }_0=9\times 10^{11}\hspace{0.17em}{\mathrm{n}\mathrm{s}}^{-1}{\mathrm{n}\mathrm{m}}^{-3}$ for TIP4P/2005. To give explicit numbers, the mean cavitation time of 1 L of water, $V=10^{-3}\hspace{0.17em}{\mathrm{m}}^3$, at a constant negative pressure of $p=-100$ bar comparable with the most extreme negative pressures in plants is ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}\approx 10^{2880}$ s for SPC/E water and ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}\approx 10^{4830}$ s for TIP4P/2005 water. In other words, pure water is not going to cavitate under biologically relevant pressure conditions and timescales, in line with earlier investigations (14, 22).

It is noted that the fits in Fig. 2A are not perfect since the slopes are fixed and dictated by the value of $\gamma$. However, in the simulations, critical bubble sizes are around 1 nm, and therefore, the continuum description can be affected by additional effects not accounted for in CNT. In SI Appendix, section 5, we test two additional fitting approaches where we 1) consider both $k_0$ and $\gamma$ as fitting parameters and 2) introduce a curvature-corrected surface tension via the concept of the Tolman length. In fact, these two additional approaches improve the fit quality but do not alter our conclusions.

While the TIP4P/2005 water model yields a more realistic surface tension, we will continue with the SPC/E water model as it reproduces very well the lipid hydration properties in combination with the Berger lipid force field (33).

Cavitation in Water with Small Solutes.

Biological liquids (and also sap) contain a wide spectrum of solutes. We consider argon and NaCl as two examples for nonpolar and ionic solutes. We perform constant rate simulations at $\stackrel{\cdot }{p}=-50$ bar/ns for a few different solute concentrations. The mean cavitation pressure in the constant rate protocol $p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}\left(c\right)$ depends mildly and approximately linearly on the solute concentration $c$ (SI Appendix, section 6 has details). This suggests the following modified form of Eq. 8:

$$p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}\left(c=0\right)+c{\left(\frac{\mathrm{d}{p}_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}\left(c\right)}{\mathrm{d}c}\right)}_{c=0}=\stackrel{\cdot }{p}{\int }_0^{\infty }{\mathrm{e}}^{-k_0\left(c\right)I\left(t\right)}\mathrm{d}t,$$ [9]

which we solve numerically to obtain the concentration-dependent kinetic prefactor $k_0\left(c\right)$ shown in Fig. 2D. In our analysis, we assume that the solutes do not modify the bubble surface tension $\gamma$, which is suggested by a simple estimate that shows that solutes do not have enough time to adsorb to or desorb from the bubble surface during the short time span in which a bubble forms (SI Appendix, section 7 has details). The simulation results in Fig. 2D reveal that the presence of nonpolar argon atoms increases the attempt frequency, whereas NaCl decreases it. This is in line with the notion that water density fluctuations are enhanced around nonpolar solutes and suppressed around polar or charged solutes (34–37). At moderate argon concentrations of $c=50$ mM, the kinetic prefactor increases by merely a factor of two. We observe that ionic solutes insignificantly increase the cavitation time while nonpolar solutes decrease it and conclude that the presence of small solutes at low concentrations does not significantly modify the cavitation time compared with pure water.

Cavitation in Lipid Bilayers.

Biological liquids not only contain small solutes but also amphiphilic lipids (27–29), which—at the concentrations measured in sap—self-assemble into aggregates, preferentially in the configuration of planar bilayers (38).

We consider lipids with PC headgroups, which are abundant lipid species in sap (29) and well studied in literature (30). Our simulation model consists of a single dilauroyl-phosphatidylcholine (DLPC) bilayer embedded in a 3-nm-thick water layer; Fig. 3 A, Upper shows a snapshot. DLPC remains in the fluid $L_{\alpha }$ phase under all conditions investigated by us, and the hydration behavior is well captured by the employed Berger force field (33). The simulation box is replicated in all three directions via periodic boundary conditions, mimicking an infinitely large bilayer stack. The pressure is controlled via the box dimension normal to the bilayer, whereas the lateral dimensions are kept fixed at an area per lipid of 0.65 ${\mathrm{n}\mathrm{m}}^2$. This simulation setup mimics a large bilayer where friction prevents the lateral flow of lipids during a rapid cavitation event. We also performed simulations with a fluctuating lateral simulation box size and found no essential differences (SI Appendix, section 8 has details). As shown in SI Appendix, section 9, the hydrophilic nature of the headgroups prevents heterogeneous cavitation events at the bilayer surface. Therefore, the most vulnerable part is the bilayer interior since the two monolayers are held together by relatively weak dispersion forces, and consequently, cavitation induced by negative pressures always occurs between the two monolayers.

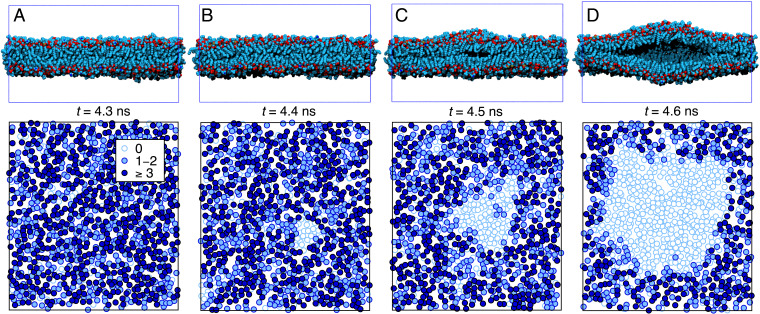
Fig. 3.

Lipid bilayer cavitation. (Upper) Consecutive bilayer cross-sections (water not shown) during a cavitation event (in steps of 0.1 ns following from A to D) at a pressure rate $\stackrel{\cdot }{p}=-50$ bar/ns occurring at $-$215 bar. The lateral surface area of the simulation box is fixed at 360 ${\mathrm{n}\mathrm{m}}^2$ (18 $\times$ 20 nm). (Lower) Map of lipid tail contacts between the monolayers.

Fig. 3 shows snapshots of a cavitation event inside a bilayer for a pressure rate of $\stackrel{\cdot }{p}=-50$ bar/ns at 0.1-ns intervals. The cross-sections in Fig. 3, Upper demonstrate that cavitation starts as an oblate bubble. Fig. 3, Lower shows top views of intermonolayer contacts. Lipid tail positions are represented by circles in Fig. 3, with the color tone indicating the number of lipid tail contacts between opposing monolayers defined as the number of ${\mathrm{C}\mathrm{H}}_3$ groups from opposing monolayers that are within a mutual distance of 0.7 nm. Empty circles in Fig. 3 denote lipid tails without opposing monolayer contacts; the cluster of empty circles becomes circular at late times, indicative of cavity formation. For a quantitative analysis of the cavity shape, we define the number of intermonolayer contacts $N_{\mathrm{c}}$ as the sum of all contacts between ${\mathrm{C}\mathrm{H}}_3$ groups of opposing monolayers. Fig. 4A shows that, during cavitation, $N_{\mathrm{c}}$ (Fig. 4 A, Lower) drastically drops, while the simulation box volume $V$ (Fig. 4 A, Upper) abruptly increases.

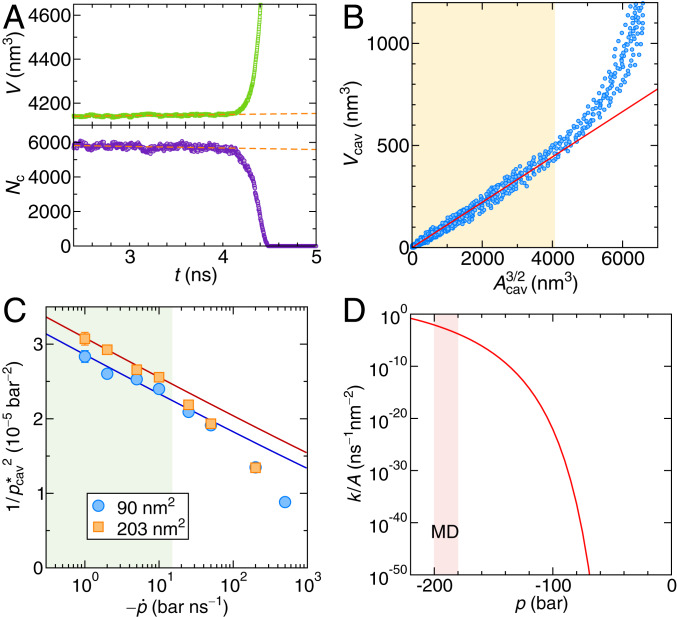
Fig. 4.

(A) Simulation box volume (Upper) and the number of intermonolayer contacts $N_{\mathrm{c}}$ (Lower) as a function of time, indicating a cavitation event in a constant rate simulation for a lipid system with a lateral area of 360 ${\mathrm{n}\mathrm{m}}^2$ and pressure rate $\stackrel{\cdot }{p}=-50$ bar/ns. The orange dashed lines are linear fits to the data prior to the cavitation event. (B) Correlation between the cavity volume $V_{\mathrm{c}\mathrm{a}\mathrm{v}}$ and the cross-section area of the cavity $A_{\mathrm{c}\mathrm{a}\mathrm{v}}^{3/2}$ (from eight independent simulations). The red line is the fit of Eq. 10 to the linear regime in the yellow shaded region, where the cavity is not affected by the finite simulation box size. (C) Inverse squared mean cavitation pressures of the bilayers vs. the pressure rate for two different lateral box sizes. The solid lines are fits of Eq. 8 using the barrier height given by Eq. 12 to the data in the green shaded region. (D) Cavitation rate density for the bilayer as a function of pressure in the constant pressure protocol. The pale red shaded area marks the regime of mean cavitation pressures probed in the constant rate MD simulations.

From $N_{\mathrm{c}}$ and $V$, we evaluate the cavity volume $V_{\mathrm{c}\mathrm{a}\mathrm{v}}$ and the cross-sectional area $A_{\mathrm{c}\mathrm{a}\mathrm{v}}$ of the cavity (SI Appendix, section 10 has details), which are shown in the correlation plot in Fig. 4B. The relation is for small areas well described (red solid line in Fig. 4B) by

$$V_{\mathrm{c}\mathrm{a}\mathrm{v}}={\alpha }_{\mathrm{l}\mathrm{i}\mathrm{p}}{A}_{\mathrm{c}\mathrm{a}\mathrm{v}}^{3/2},$$ [10]

with a proportionality constant ${\alpha }_{\mathrm{l}\mathrm{i}\mathrm{p}}=$ 0.11, which measures the volume-to-area ratio of the cavity: for a perfectly spherical cavity, one would have ${\alpha }_{\mathrm{s}\mathrm{p}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}}=4/\left(3\sqrt{\pi }\right)\simeq 0.75$. In the orange shaded region in Fig. 4B, the diameter of the cavity is smaller than the simulation box size of $L=18$ nm, which corresponds to $A_{\mathrm{c}\mathrm{a}\mathrm{v}}^{3/2}=\mathrm{4,000}\hspace{0.17em}{\mathrm{n}\mathrm{m}}^3$ and for which the fit indeed is quite accurate. We can now write down the cavity free energy in the bilayer using the cavity area $A_{\mathrm{c}\mathrm{a}\mathrm{v}}$ as the reaction coordinate:

$$\mathrm{\Delta }{G}_{\mathrm{l}\mathrm{i}\mathrm{p}}=w_{\mathrm{l}\mathrm{i}\mathrm{p}}{A}_{\mathrm{c}\mathrm{a}\mathrm{v}}+p{V}_{\mathrm{c}\mathrm{a}\mathrm{v}}\left(A_{\mathrm{c}\mathrm{a}\mathrm{v}}\right).$$ [11]

The first term is the adhesion energy between the monolayers, which is proportional to the adhesion energy density $w_{\mathrm{l}\mathrm{i}\mathrm{p}}$, and the second term is the work done by the volume expansion. The free energy of the bilayer cavity has essentially the same functional form as in the case of a bubble in water (SI Appendix, section 11). Using the relation Eq. 10, the critical cavity area and the free energy barrier follow as

$$A_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}={\left(\frac{2w_{\mathrm{l}\mathrm{i}\mathrm{p}}}{3{\alpha }_{\mathrm{l}\mathrm{i}\mathrm{p}}p}\right)}^2\hspace{1em}\mathrm{a}\mathrm{n}\mathrm{d}\hspace{1em}\mathrm{\Delta }{G}_{\mathrm{l}\mathrm{i}\mathrm{p}}^{*}=\frac{4w_{\mathrm{l}\mathrm{i}\mathrm{p}}^3}{27{\alpha }_{\mathrm{l}\mathrm{i}\mathrm{p}}^2{p}^2}.$$ [12]

The adhesion energy density $w_{\mathrm{l}\mathrm{i}\mathrm{p}}$ is obtained from integrating the pressure–distance curve as two monolayers are pulled apart (SI Appendix, section 12). Note that a negative pressure weakens the lipid–lipid interactions and, thereby, decreases the adhesion energy density from $w_{\mathrm{l}\mathrm{i}\mathrm{p}}=$ 7.6 kJ mol⁻¹nm⁻² at 0 pressure to $w_{\mathrm{l}\mathrm{i}\mathrm{p}}=7.4$ kJ mol⁻¹nm⁻² at p =−100 bar. The ratio of the free energy barriers of lipid and water cavities follows from Eqs. 2 and 12 as $\mathrm{\Delta }{G}_{\mathrm{lip}}^{*}/\mathrm{\Delta }{G}_{\mathrm{w}}^{*}={\left(36\pi {\alpha }_{\mathrm{l}\mathrm{i}\mathrm{p}}^2\right)}^{-1}{\left(w_{\mathrm{l}\mathrm{i}\mathrm{p}}/\gamma \right)}^3\simeq 8\times 10^{-3}$. Thus, the bilayer cavitation barrier is more than two orders of magnitude lower than the bulk water cavitation barrier, which suggests much higher cavitation rates in bilayers.

In order to determine the kinetic prefactor, we again perform constant rate simulations. Fig. 4C shows ${1/p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}}^2$ vs. the pressure rate $-\stackrel{\cdot }{p}$ from simulations for two different bilayer surface areas. The cavitation events at the lowest rates occur at pressures around $p_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}\approx -190$ bar, for which the adhesion energy density to be used in the free energy barrier expression Eq. 12 is reduced to $w_{\mathrm{l}\mathrm{i}\mathrm{p}}=6.6$ kJ mol⁻¹nm⁻² (SI Appendix, Fig. S9C). We fit Eq. 8 to the simulation data in the linear regime for $-\stackrel{\cdot }{p}<$ 15 bar/ns and obtain ${\kappa }_0^{\mathrm{l}\mathrm{i}\mathrm{p}}=65\pm 4\hspace{0.17em}{\mathrm{n}\mathrm{s}}^{-1}{\mathrm{n}\mathrm{m}}^{-2}$. Note that the kinetic prefactor for a lipid bilayer scales linearly with the surface area according to $k_0^{\mathrm{l}\mathrm{i}\mathrm{p}}={\kappa }_0^{\mathrm{l}\mathrm{i}\mathrm{p}}A$. Interestingly, the attempt frequency per volume obtained by dividing ${\kappa }_0^{\mathrm{l}\mathrm{i}\mathrm{p}}$ by the lipid bilayer thickness $d_{\mathrm{l}\mathrm{i}\mathrm{p}}\approx$ 3 nm is obtained as ${\kappa }_0={\kappa }_0^{\mathrm{l}\mathrm{i}\mathrm{p}}/d_{\mathrm{l}\mathrm{i}\mathrm{p}}\approx$ 10 ${\mathrm{n}\mathrm{s}}^{-1}{\mathrm{n}\mathrm{m}}^{-3}$ and thus, is by a factor ${\mathrm{10}}^{10}$ smaller than the corresponding value in water, which is ${\kappa }_0\approx 10^{11}\hspace{0.17em}{\mathrm{n}\mathrm{s}}^{-1}{\mathrm{n}\mathrm{m}}^{-3}$. This presumably reflects primarily the dynamics in lipid bilayers, which is much slower compared with water.

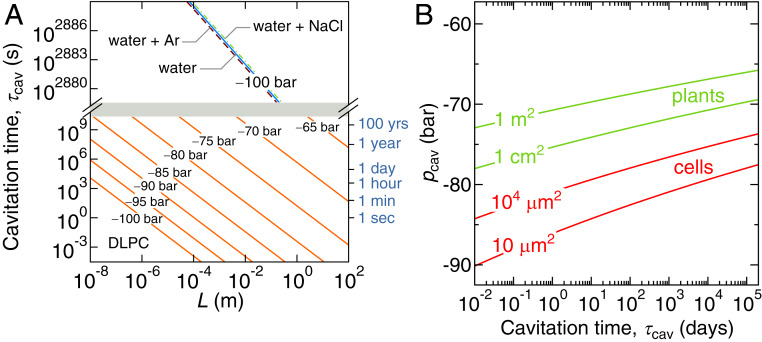
We finally show the lipid cavitation rate density in the constant pressure protocol, $k/A={\kappa }_0^{\mathrm{l}\mathrm{i}\mathrm{p}}\hspace{0.17em}\exp \left(-\beta \mathrm{\Delta }{G}_{\mathrm{l}\mathrm{i}\mathrm{p}}^{*}\right)$, in Fig. 4D as a function of the negative pressure. Fig. 5A plots the mean cavitation time ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}=k^{-1}$ as a function of the bilayer linear dimension $L=A^{1/2}$ for various fixed pressures. For comparison, we also show the cavitation times for pure bulk water and water containing Ar or NaCl as a function of the linear dimension $L=V^{1/3}$ in Fig. 5 A, Upper. We see that the bilayer cavitation time for a given length $L$ and negative pressure is much smaller than the water cavitation time. Conversely, the negative pressure at which cavitation occurs is decreased dramatically in the presence of lipid bilayers, and the cavitation time reaches biologically accessible timescales for pressures around $-$100 bar. It is interesting to note that bilayer cavitation has been suggested to be also induced by ultrasound absorption (39).

Fig. 5.

(A) Mean cavitation time ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}$ in a bilayer with lateral dimensions $L\times L$ for various imposed constant pressures (orange lines). We also show the cavitation time in a box of pure water with dimensions $L\times L\times L$ (blue line), in water containing 50 mM argon (dashed line), and in water containing 50 mM NaCl (dashed–dotted line). Note the broken scale. (B) Negative cavitation pressure vs. the mean cavitation time computed from Eq. 13 for different bilayer areas relevant for vascular systems in plants (green lines) and individual cells (red lines).

One key quantity is the most negative pressure that a lipid bilayer with the surface area $A$ can sustain over the time span ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}$. Combining Eqs. 3 and 12, we obtain

$$p_{\mathrm{c}\mathrm{a}\mathrm{v}}=-\frac{2}{{\alpha }_{\mathrm{l}\mathrm{i}\mathrm{p}}}{\left(\frac{w_{\mathrm{l}\mathrm{i}\mathrm{p}}}{3}\right)}^{3/2}\frac{1}{\sqrt{k_{\mathrm{B}}T\hspace{0.17em}\ln \left({\kappa }_0^{\mathrm{l}\mathrm{i}\mathrm{p}}A{\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}\right)}},$$ [13]

which is shown in Fig. 5B for various lipid surface areas. It is seen that $p_{\mathrm{c}\mathrm{a}\mathrm{v}}$ is only weakly dependent on $A$ and ${\tau }_{\mathrm{c}\mathrm{a}\mathrm{v}}$ owing to the square root logarithmic dependence in Eq. 13. For lipid surface areas relevant for vascular systems in plants, in the centimeter squared to meter squared range, the cavitation pressure range is rather narrow and between $-$65 and $-$80 bar on the biologically relevant timescale, which is in striking agreement with the most negative pressures in the sap of plants (3).

The cavitation of water under negative pressure also plays a central role in spore ejection in ferns. The spores are enclosed in a ring-shaped capsule, the sporangium. The water inside the 12 to 13 cells that form the crest of the capsule evaporates, which builds up tension in the cells (7, 8, 40). As the water pressure reaches a critical value of around $-$90 bar (8, 40), cavitation occurs, and the elastic energy stored in the capsule is instantly released, which catapults the spores into the air. In a typical eukaryotic cell, the total surface area of bilayers is $A\hspace{0.17em}=\hspace{0.17em}10$ to ${\mathrm{10}}^4\hspace{0.17em}\mathrm{\mu }{\mathrm{m}}^2$. The negative cavitation pressure threshold for such surface areas on the timescales of hours to days is, according to Eq. 13, around $-$90 bar (Fig. 5B), which is in excellent agreement with the reported value for fern spore ejection.

Discussion and Conclusions

As follows from Eq. 13, the predicted cavitation pressure depends significantly on the lipid adhesion energy density $w_{\mathrm{l}\mathrm{i}\mathrm{p}}$ with a relative variation $\delta p_{\mathrm{c}\mathrm{a}\mathrm{v}}/p_{\mathrm{c}\mathrm{a}\mathrm{v}}=\left(3/2\right)\hspace{0.17em}\left(\delta w_{\mathrm{l}\mathrm{i}\mathrm{p}}/w_{\mathrm{l}\mathrm{i}\mathrm{p}}\right)$. Thus, a 10% modification in the lipid adhesion energy density (for example, due to different lipid architectures or due to simulation force-field issues) will change the cavitation pressure by 15%. This might explain why the thermodynamic state of lipid bilayers, which presumably alters the lipid adhesion energy density, was experimentally demonstrated to influence the ultrasound-induced cavitation in aqueous vesicle suspensions (11, 41).

The bilayer area $A$ that appears in Eq. 13 is the sum of all individual lipid bilayer patches that are present in the entire system. Clearly, in order for our model to be valid, the area of individual bilayer patches must be larger than the critical cavity area $A_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}$, which is of the order of $A_{\mathrm{c}\mathrm{a}\mathrm{v}}^{*}=$ 50 ${\mathrm{n}\mathrm{m}}^2$ at a pressure of $-$100 bar (Eq. 12).

According to CNT, for a bubble nucleating at a smooth planar surface, the free energy barrier is modified as $\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}^{*}=\mathrm{\Delta }{G}_{\mathrm{w}}^{*}\hspace{0.17em}\left(2-\cos \theta \right){\cos }^4\left(\theta /2\right)$ (31, 42, 43) and decreases drastically as the surface contact angle $\theta$ goes up (SI Appendix, section 13 has details). At the hydrophilic–hydrophobic threshold (i.e., for $\theta =90^{○}$), the free energy barrier is reduced by half compared with the homogeneous cavitation result $\mathrm{\Delta }{G}_{\mathrm{w}}$ (Eq. 2) and is still very high. Only for a contact angle as high as $\theta \simeq 150^{○}$ is the barrier reduced down to $\mathrm{\Delta }{G}_{\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}}^{*}/\mathrm{\Delta }{G}_{\mathrm{w}}^{*}\simeq 10^{-2}$ and comparable with the free energy barrier for cavitation in the lipid bilayer, $\mathrm{\Delta }{G}_{\mathrm{l}\mathrm{i}\mathrm{p}}^{*}$.

The most hydrophobic smooth surfaces exhibit contact angles of the order of $\theta \approx {\mathrm{120}}^{○}$ (44, 45). Contact angles as high as $\theta \simeq 150^{○}$ are achieved with nano- or microtextured hydrophobic surfaces (46–48). While such superhydrophobic surfaces are frequently found on the outside of plant leaves and give rise to the lotus effect, there are no reports of such extremely hydrophobic surfaces inside the plant vascular system, where the contact angles are typically between ${\mathrm{40}}^{○}$ and ${\mathrm{55}}^{○}$ (49). It is therefore unlikely that heterogeneous cavitation inside plants produces similarly high rates as cavitation inside lipid bilayers. On the other hand, preexisting gas bubbles in hydrophobic surface crevices can significantly enhance the cavitation rate (19, 20, 24, 43), which is also the accepted explanation of why, in typical daily life situations, water cannot sustain even weak negative pressures. One can thus speculate that the presence of surfactants or lipids stabilizes small bubbles and prevents coalescence and the formation of bubbles that are larger than the critical bubble size (28), which is also in line with recent experiments of water with surfactants under tension (50).

It is also interesting to compare the cavitation rates of lipid bilayers with those in liquid alkanes, which have a similar chemical architecture as lipid tails. In SI Appendix, section 14, we demonstrate that cavitation in liquid decane is characterized by a similar free energy barrier and similar cavitation rates as bilayers of comparable simulation box sizes. This implies that oil droplets caught under negative pressure environments can impose similar stability limits to biological systems as lipid bilayers.

In conclusion, we introduced a constant pressure rate method to study rare events in metastable systems under tension. It is an alternative to other methods [e.g., forward flux sampling (51, 52)], with the advantage that one does not need to know a priori where the cavitation will occur. It is hence suitable for heterogeneous systems, such as bilayer systems, where cavitation could occur between the monolayers, at the water–bilayer interface, or in the water phase. The method will be helpful as a complementary method in future studies on cavitation in complex systems.

From our analysis, we conclude that cavitation within lipid bilayers at negative pressures commonly found in plants ($-$5 to $-$50 bar) is very unlikely but that the comparatively high cavitation rate in the interior of lipid bilayers practically limits tolerable negative pressures in plants to values above $-$100 bar and might therefore also limit where plants in dry environments can grow. Our results apply to cavitation instabilities induced by negative pressure in all systems that contain lipid bilayer aggregates, and our predictions should be testable directly in experiments.

Methods

Simulation Model.

The simulations of water and phospholipid bilayers employ classical atomistic representations. The bilayer is composed of DLPC lipids in the fluid $L_{\alpha }$ phase using the united-atom Berger force field (53) with the SPC/E (54) water model. Comparative bulk water simulations are conducted using the TIP4P/2005 (32) water model. The MD simulations are performed with the GROMACS simulation package (55, 56) with an integration time step of 2 fs. Electrostatic interactions are treated using the particle mesh Ewald method (57, 58) with a 0.9-nm real-space cutoff. The Lennard-Jones (LJ) interactions are cut off at $r_{\mathrm{L}\mathrm{J}}=0.9$ nm except for the simulations for TIP4P/2005 water, where $r_{\mathrm{L}\mathrm{J}}=1.4$ nm. Temperature is maintained at 300 K using the velocity-rescale thermostat (59) with a time constant of 0.1 ps. The pressure is controlled with the Berendsen barostat (60) with a time constant of 1 ps, which is also suitable for negative pressures. The advantage of the Berendsen barostat is its efficiency and numerical stability in box scaling even for large applied differences in the pressure. We have verified that identical results are obtained with the Parrinello–Rahman barostat (61), which reproduces the volume fluctuations more accurately (SI Appendix, section 15).

Time-Dependent Rate Equations.

In the Arrhenius description, the transition rate $k\left(t\right)$ for crossing over a time-dependent free energy barrier, $\mathrm{\Delta }G*\left(t\right)$, is given as

$$k\left(t\right)=k_0\hspace{0.17em}{\mathrm{e}}^{-\beta \mathrm{\Delta }G*\left(t\right)}.$$ [14]

The probability $f\left(t\right)$ that the system has not yet crossed the barrier obeys the first-order rate equation $\stackrel{\cdot }{f}\left(t\right)=-k\left(t\right)f\left(t\right)$, with the solution

$$f\left(t\right)={\mathrm{e}}^{-k_{0}I\left(t\right)},$$ [15]

where

$$I\left(t\right)={\int }_0^t{\mathrm{e}}^{-\beta \mathrm{\Delta }G*\left(t^{\prime }\right)}\mathrm{d}{t}^{\prime }.$$ [16]

When the free energy barrier decays inversely with the square of time as is the case in our model, $\beta \mathrm{\Delta }G*\left(t\right)={\left({\tau }_0/t\right)}^2$, the integral $I\left(t\right)$ has the closed form solution

$$I\left(t\right)=t\exp \left[-{\left(\frac{{\tau }_0}{t}\right)}^2\right]-\sqrt{\pi }\hspace{0.17em}{\tau }_0\hspace{0.17em}\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(\frac{{\tau }_0}{t}\right),$$ [17]

where $\mathrm{e}\mathrm{r}\mathrm{f}\mathrm{c}\left(x\right)$ is the complementary error function.

Data Availability.

The data that support the findings of this study are included in SI Appendix. Original simulation files are available at https://gitlabph.physik.fu-berlin.de/ag-netz/constant-rate-simulation-files.