Detected climatic change in global distribution of tropical cyclones

Significance

Little had been known about whether the ongoing climate changes had already affected observed global tropical cyclones (TCs). This study revealed that a climate change in global TC activity over 1980 to 2018 has been more evident in the spatial pattern of TC occurrence, rather than the number of global TCs. The total effect of anthropogenic greenhouse gases, aerosols, and volcanic eruptions on global TC distribution is spatially inhomogeneous: Increases and decreases in TC occurrence depend on the region. However, our climate models project decreases in the number of global TCs toward the end of the 21st century due to the dominant effect of greenhouse gases on decreasing TC occurrence in most of the tropics, consistent with many previous studies.

Abstract

Owing to the limited length of observed tropical cyclone data and the effects of multidecadal internal variability, it has been a challenge to detect trends in tropical cyclone activity on a global scale. However, there is a distinct spatial pattern of the trends in tropical cyclone frequency of occurrence on a global scale since 1980, with substantial decreases in the southern Indian Ocean and western North Pacific and increases in the North Atlantic and central Pacific. Here, using a suite of high-resolution dynamical model experiments, we show that the observed spatial pattern of trends is very unlikely to be explained entirely by underlying multidecadal internal variability; rather, external forcing such as greenhouse gases, aerosols, and volcanic eruptions likely played an important role. This study demonstrates that a climatic change in terms of the global spatial distribution of tropical cyclones has already emerged in observations and may in part be attributable to the increase in greenhouse gas emissions.

The effect of anthropogenic forcing on global tropical cyclone (TC) activity is of great interest and an important topic among the science community and public (1–3). Previous studies have reported possible future changes in global TC activity for the late 21st century as projected by numerical dynamical models (2, 4). Most studies have focused on projected changes in the global TC number, mean TC intensity, and the mean precipitation associated with TCs (2, 4). However, projected changes in the spatial distribution of TCs, as well as regional changes in TC frequency, are regarded as relatively more uncertain (2), despite their societal importance.

Compared to studies of future projections, detecting any climatic change in the observed record for global TC activity is challenging, mainly due to two factors (1). The first is the lack of a reliable long-term observed TC record, which is a limitation when it comes to confidently differentiating between real climatic trends and artificial trends (1, 5, 6). Because reliable observed TC intensity data at the global scale for climate trends analysis have only been available since 1980, when satellite observations began (7), any trend analysis using data before 1980 may involve artificial trends owing to evolution of the observational method (6). Although there are a few studies that have shown observed trends in global TC activity, such as poleward shifts in the location of lifetime maximum TC intensity (8) and slower TC motion (9), there are uncertainties in these trends because of the low quality of the observed data employed (5, 6). Another complicating factor is the effect of multidecadal internal variability on TC variations (10–12). Although some trends in the short-term observed record appear to be statistically significant, it is difficult to distinguish such trends from intrinsic multidecadal internal variability.

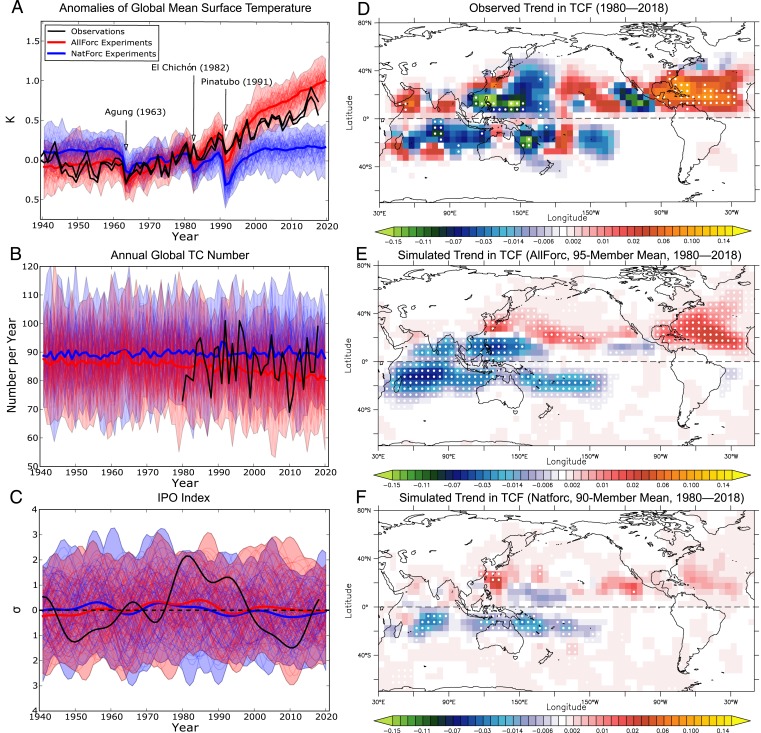
Many studies have shown that global mean temperature has been rising since the mid-20th century, and that the increase is attributable to increases in emissions of greenhouse gases (Fig. 1A and refs. 13 and 14). In contrast, the annual number of global TCs exhibits no clear trend and has remained steady at around 86 since 1980 (Fig. 1B and ref. 15). The presence of large interannual and decadal variations (the SD of the annual mean number is eight as an indication of interannual variability; Fig. 1B) may suggest no significant trend for global TC activity. However, when we look at a global map of the trend in TC frequency of occurrence (TCF; Observed Data) since 1980 (Fig. 1D), there is a pronounced spatial pattern in the trends, namely, decreasing trends in the southern Indian Ocean, western North Pacific, Coral Sea off the northeast coast of Australia, and the far eastern tropical North Pacific, but increasing trends in the Arabian Sea, central Pacific including Hawaii, and the North Atlantic. We wish to assess whether anthropogenic climate change could play a role in driving this spatial pattern in the global trends of TCF.

Fig. 1.

Time series of surface temperature, global TC number, IPO, and linear trends in TCF. (A) Anomalies of global mean surface temperature relative to the 1961 to 1990 mean based on observations (black), the AllForc large-ensemble experiments (red), and the NatForc experiments (blue), using all of the models (i.e., FLOR-FA, FLOR, and SPEAR [units: K]). Thin lines represent each ensemble member (95 members for AllForc and 90 members for NatForc); thick lines represent the ensemble means. Shading indicates the minimum and maximum ranges among the ensemble members. (B) As in A, but for global TC number (units: number per year). (C) As in A, but for the IPO index (IPO and AMV) (units: σ). (D) Observed linear trends in TCF for the period 1980 to 2018 (number per year). (E) As in D, but for the ensemble mean of the AllForc experiments. (F) As in D, but for the ensemble mean of the NatForc experiments. The arrows in A highlight the major volcanic eruptions in history. The white dot in D–F indicates the linear trend over the grid cell is statistically significant at the 95% level according to the Mann–Kendall significance test. Observations used are (A) HadCRUT4 and GISTEMv4, (B and D) IBTrACS, and (C) HadISST1.1.

Previous studies reported that intrinsic multidecadal internal variability, such as the Interdecadal Pacific Oscillation (IPO; refs. 16 and 17) and Atlantic Multidecadal Variability (AMV, as also referred to as the Atlantic Multidecadal Oscillation [AMO]; ref. 18), could influence TC activity on a global scale (10–12, 19–21). Indeed, observations showed a positive phase of the IPO and a negative phase of the AMV during 1980 to 1997, with a change in sign thereafter (Fig. 1C and SI Appendix, Figs. S1A and S2A; see IPO and AMV for computing IPO and AMV indices). The decadal phase changes in the IPO and AMV on around 1997 could be another potential factor responsible for the observed spatial pattern of TCF trends over 1980 to 2018. To clarify the extent to which the spatial pattern of the observed TCF trends was attributable to the externally forced climate change or internal multidecadal variability, we use two statistical methods on both the observations and the climate model simulations as described in the following sections.

Effect of Natural Variability and External Forcing on the Trends in Global TCF

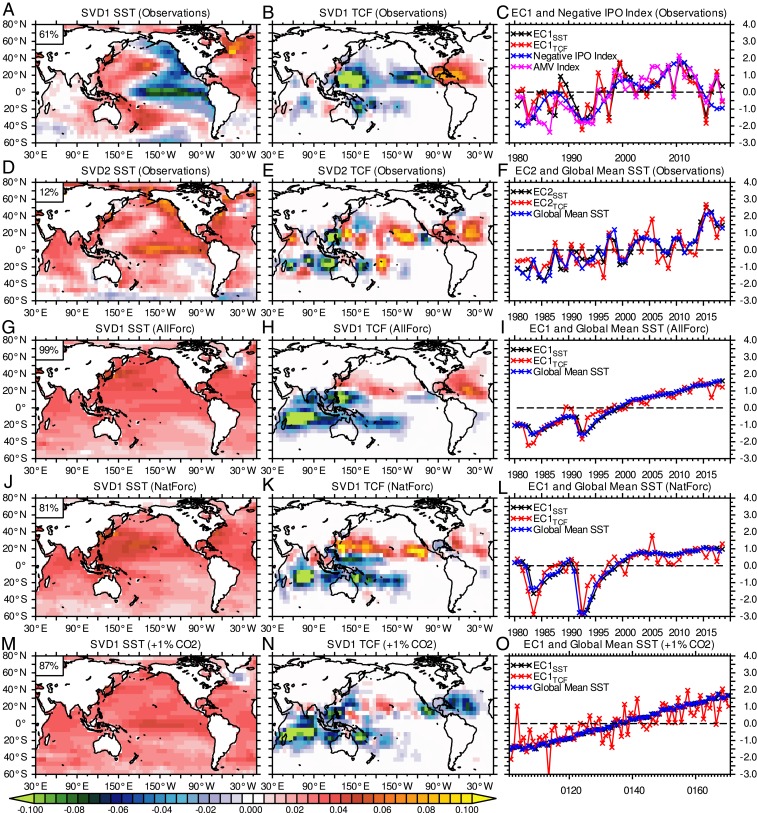
As indicated in Fig. 1A, the global warming trend is much stronger after 1980 than before. This implies that the warming trend is nonlinear (22). Therefore, it may be difficult to attribute the observed linear trends in TCF (Fig. 1D) to nonlinear increases in anthropogenic forcing or oscillatory internal natural variability because a linear TCF trend could be a mixed result from both effects. One method that successfully splits the climate variability into a long-term nonlinear trend and other natural internal modes is the singular value decomposition analysis (SVD; ref. 23; see SVD Analysis for more details). The SVD analysis method is an extension of the empirical orthogonal function (EOF) analysis method (24). Unlike the EOF analysis method, the SVD analysis method utilizes two variables for the inputs and identifies the patterns in each variable that explain the maximum amount of covariance (25). Although the SVD analysis itself does not always guarantee a separation between a nonlinear warming trend and other modes, Wang et al. (23) reported that the SVD analysis using the observed anomalies of sea surface temperatures (SSTs) and annual TCF over 1965 to 2008 successfully separated the nonlinear global warming mode from other natural internal modes. We will revisit Wang et al. (23) by applying the SVD analysis to the observed TCF and SST datasets over 1980 to 2018 (Fig. 2 A–F). As will be discussed later, we will also show the SVD results applied to the model outputs (Fig. 2 G–O) to compare the observed results.

Fig. 2.

SVD analysis using SST and TCF. (A–C) The first SVD mode derived from the observations. (A) The first SVD mode for SST (SVD1_SST) and (B) TCF (SVD1_TCF). (C) Time series of the expansion coefficient (EC) for SST (EC1_SST, black) and TCF (EC1_TCF, red) superimposed on the observed IPO index with flipped sign (blue) and AMV index (pink) (units: σ). (D–F) As in A–C, but for the second SVD mode and standardized global mean SST in F for the blue line. (G–I) As in D–F, but for the first SVD mode derived from the ensemble mean of the 95-member AllForc experiments. (J–L) As in D–F, but for the first SVD mode of the 90-member NatForc experiments. (M–O) As in D–F, but for the three-member Transient 2×CO₂ experiments.

We found that SVD analysis applied to observations over 1980 to 2018 also identified the long-term nonlinear warming mode and natural variability mode as consistent with Wang et al. (23) (Fig. 2 A–F). The first SVD mode using observations explains 61% of the total covariance between SST and TCF (Fig. 2 A–C). The expansion coefficient for the first SST mode (EC1_SST) is highly correlated with both the observed IPO index (IPO and AMV) with reversed sign (r = 0.71) and the AMV index (IPO and AMV) (r = 0.73) (Fig. 2 A and C). The spatial pattern of the first SVD TCF (Fig. 2B) corresponds fairly well to that of the observed TCF trends (Fig. 1D), suggesting an influence of the IPO and AMV on the observed TCF trends. However, the spatial pattern of the first SVD TCF does not completely agree with the observed TCF trends in terms of its smaller negative TCF loading in the southern Indian Ocean as well as an inconsistent sign of TCF change in the central Pacific near Hawaii. By contrast, the second SVD mode reveals a nonlinear global warming pattern in which the TCF pattern (Fig. 2E) shows a marked negative TCF loading over the southern Indian Ocean and a positive TCF loading in the central Pacific, which appears to be more consistent with the observed TCF trends than the first SVD mode (Fig. 1D).

Meanwhile, it is uncertain if the first SVD TCF spatial pattern in observations, shown in Fig. 2B, is a true response of TCF to IPO and AMV, owing to the short analysis period. We investigated the modeled TCF response to the simulated IPO and AMV using the long-term preindustrial control simulations of two fully coupled dynamical global models developed at the Geophysical Fluid Dynamics Laboratory (GFDL): Forecast-oriented Low Ocean Resolution model with flux adjustments (FLOR-FA; ref. 26–28) and Seamless System for Prediction and Earth System Research (SPEAR; ref. 29) (piControl; Models and piControl Experiments). The two models reasonably reproduced the IPO- and AMV-like variability (SI Appendix, Figs. S1 B, E, and I and S2 B, E, and I). The simulated TCF spatial patterns regressed onto the simulated negative IPO index (SI Appendix, Fig. S1 G and K) and AMV index (SI Appendix, Fig. S2 G and K) partially agree with the observed first SVD TCF patterns in the western North Pacific and North Atlantic (Fig. 2B); however, there are marked differences between Fig. 2B and SI Appendix, Figs. S1 G and K, especially in the Indian Ocean and South Pacific. Therefore, the spatial pattern of the observed TCF trends is not completely explained by IPO and AMV, indicating that other factors, such as external forcing, need to be explored. Note that previous studies (e.g., ref. 30) suggest that the observed IPO and AMV may reflect the response to a combination of natural and anthropogenic forcing during the historical period. Although it remains uncertain to what extent the first SVD results from external forcing, we hypothesize that the second SVD represents an externally forced mode responsible for the global TCF trends (Fig. 2 D–F).

Because of the short duration of the observed record, we primarily rely on climate model simulations to understand forced climate change (e.g., anthropogenic forcing) and internal natural variability (e.g., IPO and AMV). However, understanding forced climate change in the presence of internal unforced climate variability and model response uncertainty is a challenge for climate change science. In the past, climate modeling centers ran a small number of realizations [e.g., phase 5 of the Coupled Intercomparison Project (31)] that may not be insufficient to distinguish all aspects of the forced response from internal climate variability. An alternative approach is to conduct a new type of climate simulation called “large-ensemble simulations” (32). Large-ensemble simulations allow one to better define a model’s forced response and to distinguish it from internal variability, taking advantage of ensemble statistics given a sufficiently large ensemble.

We conducted new large-ensemble simulations using fully coupled models developed at GFDL that incorporate 50-km mesh atmospheric component, enabling realistic TC simulations (33, 34). In order to investigate the impact of different models on the results, we conducted large-ensemble simulations with three configurations using the GFDL models (Large-Ensemble Experiments and SI Appendix, Table S1). The first is the simulation using FLOR-FA. The second is that using FLOR without flux adjustment (referred to as FLOR). The last is that using a very new model developed at GFDL (SPEAR; ref. 29). We utilized SPEAR in addition to FLOR considering the potential model dependence of results. SPEAR can be considered as an independent model from FLOR and FLOR-FA with substantial upgrades in the physical and dynamical packages in SPEAR (29). Each configuration runs 30- to 35-member ensemble simulations. Each ensemble member was initialized from a different year from the long-term control simulations and integrated forward by prescribing time-varying historical external forcing such as greenhouse gases, aerosols, volcanic aerosols, and solar radiation (hereafter referred to as AllForc). The simulated global mean temperature rises year by year, as observed (red lines in Fig. 1A). Because each ensemble member shows a different phase of internal variability at a specific time, taking the mean of the ensemble members can filter out the internal variability (e.g., Fig. 1C); thus, the resultant mean field can be regarded as an estimated modeled response to the external forcing. Another set of large-ensemble simulations was also conducted with similar settings as AllForc but with a fixed level of greenhouse gases and aerosols at 1941 for FLOR and FLOR-FA (1921 for SPEAR), along with time-varying volcanic forcing and solar radiation (hereafter referred to as NatForc). This meant that there is no apparent trend in global mean temperature except for a few significant cooling events after the volcanic eruptions (blue lines in Fig. 1A).

The simulated TCF trends for the period 1980 to 2018 computed by the ensemble mean of the AllForc experiments, throughout the configurations (Fig. 1E), as well as NatForc (Fig. 1F), show spatial patterns similar to the observed TCF trends (Fig. 1D). These results indicate the possibility that external forcing has played an important role in the observed global TCF trends. We also applied SVD analysis to the ensemble mean of SSTs and TCFs simulated by the AllForc (95 members) and NatForc (90 members) experiments. Because model-simulated internal natural variabilities are cancelled out by averaging ensemble members, the first SVD mode now represents a global warming mode (Fig. 2 G–L), which is related to the TCF patterns (Fig. 2 H and K) resembling the observed TCF trends (Fig. 1D) and the observed second SVD mode of TCF (Fig. 2E). A recent study indicated that mean TC genesis locations were potentially shifted equatorward after the volcanic eruptions that occurred in the Northern Hemisphere (35). This is somewhat consistent with the first SVD TCF mode of NatForc (Fig. 2K), in that the TCF anomaly is negative in the Northern Hemisphere and positive in the Southern Hemisphere during years after the two big volcanic eruptions of El Chichón in 1982 and Pinatubo in 1991 (Fig. 2L). The low level of TC activity during the period of cooler surface ocean conditions in the earlier decades (1980 to 2001) and high level of TC activity during the recovery period from the cooling in the later decades (2002 to 2018) in the Northern Hemisphere might have partially caused the observed spatial pattern of TCF trends. To isolate the effect of CO₂ increases, we conducted another set of experiments, called “Transient 2×CO_2,” in which CO₂ was increased by +1% per year as a boundary condition until the CO₂ level had doubled relative to the 1990 level (ref. 36 and Transient 2×CO₂ Experiment). The first SVD mode derived from the ensemble mean of the Transient 2×CO₂ experiments (three members) is again a global warming mode (Fig. 2 M–O), revealing a spatial pattern of TCF similar to the observed TCF trends (Fig. 1D), except over the North Atlantic. Overall, based on the results of the large-ensemble experiments, we hypothesized that the observed spatial pattern of global TCF trends during 1980 to 2018 was highly likely to have been caused by the changes in external forcing, such as greenhouse gases, aerosols, volcanic eruptions, and solar radiation, although IPO and AMV were still important factors for the decreasing (increasing) TCF over the western North Pacific (North Atlantic).

Detected Climatic Change in the Observed Trends in Global TCF

A high similarity between the observed (Fig. 1D) and simulated (Fig. 1E) spatial patterns in the global TCF trends indicates that it is likely that external forcing played an important role for the observed TCF change. However, it is still unclear how much of the observed TCF trends over 1980 to 2018 can be statistically distinguishable from internally generated noise. If they can be distinguished from noise, by what year did this occur? One of the objective methods to answer the question is so-called optimal fingerprint analysis (37–39). We conducted the optimal fingerprint analysis using observations and the model simulations (Optimal Fingerprint Analysis).

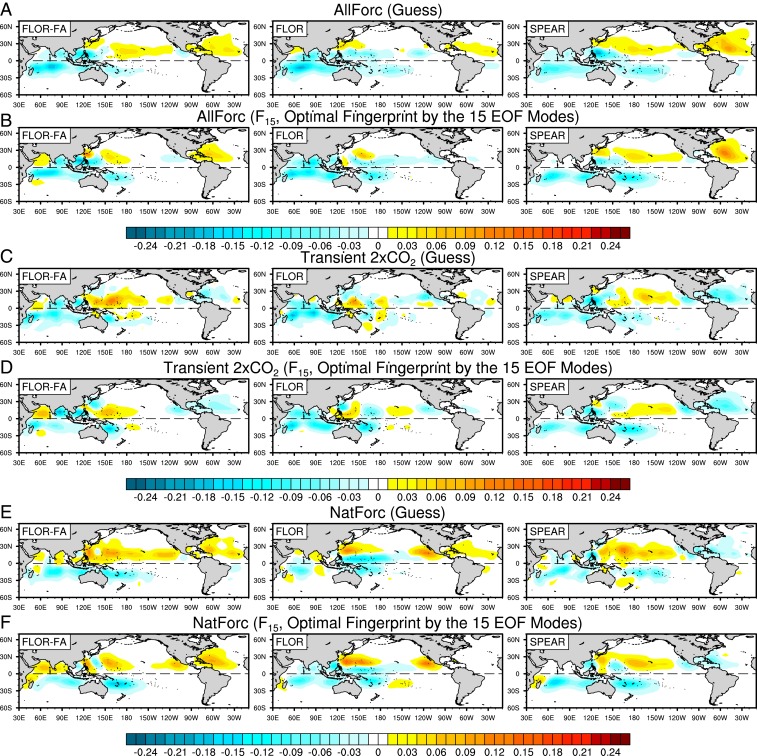
We first identified expected spatial patterns of climate change in TCF (i.e., so-called guess patterns) from the first SVD modes using the ensemble mean outputs for each configuration (i.e., FLOR-FA, FLOR, and SPEAR). The obtained guess patterns were for AllForc (Fig. 3A), NatForc (Fig. 3E), and Transient 2×CO₂ (Fig. 3C). The optimal fingerprint patterns (Fig. 3 B, D, and F) were obtained by rotating the guess patterns by weighing the EOF modes derived from the long-term piControl experiments (Optimal Fingerprint Analysis). In the fingerprint analysis, we searched for an increasing expression of the fingerprint (or guess) pattern in the observed TCF data and estimated the detection time at which the pattern would become identifiable at a 5% significance level. The detection time is referenced to 1980, the start year of the observed data. “Detected at year X” implies that the observed spatial pattern of the global TCF trends between 1980 and year X is unlikely to be due entirely to modeled internal variability. The climate noise estimates required for statistical significance were obtained from 1,000-y piControl runs using FLOR-FA and SPEAR (Optimal Fingerprint Analysis).

Fig. 3.

Fingerprints for TCF changes. The guess patterns (A, C, and E) were derived from the first SVD modes using the ensemble mean of the large-ensemble experiments for each model. The fingerprint patterns (B, D, and F) were obtained by rotating the guess patterns by the first m modes of the EOF derived from the long-term piControl experiments. We tested m = 5, 10, or 15, and m = 15 results shown in B, D, and F (A and B) are for AllForc, (C and D) for Transient 2×CO₂, and (E and F) for NatForc. Left-hand panels are for FLOR-FA, middle for FLOR, and right for SPEAR.

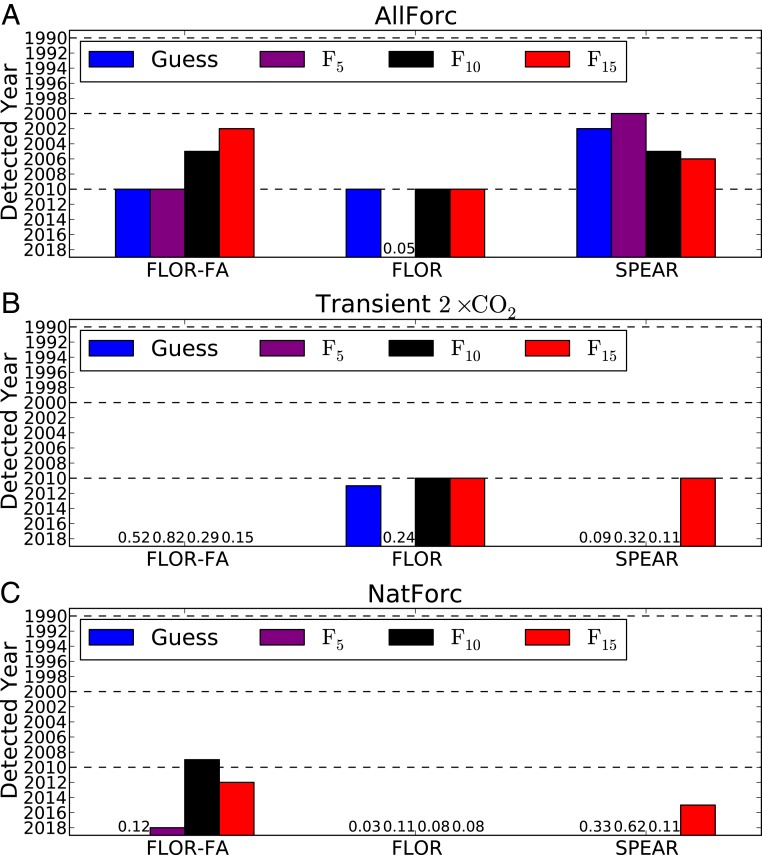
The fingerprint analysis revealed that the observed spatial pattern of TCF trends since 1980 was detected around 2010 with the fingerprints by AllForc (Fig. 4A). In other words, the probability that the observed TCF trends between 1980 and 2010 are due entirely to internal variability is less than 5%. These results support our hypothesis that the observed spatial pattern of TCF trends cannot be explained entirely by internal variability. The observed spatial pattern of TCF trends is also detected after 2010 using the fingerprints of Transient 2×CO₂, except for FLOR-FA (Fig. 4B), and the fingerprints of NatForc, except for FLOR (Fig. 4C), although the detection is not as robust as in AllForc. The results from Fig. 4B highlight that the observed global TCF trend may in part be attributable to the increase in greenhouse gas emissions.

Fig. 4.

Detection times for TCF fingerprints in observations. The detection analysis was applied using the guess and fingerprints from (A) AllForc (greenhouse gases, aerosols, volcanic forcing, and solar forcing), (B) Transient 2×CO₂ (greenhouse gas), and (C) NatForc (volcanic and solar forcing), with a 5% significance level (i.e., P value = 0.025 for a one-side test) as the detection threshold. The color bars indicate the earliest detection time (i.e., the longer bar, the earlier the detection time). “Guess” denotes the detection time using the guess pattern; F denotes the optimal fingerprint, with the subscript number indicating the truncation dimension of the EOF. The detection analysis was performed using three different fingerprints, obtained by FLOR-FA, FLOR, and SPEAR. In cases where the detected variable was lacking statistical significance, the number indicates the P value for the 1980 to 2018 trend.

Summary and Discussion

Recent studies suggest that the state-of-the-art climate models commonly project statistically significant reduction in the mean number of global TCs at the end of the 21st century (2, 4). In contrast, observations reveal no clear trend in the global TC number since 1980, although the nature of observed global TC number remains uncertain due to the limited length of available TC data and the substantial impact of natural internal variability on global TC activity. Despite the limited length of the observed record, there are pronounced trends in the observed TC frequency of occurrence (TCF, or say TC density) in some regions over the period 1980 to 2018: decreasing trends in the southern Indian Ocean, tropical western North Pacific, and South Pacific and increasing trends in the Arabian Sea, central Pacific, and North Atlantic. The different sign of TCF trends among the regions could lead to no significant trend in the overall global TC number. As indicated in the previous studies (10–12), the effect of natural decadal variability such as the IPO and/or AMV could be a potential factor responsible for the observed spatial patterns in TCF trends since 1980. However, our model simulations revealed that the observed TCF trends cannot be entirely explained by such variability. Therefore, this study aimed to address other external factors responsible for the observed global TCF trends over the period 1980 to 2018.

Using large ensembles of climate model simulations, we found that external forcing (i.e., greenhouse gases, aerosols, and volcanic eruptions) played an important role in the observed TCF trends since 1980. The application of two statistical methods (SVD and optimal fingerprint analysis) showed that the model-estimated pattern of the changes in TCF from external forcing had emerged in observations around 2010. Furthermore, the analysis indicates that the two volcanic eruptions in 1980s and 1990s exerted substantial influence on global TCF trends, as also indicated by a recent study (35). However, the current study also highlights that increases in greenhouse gases are also another important external forcing for the observed TCF trends since 1980. Indeed, the model experiments forced only with monotonically increasing greenhouse gases revealed a spatial pattern of the TCF trends similar to the observed TCF trends except for the North Atlantic, where the model showed decreasing TCF trends whereas observations showed increasing TCF trends. Conversely, the model experiments forced with the all external forcing showed increasing TCF trends in the North Atlantic. These mixed results among the model experiments, and additional evidence shown in SI Appendix, Fig. S3, suggest that the observed positive TCF trends in the North Atlantic over 1980 to 2018 could be partially attributable to the diminishing effect of anthropogenic aerosols and volcanic eruptions that are in line with the literature (35, 40–42). However, as shown in SI Appendix, Fig. S3B, our climate models project decreasing trends in the number of TCs in the North Atlantic toward the end of the 21st century because of the dominant effect of increases in CO₂ concentrations, assuming no volcanic eruption.

Regarding natural variability, the IPO and AMV are still major contributors to influence the spatial distribution of TCs around the world, especially in the western North Pacific and North Atlantic. The IPO and AMV might have changed the sign in the mid-2010s (blue and pink lines in Fig. 2C). If the current phases persist, we would expect to see more (less) frequent active TC seasons in the western North Pacific (North Atlantic) in the upcoming decades owing to the variability of IPO and AMV (SI Appendix, Figs. S1 G and K and S2 G and K). However, consistent with previous studies (2, 4), our models project a decrease in TCF over most of the tropics toward the end of the 21st century due to the anticipated increase in greenhouse gases. This, in turn, leads to a projected decrease in global TC number (SI Appendix, Figs. S3A and S4), but the decrease in global TC number is not yet detectable in the observed record (Fig. 1B) because of the relatively small signal-to-noise ratio for global TC number owing to the large spatial variations in changes in TC activity.

Although we found consistent results with a different climate model (SI Appendix, Figs. S5 and S6), projected future changes in global TC activity still vary considerably among the state-of-the-art climate models (36). Therefore, it would be preferable to adopt a multiple-model approach to reduce the uncertainty. Another caveat is that in the optimal fingerprint analysis the detection time was computed based on the statistics using linear trends following previous studies (37–39). However, as indicated in Fig. 1A, the observed warming trend is much stronger since 1980 than before. This implies that the warming trends and the response could be nonlinear. Therefore, the detected time in this study may include uncertainty. As discussed above, anthropogenic aerosols could have also influenced the TCs over the North Atlantic. Additional large-ensemble experiments that are forced with a single external forcing (e.g., anthropogenic aerosols only) will be useful to clarify the impact of the single forcing to the regional TC activity.

Methods

Observed Data.

For the observed TC data, we utilized the International Best Track Archive for Climate Stewardship (IBTrACS; ref. 43), version 4, for the period 1980 to 2018. The IBTrACS dataset consists of TC tracks compiled by multiple organizations. In this study, we utilized the combination of the National Hurricane Center, the Joint Typhoon Warning Center, and the Central Pacific Hurricane Center, which is flagged as “USA Agency” in the IBTrACS dataset. TC positions were counted for each 5° × 5° grid box within the global domain. The total count for each grid box was defined as the TC frequency of occurrence (TCF). Following Wang et al. (23), the raw TCF fields were smoothed using a nine-point moving average weighted by distance from the center of the grid box. We also used the UK Met Office Hadley Centre SST product (HadISST1.1; ref. 44) for SST and HadCRUT4 (45) and GISS Surface Temperature Analysis (46), version 4, for surface temperatures.

IPO and AMV.

We calculated the IPO index for both observations and models (Fig. 1C) following previous studies (16, 17, 47). The IPO index is the standardized second principal component of the EOF for the 13-y low-pass-filtered global SST. The AMV index was calculated following Trenberth and Shea (48). and Deser et al. (49). The AMV index is defined as the area-average SST anomaly over the North Atlantic (0–70°N, 90°W–0) minus the global mean SST anomaly. The AMV index was standardized after calculating the anomalies.

SVD Analysis.

SVD analysis is the multivariate statistical method that is widely used in climate sciences (e.g., refs. 50 and 51). It is also known as principal-component analysis. In the atmosphere and ocean sciences, data often exhibit large spatial correlations. SVD analysis produces representation of these correlations and provides insight into spatial and temporal variations that synchronize among multiple fields of data analyzed.

To detect dominant modes of variability in TCF coupled to SST as the lower boundary forcing, we performed the SVD analysis in which a covariance matrix is constructed using annual mean TCF and SST fields. We utilized the SVD code written in Python that is online available at the PyClimate website (http://www.ehu.eus/eolo/pyclimate/about_en.html).

We first prepared input data for SVD: X and Y for TCF and SST, respectively, which are annual values consisting longitude, latitude, and time. Annual mean SST fields are interpolated onto the same grids of annual TCF values (i.e., 5° × 5° grid box within the global domain). A covariance matrix $C_{xy}=X^{T}Y/N$ is constructed, where T denotes transpose operator and N represents total number of years. Passing the covariance matrix to the SVD function in PyClimate returns a tuple of three arrays U, Σ, and V. Each column u_i of U holds the i-th singular vector of the left (X) field. Same conversion is followed by the ordering of elements in V to obtain singular vector v_i for Y field. Σ is a one-dimensional array which holds the singular values σ_i. The singular vectors are orthonormal $\left(u_i\cdot u_j=v_i\cdot v_j={\sigma }_{i,j}\right)$ and can be used to linearly project each of the fields to define the expansion coefficients $p_i\left(t\right)=x\left(t\right)\cdot u_i$ and $q_i\left(t\right)=y\left(t\right)\cdot v_i$ whose covariance is the same as the singular value associated to that mode $p_i,q_i={\sigma }_i$. Note that the datasets, X and Y, are centered (i.e., sample mean is removed for each grid box) inside the function prior to the SVD computation in PyClimate; however, they are not detrended.

Models.

We used the GFDL FLOR (26) and SPEAR (29). FLOR comprises 50-km mesh atmosphere and land components, and 100-km mesh sea-ice and ocean components. The atmosphere and land components of FLOR are taken from the Coupled Model, version 2.5 (CM2.5; ref. 52), developed at GFDL, whereas the ocean and sea-ice components are based on the GFDL Coupled Model version 2.1 (CM2.1; refs. 53–55). SPEAR is a newly developed coupled model consisting of the new AM4-LM4 atmosphere and land-surface model (56, 57), and the MOM6 ocean (58), and the SIS2 sea-ice model. The horizontal resolution of SPEAR is almost of identical to that of FLOR. A detailed description and performance and evaluation of FLOR and SPEAR are available in Vecchi et al. (26) and Delworth et al. (29), respectively.

A suite of simulations using FLOR were also conducted with the “flux adjustments” approach (26) (referred to as FLOR-FA), which adjusts the model’s momentum, enthalpy, and freshwater fluxes from the atmosphere to ocean and so brings the long-term climatology of the SST and surface wind stress closer to the observations.

Model-generated TCs were detected directly from six-hourly output, using the following tracking scheme developed by Harris et al. (59), as implemented in Murakami et al. (60). In the detection scheme, the flood fill algorithm is applied to find closed contours of a specified negative sea-level pressure anomaly with a warm core. The storm detection must maintain a warm core and a wind criterion of 16.5 m⋅s⁻¹ for at least 36 consecutive hours.

piControl Experiments.

We generated long-term preindustrial climate simulations using FLOR-FA (3,500 y) and SPEAR (3,000 y), respectively, by prescribing fixed radiative forcing and land-use conditions representative of the preindustrial conditions (piControl). A summary of the configuration is provided in SI Appendix, Table S1. The fixed forcing agents for the control simulations were atmospheric CO₂, CH₄, N₂O, halons, tropospheric and stratospheric O₃, anthropogenic tropospheric sulfates, black and organic carbon, and solar irradiance. We analyzed the last 1,000 y in the simulations; however, the overall conclusions were the same even when using all of the years.

Large-Ensemble Experiments.

We conducted two types of multidecadal simulations using the dynamical models. A summary of the configuration is provided in SI Appendix, Table S1. For the AllForc experiments, the historical anthropogenic forcing was prescribed for the period 1941 to 2004 (but 1921 to 2014 for SPEAR), and the anticipated future anthropogenic forcing was prescribed for the period 2006 to 2050 based on RCP8.5 (31) for FLOR, 2006 to 2050 based on RCP4.5 (31) for FLOR-FA, and 2015 to 2100 based on the Shared Socioeconomic Pathway 5–85 (SSP5-85; refs. 61 and 62) for SPEAR. In the simulations, no volcanic forcing was prescribed after 2006. Although the prescribed level of anthropogenic forcing among the models was different after 2005, the effect of the difference was small for the period 1980 to 2018, which is the main focus of this study (e.g., Fig. 1A). These multidecadal simulations were initiated from the restart files derived from the piControl experiments every 20 y from the year 101 for each ensemble member (e.g., year 101 for ensemble 1, year 121 for ensemble 2); thus, the simulated internal variability, such as IPO and AMV, was out of phase among the ensemble members (e.g., Fig. 1C).

The other simulation type comprised the NatForc experiments, for which the experimental settings were identical to AllForc apart from the greenhouse gases and aerosols were fixed at their levels in 1941 for FLOR and FLOR-FA and 1921 for SPEAR. The difference between AllForc and NatForc was time-varying greenhouse gases and anthropogenic aerosols.

Transient 2×CO₂ Experiment.

To estimate the responses of TCF to increasing CO₂, we conducted Transient 2×CO₂ experiments (36) using FLOR, FLOR-FA, and SPEAR. Using each model, we preliminarily conducted a long-term fully coupled 1990 control simulation in which anthropogenic forcing was fixed at the 1990 level (i.e., 353 ppm for CO₂). Using a restart file at the year 101 in the 1990 control experiment, we ran the same fully coupled simulation except with a CO₂ increase of +1% per year. After 70 y (i.e., year 170), the CO₂ level had doubled (i.e., 707 ppm) relative to the 1990 level. We conducted the SVD analysis (refs. 23 and 25 and SVD Analysis) using the simulated SST and TCF during the period of CO₂ increase (i.e., years 101 to 170). Note that we only conducted the simulation with a single member for each of FLOR, FLOR-FA, and SPEAR.

Optimal Fingerprint Analysis.

We applied an optimal fingerprint analysis method (37–39) to determine if expected spatial patterns of trends in TCF induced by external forcing derived from the models could be identified in the observations. A detailed description is also available in Santer et al. (39). First, we assumed that the first SVD mode for the TCF pattern (e.g., Fig. 2 H, K, and N), computed from the ensemble mean of the simulated SST and TCF, is the expected climate change signal pattern (i.e., guess or nonoptimized pattern). Letting f(x,y) represents the guess pattern, where x is longitude and y is latitude defined over the 5° × 5° grid cells, the detection variable for observations (d_o) is obtained by projecting the observed annual TCF on f as follows:

$$d_o\left(t\right)=f\left(x,y\right)\cdot TC{F}_o\left(x,y,t\right),$$ [1]

where t denotes time (i.e., year) and TCF_o represents the observed TCF. The same projection was also applied to the piControl experiment as

$$d_m\left(t\right)=f\left(x,y\right)\cdot TC{F}_m\left(x,y,t\right),$$ [2]

where TCF_m represents the TCF simulated by a piControl experiment. Then, we fitted the least-squares linear trend for the L-length data to obtain the linear trend for observations (a_o):

$$d_o\left(t\right)\approx a_o\left(L\right)\times t+b_o\left(L\right)t=1,\mathrm{...},L$$ [3]

and piControl experiments (a_m):

$$d_m\left(t+t_0\right)\approx a_m\left(t_0,L\right)\times t+b_m\left(t_0,L\right)t=1,\mathrm{...},L,t_0=0,\dots ,t_{max}-L,$$ [4]

where t_max is the total number of years used in piControl (i.e., t_max = 1,000) and t₀ denotes the staring year of a period with L-years long. Then, we applied a Gaussian fit for the derived t_max – L samples of a_m(t_0, L) and compared it with the a_o(L). If a_o(L) fell above the 97.5% range (critical P value for statistical significance is 0.025 for the 95% statistical level in a one-tailed test) of the fitted Gaussian distribution derived from piControl, we considered that the observed trend as having been detected. The detection time was referenced to 1980, the start year of the observed data. We used a minimum trend length of 10 y (i.e., L = 10) so that the earliest possible detection year was 1990. It was necessary to use independent models for estimating f and TCF_m. If f was derived from FLOR (or FLOR-FA), for example, TCF_m was derived from SPEAR, and vice versa.

Optimized detection times were computed in a similar way but by applying projections of TCF_o and TCF_m on f*, which is the optimal fingerprint, that had been rotated away from high-noise directions. This rotation was performed using the first m EOF models of TCF_m. Following Santer et al. (39), weighting coefficients were derived as follows:

$${\alpha }_j=f\left(x,y\right)\cdot e_j\left(x,y\right),j=1,\dots ,m,$$ [5]

where e_j denotes the j-th EOF eigenvector derived from piControl (i.e., TCF_m). The optimal fingerprint f* was obtained by the EOF eigenvectors by weighting α_j and the inverse of the noise eigenvalue l_j as follows:

$$f^{\ast }\left(x,y\right)=\sum _{j=1}^m{\alpha }_j{e}_j\left(x,y\right)l_j^{-1}.$$ [6]

If f resembled higher EOF modes (i.e., higher noise), this optimization kept f* away from the higher EOF modes. We explored the sensitivity of the optimized detection times to a truncation of the EOF models (i.e., m). We chose 5, 10, and 15 EOF modes as the truncation to construct f* and applied Eqs. 1 and 2 instead of using f. To avoid the introduction of artificial skill, when a model was used for optimization (i.e., Eqs. 5 and 6), a piControl run by another model was used for estimating the internal variability statistics as used for Eq. 2. For example, when a fingerprint f* was computed using the EOF models derived from the piControl of SPEAR, we utilized the piControl of FLOR-FA for computing d_m in Eq. 2.

Data and Materials Availability.

The source code of the climate model can be accessed from the Geophysical Fluid Dynamics Laboratory (https://www.gfdl.noaa.gov/cm2-5-and-flor/) (27). The data that support the findings of this study are available in ref. 28.