Significance
Networks of actin filaments form the structural scaffold of cells. Energy-consuming protein motors such as the myosins that exert forces on the network by “walking” on actin filaments as well as polymerization of actin polymers are necessary for the movement, growth, and division of cells. The dynamics of actomyosin networks is regulated by actin-binding proteins. One of the most important of these binding proteins is the actin-related protein 2/3 (Arp2/3) complex that nucleates branched filaments, thereby altering network topology. In this work, we simulated the dynamics of actomyosin networks both with and without Arp2/3 complexes. The branched networks with Arp2/3 exhibit rare convulsive movements, which we call “avalanches,” that are reminiscent of recent experimental reports of “cytoquakes.”
Keywords: actin reorganization, marginal stability, avalanche
Abstract
Actomyosin networks give cells the ability to move and divide. These networks contract and expand while being driven by active energy-consuming processes such as motor protein walking and actin polymerization. Actin dynamics is also regulated by actin-binding proteins, such as the actin-related protein 2/3 (Arp2/3) complex. This complex generates branched filaments, thereby changing the overall organization of the network. In this work, the spatiotemporal patterns of dynamical actin assembly accompanying the branching-induced reorganization caused by Arp2/3 were studied using a computational model (mechanochemical dynamics of active networks [MEDYAN]); this model simulates actomyosin network dynamics as a result of chemical reactions whose rates are modulated by rapid mechanical equilibration. We show that branched actomyosin networks relax significantly more slowly than do unbranched networks. Also, branched networks undergo rare convulsive movements, “avalanches,” that release strain in the network. These avalanches are associated with the more heterogeneous distribution of mechanically linked filaments displayed by branched networks. These far-from-equilibrium events arising from the marginal stability of growing actomyosin networks provide a possible mechanism of the “cytoquakes” recently seen in experiments.
Actomyosin networks are systems of actin filaments that are organized both by their interaction with myosins—a group of active motor proteins—and by their interaction with passive cross-linkers. The nonequilibrium activity of actomyosin networks gives cells the ability to grow, move, and divide (1, 2). The contraction of actomyosin networks has been recapitulated in vitro using reconstituted solutions of actin filaments containing several types of actin-binding proteins that merely act as cross-linkers along with active myosins (3–6). Contractility of the network appears to require a threshold concentration of myosin and the presence of ATP but is only seen at an intermediate concentration of bivalent cross-linkers. Early studies of reconstituted solutions of actin filaments in vitro generally lacked many of the key constituents of the cytoskeleton, notably the actin-related protein 2/3 (Arp2/3) complex. The Arp2/3 complex specifically alters the topology of actin filament networks by forming branches. One of many examples of actomyosin networks with the Arp2/3 complex is the dendritic spine. Dendritic spines are small membranous actin-filled protrusions attached to neuronal dendrites whose morphological plasticity is commonly hypothesized to underlie learning and retrieving memory (2, 7, 8). While the structure of the Arp2/3 complex has been explored extensively (9–18), how the Arp2/3 complex changes the architectural dynamics of the actomyosin network raises many questions. Indeed, recent experimental studies have shown that the Arp2/3 complex qualitatively changes the dynamics of the network (4, 5, 19).
Here, we employ a powerful computational software for flexibly modeling the complexity of cytoskeletons, mechanochemical dynamics of active networks (MEDYAN), that was developed by Papoian and his group (20–24). The MEDYAN computational framework incorporates a stochastic description of individual chemical reaction events appropriate to the nanoscale and simultaneously employs a deterministic treatment of the mechanics of the cellular assembly at micrometer scales through cycles of mechanochemical feedback. Using a predecessor of the MEDYAN model, Papoian and his group (25–28) have modeled unmotorized branched actin networks and have studied the effects of branchers and capping proteins on the speed of protrusion of a flexible membrane. The mechanochemical aspects of MEDYAN make it possible to investigate how the nucleation and branching initiated by the Arp2/3 complex change the dynamics and structures of actomyosin systems. Here, we report on a computational investigation of how branchers influence network contractility.
Several other computational frameworks have been developed for modeling the dynamics of actomyosin networks (29–33). One code, Cytosim, models the actomyosin network at the mesoscopic scale (29) but lacks the mechanochemical feedback that is critical to describe active processes. Another code, AFiNeS (30), has been used to study a two-dimensional model of an actomyosin network and describes network rheology under mechanical stress. AFiNeS lacks, however, the volume exclusion for actin filaments, which we believe is important for correctly determining the mechanics of jammed states. MEDYAN captures all these features, which we believe are crucial to understanding the actual biological system.
Contractile motions of actomyosin networks can be caused by the forces generated by motors (across actin filaments) but may also be driven by compression and expansion (along actin filaments) due to polymerization. These forces deform the network and build up strains through the expenditure of free energy (34, 35). These strains then feed back into various biochemical processes. Our focus is on exploring the contrast between the dynamics of branched and unbranched networks, via conducting simulations both with and without Arp2/3. We show that the branched networks (with Arp2/3) can become marginally unstable. Fluctuations continually cause local collapse events, which are directly connected to this marginal stability. In systems that are far from equilibrium and active, marginal stability does not occur at a specific concentration but depends on both the initial configuration of the network and the history of the system. The marginal stability of branched actomyosin assemblies resembles what is found in jammed granular assembles and colloidal glasses (36–38).
Results
Linkers Modulate Contraction in Unbranched Actomyosin Networks.
Our basic approach is the simulation of actin molecular assemblies in solution with various mixtures of actin-binding proteins, all in a fixed geometry. To study unbranched networks, we considered nine different concentration ratios of nonmuscle myosin IIA heavy chain (NMIIA) motor proteins to actin monomers and eight concentration ratios of α-actinin linker molecules to actins in our simulations. In total, then, we studied 72 distinct actomyosin network assembly scenarios. All simulations were confined to a 1 μm × 1 μm × 1 μm box with 25 µM of actin in total. The concentration of actin, 25 µM, was specifically chosen to replicate the in vitro experiments from the Weitz group (3). The monomers, the filaments, the motors, the linkers, and the branchers were initially distributed randomly within a cubic container. Other various physical parameters characterizing simulated systems are described in detail in SI Appendix, Table S3. In our discussion, we will highlight four representative conditions of and from these scenarios to elucidate the role of linkers in unbranched networks: 1) low motor and low linker concentrations ( and ), 2) high motor and low linker concentrations ( and ), 3) high motor and high linker concentration ( and ), and 4) medium motor and medium linker concentrations ( and ). Note that for every combination of motor and linker to actin ratios, 16 simulation replicates were performed, differing only in their random initializations. The average length of a filament in unbranched networks is ∼0.85 μm. Throughout the simulations, we recorded the structure of the networks once every 10 s. In addition to plotting the time courses of these parameters, in some cases we have also plotted the changes of the parameters that take place between successive pairs of snapshots to highlight when large sudden changes in the parameters occur.
In order to follow the assembly process, we show in Fig. 1 how the radius of gyration of the whole system normalized by the “initial” value , , changes with time. is actually the radius of gyration measured after an initialization run without motors of 10 s, so as to allow the filament length distribution to reach a steady state before the motors are turned on. When an actomyosin network contracts due to the motor action, the radius ratio will become less than 1, while, in contrast, when becomes greater than 1 it indicates that the system has expanded during assembly. Unbranched actomyosin systems with low motor concentration and low linker concentration expand rather slowly (Fig. 1A) in comparison with what occurs for the other three conditions. The expansions are caused by actin polymerization without any significant countervailing forces being exerted by motors that would pull the actin filaments together.
Fig. 1.
The time courses of the ratio indicate contractile or extensile motion in unbranched actomyosin networks at several conditions of motors and linkers. (A) Systems with low motor and low linker concentrations ( and ). (B) Systems with high motor and low linker concentrations ( and ). (C) Systems with high motor and high linker concentrations ( and ). (D) Systems with medium motor and medium linker concentrations ( and ). The pink-dotted lines show the single exponential fits to the sets of the time courses of for each simulation condition. The traces for simulation replicates are indicated with light gray lines, and their averages are shown in black lines. τ is the single exponential fitting time constant (see SI Appendix for more details).
Adding linkers leads to a competition between actin polymerization and motor pulling. This competition accounts for the differing extent of contraction. We calculated , which is the average of the normalized radius of gyration ratio taken over all replicates for a given condition, varying motor and linker concentrations for both unbranched and branched networks. The radius ratios achieved at steady state for the high motor concentration and high linker concentration systems ( and ; Fig. 1C) are ∼16% lower than the steady-state ratios for high motor concentration and low linker concentration systems ( and ; Fig. 1B). Contractility is only manifested for unbranched systems when the motor concentration exceeds a threshold of (Fig. 1 B–D).
Assembly dynamics depends on the fraction of the linkers that are unmotorized. For the unbranched systems with and (high motor and low linker concentrations), whose time courses of the radius ratio are depicted in Fig. 1B, the pulling forces from motors lead to the rapid reduction in the radius ratio during the first 130 s. When we increased the concentration of linkers to and , the actin network contracts much more slowly as shown in Fig. 1C. These results semiquantitively agree with the experimental data from the Weitz laboratory (3), which studied these unbranched systems.
Branched Actomyosin Networks Display Convulsive Movements.
Next, we included Arp2/3 protein complexes to simulate branched networks. The radius of gyration ratios for the branched networks (Fig. 2) behave differently during assembly from what was seen for the unbranched networks (Fig. 1). The branched networks with low concentrations of motors and low concentrations of linkers ( and ; Fig. 2A) contract rather than expand as did the unbranched assemblies (Fig. 1A). The overall contraction of the branched assemblies results from the creation of branches that inhibit actin polymerization and depolymerization. Adding a brancher prevents the actin depolymerization reaction at the minus end of a daughter filament because the brancher positions itself at the branch junction once a daughter filament has been created from its mother filament. When there is depolymerization at the minus end of a filament that is faster than the dissociation of a brancher from the filament, the brancher will inhibit the depolymerization reactions at the minus end of a mother filament. Actin polymerization and depolymerization, which require actin turnover, are thus significantly inhibited by the presence of branchers. The concentration of filamentous actin (F-actin) in the branched simulations is larger than the concentration of F-actin in the unbranched simulations. The increased F-actin concentration is due to the capping of the minus end of the mother and the daughter filaments, as well as the new F-actin plus ends created by Arp2/3 nucleation. Nevertheless, due to the increased number of total filaments, the average length of a filament is in fact reduced when Arp2/3 is added. The average length of a filament in branched networks is ∼0.16 μm. Unbranched networks turn out to consist of long and parallel filaments displaying liquid crystalline order, while branched networks are composed of short and bifurcated filaments and appear more nearly isotropic.
Fig. 2.
The time courses of radius gyration ratios for contractile and extensile motions in branched actomyosin networks at several conditions of motors and linkers. (A–D) The indications for concentrations of motors and linkers are the same as those used in Fig. 1. τ is the single exponential fitting time constant (see SI Appendix for more details).
The contraction of branched networks occurs in a more irregular fashion than does the contraction of unbranched assemblies. The contraction of the assemblies is rather intermittent, occurring by unpredictable abrupt drops of the radius of gyration ratio . These convulsive events are inherently stochastic and hence do not occur at the same time in different simulation replicate runs. These abrupt drops of occur very quickly. Individually, these events have a duration of less than 10 s. The sharpest drops can be as large as 20%. These drops, which we call avalanches, are observed more frequently at higher concentrations of motors (Fig. 2 B and C) than at lower concentrations (Fig. 2A). For the range of parameters studied in our simulations, we have never observed such discrete and large-scale avalanches in the unbranched actomyosin networks created whenever Arp2/3 was absent.
To get a better picture of the mechanism underlying the avalanches, we examined changes in the ratio of the radius of gyration after an event and we have also visualized snapshots of the system to uncover the corresponding structural changes. Snapshots for medium motor concentration and medium linker concentration ( and ) are shown in Fig. 3. corresponds to the successive temporal changes of the radius of gyration ratios . An abrupt drop in the radius of gyration ratio occurs after 440 s (Fig. 3A). At this point, we note that the network contains several regions of high tension. These regions are shown in a white color inside a blue square in Fig. 3B. The tension is rather heterogeneously distributed immediately prior to the avalanche. The high-tension regions are created by the stalling of motors. Once the motors have successfully reorganized the actin filaments, the regions of high tension disappear as shown in Fig. 3C. No motor or linker unbinding was seen immediately prior to an avalanche. Instead a motor, which was previously walking on a short filament and on a filament bound by Arp2/3 branchers, became jammed before an avalanche was triggered.
Fig. 3.
Changes in the tension of a branched network occur during an avalanche. (A) The time courses of the successive values of temporal changes over a 10-s time interval in the ratio of the radius of gyration normalized by the value at 10 s. The quantity is shown for a branched network simulation with medium motor and medium linker concentrations ( and ) over time. (B and C) Two snapshots of actin filaments, motors, and linkers where the tension is indicated by color; these show the morphology of the network before (B) and after (C) the abrupt drop of when an avalanche occurs. The dimensions of the cubic simulation box are 1 μm × 1 μm × 1 μm. A blue square highlights a concentrated high-tension region that can be seen prior to the drop, which then becomes a dispersed low-tension area after the drop.
Mechanistic Insights into the Convulsive Movements during an Avalanche.
The mean of the displacements of the center of mass of each actin filament at time is defined by the following:
| [1] |
where is the center of mass of filament and is the number of filaments in a system. The between each successive pair of snapshots (black curves) turns out to be a useful parameter to identify and characterize avalanches, as shown in Fig. 4.
Fig. 4.
Examples of avalanches in a branched network containing 16 motors and 3,000 linkers. In A, the time course of the changes in the ratio of the radius of gyration normalized by the value at the initial 10-s point between successive pairs of snapshots that are separated by 10 s, , is plotted in red. In B, the time course of the changes in the shape parameter between successive pairs of snapshots that are separated by 10 s, , is plotted in blue. In both A and B, the time course of the mean filament displacement is plotted in black.
In addition, we studied the changes in the shapes of the actin assemblies using the shape parameter . This is defined for an actomyosin network by Eq. 2 (39):
| [2] |
is the geometrical inertia tensor of an assembly as described in Eq. 3, while the are the eigenvalues of the inertia tensor , and is the average eigenvalue of the inertia tensor :
| [3] |
Here, is the number of beads in the network. Each bead represents an end of a cylindrical actin segment. is the projection of bead on the axis, where can be .
There appear to be two types of avalanches that display differences in their shape and in the size of the reconfigured regions. In one group, corresponding to shear events, the temporal changes are manifested by large changes of the shape parameter between successive pairs of snapshots, changes that occur through filament sliding (e.g., labeled as avalanche 1 in Fig. 4). A second group of avalanches involve collapses of local regions and are characterized by significant changes in the normalized radius of gyration ratio between successive pairs of snapshots (e.g., labeled as avalanche 2 in Fig. 4). We believe that the type of avalanches described here are examples of two extremes of a broad distribution of avalanches.
The underlying mechanism for these abrupt behaviors seems to reflect the rather wide distribution of sizes of F-actin connectivity clusters in the network. We calculated the distributions of connectivity cluster sizes and used those distributions to compute the weighted averages of the cluster size found in both the unbranched and the branched networks. This was done for all 72 concentration scenarios while also analyzing whether avalanches occur or not. The weighted mean cluster size was calculated in units of actin monomers. represents the average cluster size of randomly selected monomers and is defined as the ratio between the first moment and the second moment of the cluster size distribution as shown in Eq. 4:
| [4] |
Here, is the number of actin monomers in a cluster and is the probability of finding a cluster of size in the system.
The weighted mean cluster size of F-actins, , provides a parameter describing heterogeneity of the cluster sizes of a network. Assemblies with a small value of contain multiple small and isolated clusters that are not connected to the rest of the system through motors, linkers, or branchers. A network with a large value of contains at least one large cluster of actins, all of which are mechanically linked.
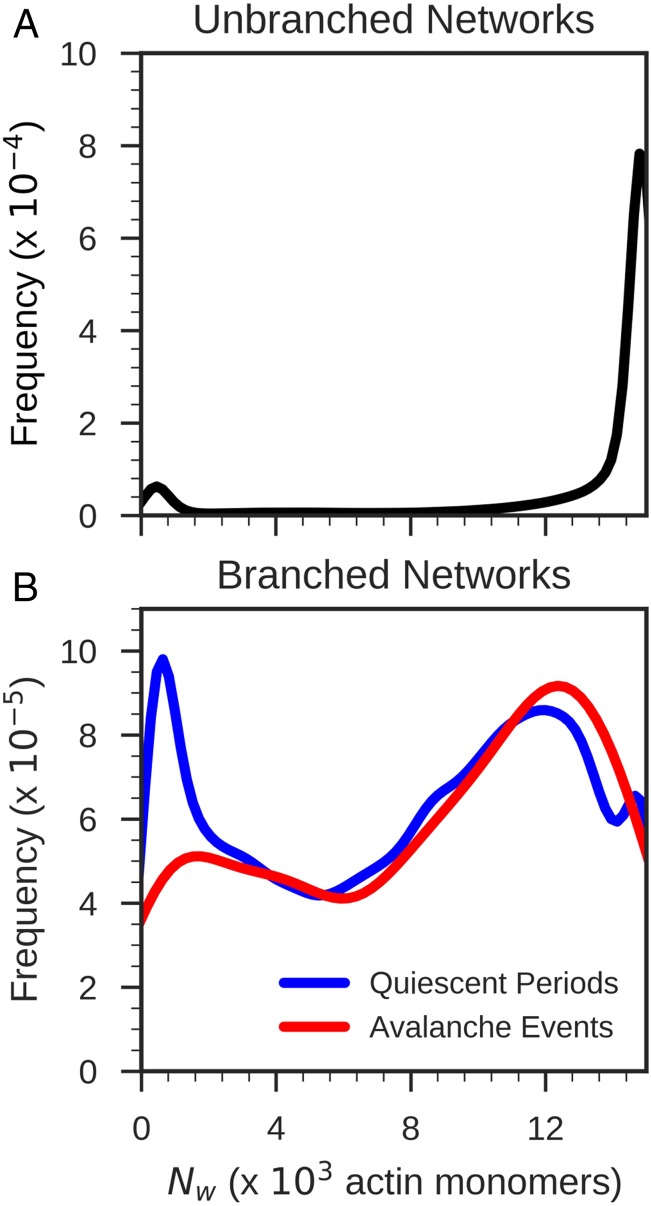
In Fig. 5, we plot histograms of the weighted mean cluster size for the unbranched and branched networks. Fig. 5A shows that for the unbranched networks, there are two predominant actin cluster sizes: one peak for small clusters having at most 2,000 actin monomers and another peak for large clusters with more than 12,000 actin monomers. The smaller connectivity clusters are typically isolated, while there is usually only a single cluster of more than 12,000 actin monomers. The unbranched networks with many small and isolated F-actin connectivity clusters generally are only weakly connected through motors or linkers, while the networks with large F-actin connectivity clusters have become fully connected, thereby allowing force to be transmitted globally throughout the networks.
Fig. 5.
Probability densities of the weighted mean cluster size of the unbranched networks (A) and branched networks (B). The branched networks were further analyzed in the event of no avalanche (blue curve) or avalanches (red curve). A total of 1,152 simulations was carried out and analyzed both for the unbranched networks and for the branched networks.
In Fig. 5B, we see that branched networks have a rather wide distribution of with a broad continuous range of intermediate size actin clusters. To characterize an event as an avalanche during an individual trajectory, we calculated the Z score of the mean filament displacement between each successive pair of snapshots separated by 10 s. We classified an event as being an avalanche when the mean filament displacement between each successive pair of snapshots is sufficiently large: that is, we require the Z score relative to the displacements for other intervals to exceed 5 in order for the interval to be classified as having an avalanche event. As shown in Fig. 5B, there is a significant difference in cluster size distributions for snapshots when an avalanche occurs and when there has been no avalanche. This comparison of the distributions of the actin cluster sizes suggests that forces build up in the branched systems with large connectivity clusters eventually resulting in an avalanche. Avalanches rarely occur in networks containing only small and isolated actin clusters.
Discussion
Contractility of Actomyosin Networks Depends on Their Topologies.
Consistent with earlier studies, we find that the contraction of unbranched actomyosin networks depends on the concentrations of motor protein and linkers (3–6). The “phase diagram” of macroscopic contractility is reentrant: Systems having an intermediate value of linker concentration contract more robustly than do systems with either a high or a low concentration of linkers. The diagram for the unbranched actomyosin networks with certain motor concentrations is shown in SI Appendix, Fig. S3. Reentrance of the transition with changing linker concentration was one of the key findings of several experimental studies (3, 4). These studies show that the macroscopic contractility in actin reconstituted systems requires a threshold concentration of motors but is strongest with an intermediate concentration of linkers. In our simulations, reentrance arises because when the concentration of linkers is low the network is not mechanically connected while at high linker concentrations the network of an unbranched actomyosin system becomes too rigid for the motors to displace fibers significantly.
Structural differences between branched actomyosin networks and the unbranched systems lead to their having a different phase diagram. The branched networks with low concentrations of motor globally contract more than do unbranched networks with the same low motor concentrations. These contractions apparently are caused by the Arp2/3 branchers inhibiting the polymerization and depolymerization of the actin fibers, which would otherwise favor the expansion of the network. In our model, an Arp2/3 brancher initially deposits at the branched junction and, once there, nucleates a daughter filament. Given that the depolymerization rate at the minus end of an actin filament is faster than the dissociation rate for branchers, the Arp2/3 branchers effectively inhibit actin filament polymerization and depolymerization.
The relaxation times of the branched actomyosin networks are longer than those of the unbranched systems, by as much as a factor of 4. The slowing due to the addition of branchers can be explained by two effects: 1) motors are not able to walk past branchers, and 2) on average, the actin filaments of the branched networks are considerably shorter than the filaments of the unbranched networks. The persistence of motor walking in the unbranched networks, which contain longer filaments, drives fast relaxation. In the branched networks, on the other hand, the motors constantly unbind and rebind to short actin filaments that are studded with branches, thereby slowing the relaxation.
The Nonequilibrium Dynamics of the Branched Actomyosin Networks Displays the Behavior of Jammed Assemblies.
The trajectories for the branched actomyosin networks show a large number of sudden variations of individual filament displacements. These events are not seen in the trajectories for the unbranched systems at the same concentrations of motors and linkers. Branched networks also have a larger variation in actin cluster size compared with what is seen for their unbranched counterparts. In branched networks, sudden releases of strain energy occur that lead to local contraction and filament sliding. We call these rare events avalanches. Avalanches in general are triggered by motor driven movements, which then in turn cause bound motors to disengage, bound linkers to rupture, and bent filaments to recoil.
It has been suggested that such avalanches occur during the remodeling of the cytoskeleton in vivo (40, 41). In these experiments, beads attached to the actomyosin cortex in cells undergo large, step-like displacements over several micrometers. Taken together with the present simulations, these findings suggest that branched actomyosin networks form marginally stable states reminiscent of jammed granular systems or colloidal glasses (36–38). The mechanical properties of jammed systems depend on their past history, a signature that the system remains far from equilibrium (36). Our findings suggest that the branched networks are more likely to become marginally stable and jammed than the unbranched networks. This feature seems to arise because branched networks have a wider distribution of F-actin cluster sizes than their unbranched counterparts have. In the branched assemblies, motors can change the conformation of the networks in a convulsive avalanche-like manner once there has been a sufficient buildup of high tension locally in the network (42).
Actin-binding proteins such as the Arp2/3 complex alter the nonequilibrium and history-dependent properties of actomyosin by changing the morphology of the networks. A full theoretical treatment of cytoskeletal dynamics must deal both with their assembly and their glassy preparation dependence.
Methods
Coarse-Grained Mechanochemical Model of Actomyosin Systems (MEDYAN).
We have used a computational implementation of a coarse-grained mechanochemical model of actomyosin systems (MEDYAN) developed by Papoian and his group (20). MEDYAN models the stochastic nature of reactions and the diffusion of chemical entities (which we will refer to as “the chemical model”) and provides simultaneously a coarse-grained physical representation of filaments, branchers, motors, and linkers (which we will refer to as “the mechanical model”). The coarse-grained actomyosin system is initialized with F-actin filaments that are made up of segments consisting of 10 G-actin monomers each, nonmuscle myosin IIA heavy chain (NMIIA) motor proteins (i.e., motors), α-actinin cross-linking proteins (i.e., linkers), and actin-related protein 2/3 (Arp2/3) branching protein complexes (i.e., branchers). The simulations of branched assemblies of filaments include the Arp2/3 protein complexes, while the unbranched simulations of filaments do not. Fig. 6 shows a typical snapshot of a simulation of unbranched filaments (Fig. 6A) and branched filaments (Fig. 6B). The monomers (G-actin), the filaments (F-actin), the motors (NMIIA), the linkers (α-actinin), and the branchers (Arp2/3) were initially distributed randomly within a cubic container. SI Appendix, Fig. S1 summarizes the four steps of a mechanochemical cycle in MEDYAN.
Fig. 6.
Typical snapshots of MEDYAN simulations without Arp2/3 protein complexes (A) or with Arp2/3 protein complexes (B). A red cylinder represents an F-actin filament. A black bead represents a positive (or a barbed) end of an F-actin filament. A white bead represents a negative (or a pointed end) of an F-actin filament. A green cylinder represents an α-actinin linker protein. A blue cylinder represents an ensemble of NMIIA motor proteins. A yellow bead represents Arp2/3 protein complexes. The angle between the mother and its daughter filaments through a brancher is 70° as reported experimentally (12, 15). Portions of the images shown on the Top are enlarged and shown on the Bottom.
We have included the polymerization reactions of F-actin at both the plus and the minus ends of the fibers, the depolymerization reactions of F-actin from both the plus and the minus ends, the binding and the unbinding reactions of α-actinin linkers, the binding and the unbinding reactions of NMIIA motors, the walking reactions of NMIIA, the branching reaction of F-actin, and the destruction reaction of short F-actin no longer than one segment in our model. We did not include the unbinding reactions of branchers because of the known high stability of Arp2/3-actin protein complexes (12, 15). We also did not include linker cross-linking between the first binding sites of mother and its daughter filaments due to geometric constraints. The motors, the linkers, and the branchers occupied same binding sites on the filaments.
All simulations were confined to a 1 μm × 1 μm × 1 μm box with 25 µM of actin in total. The concentration of actin, 25 µM, was specifically chosen to replicate the in vitro experiments from the Weitz group (3). We considered nine different concentration ratios of motor proteins to actin monomers and eight concentration ratios of linker molecules to actins in our simulations. We set to be 0.0, 0.005, 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, and 1.0, whereas was set to be 0.0, 0.01, 0.02, 0.05, 0.1, 0.2, 0.5, and 1.0. All branched simulations contained 0.5 µM of Arp2/3 branchers in total to create sufficient branching structures in the simulation. Moreover, we used the filament branching rate of 0.0001 s−1 and the short filament destruction rate of 1.0 s−1. Furthermore, we have also included actin filament bending, stretching, branching, and exclusion volume potentials, motor and linker stretching harmonic potentials, and filament-boundary interaction potential (see SI Appendix for more details). The reaction rates and the parameters of our model are listed in SI Appendix, Tables S1, S2, and S3.
Cluster Size Distribution.
To analyze how each monomer in a filament connects to another, we defined a cluster as a group of monomers in an F-actin that are connected through the plus ends (p), the minus ends (m), or through binding sites (c) as shown in Fig. 7. A motor (M) or a linker (L) can connect two actin monomers through their binding sites (c). A brancher (B) connects two F-actin monomers through the binding site (c) of one to the minus end (m) of the other one.
Fig. 7.

Schematic diagram of a cluster. A cluster is a group of F-actin monomers (F) that are connected through their binding sites (c), the plus ends (p), or the minus ends (m). The motor (M) and the linkers (L) connect the F-actin monomers through the binding sites. The brancher (B) connects two F-actin monomers by binding on the minus end (m) of one and on the binding site (c) of the other one.
Data Availability.
The dataset is hosted by Zenodo (DOI: 10.5281/zenodo.3714167). MEDYAN is available to download at http://medyan.org/.
Supplementary Material
Acknowledgments
We thank Garyk Papoian and his group for sharing the MEDYAN code with us. The assistance of James Komianos and Aravind Chandrasekaran in implementing Arp2/3 branchers into the code is greatly appreciated. This work was supported by National Science Foundation Grants CHE 1743392, PHY 1522550, and Center for Theoretical Biological Physics Grant PHY 1427654. We acknowledge the use of the uHPC OAC 1531814 and Sabine clusters managed by the core facility for Advanced Computing and Data Science at the University of Houston. Additional support was also provided by the D. R. Bullard-Welch Chair at Rice University, Grant C-0016, and an endowment from the William Wheless III Professorship at the University of Texas Health Science Center at Houston.
Footnotes
The authors declare no competing interest.
Data deposition: The simulation trajectories reported in this paper have been deposited in Zenodo (DOI: 10.5281/zenodo.3714167).
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1922494117/-/DCSupplemental.
References
- 1.Murrell M., Oakes P. W., Lenz M., Gardel M. L., Forcing cells into shape: The mechanics of actomyosin contractility. Nat. Rev. Mol. Cell Biol. 16, 486–498 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cingolani L. A., Goda Y., Actin in action: The interplay between the actin cytoskeleton and synaptic efficacy. Nat. Rev. Neurosci. 9, 344–356 (2008). [DOI] [PubMed] [Google Scholar]
- 3.Bendix P. M. et al., A quantitative analysis of contractility in active cytoskeletal protein networks. Biophys. J. 94, 3126–3136 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ennomani H. et al., Architecture and connectivity govern actin network contractility. Curr. Biol. 26, 616–626 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Tan T. H. et al., Self-organized stress patterns drive state transitions in actin cortices. Sci. Adv. 4, r2847 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Janson L. W., Kolega J., Taylor D. L., Modulation of contraction by gelation/solation in a reconstituted motile model. J. Cell Biol. 114, 1005–1015 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Honkura N., Matsuzaki M., Noguchi J., Ellis-Davies G. C. R., Kasai H., The subspine organization of actin fibers regulates the structure and plasticity of dendritic spines. Neuron 57, 719–729 (2008). [DOI] [PubMed] [Google Scholar]
- 8.Baudry M., Bi X., Gall C., Lynch G., The biochemistry of memory: The 26 year journey of a “new and specific hypothesis.”. Neurobiol. Learn. Mem. 95, 125–133 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Smith B. A., Daugherty-Clarke K., Goode B. L., Gelles J., Pathway of actin filament branch formation by Arp2/3 complex revealed by single-molecule imaging. Proc. Natl. Acad. Sci. U.S.A. 110, 1285–1290 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wachsstock D. H., Schwartz W. H., Pollard T. D., Affinity of alpha-actinin for actin determines the structure and mechanical properties of actin filament gels. Biophys. J. 65, 205–214 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Luo W. et al., Analysis of the local organization and dynamics of cellular actin networks. J. Cell Biol. 202, 1057–1073 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Svitkina T. M., Borisy G. G., Arp2/3 complex and actin depolymerizing factor/cofilin in dendritic organization and treadmilling of actin filament array in lamellipodia. J. Cell Biol. 145, 1009–1026 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wagner B., Tharmann R., Haase I., Fischer M., Bausch A. R., Cytoskeletal polymer networks: The molecular structure of cross-linkers determines macroscopic properties. Proc. Natl. Acad. Sci. U.S.A. 103, 13974–13978 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kane R. E., Interconversion of structural and contractile actin gels by insertion of myosin during assembly. J. Cell Biol. 97, 1745–1752 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mullins R. D., Heuser J. A., Pollard T. D., The interaction of Arp2/3 complex with actin: Nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc. Natl. Acad. Sci. U.S.A. 95, 6181–6186 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stachowiak M. R. et al., Self-organization of myosin II in reconstituted actomyosin bundles. Biophys. J. 103, 1265–1274 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kovar D. R., Harris E. S., Mahaffy R., Higgs H. N., Pollard T. D., Control of the assembly of ATP- and ADP-actin by formins and profilin. Cell 124, 423–435 (2006). [DOI] [PubMed] [Google Scholar]
- 18.Zalevsky J., Lempert L., Kranitz H., Mullins R. D., Different WASP family proteins stimulate different Arp2/3 complex-dependent actin-nucleating activities. Curr. Biol. 11, 1903–1913 (2001). [DOI] [PubMed] [Google Scholar]
- 19.Lombardo A. T. et al., Myosin Va transport of liposomes in three-dimensional actin networks is modulated by actin filament density, position, and polarity. Proc. Natl. Acad. Sci. U.S.A. 116, 8326–8335 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Popov K., Komianos J., Papoian G. A., MEDYAN: Mechanochemical simulations of contraction and polarity alignment in actomyosin networks. PLoS Comput. Biol. 12, e1004877 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Komianos J. E., Papoian G. A., Stochastic ratcheting on a funneled energy landscape is necessary for highly efficient contractility of actomyosin force dipoles. Phys. Rev. X 8, 21006 (2018). [Google Scholar]
- 22.Floyd C., Papoian G. A., Jarzynski C., Quantifying dissipation in actomyosin networks. Interface Focus 9, 20180078 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chandrasekaran A., Upadhyaya A., Papoian G. A., Remarkable structural transformations of actin bundles are driven by their initial polarity, motor activity, crosslinking, and filament treadmilling. PLoS Comput. Biol. 15, e1007156 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ni Q., Papoian G. A., Turnover versus treadmilling in actin network assembly and remodeling. Cytoskeleton (Hoboken) 76, 562–570 (2019). [DOI] [PubMed] [Google Scholar]
- 25.Hu L., Papoian G. A., Mechano-chemical feedbacks regulate actin mesh growth in lamellipodial protrusions. Biophys. J. 98, 1375–1384 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hu L., Papoian G. A., Molecular transport modulates the adaptive response of branched actin networks to an external force. J. Phys. Chem. B 117, 13388–13396 (2013). [DOI] [PubMed] [Google Scholar]
- 27.Lan Y., Papoian G. A., The stochastic dynamics of filopodial growth. Biophys. J. 94, 3839–3852 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hu L., Papoian G. A., How does the antagonism between capping and anti-capping proteins affect actin network dynamics? J. Phys. Condens. Matter 23, 374101 (2011). [DOI] [PubMed] [Google Scholar]
- 29.Nedelec F., Foethke D., Collective Langevin dynamics of flexible cytoskeletal fibers. New J. Phys. 9, 427 (2007). [Google Scholar]
- 30.Freedman S. L., Banerjee S., Hocky G. M., Dinner A. R., A versatile framework for simulating the dynamic mechanical structure of cytoskeletal networks. Biophys. J. 113, 448–460 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wang S., Wolynes P. G., Active contractility in actomyosin networks. Proc. Natl. Acad. Sci. U.S.A. 109, 6446–6451 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wang S., Wolynes P. G., Active patterning and asymmetric transport in a model actomyosin network. J. Chem. Phys. 139, 235103 (2013). [DOI] [PubMed] [Google Scholar]
- 33.Aström J. A., Kumar P. B. S., Vattulainen I., Karttunen M., Strain hardening, avalanches, and strain softening in dense cross-linked actin networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 77, 51913 (2008). [DOI] [PubMed] [Google Scholar]
- 34.Feng J., Levine H., Mao X., Sander L. M., Nonlinear elasticity of disordered fiber networks. Soft Matter 12, 1419–1424 (2016). [DOI] [PubMed] [Google Scholar]
- 35.Kim J. et al., Stress-induced plasticity of dynamic collagen networks. Nat. Commun. 8, 842 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lubchenko V., Wolynes P. G., Aging, jamming, and the limits of stability of amorphous solids. J. Phys. Chem. B 122, 3280–3295 (2018). [DOI] [PubMed] [Google Scholar]
- 37.Lubchenko V., Wolynes P. G., Theory of structural glasses and supercooled liquids. Annu. Rev. Phys. Chem. 58, 235–266 (2007). [DOI] [PubMed] [Google Scholar]
- 38.Wang S., Wolynes P. G., Microscopic theory of the glassy dynamics of passive and active network materials. J. Chem. Phys. 138, 12A521 (2013). [DOI] [PubMed] [Google Scholar]
- 39.Dima R. I., Thirumalai D., Asymmetry in the shapes of folded and denatured states of proteins. J. Phys. Chem. B 108, 6564–6570 (2004). [Google Scholar]
- 40.Alencar A. M. et al., Non-equilibrium cytoquake dynamics in cytoskeletal remodeling and stabilization. Soft Matter 12, 8506–8511 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shi Y., Porter C. L., Crocker J. C., Reich D. H., Dissecting fat-tailed fluctuations in the cytoskeleton with active micropost arrays. Proc. Natl. Acad. Sci. U.S.A. 116, 13839–13846 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lootens D., Van Damme H., Hébraud P., Giant stress fluctuations at the jamming transition. Phys. Rev. Lett. 90, 178301 (2003). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The dataset is hosted by Zenodo (DOI: 10.5281/zenodo.3714167). MEDYAN is available to download at http://medyan.org/.