Metabolic cost of rapid adaptation of single yeast cells

Significance

We establish, using single-cell analysis of metabolism and division in a droplet microfluidic system, that yeast can adapt, resuming division, extremely rapidly to an unforeseen environmental challenge, and that adaptation is an active process, requiring the consumption of a characteristic amount energy. The adapted state is stable over at least several days, showing that this is a genuine adaptation process. The adaptation rate (10⁻³ cells per hour) is orders of magnitude higher than expected based on known mutation rates, suggesting an epigenetic origin, and the tight energetic coupling implies that there is active exploration of different states, and fixation of the solution(s) that allow adaptation.

Abstract

Cells can rapidly adapt to changing environments through nongenetic processes; however, the metabolic cost of such adaptation has never been considered. Here we demonstrate metabolic coupling in a remarkable, rapid adaptation process (1 in 1,000 cells adapt per hour) by simultaneously measuring metabolism and division of thousands of individual Saccharomyces cerevisiae cells using a droplet microfluidic system: droplets containing single cells are immobilized in a two-dimensional (2D) array, with osmotically induced changes in droplet volume being used to measure cell metabolism, while simultaneously imaging the cells to measure division. Following a severe challenge, most cells, while not dividing, continue to metabolize, displaying a remarkably wide diversity of metabolic trajectories from which adaptation events can be anticipated. Adaptation requires a characteristic amount of energy, indicating that it is an active process. The demonstration that metabolic trajectories predict a priori adaptation events provides evidence of tight energetic coupling between metabolism and regulatory reorganization in adaptation. This process allows S. cerevisiae to adapt on a physiological timescale, but related phenomena may also be important in other processes, such as cellular differentiation, cellular reprogramming, and the emergence of drug resistance in cancer.

How populations of cells adapt to changing environments remains a major question in evolutionary biology. In the classical neo-Darwinian picture, random genetic mutations cause phenotypic variations, enabling adaptation to the new environment. However, adaptation may also be mediated by nongenetic processes (1). Phenotypic plasticity can, for example, allow cells to survive severe environmental challenges, which is essential for adaptive evolution (2). It is also suggested to play an important role in diverse biological processes, including cell differentiation and the emergence and progression of diseases such as cancer (3).

Proliferating (adapted) cells are expected to have higher metabolic activity than quiescent (nonadapted) cells as they need to replicate the entire cellular content in order to divide, although high metabolic activities have also been reported in certain quiescent cells, including respiring yeast and fibroblasts (4, 5). However, the connection between metabolic activity and the process of adaptation has remained elusive.

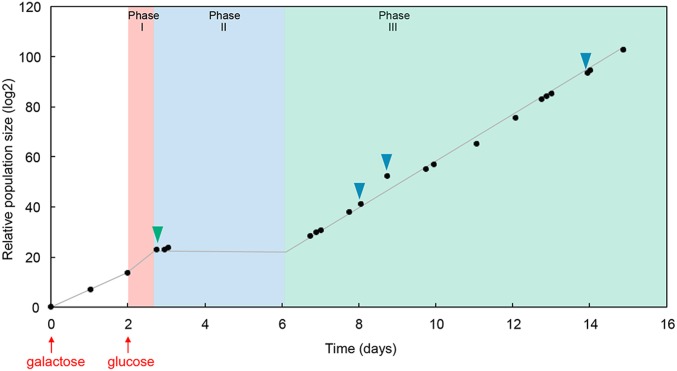
To investigate adaptation of the yeast Saccharomyces cerevisiae confronted with a severe environmental challenge, we genetically “rewired” cells by detaching the essential HIS3 gene of the histidine biosynthesis system from its native regulatory system and placed it under the control of the GAL system, which is highly induced in the presence of galactose and strongly repressed in glucose (6). Switching cells from galactose to glucose in a medium lacking histidine presents the yeast with the challenge of reinitiating histidine synthesis in order to resume growth and prevent extinction. The population dynamics of this system have previously been studied in detail (6–12). After switching to glucose, growth continues for ∼1 d (phase I) then, after a few days with little or no growth (phase II), normal growth is resumed at the population level (phase III) with a doubling time similar to that before the challenge, indicating that after only a few days the population is fully adapted (Fig. 1).

Fig. 1.

Population growth in bulk cultures during adaptation. The culture of rewired cells started with galactose as the sole carbon source (first red arrow). Then, the medium was switched to glucose (second red arrow). The culture continued to grow during the “initial growth phase” (phase I), before entering the latent phase (phase II) where growth stopped. Finally, the population grew again, entering the adapted phase (phase III). Green and blue triangles indicate time points when samples were taken for single-cell measurements in droplets (green triangle: 3 h after the beginning of phase II; blue triangles: 2, 3, and 6 d after the onset of phase III).

Results and Discussion

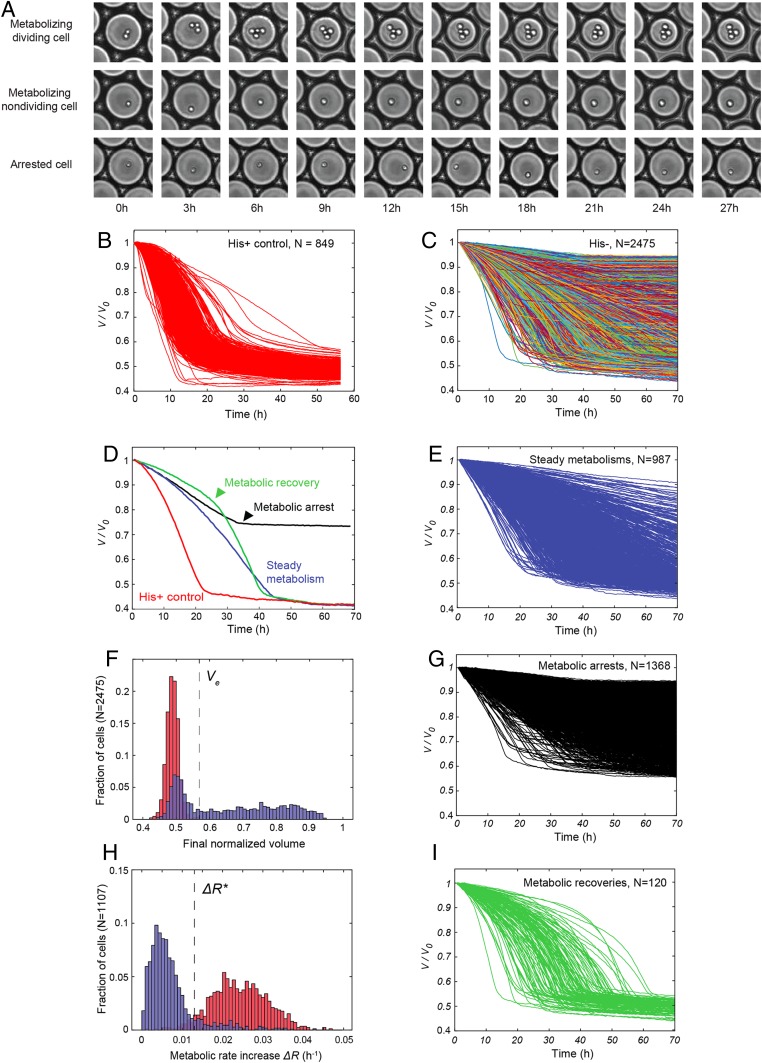
To track adaptation at the single-cell level, we used a droplet microfluidic system that allows simultaneous measurements of growth and metabolism of several thousands of single yeast cells over time (13). Individual cells, harvested from batch cultures 3 h after the beginning of phase II (Fig. 1, green triangle), were compartmentalized in 30-pL aqueous droplets in an inert carrier oil and immobilized in a two-dimensional (2D) array in a closed glass observation chamber and incubated at 30 °C for 65–70 h (Fig. 2A). A small fraction of the droplets contained single cells (typically 6%), and these were surrounded by empty droplets. In the presence of glucose, yeast metabolism is dominated by anaerobic fermentation (C₆H₁₂O₆ + 2ADP + 2Pi → 2C₂H₅OH + 2CO₂ + 2ATP). Loss of C₂H₅OH + 2CO₂ by solubilization in the continuous phase leads to an osmotic imbalance, resulting in water flux, inducing the shrinkage of droplets containing a yeast cell, while neighboring cell-free droplets tend to swell by a few percent, then reequilibrate to their initial size (Movie S1 and SI Appendix, Fig. S1). The consumption of a specific amount of glucose corresponds to a specific amount of energy. Therefore, the osmotic shrinkage of the droplet is a direct measurement of glucose and energy consumption (see ref. 13 and SI Appendix, Measurement of glucose consumption using osmotic volume variation, for a detailed explanation). Images were taken every 20 or 30 min over 3 d and used to determine the change in volume of each droplet as a function of time, reflecting cell metabolism (13), while simultaneously imaging the cells to measure division (Materials and Methods). Three independent batch cultures were analyzed; however, only the consolidated data from these three independent experiments are plotted and analyzed. For analysis of individual experiments, time-course data, and analysis code, see ref. 14 and SI Appendix,Table S1.

Fig. 2.

Single-cell analysis of metabolic dynamics in droplets. (A) Time-lapse sequences of droplets containing a metabolizing dividing cell, a metabolizing nondividing cell, and an arrested cell. Each image is 150 × 150 µm. (B) Traces of droplet volumes V normalized by the initial volume V₀, in the absence of metabolic challenge (with histidine). (C) Traces of normalized droplet volumes starting 3 h after switching from galactose to glucose. Lines are randomly color coded. (D) Examples of traces of normalized droplet volumes of the His+ control (red) and of each category of metabolic response observed in the adaptation experiment. (E) Subset of steady metabolisms from C. (F) Distribution of final normalized droplet volume (V_f/V₀) in the presence (red) and absence (blue) of histidine. V_e indicates the largest final droplet volume with histidine. (G) Subset of arrested metabolisms from C. (H) Distributions of the difference ΔR (metabolic rate increase) between the initial (at 2 h) and maximum metabolic rates in the presence (red) and absence (blue) of histidine. ΔR* indicates the cross-over between the two distributions. (I) Subset of metabolic recoveries from C.

Metabolic activity was detectable for 88% of cells (final droplet volume <0.95 of initial volume; see Materials and Methods and SI Appendix, Fig. S2). The volume variation of droplets containing cells displaying metabolic activity was plotted for both the control experiment, with histidine in the medium (Fig. 2B), and the adaptation experiment, in the absence of histidine (Fig. 2C). Cells in medium lacking histidine showed remarkably diverse metabolic trajectories (coefficient of variation, CV = 0.60 at 10 h), while in the presence of histidine the diversity of the metabolic trajectories was more restricted (CV = 0.24 at 10 h, SI Appendix, Fig. S3) and similar to wild-type yeast (13). Initial cell size made a small, but statistically significant, contribution to metabolic rate variability in the adapting population (R² = 0.27, P < 10⁻⁵). This contrasts with the control experiment in the presence of histidine, where no correlation was observed (SI Appendix, Fig. S4). Note that neither the presence of neighboring droplets containing cells, nor rare cases where droplets had five rather than six neighbors had a detectable effect on the measured metabolic rate (SI Appendix, Figs. S5 and S6).

Analysis of the change of droplet volumes over time (SI Appendix, Figs. S2, S3, and S7–S9) revealed three different classes of metabolizing cells (Fig. 2D and Materials and Methods): 1) steadily metabolizing cells (35% of the total population) (Fig. 2E); 2) cells that underwent metabolic arrest (49% of the total population), the volume curve flattening before nutrient exhaustion, i.e., at a value larger than the final volume of cells grown with histidine (Fig. 2 F and G), and 3) cells that underwent metabolic recovery (4% of the total population), the shrinkage rate increasing to a similar level as for cells under nonstressed conditions (in the presence of histidine) (Fig. 2 H and I). The time of metabolic arrest (T_arr) and time of metabolic recovery (T_rec) were determined as the minimum and the maximum of the second derivative of the drop-shrinkage curves, respectively (arrowheads in Fig. 2D, and Materials and Methods).

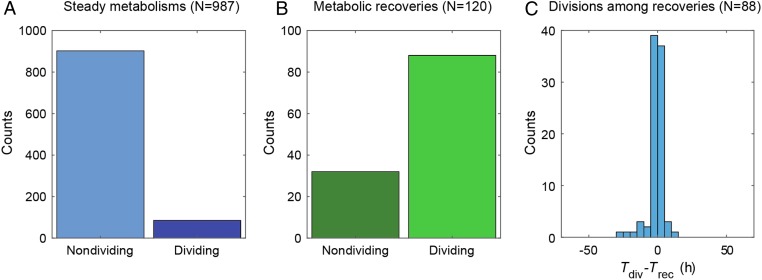
We next addressed the question of the correlation between metabolic profiles and adaptation—the resumption of division. Each metabolizing cell within the shrinking drops was visualized to determine if division occurred at least once and at what time, the time of division T_div being defined as the time of appearance of a first bud eventually leading to a division event. We found that within the subset of cells showing steady metabolism, only 9% of the cells resumed division, whereas within the metabolic recovery class, 73% resumed division (Fig. 3 A and B). Plotting the distribution of the time difference between the onset of cell division (T_div) and metabolic recovery (T_rec) shows that the two events are strongly correlated (R² = 0.79, P < 10⁻⁵, SI Appendix, Fig. S10), with a mean value T_div – T_rec ∼ −1.35 ± 5.5 h (Fig. 3C), which is significantly smaller than the average time of recovery (29 h). This indicates that division starts when the maximum metabolic acceleration is reached.

Fig. 3.

Relation between onset of division and metabolic recovery. (A) Fraction of dividing cells in steady metabolisms. (B) Fraction of dividing cells in metabolic recoveries. (C) Distribution of the difference between division time (T_div) and metabolic recovery time (T_rec).

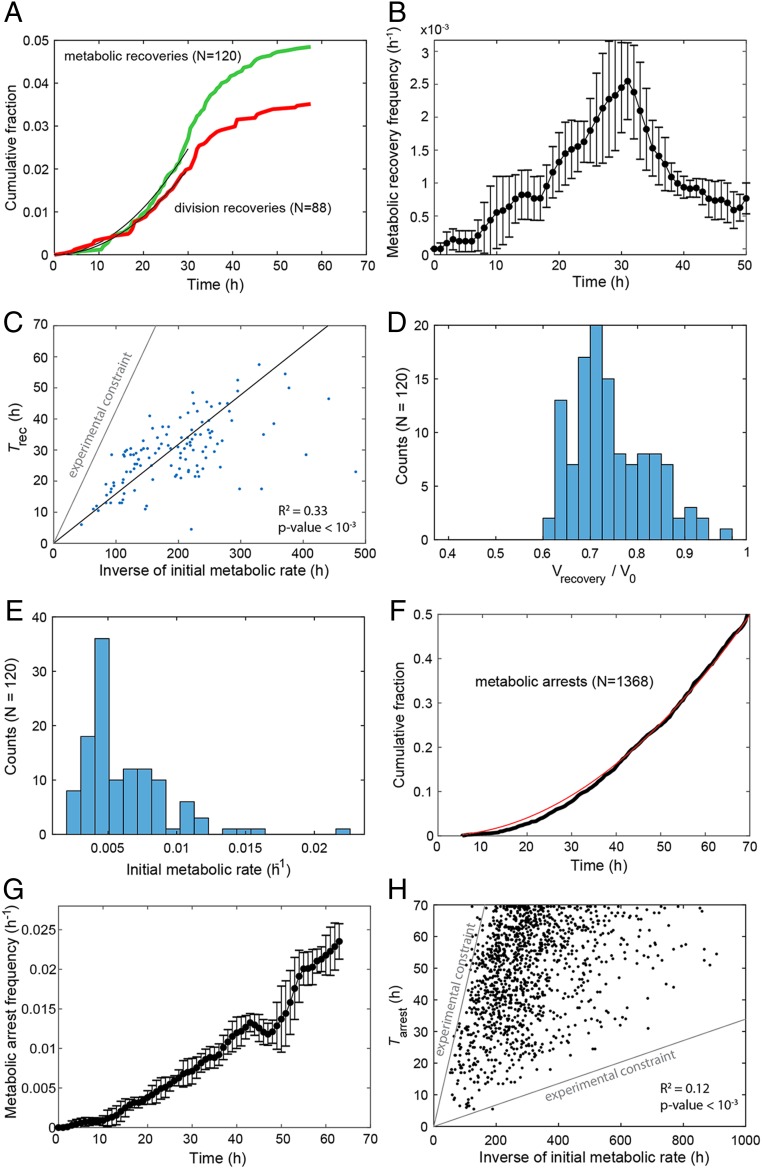
The cumulated fraction of metabolic recoveries (Fig. 4A, green) and cells recommencing division (Fig. 4A, red) both displayed a sigmoidal shape, with a quadratic increase up to 30 h, followed by a leveling off. The instantaneous rate of adaptation also increased up to 30 h, reaching a maximum of ∼10⁻³ cells per hour (Fig. 4B). Plotting the recovery time (T_rec) as a function of the inverse initial metabolic rate (R₀⁻¹) revealed a clear linear correlation (R² = 0.33, P < 10⁻³, Fig. 4C). The droplet volume on recovery peaks at ∼74% of the initial droplet volume (Fig. 4D and SI Appendix, Table S1), indicating that, on average, a characteristic amount of glucose (156 pg) and hence a characteristic amount of energy (6.24 × 10⁻⁷ cal) is consumed at the moment a cell adapts. The distribution of adaptation times is explained by the distribution of the initial metabolic rates which peaks at low values (Fig. 4E and Materials and Methods). In contrast, the cumulated fraction of metabolic arrests increases quadratically throughout the course of the experiments (Fig. 4F), leading to an instantaneous death rate that continuously increases with time (Fig. 4G). The time of metabolic arrest (T_arr) is, however, poorly correlated with the initial metabolic rate (R² = 0.12, P < 10⁻³, Fig. 4H), in agreement with an age-driven mechanism essentially independent of the initial metabolic rate. We also performed a simulation of a bulk adaptation based on the experimentally observed adaptation events in our system over 70 h (SI Appendix, Fig. S11), which corresponds roughly to the length of the “latent phase” (phase II) where bulk population growth is stalled (Fig. 1). This showed that the final population has a low diversity, dominated by the progeny of a few adapted cells: from the initial pool of 2,475 cells, the first two adapters make up 37% of the adapted population, and the 10 first adapters (0.4% of the initial population) make up 90% (SI Appendix, Fig. S11). Overall, the rate of adaptation (1 in 1,000 cells per hour) measured at the single-cell level is fully consistent with the recovery observed in bulk culture. Indeed, at the beginning of phase I, the culture contains 3.75 × 10⁷ cells, and the first few adapters are expected to appear within the first hour. Given the measured doubling time of 3.1 h of recently adapted cells, the population size is expected to start to increase again (double) 78 h after the stress event, corresponding to the duration of phase II (Fig. 1).

Fig. 4.

Characterization of adaptation. (A) Cumulative fraction over time for metabolic recoveries (green) and division recoveries (red). Black lines are a quadratic fit over the first 30 h. (B) Instantaneous frequency of metabolic recoveries of cells. At each time point, frequencies are computed over seven consecutive points and error bars are SDs over the values obtained over these points. (C) Plot of metabolic recovery time (T_rec) as a function of inverse initial metabolic rate (R₀⁻¹). The parameter region above the gray line corresponds to cells that have exhausted droplet resources before being able to recover (Materials and Methods). The black line is the linear fit. (D) Distribution of normalized droplet volume at T_rec. (E) Distribution of R₀ for the subset of metabolic recoveries. (F) Cumulative fraction over time for metabolic arrests (black). The red line is a quadratic fit. (G) Instantaneous frequency of arrests of cells that have neither recovered nor arrested their metabolism. Frequencies and error bars were computed as in B). (H) Plot of time of metabolic arrest (T_arr) as a function of R₀⁻¹. The parameter region above the upper gray line corresponds to cells that have exhausted droplet resources before arresting. The parameter region below the lower gray line corresponds to curves whose final volume is indistinguishable from curves of empty droplets (overall volume variation <5%). The contribution of the constraints in C and H has been accounted for to compute the coefficients of determination R² (Materials and Methods).

We finally examined the metabolism of single cells in the adapted populations taken 2, 4, and 7 d after the batch population entered phase III (Fig. 1, blue arrows). The overall dynamics of the adapted population (SI Appendix, Fig. S12A) are highly comparable with cells in the absence of stress (Fig. 2B), with a similar spread of final droplet volumes (SI Appendix, Fig. S12B) and metabolic rates (SI Appendix, Fig. S12C, CV = 0.35 for adapted compared to CV = 0.24 for nonstressed cells). None of the 174 dividing cells analyzed underwent metabolic arrest, demonstrating stability of the adapted state over days, consistent with results at the population level (Fig. 5) (6, 11).

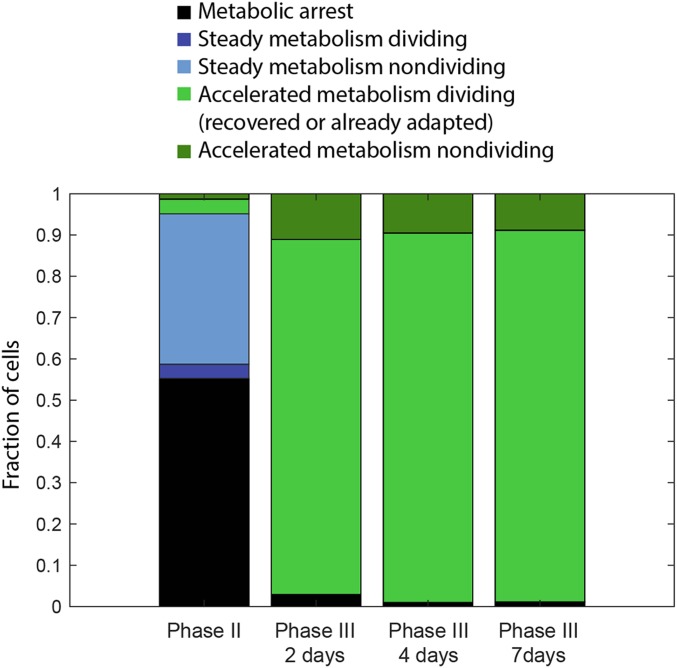
Fig. 5.

Metabolic categories in phase II (adapting population) and phase III (adapted population). Fraction of each cell type during adaptation (phase II), and 2, 4, and 7 d after entering the adapted phase (phase III). Phase II: metabolic arrest (55%), steady metabolism: dividing (3.4%), nondividing (36%), accelerated metabolism: dividing (3.5%), nondividing (1.3%). Phase III: The proportions of the different classes of cells are very similar at the three time points: metabolic arrest (1.6 ± 1%), accelerated metabolism nondividing (10 ± 1%), and accelerated metabolism dividing (89 ± 2%). Steady metabolism is not observed in phase III, since the cells are already adapted. Consistent with adaptation observed at the population level, the fraction of dividing cells is >10-fold higher than at the beginning of phase II (7).

What mechanism might explain this rapid adaptation? Previous results using the same “rewired” yeast system indicate that cells do not adapt by simply expressing the HIS3 gene that was placed under the control of the GAL system (6). Also, consistent with previous results (9), the adaptation process observed here appears to differ from known S. cerevisiae stress responses, including the response to amino acid starvation (15), in a number of ways. Known stress responses are rapid and transient (with changes in gene expression typically peaking after <2 h) (16, 17), and all cells respond broadly similarly (17). In contrast, the characteristic timescale of adaptation of single cells that we observe is much longer (∼10³ h; see Fig. 4B) and only a fraction of cells adapt. However, the rate of adaptation (∼10⁻³ h⁻¹) is also several orders of magnitude higher than rates reported based on genetic mechanisms (18–20), for example, the spontaneous reversion rates by point mutation in quiescent histidine auxotrophic yeast cells in the absence of histidine is only 10⁻⁵ to 10⁻⁹ h⁻¹ (19). This may point to an epigenetic mechanism, as recently suggested for a similar engineered yeast system (21).

The GAL1/10 promoter is naturally controlled by the yeast galactose signaling network, which contains multiple nested feedback loops, and, in the presence of certain concentrations of galactose can exhibit multistability, and memory of previous galactose exposure can be maintained for hundreds of generations (22). Memory persistence, which is controlled by the rate of stochastic switching between ON and OFF states, can be modulated by varying the concentration of the inhibitor Gal80p in engineered yeast strains. However, in our experiments, memory of previous galactose exposure cannot explain the results, as the switch to an adapted phenotype occurs after a period of time in the absence of galactose and in a rich glucose medium (in phase II). Neither can our results be explained by stochastic switching, as in the absence of galactose the system is monostable and OFF (22).

In conclusion, this work establishes that, in yeast, rapid adaptation necessitates consumption of a characteristic amount of glucose, which corresponds to a characteristic amount of energy, causing certain cells that metabolize more efficiently to adapt more rapidly. The adapted state is stable, backing up previous observations in bulk, which indicates that the adapted state is stably inherited across generations (6, 11), showing that this is a genuine adaptation process. It is also an active process, requiring the consumption of energy, which implies exploration of different states, and fixation of the solution(s) that allow adaptation. Interestingly, the characteristic cost of adaptation implies that cells with an initially higher metabolic rate adapt and start to multiply earlier, thereby providing a selective advantage.

Finally, it is tempting to speculate that a related system may also play a role in other important processes, including cellular differentiation and development. Indeed, stochastic fluctuations at the single-cell level have been proposed to play an important role in early-stage embryonic stem-cell differentiation (23–25) and epigenetic mechanisms are increasingly believed to play an important role the development, progression, and emergence of drug resistance in cancer (26, 27). Furthermore, it may have implications for important biotechnologies, such as reprogramming of human somatic cells to generate induced Pluripotent Stem Cells (28).

Materials and Methods

Chemicals.

All chemicals were purchased from Sigma–Aldrich unless otherwise mentioned.

Strains and Culture Conditions.

The rewired yeast strain was the same as in previous bulk experiments (6). Briefly, it is a haploid S. cerevisiae strain YPH499 (MATa ura3-52 lys2-801_amber ade2-101_ochre trp1-Δ63 his3-Δ200 leu2-Δ1), lacking the entire HIS3 coding region plus the upstream promoter region, and carrying the plasmid vector pESC-LEU (Agilent Technologies), which contains the GAL1/GAL10 divergent promoter, and into which a GFPS65T reporter gene was cloned under control of the GAL10 promoter and an HIS3 gene was cloned under control of the GAL1 promoter (for further details see refs. 6, 29 and SI Appendix, Fig. S13).

Cells were grown from colonies on plates in 25 mL of culture medium comprising: 1.7 g/L of yeast nitrogen base without amino acids and ammonium sulfate, 5 g/L ammonium sulfate, 1.4 g/L amino acid dropout powder (without Trp, His, Leu, Ura), 0.004 g/L l-tryptophan, and 0.002 g/L uracil, 20 g/L of galactose or glucose, and incubated at 30 °C, shaking at 200 rpm in 100-mL Erlenmeyer flasks. Cultures were diluted every 12 h to maintain optical density (OD) < 1.0 and 3 × 10⁶ cells or more were transferred into fresh medium at each dilution step. The exact volume of culture transferred at each dilution was calculated in order to have an OD of 0.005 in the fresh culture.

Rewired yeast cells were first grown in a batch culture with galactose medium lacking histidine. The OD (OD_600nm) of the culture was monitored and it was maintained in the exponential phase of growth by serial dilutions for 2 d. The medium was then switched from galactose to glucose: 0.25 mL of culture in galactose medium was transferred into 25 mL of fresh glucose medium (a 100-fold dilution; hence, 0.2 g/L of residual galactose was present in the first glucose culture). As previously reported (6, 11), naive cells (i.e., rewired cells that had never been grown in glucose before) were able to grow for about 20 h in glucose media lacking histidine with a doubling time, t_D, of 1.9 h (phase I). Following this phase, growth slowed considerably (t_D 17.1 h), leaving the OD_600nm approximately constant (phase II, the “latent phase”). At the end of this phase, after durations that varied across repeated experiments from (1 to 6 d), the population adapted and started growing and proliferating (phase III, the “adapted phase”). The doubling time of the adapted population was reduced from 3.1 h after 1 d in phase III, to 2.1 h after 8 d in phase III, reflecting the fact that the population continues to adapt after resuming growth (7). Three independent batch cultures were analyzed and the growth curve for one of these experiments is shown in Fig. 1.

Microfluidic Device Fabrication.

Microfluidic devices were obtained using conventional soft lithography methods (30) as described (31). Molds were prepared using SU8-2015 or SU8-2075 photoresist (MicroChem Corp.) and used to pattern 20- and 75-µm-deep channels onto silicon wafers (Siltronix). The channels of the devices were passivated with Aquapel in HFE7100 (3M) and subsequently flushed with compressed nitrogen gas.

Formation and Imaging of Droplet Arrays.

Single-cell metabolic and growth dynamics of yeast cells from batch cultures were measured as in Boitard et al. (13). Yeast cells were harvested from batch cultures 3 h after the beginning of phase II (Fig. 1, green triangle), or 2, 4, and 7 d after the batch population entered phase III (Fig. 1, blue arrows). The harvested cells were centrifuged (5 mL of culture at 3,000 g for 30 min) and washed again with fresh glucose medium (the supernatant was discarded, the cells resuspended into 2 mL of fresh medium, and centrifuged at 3,000 g for 30 min). The process was repeated two times; then the cells were suspended into 1 mL of fresh medium and diluted with the appropriate volume of glucose medium to reach OD of 0.17, ensuring that ∼10% of the droplets would contain a single cell, and ∼90% would be empty (assuming a Poisson distribution). For the cells harvested from phase II, the final residual galactose concentration is estimated to be ∼4 × 10⁻⁵ g/L. The yeast cells were then individually compartmentalized in monodisperse 30-pL-volume (38-µm diameter) aqueous droplets containing fresh glucose medium lacking histidine by hydrodynamic flow focusing (32) with a fluorinated oil phase containing fluorosurfactant (33). For each experiment, about 200,000 droplets were incubated at 30 °C in a 2D array and images were taken every 30 min over 3 d. Briefly, a flow-focusing device (32) was used for droplet generation and flow rates were controlled using standard-pressure infuse/withdraw PHD 22/2000 syringe pumps (Harvard Apparatus Inc.). Syringes (Hamilton) connected to the microfluidic device using 0.6 × 25 mm Neolus needles (Terumo Corporation) and polytetrafluoroethylene (PTFE) tubing with an internal diameter of 0.56 mm and an external diameter of 1.07 mm (Fisher Bioblock Scientific). The aqueous phase, comprising cells suspended in culture medium, was injected at 300 µL/h and dispersed in a continuous phase consisting of HFE-7500 fluorinated oil (3M) containing 2% (wt/wt) EA surfactant (Raindance Technologies), a perfluoropolyether-polyethylene glycol-perfluoropolyether (PFPE-PEG-PFPE) amphiphilic triblock copolymer (33), injected at 150 µL/h, forming 30-pL-volume (38-µm-diameter) droplets at 2,800 droplets s⁻¹. Droplets were produced in a compact manner and were directly incubated in a glass chamber of 3.5 × 1.5 cm to form a compact 2D droplet array (13). Compaction of the emulsion prevents droplet movement to enable their tracking over long timescales. The chamber was maintained at 30 °C on a Nikon T300 inverted microscope with a Thorlabs MAX202 XY stage. Images of the droplet array were taken every 30 min using a Hamamatsu Orca-ER camera. Custom-made LabVIEW software was used to automate image acquisition and microscope control.

Data Processing.

For a schematic representation see SI Appendix, Fig. S9.

Droplet Tracking and Normalization.

Droplets were detected with an in-house MATLAB segmentation routine and tracked over time by a nearest-neighbor criterion, knowing that displacements from image to image are much smaller than the characteristic droplet diameter. Images in which large displacements occurred were easily detected as they displayed strongly discontinuous volume traces and were discarded. In order to minimize volume fluctuations caused by defocusing in time, volumes were normalized by the time course of the average of more than 10 empty droplets for each image. Images for which normalization failed were discarded (SI Appendix, Fig. S9). The first and second derivatives of the normalized volume over time were computed over a five-time-point sliding windows and provided the metabolic rate and metabolic acceleration, and were used to automatically determine the maximum metabolic rate, time of metabolic acceleration, and time of metabolic arrest (SI Appendix, Fig. S7).

Significantly Shrinking Droplets.

A droplet was considered to be significantly shrinking (i.e., the compartmentalized cell showed detectable metabolism) if its final normalized volume V_end was smaller than V_s = 1 – 3σ, where σ is the coefficient of variation of empty droplet final volumes taken over all experiments. We measured V_s = 0.95. Shrinking but empty droplets that passed this filter were removed by visual inspection of the droplet content.

Poisson Parameter and Initial Fraction of Dead Cells.

The Poisson parameter λ (the mean number of cells per droplet) was determined from the frequency of occupied droplets on a sample of 10 initial images (∼1,500 droplets) per experiment. The number of droplets containing cells arrested from the start was estimated by calculating the difference between λ and the number of significantly shrinking droplets (SI Appendix, Fig. S1).

Metabolic Arrest.

Metabolically arrested cells were defined as cells: 1) which do not consume all of the nutrients available in the droplets within the timeframe of the experiment, as defined by V_end > V_e, where V_end is the final droplet volume and V_e = 0.55 is the maximal normalized volume reached by cells in the control experiment (with histidine), and 2) for which the volume trace significantly flattens during the time course of the experiment. The latter was determined as the existence of an inflection in the volume curve leading to reach a rate R < R_max/10, where R_max is the maximum rate observed for this cell. The metabolic arrest point is defined as the time at which R reaches R_max/10 (SI Appendix, Fig. S7). In the presence of histidine, an abrupt decrease in metabolic rate was reached when glucose in the droplet was exhausted by the cells (13), corresponding to a mean final droplet volume of 0.49 ± 0.002 of the initial value, and always <0.55 of the initial value (Fig. 2F, red). In contrast, in the adaptation experiment in the absence of histidine (Fig. 2F, blue), 54% of cells had a final volume >0.55 of the initial value, indicating that they had not consumed all of the glucose in the droplet. These cells fall into two categories. In the first category are cells (49%) that arrested their metabolism during the experiment (Fig. 2G), as they were initially metabolically active and showed an abrupt metabolic deceleration and a stable volume, indicating that the cells were not metabolically active from that point in time (T_arr). A second category of cells (5%) neither arrested nor recovered, but had a metabolism slow enough that glucose was not exhausted at the end of the experiment.

Metabolic Recovery.

Metabolic recoveries in the adaptation experiment were determined as those cells whose metabolic rate increased to levels comparable to the control with histidine, as computed by the difference (ΔR) between the maximum rate (R_max) and the initial rate (R₀) (2 h after compartmentalization) obtained from the volume time course of each droplet (Fig. 2C). For this we determined the lower and upper bounds of the crossing values for the histograms of ΔR (Fig. 2H) for different binning intervals in the presence and absence of histidine (SI Appendix, Fig. S8). The threshold value ΔR* = 0.013 h⁻¹, which indicates the cross-over between the two distributions, was obtained when these bounds converged. Cells with ΔR > ΔR* were classed as metabolic recoveries. In the control, with histidine, the metabolic rate of cells steadily increased due to cell growth and division before glucose exhaustion (Fig. 2B) (13), with a mean rate increase of 3.6 ± 0.7 × 10⁻² h⁻¹ (Fig. 2H, red). In the adaptation experiment, 4% of cells accelerated their metabolic rates (n = 120, Fig. 2H, blue) to values similar to those observed in the control with histidine (>1.3 × 10⁻² h⁻¹).

Computation of Instantaneous Rates of Arrest and Metabolic Recovery.

Three distinct cell fates were categorized from the metabolic curves: metabolic arrest, metabolic recovery, and steady metabolism. Calling N the total number of cells observed during the experiment, N_a and N_r the respective cumulative number of arrested and recovering cells, the instantaneous rate of arrest and recovery were respectively computed as $d{N}_a/dt/(N-N_a-N_r)$ and $d{N}_r/dt/(N-N_a-N_r)$.

Effective Coefficients of Determinations.

The correlations of Fig. 4 C and H display regions of experimentally inaccessible parameter values, due to the finite amount of resource available in each droplet and the noise in droplet volume measurements. The coefficient of determination R_a² computed directly from the data thus comprises a contribution of these boundary constraints. This contribution R_b² to the total covariance was estimated using a Monte Carlo approach preserving the marginal distributions: 10⁵ random permutations of the measured values were generated under the boundary constraints, taking R_b² as the mean coefficient of determination of the last 10⁴ realizations. Assuming independence between the experimental constraints and cell fates in the absence of resource exhaustion, the additive contribution of these phenomena to the covariance leads to effective coefficients of determinations R² = R_b² − R_a².

Data Availability.

MATLAB analysis codes and data from yeast cells adaptation tracking in droplets are available in the database "Hyper Articles en Ligne" (HAL) of the Centre National de la Recherche Scientifique (CNRS), France, at https://hal.archives-ouvertes.fr/hal-02508076. All other data are available within the main text or SI Appendix.