Controlling photoionization using attosecond time-slit interferences

Significance

The photoelectric effect, in which an electron is emitted from matter after absorption of a high-energy photon, is one of the most fundamental and fastest processes in nature. Ruled by energy quantization and parity conservation, this process provides a general approach to study electronic properties of matter. Using a few attosecond pulses and a weak low-frequency control laser field to photoionize helium atoms, we show that these rules can be circumvented. This work represents a step toward time domain coherent control of photo-induced processes, using a tailored sequence of attosecond pulses.

Abstract

When small quantum systems, atoms or molecules, absorb a high-energy photon, electrons are emitted with a well-defined energy and a highly symmetric angular distribution, ruled by energy quantization and parity conservation. These rules are based on approximations and symmetries which may break down when atoms are exposed to ultrashort and intense optical pulses. This raises the question of their universality for the simplest case of the photoelectric effect. Here we investigate photoionization of helium by a sequence of attosecond pulses in the presence of a weak infrared laser field. We continuously control the energy of the photoelectrons and introduce an asymmetry in their emission direction, at variance with the idealized rules mentioned above. This control, made possible by the extreme temporal confinement of the light–matter interaction, opens a road in attosecond science, namely, the manipulation of ultrafast processes with a tailored sequence of attosecond pulses.

Since the seminal scientific contributions of Planck (1) and Einstein (2) at the beginning of the 20th century, it is well known that matter absorbs light in the form of discrete energy quanta ($h\nu$, the photon), where $h$ is the Planck constant and $\nu$ is the light frequency. Photoabsorption in centrosymmetric systems such as free atoms or molecules follows strict selection rules, with a change of parity between the initial and final states (3). When the absorbed energy is above the binding energy ($I_p$), a photoelectron is emitted with kinetic energy equal to $h\nu -I_p$ (2), and its probability of emission is symmetric relative to the origin (4, 5). These rules are based on first-order perturbation theory within the dipole approximation. With the advent of bright monochromatic light sources such as lasers (6) and synchrotron radiation sources (7) as well as the progress in photoelectron detection technology, in-depth studies of photoemission in a variety of systems with ever-increasing energy and angle resolution have confirmed these quantum mechanical predictions (8, 9).

As the light intensity increases, nonlinear multiphoton processes become possible, leading to new ionization mechanisms. In above-threshold-ionization (ATI) processes, electrons are emitted at kinetic energies equal to $nh\nu -I_p$, where $n$ is the number of photons absorbed (10, 11) and angular distributions remain centrosymmetric, except in some particular multiphoton schemes using several frequencies that mix parity in the final state (12, 13). In fact, electron spectra can be interpreted as resulting from the interference of “attosecond” electron wave packets (EWPs) emitted by strong-field (tunneling) ionization at each half-laser cycle (14, 15). The width of the electron peaks depends on the number of interfering wave packets, and therefore on the laser pulse duration. When ionization takes place during just a few cycles, the electron distribution presents broad spectral features and varies with the carrier-to-envelope phase (CEP) offset of the electric field of the laser pulse relative to its envelope. The “stereo ATI” technique (16, 17) uses the asymmetry of the electron distribution relative to the plane perpendicular to the laser polarization direction to characterize the CEP phase offset of the laser pulses.

With even shorter pulses, produced through high-harmonic generation in gases (18, 19) in the attosecond extreme ultraviolet (XUV) range, new tools become available for the study of time-resolved photoemission processes in atoms (20–23), molecules (24–26), and solids (27, 28). The “streaking” technique (29, 30) combines a single attosecond pulse with an intense infrared (IR) laser pulse. In this case, the kinetic energy distribution of the photoelectrons, imposed by the attosecond pulse bandwidth, is very broad, typically several electronvolts, and can be continuously varied depending on the delay between the XUV and IR fields. The energy shift can be understood classically by momentum transfer from the IR electromagnetic field to the electron which is released by absorption of an XUV photon. At the delays when the energy transfer is not zero, the angular distribution is asymmetric. The reconstruction of attosecond harmonic beating by interference of two-photon transitions (RABBIT) technique (31–33) uses a train of attosecond pulses together with a weak IR laser pulse. In this case, the photoelectron momentum distribution remains symmetric, and the kinetic energy spectrum presents discrete peaks separated by the IR photon energy.

This brief description of the state of knowledge of light–matter interaction shows that the rules of energy quantization and parity conservation, established at the beginning of the last century for describing the photoelectric effect, are not universal, in particular for short and intense optical fields. To the best of our knowledge, the limits of these rules in photoelectron spectroscopy, in particular concerning energy quantization, have not been discussed in the case of weak optical fields.

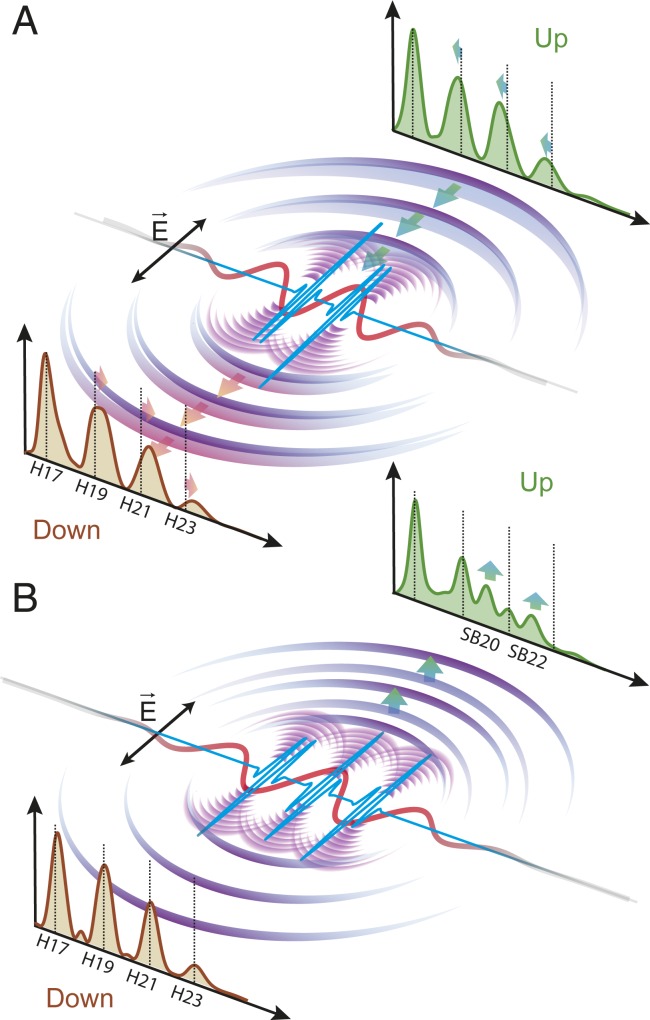
In this work, we study the photoionization of helium by tailored sequences of a few attosecond pulses in the presence of a weak IR laser field using three-dimensional (3D) momentum electron detection, which is becoming an essential tool in attosecond science (34, 35). The principle of our experiment is illustrated in Fig. 1. Helium atoms interact with two (Fig. 1A) or three (Fig. 1B) attosecond pulses, and the IR field. EWPs are emitted, which carry the phase of the ionizing attosecond pulse and a phase modulation due to the IR field at the time of ionization. The resulting momentum distribution is determined by the interference of these wave packets. When helium atoms are photoionized by two attosecond pulses separated by half of the laser period, the electron energy is shifted relative to the kinetic energy for the XUV-only case by a continuous amount which depends on the IR light field as well as on the direction of emission. When helium atoms are photoionized by three attosecond pulses, we recover discrete energies equal to the energy of the absorbed photons minus the ionization energy. The emission direction is, however, strongly asymmetric. A theoretical analysis shows that this behavior can be explained by time-slit interferences of EWPs when the light–matter interaction is temporally confined to approximately an IR cycle, shedding light on the possibility to control the photoelectric effect in the time domain.

Fig. 1.

Principle of the experiment: Helium atoms are exposed to (A) two or (B) three XUV attosecond pulses (blue) in the presence of a weak IR laser field (red) at a fixed delay. EWPs (violet) are emitted with an up–down asymmetry relative to the direction of polarization, resulting in different spectra (brown and green) when recording electrons emitted in the two opposite directions. In the case of two pulses (in A), the photoelectron spectrum is shifted toward higher or lower energies, while, for three pulses (in B), peaks at different frequencies, called sidebands, are observed, mostly in the up direction.

Results

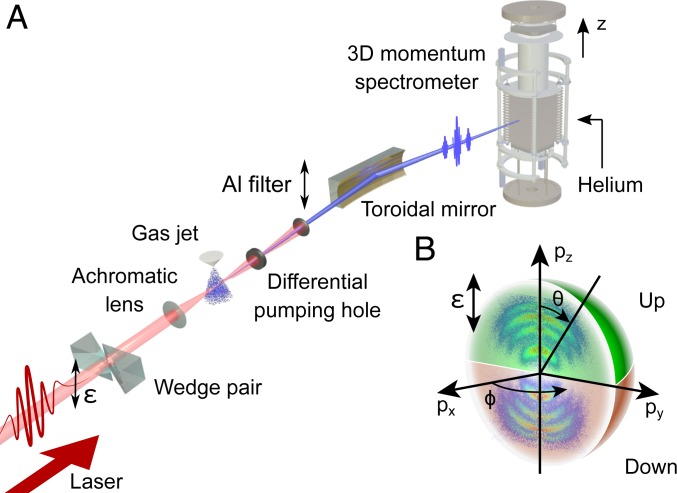
Details of the experiment are presented in Fig. 2A and explained in Materials and Methods. Briefly, a 200-kHz repetition-rate CEP-stable few-cycle laser generates a few attosecond pulses separated by half of the laser period (1.3 fs) (36). Helium atoms are ionized by the attosecond pulses, in the presence of a weak fraction of the IR laser pulse. In contrast to RABBIT or streaking experiments, the delay between the XUV and the IR fields is kept fixed. Charged particles are detected using a 3D momentum spectrometer based on an electron–ion coincidence scheme (37, 38). Fig. 2B shows an example of a 3D photoelectron momentum distribution obtained in helium with XUV-only radiation. Since the momentum distribution has rotational symmetry along the polarization axis, we can define the photoelectron direction with positive (negative) $p_z$ as up (down). Simulations based on the Strong Field Approximation (39, 40) are described in Materials and Methods.

Fig. 2.

Experimental setup. (A) The 200-kHz 6-fs IR laser pulses with vertical polarization are sent through a wedge pair for CEP control and focused with an achromatic lens into a high-pressure argon gas jet. A tailored sequence of a few XUV attosecond pulses is then generated and focused by a gold-coated toroidal mirror into a 3D momentum spectrometer, where it intersects an effusive helium jet. An Al filter can be introduced to eliminate the copropagating IR field. (B) A 3D representation of electron momentum distribution as a function of azimuthal angle $\varphi$ and angle $\theta$ for XUV-only radiation.

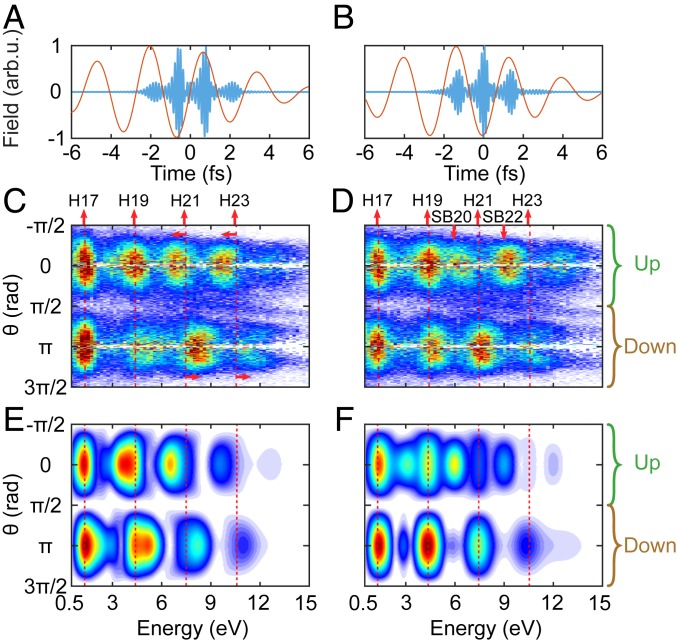
Fig. 3 shows photoelectron distributions as a function of angle and energy, in two cases corresponding to attosecond pulse trains generated by IR fields with CEPs equal to $\pi /2$ (Fig. 3A) and 0 (Fig. 3B). Measured and simulated results are shown in Fig. 3 C and D and Fig. 3 E and F, respectively. The XUV field, indicated by the blue solid line in Fig. 3 A and B, is obtained using a model (36) based on the three-step picture of high-order harmonic generation (41, 42), with ionization rates from ref. 43 and photoionization cross-sections from ref. 44. The predictions of the model have been checked against detailed experimental studies of HHG spectra as a function of dispersion (36).

Fig. 3.

XUV attosecond pulse trains and angular-resolved spectrograms. (A and B) XUV (blue) and IR (red) electric fields with (A) CEP = $\pi /2$ and (B) CEP = 0. (C–F) Color plots representing the photoelectron angular distributions as function of energy. The experimental results are shown in C and D, while corresponding simulated photoelectron spectra are shown in E and F. The red dashed lines indicate the photoelectron kinetic energies after absorption of XUV radiation. When two attosecond pulses are used, the electron distribution shifts in energy, in opposite ways for the up and down emission directions (in C and E). In the three-pulse case, sidebands appear, but only in the up direction (in D and F).

As shown in Fig. 3A, laser pulses with CEP equal to $\pi /2$, antisymmetric with respect to time reversal, lead to the generation of an even number of attosecond pulses. In our conditions, we obtain mainly two similar pulses with a phase difference of $\pi$, since they are generated by two consecutive half-cycles of the IR field. The resulting photoelectron distributions, shown in Fig. 3 C and E, are shifted toward lower energy in the up direction and higher energy in the down direction. The shift increases with kinetic energy.

As shown in Fig. 3B, laser pulses with CEP equal to 0, symmetric with respect to time reversal, lead to the generation of an odd number of attosecond pulses, with a main central pulse. In our conditions, we obtain three pulses. The resulting photoelectron distributions, shown in Fig. 3 D and F, depend on the direction of emission. In the down direction, photoelectrons are emitted with kinetic energies corresponding to absorption of harmonics 17 to 23. In the up direction, photoabsorption of harmonics 21 and 23 is strongly reduced, while new peaks corresponding to additional absorption/emission of an IR photon appear, so-called sidebands (SB20 and SB22). In general, measurements performed with different laser CEPs show both energy shifts and asymmetric appearance of sidebands. When the CEP is equal to $3\pi /2$ or $\pi$, very similar results to those shown in Fig. 3 C and D are obtained, except that the up and down directions are now reversed. In all of these cases, very good agreement is found between experiment and simulation.

Discussion

We now examine the behavior of the photoelectron distribution in the two cases by using an analytical derivation described in Materials and Methods. Assuming two pulses with the same amplitude and a spectral phase difference of $\pi$, the photoionization probability is proportional to

$${\left|a\left(\mathbf{p}\right)\right|}^2\propto {\sin }^2\left[\pi \mathrm{\Omega }/\left(2\omega \right)-{\eta }_p\right],$$ [1]

where $\mathrm{\Omega }=I_p/\hslash +{\mathbf{p}}^2/\left(2m_e\hslash \right)$ is the XUV frequency, with $\mathbf{p}$ as the final momentum of the photoelectron, $m_e$ as the electron mass, $\hslash$ as the reduced Planck constant, and $I_p$ as the ionization potential of helium. The phase shift ${\eta }_p$ is proportional to $\mathbf{p}\cdot {\mathbf{A}}_0$, where ${\mathbf{A}}_0$ is the maximum amplitude of the vector potential. The photoelectron distribution in frequency is modulated due to the interference between the EWPs created by the two attosecond pulses. In this case, the interaction with the IR field does not lead to new photoelectron structures (sidebands) but to a shift of the photoelectron peaks. These peaks appear at $\mathrm{\Omega }=\left(2q+1\right)\omega +2{\eta }_p\omega /\pi$, where q is an integer, which corresponds to the position of absorption by odd harmonics, shifted by a quantity proportional to ${\eta }_p$, thereby depending on the emission direction of the electron as shown in the spectra presented in Fig. 3 C and E.

In the case of a main attosecond central pulse and two similar side pulses as in Fig. 3B, as described in Materials and Methods, the photoionization probability is proportional to

$${\left|a\left(\mathbf{p}\right)\right|}^2\propto 1+4r^2{\cos }^2\left(\frac{\pi \mathrm{\Omega }}{\omega }\right)-4r\cos \left(\frac{\pi \mathrm{\Omega }}{\omega }\right)\cos \left[s\left(\mathrm{\Omega }\right)-2{\eta }_p\right],$$ [2]

where $s\left(\mathrm{\Omega }\right)$ is the difference in spectral phase, and $r$ is the amplitude ratio between the side and the central pulses. The second term comes from interference between the first and third EWPs, resulting in peaks at all harmonic frequencies. The third term describes interference between the central EWP and the other two, leading to enhancement or reduction of the sidebands with respect to the main peaks. This interpretation, based on the interference of a few EWPs, is consistent with a recent theoretical prediction (45). In traditional RABBIT, the spectral phase difference $s\left(\mathrm{\Omega }\right)$ is very small since it rapidly decreases as the pulse duration increases (36), so that the photoelectron distribution remains up–down symmetric. In our case, $s\left(\mathrm{\Omega }\right)$ is not negligible and leads to an up–down asymmetry of the photoelectron emission spectra. Finally, we verified that the difference in IR amplitude for the first and third attosecond pulses (Fig. 3B) does not change significantly the theoretical predictions.

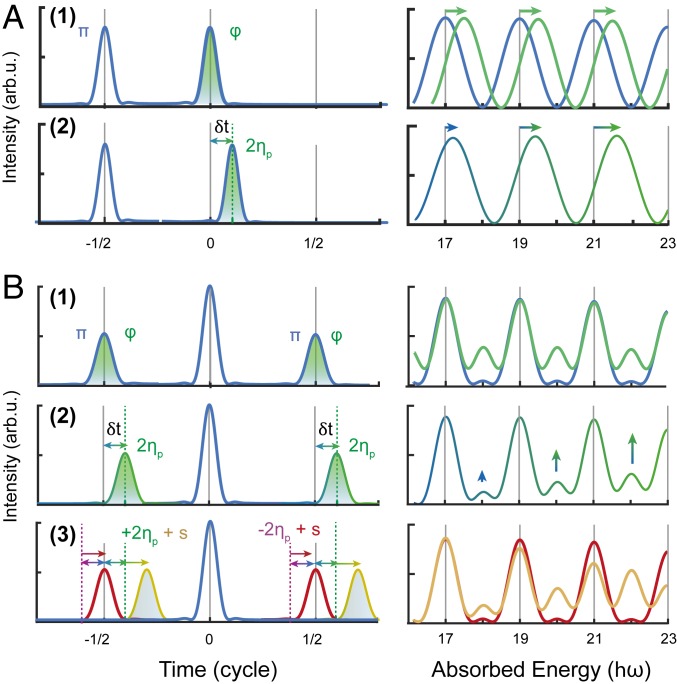
Finally, we give a simple interpretation of these results based on an analogy with diffraction through two or three slits (15, 46). Fig. 4A illustrates the two-EWP (or two-slit) case. The Fourier transform of a pair of pulses separated by $\pi /\omega$ leads to a modulation in the frequency domain equal to $2\omega$. When the phase difference between the pulses is $\pi$, constructive interferences take place at frequencies $\mathrm{\Omega }=\left(2q+1\right)\omega$, where $q$ is an integer, as illustrated in Fig. 4 A, 1. An additional constant phase ($\phi$) imparted in one of the EWPs shifts the interference fringes, as shown by the green curve. In our experiment, the phase difference between the two EWPs, equal to $2{\eta }_p$, increases with $\left|\mathbf{p}\right|$, which leads to a (small) time delay ($\delta t\approx$ 100 as) between the two EWPs and a shift increasing with frequency as shown in Fig. 4 A, 2. The sign of the frequency shift depends on the direction of emission of the photoelectron with respect to the polarization, resulting in an asymmetric angular distribution.

Fig. 4.

Interference through multiple temporal slits. (A) The interference of two EWPs separated by half of a laser cycle with a $\pi$ phase difference (Left, 1) leads to a modulation in the energy (frequency) domain, with maxima at the energies corresponding to excitation by odd harmonics (Right, 1, blue curve). A phase change, $\phi$, of one EWP shifts the interference fringes (1, green curve). A momentum-dependent phase change, $2{\eta }_p$ (2), leads to an energy-dependent shift of the interference fringes, as well as to a temporal shift ($\delta t$) of one EWP relative to the other. (B) The interference of three EWPs separated by half of a laser cycle with a $\pi$ phase difference (Left, 1) leads to interferences with maxima at the energies corresponding to excitation by odd harmonics, and weak “secondary” maxima at the SB position (Right, 1, blue curve). A phase change between the side and central EWPs ($\phi$) enhances the SB relative to the main peak (1, green curve). A momentum-dependent phase change ($2{\eta }_p$) leads to energy-dependent sideband amplitudes, but no energy shift (Right, 2). The spectral phase difference between consecutive attosecond pulses ($s$) enhances (yellow curve) or reduces (red curve) this effect depending on the direction of emission (3).

Fig. 4B illustrates the three-slit case. The Fourier transform of three pulses separated by $\pi /\omega$ and with $\pi$ phase difference leads to interference fringes still separated by $2\omega$ (Fig. 4 B, 1, blue), with a small contribution at frequencies $\mathrm{\Omega }=2q\omega$ (sidebands), called “secondary maxima” in the theory of diffraction. An additional phase shift ($\phi$) between consecutive EWPs (Fig. 4 B, 1, green) leads to an enhancement of the sideband peaks. In our experiment, the phase difference between consecutive EWPs due to the interaction with the IR field leads to time delays between the EWPs and to sideband intensities increasing with frequency, as shown in Fig. 4 B, 2. The spectral phase between the side and the central attosecond pulses, $s\left(\mathrm{\Omega }\right)$, can enhance (compensate for) this effect, increasing (reducing) the sideband intensities; see Fig. 4 B, 3. Since $s\left(\mathrm{\Omega }\right)-2{\eta }_p$ depends on the photoelectron emission direction, the angular distribution becomes asymmetric. The difference with the two-slit case comes from the fact that the two smaller EWPs have the same phase, which fixes the position of the constructive interferences at $\mathrm{\Omega }=q\omega$.

The asymmetry in the photoelectron direction of emission is here due to the difference in spectral phase between consecutive attosecond pulses, that is, the femtosecond chirp of the harmonic emission. This result has a simple interpretation in the spectral domain. The harmonic width becomes broad enough for spectral overlap between the continua reached by two-photon (XUV+IR) and one-photon (XUV) ionization, leading to parity mixing and asymmetric electron emission.

Summary and Outlook

The analogy with diffraction by multiple slits allows us to understand the difference in electron spectra observed in our experiments, depending on the XUV pulse sequence used for the photoionization. The underlying physics presented has a strong analogy to the physics of atoms or molecules in strong laser fields, where ATI and high-order harmonic generation spectra can be explained in terms of time-slit interferences between EWPs created by tunneling at each half laser cycle (15). Here, EWPs are created by single-photon absorption of XUV radiation. Their interference is controlled both by the relative amplitude and phase of the XUV attosecond pulses and by an additional phase modulation due to the weak IR field.

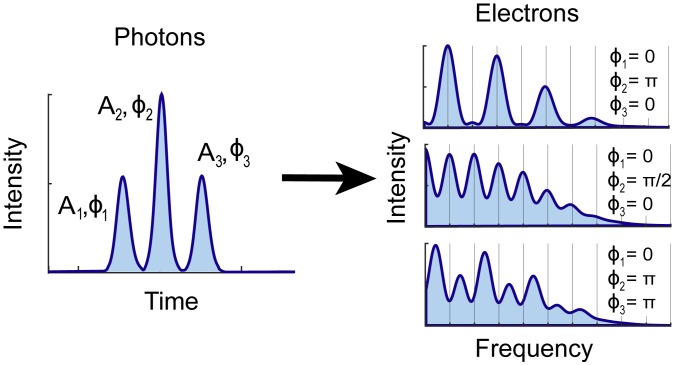
In general, as illustrated in Fig. 5, attosecond time domain control using a sequence of attosecond XUV pulses in combination with a weak synchronized IR field allows the manipulation of the electron spectrum by (time-slit) quantum interferences. This is the reverse of traditional optical pulse shaping, with aim to obtain a well-defined pulse sequence, by manipulating frequency components in the Fourier plane (47, 48). The achieved control enables generation of electrons at any energy and in a certain emission direction, thus circumventing the well-established (but idealized) rules of the photoelectric effect.

Fig. 5.

Attosecond time domain control: By manipulating the phase and amplitude of a sequence of attosecond pulses, photoionization of atoms and molecules can be controlled in the frequency domain. The addition of a weak IR pulse allows for additional phase control.

Our results open a road in attosecond science, namely, the manipulation of ultrafast processes with a tailored sequence of attosecond pulses, combined with a synchronized weak IR field. From the experimental point of view, this achievement is possible thanks to the high CEP stability and short pulse duration of our laser system. In addition, the high repetition rate of our experiment allows us to measure 3D momentum electron distributions with electron–ion coincidence detection, thus providing a complete kinematic description of the interaction. We envision numerous applications of the time domain coherent control shown in the present work, for example, toward 2D spectroscopy of more-complex systems at the attosecond temporal resolution and in the XUV spectral range.

Materials and Methods

Experiment.

The experiment was performed with a 200-kHz-repetition rate CEP-stable optical parametric chirped pulse amplification laser system with 5 $\mathrm{\mu }$J of energy per pulse, 820-nm central wavelength, and 6-fs pulse duration. The CEP of the laser can be varied with a fused silica wedge pair, as shown in Fig. 2A. The laser pulses are focused using an achromatic lens with 5-cm focal length in an argon gas jet with a 10-bar backing pressure (49). High-order harmonics are generated, corresponding, in the time domain, to a train of (primarily) two to three attosecond pulses (36). An aluminum filter can be introduced to eliminate the IR field, and a concave grating (not shown in Fig. 2) can be inserted after the differential pumping hole in order to disperse the XUV radiation and measure its spectrum with microchannel plate detector. The IR field, with an intensity less than ${\mathrm{10}}^{12}$ W/${\mathrm{c}\mathrm{m}}^2$, and the XUV radiation are focused by a gold-coated toroidal mirror into a vacuum chamber containing an effusive helium gas jet and a 3D momentum spectrometer (Fig. 2A). This spectrometer is based on a revised “Coïncidences entre Ions et Électrons Localisés” design, providing a complete kinematic momentum picture of the emitted ions and electrons without losing data due to magnetic nodes (50). The spectrometer orientation is chosen so that the time-of-flight axis coincides with the optical polarization direction. Electron–ion coincidence data are recorded at a typical rate of $\sim$35 kHz, with a negligible amount of false coincidence.

The rotational symmetry of the momentum distribution around the $p_z$ axis (polarization axis) means that the signal can be integrated along the azimuthal angle $\varphi$ and subsequently divided by $\sin \theta$, giving the differential cross-section. In the XUV-only case, four rings can be identified (Fig. 2B), corresponding to ionization ($1s\to ϵp$) by absorption of harmonics 17, 19, 21, and 23.

Simulations.

The simulations presented in Fig. 3 E and F have been performed by evaluating the probability amplitude for emission with momentum $\mathbf{p}$ (40),

$$a\left(\mathbf{p}\right)=-i{\int }_{-\infty }^{\infty }dt\hspace{0.17em}\mathbf{d}\left(\mathbf{p}\right)\cdot {\mathbf{E}}_{\mathrm{X}\mathrm{U}\mathrm{V}}\left(t\right)\hspace{0.17em}{e}^{\frac{i}{\hslash }\left(I_p+\frac{{\mathbf{p}}^2}{2m_e}\right)t+i{\mathrm{\Phi }}_{\mathrm{I}\mathrm{R}}\left(\mathbf{p},t\right)},$$ [3]

where $\mathbf{p}$ denotes the final electron momentum, $\mathbf{d}$ is the dipole moment, E_XUV is the XUV field, $m_e$ is the electron mass, $\hslash$ is the reduced Planck constant, and $I_p$ is the ionization potential of helium. In the relatively weak field case which is considered in the present work, the action of the laser field reduces to a phase modulation, approximated by

$${\mathrm{\Phi }}_{\mathrm{I}\mathrm{R}}\left(\mathbf{p},t\right)\approx -\frac{e}{m_e\hslash }{\int }_t^{+\infty }dt\prime \mathbf{p}\cdot \mathbf{A}\left(t\prime \right),$$ [4]

where $\mathbf{A}$ is the vector potential of the IR field. The dipole moment $\mathbf{d}\left(\mathbf{p}\right)$ is calculated with an hydrogenic approximation (39), while both the IR and the XUV fields have been chosen to reproduce the experimental conditions as closely as possible. The XUV attosecond pulses are generated at an IR intensity of $1.1\times 10^{14}$ W/${\mathrm{c}\mathrm{m}}^2$, and the IR intensity in the detector chamber is $6\times 10^{11}$ W/${\mathrm{c}\mathrm{m}}^2$. For a temporal offset $\tau$ between attosecond pulses and the IR dressing field of $\sim$0.6 optical cycle, excellent agreement between experiment and theory is achieved.

Analytical Derivation.

The XUV field, ${\mathbf{E}}_{\mathrm{X}\mathrm{U}\mathrm{V}}\left(t\right)={\sum }_m{\mathbf{E}}_m\left(t-m\pi /\omega \right)$, can be decomposed into a sum of attosecond pulses ${\mathbf{E}}_m$, separated by half of the laser period $\pi /\omega$ and centered at $m\pi /\omega$. The XUV and IR fields have the same linear polarization, so we may drop the vector notation unless needed. Assuming that the phase ${\mathrm{\Phi }}_{\mathrm{I}\mathrm{R}}\left(\mathbf{p},t\right)$ does not vary much over the duration of the attosecond pulse, introducing the XUV frequency $\mathrm{\Omega }=I_p/\hslash +{\mathbf{p}}^2/\left(2m_e\hslash \right)$ and changing the variable in the temporal integral, $t\to t-m\pi /\omega$, Eq. 3 becomes

$$a\left(\mathbf{p}\right)\approx -id\left(\mathbf{p}\right)\sum _m{e}^{i{\mathrm{\Phi }}_{\mathrm{I}\mathrm{R}}\left(\mathbf{p},\frac{m\pi }{\omega }\right)}{\int }_{-\infty }^{+\infty }dt\hspace{0.17em}{E}_m\left(t\right)\hspace{0.17em}{e}^{i\mathrm{\Omega }\left(t+\frac{m\pi }{\omega }\right)}.$$ [5]

Using $\mathbf{A}\left(t\right)=-{\mathbf{A}}_0\sin \left[\omega \left(t-\tau \right)\right]$, Eq. 4 is equal to

$${\mathrm{\Phi }}_{\mathrm{I}\mathrm{R}}\left(\mathbf{p},\frac{m\pi }{\omega }\right)=\frac{e\mathbf{p}\cdot {\mathbf{A}}_0}{m_e\hslash \omega }{\left(-1\right)}^m\cos \left(\omega \tau \right),$$ [6]

which we can write in a more compact form as ${\left(-1\right)}^m{\eta }_p$. The Fourier transform of $E_m\left(t\right)$ is the spectral amplitude $E_m\left(\mathrm{\Omega }\right)=\left|E_m\left(\mathrm{\Omega }\right)\right|\exp \left[im\pi +i{\mathrm{\Phi }}_m\left(\mathrm{\Omega }\right)\right]$, where the first phase term describes the $\pi$ change between consecutive attosecond pulses, and ${\mathrm{\Phi }}_m\left(\mathrm{\Omega }\right)$ is the spectral phase of the attosecond pulse. Eq. 3 can be written in a compact form as

$$a\left(\mathbf{p}\right)\approx -id\left(\mathbf{p}\right)\sum _m{e}^{i{\left(-1\right)}^m{\eta }_p}{e}^{\frac{im\pi \mathrm{\Omega }}{\omega }}{E}_m\left(\mathrm{\Omega }\right).$$ [7]

In the perturbative limit (${\eta }_p\ll 1$), Eq. 7 can be written as the sum of two terms. The first term describes ionization by absorption of one photon,

$$a_1\left(\mathbf{p}\right)\approx -id\left(\mathbf{p}\right)\sum _m{e}^{i\frac{m\pi \mathrm{\Omega }}{\omega }}{E}_m\left(\mathrm{\Omega }\right).$$ [8]

When consecutive attosecond pulses have approximately the same amplitude and a phase difference of $\pi$, $a_1\left(\mathbf{p}\right)$ is maximum when $\mathrm{\Omega }=\left(2q+1\right)\omega$, where $q$ is an integer, corresponding to ionization by absorption of odd-order harmonics of the laser field. The second term includes the interaction with the IR field,

$$a_2\left(\mathbf{p}\right)={\eta }_{p}d\left(\mathbf{p}\right)\sum _m{\left(-1\right)}^m{e}^{\frac{im\pi \mathrm{\Omega }}{\omega }}{E}_m\left(\mathrm{\Omega }\right).$$ [9]

When consecutive attosecond pulses have approximately the same amplitude and a phase difference of $\pi$, $a_2\left(\mathbf{p}\right)$ is maximum when $\mathrm{\Omega }=2q\omega$, where $q$ is an integer, leading thus to sideband peaks in the photoelectron distribution, at energies that would correspond to ionization by absorption of even-order harmonics.

When the two terms do not overlap spectrally, ${\left|a\left(\mathbf{p}\right)\right|}^2\approx {\left|a_1\left(\mathbf{p}\right)\right|}^2+{\left|a_2\left(\mathbf{p}\right)\right|}^2$, and the photoelectron spectrum, which consists of a series of peaks at energies corresponding to absorption of both an odd and even number of IR photons, is symmetrical with respect to the $p_x$, $p_y$ plane. If, on the other hand, the two contributions overlap spectrally, the photoelectron spectrum will become asymmetric, due to the term ${\eta }_p\propto \mathbf{p}\cdot {\mathbf{A}}_0$, which is opposite for the photoelectrons emitted upward or downward. We now examine photoionization by two and three attosecond pulses.

Two Pulses.

In the case of two pulses ($m=\mathrm{0,1}$) with equal amplitude $\left|E_0\left(\mathrm{\Omega }\right)\right|$, spectral phase ${\mathrm{\Phi }}_0\left(\mathrm{\Omega }\right)$, and a phase difference of $\pi$, Eq. 7 simplifies to

$$a\left(\mathbf{p}\right)=-id\left(\mathbf{p}\right)E_0\left(\mathrm{\Omega }\right)\left(e^{i{\eta }_p}-e^{-i{\eta }_p+i\frac{\pi \mathrm{\Omega }}{\omega }}\right),$$ [10]

so that (Eq. 1)

$${\left|a\left(\mathbf{p}\right)\right|}^2=4{\left|d\left(\mathbf{p}\right)\right|}^2{\left|E_0\left(\mathrm{\Omega }\right)\right|}^2{\sin }^2\left(\frac{\pi \mathrm{\Omega }}{2\omega }-{\eta }_p\right).$$ [11]

Three Pulses.

We now consider three pulses, $m=-\mathrm{1,0,1}$, with a central pulse and two smaller, identical, satellite pulses (Fig. 3B). We introduce the ratio $r=\left|E_{\pm 1}\left(\mathrm{\Omega }\right)\right|/\left|E_0\left(\mathrm{\Omega }\right)\right|$ and the difference in spectral phase $s\left(\mathrm{\Omega }\right)={\mathrm{\Phi }}_{\pm 1}\left(\mathrm{\Omega }\right)-{\mathrm{\Phi }}_0\left(\mathrm{\Omega }\right)$. We obtain

$$a\left(\mathbf{p}\right)=-id\left(\mathbf{p}\right)E_0\left(\mathrm{\Omega }\right)\left(e^{i{\eta }_p}-2r{e}^{-i{\eta }_p+is\left(\mathrm{\Omega }\right)}\cos \left(\frac{\pi \mathrm{\Omega }}{\omega }\right)\right).$$ [12]

The absolute square of the parenthesis is Eq. 2.

Temporal Slits.

Finally, the temporal slit analogy mentioned in the main text is formally based on Eq. 5, representing a sum of attosecond EWPs.

Data Availability Statement.

All data discussed in the paper are available on the Swedish National Data Service (51).