Highlights
-
•
Compartmental SIQR model to study COVID-19 evolution in Rio de Janeiro.
-
•
Implementation of containment rules.
-
•
Analysis of the efficacy of social distancing policies.
Keywords: Dynamics of social systems, Epidemic modeling, Collective phenomena, Data analysis
Abstract
The recent Coronavirus has been spreading through all the world fastly. In this work we focus on the evolution of the COVID-19 in one of the most populous Brazilian states, namely the Rio de Janeiro state. The first case was reported in March 5, 2020, thus we have a considerable amount of available data to make a good analysis. We study the dynamics of COVID-19 through a Susceptible-Infectious-Quarantined-Recovered (SIQR) model with an additional mechanism that represents the implementation of public policies of social isolation. Based on the data collected from the Rio de Janeiro state Department of Health from March 5, 2020 through April 26, 2020, we observed that the implementation of social distancing policies changed the initial exponential growth to a sub-exponential one. The SIQR model with the above-mentioned mechanism is capable of reproducing the data of confirmed cases in Rio de Janeiro, and it explains how that change occurred. The model also predicts an important mitigation effect, namely the flattening effect, i.e., the considerably decrease of the maximum number of confirmed cases. Through the results of the model, this effect can be directly related to the social isolation policies. Finally, we consider the relaxation of such policies, and discuss about the ideal period of time to release people to return to their activities.
1. Introduction
The world observed recently the emergence of a new pandemic, the COVID-19 (coronavirus 2) caused by severe acute respiratory syndrome SARS-CoV-2 [1]. As other pandemics observed during the time, COVID-19 has been caused a lot of fatal victims. The emergence of diverse epidemics led the scientific community to developed diverse methods to study and analyze the evolution of diseases. The classical compartmentals mathematical models are usually the starting point for the study of epidemics [2], [3].
In the last two months a considerable number of works was published considering studies related to the COVID-19 evolution through the world [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22]. Some of such papers considered the case of Brazil. Our interest in this work is to study the evolution of COVID-19 in one of the most populous Brazilian states, namely the Rio de Janeiro state.
The first case in the Rio de Janeiro state was reported in the Rio de Janeiro city in March 5, 2020. After that, the disease spreaded to all the State, achieving the majority of state’s cities. To avoid the rapid growth of the number of cases, the Rio de Janeiro state government implemented some policies of social isolation. Such policies were started at March 17, 2020, and of course they lead some days to produce effective results. The government did not imposed a lockdown, they suggested people to stay in home, schools and universities were closed, public events were banning, and only the essential activities are in progress, for example delivery of food, drugstories, supermarkets, and so on. The mentioned policies continue to be implemented in May, 2020: no lockdown was imposed to the population, the government continues asking population to stay home, and the police is monitoring agglomerations to avoid the rapid dissemination of the virus.
The target of this work is to implement social isolation in a simple way in a compartmental epidemic model, and study it impact on the evolution of cases in Rio de Janeiro state. In this case, we consider a Susceptible-Infectious-Quarantined-Recovered (SIQR) model. Based on the data collected from the Rio de Janeiro state Department of Health [23], one observed that the social distancing policies led about 7 days to effectively decrease the rate of growth of confirmed cases in Rio de Janeiro. In this case, we observe a sub-exponential growth of cases, and this nonexponential behavior is reproduced by our model. Finally, we used the model to discuss about the relaxation of such isolation policies, since this is in discussion by the Rio de Janeiro state government.
This work is organized as follows. Section 2 is divided in two subsctions. In the first one, we present the SIQR model, and define its parameters, in order to study the early evolution of the COVID-19 in Rio de Janeiro state. In the second subsection we consider the implementation of isolation policies, and study their impact on the dynamics of the SIQR model. Finally, we present a discussion in Section III. Some other details are presented in the Appendix.
2. Methodologies and COVID-19 overview
2.1. Model
To study the evolution of the COVID-19, we consider a Susceptible-Infectious-Quarantined-Recovered (SIQR) model with containment [5], [15], [24]. The individuals in the population are divided in 4 compartments, namely:
-
•
Susceptible individuals (S): the healthy ones. They are individuals that were not contaminated by COVID-19;
-
•
Quarantined individuals (Q): we are observing that the governments (including the Rio de Janeiro governor’s) are forcing individuals tested positive (confirmed cases) to self-isolate from the community (quarantine). These individuals will be called Quarantined individuals;
-
•
Infectious individuals (I): represent individuals infected by COVID-19 but that did not develop symptoms and are not aware of actually being infectious, or individuals with mild symptoms;
-
•
Recovered individuals (R): the individuals that have recovered from COVID-19.
The dynamics of the model is defined as follows. A Susceptible individual can be infected by COVID-19 with rate β if he/she is in contact with an Infected (I) individual (S → I). A given I individual can be tested for COVID-19 with rate η, and in this case he/she is forced to quarantine (I → Q). On the other hand, the I individuals that did not develop symptoms or present mild symptoms are not quarantined, and they can recover from COVID-19 with rate α (I → R). A Quarantined (Q) individual, after being isolated, will recover from the disease with rate γ (Q → R). Finally, we have to consider the self-isolation of individuals due to the implementation of public policies of social distancing. A simple form to modeling the isolation policies is to consider a mechanism that can be interpreted as a process of removing susceptibles from the transmission process, as discussed recently [15]. Thus, we consider that S individuals are removed from the dynamics with a containment rate k 0.
Thus, our model may be described by the following equations:
| (1) |
| (2) |
| (3) |
| (4) |
Eqs. (1) –(4) describes the dynamics of the disease spreading, taking into account the parameters β, k 0, α, η and γ, denoting the infection rate, the containment rate, the recovering of asymptomatic individuals, detection of infected individuals and recovering of quarantined individuals, respectively. The simplified case case corresponds the to a scenario in which the general population is unaffected by policies or does not commit behavioral changes in response to an epidemic.
In the next subsections, we discuss separately two stages of the evolution of COVID-19 in Rio de Janeiro state. The first one is the early evolution of the disease, in the last 20 days since the first confirmed case, where the growth of cases show the usual exponential behavior. After that, the implementation of public policies of social distancing changed the growth of cases, and we study this second phase separately.
2.2. Initial evolution of COVID-19
First, we wil consider the early evolution of COVID-19 in Rio de Janeiro state. As pointed in the Introduction, the first documented case occurred in March 5, 2020 [23]. So, we considered the first days of the evolution of the disease, namely from March 5, 2020 through March 24, 2020. As it is usual, we expect an exponential growth of the number of confirmed cases in such initial phase of the epidemics.
To study the initial evolution of the COVID-19, we consider the model defined in Eqs. (1)–(4) with . As pointed above, the simpler case case corresponds to a scenario in which the general population is unaffected by policies or does not commit behavioral changes in response to an epidemic. Indeed, the social isolations policies were not implemented in the initial stage of the disease in Rio de Janeiro.
We are discussing the early evoution of COVID-19 in Rio de Janeiro (first 20 days). Thus, a relatively small fraction of the state’s population has been found positive for COVID-19, which means we have S/N ≈ 1. In this case Eq. (2) can be approximated to that can be directed integrated to obtain
| (5) |
where I 0 is the number of infectious individuals at the beginning of the outbreak. Eq. (5) can be rewriten as and one can obtain the expression for the basic reproduction number R 0,
| (6) |
One can found a relevant analytical expression summing Eqs. (3) and (4),
| (7) |
Substituting the result (5) in Eq. (7) and integrating over t, one obtains
| (8) |
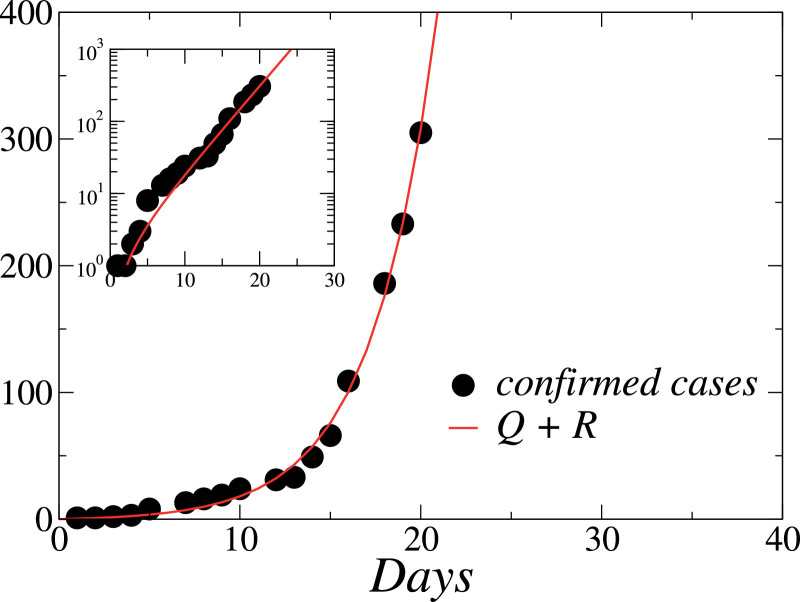
We fitted Eq. (8) to the Rio de Janeiro state COVID-19 data [23] from March 5, 2020 through March 24, 2020. The estimated values were and . First, we can estimate I 0, the number of infectious individuals at the beggining of the outbreak. Based on the data, we take . Considering this value, the above fitted results give us and . Following the discussion in Pedersen and Meneghini [5], we have and . Considering those estimates, we plot in Fig. 1 the temporal evolution of the number of cases together with Eq. (8).
Fig. 1.
(Color online) Comparison between the number of confirmed cases in Rio de Janeiro state (circles) and Eq. (5) (full line), for the initial epidemic phase. In this case, we considered i.e., no implementation of isolation policies. The parameters are as discussed in the text. In the inset we exhibit the graphic in the log-linear scale, showing the typical linear behavior of the exponential function.
Taking the estimated values, from Eq. (6) we estimate R 0 ≈ 7.7, that is compatible with the range 1.4 < R 0 < 6.5 estimated for China [7], [10], [11], [12]. One can also estimate the epidemic doubling time, that characterize the sequence of intervals at which the cumulative incidence doubles. From Eq. (5) the doubling time is given by
| (9) |
Based on Eq. (9), and on the estimated parameters, we have τ ≈ 2.5 days, which falls in the range 1.4 < τ < 3.1 estimated for China [13].
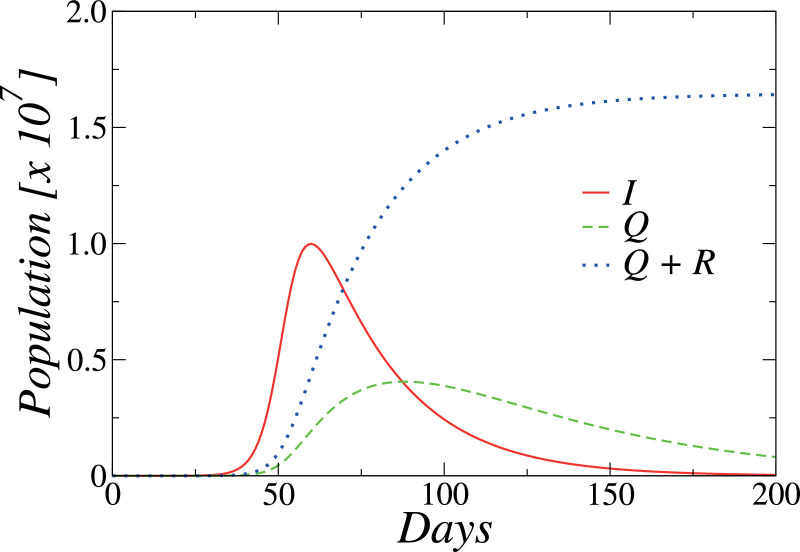
Considering the estimated parameters, we exhibit in Fig. 2 the time evolution of the number of Infected (I), Quarantined (Q) and total confirmed cases (Q+R), obtained by the numerical integration of the Eqs. (1)–(4). For these curves, we considered N as the total population of the Rio de Janeiro state, . One can see that the number of infected and nonconfirmed cases I grows faster than the number of quaratined individuals Q (confirmed cases). This unbalance is observed in all the world, since there is a huge number of undocumented infection cases for the COVID-19, as discussed in a recent work [4].
Fig. 2.
(Color online) Time evolution of the number of Infected (I), Quarantined (Q) and total confirmed cases (Q+R) predicted by the SIQR model, for the initial epidemic phase, obtained by the numerical integration of Eqs. (1)–(4) with (no isolation policies). The parameters are and .
The above-mentioned unbalance among I and Q individuals can be estimated by the model. Taking the ratio of Eqs. (3) and (2), and considering the obtained approximated result for short times, one can obtain [5]
| (10) |
Eq. (6) gives us I/Q ≈ 14.5, i.e., for each patient in quarantine approximately 14 infectious individuals are present in the population. This number is greater than the estimated for Italy (I/Q ≈ 10) [5] and China (I/Q ≈ 7) [4], but due to the very small number of tests made in all Brazilian states, it is compatible with the estimate 12–15 made in brazilian studies [25].
2.3. Implementation of isolation policies
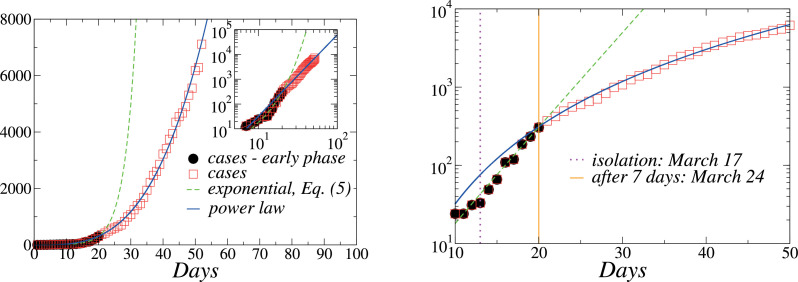
In Fig. 3 (left side) we plot the data of confirmed cases of COVID-19 for the Rio de Janeiro state, now considering all the evolution of cases, from March 5, 2020 through April 26, 2020, obtained from [23]. For comparison, we also plot Eq. (8) (dashed line) together with data of the initial epidemic phase. As one can see, the behavior is not purely exponential, as was the case for the early growth of cases discussed in the previous subsection. This is consequence of the policies of social isolation implemented by the Rio de Janeiro state governement. Indeed, the number of confirmed cases is still growing, but this growth is slower than the initial exponencial behavior. We observed a linear behavior when we plot the data in the log-log scale, as observed in the data from several provinces of China [15], as well for some other countries [26]. Thus, to guide the eyes, we also exhibit a power law function (full line).1 As one can see in Fig. 3 (left side), the confirmed cases are growing sub-exponentially. We also exhibit in Fig. 3 (right side) the same curves in the log-linear scale. The vertical dotted line marks the beginning of the isolation policies in Rio de Janeiro (March 17, 2020). One can see that the social distancing policies changed the initial exponential growth after 7 days (March 24, 2020).
Fig. 3.
(Color online) Left panel:Time evolution of the total number of confirmed cases from March 5, 2020 through April 26, 2020 (squares). The dashed line is given by Eq. (5). As a guide to the eyes, we also show a power law fit of the data (full line). In the inset we exhibit the same data in the log-log scale. Right panel: Log-linear plot of the same quantities. The vertical dotted line marks the beginning of the isolation policies in Rio de Janeiro (March 17, 2020). One can see that the social distancing policies changed the initial exponential growth after 7 days (March 24, 2020).
In this case, to reproduce the mentioned sub-exponential behavior of the number of confirmed cases, we have to consider the model defined by Eqs. (1)–(4) with k 0 ≠ 0, which represents the implementation of public policies of social distancing.
Typically in outbreaks a small number of people are infected initially. In this case, we have for small times S/N ≈ 1 and I ≈ 0, such that Eq. (1) can be linearized, yielding the solution [15]
| (11) |
which implies that the depletion of susceptibles available to the transmission process will be dominated by shutdown policies. Considering this result, one can integrate Eq. (2) to obtain
| (12) |
For small values of t we can expand the exponential in the last term to obtain the approximate growth function
| (13) |
The first factor implies that quarantining infecteds merely decreases the rate with which their number will grow exponentially, as occurred in the SIQR model studied in the previous subsection. On the other hand, the second term suppresses the whole transmission process well enough to alter the growth behavior, due to the quadratic term t 2. This implies that public shutdown policies facilitate epidemic containment in a more effective way than quarantine measures [15].
We can add Eqs. (6) and (7), one obtains . Using Eq. (13) in this last result and integrating over t, one obtains
| (14) |
where erf(x) is the error function, and we have and and .
Observe that we are not anymore in the early evolution of COVID-19. In such case, Eqs. (11)–(14) are poor approximations for the real evolution of Eqs. (1)–(4). Thus, a fitting procedure based on the data together with Eq. (14) will not give accurate parameters, but they can be usefull. In such case, fitting Eq. (14) to the data of confirmed cases from March 5, 2020 through April 26, 2020, we obtained and . Based on such values, the estimated parameters are (considering see bellow) and . Eq. (14) can fit well the data, however if we consider the estimated parameters and perform a numerical integration of the model’s Eqs. (1)–(4), there is a good agreement only for short times. This explains why we will fit the data for the window March 5, 2020 through April 26, 2020, with other values of the parameters, namely and . Finally, the time in our graphics were counted after the first confirmed case in Rio de Janeiro state, i.e., Day 1 was March 5, 2020. The number of confirmed cases kept almost constant for some days, and start to grow faster since day 10 (March 14, 2020), where 24 cases were confirmed. In this case, we take the number of initial cases as for the model’s purposes.
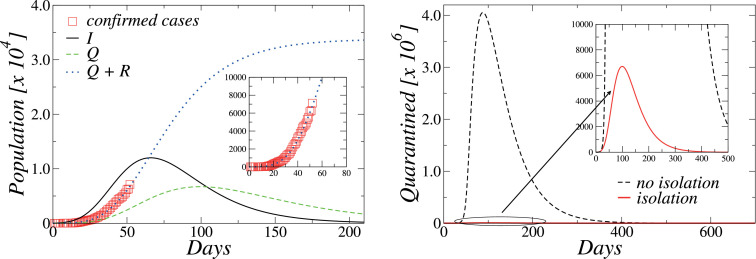
In Fig. 4 (left side) we plot the total number of confirmed cases of COVID-19 in Rio de Janeiro state, as well as the temporal evolution of the quantity numerically predicted by the model. There is a good agreement between data and model for the adjusted parameters and . For comparison with the model with no isolation policies, we also plot in Fig. 4 (right side) the evolution of the Quarantined (Q) individuals for the above-mentioned parameters, and the same quantity obtained in the absence of isolation measures (namely, for ). One can see the flattening of the curve: the maximum number of quarantined individuals decreases considerably, even for a small value of k 0.
Fig. 4.
(Color online) Left panel: Time evolution of the number of Infected (I), Quarantined (Q) and total confirmed cases (Q + R) considering isolation policies, obtained by the numerical integration of Eqs. (1)–(4). Data of confirmed cases are exhibited as well (squares). In the inset we show a zoom in the region of the current data (from March 5, 2020 through April 26, 2020), to highlight the agreement of the model with the data. Right panel: Flattening the curve: comparison between the predicted number of Quarantined individuals for the model with (full line) and without (dashed line) the implementation of isolation policies. The peak of the curve is considerably reduced. In both figures the parameters are and .
Considering the result of Fig. 4 (right side), the peak of the Quarantined individuals is expected to occur in the Day 99, i.e., June 11. Some local governments in Brazil are discussing about the relaxation of isolation of people including the Rio de Janeiro state government. A question of practical interest arises: when is it really safe to relax the isolation policies? To address this issue, we considered the following slight modification of the model presented in this section. In this case, the dynamics is implemented normally considering Eqs. (1)–(4) from the initial time until a given time step t′. After t′, we take in order to simulate the relaxation of isolation policies, and the model is reduced to the SIQR model presented in section II.A. The equations are integrated numerically, and the results for distinct times t′ are exhibited in Fig. 5 . One can see that if the relaxation of isolation policies is started at (May 4, 2020), the result is disastrous: the peak of Quarantined individuals increases fast. However, one can also see in Fig. 5 that after June 1, 2020, there is no considerably change in the peak, suggesting a security date to relax the isolation policies. Even after May 20 the peak does not increase considerably, which lead us to conclude that if the end of isolation procedures occurs about June 1 the damage will not be considerable.
Fig. 5.
(Color online) Time evolution of the number of Quarantined (Q) individuals. The full line represents the main result of section 2.2, i.e., the original model with isolation policies (). The other curves represent the relaxation of such policies, starting from the days t′ indicated in the graph. The inset shows a zoom of the smallest peaks. One can see that after June 1, 2020 there is no considerably change in the peak.
3. Results
To summarize, in this work we study the evolution of COVID-19 cases in the Rio de Janeiro state, Brazil. The number of confirmed cases are still growing. Based on the data, we considered a SIQR model on a fully-connected population in order to study the evolution of the disease. Initially, when we do not have social isolation policies, the growth of cases is fast, and we identified a exponential growth. The parameters of such early epidemic phase such as the epidemic doubling time and the ratio unidentified infected and confirmed infected indiviudals were estimated, based on the data.
After the initial exponential growth, the implementation of isolation policies changed the growth to a sub-exponential one. The model is capable of reproduce the data, since we considered an additional mechanism in the SIQR model, simulating the action of public policies of social distancing. The model also predicts the so-called flattening the curve effect, when the maximum number of confirmed cases is reduced due to social isolation.
However, this isolation can not lead an infinite time, due to economic consequences for the state. In this case, the government is discussing about the relaxation of the isolation policies. In this case, we simulated the relaxation of isolation policies in our model, considering that the isolation procedures will be adopted by the population until a given number of days, namely until a time step t′ in the model. Thus, after such time step t′ the isolation parameter k 0 is taken to zero, simulating the relaxation of people isolation at home. Analyzing distinct values of t′, we concluded that if the end of isolation procedures occurs about June 1 the damage will not be considerably. A recent work, considering some countries, also suggested that the social distancing policies need to continued for some time in order to really produce effective results [26].
4. Discussion
As as discussed in the text, the Rio de Janeiro state governement implemented isolation policies in March 17, 2020, in order to avoid the explosion of cases of COVID-19. After the initial exponential growth of cases (from March 5 to March 24), the cases continue to growth, but it exhibits a distinct, sub-exponential behavior. The SIQR model with containment is capable of reproduce the mentioned sub-exponential behavior. Considering the data, we have observed that the initial exponential behavior changed to the sub-exponential one about 7 days after the implementation of social distancing policies.
We found that the isolation policies really work, i.e., the fact of isolate people in home, to avoid social contacts, decreased the growth rate of the number of cases. For the considered parameters, we observed that the number of quarantined individuals grows, stabilizes and after it decays to zero, as it is standard in compartmental models. Based on the data, we can see that the number of such isolated individuals grows until Day 99 from the beginning (March 5, 2020) of the disesase spreading. Thus, the model predicts that the maximum number of quarantined individuals will occur about June 11, 2020. This is in line with a recent estimate [9]. That peak is associated with the quarantine of about 0.041% of the Rio de Janeiro state population (about 6700 individuals). This number is about 600 times lower than the one predicted by the SIQR model without isolation policies (taking ), suggesting the effectiveness of the social isolation. In fact, combining quarantine of individuals tested positive (confirmed cases) with social distance, i.e., multiple interventions, appears to be effective to contain the rapid evolution of confirmed cases seen in the early evolution of the COVID-19 in Rio de Janeiro state. This is in line with a recent work [9], where the authors analyzed the potential role of nonpharmaceutical interventions in UK and USA. They conclude that the effectiveness of any one intervention in isolation is likely to be limited, requiring multiple interventions to be combined to have a substantial impact on transmission.
5. Conclusion and future research
Concluding, we proposed in this work to study the dynamics of COVID-19 in Rio de Janeiro state, Brazil, by means of a SIQR model with containment policies. We confronted the model results with data from the Rio de Janeiro state Department of Health [23], and the agreement among data and our numerical results is very good. The data shows that the social distancing policies led about 7 days to change the initial exponential growth of cases and to effectively decrease the rate of growth of confirmed cases in Rio de Janeiro. The relaxation of isolation policies was also discussed, in order to avoid a second wave of cases.
The impact of isolation policies in the economy is important to be adressed. There is a fraction of the population related to the informal economy sector. These individuals are less propensed to self isolate, which impacts in the spreading of COVID-19. It can be interesting to split the population in two groups: one related to the informal economy, and another group that has the option of self-isolation. This analysis will enrich the model, and it can help the polciy makers to improve both the social isolation policies and the support to the fraction of the population that cannot afford for the self-isolation. The explicity analysis of deaths also need to be studied. Those proposals certainly will be considerd in future works.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The author acknowledges financial support from the Brazilian scientific funding agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq, Grant 303025/2017-4) and Fundação de Amparo à Pesquisa do Estado do Rio de Janeiro (FAPERJ, Grant 203.217/2017). Further discussions with Lucas Sigaud are also acknowledged.
Footnotes
We obtained from a least square fitting and .
References
- 1.Gorbalenya A. L.. Severe acute respiratory syndrome-related coronavirus: the species and its viruses a statement of the Coronavirus Study Group. 2020. BioRxiv10.1101/2020.02.07.937862.
- 2.Anderson R.M., May R.M. Oxford University Press; Oxford: 1991. Infectious diseases of humans: dynamics and control. [Google Scholar]
- 3.Bailey N.T.J. Hafner Press; New York: 1975. The mathematical theory of infectious diseases and its application. [Google Scholar]
- 4.Li R. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2) Science. 2020;368:489. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Pedersen M.G., Meneghini M.. Quantifying undetected COVID-19 cases and effects of containment measures in Italy: predicting phase 2 dynamics. 2020. Preprint, ResearchGate10.13140/RG.2.2.11753.85600
- 6.Zhou F. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. Lancet Online First. 2020 doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhou T. Preliminary prediction of the basic reproduction number of the Wuhan novel coronavirus 2019-nCoV. J Evid Based Med. 2020;13:3–7. doi: 10.1111/jebm.12376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kraemer M.U.G.. The effect of human mobility and control measures on the COVID-19 epidemic in China. 2020. Science10.1126/science.abb4218. [DOI] [PMC free article] [PubMed]
- 9.Ferguson N.M. Imperial college COVID-19 response team. 16 March 2020. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. [DOI] [PMC free article] [PubMed] [Google Scholar]; DOI: 10.25561/77482
- 10.Lai A. Early phylogenetic estimate of the effective reproduction number of SARS-CoV2. J Med Virol. 2020 doi: 10.1002/jmv.25723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhao S. Preliminary estimation of the basic reproduction number of novel coronavirus 2019-nCoV) in China, from 2019 to 2020: adata-driven analysis in the early phase of the outbreak. Int J Infect Dis. 2020;92:P214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Liu Y., Gayle A.A., Wilder-Smith A., Rocklov J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. Journal of Travel Medicine. 2020;27(2) doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Muniz-Rodriguez K., Chowell G., Cheung C.-H., Jia D., Lai P.-Y., Lee Y. Doubling time of the COVID-19 epidemic by province, China. Emerg Infect Dis. 2020 doi: 10.3201/eid2608.200219. August [date cited] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Roques L., Klein E.K., Papaix J., Sar A., Soubeyrand S. Using early data to estimate the actual infection fatality ratio from COVID-19 in france. Biology. 2020;9(5):97. doi: 10.3390/biology9050097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maier B.F., Brockmann D. Effective containment explains sub-exponential growth in confirmed cases of recent COVID-19 outbreak in mainland China. Science. 2020 doi: 10.1126/science.abb4557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Reis R.F. Characterization of the COVID-19 pandemic and the impact of uncertainties, mitigation strategies, and underreporting of cases in south korea, italy, and brazil. Chaos, Solitons & Fractals. 2020;136:109888. doi: 10.1016/j.chaos.2020.109888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Mandal M. A model based study on the dynamics of COVID-19: Prediction and control. Chaos, Solitons & Fractals. 2020;136:109889. doi: 10.1016/j.chaos.2020.109889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chimmula V.K.R., Zhang L. Time series forecasting of COVID-19 transmission in canada using LSTM networks. Chaos Solitons Fractals. 2020;135:109864. doi: 10.1016/j.chaos.2020.109864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Abdo M.S., Shah K., Wahash H.A., Panchal S.K. On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fractals. 2020;135:109867. doi: 10.1016/j.chaos.2020.109867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ribeiro M.H.D.M., da Silva R.G., Mariani V.C., Coelho L.S. Short-term forecasting COVID-19 cumulative confirmed cases: perspectives for Brazil. Chaos Solitons Fractals. 2020;135:109853. doi: 10.1016/j.chaos.2020.109853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Boccaletti S., Ditto W., Mindlin G., Atangana A. Modeling and forecasting of epidemic spreading: the case of COVID-19 and beyond. Chaos Solitons Fractals. 2020;135:109794. doi: 10.1016/j.chaos.2020.109794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Chakraborty T., Ghosh I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: a data-driven analysis. Chaos Solitons Fractals. 2020;135:109850. doi: 10.1016/j.chaos.2020.109850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.de R.. Janeiro state department of health. http://painel.saude.rj.gov.br/monitoramento/covid19.html.
- 24.Hethcote H., Zhien M., Shengbing L. Effects of quarantine in six endemic modelsfor infectious diseases. Math Biosci. 2002;180:141â160. doi: 10.1016/s0025-5564(02)00111-6. [DOI] [PubMed] [Google Scholar]
- 25.COVID-19. Brazil. https://ciis.fmrp.usp.br/covid19/.
- 26.Manchein C., Brugnago E.L., da Silva R.M., Mendes C.F.O., Beims M.W. Strong correlations between power-law growth of COVID-19 in four continents and the inefficiency of soft quarantine strategies. Chaos. 2020;30:041102. doi: 10.1063/5.0009454. [DOI] [PMC free article] [PubMed] [Google Scholar]