Abstract
This study examines how financial contagion occurs through financial and nonfinancial firms between China and G7 countries during the COVID–19 period. The empirical results show that listed firms across these countries, financial and non-financial firms alike, experience significant increase in conditional correlations between their stock returns. However, the magnitude of increase in these correlations is considerably higher for financial firms during the COVID-19 outbreak, indicating the importance of their role in financial contagion transmission. They also show that optimal hedge ratios increase significantly in most cases, implying higher hedging costs during the COVID-19 period.
Keywords: COVID–19, financial contagion, spillover index, financial firms, nonfinancial firms, hedge ratios
1. Introduction
The outbreak of COVID–19 has been declared as a global pandemic on March 11, 2020 by the World Health Organisation. As of April 21, 2020, there are 2,397,216 confirmed cases and 162,956 deaths across the world (WHO, 2020a). China and G7 countries account for the majority of COVID–19 confirmed cases and deaths (WHO, 2020a). The outbreak of COVID–19 has shaken the global financial markets. Level 1 market-wide circuit-breakers based on drops of 7% from the previous close were triggered four times on 9, 12, 16 and 18 March 2020 in the US stock market to prevent larger crashes (World Economic Forum, 2020).1 This mechanism has been triggered only once in 1997 since its implementation in 1988. Dow Jones Industrial Average (DJIA) and S&P500 indices dropped by 33% and 29%, respectively on March 20, 2020 from December 31, 2019, when the first confirmed case is reported by the World Health Organisation (World Economic Forum, 2020). Also, March 16, 2020 (12.93% drop) and March 12, 2020 (9.99% drop) were recorded third and sixth largest daily drops, respectively in DJIA (World Economic Forum, 2020). FTSE100, the UK main index suffered the worst quarter since 1987, recording a drop of 24.80% (The Guardian, 2020). Japan experienced more than 20% drop from December 2019 high (Bloomberg, 2020).
Central banks, government agencies, and multilateral organisations have engaged in an ongoing series of interventions in the financial market to stimulate economies. The International Monetary Fund (IMF) estimated that government stimulus packages adopted during the COVID–19 pandemic amounted to USD3.3 trillion, and that additional loans, equity injections and guarantees amounted to USD4.5 trillion (Congressional Research Service, 2020). The Federal Reserve has taken exceptional steps to address the economic effects of COVID–19 and announced a zero-percent interest rate policy on March 15, 2020 and declared a USD700 billion Quantitative Easing (QE) program. Central banks in other countries have reduced policy interest rates and reserve requirements and announced additional financing facilities. Also, some of the central banks have relaxed capital and countercyclical buffers for financial institutions (Congressional Research Service, 2020). IMF predicted that “the increase in borrowing by governments globally will rise from 3.7% of global gross domestic product (GDP) in 2019 to 9.9% in 2020” (Congressional Research Service, 2020, p. 1).
Following such a huge worldwide impact, the literature on the economic effects of COVID–19 has started to grow rapidly (Baker et al., 2020; Conlon & McGee, 2020; Corbet et al., 2020; Kristoufek, 2020; McKibbin & Fernando, 2020; Ramelli & Wagner, 2020; Zhang et al., 2020). Baker et al., 2020 and Zhang et al., 2020 investigate the effects of COVID–19 on the aggregate markets. Conlon and McGee (2020) explore whether Bitcoin is a safe haven during the COVID–19 bear market. McKibbin and Fernando (2020) show how the outbreak of COVID–19 is impacting the global economy. Sharif et al. (2020) find that the effect of COVID-19 on the US economic uncertainty is much lower than that on the geopolitical risk. Yarovaya et al. (2020) do not detect any herding behavior in cryptocurrency markets during the COVID-19 pandemic.
However, to the best of our knowledge, none of these studies has attempted to examine the effects of COVID–19 on financial firms compared to nonfinancial firms, financial contagion originated by them, and its implications on the portfolio design. Our study fills this void in the literature by investigating whether the financial contagion occurs across Chinese and G7 listed firms, financial and nonfinancial alike, and how the optimal portfolio design changes during the COVID–19 pandemic era.
The empirical results show that dynamic conditional correlations (DCCs) between Chinese and G7 stock returns, financial and nonfinancial alike, increased significantly during the COVID–19 period. However, the magnitude of the increase in DCCs is higher for financial firms, implying that they play a more important role in transmitting financial contagion than nonfinancial firms do. During the outbreak, China and Japan appear to be net transmitters of spillovers, suggesting that financial contagion follows a similar pattern to that of the virus contagion. Finally, optimal hedge ratios increase significantly in most cases during the COVID–19 period, implying higher hedging costs during this period of extreme turbulence. These results provide guidance to policymakers, regulators, practitioners, and other market participants to devise strategies to cope with financial contagion.
The rest of the paper is organized as follows. Section 2 presents the empirical strategy. Section 3 explains the data. Section 4 presents the results, while Section 5 conducts robustness checks. Section 6 concludes.
2. Empirical strategy
2.1. VARMA (1,1) DCC-GARCH model
This study employs alternative specifications of GARCH models to choose the best fit GARCH model and then estimates a VARMA (1,1) DCC-GARCH model based on information criteria.2
| (1) |
| (2) |
where α is the vector of constants. rt refers to a n × 1 vector of returns on Chinese, G7 and World financial and nonfinancial returns. ϕ and ω refer to a n × 1 vector of co-efficients for AR (1) and MA (1), respectively. εt is the vector of residuals. ηt refers to independently and identically distributed (i.i.d) random errors. Ht is the conditional variance-covarianc matrix estimated by the DCC methodology of Engle (2002).
2.2. Optimal portfolio design and hedging ratios
In the second step of our analysis, we investigate how the optimal portfolio design changes during COVID–19 pandemic. Following Kroner and Ng (1998), we estimate the optimal weight of Chinese financial/nonfinancial sector in a one-dollar portfolio of G7 countries (or world). The optimal weight at time t is denoted by :
| (3) |
where , and are the conditional volatility of G7 countries (or world) financial/nonfinancial firm returns and China financial/non-financial firm returns, respectively, and is the covariance between China and G7 countries (or world) financial/nonfinancial firm returns at day t. The conditional variances and covariances at day t are estimated using the benchmark model, VARMA (1,1) DCC GRACH, as explained above. However, the portfolio optimization process imposes the following constraints to assume no short-selling.
| (4) |
A long position of one-dollar in China financial/non-financial sector must be hedged by shorting dollars in the G7 countries (or world) financial/nonfinancial sector, to minimise the portfolio risk where is the optimal hedge ratio (see Kroner & Sultan, 1993) calculated as:
| (5) |
2.3. Directional spillover model
We use Diebold and Yilmaz's (2012) model (hereafter, DY model) to examine the return and volatility spillovers across financial and nonfinancial firms of China and G7 countries. The DY model measures the spillovers in a “generalised vector autoregression (VAR)” framework that removes the order-dependent results using “Cholesky factor orthogonalization” (see Diebold & Yilmaz, 2009).
Assuming an N-variable VAR(p), , where ɛ ~ (0, ∑ ) is a vector of i.i.d disturbances. The moving average (MA) is
where Ai is an N × N matrix of a recursive pattern:
The DY model calculates the H-step-ahead “Forecast Error Variance Decompositions” (FEVD) as
| (6) |
where σjj is the standard deviation of the residuals, ei is a selection vector, with 1 as the ith element and 0 otherwise. . The row sum normalises each element.
| (7) |
with and
Following the DY model, the spillover index is estimated in Equation (8):
| (8) |
The directional spillover to market i from all other markets j is measured in Equation (9):
| (9) |
Similarly, the directional spillover to all other markets j from market i is measured in Equation (10)
| (10) |
The net spillover to all markets j from market i is measured by subtracting Equation (10) from Equation (9)
| (11) |
3. Data and descriptive statistics
3.1. Data
Our sample period covers both pre-COVID–19 period (January 1, 2013– December 30, 2019) and COVID–19 period (December 31, 2019–March 20, 2020). We take the starting date of COVID–19 period as December 31, 2019, the date when the first case of COVID–19 was reported to the World Health Organisation (WHO) by China (WHO, 2020b). On the other hand, we choose the first date of pre-COVID–19 period as January 1, 2013, to not overlap with the global financial crisis (2007–2009) and European sovereign debt crisis (2010–2012). To investigate the financial contagion due to COVID–19 outbreak, we have chosen China and G7 countries in our sample for the following reasons. First, China is a source of COVID–19. Second, China and G7 countries are among the most affected countries as they account for 68.19% of total confirmed cases as of 20 March 2020 (WHO, 2020c). Third, China and G7 countries account for 61.11% of global GDP as of 2018 (World Bank, 2020). For robustness, we also use the world financial and nonfinancial stock returns to compare our results with those obtained from G7 countries.
Data on the return indices of financial and nonfinancial sectors from China, G7 countries, and the world are obtained from DataStream. Financial sector and non-financial sector have been categorised following DataStream Level 2.3 We have used USD denominated return series to calculate daily returns.4 Daily returns were computed from the return index: rt = ln(RIt/RI t − 1), where rt is return and RIt is the Return Index obtained from DataStream.5 Data on confirmed cases are obtained from the World Health Organisation and European Centre for Disease Prevention and Control.
3.2. Descriptive statistics
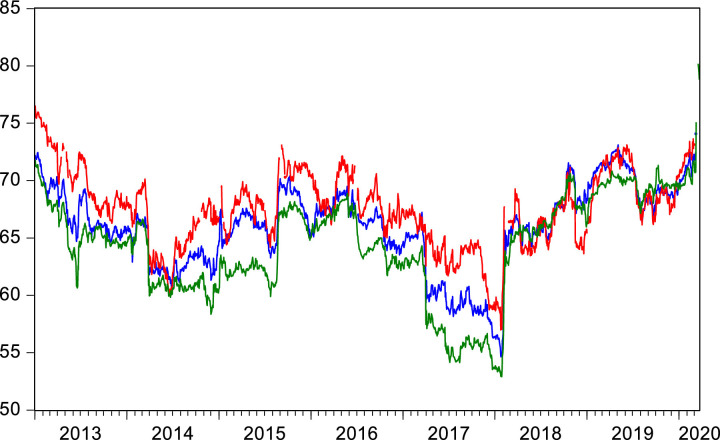
The mean financial and nonfinancial stock returns of China, G7 countries, and world indices during COVID–19 period are negative while the pre-COVID–19 period has positive daily returns. Italian financial firms experienced the highest negative return during COVID–19 period, while the UK had the highest negative return for its nonfinancial firms during the same period. Negative returns are associated with the number of confirmed cases in China and G7 countries (see, Figure 1 ). The UK market return dropped by 40% during the period (December 31, 2019–March 20, 2020). Similarly, market indices in other G7 countries experienced a significant drop during the COVID–19 period (see, Figure 1).
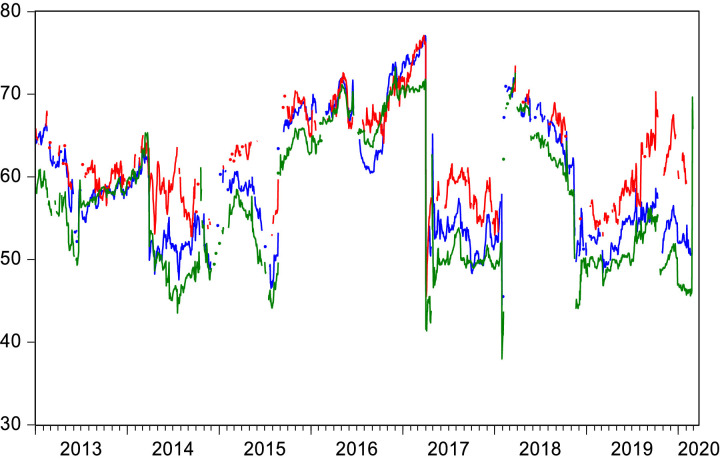
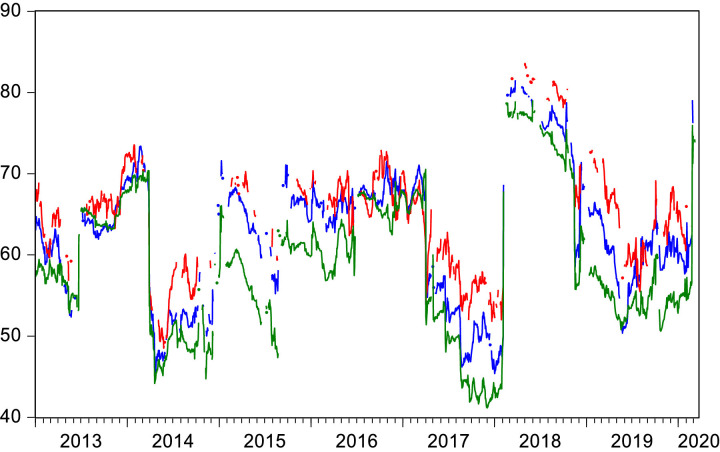
Figure 2.
Return volatility
Figure 3.
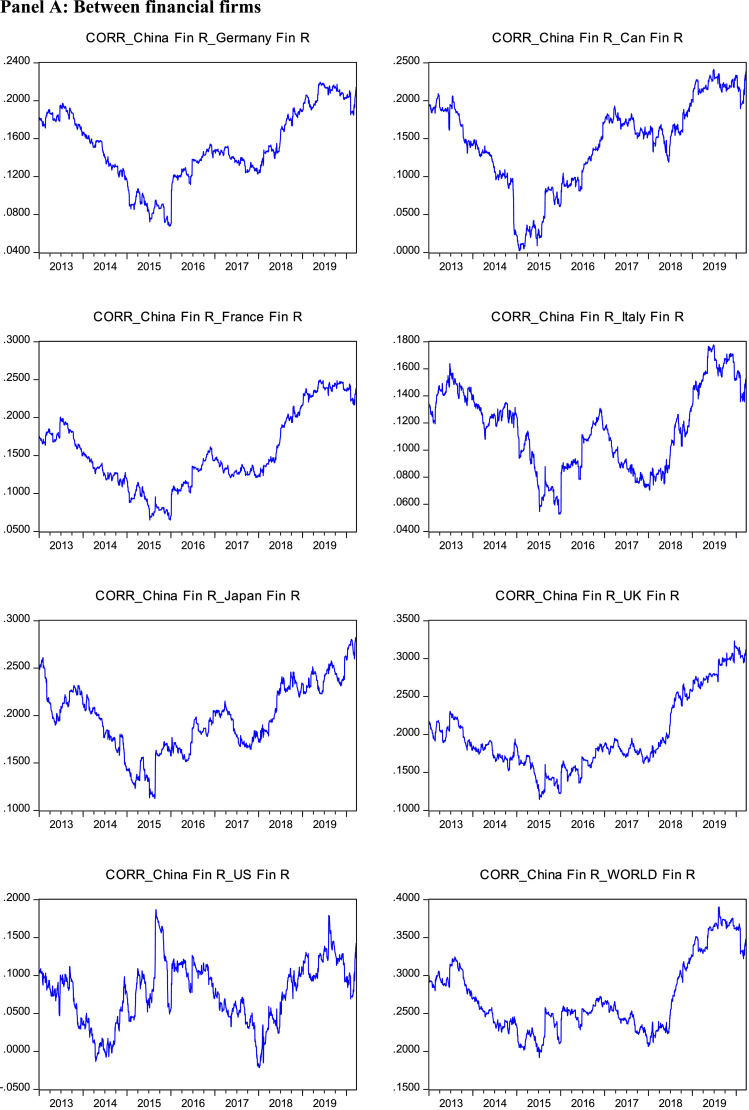
DCCs between China and G7 countries and World
Note: CORR_China_Fin_R_Germany and CORR_China_NF_R_Germany mean DCCs between Chinese and German financial and nonfinancial stock returns, respectively and likewise.
Figure 1.
Return indices and daily changes in confirmed cases of COVID–19
Notes:
USD return indices are created for World, China, and G7 countries with a base of 100 on December 31, 2019 when the first confirmed case of COVID–19 is reported. The right axis represents daily changes in confirmed cases of COVID–19, and the left axis represents the base percentage of return indices.
Source: Datastream and https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide.
The volatility of financial and nonfinancial stock returns is higher during COVID–19 period compared to those during the pre-COVID–19 period as evidenced by increased standard deviations. The skewness of all returns is far from zero and the kurtosis is well over 3 in all cases, indicating the non-normality of return series. This is formally confirmed by the Jarque-Bera test. All portfolio return series appear not to have unit roots. The Box–Pierce–Ljung portmanteau test shows that most returns have autocorrelation. Both financial and nonfinancial stock returns do not have unit roots during the pre-COVID–19 period. However, most of them have unit roots during the COVID–19 period because stock indices experienced a trend of negative returns during the same period. Pearson correlations between Chinese and G7 (or world) financial and nonfinancial stock returns appear to be much higher during the COVID–19 period as compared to those during the pre-COVID–19 period, suggesting some preliminary results on financial contagion (Table 1 ).
Table 1.
Descriptive statistics.
| Panel A: Financial firm return: Pre-COVID–19 period (January 1, 2013−December 30, 2019) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| China | Canada | France | Germany | Italy | Japan | UK | US | World | |
| Mean | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0002 | 0.0001 | 0.0001 | 0.0005 | 0.0003 |
| Std.Dev | 0.0152 | 0.0082 | 0.0124 | 0.0097 | 0.0175 | 0.0123 | 0.0118 | 0.0089 | 0.0069 |
| Skewness | –0.3822 | –0.0973 | –1.0666 | –0.6513 | –1.1087 | –0.0391 | –2.5147 | –0.4952 | –0.9315 |
| Kurtosis | 9.4909 | 5.8654 | 17.4658 | 8.7996 | 16.9558 | 6.6088 | 44.9585 | 6.1164 | 9.2479 |
| Jarque-Bera (x103) | 3.2*** | 0.63*** | 16.3*** | 2.7*** | 15.2*** | 0.99*** | 135.7*** | 0.81*** | 3.2*** |
| Observations | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 |
| Q (10) | 30.40*** | 46.07*** | 22.23** | 24.22** | 16.49* | 36.05*** | 60.42*** | 15.51* | 96.96*** |
| ADF | –41.4*** | –38.7*** | –40.0*** | –41.8*** | –42.5*** | –48.2*** | –22.4*** | –43.6*** | –34.6*** |
| Pearson Correlation with China | 1.0000 | 0.1391 | 0.1289 | 0.1366 | 0.0912 | 0.1562 | 0.1615 | 0.1269 | 0.2870 |
| Panel B: Financial firm return: COVID–19 period (December 31, 2019−March 20, 2020) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| China | Canada | France | Germany | Italy | Japan | UK | US | World | |
| Mean | –0.0027 | –0.0077 | –0.0100 | –0.0082 | –0.0088 | –0.0060 | –0.0085 | –0.0081 | –0.0076 |
| Std.Dev | 0.0186 | 0.0362 | 0.0340 | 0.0321 | 0.0345 | 0.0155 | 0.0256 | 0.0391 | 0.0258 |
| Skewness | –1.6583 | –1.1801 | –2.7389 | –2.3737 | –2.8101 | –2.2496 | –2.6733 | –0.8660 | –2.0971 |
| Kurtosis | 8.8833 | 9.6082 | 12.5255 | 10.4504 | 14.7099 | 9.0253 | 12.3601 | 6.6663 | 8.5486 |
| Jarque-Bera | 112*** | 121*** | 297*** | 192*** | 415*** | 139*** | 286*** | 40*** | 119*** |
| Observations | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 |
| Q (10) | 8.26 | 27.31*** | 19.40*** | 16.74* | 16.11* | 15.65 | 13.61 | 45.72*** | 23.32*** |
| ADF | –9.1*** | 0.5 | 0.5 | 1.32 | –0.05 | –2.27 | 0.67 | –0.42 | 0.80 |
| Pearson Correlation with China | 1.0000 | 0.2646 | 0.3349 | 0.3208 | 0.1978 | 0.2875 | 0.3836 | 0.2863 | 0.3840 |
| Panel C: Nonfinancial firm return: Pre-COVID–19 period (January 1, 2013−December 30, 2019) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| China | Canada | France | Germany | Italy | Japan | UK | US | World | |
| Mean | 0.0002 | 0.0003 | 0.0004 | 0.0002 | 0.0003 | 0.0004 | 0.0002 | 0.0005 | 0.0003 |
| Std.Dev | 0.0147 | 0.0082 | 0.0097 | 0.0098 | 0.0110 | 0.0107 | 0.0094 | 0.0080 | 0.0063 |
| Skewness | –1.0272 | –0.0973 | –0.4944 | –0.5115 | –0.6667 | –0.3174 | –0.8187 | –0.4980 | –0.6763 |
| Kurtosis | 9.5130 | 5.8654 | 7.4409 | 6.4318 | 8.1531 | 6.6691 | 14.3710 | 6.6057 | 6.8862 |
| Jarque-Bera | 3547*** | 627*** | 1574*** | 975*** | 2154*** | 1054*** | 10036*** | 1064*** | 1288*** |
| Observations | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 | 1825 |
| Q (10) | 39.18*** | 19.67** | 23.72*** | 18.65*** | 23.01** | 99.65*** | 46.19*** | 13.03 | 95.13*** |
| ADF | –8.12*** | –39.48*** | –21.89*** | –20.75*** | –18.00*** | –23.62*** | –22.18*** | –31.56*** | –21.70*** |
| Pearson Correlation with China | 1.0000 | 0.1441 | 0.1601 | 0.1697 | 0.1280 | 0.2034 | 0.1819 | 0.1486 | 0.2752 |
| Panel D: Nonfinancial firm return: COVID–19 period (December 31, 2019−March 20, 2020) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| China | Canada | France | Germany | Italy | Japan | UK | US | World | |
| Mean | –0.0012 | –0.0077 | –0.0064 | –0.0071 | –0.0066 | –0.0048 | –0.0084 | –0.0053 | –0.0056 |
| Std.Dev | 0.0204 | 0.0328 | 0.0254 | 0.0247 | 0.0324 | 0.0138 | 0.0251 | 0.0321 | 0.0235 |
| Skewness | –1.7575 | –2.1937 | –2.6429 | –2.2157 | –3.5850 | –1.7165 | –3.0288 | –1.0107 | –1.8450 |
| Kurtosis | 8.9188 | 9.2108 | 13.5835 | 8.5982 | 21.0208 | 7.9480 | 14.5055 | 6.6343 | 7.9011 |
| Jarque-Bera | 116*** | 142*** | 344*** | 125*** | 925*** | 89*** | 416*** | 43*** | 93***1 |
| Observations | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 | 59 |
| Q (10) | 6.74 | 22.73*** | 11.09 | 16.04* | 8.31 | 8.83 | 13.25 | 44.38*** | 25.73*** |
| ADF | 8.51*** | –0.16 | 0.28 | –0.34 | 1.25 | –5.47*** | 1.28 | 0.07 | 0.34 |
| Pearson Correlation with China | 1.0000 | 0.3462 | 0.3905 | 0.4390 | 0.2723 | 0.4064 | 0.4539 | 0.3273 | 0.4267 |
Notes: The Jarque–Bera test is used to check whether the return distribution is normal. The Box–Pierce–Ljung statistic, Q (10) statistic is distributed as a χ2 with 10 degrees of freedom. The augmented Dickey–Fuller (ADF) is used to check the unit root of return series. *, **, and *** represent significance at the 10%, 5%, and 1% levels, respectively.
4. Empirical results
4.1. Dynamic Conditional Correlations (DCCs)
DCCs between Chinese and G7 (world) financial and nonfinancial stock returns are higher during the COVID–19 period as compared to those during the pre-COVID–19 period. The difference in DCCs between crisis period and non-crisis period varies across countries. The UK exhibits the highest difference (0.1101) for financial firms, whereas Germany has the highest difference (0.0776) for nonfinancial firms. Empirical results pass diagnostic tests. The Lagrange multiplier test of Tse (2000) rejects constant correlations. Hosking (1980) test presents no evidence of serial correlation, and Li and McLeod (1981) test provides no evidence of misspecification in the model. Also, t-test shows that there is a significant difference between DCCs in the pre-COVID–19 period and DCCs in the COVID–19 period. The results of higher DCCs during this crisis period are consistent with those studies on the global financial crisis (Akhtaruzzaman et al., 2014; Dimitriou et al., 2013; Kim et al., 2015). Except for Germany and the US, the increase in dynamic correlations is much higher for the financial compared to non-financial firms. The results not only confirm the existence of financial contagion between China and G7 countries, but also show that the degree of contagion is much higher for financial compared to non-financial companies. Evidence points out to the fact that investors and policymakers should be particularly cautious with regards to the price behaviour of financial firm stocks (Table 2, Table 3, Table 4 ).
Table 2.
DCCs between China and G7 countries and the World.
| Panel A: Between financial firms | ||||||||
|---|---|---|---|---|---|---|---|---|
| Canada | France | Germany | Italy | Japan | UK | US | World | |
| Pre-COVID19 Mean DCC | 0.1420 | 0.1512 | 0.1502 | 0.1146 | 0.1951 | 0.1956 | 0.0758 | 0.2686 |
| COVID19 Period Mean DCC | 0.2134 | 0.2309 | 0.1988 | 0.1476 | 0.2719 | 0.3066 | 0.0939 | 0.3459 |
| Difference in DCC^ | 0.0714 | 0.0797 | 0.0486 | 0.0330 | 0.0768 | 0.1110 | 0.0181 | 0.0773 |
| t–stat difference | –30.25*** | –49.12*** | –31.80*** | –24.98*** | –60.60*** | –80.00*** | –6.55*** | –32.93** |
| Diagnostic Tests: | ||||||||
| Tse (2000) test | 2.26** | 2.27** | 2.66*** | 2.87*** | 2.99*** | 4.60*** | 5.02*** | 3.12*** |
| Hosking (1980) test | 40.42 | 34.98 | 47.78 | 40.59 | 40.03 | 44.60 | 35.96 | 43.20 |
| Li and McLeod (1981) test | 40.43 | 34.97 | 47.73 | 40.57 | 40.04 | 44.58 | 35.97 | 43.19 |
| Panel B: Between nonfinancial firms | ||||||||
|---|---|---|---|---|---|---|---|---|
| Canada | France | Germany | Italy | Japan | UK | US | World | |
| Pre-COVID19 Mean DCC | 0.1480 | 0.1589 | 0.1713 | 0.1576 | 0.1812 | 0.1959 | 0.1199 | 0.2253 |
| COVID19 Period Mean DCC | 0.1737 | 0.1783 | 0.2489 | 0.1532 | 0.2314 | 0.2602 | 0.1506 | 0.2511 |
| Difference in DCC^ | 0.0257 | 0.0194 | 0.0776 | –0.0044 | 0.0502 | 0.0643 | 0.0307 | 0.0258 |
| t–stat difference | –8.61*** | –3.81*** | –14.80** | 0.88 | –19.77*** | –24.64*** | –11.42*** | –5.12*** |
| Diagnostic Tests: | ||||||||
| Tse (2000) test | 3.58*** | 5.33*** | 5.50*** | 6.47*** | 5.62*** | 5.59*** | 3.75*** | 4.45*** |
| Hosking (1980) test | 45.65 | 19.35 | 34.25 | 34.34 | 30.09 | 23.88 | 50.01 | 43.57 |
| Li and McLeod (1981) test | 46.30 | 21.39 | 34.11 | 35.21 | 31.61 | 25.56 | 49.64 | 43.43 |
^ Difference is calculated from COVID19 mean minus pre-COVID19 mean.
Notes:
1. Tse (2000) tests the null hypothesis of constant correlation: H0: δij = 0 for the equation: ρij,t = ρij + δijεi,t − 1εj,t − 1, where εi,t − 1 and εj,t − 1 are the standard residuals in Chinese (i), G7 and World (j) financial stock returns, respectively from the best fit GARCH (1,1) process.
2. Hosking (1980) test checks the null hypothesis of no serial correlation.
3. Li and McLeod (1981) test checks the null hypothesis of no misspecification in the model.
4. t-test for the difference in mean DCC is conducted.
*, **, and *** represent significance at the 10%, 5%, and 1% levels, respectively.
Table 3.
Optimal weights and hedge ratios
| Panel A: Optimal weights-Financial firms | ||||||||
|---|---|---|---|---|---|---|---|---|
| Canada | France | Germany | Italy | Japan | UK | US | World | |
| Pre-COVID19 Mean Optimal Weights | 0.2460 | 0.4432 | 0.3389 | 0.6001 | 0.4229 | 0.3629 | 0.2949 | 0.1399 |
| COVID19 Period Mean Optimal Weights | 0.2561 | 0.3922 | 0.3669 | 0.5088 | 0.2621 | 0.3969 | 0.4199 | 0.2569 |
| Difference in Optimal weights^ | 0.0102 | –0.0510 | 0.0279 | –0.0913 | –0.1608 | 0.0344 | 0.1250 | 0.1171 |
| t–stat difference | –0.23 | 1.46 | –0.80 | 3.17*** | 6.00*** | –0.99 | –3.08*** | –2.76*** |
| Panel B: Optimal weights-Nonfinancial firms | ||||||||
|---|---|---|---|---|---|---|---|---|
| Canada | France | Germany | Italy | Japan | UK | US | World | |
| Pre-COVID19 Mean Optimal Weights | 0.3114 | 0.3533 | 0.3693 | 0.4278 | 0.3741 | 0.3138 | 0.2563 | 0.1436 |
| COVID19 Period Mean Optimal Weights | 0.2579 | 0.3557 | 0.3578 | 0.4049 | 0.2716 | 0.3481 | 0.3819 | 0.2719 |
| Difference in Optimal weights^ | –0.0535 | 0.0024 | –0.0115 | –0.0228 | –.0.1026 | 0.0342 | 0.1255 | 0.1283 |
| t–stat difference | 1.32 | –0.07 | 0.38 | 0.69 | 4.25*** | –0.99 | –3.17*** | –3.23*** |
| Panel C: Optimal hedge ratios-Financial firms | ||||||||
|---|---|---|---|---|---|---|---|---|
| Canada | France | Germany | Italy | Japan | UK | US | World | |
| Pre-COVID19 Mean Optimal hedge ratios | 0.2736 | 0.2003 | 0.2431 | 0.1151 | 0.2645 | 0.3213 | 0.1825 | 0.6380 |
| COVID19 Period Mean Optimal hedge ratios | 0.4048 | 0.2803 | 0.2334 | 0.1355 | 0.4252 | 0.3056 | 0.1536 | 0.5441 |
| Difference in Optimal hedge ratios^ | 0.1312 | 0.0800 | –0.0097 | –0.0204 | 0.1608 | –0.0148 | –0.0289 | –0.0939 |
| t–stat difference | –5.19*** | –4.87*** | 0.94 | –2.96*** | 6.54*** | 0.80 | 2.72*** | 2.95*** |
| Panel D: Optimal hedge ratios-Nonfinancial firms | ||||||||
|---|---|---|---|---|---|---|---|---|
| Canada | France | Germany | Italy | Japan | UK | US | World | |
| Pre-COVID19 Mean Optimal hedge ratios | 0.2244 | 0.2214 | 0.2293 | 0.1916 | 0.2788 | 0.3044 | 0.1976 | 0.5024 |
| COVID19 Period Mean Optimal Weights Optimal hedge ratios | 0.3337 | 0.2504 | 0.2646 | 0.1992 | 0.4240 | 0.3200 | 0.1578 | 0.4155 |
| Difference in Optimal hedge ratios^ | 0.1093 | 0.0287 | 0.0353 | 0.0076 | 0.1452 | 0.0156 | –0.0398 | –0.0869 |
| t–stat difference | –5.47*** | –1.88* | –3.24*** | –0.67 | –6.53*** | –0.70 | 2.83*** | 3.06** |
Notes:
1) Optimal weights and optimal hedge ratios are computed using Equation (4) and Equation (5), respectively.
2) t-test for the difference in mean optimal weights and hedge ratios is conducted.
^Difference is calculated from COVID19 mean minus pre-COVID19 mean.
*, **, and *** represent significance at the 10%, 5%, and 1% levels, respectively.
Table 4.
Structural breaks in hedge ratios
| Canada | France | Germany | Italy | Japan | UK | US | World | |
|---|---|---|---|---|---|---|---|---|
| Date | 31 Dec 2019 | 31 Dec 2019 | 31 Dec 2019 | 31 Dec 2019 | 31 Dec 2019 | 31 Dec 2019 | 31 Dec 2019 | 31 Dec 2019 |
| Financial firms | ||||||||
| F (1,1882) | 41.39*** | 36.84*** | 0.44 | 9.51*** | 88.52*** | 0.62 | 4.07** | 7.08*** |
| Nonfinancial firms | ||||||||
| F (1,1882) | 39.22*** | 2.77* | 3.07* | 0.43 | 42.74*** | 0.88 | 4.68** | 6.62*** |
Notes: Chow Breakpoint test is conducted with a null hypothesis that there is no structural break on December 31, 2019 when the first confirmed case is reported by the WHO, with only regressor, constant allowed to vary across breakpoints.
*, **, and *** represent significance at the 10%, 5%, and 1% levels, respectively.
4.2. Optimal portfolio design and hedging ratios
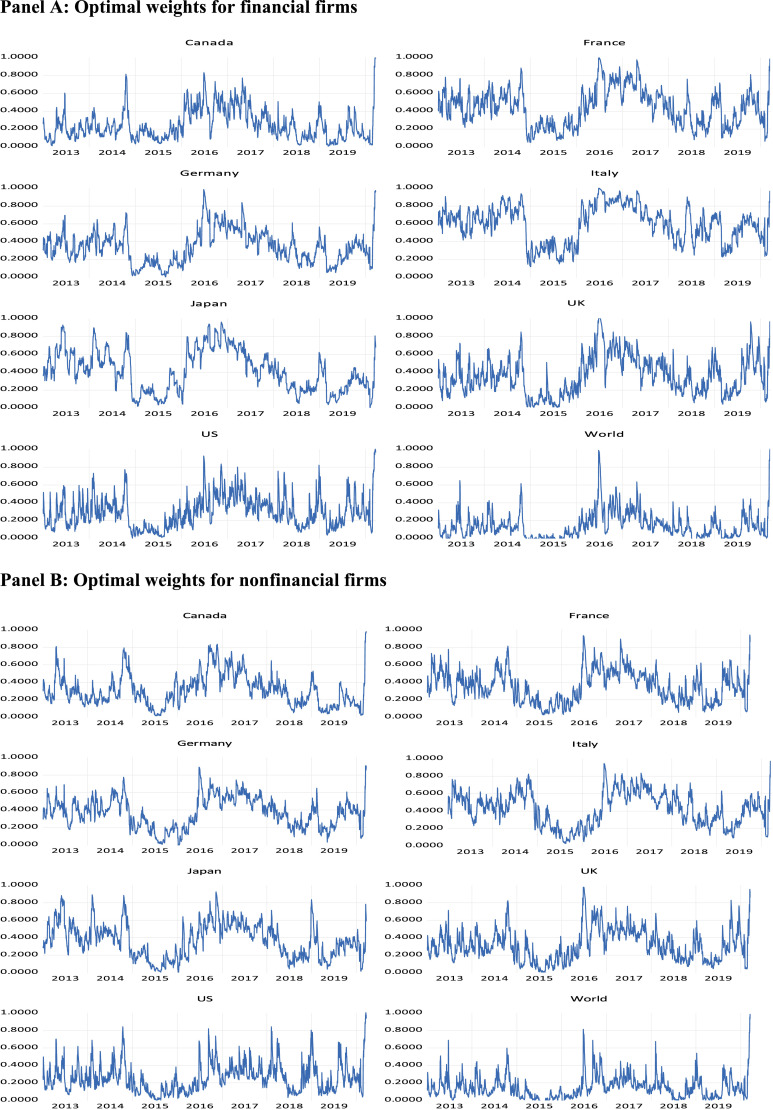
The optimal weights have been estimated using Equation (3). The results show that the optimal weights in the Chinese financial and nonfinancial sectors are less than 0.50 except for the Italian financial sector in both periods. The results imply that investors should allocate less than half of a one-dollar portfolio in the Chinese financial (nonfinancial) sector to reduce the portfolio's risk without decreasing its return. Interestingly, the optimal weights appear to be time-varying (see, Figure 4 ) and change during the COVID–19 period. For instance, the optimal weight of the Chinese financial sector in the portfolio of Chinese and US financial sector increased from 0.2949 in the pre-COVID–19 period to 0.4199 during the COVID–19 period. This might be due to the fact that towards the end of our sample, Chinese markets start to recover whereas western markets continue to experience big drops. In this case, adding Chinese securities to such portfolios can balance the outcomes and improve the overall performance (Table 3).
Figure 4.
Optimal weights.
The optimal hedge ratios are estimated using Equation (5) with a VARMA (1,1) DCC GARCH model. Figure 5 shows that these optimal ratios are time-varying. The results provide interesting insights for portfolio design. First, it seems that most of the optimal hedge ratios for financial and nonfinancial sectors have significantly changed during the COVID–19 period. Some of them have increased while others have decreased. For example, the hedge ratio for China-Japan financial (nonfinancial) firms increased from 0.2645 (0.2788) in the pre-COVID–19 period to 0.4252 (0.4240) in the COVID–19 period. The increase in hedging ratios suggests higher hedging costs during the COVID–19 period due to the larger number of contracts required to short Chinese financial and non-financial sectors. The results are consistent with the literature that shows higher hedge ratios during crisis periods (Antonakakis et al., 2018; Batten et al., 2019). Also, Chow breakpoint test indicates that there is a structural break in hedge ratios on December 31, 2019, when the first confirmed case of COVID–19 is reported by the WHO (Table 4). Second, the hedge ratios for China-World financial and nonfinancial sectors appear to be higher than those of developed countries (G7). This implies that compared to G7 countries, the hedging cost is higher for the global financial and nonfinancial sectors when shorting Chinese financial and nonfinancial sectors. These results suggest the increased challenges for financial risk management during COVID-19 period and show that the situation is more challenging when hedging financial firm stocks (see, Figure 5).
Figure 5.
Optimal hedge ratios.
4.3. Return and volatility spillovers
This section examines spillovers within a DY framework. The empirical results show that financial (nonfinancial) return and volatility spillovers amount, on average, to 61.99% (64.09%) and 60.13% (65.51%), respectively.6 According to Figure 6 , both return and the volatility spillover indices are high, indicating that shock transmission between Chinese and G7 financial and nonfinancial firms is high. These results also indicate that shock transmission between Chinese and G7 financial and nonfinancial firms is high.
Figure 6.
Total spillover plots.
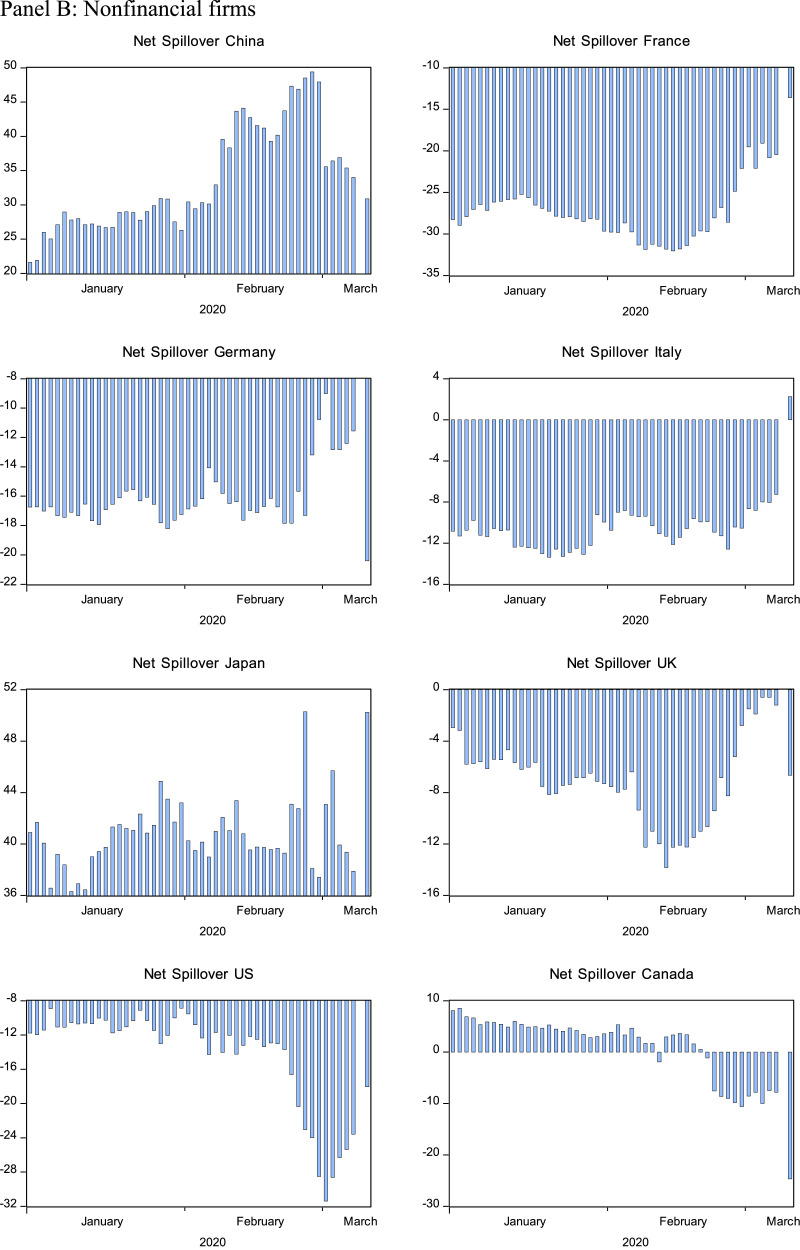
Following the DY model, we measure the return and volatility spillover using a 200-day rolling window to examine the magnitude and type of spillovers during the pre-COVID–19 and COVID–19 periods. The spillover plots demonstrate that both return and volatility spillovers increased significantly during the COVID–19 period. These results corroborate previous studies (Elsayed & Yarovaya, 2019; Lau et al., 2017; Zhang & Broadstock, 2018). Moreover, Figure 7 demonstrates the net spillover measured by in Equation (11). Figure 7 shows that Chinese and Japanese financial and nonfinancial firms are net transmitters of spillover to other G7 countries during the COVID–19 period, indicating that financial contagion trails the same path to that of COVID-19.7 Thus, policymakers in G7 countries should pay special attention to the market movements in these countries.
Figure 7.
Net spillover plots
Notes: Net spillover plots have been created using Diebold and Yilmaz (2012) model.
5. Robustness checks
We consider several alternative specifications to check the robustness of our results. In particular, we investigate whether the results from local currency returns differ from those obtained from USD returns. The results demonstrate that findings from local currency returns appear to be similar to those from USD return (See, Figure A1 ). Also, we generate the spillover indices for a forecast horizon of 5, 10, and 15 days with a VAR lag structure of 5, 10, and 15 days, and rolling windows of 200 days. We find that spillover indices from alternative specifications appear to be similar in magnitude and trend to those from the baseline specification (see, Figures A2 to A7 ), suggesting that our findings are robust to alternative specifications.
Figure A3.
Sensitivity of the return spillover index (financial firms) to the forecast horizon (5, 10 and 15 days).
Figure A4.
Sensitivity of the return spillover index (nonfinancial firms) to the VAR lag structure (orders of 5, 10 and 15).
Figure A5.
Sensitivity of the return spillover index (nonfinancial firms) to the forecast horizon (5, 10 and 15 days).
Figure A6.
Sensitivity of the volatility spillover index (financial firms) to the VAR lag structure (orders of 5, 10 and 15).
Figure A1.
DCCs from local currency return.
Figure A2.
Sensitivity of the return spillover index (financial firms) to the VAR lag structure (orders of 5, 10 and 15).
Figure A7.
Sensitivity of the volatility spillover index (nonfinancial firms) to the VAR lag structure (orders of 5, 10 and 15).
6. Conclusion
This paper analyses how financial contagion occurs through financial and nonfinancial firms between China and G7 countries. The empirical results show that dynamic conditional correlations (DCCs) between Chinese and G7 financial and nonfinancial stock returns increased significantly during the COVID–19 period. However, the magnitude of the increase in DCCs was higher for financial firms, implying that they play a more important role in financial contagion transmission than nonfinancial firms do. The results also show that China and Japan appear to be net transmitters of spillovers during the COVID–19 period. Hence, the role of Chinese and Japanese financial and nonfinancial firms in the cross-market transmission of shocks to G7 countries may be of interest to policymakers, regulators, practitioners, and other market participants. Optimal hedge ratios have increased significantly in most cases during the COVID–19 period, implying larger hedging costs during the crisis. These results provide a snapshot of what has happened in the past few weeks following the COVID–19 pandemic outbreak.
Our findings offer many suggestions to investors in optimising their portfolios and provide guidance to policymakers and regulators. During this COVID–19 phase, not only international stock markets but also foreign exchange markets had extremely volatile days. More important hedging costs in equity markets combined with currency mismatches in portfolios have increased both market and credit risk for international investors. These developments force market participants (in particular banks) to reduce their risk-taking capacity and dampen the growth in both financial markets and global economies. In order to prevent these actions, policymakers should keep providing liquidity to international markets as illustrated by the recent global swap arrangements made by the Federal Reserve. Research on the effects of COVID–19 is still in a very nascent stage. Further future research is warranted on the topic, particularly with the availability of longer time periods under the COVID–19.
CRediT authorship contribution statement
Md Akhtaruzzaman: Conceptualization, Methodology, Formal analysis, Data curation, Investigation, Writing - original draft, Writing - review & editing. Sabri Boubaker: Conceptualization, Writing - review & editing, Supervision, Resources. Ahmet Sensoy: Conceptualization, Methodology, Writing - review & editing, Validation.
Footnotes
Level 1 circuit breaker is triggered when the market index falls by 7% in a day (World Economic Forum, 2020).
Alternative specifications of GARCH models include GARCH, GJR-GARCH, EGARCH, PARCH and APARCH. VARMA (1,1) DCC-GARCH model is the best-fit model based on both information criteria (Akaike and Schwarz).
DataStream industry levels follow the Industry Classification Benchmark (ICB) (https://www.ftserussell.com/data/industry-classification-benchmark-icb). DataStream Global Equity Indices break down to six levels. Level 1 is the market index. Level 2 divides the market to industry sectors. Levels 3 to 6 further break down to industry sub-sectors. Nonfinancial sector includes all industry sectors except the financial sector.
Mink (2015) argues for using local currency-denominated returns than common currency returns. Studies such as Akhtaruzzaman et al. (2019), Akhtaruzzaman and Shamsuddin (2016) and Forbes and Rigobon (2002) find similar results irrespective whether examining financial contagion using local currency returns or USD returns.
Return Index (RI) from Datastream is a price index adjusted by the dividend yield.
Spillover tables are not provided here for sake of brevity. The results are available from the authors upon request.
In the initial phase of the COVID-19, Japan had higher number of confirmed cases of COVID-19 as compared to other G7 countries.
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.frl.2020.101604.
Appendix
Appendix B. Supplementary materials
References
- Akhtaruzzaman M., Abdel-Qader W., Hammami H., Shams S. Is China a source of financial contagion? Finance Research Letters. 2019 [Google Scholar]
- Akhtaruzzaman M., Shamsuddin A. International contagion through financial versus non-financial firms. Economic Modelling. 2016;59:143–163. [Google Scholar]
- Akhtaruzzaman M., Shamsuddin A., Easton S. Dynamic correlation analysis of spill-over effects of interest rate risk and return on Australian and US financial firms. Journal of International Financial Markets, Institutions and Money. 2014;31(July):378–396. [Google Scholar]
- Antonakakis N., Cunado J., Filis G., Gabauer D., De Gracia F.P. Oil volatility, oil and gas firms and portfolio diversification. Energy Economics. 2018;70:499–515. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Kost K.J., Sammon M.C., Viratyosin T. The Unprecedented Stock Market Impact of COVID-19. NBER Working paper. 2020 [Google Scholar]
- Batten J.A., Kinateder H., Szilagyi P.G., Wagner N.F. Hedging stocks with oil. Energy Economics. 2019 [Google Scholar]
- Bloomberg. (2020). Perfect storm plunges Asia stocks into bear markets one by one. Retrieved from https://www.bloomberg.com/news/articles/2020-03-09/perfect-storm-is-plunging-asia-stocks-to-bear-markets-one-by-one.
- Congressional Research Service Global Economic Effects of COVID-19. 2020 https://crsreports.congress.gov Retrieved from. [Google Scholar]
- Conlon T., McGee R. Bitcoin during the Covid-19 Bear Market (March 24, 2020) 2020. Safe Haven or Risky Hazard? Bitcoin during the Covid-19 Bear Market. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbet S., Hu Y., Lucey B.M., Oxley L. The Contagion Effects of Being Named Corona during the COVID-19 Pandemic (March 26, 2020) 2020. Aye Corona! The Contagion Effects of Being Named Corona During the COVID-19 Pandemic. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diebold F.X., Yilmaz K. Measuring financial asset return and volatility spillovers, with application to global equity markets. The Economic Journal. 2009;119(534):158–171. [Google Scholar]
- Diebold F.X., Yilmaz K. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting. 2012;28(1):57–66. [Google Scholar]
- Dimitriou D., Kenourgios D., Simos T. Global financial crisis and emerging stock market contagion: A multivariate FIAPARCH–DCC approach. International Review of Financial Analysis. 2013;30:46–56. [Google Scholar]
- Elsayed A.H., Yarovaya L. Financial stress dynamics in the MENA region: Evidence from the Arab Spring. Journal of International Financial Markets, Institutions and Money. 2019;62:20–34. [Google Scholar]
- Engle R.F. Dynamic conditional correlation: a simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics. 2002;20(3):339. [Google Scholar]
- Forbes K.J., Rigobon R. No contagion, only interdependence: measuring stock market comovements. The Journal of Finance. 2002;57(5):2223–2261. [Google Scholar]
- Hosking J.R. The multivariate portmanteau statistic. Journal of the American Statistical Association. 1980;75(371):602–608. [Google Scholar]
- Kim B.-H., Kim H., Lee B.-S. Spillover effects of the US financial crisis on financial markets in emerging Asian countries. International Review of Economics & Finance. 2015;39:192–210. [Google Scholar]
- Kristoufek, L. (2020). Grandpa, grandpa, tell me the one about Bitcoin being a safe haven: Evidence from the COVID-19 pandemics. arXiv preprint arXiv:2004.00047.
- Kroner K.F., Ng V.K. Modeling asymmetric comovements of asset returns. The Review of Financial Studies. 1998;11(4):817–844. [Google Scholar]
- Kroner K.F., Sultan J. Time-varying distributions and dynamic hedging with foreign currency futures. Journal of Financial and Quantitative Analysis. 1993;28(4):535–551. [Google Scholar]
- Lau M.C.K., Vigne S.A., Wang S., Yarovaya L. Return spillovers between white precious metal ETFs: The role of oil, gold, and global equity. International Review of Financial Analysis. 2017;52:316–332. doi: 10.1016/j.irfa.2017.04.001. [DOI] [Google Scholar]
- Li W., McLeod A. Distribution of the residual autocorrelations in multivariate ARMA time series models. Journal of the Royal Statistical Society. Series B (Methodological) 1981:231–239. [Google Scholar]
- McKibbin, W. J., & Fernando, R. (2020). The global macroeconomic impacts of COVID-19: Seven scenarios.
- Mink M. Measuring stock market contagion: Local or common currency returns? Emerging Markets Review. 2015;22(March):18–24. [Google Scholar]
- Ramelli, S., & Wagner, A. F. (2020). Feverish stock price reactions to covid-19.
- Sharif A., Aloui C., Yarovaya L. Oil Prices, Stock Market and Policy Uncertainty Nexus in the US Economy: Fresh Evidence from the Wavelet-Based Approach (April 13, 2020) 2020. COVID-19 Pandemic, Oil Prices, Stock Market and Policy Uncertainty Nexus in the US Economy: Fresh Evidence from the Wavelet-Based Approach. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The Guardian. (2020). FTSE 100 suffers worst quarter since 1987 as Covid-19 recession looms - as it happened.
- Tse Y.K. A test for constant correlations in a multivariate GARCH model. Journal of Econometrics. 2000;98(1):107–127. [Google Scholar]
- WHO. (2020a). Novel Coronavirus (2019-nCOV) Situation Report -92. Retrieved from https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports.
- WHO. (2020b). Novel Coronavirus (2019-nCOV) Situation Report -1. Retrieved from https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports.
- WHO. (2020c). Novel Coronavirus (2019-nCOV) Situation Report -60. Retrieved from https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports.
- World Bank. (2020). World Development Indicators. Retrieved from https://datacatalog.worldbank.org/dataset/world-development-indicators.
- World Economic Forum. (2020). Mad March: how the stock market is being hit by COVID-19. Retrieved from https://www.weforum.org/agenda/2020/03/stock-market-volatility-coronavirus/.
- Yarovaya L., Matkovskyy R., Jalan A. EUR, JPY and KRW Markets (April 27, 2020) 2020. The Effects of a'Black Swan'Event (COVID-19) on Herding Behavior in Cryptocurrency Markets: Evidence from Cryptocurrency USD, EUR, JPY and KRW Markets. [Google Scholar]
- Zhang D., Broadstock D.C. Global financial crisis and rising connectedness in the international commodity markets. International Review of Financial Analysis. 2018 [Google Scholar]
- Zhang D., Hu M., Ji Q. Financial markets under the global pandemic of COVID-19. Finance Research Letters. 2020 doi: 10.1016/j.frl.2020.101528. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.