Abstract
The field of neuroimaging has recently witnessed a strong shift towards data sharing; however, current collaborative research projects may be unable to leverage contemporary institutional architectures that collect and store data in local, centralized data centers. Although research groups are willing to grant access for collaborations, they often wish to maintain control of their data locally. This may stem from research culture as well as privacy and accountability concerns. In order to leverage the potential of these aggregated larger data sets, we require tools that perform joint analyses without transmitting the data. Ideally, these tools would have similar performance and ease of use as their current centralized counterparts. In this paper, we propose and evaluate a new algorithm, decentralized joint independent component analysis (djICA), which meets these technical requirements. djICA shares only intermediate statistics about the data, retaining privacy of the raw information to local sites and, thus, making it amenable to further privacy protections, for example via differential privacy. We validate our method on real functional magnetic resonance imaging (fMRI) data and show that it enables collaborative large-scale temporal ICA of fMRI, a rich vein of analysis as of yet largely unexplored, and which can benefit from the larger-N studies enabled by a decentralized approach. We show that djICA is robust to different distributions of data over sites, and that the temporal components estimated with djICA show activations similar to the temporal functional modes analyzed in previous work, thus solidifying djICA as a new, decentralized method oriented toward the frontiers of temporal independent component analysis.
Keywords: Independent Component Analysis, temporal Independent Component Analysis, Decentralization, Collaborative Analysis, fMRI
1. Introduction
The benefits to collaborative analysis on fMRI data are deep and far-reaching. Research groups studying complex phenomena (such as certain diseases) often gather data with the intent of performing specific kinds of analyses. However, researchers can often leverage the data gathered to investigate questions beyond the scope of the original study. For example, a study focusing on the role of functional connectivity in mental health patients may collect a brain scan using magnetic resonance imaging (MRI) from all enrolled subjects, but may only examine a particular aspect of the data. The scans gathered for the study, however, are often saved to form a data set associated with that study, and therefore remain available for use in future studies. This phenomenon often results in the accumulation of vast amounts of data, distributed in a decentralized fashion across many research sites. In addition, since technological advances have dramatically increased the complexity of data per measurement while lowering its cost, researchers hop to leverage data across multiple research groups to achieve sufficiently large sample sizes that may uncover important, relevant, and interpretable features that characterize the underlying complex phenomenon.
The standard industry solution to data sharing involves each group uploading data to a shared-use data center, such as a cloud-based service like the openFMRI data repository [1], or the more-recently proposed OpenNeuro service [2]. Despite the prevalence of such frameworks, centralized solutions may not be feasible for many research applications. For example, since neuroimaging uses data taken from human subjects, data sharing may be limited or prohibited due to issues such as (i) local administrative rules, (ii) local desire to retain control over the data until a specific project has reached completion, (iii) a desire to pool together a large external dataset with a local dataset without the computational and storage cost of downloading all the data, or (iv) ethical concerns of data re-identification. The last point is particularly acute in scenarios involving genetic information, patient groups with rare diseases, and other identity-sensitive applications. Even if steps are taken to assure patient privacy in centralized repositories, the maintainers of these repositories are often forced to deal with monumental tasks of centralized management and standardization, which can require many hours of additional processing, occasionally reducing the richness of some of the contributed data [3].
In lieu of centralized sharing techniques, a number of practical decentralization approaches have recently been proposed by researchers most often looking to perform privatized analyses. For example, the “enhancing neuroimaging genetics through meta analysis” (ENIGMA) consortium [4], allows for the sharing of local summary statistics rather than centralizing the analysis of the original imaging data at a single site. This method has proven very successful when using both mega- and meta-analysis approaches [5, 4, 6, 7]. Particularly, the meta-analysis at work in ENIGMA has been used for large-scale genetic association studies, with each site performing the same analysis, the same brain measure extraction, or the same regressions, and then aggregating local results globally. Meta-analyses can summarize findings from tens of thousands of individuals, so the summaries of aggregated local data need not be subject to institutional firewalls or even require additional consenting from subjects [8, 7]. This approach represents one proven, widely used method for enabling analyses on otherwise inaccessible data.
Although ENIGMA has spurred innovation through massive international collaborations, there are some challenges which complicate the approach. Firstly, the meta-analysis at work in ENIGMA are effectively executed manually and, thus, is time-consuming. For each experiment, researchers have to write analysis scripts, coordinate with personnel at all participating sites to make sure scripts are implemented at each site, adapt and debug scripts at each site, and then gather the results through the use of proprietary software. In addition, an analysis using the ENIGMA approach described above is typically “single-shot,” i.e., it does not iterate among sites to compute results holistically, as informed by the global data. From a statistical and machine learning perspective, single-shot model averaging has asymptotic performance with respect to the number of subjects for some types of analysis [9, 10]. However, simple model averaging does not account for variability between sites driven by small sample sizes and cannot leverage multivariate dependence structures that might exist across sites. Further-more, the ability to iterate over local site computations not only enables continuous refinement of the solution at the global level but also greater algorithmic complexity, enabling multivariate approaches like group ICA [11] and support vector machines [12], and increased efficiency due to parallelism, facilitating the processing of images containing thousands of voxels.
These, together with the significant amount of manual labor required for single-shot approaches to decentralization, motivates decentralized analyses which favor more frequent communication, for example, between each iteration or after a number of iterations, in a global optimization algorithm. In this paper, we further previous work in this direction [13] to develop iterative algorithms for collaborative, decentralized feature learning. Namely, we implement a real-data application of a successful algorithm for decentralized independent component analysis (ICA), a widely-used method in neuroimaging applications. Specifically, we show that our decentralized implementation can help further advance the as-of-yet mostly unexplored domain of temporal ICA of functional magnetic resonance imaging (fMRI) data.
In resting-state fMRI studies, we can assume that the overall spatial networks remain stable across subjects and experiment duration, while the activation of certain neurological regions varies over time and across subjects. Temporal ICA, in contrast to spatial ICA, locates temporally independent components corresponding to independent activations of a subjects’ intrinsic common spatial networks. Historically, due to its computational complexity and dependence on statistical sample size, temporal ICA requires more data points in the time dimension than the typical fMRI timeseries can offer. Specifically, the ratio of spatial to temporal dimensions often requires the temporal dimension to be at least similar to the voxel dimension, motivating the temporal aggregation of datasets over multiple subjects via temporal concatenation. This is also a key feature of the well-established group spatial ICA of fMRI literature [14, 15, 16].
Although temporal ICA would benefit tremendously from analyzing a large number of subjects at a central location, as mentioned above, this is not always feasible. To overcome the challenges of centralized temporal ICA, we illustrate an approach that allows for the computation of aggregate spatial maps and local independent time courses across decentralized data stored at different servers belonging to independent labs. The approach combines individual computation performed locally with global processes to obtain both local and global results. Our approach to temporal ICA produces results with similar performance to the pooled-data case and provides estimated components in line with previous results, thus demonstrating the effectiveness of decentralized collaborative algorithms for this difficult task.
2. Materials and Methods
2.1. Independent Component Analysis
ICA is a popular blind source separation (BSS) method, which attempts to decompose mixed signals into underlying sources without prior knowledge of the structure of those sources. Empirically, ICA applied to brain imaging data produces robust features which are physiologically interpretable and markedly reproducible across studies [16, 17, 18, 19]. Indeed, while justification for successful ICA of fMRI results had been previously attributed to sparsity alone [20], it has been shown that statistical independence between the underlying sources is in fact a key driving mechanism of ICA algorithms [21], with additional benefits possible by trading off between the two [22].
In linear ICA, we model a data matrix as a product is composed of N observations from r statistically independent components, each representing an underlying signal source.
We interpret ICA in terms of a generative model in which the independent sources S are submitted to a linear mixing process described by a mixing matrix forming the observed data X. Most algorithms attempt to recover the “unmixing matrix” W = A−1, assuming the matrix A is invertible, by trying to maximize independence between rows of the product WX.
Maximal information transfer (Infomax) is a popular heuristic for estimating W by maximizing an entropy functional related to WX. More precisely, with some abuse of notation, let
| (1) |
be the sigmoid function with g(Z) being the result of element-wise application of g(·) on the entries of a matrix or vector Z. The entropy of a random vector Z with joint density p is
| (2) |
The objective of Infomax ICA then becomes
| (3) |
Other classes of ICA algorithms proceed toward a similar objective, but optimize a different function, such as the maximum likelihood [23]. Another class of algorithms includes the famous family of fixed-point methods, such as so-called “Fast ICA” [24, 25, 26] which locally optimizes a ‘contrast’ function such as kurtosis, or negentropy.
ICA, along with other methods for BSS, has celebrated a wide breadth of applications in a number of fields. In particular, functional magnetic resonance imaging (fMRI) and other domains in biomedical imaging have found ICA models useful as tools for interpreting subject imaging data [18]. With regards to fMRI, many applications assume that functionally connectivity in the brain are systematically nonoverlapping. ICA has thus found a number of useful applications in interpreting physiology or task-related signals in the spatial or temporal domain.
Additionally, a number of extensions of ICA exist for the purpose of joining together various data sets [27] and performing simultaneous decomposition of data from a number of subjects and modalities [28]. Group spatial ICA (GICA) stands out as the leading approach for multi-subject analysis of task- and resting-state fMRI data [29], building on the assumption that the spatial map components (S) are common (or at least similar) across subjects. Another approach, called joint ICA (jICA) [30], is popular in the field on multimodal data fusion and assumes instead that the mixing process (A) over a group of subjects is common between a pair of data modalities.
A largely unexplored area of fMRI research is group temporal ICA, which, like spatial ICA, also assumes common spatial maps but pursues statistical independence of time-courses instead. Group temporal ICA has been most commonly applied to EEG data [31]. but less so to fMRI data. Consequently, like jICA, in the fMRI case, the common spatial maps from temporal ICA describe a common mixing process (A) among subjects. While very interesting, temporal ICA of fMRI is typically not investigated because of the small number of time points in each data set, which can lead to unreliable estimates. Our decentralized jICA approach overcomes that limitation by leveraging information from data sets distributed over multiple sites, and thus represents an important extension of single-subject temporal ICA, and a further contribution to methods which can leverage data in collaborative settings.
2.2. Decentralized Joint ICA
Our goal in this paper is to show that the decentralized joint ICA algorithm can be applied to decentralized fMRI data and produce meaningful results for performing temporal ICA.
Suppose that we have s total sites; each site i has a data matrix consisting of a total time course of length Ni time points over d voxels. Let be the total length. We model the data at each site as coming from a common (global) mixing matrix applied to local data sources Thus, the total model can be written as
| (4) |
Our algorithm, decentralized joint ICA (djICA), uses locally computed gradients to estimate a common, global unmixing matrix corresponding to the Moore-Penrose pseudo-inverse of A in (4), denoted A+.
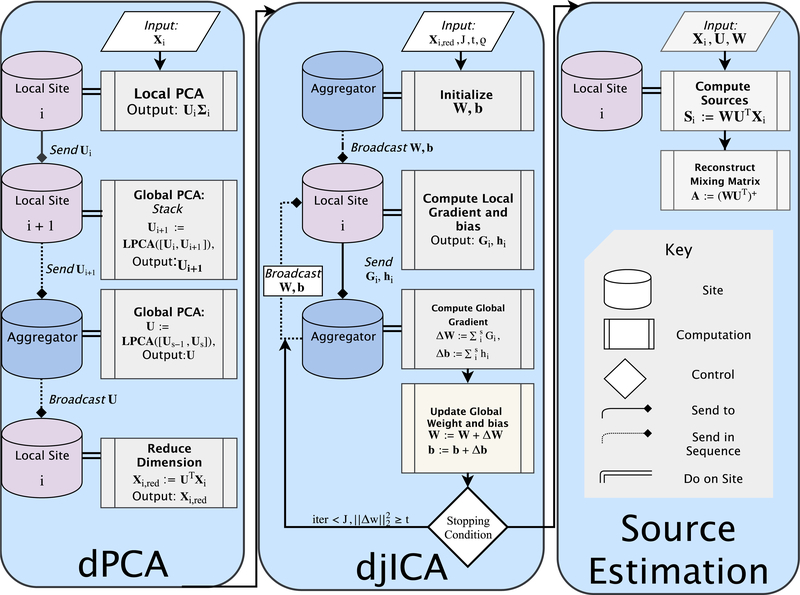
Fig. 1 summarizes the overall algorithm in the context of temporal ICA for fMRI data. Each site i has data matrices corresponding to subjects m = 1, 2, . . . , Mi with d voxels and ni time samples. Sites concatenate their local data matrices temporally to form a d × niMi data matrix Xi, so Ni = niMi. In a two-step distributed principal component analysis (dPCA) framework, each site performs local PCA (Algorithm 2) by means of singular value decomposition (SVD), with matrices corresponding to the top singular vectors and values, respectively. The sites then compute a global PCA (Algorithm 3) to form a common projection matrix Alternatively, in a one-step dPCA framework, we can compute the global U directly but at the expense of communicating a large d × d matrix between sites. Finally, all sites project their data onto the subspace corresponding to U to obtain reduced datasets The projected data is the input to the iterative djICA algorithm that estimates the unmixing matrix as described in Algorithm 1. The full mixing matrix for the global data is modeled as
Figure 1:
An overview of the djICA pipeline. Each panel in the flowchart represents one of the distinct stages in the pipeline, and provides an overview of the processes done on local sites, and on the aggregator site, as well as communication between nodes. The PCA panel corresponds to algorithms 2 and 3, the djICA panel corresponds to algorithm 1, and the Source Estimation panel corresponds to the procedure for computing sources given in equation 5. On each panel, local site i is an arbitrary i-th site in the decentralized network, and local site i + 1 represents the next site in some ordering over the decentralized network. Broadcast communication sends data to all sites, and S end communication sends data to one site. Lines with arrowhead endpoints indicate procedural flow. Lines with diamond endpoints indicate communication flow. Dotted lines with diamond endpoints indicate that the sending process occurs iteratively to neighbors until the aggregator is reached, or in the case of broadcasting, indicates that all nodes are sent the latest update. Double-lines indicate that computations occur on a particular site.
After initializing W (for example, as the identity matrix), the djICA algorithm iteratively updates W using a distributed natural gradient descent procedure [32]. At each iteration j the sites update locally: in lines 4 and 5, the sites adjust the local source estimates Zi by the bias estimates followed by the sigmoid transformation g(·); they then calculate local gradients with respect to Wi and bi in lines 6 and 7. Here ym,i(j) is the m-th column of Yi(j).
The sites then send their local gradient estimates Gi(j) and hi(j) to an aggregator site, which aggregates them according to lines 11–13.
After updating W(j) and b(j), the aggregator checks if any values in W(j) increased above an upper bound of 109 in absolute value. If so, the aggregator resets the global unmixing matrix, sets j = 0, and anneals the learning rate by ρ = 0.9ρ. Otherwise, before continuing, if the angle between is above 60°, the aggregator anneals the learning rate by ρ = 0.9ρ, preventing W from scaling down too quickly without learning the data. The aggregator sends the updated W(j) and b(j) back to the sites. Finally, the algorithm stops when
In order to recover the statistically independent source estimates Si, each site computes
| (5) |
Algorithm 1.
decentralized joint ICA (djICA)
| Require: data where r is the same across sites, tolerance level t = 10−6, j = 0, maximum iterations initial learning rate ρ = 0.015/ln(r) | ||
| 1: | Initialize | ⊳ for example, W = I |
| 2: | while ≥ t do | |
| 3: | for all sites i = 1, 2, . . . , s do | |
| 4: | ||
| 5: | ||
| 6: | ||
| 7: | ||
| 8: | Send Gi(j) and hi(j) to the aggregator site. | |
| 9: | end for | |
| 10: | At the aggregator site, update global variables | |
| 11: | ||
| 12: | ||
| 13: | ||
| 14: | Check upper bound and learning rate adjustment. | |
| 15: | Send global W(j) and b(j) back to each site | |
| 16: | end while | |
For the pooled-data case, Amari et. al [33] demonstrate theoretically that W will converge asymptotically to A−1 in Infomax ICA. In the decentralized-data case, djICA acts as in the pooled-data case in terms of convergence. The assumption of a common mixing matrix across subjects assures that the global gradient sum will be identical to the pooled-data gradient on average, likewise moving the global weight matrix towards convergence.
Beyond normal djICA, a number of decentralization-friendly, heuristic choices can be added to improve runtime or performance. Namely, in Infomax ICA, one can compute the gradient for weight updates over blocks of data in order to improve runtime. Thus the blocksize b can be chosen as a heuristic or evaluated as a hyperparameter in order to examine a tradeoff between algorithm runtime and performance. Other hyperparameters worth investigation are the tolerance level t, initial learning rate ρ, maximum iterations J, and the number of components chosen for local PCA.
In a pooled environment with a known ground-truth, it makes sense to find optimal values for these hyper-parameters using a grid search. In many real-life collaborative environments, a decentralized grid search across sites is not always practical. What’s more, in certain problem settings where no reliable ground-truth is available, verifying the effectiveness of many different hyper-parameters can become an even more difficult and time-consuming matter.
In situations where reliable ground truth is available, such as a reliable simulation, one solution may be to take an average of locally searched hyper-parameters; however, this will not likely perform well in situations where the underlying distribution of subjects varies widely between sites, or where there are many sites with a small amount of data. Another potential solution would be to have each site participate in a global search using a randomly sampled subset of the local data. This may prove effective, provided that each site can provide a sufficient subset in order to provide a reliable heuristic for the global data; however, it comes at the expense of involving all of the collaborators in a separate analysis.
In the setting of independent component analysis for fMRI, however, it is not often the case that collaborators possess a reliable ground-truth which can be used to perform such a hyperparameter search. Though certain auxiliary measures, such as the cross-correlation between components, or the kurtosis of estimated spatial independent components, could be used to measure the success of the algorithm, it will usually be more practical to run an analysis with some initial choice of heuristic parameters, and to make adjustments if auxiliary measures or other indirect validation techniques indicate it would be helpful to do so.
2.3. PCA preprocessing.
Here, we describe the decentralized principal component analysis (dPCA) algorithms used for dimension reduction and whitening in the djICA pipeline. dPCA serves as a preprocessing step to standardize the data prior to djICA, and should also be decentralized so that the benefits of using a decentralized joint ICA are not made moot by dependence on a previous pooled step.
We first choose to examine dPCA from Bai et al. [34]. Their proposed dPCA algorithm bypasses local data reduction, which increases the level of decentralization in the full pipeline, thus motivating its choice for some of our simulated experiments. One major downside of their approach, however, is that it requires the transfer of large orthogonal matrix between all sites, thus increasing bandwidth usage significantly. As an alternative to the approach presetend by Bai et al., a two-step dPCA approach was considered based on the STP and MIGP [35] approaches recently developed for large PCA of multi-subject fMRI data. One advantage provided through the utilization of this approach is that only a small whitening matrix is transmitted across sites, a significant decrease compared to the large d × d R-matrix in Bai’s algorithm [34]. The downside of this approach is that there are no bounds on the accuracy of U, and results can vary slightly with the order in which sites and subjects are processed. Nonetheless, our results suggest that the two-step dPCA approach, described in Algorithms 2 and 3, yields a fairly good estimate of U. In principle, any suitable decentralized PCA algorithm could replace the two methods tested here, and we thus leave room for future extensions of this framework which compare the effects of many different dPCA approaches within the djICA pipeline.
Algorithm 3 uses a peer-to-peer scheme to iteratively refine P(j), with the last site broadcasting the final U to all sites. U is the matrix containing the top r′ columns of P(s) with largest L2-norm, but normalized to unit L2-norm instead. Following
Algorithm 2.
Local PCA algotithm (LocalPCA)
| Require: data and intended rank k | |
| 1: | Compute the |
| 2: | Let contain the largest k singular values and the corresponding singular vectors. |
| 3: | Save locally and return |
Algorithm 3.
Global PCA algorithm (GlobalPCA)
| Require: s sites with data , intended final rank r, local rank k ≥ r. | ||
| 1: | Choose a random order π for the sites. | |
| 2: | P(1) = LocalPCA(Xπ(1), min{k, rank(Xπ(1))}) | |
| 3: | for all j = 2 to s do | |
| 4: | i = π(j) | |
| 5: | Send P(j − 1) from site π(j − 1) to site π(j) | |
| 6: | k′ = min{k, rank(Xi)} | |
| 7: | P′ = LocalPCA(Xi, k′) | |
| 8: | k′ = max{k′, rank(P(j − 1))} | |
| 9: | P(j) = LocalPCA([P′ P(j − 1)], k′) | |
| 10: | end for | |
| 11: | r′ = min{r, rank(P(s))} | |
| 12: | U = NormalizeTopColumns(P(s),r′) | ⊳ At last site |
| 13: | Send U to sites π(1), . . . ,π(s − 1). | |
| 14: | for all i = 1 to s do | |
| 15: | Xi,red = U⊤Xi | ⊳ The locally reduced data |
| 16: | end for | |
the recommendation in [35], we set r = 20 and k = 5 · r for our simulations.
2.4. Evaluation Strategy
All of our experiments were run using the MATLAB 2007b parallel computation toolbox, on a Linux Server running Ubuntu 12.04 LTS, with a 9.6GHz - Four Intel Xeon E7-4870 @ 2.40GHz processor, with a 120MB L3 cache - 30MB L3 cache per processor, and with 512GB of RAM. For any one experiment, we only used a maximum of 8 cores, due to a need to share the server with other researchers.
As a performance metric for our experiments we choose the Moreau-Amari inter-symbol interference (ISI) index [32], which is a function of the square matrix where where W is the estimated unmixing matrix from before, and U is the orthogonal projection matrix retrieved from PCA. In particular, a lower ISI measure indicates a better estimation of a given ground-truth component.
3. Experiments with Simulated Data
First, we test djICA in a simulated environment, where we can manufacture a known grown-truth and use djICA to reconstruct this ground truth under some different mixing scenarios. We evaluated 5 different scenarios for creating synthetic data, as summarized in Table 1.
Table 1:
A brief summary of the five preprocessing methods tested for simulated data experiments.
| scenario | preprocessing | mixing matrix A |
|---|---|---|
| 1. ICA (pooled) | none | i.i.d. Gaussian |
| 2. djICA | none | i.i.d. Gaussian |
| 3. ICA (pooled) | LocalPCA | simTB map |
| 4. djICA | One-Step dPCA [34] | simTB map |
| 5. djICA | GlobalPCA | simTB map |
Two kinds of mixing matrices were used for experimentation:
Lower dimensional mixing matrices were generated using MATLAB’s randn function [36], which generates matrices whose elements are selected from a i.i.d. Gaussian distribution.
Higher dimensional mixing matrices were generated using the Mind Research Network’s simulated fMRI toolbox [37]. The simTB spatial maps are intended to simulate spatial components of the brain which contribute to the generation of the simulated time course. Higher dimensional mixtures were masked using a simple circular mask which drops empty voxels outside of the generated spatial map.
The S signals were simulated using a generalized autoregressive (AR) conditional heteroscedastic (GARCH) model [38, 39], which has been shown to be useful in models of causal source separation [40] and time-series analyses of data from neuroscience experiments [40, 41], especially resting-state fMRI time courses [42, 43]. We simulated fMRI time courses using a GARCH model by generating an AR process (no moving average terms) randomly such that the AR series converges. We chose a random order between 1 and 10 and random coefficients such that α[0] ∈ [0.55, 0.8] and ∈ [−0.35, 0.35] for > 0. For the error terms we used an ARMA model driven by from a generalized normal distribution with shape parameter 100 (so it was approximately uniform on For each of 2048 simulated subjects, we generated 20 time courses with 250 time points, each after a “burn-in” period of 20000 samples, checking that all pair-wise correlations between the 20 time courses stayed below 0.35. We generated a total of 2048 mixed datasets for each experiment.
For the one-step dPCA scenario, we use Bai et al.’s dPCA algorithm without updates [34], and for the two-step dPCA scenario, we use the LocalPCA algorithm (Algorithm 2), followed by GlobalPCA (Algorithm 3). For the first two scenarios, we generated i.i.d. Gaussian mixing matrices For the higher-dimensional problems (scenarios 3–5), we used the fMRI Simulation Toolbox’s simTB spatial maps [37] to generate different mixing matrices.
3.1. Simulated Results
In this section, the results for simulated experiments are presented. We are particularly interested in understanding how our algorithm performs when using different kinds of preprocessing, and how the results improve as a function of the global number of subjects, the global number of sites, or how the subjects are distributed over sites. For each experiment, we tested five different preprocessing strategies, summarized in Table 1: pooled temporal ICA with no preprocessing and an i.i.d Gaussian mixing-matrix, djICA with no preprocessing and an i.i.d Gaussian mixing-matrix, pooled temporal ICA with LocalPCA preprocessing (algorithm 2) and a simTB mixing matrix, djICA with One-Step dPCA from Bai et al. 2005 [34], and djICA with GlobalPCA (algorithm 3).
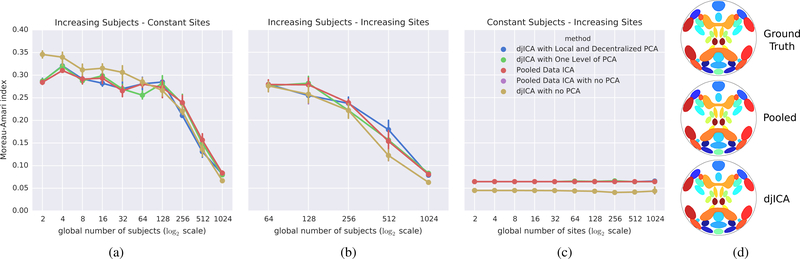
To test how the algorithms compare as we increase the data at a fixed number of sites, we fixed s = 2 sites and evaluated five different preprocessing strategies. For the distributed settings we split the data evenly per site. Fig. 2a shows ISI versus the total data set size. As the data increases all algorithms improve, and more importantly, the distributed versions perform nearly as well as the pooled-data counterparts. Results are averaged over 10 randomly generated mixing matrices.
Figure 2:
The ISI for pooled ICA and djICA for different distributions of subjects over sites, and for five different pre-processing strategies. Panel 2a illustrates an increasing number of subjects over two, fixed sites. Panel 2b illustrates an increasing number of sites, with the number of subjects per site staying constant. Panel 2c illustrates 1024 global subjects distributed of an increasing number of sites. Panel 2d shows the 20 Ground-Truth spatial-maps, along with the estimated spatial-maps from Pooled ICA and djICA.
To test how the algorithms compare as we increase the number of sites with a fixed amount of data sets per site, we fixed the total 2048 subjects but investigated the effect of increasing s where Mi = 32 subjects at each site. Results are averaged over 10 randomly generated mixing matrices. Fig. 2b demonstrates the convergence of ISI curve with the increase of the combined data. Again, we see that the performance of djICA is very close to the centralized pooled performance, even for a small number of subjects per site.
To test how splitting the data sets across more sites affects performance, we examined splitting the 2048 data subjects across more and more sites (increasing s), so for small s each site had more data. Fig. 2c shows that the performance of djICA is very close to that of the pooled-data ICA, even with more and more sites holding fewer and fewer data points. This implies that we can support decentralized data with little loss in performance.
4. Experiments with Real Data
In this section, we describe the methods used for real-data experiments using resting-state fMRI datasets. These experiments are intended to illustrate the effectiveness of djICA (Algorithm 1) in one particular domain of data analysis. As mentioned earlier, the benefits of using this algorithm for fMRI analysis are numerous, and the experiments here aim to both highlight those benefits and illustrate the robustness of the algorithm when compared to pooled analyses.
4.1. Data Description
In this section, we describe the data sets used for real data analysis. The purpose here is to indicate preprocessing steps specific to the data used, and to indicate how certain aspects of the data illustrate specific usefulness and general robustness of djICA. Experiments used data from the Human Connectome Project (HCP) [44]. The data underwent rigid body head motion, slice-time correction, spatial normalization to MNI space (using SPM5), regression of 6 motion parameters and their derivatives in addition to any trends (up to cubic or quintic), and spatial smoothing to 10 mm3 using a full-width, half-maximum Gaussian kernel.
We also used a minimum description length (MDL) [45] criterion to estimate the number of independent components for each specific subject. We ran an MDL-driven estimation algorithm from the MIALab’s Group ICA of fMRI toolbox (GIFT) [46, 47, 11] over 3050 smoothed subjects, including the 2000 subjects used in the experiment. The median number of components was 50, and the mean was 49.4636. In all experiments, we thus elected to estimate 50 real components from the HCP2 data.
4.2. Real Data with “Real” Ground-Truth
In the previous section, we established that djICA can extract simulated components that have been mixed with real fMRI data. The benefit of this experiment was that we could still provide a known ground-truth which can be used to measure the ISI of estimated components; however, our ultimate goal is to show that djICA can provide reasonable estimations for real fMRI components. Since the goal of djICA is to provide results which are just as good as the pooled case, but in a decentralized environment, we decide to perform such a pooled analysis ourselves, in order to create a pseudo ground-truth, which can be used to evaluate djICA for the task of real component estimation.
In order to provide our pseudo ground-truth, w e generated 50 real independent components for 2038 subjects by running a pooled instance of ICA on a single node, matching estimated distributed components via the Hungarian Algorithm, and then computing the ISI of estimated components from djICA with those estimated by the pooled case.
Using the pooled estimations as our basis for comparison, we then tested djICA in four distinct scenarios for the distribution of subjects across a network:
when the global number of subjects in the network increases, but the number of sites in the network stays constant,
when the number of subjects per site stays constant, and the number of sites in the network increases,
when the global number of subjects in the network stays constant, but the number of sites in the network increases, and
when the number of subjects in the network stays constant, and subjects are randomly distributed across sites.
For the scenario where subjects are randomly distributed across sites, we first select a probability distribution P(Θ), with parameters Θ. We then sample 100 different values from P, where each value vi corresponds with a potential number of subjects on the i-th site. We discard any values below 4, so that each site has a minimum of 4 subjects per site, and we take the ceiling of each real value so that site distributions are given as natural numbers. We then select the first s − 1 remaining values, with s being the number of sites, such that where N is the global number of subjects in the network. For the final, site, we set so that the total number of subjects in the network will remain constant at N. This process results in a varying number of sites between successive runs; however, we found it to be computationally more favorable for testing as opposed to a randomized method that would distribute a fixed number of subjects across a fixed number of sites.
In order to test how the shape of each different distribution affects the performance of djICA, we also run basic searches over the parameters Θ.
4.3. “Real” Ground Truth Results
In this section, we present the results of djICA on the HCP2 fMRI data set. All of our experiments involving djICA are compared with a pooled case involving 2000 subjects, and we compare these cases using the Moreau-Amari Index as we did in the simulated experiments, now treating the pooled cased as a our real-data ground-truth.
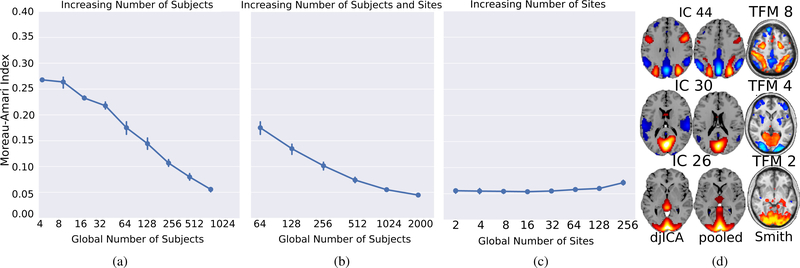
4.3.1. How do the algorithms compare as we increase the data at a fixed number of sites?
In Figure 3a we compare the estimated ISI of djICA using real-data in a scenario where the global number of subjects increases, but the number of sites in the network is fixed. This figure illustrates that as the number of subjects increases, the estimated djICA components converge towards the components computed in the pooled case with 2038 subjects.
Figure 3:
The ISI for real-data djICA for different distributions of subjects over sites. Panel 3a illustrates an increasing number of subjects over two, fixed sites. Panel 3b illustrates an increasing number of sites, with the number of subjects per site staying constant. Panel 3c illustrates 1024 global subjects distributed of an increasing number of sites. Panel 3d shows three of the spatial maps from djICA, the pooled ICA ”pseudo ground-truth”, and the corresponding components from Smith et al. [48].
4.3.2. How do the algorithms compare as we increase the number of sites with a fixed amount of data sets per site?
In Figure 3b we compare the estimated ISI of djICA using real-data in a scenario where the number of subjects on each site is held constant, while the number of sites in the network increases. This figure further illustrates that as the number of subjects increases, the estimated djICA components converge towards the components computed in the pooled case with 2038 subjects.
4.3.3. How does splitting the data sets across more sites affect performance?
In Figure 3c we compare the estimated ISI of djICA using real-data in a scenario where the number of subjects across the entire network is held constant, while the number of sites in the network increases. This figure illustrates that it is the global number of subjects included in the analysis, rather than the number of subjects per site that a_ects the performance of djICA.
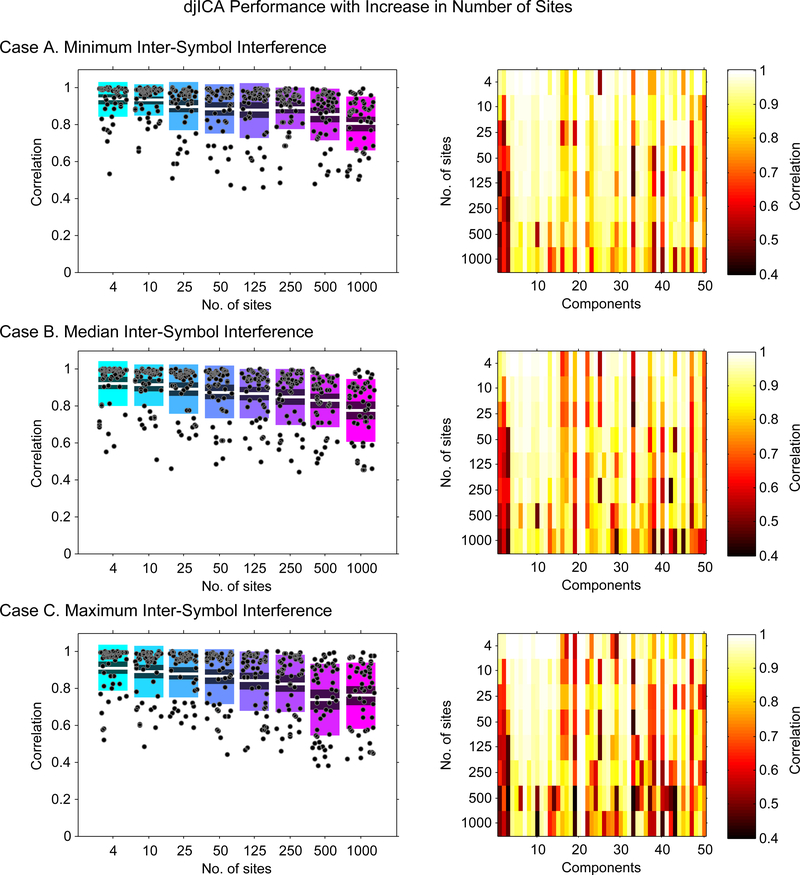
The three cases A, B and C in Figure 4 illustrate the performance of the algorithm for the minimum, median and maximum inter-symbol interference (ISI) scenarios respectively on an increasing number of sites. The boxplots on the left (for all three cases) illustrate the correlations of each reference component with their corresponding match in the number-of-site specific decompositions. It is evident from these plots that the correlation values for majority of the 50 components clustered tightly above the mean correlation values for the entire range of number of sites (thus suggesting that the mean correlation values for all cases was driven to a lower value by a few outliers); however, in general, the mean value of the component correlations for any given case decreased with an increase in number of sites.
Figure 4:
Keeping the number of subjects fixed at 2000, and increasing the number of sites, we examine the correlations of the estimated components from djICA with the reference component being the corresponding best match from the pooled ICA case. We plot the correlations for the estimations from runs with the minimum, maximum, and median ISI selected out of 10 total runs.
The one-way analysis of variance and multiple comparison of means tests were used to determine the specific cases in which mean correlation estimates were significantly different (at significance level 5%). For the minimum ISI case, it was found that the mean correlation values for the first two decompositions (s = 4 and 10) were significantly different than the last two decompositions (s = 500 and 1000), and the third and fourth decompositions (s = 25 and 50) were significantly different than the last (s = 1000) decomposition. The median ISI case also highlighted significant difference in mean estimates of the fifth (s = 125) decomposition as compared to the last two (s = 500 and 1000) decompositions in addition to highlighting differences in the decomposition pairs for the maximum ISI case. Finally, for the maximum ISI case, the first four decompositions (s = 4, 10, 25, 50) had mean correlation estimates significantly different than the last two decompositions (s = 500 and 1000), the fifth decomposition (s = 125) significantly different mean than the seventh decomposition (s = 500) while the sixth decomposition (s = 250) was found not significantly different to any of the decompositions. This overall pattern clearly indicates: (1) deterioration of performance with increase in ISI; (2) significantly different mean estimates of the (s = 500 and 1000) decompositions than the other decompositions on all three ISI scenarios.
For all ISI scenarios, the component-specific performance of the algorithm can be traced in the correlation intensity images on the right. It is evident that for the maximum ISI scenario, the correlations are high for most of the components for most of the lower order (number of sites) decompositions; however, few components that exhibit poor (or outlier) performance do exist. For example, correlations for components 1, 2 and 50 degrade significantly and correlations for component 25 is unexpectedly low for the first (s = 4) decomposition but better for the other higher order decompositions for the maximum ISI case. Finally, it can be concluded from these correlation images that the algorithm performance degrades with increasing ISI which suggests that ISI is a key parameter to control in djICA.
4.3.4. How does randomly splitting the data sets across more sites affect performance?
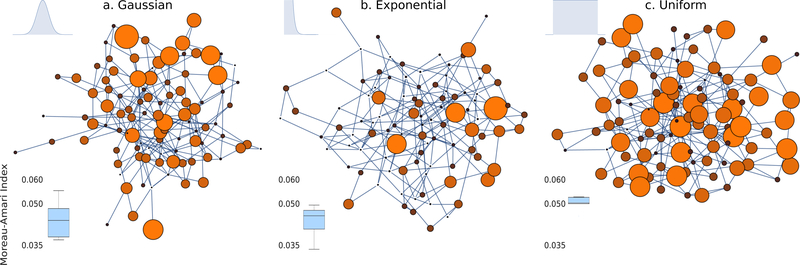
In Figure 5 we compare the estimated ISI of djICA using real-data in a scenario where 2000 subjects are randomly distributed by sampling from a given distribution P(Θ). We tested three different distributions: normal, exponential, and uniform, setting the mean and standard deviation both at 128. We ran djICA five times, and then blotted the ISI for each run side-by-side for each distribution. As the figure shows, uniformly distributing subjects across the network reduces variance in computations when compared to normally distributed subjects; however, all of the given runs do not vary more than 0.02 with respect to the ISI, and all fall below 0.1 ISI, indicating favorable performance.
Figure 5:
An illustration of different subject/site distributions in distributed networks for (a) gaussian-distributed subjects, (b) exponentially distributed subjects, and (c) uniformly distributed subjects. We plot the ISI for each different distribution in the bottom-left corner for 2000 randomly distributed subjects.
4.3.5. How do the estimated maps compare with previous results?
In Figure 3d we have plotted the spatial maps from three of the highest-correlated components estimated using djICA and pooled ICA in comparison to corresponding TFMs from Smith et al. [48]. We discuss the comparison to the results in Smith et al. 2012 in the following section.
5. Discussion
In contrast to systems optimized for processing large amounts of data by making computation more effcient (Apache Spark, H2O and others), we focus on a different setting common in research collaborations: data is expensive to collect and spread across many sites. To that end we proposed a distributed data ICA algorithm that (in synthetic experiments) finds underlying sources in decentralized data nearly as accurately as its centralized counterpart. This shows that algorithms like djICA may enable collaborative processing of decentralized data by combining local computation and communication. djICA represents an important iteration towards toolboxes for distributed computing with an emphasis on collaboration. While other distributed methods for decentralized fMRI analysis have been recently proposed [49, 50], djICA in particular is able to benefit from the unique opportunity of globally accumulated subject-data.
To further validate this proof-of-concept we have evaluated this method on real fMRI experiments. Our use of djICA to perform tICA produces results which compare well to the pooled version of the algorithm, and produce estimated components which compare well with other work on temporal fMRI analysis [48]. Additionally, djICA is robust to a random allocation of subjects to sites, generally performing well when with a high number of globally accumulated subjects, regardless of how these subjects are shared across the sites. We have discovered one edge-case for real-data djICA : where having less than four subjects across all sites in the network correlates with a slight decrease in global performance. While it is possible that performing a robust hyper-parameter search, which we do not investigate in this paper, may mitigate this loss, the scenario where all or many sites in a collaborative analysis would each have fewer than four subjects is highly unlikely. Other decentralized approaches to fMRI analysis, such as approaches which use the ENIGMA consortium [4], do not explore this edge-case. Indeed, the lowest number of subjects on an site within the ENIGMA consortium was 36, with the majority of other sites in the consortium possessing above 200 subjects [7].
As temporal ICA networks from resting state neuroimaging data are rarely reported in literature, a straightforward comparison of our observed ground truth networks is not possible. However our maps should be comparable to some extent to temporal fluctuation modes (TFMs) reported in Smith et al. 2012 [48] in which they perform temporal ICA on denoised spatial ICA component time courses. A comparison of the observed ground truth maps in our work to the TFM maps reported in their work suggests similarities in certain spatial map activation patterns between the two. Component 44 resembles TFM 8 with task positive regions (dorsal visual regions and frontal eye fields) anti correlated to the default mode (posterior cingulate, angular gyri and medial prefrontal cortex). Component 30 with anti-correlated foveal and high eccentricity visual areas corresponding to surround suppression observed in task studies shows a good resemblance to TFM 4 in their work. As observed in TFM 2 in their work, Component 26 shows coactivation patterns of lateral visual areas and parts of thalamus. Component 48 from our work shows a good correspondence to TFM 13 in their work with DMN regions anti-correlated with bilateral supramarginal gyri and language regions albeit without strong lateralization reported in their work. TFM 1 and component 41 in this work demonstrate anti-correlated somatosensory regions to DMN regions of the brain. A couple other TFMs 12 and 15 show moderate correspondence to components 36 and 32 respectively. The differences between the networks we observe and the TFMs reported in their work can stem from methodological differences and choice of number of independent components.
In their work, instead of performing direct temporal ICA on preprocessed data to identify fluctuation modes, Smith et al. [48] use a two step approach where in they perform a high model order spatial ICA, identify artifactual components and regress out their variance from the time courses of seemingly non-artifactual components and then perform a temporal ICA on these denoised time courses. In our work we perform direct temporal ICA leveraging on the large number samples available from large collaborative studies. Therefore, the amount of variance captured during PCA step in both methods differs. Although the model order for temporal ICA differs (50 versus 21 in their work), coincidentally we could identify 21 non-artifactual spatial modes out of 50 network decomposition with spatial map activation patterns localized to gray matter regions and corresponding power spectra of independent time courses showing higher low frequency amplitude as observed for intrinsic connectivity networks from spatial ICA analyses.
6. Conclusions & FutureWork
Additional extensions to the analysis provided here include reducing the bandwidth of the method and designing privacy-preserving variants that guarantee differential privacy, which we have previously investigated for simulated cases [51]. In such cases, reducing the iteration complexity will help guarantee more privacy and hence incentivize larger research collaborations. If we were to return to the simulated data case, additional explorations into robust hyper-parameter searches and the addition of noise may prove interesting for discovering and ameliorating further edge-cases for djICA. Finally, InfoMax ICA represents only one optimization approach to perform ICA, and while it is amenable to decentralization, other algorithms for ICA, such as fastICA [25] or more flexible ICA approaches such as entropy bound minimization [52] may provide other benefits beyond easy decentralization.
Table 2:
Statistics on Number of Timepoints in HCP2 Data
| statistic | HCP2 |
|---|---|
| mean | 157.69 |
| std | 9.2102 |
| median | 158 |
| mode | 158 |
| max | 301 |
| min | 64 |
| range | 237 |
Acknowledgments
This work was supported by grants from the NIH grant numbers R01DA040487, P20GM103472, and R01EB020407 as well as NSF grants 1539067 and 1631838. The author(s) declare that there was no other financial support or compensation that could be perceived as constituting a potential conflict of interest.
7. Bibliography
- [1].Poldrack RA, Barch DM, Mitchell JP, Wager TD, Wagner AD, Devlin JT, Cumba C, Koyejo O, Milham MP, Toward open sharing of task-based fmri data: the openfmri project, Frontiers in neuroinformatics 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Gorgolewski K, Esteban O, Schaefer G, Wandell B, Poldrack R, Openneuro—a free online platform for sharing and analysis of neuroimaging data, Organization for Human Brain Mapping; Vancouver, Canada: (2017) 1677. [Google Scholar]
- [3].Poldrack RA, Gorgolewski KJ, Making big data open: data sharing in neuroimaging, Nature neuroscience 17 (11) (2014) 1510–1517. [DOI] [PubMed] [Google Scholar]
- [4].Thompson PM, Stein JL, Medland SE, Hibar DP, Vasquez AA, Renteria ME, Toro R, Jahanshad N, Schumann G, Franke B, et al. , The enigma consortium: large-scale collaborative analyses of neuroimaging and genetic data, Brain imaging and behavior 8 (2) (2014) 153–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Jack CR, Bernstein MA, Fox NC, Thompson P, Alexander G, Harvey D, Borowski B, Britson PJ, L Whitwell J, Ward C, et al. , The alzheimer’s disease neuroimaging initiative (adni): Mri methods, Journal of magnetic resonance imaging 27 (4) (2008) 685–691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Thompson PM, Andreassen OA, Arias-Vasquez A, Bearden CE, Boedhoe PS, Brouwer RM, Buckner RL, Buitelaar JK, Bulayeva KB, Cannon DM, et al. , Enigma and the individual: predicting factors that a_ect the brain in 35 countries worldwide, Neuroimage 145 (2017) 389–408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].van Erp TG, Hibar DP, Rasmussen JM, Glahn DC, Pearlson GD, Andreassen OA, Agartz I, Westlye LT, Haukvik UK, Dale AM, et al. , Subcortical brain volume abnormalities in 2028 individuals with schizophrenia and 2540 healthy controls via the enigma consortium, Molecular psychiatry 21 (4) (2016) 547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Hibar DP, Stein JL, Renteria ME, Arias-Vasquez A, Desrivières S, Jahanshad N, Toro R, Wittfeld K, Abramovic L, Andersson M, et al. , Common genetic variants influence human subcortical brain structures, Nature 520 (7546) (2015) 224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Mcdonald R, Mohri M, Silberman N, Walker D, Mann GS, Efficient large-scale distributed training of conditional maximum entropy models, in: Advances in Neural Information Processing Systems, 2009, pp. 1231–1239. [Google Scholar]
- [10].Zinkevich M, Weimer M, Li L, Smola AJ, Parallelized stochastic gradient descent, in: Advances in neural information processing systems, 2010, pp. 2595–2603. [Google Scholar]
- [11].Calhoun VD, Adalı T, Multisubject independent component analysis of fMRI: A decade of intrinsic networks, default mode, and neurodiagnostic discovery, IEEE Reviews in Biomedical Engineering 5 (2012) 60–73. doi: 10.1109/RBME.2012.2211076. URL 10.1109/RBME.2012.2211076 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Plis S, Sarwate AD, Wood D, Dieringer C, Landis D, Reed C, Panta SR, Turner JA, Shoemaker JM, Carter KW, Thompson P, Hutchison K, Calhoun VD, COINSTAC: A privacy enabled model and prototype for leveraging and processing decentralized brain imaging data, Frontiers in Neuroscience 10 (365). doi: 10.3389/fnins.2016.00365. URL 10.3389/fnins.2016.00365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Baker BT, Silva RF, Calhoun VD, Sarwate AD, Plis SM, Large scale collaboration with autonomy: Decentralized data ica. [Google Scholar]
- [14].Calhoun VD, Adali T, Pearlson GD, Pekar J, A method for making group inferences from functional mri data using independent component analysis, Human brain mapping 14 (3) (2001) 140–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Correa N, Adalı T, Calhoun VD, Performance of blind source separation algorithms for fmri analysis using a group ica method, Magnetic resonance imaging 25 (5) (2007) 684–694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Calhoun VD, Liu J, Adalı T, A review of group ica for fmri data and ica for joint inference of imaging, genetic, and erp data, Neuroimage 45 (1) (2009) S163–S172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Svensén M, Kruggel F, Benali H, Ica of fmri group study data, NeuroImage 16 (3) (2002) 551–563. [DOI] [PubMed] [Google Scholar]
- [18].Calhoun VD, Adalı T, Unmixing fMRI with independent component analysis, IEEE Engineering in Medicine and Biology Magazine 25 (2) (2006) 79–90. [DOI] [PubMed] [Google Scholar]
- [19].Biswal BB, Ulmer JL, Blind source separation of multiple signal sources of fmri data sets using independent component analysis, Journal of computer assisted tomography 23 (2) (1999) 265–271. [DOI] [PubMed] [Google Scholar]
- [20].Daubechies I, Roussos E, Takerkart S, Benharrosh M, Golden C, D’Ardenne K, Richter W, Cohen J, Haxby J, Independent component analysis for brain fMRI does not select for independence, PNAS 106 (26) (2009) 10415–10422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Calhoun V, Potluru V, Phlypo R, Silva R, Pearlmutter B, Caprihan A, Plis S, Adalı T, Independent component analysis for brain fMRI does indeed select for maximal independence, PloS One 8 (8) (2013) e73309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Boukouvalas Z, Levin-Schwartz Y, Calhoun VD, Adalı T, Sparsity and independence: Balancing two objectives in optimization for source separation with application to fmri analysis, Journal of the Franklin Institute. [Google Scholar]
- [23].MacKay DJ, Maximum likelihood and covariant algorithms for independent component analysis, Tech. rep., Technical Report Draft 3.7, Cavendish Laboratory, University of Cambridge, Madingley Road, Cambridge CB3 0HE (1996). [Google Scholar]
- [24].Hyvarinen A, A family of fixed-point algorithms for independent component analysis, in: Acoustics, Speech, and Signal Processing, 1997. ICASSP-97., 1997 IEEE International Conference on, Vol. 5, IEEE, 1997, pp. 3917–3920. [Google Scholar]
- [25].Hyvarinen A, Fast and robust fixed-point algorithms for independent component analysis, IEEE transactions on Neural Networks 10 (3) (1999) 626–634. [DOI] [PubMed] [Google Scholar]
- [26].Hyvärinen A, Oja E, Independent component analysis: algorithms and applications, Neural networks 13 (4) (2000) 411–430. [DOI] [PubMed] [Google Scholar]
- [27].Sui J, Adalı T, Pearlson G, Calhoun V, An ICA-based method for the identification of optimal fMRI features and components using combined group-discriminative techniques, NeuroImage 46 (1) (2009) 73–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Liu J, Calhoun V, Parallel independent component analysis for multimodal analysis: Application to fmri and eeg data, in: Proc. IEEE ISBI: From Nano to Macro, 2007, pp. 1028–1031. [Google Scholar]
- [29].Allen E, Erhardt E, Damaraju E, Gruner W, Segall J, Silva R, Havlicek M, Rachakonda S, Fries J, Kalyanam R, Michael A, Caprihan A, Turner J, Eichele T, Adelsheim S, Bryan A, Bustillo J, Clark V, Feldstein Ewing S, Filbey F, Ford C, Hutchison K, Jung R, Kiehl K, Kodituwakku P, Komesu Y, Mayer A, Pearlson G, Phillips J, Sadek J, Stevens M, Teuscher U, Thoma R, Calhoun V, A baseline for the multivariate comparison of resting state networks, Front in Syst Neurosci 5 (2). doi: 10.3389/fnsys.2011.00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Calhoun V, Adalı T, Giuliani N, Pekar J, Kiehl K, Pearlson G, Method for multimodal analysis of independent source differences in schizophrenia: Combining gray matter structural and auditory oddball functional data, Hum Brain Mapp 27 (1) (2006) 47–62. doi: 10.1002/hbm.20166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Eichele T, Rachakonda S, Brakedal B, Eikeland R, Calhoun VD, EEGIFT: A toolbox for group temporal ICA event-related EEG, Computational Intelligence and Neuroscience 2011 (2011) Article ID 129365. doi: 10.1155/2011/129365. URL 10.1155/2011/129365 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Amari S-I, Cichocki A, Yang H, A new learning algorithm for blind signal separation, Advances in NIPS (1996) 757–763. [Google Scholar]
- [33].Amari S-I, Chen T-P, Cichocki A, Stability analysis of learning algorithms for blind source separation, Neural Networks 10 (1997) 1345–1351. doi: 10.1016/S0893-6080(97)00039-7. [DOI] [PubMed] [Google Scholar]
- [34].Bai Z-J, Chan R, Luk F, Principal component analysis for distributed data sets with updating, in: Proc. APPT, 2005, pp. 471–483. [Google Scholar]
- [35].Calhoun V, Silva R, Adalı T, Rachakonda S, Comparison of PCA approaches for very large group ICA, NeuroImage, In Press-doi: 10.1016/j.neuroimage.2015.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].MATLAB, rand:Uniformly distributed random numbers, mathworks. URL https://www.mathworks.com/help/matlab/ref/rand.html [Google Scholar]
- [37].Erhardt E, Allen E, Wei Y, Eichele T, Calhoun V, SimTB, a simulation toolbox for fMRI data under a model of spatiotemporal separability, NeuroImage 59 (4) (2012) 4160–4167. doi: 10.1016/j.neuroimage.2011.11.088. URL http://www.sciencedirect.com/science/article/pii/S105381191101370X [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Engle R, Autoregressive conditional heteroscedasticity with estimates of the variance of united kingdom inflation, Econometrica 50 (4) (1982) 987–1007. [Google Scholar]
- [39].Bollerslev T, Generalized autoregressive conditional heteroskedasticity, J Econometrics 31 (1986) 307–327. [Google Scholar]
- [40].Zhang K, Hyvärinen A, Source separation and higher-order causal analysis of MEG and EEG, in: Proc. UAI, AUAI Press, Catalina Island, California, 2010. [Google Scholar]
- [41].Ozaki T, Time Series Modeling of Neuroscience Data, CRC Press, 2012. [Google Scholar]
- [42].Luo Q, Tian G, Grabenhorst F, Feng J, Rolls E, Attention-dependent modulation of cortical taste circuits revealed by Granger causality with signal-dependent noise, PLoS Comp. Bio 9 (10) (2013) e1003265. doi: 10.1371/journal.pcbi.1003265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lindquist M, Xu Y, Nebel M, Caffo B, Evaluating dynamic bivariate correlations in resting-state fMRI: A comparison study and a new approach, NeuroImage 101 (2014) 531–546. doi: 10.1016/j.neuroimage.2014.06.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Essen DV, Ugurbil K, Auerbach E, Barch D, Behrens T, Bucholz R, Chang A, Chen L, Corbetta M, Curtiss S, Penna SD, Feinberg D, Glasser M, Harel N, Heath A, Larson-Prior L, Marcus D, Michalareas G, Moeller S, Oostenveld R, Petersen S, Prior F, Schlaggar B, Smith S, Snyder A, Xu J, Yacoub E, The human connectome project: A data acquisition perspective, NeuroImage 62 (4) (2012) 2222–2231, connectivityConnectivity. doi: 10.1016/j.neuroimage.2012.02.018. URL http://www.sciencedirect.com/science/article/pii/S1053811912001954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Balan R, Estimator for number of sources using minimum description length criterion for blind sparse source mixtures, in: International Conference on Independent Component Analysis and Signal Separation, Springer, 2007, pp. 333–340. [Google Scholar]
- [46].Egolf E, Kiehl KA, Calhoun VD, Group ica of fmri toolbox (gift), Proc. HBM Budapest, Hungary [Google Scholar]
- [47].Medical MRN Image Analysis Lab, Group ICA Of fMRI Toolbox (GIFT) [cited February 11, 2018]. URL http://mialab.mrn.org/software/gift
- [48].Smith SM, Miller KL, Moeller S, Xu J, Auerbach EJ, Wool-rich MW, Beckmann CF, Jenkinson M, Andersson J, Glasser MF, et al. , Temporally-independent functional modes of spontaneous brain activity, Proceedings of the National Academy of Sciences 109 (8) (2012) 3131–3136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Wojtalewicz NP, Silva RF, Calhoun VD, Sarwate AD, Plis SM, Decentralized independent vector analysis, in: Acoustics, Speech and Signal Processing (ICASSP), 2017. IEEE International Conference on, IEEE, 2017, pp. 826–830. [Google Scholar]
- [50].Lewis N, Plis S, Calhoun V, Cooperative learning: Decentralized data neural network, in: Neural Networks (IJCNN), 2017. International Joint Conference on, IEEE, 2017, pp. 324–331. [Google Scholar]
- [51].Imtiaz H, Silva R, Baker B, Plis SM, Sarwate AD, Calhoun VD, Privacy-preserving source separation for distributed data using independent component analysis, in: Proceedings of the 2016 Annual Conference on Information Science and Systems (CISS), Princeton, NJ, USA, 2016, pp. 123–127. doi: 10.1109/CISS.2016.7460488 URL 10.1109/CISS.2016.7460488 [DOI] [Google Scholar]
- [52].Li X-L, Adali T, Complex independent component analysis by entropy bound minimization, IEEE Transactions on Circuits and Systems I: Regular Papers 57 (7) (2010) 1417–1430. [Google Scholar]