A Novel Hybrid Model for VAT Prediction using Shape Descriptors

Abstract

Obesity is gaining increasing attention in modern society since it is associated with various health issues. The visceral adipose tissue (VAT) deposits around the abdominal organs and is considered an extremely important indicator of health risk. VAT can be assessed through magnetic resonance imaging (MRI) or computed tomography (CT) accurately, but the cost is prohibitive. Shape-based body composition prediction has become a promising topic thanks to the prevalence of commodity optical body scan systems, from which numerous anthropometries can be extracted automatically. In this paper, we propose an innovative shape-based hybrid VAT prediction model. The most appealing benefit of our method is to robustly handle the lack of knowledge about gender and demographics. First, we train a baseline VAT prediction model for each gender separately. Second, we train a classifier to predict the gender likelihood and a classifier to predict the shape likelihood of being overestimated in VAT baseline prediction. Third, we integrate the gender likelihood and shape likelihood into the baseline models to derive one hybrid VAT prediction model. We compare our prediction model with other state-of-the-art VAT prediction methods. The result shows that our method outperforms the comparison methods by 21.8% on average.

I. Introduction

The obesity rate is surging at an alarming rate worldwide. It is widely recognized that the obese suffer from a higher risk of developing serious metabolic or cardiovascular diseases such as insulin resistance, type 2 diabetes, dyslipidemia, and hypertension, and the excessive visceral fat has been considered an important cause. Whole-body body fat, as an advanced indicator of obesity, can be reliably measured by various civil or medical devices, such as Biomedical Impedance Analysis (BIA), Bod Pod®, and Dual-energy X-ray Absorptiometry (DXA) but they do not distinguish different types of adipose, i.e., subcutaneous fat and visceral fat. Unlike the Subcutaneous Adipose Tissue (SAT), which is typically located beneath the skin, the Visceral Adipose Tissue (VAT) deposits around the abdominal organs and is more likely to release free fatty acids into the circulation, leading to metabolic disturbances[1]. The VAT can be measured accurately by magnetic resonance imaging (MRI) or computed tomography (CT). However, the prohibitive cost and low accessibility of these technologies limit its usage. Moreover, the CT exposes users to significant amounts of ionizing radiation. The CoreScan®[2] (GE Healthcare, Madison, WI), a DXA-based VAT assessment software has been developed to reduce the cost and radiation damages of the measurement. Although the CoreScan® evaluates VAT based on a statistical model, its accuracy has been validated by multiple studies with sufficient and well-distributed populations[3][4]. In spite of this new technology, the general public still has a low accessibility to VAT assessment.

The advance of optical 3D scan technologies has facilitated highly precise body shape information[5][6][7][8]. Laser-based body scan systems have been widely used in large-scale body shape data collection[9][10]. However, this type of system is typically space-consuming. Light-weight stereo vision based or RGB-D sensor based body scan systems[5][6][7] are more accessible and affordable for the public.

Early medical studies have found that the waist circumference and waist-to-hip ratio (WHR) are effective shape descriptors to assess abdominal fat. With the maturation of 3D scan technologies, body shape can be recorded and analyzed digitally, and thus, more comprehensive shape descriptors have been explored for the VAT prediction. Sun et al. [8] extensively investigated low-order shape descriptors extracted directly from 3D geometry and adopted stepwise regression to select the most effective descriptors for the prediction. Hanen et al. [11] proposed an innovative feature selection scheme for VAT prediction by considering the feature correlations to VAT and abdominal SAT simultaneously. However, the existing works are based on discretized primitive shape descriptors, which neglect the functional property of the 3D body shape data[12]. Under the functional hypothesis of the geometry data, functional shape descriptors can be extracted to learn the body shapes at an abstract level. The gender likelihood is one type of abstract information that can be learned from the functional shape descriptors. According to the large population cohort anthropometry study conducted by Löffler-Wirth et al. [10], there are gender specific and unspecific body types. Perceptual level shape information, such as lean or non-lean[13], is another example. In our work, we hypothesize our prediction model can benefit from this high-level information.

In this paper, we present a highly innovative shape-based hybrid VAT prediction model, which integrates high-level shape-related information from different aspects. The main contribution of this paper is threefold. First, to the best of our knowledge, this is the first total shape-based VAT prediction model. Our hybrid model robustly handles the lack of gender and other demographic information (e.g., weight, age), which makes our model more general. Second, our method improves the prediction accuracy by taking genderrelated shape ambiguity into account. Third, our model works robustly with data derived from commodity level sensor based body scan systems. Thus, our prediction model has the potential to be used by the general public for routinely monitoring health.

II. Methods

A. Baseline VAT Prediction Model

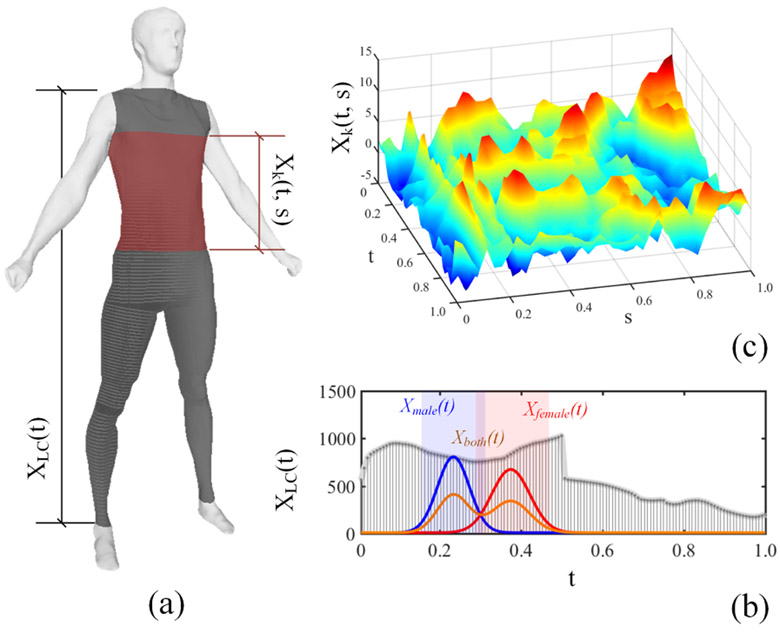
We collect the 3D body shape data (Fig. 1-a) using a commodity level optical body scanner[7], from which the shape descriptors are extracted. The level circumference is noted as an effective shape descriptor[13][9], which preserves the functional property of the original geometry data[12]. We extract the level circumferences from the 3D geometry from the neck to ankle with a sample rate of 128 (see Fig. 1-a), and the functional representation of the feature X_LC(t) is illustrated in Fig. 1-b. The training response for the baseline model is the VAT volume assessed by the CoreScan®.

Fig. 1.

Functional features extracted from the 3D body shape. (a) The 3D body shape geometry, where the level circumference feature is extracted from the black region and the curvature feature is extracted from the red region. (b) The level circumference functional feature. (c) The curvature functional feature.

The domain of the level circumference functional feature is [0, 1]. However, due to the locality of the visceral fat distribution, the feature on the sub-interval of the domain works better for the prediction. The previous works tend to build different prediction models for males and females respectively[9][11]. The effective regions of the level circumference significantly differ between genders. In Fig. 1-b, the effective region for males is highlighted in blue, corresponding to the sub-interval [0.156, 0.313], and that of females is highlighted in red, corresponding to the sub-interval [0.289, 0.469]. We extract the functional features, X_male(t) and X_female(t), corresponding to the two sub-intervals as predictors in our baseline model. We transform the functional features using the eigenfunctions obtained from functional principal component analysis (FPCA)[12]. The top C_n principal components (PCs) are considered sufficient for the training model, which explain at least η = 0.95 proportion of the predictor variance.

$$C_n=\underset{k⩽N}{arg\text{min}}\left(\sum _{i=1}^k{\lambda }_i∕\sum _{i=1}^N{\lambda }_i⩾\eta \right)$$ (1)

We adopt a Gaussian Process Regression (GPR)[14] with Matern kernel to train a baseline VAT prediction model for males and females respectively as in Eq. (2), where h_male, h_female are predicted VAT.

$$\{\begin{array}{c}{h}_{male}={\Phi }_{gpr}(FPCA(X_{male}(t)))\hfill \\ h_{female}={\Phi }_{gpr}(FPCA(X_{female}(t)))\hfill \end{array}\phantom{\}}$$ (2)

B. Gender Likelihood Model

The previous works[9][11] predict the VAT by training prediction models for males and females separately, in which they take prior knowledge about the gender for granted. In this paper, we present a more general VAT prediction model without this prior knowledge. According to the work of Löffler-Wirth et al. [10], there are gender specific and unspecific body types based on analyzing anthropometries of a large population cohort. Motivated by this study, we propose a gender likelihood model to estimate the probability of a given body shape belonging to each gender. The benefit of this model is two-fold. First, we robustly handle the lack of gender information for the input body shapes, which makes our prediction model more general. Second, our model evaluates the degree of the gender ambiguity of the input shape. This information is important to improve the VAT prediction accuracy.

We adopt the linear support vector machine (SVM) classifier[15] to train a classification model as well as a sigmoid function to obtain the conditional probability of gender given shape. The calculation process is shown in Eq. (3). The functional feature X_both(t) is extracted from the union of the red and blue regions in Fig. 1-b, corresponding to the sub-interval [0.156, 0.469]. The training parameters ω, b, ξ and φ can be determined during the learning process.

$$\{\begin{array}{c}\underset{sigmoid}{\underbrace{P_{feamle,male}=\frac{1}{1+e^{\xi f(x)+\phi }}}}\hfill \\ \underset{svm}{\underbrace{f(x)={\omega }^{\prime }\varphi (x)+b}}\hfill \end{array}\phantom{\}},x=FPCA(X_{both}(t))$$ (3)

Then, we integrate the gender likelihood information into the baseline VAT prediction model to derive the gender model. The probability P virtually determines which candidate model in Eq. (1) is appropriate. We hypothesize that a large discrepancy between the P_male and P_female indicates a gender specific body type, whereas the small discrepancy indicates a gender unspecific body type. We aim to improve the VAT prediction performance of the baseline model by integrating this information. We take the probability P_male and P_female as weighted coefficients to balance the female and male VAT prediction model. We, therefore, get a more accurate and general VAT result h′ as Eq. (4).

$$h^{\prime }=P_{male}\cdot h_{male}+P_{female}\cdot h_{female}$$ (4)

The gender model omits the gender labels, which makes the VAT prediction behave more robust and general. The weighting processing in Eq. (4) improves the VAT prediction accuracy.

C. Shape Likelihood Model

Previous literature has suggested that the body shape (i.e., lean or non-lean) influences the prediction result and usually leads to overestimating the VAT and whole-body body fat of the lean[16][17][13]. Likewise, we find the same trend in our baseline model. Thus, we are motivated to develop a shape likelihood model to discriminate the lean body shape which is likely to be overestimated in VAT prediction.

We divide all subjects into lean and non-lean and label them as in Eq. (5), where h is the VAT value. According to VAT distributions of the two genders, we set threshold τ as 4 for males and 2.5 for females.

$$L=\{\begin{array}{c}1,h⩽\tau \hfill \\ 0,h>\tau \hfill \end{array}\phantom{\}}$$ (5)

Since the level circumferences are low-order features, they are not effective in classifying the body shapes[13]. Hence, we extract a higher order feature, i.e., surface curvature, from the 3D body surface, or explicitly the red region in Fig. 1-a. For the convenience of data processing, the 3D body shape is registered into a cylinder, on which the curvature information is projected. The 2D curvature map (Fig. 1-c) is generated by unfolding the cylinder wall.

We propose an accurate classifier to evaluate the likelihood of the lean body shape. The curvature feature cannot be directly used to construct the model. We adopt the Haar-like basis functions to extract useful patterns to discriminate the lean and non-lean body shapes. The Haar-like features are highly redundant, and thus we use agglomerative hierarchical clustering to merge the redundant feature space. We choose the top five merging features and apply them to build the shape likelihood model. We choose the SVM classifier with Gaussian Kernel to classify the body shape, as in Eq. (6).

$$\widehat{L}=svm(x),x\leftarrow T_{Haarlike}(X_k(s,t))$$ (6)

We then use the body shape classification results to compensate the VAT prediction of Eq. (4). The compensation function $\theta (\widehat{L})$ in Eq. (7) is a step function.

$$h^{″}=h^{\prime }+\theta (\widehat{L}),\widehat{L}=0,1$$ (7)

The $\theta (\widehat{L})=\theta \cdot (-1{)}^{\widehat{L}}$ can be determined by minimizing the objective function f (θ) in Eq. (8).

$$f(\theta )=\Vert h-h^{\prime }-\theta (\widehat{L}){\Vert }_2$$ (8)

We estimate the compensation coefficients $\theta (\widehat{L})$ by the Least Square Method (LSM).

D. Hybrid Model

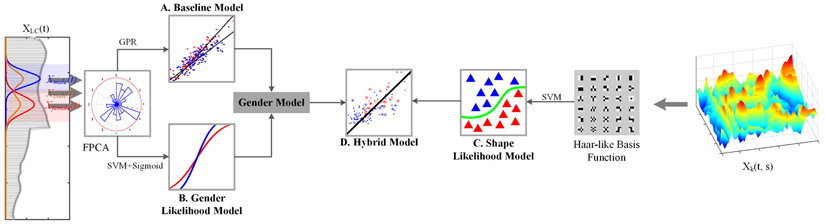
The hybrid model architecture is shown in Fig. 2. The baseline model and the gender likelihood model are developed based on the level circumference features. The shape likelihood model is developed based on the surface curvature feature. The three models are combined to construct the final hybrid model. The hybrid model is highly general and robust since it does not require any additional information other than the 3D body shape. The accuracy of the hybrid model will be evaluated in the next section.

Fig. 2.

Illustration of our proposed method. The whole method can be divided into four sub-modules: baseline model, gender likelihood model, shape likelihood model and hybrid model. The combination of the baseline and gender likelihood models derives the gender model.

III. Results

In this section, we evaluate the performance of the proposed method. The experiment dataset includes 87 female subjects and 60 male subjects. The data collection and study presented in this paper involved human subjects, which were approved by the Institutional Review Board (IRB) of the George Washington University. For the data collection details see Lu et al.[7].

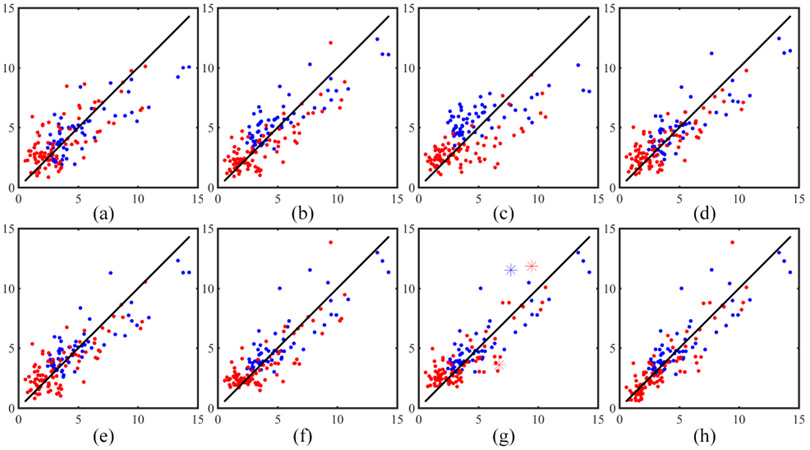
To evaluate the proposed method, the experiment adopts Leave-One-Out Cross Validation (LOOCV). We compare our method with the cutting-edge methods in [1][11][9], all of which are based on linear regression. Both Root-Mean-Square-Error (RMSE) and R-Squared are computed for all methods. Fig. 3 visualizes the VAT prediction results for different methods and the corresponding values are listed in Table I. It is worth noting that both Hanen et al. [11] and Sun et al. [9] involve gender and other shape-unrelated information such as age. Therefore, our hybrid model is more robust and general compared to these state-of-the-art methods. We also compare with the BMI, waist, and waist-to-hip ratio based VAT prediction model because they have been widely used as the VAT indicators in medical domain[1].

Fig. 3.

The VAT prediction result for different methods. (a) BMI. (b) Waist. (c) Waist-to-hip ratio. (d) Hanen et al. [11]. (e) Sun et al. [9]. (f) Baseline model. (g) Gender model (i.e., Baseline + Gender Likelihood) (h) Hybrid model (i.e., Baseline + Gender Likelihood + Shape Likelihood). The blue markers denote the male. The red markers denote the female. The X axis denotes the actual VAT. The Y axis denotes the predicted VAT. The asterisk corresponds to gender misclassified cases.

TABLE I.

Experiment results comparison

Methods	Index	RMSE	R-Squared
BMI	(a)	1.71	0.60
Waist	(b)	1.45	0.70
Waist-to-hip-ratio	(c)	1.95	0.48
Hanen et al.	(d)	1.45	0.70
Sun et al.	(e)	1.54	0.68
Baseline model	(f)	1.39	0.73
Gender model	(g)	1.35	0.74
Hybrid model	(h)	1.25	0.77

Both Table I and Fig. 3 demonstrate that the hybrid model, which integrates the gender and shape information into the baseline VAT prediction, achieves the best prediction results in terms of both RMSE (1.252, the smallest) and R-Squared (0.77, the largest). The hybrid model outperforms the comparison methods by 21.8%, on average in the RMSE.

The gender model (Fig. 2-Gender Model) integrates the gender probability into the baseline prediction to balance the gender disparity in the VAT baseline prediction. Table I shows the gender model outperforms the baseline model by 2.81% in RMSE. The gender classification achieves a very high classification accuracy (> 95%, see Fig. 3-g). We find the baseline model (Fig. 3-f) and the gender model (Fig. 3-g) indeed overestimate the VAT of the lean, and our hybrid model (Fig. 3-h) with a body shape compensation improves the baseline model by 10.1% and improves the gender model by 7.4%.

From the results, we conclude that the hybrid model not only can robustly handle the missing information about gender and other demographics (e.g., age, weight), but also enhances the prediction accuracy by introducing the gender likelihood and shape likelihood analyses.

IV. Conclusions

In this paper, we propose a novel VAT prediction approach using shape descriptors derived only from the 3D geometry. The proposed approach comprehensively considers the disparities of gender and body shapes. A shape-based gender likelihood model is developed to predict the probability of the 3D body shape belonging to different genders and integrates this information to enhance the VAT prediction robustness and accuracy. A shape likelihood model is presented to compensate the VAT prediction overestimation for the lean. We compare our proposed models with the other state-of-the-art methods. The result illuminates the novel effectiveness of our proposed approach. Moreover, our method is totally shape-based without the knowledge of the subjects’ demographics. Besides, the 3D body shapes are derived from the commodity level sensor based body scan system [6]. These merits indicate that our approach has the potential to provide easy access by the general public to routinely monitor their VAT variation.