Metal ion coordination delays amyloid-β peptide self-assembly by forming an aggregation–inert complex

Abstract

A detailed understanding of the molecular pathways for amyloid-β (Aβ) peptide aggregation from monomers into amyloid fibrils, a hallmark of Alzheimer's disease, is crucial for the development of diagnostic and therapeutic strategies. We investigate the molecular details of peptide fibrillization in vitro by perturbing this process through addition of differently charged metal ions. Here, we used a monovalent probe, the silver ion, that, similarly to divalent metal ions, binds to monomeric Aβ peptide and efficiently modulates Aβ fibrillization. On the basis of our findings, combined with our previous results on divalent zinc ions, we propose a model that links the microscopic metal-ion binding to Aβ monomers to its macroscopic impact on the peptide self-assembly observed in bulk experiments. We found that substoichiometric concentrations of the investigated metal ions bind specifically to the N-terminal region of Aβ, forming a dynamic, partially compact complex. The metal-ion bound state appears to be incapable of aggregation, effectively reducing the available monomeric Aβ pool for incorporation into fibrils. This is especially reflected in a decreased fibril-end elongation rate. However, because the bound state is significantly less stable than the amyloid state, Aβ peptides are only transiently redirected from fibril formation, and eventually almost all Aβ monomers are integrated into fibrils. Taken together, these findings unravel the mechanistic consequences of delaying Aβ aggregation via weak metal-ion binding, quantitatively linking the contributions of specific interactions of metal ions with monomeric Aβ to their effects on bulk aggregation.

Introduction

Association and dissociation of protein–protein and metal–protein complexes are highly relevant in biological systems, both for function and misfunction related to diseases (1). The interplay between proteins and metal ions, including the stability/lifetime of such complexes, might be key for an understanding of the disease-associated molecular processes. One central event in Alzheimer's disease is the formation of cerebral senile plaques consisting of aggregated amyloid-β (Aβ)² peptides (2, 3). The self-assembly of the Aβ peptide can be described as a nucleation-dependent process, and detailed information about the fibrillization and nucleation mechanisms may be of importance for an understanding of the disease pathology (4–7). Metal ions have been shown to be potent modulators of Aβ aggregation (8–10), exhibiting specific binding to the intrinsically disordered Aβ monomer (8–14). Their small size and variable charge makes them suitable agents to elucidate the effect of modulating the Aβ monomer structure upon metal-ion binding on the overall Aβ fibrillization process. In general, metal ions such as copper, zinc, and iron are implicated in Alzheimer's disease pathology (15–17) and are also abundantly sequestered in senile plaques (18), but also other metal ions may take key roles, e.g. through exogenous contamination and competition with the same binding ligands as endogenous metal ions (13, 19–23). Here we use metal ions in substoichiometric concentrations as amyloid aggregation modulators to disturb the aggregating system to obtain further insights into the fundamental self-assembly mechanisms.

The monomeric Aβ peptides are predominantly unstructured (24, 25), yet are prone to self-assembly into larger aggregates, and eventually they form fibrils with a stable cross-β structure (26, 27). The main coordinating metal ligands in the Aβ peptide are in the hydrophilic N-terminal part (12, 28–30). Findings from NMR and molecular modeling studies suggest one main binding mode consisting of three histidines and the N-terminal aspartic acid (28–30), where Glu¹¹ is an alternative potential fourth ligand (20). A specific metal-binding mode affects the structure of the Aβ peptide and hence its properties. The net charge of the Aβ peptide at physiological pH is approximately −3, and interactions with cations decrease the net charge and the intra- and interpeptide electrostatic repulsions. The metal ion effects on the Aβ aggregation kinetics are concentration-dependent. Superstoichiometric concentrations of Cu(II) and Zn(II) easily induce rapid formation of amorphous aggregates without amyloid structures, where the metal ion might bind to a second binding site and possibly bridge between Aβ peptides (9, 31, 32). In contrast, substoichiometric Cu(II) (33, 34) or Zn(II) concentrations retard the overall fibrillization process, and our previous study on Zn(II) revealed the specific reduction of the fibril-end elongation (14). In addition to Cu(II) and Zn(II), several other transition metal ions bind to the Aβ peptide, competing for similar ligands with slightly different coordination modes (13, 19–21).

Silver ions are well-known protein-binding ions and substantially used in the past as a protein-staining agent (35, 36). In addition to changes in charge, the ionic radii of Ag(I) and divalent metal ions differ, together with small deviations in preferred binding ligands and coordination geometry (Table S1). Both in vitro and in vivo studies showed Cu(I) replacement by Ag(I) ions in copper-containing proteins (37–39). Ag(I) ions exhibit a larger Pauling radius and a smaller charge density than Cu(I) ions (Table S1), but because of the same electric charge number, the more stable Ag(I) ions have been used as a probe for the readily redox-active Cu(I) ions in in vitro studies (40–42). In fact, a recent study investigated Cu(I) and Ag(I) binding toward the model peptide Aβ₁₆ and showed similar but slightly different binding modes (42). Furthermore, silver ions are not paramagnetic, in contrast to Cu(II), and are thus a useful substitute for interaction studies using NMR.

Studying misfolding and aggregation of amyloidogenic proteins by varying the experimental conditions such as pH, electrostatics, ionic strength, temperature, and local concentration is a valuable tool, because the aggregation processes can be understood in more detail (43–47). Modulation of electrostatic repulsion of Aβ has been shown to greatly influence the Aβ self-assembly mechanism by promoting surface-catalyzed secondary nucleation reactions (46, 47). Hence, in contrast to the divalent ions Zn(II) and Cu(II), the net charge of +1 makes Ag(I) ions a valuable comparative agent for studying the impact of electrostatics for metal ion modulation of peptide/protein aggregation.

In this project we used a combination of biophysical methods to study the characteristics of Aβ metal-ion binding to Ag(I) ions by characterizing the exchange dynamics and thermodynamics of the binding reaction and how this binding affects the fibrillization kinetics. Further, together with our previous results on Zn(II) (14), we rationalized a model for the determinants of modulation of Aβ self-assembly by transition metal ions. In short, 1) monomeric Aβ binds Ag(I) ions specifically in the N-terminal part, forming a dynamic metal-ion bound complex; 2) the weak metal-ion binding prevents monomeric Aβ from incorporation into fibrils; and 3) this leads to attenuation of the Aβ fibrillization kinetics in particular by reduction of the fibril-end elongation rate. Remarkably, these results are strikingly similar to effects of Zn(II) ions (14), which suggests a common mechanism of interaction of monovalent Ag(I) and divalent Zn(II) ions with Aβ peptides. Taken together, the metal-ion binding redirects Aβ monomers from fibril formation, retarding the overall Aβ fibrillization, in particular by reducing fibril-end elongation. This study hence links quantitatively the microscopic perturbation of metal-ion binding to Aβ monomers with its effect on the bulk peptide aggregation process.

Results and discussion

Ag(I) ions predominately retard Aβ fibril-end elongation

Fibrillization kinetics can be monitored using different fluorescent dyes that detect amyloid formation (48, 49). In this study, we simultaneously measured the aggregation kinetics of 20 μm Aβ₄₀ and 5 μm Aβ₄₂ at +37 °C under quiescent conditions using pentameric formyl thiophene acetic acid (pFTAA) (49) and thioflavin T (ThT) (48) (Figs. S1 and S2). With pFTAA we observed the typical sigmoidal aggregation kinetic traces (6, 50), whereas the monitoring of aggregation by ThT is interfered by interactions of Ag(I) and ThT (52, 53) (Fig. S1), which makes ThT unsuitable for aggregation kinetics in the presence of Ag(I) (supporting text).

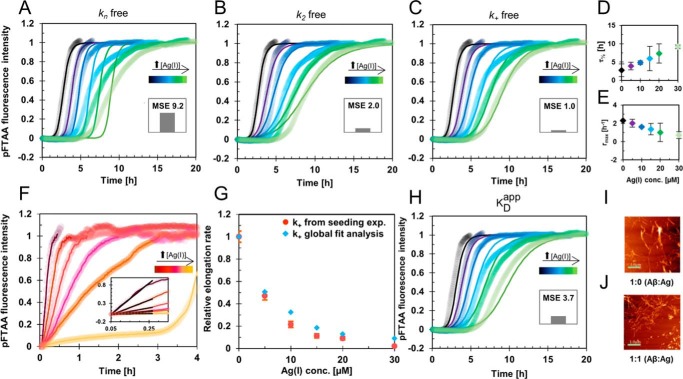
From pFTAA fluorescence experiments, we observed that the fibrillization kinetics of Aβ₄₀ and Aβ₄₂ are retarded by Ag(I) ions in a concentration-dependent manner (Fig. 1, A–C, and Fig. S1). We quantitatively analyzed the effect of Ag(I) ions on Aβ aggregation and found a clear Ag(I) concentration dependence of the aggregation halftime, τ_½, and the maximum growth rate, r_max (Fig. 1, D and E), obtained from fitting a sigmoidal function to the aggregation trace. To obtain insights into the microscopic nucleation process of Aβ₄₀, we analyzed the aggregation kinetics applying a global fit analysis using an integrated rate law (6, 50, 54, 55) (Fig. 1, A–C). The fibrillization process can selectively be differentiated into distinct nucleation events with their related microscopic rate constants, such as primary nucleation (k_n), surface-catalyzed secondary nucleation (k₂), and fibril-end elongation (k₊) (5, 54, 55), and we assumed that similar microscopic nucleation events occur also in the presence of Ag(I).

Figure 1.

Aβ fibrillization retardation in the presence of Ag(I) ions. A–C, global fit analysis of aggregation traces of 20 μm monomeric Aβ₄₀ incubated in the presence of 0–30 μm Ag(I) in 10 mm MOPS buffer, pH 7.2, at +37 °C under quiescent conditions. The global fits were constrained such that only one nucleation rate (k_n, k₂, or k₊) is the single free fit parameter, revealing the best fit for k₊ (normalized mean squared error (MSE), 1.0), followed by k₂ (normalized MSE, 2.0) and k_n (normalized MSE, 9.2). D and E, parameters from sigmoidal curve fitting of the kinetic traces in A–C. The error bars represent standard deviation values from individual fits to four replicates (Fig. S1). F, elongation rates obtained from the initial slopes of highly seeded aggregation kinetics experiments, where 1 μm seeds were added to 20 μm monomeric Aβ₄₀ with 0–30 μm Ag(I). The weighted average values calculated from four replicates are shown in A–C and F. G, relative k₊ values obtained from the global fit analysis in C compared with values from seeding experiments in F, showing the same Ag(I) dependence of k₊. H, global fit analysis applying a model, where the apparent free Aβ monomer concentration is determined by the dissociation constant K_D^app, revealing K_D^app = 14.5 ± 0.2 μm (normalized MSE, 3.7). I and J, images from solid-state AFM of samples taken after fibrillization kinetic experiments showing similar Aβ₄₀ fibril structures in the absence (I) and presence (J) of Ag(I) ions at 1:1 ratio. The scale bar represents 1 μm.

To test the contribution of each microscopic rate constant, we globally fitted the kinetic curves with one single microscopic rate constant as an effective free fitting parameter by fixing the other two rate constants to constant values (Fig. 1, A–C). We found that the aggregation behavior could not be described with k_n as the sole fitting parameter. Although letting k₊ be free better explains the observed aggregation data, using k₂ as free parameter yields a better fit than for k_n but significantly worse than for k₊ (Fig. 1 and Fig. S3).

To confirm that it is the elongation rate that is most affected by Ag(I) ions, we performed kinetics experiments in the presence of preformed seeds (Fig. 1F and Figs. S4 and S5). The initial slope of such kinetic trace is directly proportional to the elongation rate, and hence the isolated effect on k₊ by silver ions can be estimated (5, 6, 14, 50). A high concentration of seeds was added to a monomeric peptide solution in the presence of different Ag(I) concentrations, and we found that the relative elongation rates obtained from these experiments agree very well with those from the global fit (Fig. 1G), providing further evidence that indeed the elongation rate is the rate constant mainly modulated by Ag(I). It is noteworthy that these findings do not exclude that there may be minor effects of Ag(I) on k_n and k₂ as well.

Additionally, the experimental data were also fitted to a model, where the metal-bound population of Aβ monomers is assumed to be unavailable for fibril formation. The reduced aggregation-prone Aβ monomer pool can be described by an apparent free Aβ monomer concentration for each Ag(I) concentration. Similarly to a global fit analysis of aggregation kinetics with different Aβ concentrations (6, 50), the combined microscopic rate constants were globally fitted and constrained to the same values across all Ag(I) concentrations. In addition, an apparent dissociation constant K_D^app was included as a global fit parameter, reflecting the apparently reduced free Aβ monomer concentration caused by the Ag(I) binding. This model describes reasonably well the observed aggregation kinetics, with K_D^app = 14.5 ± 0.2 μm (Fig. 1H).

To investigate whether Ag(I) affects the final state of the Aβ₄₀ fibrils, we used atomic force microscopy (AFM) and recorded images of the end-point samples from the aggregation experiments (Fig. 1, I and J, and Fig. S6). No detectable difference in the fibril morphology was found. This was further supported by circular dichroism (CD), which exhibit spectra showing similar β-structures of the aggregated state at all Ag(I) concentrations (Fig. S1, G and H).

We conclude that Ag(I) ions predominantly retard fibril-end elongation, whereas the structural state and the amount of the end-point fibrils are not affected (Fig. S1C). Hence, these metal ion interactions only modulate the fibrillization process, solely resulting in a delay of the aggregation process, whereas the aggregation mechanism and the final products are not altered.

Interaction between Aβ monomers and Ag(I) ions

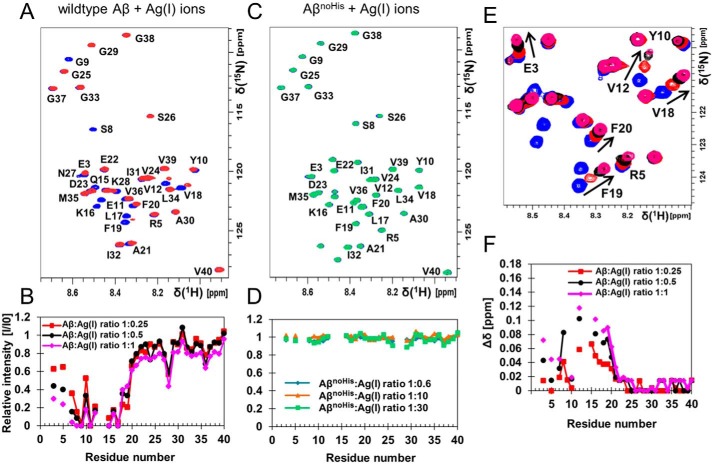
Although aggregation experiments showed a reduction in the fibril-end elongation rate, these kinds of experiments do not reveal any details on the mechanism of metal-ion binding to monomeric peptide. To obtain high resolution information on the binding mechanism, we opted for NMR spectroscopy and recorded 2D ¹H-¹⁵N HSQC and ¹H-¹³C HSQC experiments (Fig. 2 and Fig. S7) at various silver ion concentrations. Addition of 20 μm Ag(I) ions to 80 μm ¹³C-¹⁵N-labeled Aβ₄₀ (Ag(I):Aβ₄₀ ratio of 1:4) resulted in an immediate attenuation of signal intensities of cross-peaks corresponding to N-terminal residues in both the ¹⁵N- (Fig. 2, A and B) and ¹³C-edited spectra (Fig. S7). In addition, induced chemical shift changes were observed (Fig. 2, E and F, and Fig. S7), indicating Ag(I)-induced conformational changes in the N terminus of Aβ. To exclude specific effects from Ag(I)–buffer interactions, we performed experiments in different buffers and found similar binding patterns (Fig. S8). The Ag(I) ion binding is reversible, as probed by an added chelator (1,10-phenanthroline) to a sample containing both Aβ and Ag(I) ions (Fig. S9). The loss of signal intensity and chemical shift differences induced by Ag(I) ions immediately returned to the original values in the presence of the chelator. SDS micelles constrain Aβ in a monomeric state while keeping the metal binding N terminus disordered in solution (56) and indeed while bound to SDS micelles similar binding pattern as in buffer solution was found (Fig. S10). Hence, we can conclude that Ag(I) ions bind to Aβ monomers (supporting text and Fig. S10). The ¹H-¹⁵N HSQC cross-peak intensities of the histidine residues (His⁶, His¹³, and His¹⁴) in Aβ are only very weak under present conditions, whereas cross-peak intensities both in the aliphatic and in the aromatic region are detectable in the ¹H-¹³C HSQC spectra, (Fig. S7). All histidines are clearly affected by the presence of Ag(I) ions and show ∼75–80% reduction of the initial signal intensity at 20 μm Ag(I). Neighboring residues to the histidines in the sequence such as Arg⁵, Ser⁸, Val¹², and Gln¹⁵ are also affected, as well as Asp¹, similar to the effect of Zn(II) ions (28).

Figure 2.

Ag(I) ions bind specifically to the N-terminal part of monomeric Aβ peptide. A, ¹H-¹⁵N HSQC spectra of 80 μm monomeric ¹³C-¹⁵N-labeled Aβ₄₀ peptides alone (blue) and with 20 μm Ag(I) ions, 4:1 Aβ₄₀:Ag(I) (red) in 20 mm sodium phosphate buffer, pH 7.4, recorded at 278 K. B, relative intensities determined from the Ag(I) ion titration. C and D, ¹H-¹⁵N HSQC spectra of ¹⁵N-labeled Aβ₄₀ H6A,H13A,H14A mutant peptides (Aβ^noHis) (blue) and in the presence of 1:30 Aβ₄₀:Ag(I) ions (green), showing no changes in cross-peak intensities (D) and chemical shifts (C) in the presence of Ag(I) ions. E, magnification of the chemical shift changes observed in A. F, combined chemical shift changes from data in A. Hence, signal attenuation and chemical shift changes upon addition of Ag(I) are most prominent for the N-terminal residues.

To further verify that the histidines are the metal-binding ligands, we performed ¹H-¹⁵N HSQC titration experiments on a histidine-free H6A,H13A,H14A-¹⁵N-Aβ₄₀ variant (Aβ₄₀^noHis), and we found that the addition of more than 10-fold excess of Ag(I) ions neither caused any signal loss nor any chemical shift changes (Fig. 2, C and D). Moreover, 1D proton experiments for nonlabeled Aβ₄₀ were conducted in D₂O (Fig. S11A). Here the nonexchangeable imidazole proton signals are observed as three peaks ∼7.7 ppm, and upon titration of Ag(I) ions these signals were broadened. We conclude that the three histidines His⁶, His¹³, and His¹⁴ are involved in silver ion coordination.

The dissociation constant can be calculated from the signal loss in NMR HSQC data, assuming that the line broadening effect is linearly coupled to the bound population and is ∼3 μm in 20 mm sodium phosphate buffer, pH 7.4 (Table S2 and Fig. S12). Calculating the dissociation constant from induced chemical shifts instead gives consistent values (Table S2 and Fig. S12). In addition, intrinsic Tyr¹⁰ fluorescence experiments were conducted in which Ag(I) ions decrease the Tyr¹⁰ fluorescence intensity, and this phenomenon was used for a direct estimation of the dissociation constant (supporting text). The obtained values agree well with the values determined by NMR data and from analysis of the kinetics data (Fig. 1H). The values for the dissociation constant vary thus in a relatively narrow interval between 3 and 15 μm depending on the applied technique and experimental conditions (Table S2).

Silver ions induce a more compact structure in Aβ

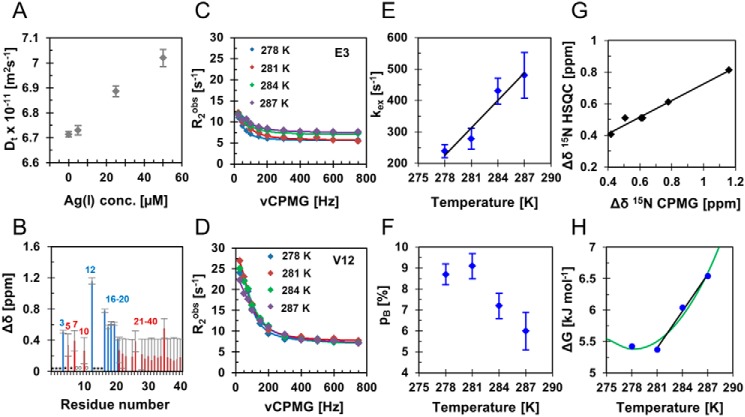
To examine whether the Ag(I) ion interaction causes the Aβ peptide to fold upon coordination of the metal ion, pulse field gradient diffusion experiments (57) were conducted at different Ag(I) concentrations. The translational diffusion coefficient for 80 μm Aβ₄₀ peptide increases in a concentration-dependent manner from 6.7 to 7.0 × 10⁻¹¹ m²/s upon increasing Ag(I) concentration from 0 to 50 μm (Fig. 3A). From the translational diffusion coefficient, the hydrodynamic radius (R_H) can be calculated using the Stokes–Einstein equation (58, 59). The apparent hydrodynamic radius decreases from 17.0 Å for Aβ₄₀ alone to 16.3 Å in the presence of 50 μm Ag(I) ions, suggesting a slightly more compact Aβ peptide structure once bound to the Ag(I) ion, without significant changes in the secondary structure content (Fig. S11B). Because the observed R_H is the population-weighted mean of the free and bound state, the hydrodynamic radius of the bound state can be estimated to be 16.0 Å, indicating a significant compactification upon metal-induced folding.

Figure 3.

Chemical exchange between free Aβ and an Aβ–Ag(I) ion complex. A, translational diffusion coefficients of 80 μm monomeric Aβ₄₀ in the absence and presence of 5–50 μm Ag(I) ions at 281 K. The average and standard deviation values were determined from five repeated measurements. B–F, relaxation dispersion was measured for 80 μm ¹⁵N-labeled Aβ₄₀ with two different Ag(I) concentrations (4 and 6 μm). B, chemical shift differences from an individual data set with 6 μm Ag(I). Blue bars show the residues exhibiting significant chemical exchange (p < 0.01), which were included in the full analysis, whereas red bars correspond to residues with no significant chemical exchange. Residues marked with an open circle were not observed because of low signal intensity, and residues marked with an asterisk exhibited too fast exchange with the solvent or spectral overlap. C and D, relaxation dispersion profiles from two selected N-terminal residues at four different temperatures with 6 μm Ag(I). E and F, the temperature dependence of the global fit parameters, the chemical exchange rate, k_ex, and bound population, p_B. G, chemical shift changes from ¹H-¹⁵N HSQC experiments plotted against the chemical shift differences from relaxation dispersion, displayed in B, revealing good correlation. H, Gibbs free energy for the four different temperatures shown for 6 μm Ag(I). At higher temperatures (≥281 K) the data points could be fitted linearly, whereas the whole data set exhibits a nonlinear dependence (green), described by an equation including a heat capacity difference (supporting text).

Chemical exchange between Aβ–Ag(I) complex and free peptide

The loss of NMR signal of ¹⁵N-Aβ₄₀ upon Ag(I) addition presumably originates from chemical exchange effects. Transient structures and dynamical features on the microsecond to millisecond time scale (typically underlying exchange broadening) are suitable to quantify using NMR relaxation dispersion experiments (60). We applied ¹⁵N Carr–Purcell–Meiboom–Gill (CPMG)–based pulse schemes (61–63) to characterize the influence of Ag(I) ions on 80 μm Aβ₄₀ (Fig. 3, B–F), and we observed relaxation dispersion profiles in the presence of 4 and 6 μm Ag(I) at four different temperatures (278–287 K) (Figs. S13 and S14, and Table S3).

Especially, the N-terminal residues exhibit high-amplitude relaxation dispersion profiles, where seven residues show significant relaxation dispersion (F-test p value <0.01), and these residues were used for further analysis (Table S3). The seven residues are in close proximity to the histidines, the metal-binding ligands. Notably, also in the presence of SDS micelles, constraining Aβ as a monomer, the same N-terminal residues show relaxation dispersion profiles, confirming that the chemical exchange process can be attributed to Ag(I) binding to monomeric Aβ (supporting text and Figs. S10 and S15). In contrast, we have previously reported that Aβ₄₀ peptides without metal ions do not show any relaxation dispersion profiles in this NMR time regime (14).

The relaxation dispersion profiles fit to a two-state exchange model (14, 64), which allows determination of the population of the free and bound states, (1 − p_B) and p_B, the chemical exchange rate, k_ex, between the two states, the absolute value of chemical shift differences, |Δδ_N|, and intrinsic transverse relaxation rate R₂⁰ (Fig. 3, E and F, and Table S4). Although the latter two parameters, R₂⁰ and |Δδ_N|, are residue-specific parameters, the exchange rate and populations can be applied as global fitting parameters and constrained to the same values for all residues. We found that a model with a temperature-dependent p_B (referred to as model 1) best describes the data (Table S5). In this model, the exchange rate k_ex linearly increases and the population p_B decreases with increasing temperatures. Under the chosen experimental conditions, ∼6–9% of the Aβ population is bound to a silver ion at any given time point (Fig. 3F) and exchanges between the Ag(I)-bound and the free state with an exchange rate of 200 to 500 s⁻¹ (Fig. 3E).

The chemical shift differences correlate well with the values obtained from the titration experiments monitored by ¹H-¹⁵N HSQC experiments, indicating that the same structural state from the same process is observed (Fig. 3G). Interestingly, the exchange and population parameters for Ag(I) are in the same order as the ones previously determined for zinc ions (14). When calculating K_D^app values from relaxation dispersion data, these values were estimated to ∼1 μm at 281 K (Table S4). This value is in the same order of magnitude compared with the K_D^app values determined by HSQC titration (Table S2). To further confirm the model with a two-state exchange process, two different Ag(I) ion concentrations were compared. The exchange rate determined from the global fit at 6 μm Ag(I) ions does not significantly differ from the one at 4 μm Ag(I) ions and can be constrained to the same value in the fitting procedure (Tables S4 and S5). In contrast, the populated state (p_B) does increase with ∼30% as expected for this increase in concentration (Table S4). This observation shows that the signal intensity loss and chemical shift changes in HSQC spectra upon Ag(I) ions titration are linearly coupled to the bound Aβ population. The p_B parameter is temperature-dependent and related to the Gibbs free energy difference, ΔG, between the free and the bound state via the equilibrium constant (supporting text and Fig. 3H). Notably, at a higher temperature (≥281 K), the data exhibit a linear temperature dependence, which reflects non–temperature-dependent contributions of the enthalpy and entropy. However, the whole data set fits best to temperature-dependent enthalpy and entropy terms, reflected in a heat capacity difference between the free and the bound state (supporting text). We found that the binding reaction is favored by enthalpy but disfavored by entropy. Together, the Gibbs free energy differences are small, yielding an unstable final fold at all temperatures (Fig. 3H, supporting text, and Tables S4 and S6).

Insights into metal-ion binding mechanisms and effects on aggregation comparing Ag(I) and Zn(II)

The weak Ag(I) binding transiently removes Aβ monomers from the pool of aggregation-prone monomeric species, which are available to be incorporated into the fibrils (Figs. 1 and 3). Because the metal-ion binding is weak, eventually all Aβ peptides fibrillate. This analysis hence directly links the metal ion interactions with monomeric Aβ to the overall retardation effect of fibril formation.

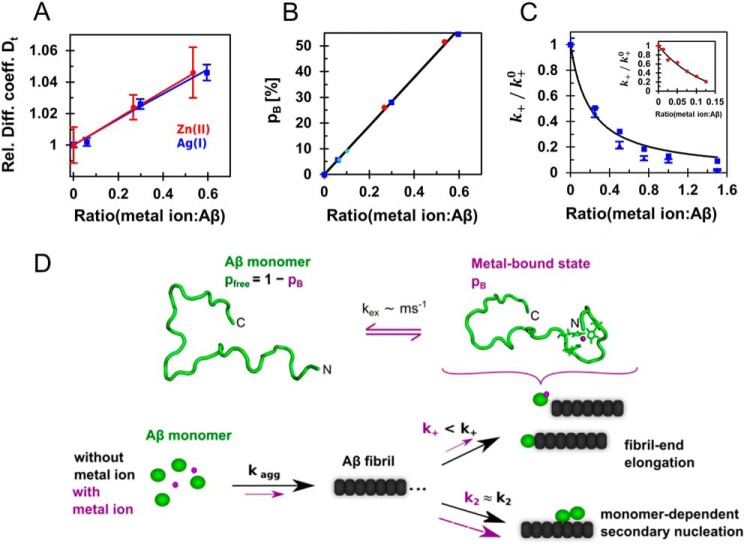
To distinguish whether this is solely a Ag(I) ion effect or whether it is a general metal-ion modulation effect of the Aβ fibrillization, we compared the results from monovalent Ag(I) with our previously reported findings from divalent Zn(II) (14) to be able to elucidate the impact of charge of the transition metal ion on the nucleation mechanism and binding characteristics. An induced folding of the N terminus upon metal-ion binding is a shared feature reflected in a decreased hydrodynamic radius of the Zn(II)–Aβ (14) and Ag(I)–Aβ complexes (Fig. 3A and Table S7). In fact, normalized diffusion data of Ag(I) and Zn(II) can be fitted together, constraining the normalized diffusion coefficient for the bound state, D_B/D_free, to the same values for both metal ions. This analysis revealed an increased value of D_B/D_free = 1.087 ± 0.002, reflecting a decreased hydrodynamic radius by a factor 0.92 for the metal ion-bound/“folded” state (Fig. 4A). Interestingly, unlike in the presence of Zn(II), we observed significant chemical shift changes in ¹H-¹⁵N HSQC resonances for Ag(I), indicating somewhat modulated exchange kinetics. Overall, both ions display similar binding regions with similar exchange dynamics; however, Zn(II) ions act at lower metal ion:Aβ ratios.

Figure 4.

Model for the role of Aβ:metal ion complexes in Aβ fibrillization using substoichiometric concentrations of Ag(I) and Zn(II) ions. A, global fit of diffusion data where data from Ag(I) (blue) were fitted together with previously reported data for Zn(II) (14) (red) using a two-state model, revealing an increased relative diffusion coefficient (Rel. Diff. coeff.) of the bound/folded state by D_B/D_free = 1.087 ± 0.002. B, the metal-bound populations, p_B, are determined by the apparent dissociation constants for the respective metal ions and exhibit a linear dependence on the metal ion:Aβ ratio, here shown for the population corresponding to the diffusion data in A. The bound populations from relaxation dispersion experiments of Ag(I) (turquoise) confirm this relation. C, the relative elongation rates, k₊, of Zn(II) (red) and Ag(I), from seeding (blue triangles) and global fit analysis (blue squares), are plotted against the metal ion:Aβ ratio, and fitted with Equation 5, revealing an apparent dissociation constant of K_D^app = 4.1 ± 0.4 μm for Ag(I) ions and K_D^app = 1.2 ± 0.2 μm for Zn(II) ions (inset). These values are similar as determined by other methods for Ag(I) (Table S2) and determined previously for Zn(II) (28). These findings indicate that Ag(I) and Zn(II) interact with monomeric Aβ in a remarkably similar manner. D, monomeric Aβ binds transition metal ions at the N terminus, forming a compact, histidine-coordinated fold. This metal–peptide complex is not stable and exchanges with the free peptide on the millisecond time scale. Aβ fibrils are formed through secondary nucleation mechanisms, in addition to fibril-end elongation, where the latter is predominantly attenuated by the presence of metal ions. Hence, these binding processes reduce the apparent available pool of free monomeric Aβ, resulting in a retardation of the overall fibrillization.

In fact, when plotting the population of the metal-bound states estimated by the K_D values against the metal ion:Aβ ratio, a linear relation is evident (Fig. 4B). Notably, the bound population of Ag(I), as determined by relaxation dispersion experiments, agrees well with this prediction (Fig. 4B). For the bound/folded state, this suggests that the association mechanisms are very similar and determined by the respective dissociation constant. Comparing the thermodynamics for the binding, it turned out that both metal ions induce an enthalpy-favorable, yet unstable, final Aβ fold, where the heat capacity in the presence of Ag(I) is consistent with the more accurately determined value for Zn(II) (Table S7). Hence, these findings suggest strikingly similar binding mechanisms for both metal ions, where the lower binding efficiency for Ag(I) ions may stem from lower charge and larger ionic radius.

Specific interaction with monomeric Aβ resulting in reduction of the elongation rate is seemingly a common mechanism for the investigated metal ions. Indeed, the relative elongation rates for both Ag(I) and Zn(II) ions (14) can be fitted with a model for metal-ion binding to Aβ monomers as a function of an apparent binding constant, revealing K_D^app = 4.1 ± 0.4 μm and 1.2 ± 0.2 μm for Ag(I) and Zn(II), respectively (Fig. 4C). These values are similar as obtained here by other methods for Ag(I) (Table S2) and reported previously for Zn(II) (28). This analysis hence suggests that the reduction of free Aβ monomer population by metal ion-bound state causes the decrease of the apparent fibril-end elongation rates.

Concluding remarks

Taken together, we rationalized the mechanisms of action of transition metal-ion binding to Aβ in a schematic model (Fig. 4D). Metal-ion binding causes a N-terminal fold in Aβ with a histidine coordination of the metal ion, where the Aβ peptide exchanges at a millisecond time scale between the free and bound, folded states. This folded state is inert to fibril elongation. Hence, the pool of monomeric species available to be incorporated into the fibrils is reduced, retarding the overall Aβ fibrillization. Whereas also primary and secondary nucleation are dependent on the Aβ monomer concentration, the metal-ion interaction mainly affects the process of fibril-end elongation, because the elongation reaction involves a folding event when integrating Aβ into the fibril. This elongation event presumably includes multiple steps, where in a first step the peptide binds to the fibril end, followed by a folding event representing the conversion from a predominantly unstructured state to a β-structure conformation (66). In contrast, primary and secondary nucleation do not require a full β-structure formation to form the amyloid state. Hence the elongation event is particularly dependent on modulation of the folding thermodynamics, where the metal-bound state is unable to adopt a productive fold on the fibril end. However, because the metal-ion binding is weak, presumably much weaker than the affinity of the monomer to the fibrillar state, eventually almost all Aβ peptides are incorporated into the fibrils. This is also reflected when comparing the Gibbs free energy values of the fibril elongation event, which was determined to approximately −38 kJ/mol (67), and the value of the metal-bound state in the range of 5–7 kJ/mol.

To conclude, our analysis hence establishes the link between microscopic metal-ion interactions with monomeric Aβ and its macroscopic retardation effect of fibril formation, providing detailed mechanistic insights into modulation of Aβ self-assembly. We hence could further develop our previous model for Zn(II) (14) for both mono- and divalent metal ions and were able to show here in a strictly quantitative manner that the population of the aggregation-inert metal ion-bound state causes the retardation of Aβ fibrillization. These insights might be beneficial to interfere with specific Aβ nucleation events, which potentially prevents toxic pathways (68–70), and thereby find efficient ways for treatment of protein/peptide misfolding-related disorders.

Experimental procedures

Sample preparation

Recombinant Aβ peptides with the sequence ¹DAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVV⁴⁰ (IA) were used in this study. Non-, ¹⁵N-, and ¹³C-¹⁵N-labeled Aβ₄₀ peptides were bought lyophilized from AlexoTech AB, and nonlabeled Aβ₄₂ peptides were purchased from rPeptide. Silver(I) acetate, silver(I) nitrate, and 1,10-phenanthroline were purchased from Sigma–Aldrich, and the Ag(I) ion concentration was determined by weight. For NMR experiments, the lyophilized peptides were dissolved in 10 mm NaOH, pH 12, at 1 mg ml⁻¹; sonicated in an ice-water bath; and diluted to the desired concentration in the selected buffer. For kinetics experiments, the lyophilized peptides were dissolved in 6 m guanidium hydrochloric acid, pH 7.2, and prepared with size-exclusion chromatography using a Superdex 75 10/300 GL column from GE Healthcare to remove preformed aggregates (supporting text).

pFTAA and ThT fibrillization kinetics using fluorescence spectroscopy

For aggregation kinetics experiments, 20 μm Aβ₄₀ in 10 mm MOPS buffer, pH 7.2, was supplemented with 0.3 μm pentameric formyl thiophene acetic acid (pFTAA) (49) or 40 μm thioflavin T (ThT) (48, 71) and different concentrations of Ag(I) ions (0–30 μm). The fluorescence intensity was monitored over time with a FLUOstar Omega microplate reader from BMG LABTECH (Germany) each minute (for seeded samples) or each third minute in a 384-well plate, 30–40 μl/well, at +37 °C. Three or four replicates per condition were measured. Both raw data and weighted average kinetic traces were analyzed using sigmoidal curve fitting (72) (supporting text). For each type of kinetic experiments, at least three measurements were performed with qualitatively similar results.

Global fit analysis

Global fit analysis of the kinetic curves using the model presented by Meisl et al. (50) was performed where the Aβ fibrillization process under quiescent conditions is described as a monomer-dependent process with three different microscopic rate constants (6), k_n as the primary nucleation rate constant with reaction order n_c = 2, k₊ as the elongation rate constant, and k₂ as the secondary nucleation rate constant with the reaction order n₂ = 2 (6, 50). The kinetic curves from 20 μm Aβ₄₀ were globally fitted to a multistep secondary nucleation model with a Michaelis constant K_M of 12.5 μm (14). Two of the rate constants k₊, k₂, and k_n were held constant, whereas the third rate constant was allowed to vary. The global fit analysis was performed with IgorPro 7 (WaveMetrics) and the Amylofit interface (73).

Seeding experiments

Seeding experiments were conducted with a fixed concentration of seeds of 1 μm supplemented to 20 μm monomeric Aβ₄₀. The seeds were prepared from homogenized fibrillated samples by sonication, and the seed concentration was determined from the initial Aβ₄₀ monomer concentration. The relative elongation rate constant, k₊, was determined from the initial rate of the derived concave kinetic curves.

We applied a model where the kinetic traces at different Ag(I) concentrations are described by an apparent free Aβ monomer concentration, which is determined by an apparent dissociation constant, K_D^app. For a two-state exchange, K_D^app can be described by Equation 1 based on the Ag(I)-bound population, p_B, and the initial concentrations of Aβ monomers and Ag(I) ions (14).

$$K_D^{\text{app}}=\frac{\left(1-p_{\text{B}}\right)·\left({\left[\text{Ag}\left(\text{I}\right)\right]}_0-p_{\text{B}}{\left[\text{A}\beta \right]}_0\right)}{p_{\text{B}}}$$ (Eq. 1)

The apparent Aβ monomer concentration is then given by [Aβ]^app = [Aβ]₀ (1 − p_B), where p_B is a function of K_D^app, which can be derived from Equation 1. The aggregation traces were then globally fitted applying a secondary nucleation model (6), where k_nk₊, k₂k₊, and K_D^app are global fit parameters, which were constrained to the same value across all values of [Aβ]^app. Hence, all fitting parameters are globally constrained, and this approach facilitates testing the model of an apparent free Aβ monomer concentration that is determined by K_D^app.

Solid-state AFM imaging and circular dichroism spectroscopy

Samples from the end of a fibrillization kinetic experiment were used for AFM imaging and CD measurements. CD spectra were also recorded for a titration series of Ag(I) ions onto monomeric Aβ₄₀ in 20 mm sodium phosphate buffer, pH 7.4 (supporting text).

NMR spectroscopy

Most NMR experiments were performed on a 700 MHz Bruker Avance spectrometer equipped with a cryogenic probe, if not stated differently. The 2D NMR ¹H-¹⁵N HSQC experiments used 80 μm WT ¹³C-¹⁵N-Aβ₄₀ or 80 μm ¹⁵N-labeled mutant Aβ₄₀ (H6A,H13A,H14A) (referred to as Aβ₄₀^noHis) in 20 mm sodium phosphate buffer, pH 7.4 (90/10 H₂O/D₂O), and were performed at 278 K. The temperature was calibrated with an external thermometer. To investigate the Ag(I) ion-binding capacity to Aβ₄₀ situated in a membrane-mimicking system, SDS micelles were used, applying 50 mm d-SDS (> critical micelle concentration) and 170 μm ¹⁵N-Aβ₄₀. For the 2D spectra, the relative intensities for each amide cross-peak were determined from the amplitude of the cross-peaks. The combined chemical shift changes were calculated from Equation 2 (74, 75).

$$\Delta \delta ={\left(\left({\left(\frac{\Delta {\delta }_{\text{N}}}{5}\right)}^2+{\left(\Delta {\delta }_{\text{H}}\right)}^2\right)/2\right)}^{1/2}$$ (Eq. 2)

The spectra were referenced to the ¹H signal of trimethylsilylpropanoic acid. The Aβ₄₀ amide cross-peak assignment in the HSQC spectra was performed by comparison with previously published work (24, 28, 56).

Pulse field gradient diffusion experiments were performed on a 600 MHz Bruker Avance spectrometer with 80 μm Aβ₄₀ in 20 mm sodium phosphate buffer, pH 7.4, in D₂O at 281 K with different Ag(I) concentrations. A standard sample of 1% H₂O, 0.1% DSS and 0.1 mg ml⁻¹ GdCl₃ in D₂O was used to calibrate the pulse field gradients. The translational diffusion coefficient (D_t) was determined by one-component analysis, and the hydrodynamic radius (r_H) was determined from the diffusion coefficient (76) using the Stokes–Einstein relation (58, 59). The diffusion data were further analyzed using a two-state model,

$$D_{\text{obs}}=p_{\text{free}}{D}_{\text{free}}+p_{\text{B}}{D}_{\text{B}}$$ (Eq. 3)

in which D_free and D_B are the diffusion coefficient of the free and the bound state, respectively, with the respective populations. Additionally, a global fit analysis of the diffusion data from Ag(I) and Zn(II) (14) was performed on normalized diffusion data (Fig. 4A), where the coefficients D_free and D_B were constrained to the same value for Ag(I) and Zn(II), and the values of p_B were calculated by resolving Equation 1 using the respective apparent dissociation constants, here 1 μm for Zn(II) and 3.5 μm for Ag(I) (from HSQC analysis at low temperature) (28) (Table S2).

¹⁵N-CPMG relaxation dispersion experiments (61–63) were recorded on 80 μm ¹⁵N-Aβ₄₀ peptides with 6 μm or 4 μm Ag(I), in 20 mm sodium phosphate or 10 mm HEPES buffer at pH 7.4. The Ag(I) concentration was adjusted and recalculated to the same signal attenuation upon Ag(I) addition based on the 2D NMR HSQC titration experiments. The experiment was repeated at four different temperatures (278–287 K) with 3 K intervals for each Ag(I) ion concentration. The ¹⁵N-CPMG relaxation dispersion experiments were performed as pseudo 3D experiments. 7 or 11 different CPMG frequencies were used as delays for the refocusing pulse with a mixing time, T_CP, of 120 ms. The transverse relaxation rate (R₂^obs) values were determined from the signal ratios by R₂^obs = 1/T_CP·ln(I/I₀). The significance of each relaxation dispersion profile was assessed based on an F-test (p value < 0.01). A global fit analysis using a two-state exchange model (14, 64) was performed by fitting the residues displaying significant relaxation dispersion profiles. The intrinsic transverse relaxation rates R₂⁰ and the chemical shift changes |Δδ_N| are residue-specific parameters, whereas the population p_B and the exchange rate k_ex were set to the same value for all residues. The chemical shift changes (|Δδ_N|) were assumed to be independent of the temperature, ≥Δδ_N(HSQC) and constrained to the same value for all temperatures in the global fit analysis. We applied two models: model 1, in which p_B is temperature-dependent, and model 2, in which p_B is temperature-independent. The models were assessed with an F-test and using the Akaike information criterion (Table S5), yielding model 1 as the preferred one. In model 1 the exchange rate for the two Ag(I) concentrations can be constrained to the same value (referred to as model 1b), resulting in the same quality of the fits (Table S5). From model 1 thermodynamic parameters for the binding and folding reaction were calculated (supporting text).

NMR data were processed with the Topspin version 3.2 software or NMRPipe. The diffusion data were analyzed using MatLab, and the ¹⁵N-CPMG relaxation dispersion data were analyzed and fitted using IgorPro 7 (WaveMetrics).

Dissociation constant determination for Ag(I) binding

Apparent dissociation constants of the Aβ–Ag(I) complex were determined for different conditions with different techniques. Relative intensities and chemical shift changes from ¹H-¹⁵N HSQC spectra were extracted and plotted against the Ag(I) ion concentration. The data were globally fitted to a model assuming one binding site (Equation 4) (65). Additionally, the apparent dissociation constant was determined from fluorescence spectroscopy data (supporting text). No buffer corrections were made.

$$I=I_0+\frac{I_{\infty }-I_0}{2·\left[\text{A}\beta \right]}·\left(K_D^{\text{app}}+\left[\text{Ag}\left(I\right)\right]+\left[\text{A}\beta \right]-\sqrt{{\left(K_D^{\text{app}}+\left[\text{Ag}\left(I\right)\right]+\left[\text{A}\beta \right]\right)}^2-4·\left[\text{Ag}\left(I\right)\right]·\left[\text{A}\beta \right]}\right)$$ (Eq. 4)

where I_∞ is the intensity upon saturation, I₀ is the initial intensity without Ag(I) ions, and K_D^app is the apparent dissociation constant. From NMR relaxation dispersion experiments, an apparent K_D^app value was determined using the bound population p_B.

The relative elongation rate constants in Fig. 4C were fitted using an equation that describes the effect of metal-ion binding to Aβ monomers on the elongation rate, in terms of an apparent dissociation constant (51).

$$k_{+}/{{{\displaystyle k}}^0}_{+}=1/\left(1+{\left[\text{Me}\right]}_0/K_D^{\text{app}}\right)$$ (Eq. 5)

Data availability

All supporting data are available from the corresponding author upon request.

Author contributions

C. W., J. D., A. G., and A. A. conceptualization; C. W., J. D., and A. A. formal analysis; C. W. and A. A. investigation; C. W. and A. A. visualization; C. W., J. D., and A. A. methodology; C. W. and A. A. writing-original draft; C. W. and A. A. project administration; J. J., H. B., and S. W. resources; J. J., H. B., and S. W. validation; J. J., H. B., S. W., J. D., and A. G. writing-review and editing; J. D., A. G., and A. A. supervision; A. G. funding acquisition.