Abstract
Global efforts around the world are focused on to discuss several health care strategies for minimizing the impact of the new coronavirus (COVID-19) on the community. As it is clear that this virus becomes a public health threat and spreading easily among individuals. Mathematical models with computational simulations are effective tools that help global efforts to estimate key transmission parameters and further improvements for controlling this disease. This is an infectious disease and can be modeled as a system of non-linear differential equations with reaction rates.
This work reviews and develops some suggested models for the COVID-19 that can address important questions about global health care and suggest important notes. Then, we suggest an updated model that includes a system of differential equations with transmission parameters. Some key computational simulations and sensitivity analysis are investigated. Also, the local sensitivities for each model state concerning the model parameters are computed using three different techniques: non-normalizations, half normalizations, and full normalizations.
Results based on the computational simulations show that the model dynamics are significantly changed for different key model parameters. Interestingly, we identify that transition rates between asymptomatic infected with both reported and unreported symptomatic infected individuals are very sensitive parameters concerning model variables in spreading this disease. This helps international efforts to reduce the number of infected individuals from the disease and to prevent the propagation of new coronavirus more widely on the community. Another novelty of this paper is the identification of the critical model parameters, which makes it easy to be used by biologists with less knowledge of mathematical modeling and also facilitates the improvement of the model for future development theoretically and practically.
Keywords: Coronavirus disease (COVID-19), Mathematical modeling, Model reduction, Sensitivity analysis, Computational simulations
1. Introduction
The history of the coronaviruses started from the 1930s when the infectious bronchitis virus (IBV) infection was caused by the domesticated chickens. In humans, it was firstly reported in the 1960s [1]. To avoid stigmatizing the virus's origins in terms of populations, geography, or animal associations the WHO termed as COVID-19 in December 2019. This virus involves serious respiratory tract infections [2,3]. Detected in Wuhan City, Hubei Province of China, this virus might be transferred to the seafood market [4,5] and then internationally via domestic/commercial air traveler carriers [6]. After that, an emergency has been declared in infected areas of the world and a serious public health concern has been paid at a global level. While to stop the impact of this infection and to avoid further spreading some mathematical estimations are also being performed at each level [7].
Spreading the novel coronavirus (COVID-19) has become a very difficult global issue. For May 15th, 2020, there were 4609,787 confirmed cases, 307, 528 deaths, and 1742,813 recovered cases around the world [8]. This virus has been spread more quickly around the world, it is very important to know its dynamics and predications. Although there were several proposed studies based on mathematical tools, computational simulations, clinical, and examination tests for controlling the disease, there are still different dimensions about this issue that can be further improved.
Recently, mathematical modeling of the COVID-19 disease has been investigated by several mathematical and computational researchers for the prediction of the disease dynamics. One of the well-known concepts in epidemiology is the basic reproduction number (or it sometimes is called the basic reproductive ratio). This ratio is a quantity and it is denoted by R0. This is the average number of secondary infections produced by a single primary infection in a population where everyone is susceptible. Based on the developed approaches of mathematical epidemiology models, this quantity becomes an essential tool to understand epidemiological concepts and identify key critical parameters for such models. The value of this quantity has been changed for the confirmed cases of Coronavirus. According to a study published recently, the median value of R0 was about 2.28 during the early stage experienced [9]. Based on another study, this quantity is about 2.489. They suggested a discrete-time stochastic epidemic model with binomial distributions to study the transmission of the disease [10]. There is also a developed compartmental model based on the clinical progression of the disease, the epidemiological status of the individuals, and intervention measures [11]. According to this study, the estimation of the basic reproduction number is very high and it was about 6.47. The idea of the next-generation matrix approach was used to calculate the basic reproduction number for the COVID-19 models, this is presented in [12]. According to their study, this ratio is bout 3.58. Furthermore, an updated model was proposed to estimate the transmission risk of the novel coronavirus, their calculations relate to a time-dependent dynamic model of contact and diagnosis rate. This helps us to re-estimated the daily reproduction number [13].
One of the key parameters that can be accumulated from the confirmed cases is the serial interval. The serial interval is a time interval between primary patients (infecters) and the second patient (infectees). This parameter helps investigators to find epidemic transmission links between confirmed cases and uses for design healthcare program strategies [14]. The serial interval is widely used for describing models dynamics of infectious disease. This may help us to understand the effect of contact among individuals and how transmits the virus more quickly. Recently, the serial interval has been calculated for the COVID-19, this estimates by 4.6 days [15]. A reported study mentioned that the mean serial interval for COVID-19 was calculated as 3.96 days. This considerably shorter than the mean serial interval calculated for SARS 8.4 days and MERS 14.6 days [16].
Although, there is a variety of modeling approaches that have been proposed so far for prediction and evaluation of the COVID-19 disease, there are more questions that can still be answered. There are some related works that sensitivity analysis used in their studies [13,17]. They used this technique only for special variables and parameters. More recently, mathematical modeling has been used to describe this disease in different views. Transmission and mitigation strategies for COVID-19 presented in [18], response strategies for COVID-19 epidemics in African settings shown in [19], the effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic explained in [20], mathematical recommendations to fight against COVID-19 investigated in [21], the feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts presented in [22], a mathematical modeling approach in the Spread of the COVID-19 described in [23], the reproductive number of COVID-19 is higher compared to SARS coronavirus presented in [24].
Defining such proposed models based on the mass action law with transmission parameters and identify some critical model elements could improve the outcomes further. An issue that has not been explained very well for this new virus is identifying the local sensitivities for non-normalizations, half normalizations, and full normalization techniques in commotional simulations. Here, we are proposing a mathematical model to estimate the transmissibility with the dynamical view of the virus transmission. For the complex model of COVID-19 given in this paper, it is vital to pay more attention to identify critical model elements based on sensitivity analysis and computational results more widely and accurately. Another contribution of this paper is analyzing the suggested model based on different values of the model parameters in commotional simulations. This is also an important step forward to understand how changing the model dynamics and predicting the spread of this virus in the future. The main contribution here is to understand the impact of each model parameter on the model states, this is given in our computational simulations and calculating the local sensitivities. This will help to quantify possible disease control strategies with further improvements and recommendations. Results in this study provide effective roles in further suggestions and preventions theoretically and practically. On possible theoretical suggestion is that these results could help biologists to understand the model dynamics and parameter transmissions. This may give further improvements and analyze the complex models in computational simulations. While the results here could also give practical suggestions. One practical improvement for controlling this disease could be reducing the contact between asymptomatic infected, reported, and unreported infected classes because their transmission parameters are very sensitive based on our computational simulations.
2. Methods
The idea of chemical kinetic theory is an important approach for understanding and representing the biological process in terms of model equations. The important assumptions to build such models are model states, parameters, and equations. This is because it helps the investigation of mathematical modeling effectively and easily [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], [35]. Therefore, we present here the basics of our calculations. We consider n irreversible chemical reactions and m chemical components with a stoichiometric equation given below
| (1) |
where are chemical species, aij and bij are stoichiometric coefficients (non-negative integers), are chemical interaction parameters. The model reaction rates are simply defined based on the classical theory of mass-action law
| (2) |
The chemical reactions can be expressed as a system of differential equations with initial components
| (3) |
where for and . Therefore, Eq. (3) takes the form
| (4) |
where The functions are often non-linear therefore model differential equations may not solve analytically. The more details and descriptions about chemical reactions and their differential equations with some applications in system biology can be found in [25,36,37]. An important technique to analyze system 4 is the idea of sensitivity analysis. According to this approach, the sensitivity of each variable concerning parameters can be calculated. The main equation of sensitivity is given below
| (5) |
The first order derivatives given in Eq. (5) represent the time-dependent sensitivities of all variables concerning each parameter value
Furthermore, the differential equations can be solved for sensitivity coefficients as below
| (6) |
Using the chain rule of differentiation, Eq. (6) can be further driven and the sensitivity equations take the Jacobian matrix as follows
| (7) |
where the matrices are defined by
For more details and applications of sensitivity analysis in the field systems biology, the reader can see in [25,[38], [39], [40], [41], [42], [43], [44], [45]]. The local sensitivity values are given in Eq. (7) can be computed using SimBiology Toolbox in MATLAB with three different techniques: non-normalizations, half normalizations, and full normalizations. Accordingly, in a complicated modeling case like new coronavirus dynamics, it is necessary to pay attention to sensitivity analysis more accurately and widely. This provides one to identify the key critical model parameters and to improve model dynamics.
3. An updated model for coronavirus disease
The classical models of epidemic diseases normally include components (individuals) and interaction changes among components in the population. In other words, for an epidemic network model, nodes are individuals, and edges are contacted among individuals. This representation helps us to understand infectious disease models in terms of a graphical network. There are some recently proposed models for presenting the dynamical equations of COVID-19 [26], [46], [47], [48], [49], [50], [51], [52], [53], [54]. The model initial populations and interaction parameters are mainly obtained for the confirmed cases in China. The main idea of the models is based on clinical progression, epidemiological individuals, and intervention measures. In this paper, we develop the previous model presented in [55]. We then extend the suggested model structure by including the recovered individuals (R), the unreported symptomatic death rate (α 1 U) and reported symptomatic death rate (α 2 W). The model network diagram and the interaction individual components demonstrated in Fig. 1 . The COVID-19 model digraph can be expressed as a graph , where is the model graph, is the set of nodes (states), is the set of links (reactions).
Fig. 1.
The model interaction individuals for the COVID–19 epidemic outbreak with reaction rates.
Thus, let us consider the human groups separated into 5 different groups.
-
1
Susceptible group (S). This group presents a healthy individual.
-
2
Asymptomatic group (I). This group presents an infected individual in the early stage of infection. They do not show any symptoms, but capable to infect through droplets or direct contact with the susceptible individual.
-
3
Symptomatic unreported group (U). This group presents an individual who gets infected, had symptoms of COVID-19 but did not detect by the government as a COVID-19 suspect.
-
4
Symptomatic reported group (W). This group presents an individual who gets infected, shows symptoms of COVID-19, and detected by the government, either from a rapid test or from voluntary action to report to the hospital. We assume that all individuals in this class will get a specific treatment and supervision, whether it's through monitored isolation or treatment in the hospital.
-
5
Recovered group (R). This group present individual who get recovered from COVID-19, and had a temporal immunity.
The transmission diagram which illustrates the interaction between each group described in Fig. 1. The developed model here has six parameters that can be analyzed in computational simulations. They are defined as interactions rate constants between individual groups. The contacts between different states (individuals) are as follows. Susceptible people (S) move into the infected people (I) when they are asymptomatic infected at the transition rate . After that, the asymptomatic infected individuals (I) either move into the reported symptomatic infected individuals (W) with the transition rate γI or turn into the unreported symptomatic infected individuals (U) with transition rate δI. Both groups W and U move into the recovered individuals (R) with the transition rates ηW and ηU, respectively. In addition to that some unreported and reported infected individuals may die with transition rates α 1 U and α 2 W, respectively.
The model reactions with their rats are shown below:
| (8) |
where
Furthermore, the model's constant parameters and initial states with their definitions are described in Table 1 . Using Eqs. (2)–(4), the model dynamics are described by the following system of non-linear ordinary differential equations
| (9) |
Table 1.
The model reaction constants (parameters) and initial individual populations for COVID–19 epidemic outbreak with their biological definitions, all data are confirmed cases in China presented in [55].
| Symbols | Biological definitions | Estimated values |
|---|---|---|
| S(0) | Initial susceptible individuals | 11.081 × 106 |
| I(0) | Initial asymptomatic infected individuals | 3.62 |
| U(0) | Initial unreported symptomatic infected individuals | 0.2 |
| W(0) | Initial reported symptomatic infected individuals | 4.13 |
| R(0) | Initially recovered individuals | 0 |
| β | Transmission rate between susceptible individuals and asymptomatic infected individuals | |
| γ | Transition rate between asymptomatic infected and reported symptomatic infected | 0.1142 |
| δ | Transition rate between asymptomatic infected and unreported symptomatic infected | 0.0285 |
| 1/η | Average time symptomatic infectious have symptoms | 1/7 |
| α1 | The unreported symptomatic death rate | |
| α2 | The reported symptomatic death rate |
The model initial populations are expressed in the following equation
| (10) |
6. Computational results
Analyzing epidemic disease models with a high number of elements sometimes cannot be well understood only by biological tools. This is why mathematical models are used, such models help and provide a good environment to analyze infectious diseases more widely and easily. Theoretical studies may help biologists to predict future model dynamics and identify critical model parameters. In the case of COVID-19, the suggested mathematical models are effective tools that give estimations and suggestions about controlling the virus and further preventions more effectively.
The values of parameters and initial populations in this study are obtained from the WHO situation report (the National Health Commission of the Republic of China) presented in [55]. We calculate the numerical approximate solutions of the model equations (9) for different parameters and initial populations using System Biology Toolbox (SBedit) for MATLAB; see Fig. 2, Fig. 3, Fig. 4, Fig. 5, Fig. 6 . Accordingly, there are different model dynamics for initial population model states and estimated parameters. Computational numerical simulations are calculated in two-dimensional planes for model parameters and initial populations. Results in this study provide a good step forward in predicting the model dynamics in the future for development programs, interventions, and health care strategies.
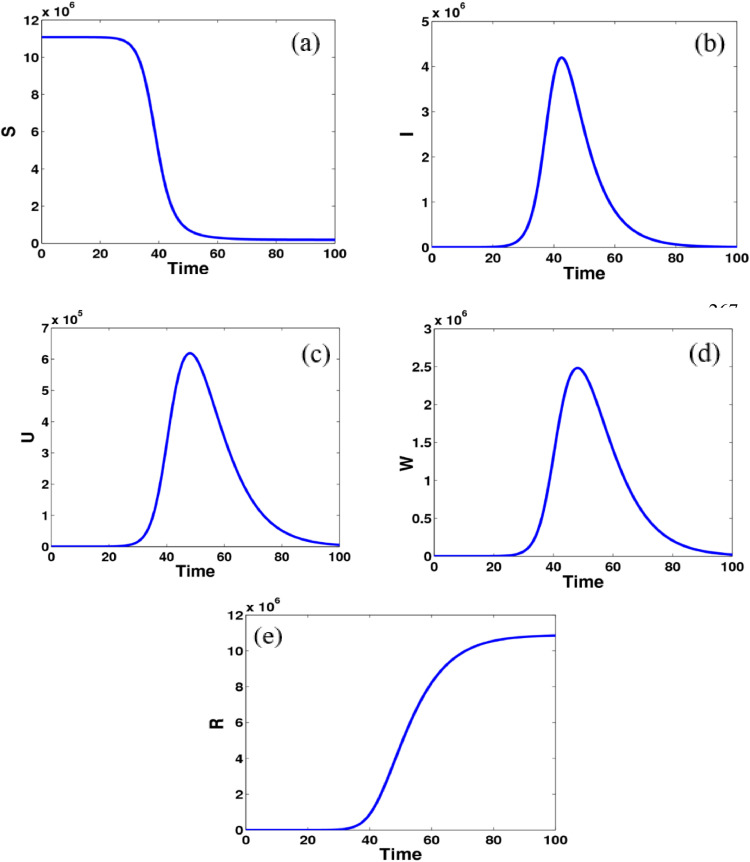
Fig. 2.
Computational simulations for the model states given in system (9) of the COVID–19 using MATLAB; there are model dynamics of (a) susceptible individuals, (b) asymptomatic infected individuals, (c) unreported symptomatic infected individuals, (d) reported symptomatic infected individuals, (e) recovered individuals.
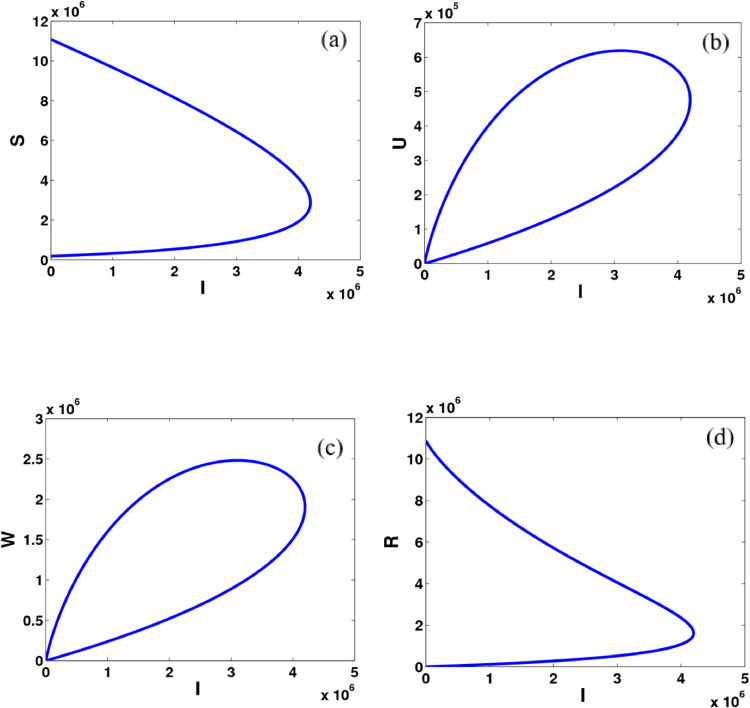
Fig. 3.
Computational simulations for the model states given in system (9) of the COVID–19 using MATLAB; there is the relationship between the asymptomatic infected people and (a) susceptible individuals, (b) unreported symptomatic infected individuals, (c) reported symptomatic infected individuals, (d) recovered individuals.
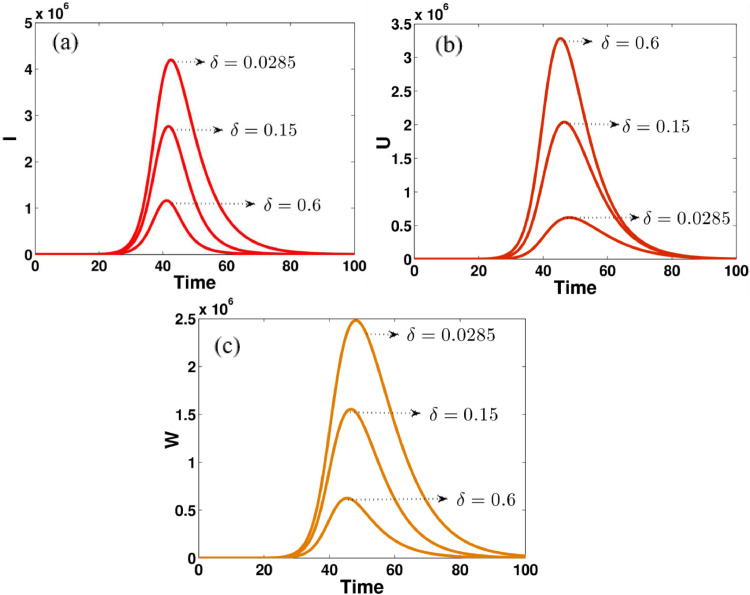
Fig. 4.
The effect of transition rate δ on (a) asymptomatic infected individuals, (b) unreported symptomatic infected individuals, (c) reported symptomatic infected individuals, in computational simulations using MATLAB parameters used
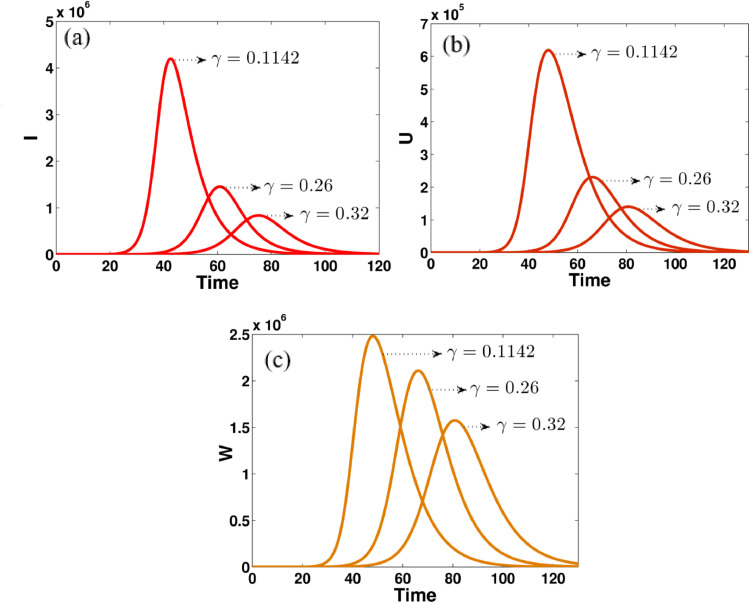
Fig. 5.
The effect of transition rate γ on (a) asymptomatic infected people, (b) unreported symptomatic infected people, (c) reported symptomatic infected people, in computational simulations using MATLAB parameters used γ = 0.1142, 0.26, 0.32.
Fig. 6.
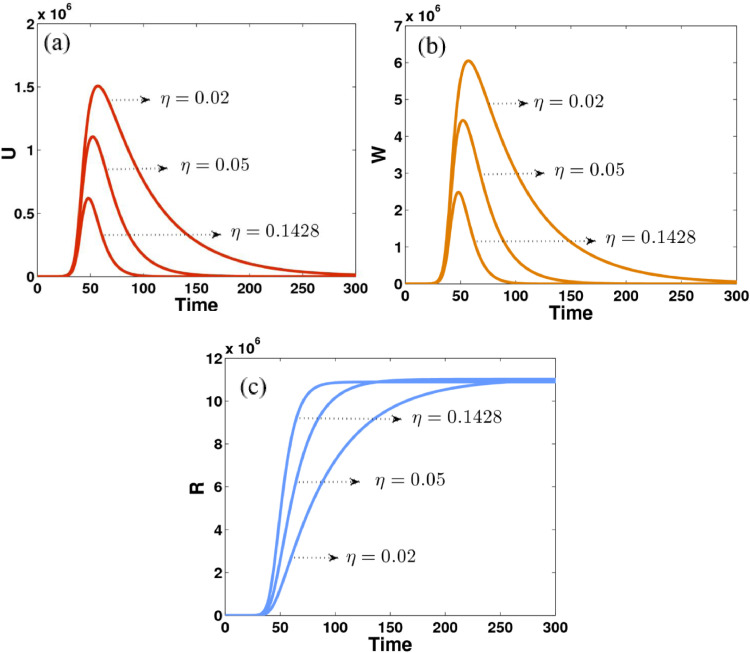
The effect of parameter η on (a) unreported symptomatic infected people, (b) reported symptomatic infected people, (c) recovered people, in computational simulations using MATLAB parameters used η = 0.1428, 0.05, 0.02.
Fig. 2 shows the model dynamics of susceptible, asymptomatic infected, reported symptomatic, and unreported symptomatic individuals. The number of susceptible populations decreases gradually and becomes stable after 60 days while the dynamics of recovered people increase and get flat again after 60 days. Interestingly, the number of infected individuals in both asymptomatic and symptomatic groups is dramatically changed between 40 days to 80 days. Furthermore, Fig. 3 explains the relationship between infected people with the other groups in the COVID-19. It can be seen that there are the same dynamical relations for reported and unreported symptomatic states whereas there are slightly different model dynamics for susceptible and recovered groups.
Fig. 4 shows that the impact of transition rate δ on asymptomatic infected reported symptomatic infected and unreported symptomatic infected individuals. The effect of this parameter can easily occur on the variables I, U, and W. For example, if the value of δ is increased from 0.0285 to 0.6 then the number of unreported symptomatic infected people is dramatically increased, see Fig. 4(b). On the other hand, there will be more asymptomatic infected and reported symptomatic infected cases when the values of transition rate δ become smaller and smaller, see Figs. 4(a) and 4(c).
Fig. 5 shows that the impact of transition rate γ on asymptomatic infected people reported symptomatic infected people and unreported symptomatic infected people. The effect of this parameter can easily occur on the variables I, U, and W. It can be seen that the model dynamics for such states become more flat when the value of γ is increased. This is an important key element for controlling this disease.
Fig. 6 shows that the impact of parameter η (average time that infected people have symptoms) on the dynamics of unreported symptomatic, reported symptomatic, and recovered individuals. The number of both unreported and reported infected people are significantly increased when the value of η becomes smaller, see Figs. 6(a) and 6(b). Conversely, the dynamics of recovered people dramatically grow and become stable very quickly when the value of η gets bigger and bigger, see Fig. 6(c)
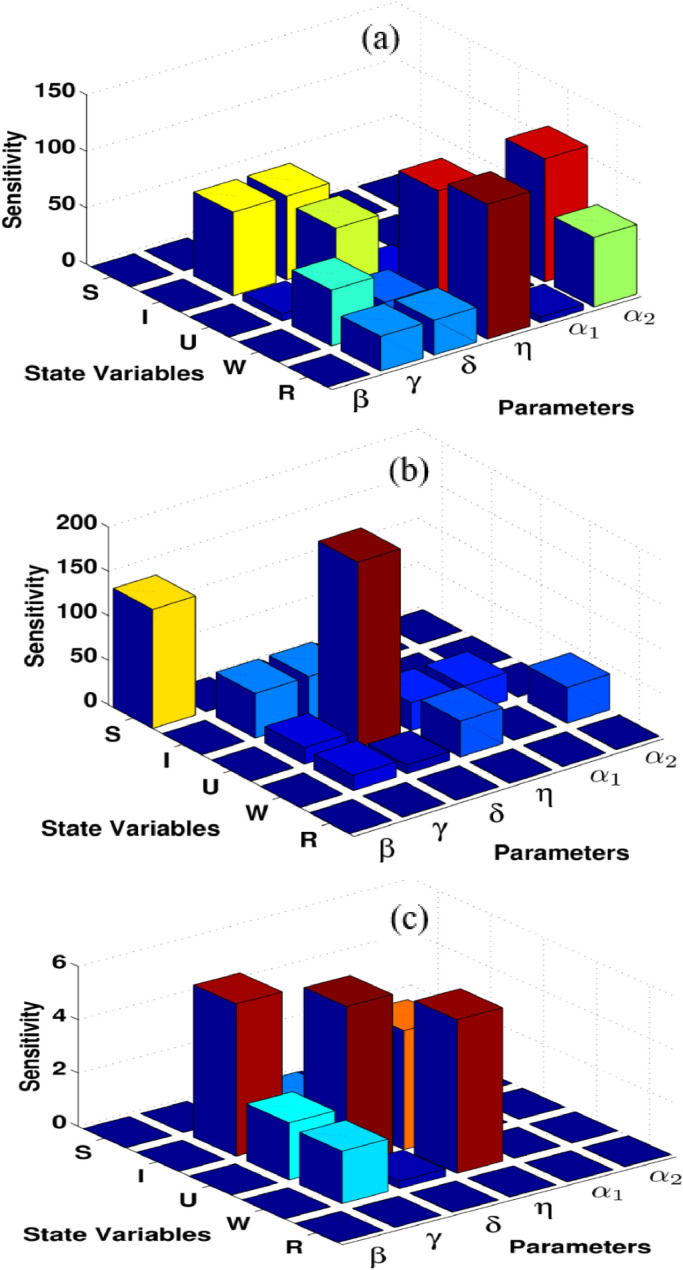
Another important step of parameter analysis is using the idea of local sensitivity analysis presented in Eq. (7). We use SimBiology Toolbox for MATLAB to calculate the local sensitivity of each model state concerning model parameters for the model equations (9). We compute the model sensitivities using three different techniques: non-normalizations, half normalizations, and full normalizations; see Figs. 7 . Interestingly, results provide us further understanding of the model and give one to identify the key critical model parameters. For example, it generally seems that the communication rate between asymptomatic infected and unreported symptomatic infected, transition rate between asymptomatic infected and reported symptomatic infected, the average time that infected people have symptoms are very sensitive parameters concerning model variables in spreading this disease among people. On the other hand, the other parameters are less sensitive to the model dynamics, they are unreported symptomatic death rate, reported symptomatic death rate and transition rate between susceptible and asymptomatic infected people. As a result, identifying critical model parameters in this study based on computational simulations is an effective way to further study the model practically and theoretically and give some suggestions for future improvements of the novel coronavirus vaccination programs, interventions, and controlling the spread of disease.
Fig. 7.
The sensitivity of each model state concerning model parameters in computational simulations for the coronavirus disease (COVID–19); (a) non-normalization sensitivity, (b) half normalization sensitivity, (c) full normalization sensitivity.
Accordingly, some findings and computational results are given based on the suggested approaches for the updated model of the COVID-19. We can mainly summarize them as the points given below:
-
1
The model dynamics of susceptible, asymptomatic infected, both reported and unreported symptomatic individuals, recovered individuals are computed using System Biology Toolbox (SBedit) in MATLAB. It can be seen that the relationship between infected people with the other groups in the COVID-19 model. There are the same dynamical relations for reported and unreported symptomatic states whereas there are slightly different model dynamics for susceptible and recovered groups.
-
2
The impact of transition rate δ on asymptomatic infected reported symptomatic infected and unreported symptomatic infected individuals is investigated. This parameter has an effective role in the dynamics of I, U, and W.
-
3
The transition rate γ has also affected asymptomatic infected people, reported symptomatic infected people, and unreported symptomatic infected people. It can be seen that the model dynamics for such states become more flat when the value of γ is increased. This is an important key element for controlling this disease.
-
4
The number of both unreported and reported infected people are significantly increased when the value of η becomes smaller whereas the dynamics of recovered people dramatically grow and become stable very quickly when the value of η becomes large.
-
5
The local sensitivity of each model state concerning the model parameters computed using three different techniques: non-normalizations, half normalizations, and full normalizations. Interestingly, results provide us further understanding and identifying the key critical model parameters. It can be concluded that the transmission parameters between asymptomatic infected and both reported and unreported symptomatic infected, the average time that infected people have symptoms are very sensitive parameters concerning model variables in computational simulations.
7. Discussions
Several healthcare strategies and preventions have been discussed and suggested as global efforts to reduce the impact of the new COVID-19 around the world. Although, this virus still spreads quickly and millions of people have been infected so far, but all scientific attempts give a great step forward to control this disease and minimizing the impact of such threats on the community. Currently, there are a variety of studies both theoretically and practically discussed and investigated in this area. One of the effective tools that could be used to describe such diseases is mathematical modeling. Mathematical modeling with computational simulations provides estimations and predictions about the dynamics of model states and parameters. However, having many suggested models in different countries makes the parameter estimations, predictions, and understandings of the disease remain unclear.
An issue that has not been well discussed and explained for this new virus is identifying the model critical elements. In this study, we computed the model dynamics for the different model parameter values. This provides us how the number of each model class changes concerning to the model parameters. Based on the results obtained here, we can simply understand the model critical parameters. For instance, the transmission parameter between asymptomatic class and the unreported symptomatic class becomes a key critical element and it has a great role in speeding this disease. However, the key critical model parameters may slightly change if we use different data reported for another country. Therefore, it can be argued that computational results and simulations based on the suggested models may give good approximations and predictions.
Another issue that can be discussed for the COVID-19 is the identification of the model sensitive parameters. This has also not well explained recently. In this work, we have used the idea of local sensitivities for non-normalizations, half normalizations, and full normalizations techniques in commotional simulations. For the complex model of COVID-19 given in this paper, it is vital to pay more attention to identify critical model elements based on sensitivity analysis and computational results more widely and accurately. Results in this paper become an important step forward to understand the model dynamics more widely. This provides to identify critical model parameters and how each model individual can be affected by the other model individuals. For example, results here show that almost all model states are sensitive to the critical model parameters { γ, δ, η} . On the other hand, such critical model parameters can be changed to the other model parameters when we use another set of initial states and parameters. Interestingly, the suggested approach here can be further developed and applied to a wide range of complex models of the COVID-19. It can work more effectively for identifying the model key elements. This provides us the suggested approaches here work very well for the COVID-19 models compared to the recently suggested techniques.
8. Conclusions
Global efforts and preventions of the speeding COVID-19 cannot be well understood only by biological and healthcare tools. Some mathematical models have been investigated for further improvements and give estimations for such model parameters. An issue that can be further studied is identifying key critical model parameters. This helps international efforts to pay more attention to the sensitive elements. The suggested coronavirus disease (COVID–19) model here is a complicated one, and it requires some mathematical tools to have improvements in interventions and healthcare programs.
The used model in this paper has further improved based on the computational results using MATLAB for different initial populations and parameters. Some main results can help in understanding the suggested model more widely and effectively. By using computational simulation, we identify some key critical parameters that have a great role in spreading this virus among the model classes. One of the identified key parameters is the transmission rate between asymptomatic infected and reported symptomatic individuals. This is an important finding in the understanding of the COVID-19 and how this virus spreads more quickly. Some other critical model parameters have investigated in this paper. For example, the transmission parameter between asymptomatic infected and unreported symptomatic individuals has a great impact on the dynamics of the model states. Besides these findings provide additional information about estimations and predictions for the number of infected individuals. Accordingly, our results in identifying key parameters are broadly consistent with clinical and biological findings.
Remaining issues are subject to sensitivity analysis. This is also an important issue that can be further studied. We have applied the idea of local sensitivity to calculate the sensitivity of each model state concerning model parameters for the updated model of the COVID-19. Three different techniques are investigated which are non-normalizations, half normalizations, and full normalizations. These provide us an important step forward to identify critical model elements. By using local sensitivity approaches we concluded that almost all model states are sensitive to the critical model parameters { γ, δ, η} . This becomes a great step forward and helps international attempts regarding the COVID-19 pandemic outbreak. This may help to reduce the number of infected individuals from the disease and to prevent the coronavirus more widely in the community. It can be concluded that the identified factors can be controlled to reduce the number of infected individuals. Overall, our results demonstrate a strong effect of the key critical parameters on the spreading COVID-19.
Therefore, based on the effect of each involved parameters over the model states, more suggestions and interventions can be proposed for controlling the COVID-19 disease. That will be useful for any interventions and vaccination programs. Accordingly, the healthcare communities should pay more attention to the quarantine places for controlling this disease more effectively. It can be strongly suggested that anyone in the quarantine places should be separated from the others and should use only their separate equipment, bedroom, and toilet to prevent the transmission of the virus through the touching of shared surfaces. Another suggestion is that reducing the contact between asymptomatic-symptomatic groups and susceptible groups, this is effectively minimizing the number of infected people. It seems necessary to plan a certain strategy to put the asymptomatic infected individuals on quarantine places sooner rather than later. Future research on identifying key critical elements might extend the explanations of the new COVID-19 more widely. It will be important that future research investigates more suggested transmissions between the model groups. For example, the model will further improve by adding two transmission paths, one of them is between unreported symptomatic infected and reported symptomatic infected, the other one is between asymptomatic infected and recovered individuals.
Declaration of Competing Interest
The authors declare that there are no competing interests.
References
- 1.Kahn J.S., McIntosh K. History and recent advances in coronavirus discovery. Pediatr Infect Dis J. 2005;24(11 Suppl):S223–S227. doi: 10.1097/01.inf.0000188166.17324.60. discussion S226PMID 16378050. [DOI] [PubMed] [Google Scholar]
- 2.Geller C., Varbanov M., Duval R.E. Human coronaviruses: insights into environmental resistance and its influence on the development of new antiseptic strategies. Viruses. November 2012;4(11) doi: 10.3390/v4113044. PMC 3509683. PMID 23202515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Zhu Na, Zhang D., Wang W., Li X., Yang Bo, Song J., Zhao X., Huang B., Shi W., Lu R., Niu P. A novel coronavirus from patients with pneumonia in China, 2019. N Engl J Med. 2020;382(8):727–733. doi: 10.1056/NEJMoa2001017. ISSN 0028-4793. PMC 7092803. PMID 31978945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 2020 doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Huang C., Wang Y., Li X., Ren L., Zhao J., Hu Y. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020 doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Bogoch I.I., Watts A., Thomas-Bachli A., Huber C., Kraemer M.U.G., Khan K. Pneumonia of unknown etiology in Wuhan, China: potential for international spread via commercial air travel. J Travel Med. 2020 doi: 10.1093/jtm/taaa008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020 doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.https://www.worldometers.info/coronavirus/
- 9.Zhang S., Diao M.Y., Yu W., Pei L., Lin Z., Chen D. Estimation of there productive number of novel coronavirus (COVID-19) and the probable outbreak size on the diamond princess cruise ship: a data-driven analysis. Int J Infect Dis. 2020;93:201–204. doi: 10.1016/j.ijid.2020.02.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.He S., Tang S., Rong L. A discrete stochastic model of the COVID-19 outbreak: forecast and control. Math Biosci Eng. 2020;17(4):13. doi: 10.3934/mbe.2020153. [DOI] [PubMed] [Google Scholar]
- 11.Tang B., Wang X., Li Q., Bragazzi N.L., Tang S., Xiao Y., Wu J. Estimation of the transmission risk of the 2019–nCoV and its implication for public health interventions. J Clin Med. 2020;9(2):462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen T.,M., Rui J., Wang Q.,.P, Zhao Z.,Y., Cui J.,A., Yin L. A mathematical model for simulating the phase–based transmissibility of a novel coronavirus. Infect Dis Poverty. 2020;9(1):1–8. doi: 10.1186/s40249-020-00640-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Tang B., Bragazzi N.L., Li Q., Tang S., Xiao Y., Wu J. An updated estimation of the risk of transmission of the novel coronavirus (2019–nCov) Infect Dis Model. 2020;5:248–255. doi: 10.1016/j.idm.2020.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vink M.A., Bootsma M.C.J., Wallinga J. Serial intervals of respiratory infectious diseases: a systematic review and analysis. Am J Epidemiol. 2014;180(9):865–875. doi: 10.1093/aje/kwu209. [DOI] [PubMed] [Google Scholar]
- 15.Nishiura H., Linton NM., Akhmetzhanov AR. Serial interval of novel coronavirus (COVID-19) infections. Int J Infect Dis. 2020 doi: 10.1016/j.ijid.2020.02.060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Du Z., Xu X., Wu Ye, Wang L., Cowling BJ., Meyers L.A. The serial interval of COVID-19 from publicly reported confirmed cases. medRxiv. 2020 doi: 10.3201/eid2606.200357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Li L., Huang T., Wang Y., Wang Z., Liang Y., Huang T., Wang Y. 2019 novel coronavirus patients’ clinical characteristics, discharge rate and fatality rate of meta–analysis. J Med Virol. 2020 doi: 10.1002/jmv.25757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tuite AR., Fisman DN., Greer AL. Mathematical modelling of COVID-19 transmission and mitigation strategies in the population of Ontario, Canada. CMAJ. 2020;192(19):E497–E505. doi: 10.1503/cmaj.200476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Van Zandvoort K., Jarvis CI., Pearson C., Davies NG., Russell TW., Kucharski AJ., Jit MJ. Response strategies for COVID-19 epidemics in African settings: a mathematical modelling study. MedRxiv. 2020 doi: 10.1186/s12916-020-01789-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Prem K., Liu Y., Russell TW., Kucharski AJ., Eggo RM., Davies N., Flasche S. The Lancet Public Health; 2020. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.GU, C., W. Jiang, T. Zhao, and B. Zheng. "Mathematical recommendations to fight against COVID-19." Available at SSRN 3551006 (2020).
- 22.Hellewell J., Abbott S., Gimma A., Bosse NI., Jarvis CI., Russell TW., Munday JD. The Lancet Global Health; 2020. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cakir Z., Savas H. A mathematical modelling approach in the spread of the novel 2019 coronavirus SARS-CoV-2 (COVID-19) pandemic. Electron J Gen Med. 2020;17(4) em205." (2020): 4. [Google Scholar]
- 24.Liu Y., Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J Travel Med. 2020 doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Khoshnaw S.H.A. University Leicester-UK; 2015. Model reductions in biochemical reaction networks. Ph.D. thesis. [Google Scholar]
- 26.Khoshnaw S.H.A, Rizgar S., Sadegh S. Mathematical modelling for coronavirus disease (COVID-19) in predicting future behaviours and sensitivity analysis. Math Model Nat Phenom. May 2020 doi: 10.1051/mmnp/2020020. Accepted: 12. [DOI] [Google Scholar]
- 27.Sultan F., Shahzad M., Ali M., Adnan W., Khan W.A. Balancing the chemical equations and their steady-state approximations in the complex reaction mechanism: linear algebra techniques. Appl Nanosci. 2020 Apr 3 doi: 10.1007/s13204-020-01370-6. [DOI] [Google Scholar]
- 28.Sultan F., Shahzad M., Ali M., Azeem Khan W. Computational analysis of the slow invariant manifold for single and multi-route reaction mechanisms. Sci Iran. 2020 Apr 14 doi: 10.24200/sci.2020.53151.3080. [DOI] [Google Scholar]
- 29.Shahzad M., Sultan F., Ali S.I., Ali M., Azeem W. Physical assessments on chemically reacting species and reduction schemes for the approximation of invariant manifolds. J Mol Liq. 2019;285:237–243. doi: 10.1016/j.molliq.2019.03.031. [DOI] [Google Scholar]
- 30.Shahzad M., Sultan F. ’Complex reaction and dynamics’ ”advanced chemical kinetics”, ISBN 978-953-51-5588-1. DOI: 10.5772/intechopen.70502. InTech (2018).
- 31.Shahzad M., Sultan F., Ali M. Modeling multi-route reaction mechanism for surfaces: a mathematical and computational approach. Appl Nanosci. 2020 doi: 10.1007/s13204-020-01275-4. [DOI] [Google Scholar]
- 32.Shahzad M., Sultan F., Ali M., Khan W.A., Irfan M. Slow invariant manifold assessments in the multi-route reaction mechanism. J Mol Liq. 2019;284:265–270. doi: 10.1016/j.molliq.2019.03.179. [DOI] [Google Scholar]
- 33.Radulescu O., Vakulenko S., Grigoriev D. Model reduction of biochemical reactions networks by tropical analysis methods. Math Model Nat Phenom. 2015;10(3):124–138. [Google Scholar]
- 34.Snowden T.J., van der Graaf P.H., Tindall M.J. Methods of model reduction for large-scale biological systems: a survey of current methods and trends. Bull. Math. Biol. 2017;79(7):1449–1486. doi: 10.1007/s11538-017-0277-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Boulier F., Lefranc M., Lemaire F., Morant P.E. Model reduction of chemical reaction systems using elimination. Math Comput Sci. 2011;5(3):289–301. [Google Scholar]
- 36.Ross J., Arkin A.P. Complex systems: from chemistry to systems biology. Proc Natl Acad Sci. 2009;106(16):6433–6434. doi: 10.1073/pnas.0903406106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Palsson B.Ø. Cambridge University Press; 2011. Systems biology: simulation of dynamic network states. [Google Scholar]
- 38.Rabitz H., Kramer M., Dacol D. Sensitivity analysis in chemical kinetics. Annu Rev Phys Chem. 1983;34(1):419–461. [Google Scholar]
- 39.Zi Z. Sensitivity analysis approaches applied to systems biology models. IET Syst Biol. 2011;5(6):336–346. doi: 10.1049/iet-syb.2011.0015. [DOI] [PubMed] [Google Scholar]
- 40.Akgül A., Khoshnaw S.H.A., Wali H.M. Mathematical model for the ebola virus disease. J Adv Phys. 2018;7(2):190–198. [Google Scholar]
- 41.Kiparissides A., Kucherenko S.S., Mantalaris A., Pistikopoulos E.N. Global sensitivity analysis challenges in biological systems modeling. Ind Eng Chem Res. 2009;48(15):7168–7180. [Google Scholar]
- 42.Babtie AC., Kirk P., Stumpf M.P.H. Topological sensitivity analysis for systems biology. Proc Natl Acad Sci. 2014;111(52):18507–18512. doi: 10.1073/pnas.1414026112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Powell D.R., Fair J., LeClaire R.J., Moore L.M., Thompson D. Proceedings of the International System Dynamics Conference. 2005. Sensitivity analysis of an infectious disease model. July. [Google Scholar]
- 44.Khoshnaw S.H.A. AIP Conference Proceedings. AIP Publishing; 2019. A mathematical modelling approach for childhood vaccination with some computational simulations. [Google Scholar]
- 45.Khoshnaw S.H.A., Najem A.M., Rizgar H.S. Identifying critical parameters in SIR model for spread of disease. Open J Model Simul. 2017;5(1) [Google Scholar]
- 46.He S., Tang S., Rong L. A discrete stochastic model of the COVID–19 outbreak: forecast and control. Math Biosci Eng. 2020;17(4):13. doi: 10.3934/mbe.2020153. [DOI] [PubMed] [Google Scholar]
- 47.Tang B., Wang X., Li Q., Bragazzi N.L., Tang S., Xiao Y., Wu J. Estimation of the transmission risk of the 2019–nCoV and its implication for public health interventions. J Clin Med. 2020;9(2):462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Munday J.D. Early dynamics of transmission and control of COVID–19: a mathematical modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chen T.M., Rui J., Wang Q.,P., Zhao Z.Y., Cui J.A., Yin L. A mathematical model for simulating the phase–based transmissibility of a novel coronavirus. Infect Dis Poverty. 2020;9(1):1–8. doi: 10.1186/s40249-020-00640-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tang B., Bragazzi N.L., Li Q., Tang S., Xiao Y., Wu J. (2020). An updated estimation of the risk of transmission of the novel coronavirus (2019–nCov) Infect Dis Model. 2020;5:248–255. doi: 10.1016/j.idm.2020.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li L., Huang T., Wang Y., Wang Z., Liang Y., Huang T., Wang Y. 2019 novel coronavirus patients' clinical characteristics, discharge rate and fatality rate of meta–analysis. J Med Virol. 2020 doi: 10.1002/jmv.25757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Roda W.C., Varughese M.B., Han D., Li. M.Y. Why is it difficult to accurately predict the COVID-19 epidemic? Infect Dis Model. 2020 doi: 10.1016/j.idm.2020.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kuniya T. "Prediction of the epidemic peak of coronavirus disease in Japan, 2020. J Clin Med. 2020;9(3):789. doi: 10.3390/jcm9030789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhou, W., A. Wang, F. Xia, Y. Xiao, and S. Tang. "Effects of media reporting on mitigating spread of COVID-19 in the early phase of the outbreak." (2020). [DOI] [PubMed]
- 55.Liu Z., Magal P., Seydi O., Webb G. Understanding unreported cases in the COVID-19 epidemic outbreak in Wuhan, China, and the importance of major public health interventions. Biology (Basel) 2020;9(3):50. doi: 10.3390/biology9030050. [DOI] [PMC free article] [PubMed] [Google Scholar]