Abstract
Given a regular language L over an ordered alphabet 
, the set of lexicographically smallest (resp., largest) words of each length is itself regular. Moreover, there exists an unambiguous finite-state transducer that, on a given word 
, outputs the length-lexicographically smallest word larger than w (henceforth called the L-successor of w). In both cases, naïve constructions result in an exponential blowup in the number of states. We prove that if L is recognized by a DFA with n states, then 
states are sufficient for a DFA to recognize the subset S(L) of L composed of its lexicographically smallest words. We give a matching lower bound that holds even if S(L) is represented as an NFA. We then show that the same upper and lower bounds hold for an unambiguous finite-state transducer that computes L-successors.
Introduction
One of the most basic problems in formal language theory is the problem of enumerating the words of a language L. Since, in general, L is infinite, language enumeration is often formalized in one of the following two ways:
A function that maps an integer
to the n-th word of L.A function that takes a word and maps it to the next word in L.
Both descriptions require some linear ordering of the words in order for them to be well-defined. Usually, radix order (also known as length-lexicographical order) is used. Throughout this work, we focus on the second formalization.
While enumeration is non-computable in general, there are many interesting special cases. In this paper, we investigate the case of fixed regular languages, where successors can be computed in linear time [1, 2, 9]. Moreover, Frougny [7] showed that for every regular language L, the mapping of words to their successors in L can be realized by a finite-state transducer. Later, Angrand and Sakarovitch refined this result [3], showing that the successor function of any regular language is a finite union of functions computed by sequential transducers that operate from right to left. However, to the best of our knowledge, no upper bound on the size of smallest transducer computing the successor function was known.
In this work, we consider transducers operating from left to right, and prove that the optimal upper bound for the size of transducers computing successors in L is in 
, where n is the size of the smallest DFA for L.
The construction used to prove the upper bound relies heavily on another closely related result. Many years before Frougny published her proof, it had already been shown that if L is a regular language, the set of all lexicographically smallest (resp., largest) words of each length is itself regular; see, e.g., [11, 12]. This fact is used both in [3] and in our construction. In [12], it was shown that if L is recognized by a DFA with n states, then the set of all lexicographically smallest words is recognized by a DFA with 
states. While it is easy to improve this upper bound to 
, the exact state complexity of this operation remained open. We prove that 
states are sufficient and that this upper bound is optimal. We also prove that nondeterminism does not help with recognizing lexicographically smallest words, i.e., the corresponding lower bound still holds if the constructed automaton is allowed to be nondeterministic.
The key component to our results is a careful investigation of the structure of lexicographically smallest words. This is broken down into a series of technical lemmas in Sect. 3, which are interesting in their own right. Some of the other techniques are similar to those already found in [3], but need to be carried out more carefully to achieve the desired upper bound.
Preliminaries
We assume familiarity with basic concepts of formal language theory and automata theory; see [8, 13] for a comprehensive introduction. Below, we introduce concepts and notation specific to this work.
Ordered Words and Languages. Let 
be a finite ordered alphabet. Throughout the paper, we consider words ordered by radix order, which is defined by 
if either 
or there exist factorizations 
, 
with 
and 
such that 
. We write 
if 
or 
. In this case, the word u is smaller than v and the word v is larger than u.
For a language 
and two words 
, we say that v is the L-successor of u if 
and 
for all 
with 
. Similarly, u is the L-predecessor of v if 
and 
for all 
with 
. A word is L-minimal if it has no L-predecessor. A word is L-maximal if it has no L-successor. Note that every nonempty language contains exactly one L-minimal word. It contains a (unique) L-maximal word if and only if L is finite. A word 
is L-length-preserving if it is not L-maximal and the L-successor of u has length 
. Words that are not L-length-preserving are called L-length-increasing. Note that by definition, an L-maximal word is always L-length-increasing. For convenience, we sometimes use the terms successor (resp., predecessor) instead of 
-successor (resp., 
-predecessor).
For a given language 
, the set of all smallest words of each length in L is denoted by S(L). It is formally defined as follows:
 |
Similarly, we define B(L) to be the set of all L-length-increasing words:
 |
A language 
is thin if it contains at most one word of each length, i.e., 
for all 
. It is easy to see that for every language 
, the languages S(L) and B(L) are thin.
Finite Automata and Transducers. A nondeterministic finite automaton (NFA for short) is a 5-tuple 
where Q is a finite set of states, 
is a finite alphabet, 
is the initial state, 
is the set of accepting states and 
is the transition function. We usually use the notation 
instead of 
, and we extend the transition function to 
by letting 
and 
for all 
, 
, and 
. For a state 
and a word 
, we also use the notation 
instead of 
for convenience. A word 
is accepted by the NFA if 
. We sometimes use the notation 
to indicate that 
. An NFA is unambiguous if for every input, there exists at most one accepting run. Unambiguous NFA are also called unambiguous finite state automata (UFA). A deterministic finite automaton (DFA for short) is an NFA 
with 
for all 
and 
. Since this implies 
for all 
, we sometimes identify the singleton 
with the only element it contains.
A finite-state transducer is a nondeterministic finite automaton that additionally produces some output that depends on the current state, the current letter and the successor state. For each transition, we allow both the input and the output letter to be empty. Formally, it is a 6-tuple 
where Q is a finite set of states, 
and 
are finite alphabets, 
is the initial state and 
is the set of accepting states, and 
is the transition function. One can extend this transition function to the product 
. To this end, we first define the 
-closure of a set 
as the smallest superset C of T with 
. We then define 
to be the 
-closure of 
and 
to be the 
-closure of 
for all 
, 
and 
. We sometimes use the notation 
to indicate that 
. A finite-state transducer is unambiguous if, for every input, there exists at most one accepting run.
The State Complexity of S(L)
It is known that if L is a regular language, then both S(L) and B(L) are also regular [11, 12]. In this section, we investigate the state complexity of the operations 
and 
for regular languages. Since the operations are symmetric, we focus on the former. To this end, we first prove some technical lemmas. The first lemma is a simple observation that helps us investigate the structure of words in S(L).
Lemma 1
Let 
with 
. Then 
or 
or 
.
Proof
Note that uy and yv are words of the same length. If 
, then 
. Similarly, 
immediately yields 
. The last case is 
, which implies 
. 
Using this observation, we can generalize a well-known factorization technique for regular languages to minimal words. For a DFA with state set Q, a state 
and a word 
, we define
 |
to be the sequence of all states that are visited when starting in state q and following the transitions labeled by the letters from w.
Lemma 2
Let 
be a DFA over 
with n states and with initial state 
. Then for every word 
, there exists a factorization 
with 
and 
such that, for all 
, the following hold:
,
, and
is not a prefix of 
.
Additionally, if 
, this factorization can be chosen such that
-
(d)
the lengths
are pairwise disjoint (i.e., 
) and -
(e)
there exists at most one
with 
.
Proof
To construct the desired factorization, initialize 
and 
and follow these steps:
If
, we are done. If 
and the states in 
are pairwise distinct, let 
and 
and we are done. Otherwise, factorize 
with 
minimal such that 
contains exactly one state twice, i.e., 
distinct states in total.Choose the unique factorization
such that 
and 
.Let
and 
.If
and 
and 
, increment 
and go back to step 1. Otherwise, let 
, 
and 
; then go back to step 1.
This factorization satisfies the first three properties by construction. It remains to show that if 
, then Properties (d) and (e) are satisfied as well.
Let us begin with Property (d). For the sake of contradiction, assume that there exist two indices a, b with 
and 
. Note that by construction, 
and 
must be nonempty. Moreover, by Property (a), the words
 |
both belong to 
. However, since 
, neither 
nor 
can be strictly smaller than w. Using Lemma 1, we obtain that 
. This contradicts Property (c).
Property (e) can be proved by using the same argument: Assume that there exist indices a, b with 
and 
. The words 
and 
have the same lengths. We define
 |
and obtain 
, which is a contradiction as above. 
The existence of such a factorization almost immediately yields our next technical ingredient.
Lemma 3
Let 
be a DFA with 
states. Let 
be the initial state of 
and let 
. Then there exists a factorization 
with 
, 
and 
such that 
. In particular, 
.
Proof
Let 
be a factorization that satisfies all properties in the statement of Lemma 2. Suppose first that all exponents 
are at most n. Using Properties (b) and (d), we obtain 
and the maximum length of w is achieved when all lengths 
are present among the factors 
and the corresponding 
have lengths 
. This yields
 |
where the last inequality uses 
. Therefore, we may set 
, 
and 
.
If not all exponents are at most n, by Property (e), there exists a unique index j with 
. In this case, let 
, 
and 
. The upper bound 
still follows by the argument above, and 
is a direct consequence of Property (b). Moreover, 
and Property (a) together imply that 
. 
For the next lemma, we need one more definition. Let 
be a DFA with initial state 
. Two tuples (x, y, z) and 
are cycle-disjoint with respect to
if the sets of states in 
and 
are either equal or disjoint.
Lemma 4
Let 
be a DFA with 
states and initial state 
. Let (x, y, z) and 
be tuples that are not cycle-disjoint with respect to 
such that
 |
Then either 
or 
only contains words of length at most 
.
Proof
Since the tuples are not cycle-disjoint with respect to 
, we can factorize 
and 
such that 
.
Note that since 
, the sets of states in 
and 
coincide for all 
. By the same argument, the sets of states in 
and 
coincide for all 
.
If the powers 
and 
were equal, then 
and 
coincide. By the previous observation, this would imply that the tuples (x, y, z) and 
are cycle-disjoint, a contradiction. We conclude 
.
By symmetry, we may assume that 
. But then, for every word of the form 
with 
, there exists a strictly smaller word 
in 
. To see that this word indeed belongs to 
, note that 
. This means that all words in 
are of the form 
with 
. 
The previous lemmas now allow us to replace any language L by another language that has a simple structure and approximates L with respect to S(L).
Lemma 5
Let 
be a DFA over 
with 
states. Then there exist an integer 
and tuples 
such that the following properties hold:
-
(i)
, -
(ii)
for all 
, and -
(iii)
where 
.
Proof
If we ignore the required upper bound 
and Property (iii) for now, the statement follows immediately from Lemma 3 and the fact that there are only finitely many different tuples (x, y, z) with 
and 
. We start with such a finite set of tuples 
and show that we can repeatedly eliminate tuples until at most 
cycle-disjoint tuples remain. The desired upper bound 
then follows automatically.
In each step of this elimination process, we handle one of the following cases:
If there are two distinct tuples
and 
with 
and 
, there are two possible scenarios. If 
, then for every word in 
there exists a smaller word in 
and we can remove 
from the set of tuples. By the same argument, we can remove the tuple 
if 
and 
.Now consider the case that there are two distinct tuples
and 
with 
and 
but 
. We first check whether 
. If true, we add the tuple 
, otherwise we add 
. If 
, we know that each word in 
has a smaller word in 
, and we remove the tuple 
. Otherwise, we can remove 
by the same argument.The last case is that there exist two tuples
and 
that are not cycle-disjoint. By Lemma 4, we can remove at least one of these tuples and replace it by multiple tuples of the form 
. Note that the newly introduced tuples might be of the form 
with 
but Lemma 4 asserts that they still satisfy 
.
Note that we introduce new tuples of the form 
during this elimination process. These new tuples are readily eliminated using the first rule.
After iterating this elimination process, the remaining tuples are pairwise cycle-disjoint and the pairs 
assigned to these tuples 
are pairwise disjoint. Properties (ii) and (iii) yield the desired upper bound on k. 
Remark 1
While S(L) can be approximated by a language of the simple form given in Lemma 5, the language S(L) itself does not necessarily have such a simple description. An example of a regular language L where S(L) does not have such a simple form is given in the proof of Theorem 2.
The last step is to investigate languages L of the simple structure described in the previous lemma and show how to construct a small DFA for S(L).
Lemma 6
Let 
. Let 
with 
and 
for all 
and 
where 
. Then S(L) is recognized by a DFA with 
states.
Proof
We describe how to construct a DFA of the desired size that recognizes the language S(L). This DFA is the product automaton of multiple components.
In one component (henceforth called the counter component), we keep track of the length of the processed input as long as at most 
letters have been consumed. If more than 
letters have been consumed, we only keep track of the length of the processed input modulo all numbers 
for 
.
For each 
, there is an additional component (henceforth called the i-th activity component). In this component, we keep track of whether the currently processed prefix u of the input is a prefix of a word in 
, whether u is a prefix of a word in 
and whether 
. Note that if some prefix of the input is not a prefix of a word in 
, no longer prefix of the input can be a prefix of a word in 
. The information stored in the counter component suffices to compute the possible letters of 
allowed to be read in each step to maintain the prefix invariants.
It remains to describe how to determine whether a state is final. To this end, we use the following procedure. First, we determine which sets of the form 
the input word leading to the considered state belongs to. These languages are called the active languages of the state. They can be obtained from the activity components of the state. If there are no active languages, the state is immediately marked as not final. If the length of the input word w leading to the considered state is 
or less, we can obtain 
from the counter component and reconstruct w from the set of active languages. If the length of the input is larger than 
, we cannot fully recover the input from the information stored in the state. However, we can determine the shortest word w with 
such that 
is consistent with the length information stored in the counter component and w itself is consistent with the set of active languages. In either case, we then compute the set A of all words of length 
that belong to any (possibly not active) language 
with 
. If w is the smallest word in A, the state is final, otherwise it is not final.
The desired upper bound on the number of states follows from known estimates on the least common multiple of a set of natural numbers with a given sum; see e.g., [6]. 
We can now combine the previous lemmas to obtain an upper bound on the state complexity of S(L).
Theorem 1
Let L be a regular language that is recognized by a DFA with n states. Then S(L) is recognized by a DFA with 
states.
Proof
By Lemma 5, we know that there exists a language 
of the form described in the statement of Lemma 6 with 
. Since 
implies 
and since 
, this also means that 
. Lemma 6 now shows that there exists a DFA of the desired size. 
To show that the result is optimal, we provide a matching lower bound.
Theorem 2
There exists a family of DFA 
over a binary alphabet such that 
has n states and every NFA for 
has 
states.
Proof
For 
, let 
be the i-th prime number and let 
. We define a language
 |
It is easy to see that L is recognized by a DFA with 
states. We show that S(L) is not recognized by any NFA with less than p states. From known estimates on the prime numbers (e.g., [4, Sec. 2.7]), this suffices to prove our claim.
Let 
be a NFA for S(L) and assume, for the sake of contradiction, that 
has less than p states. Note that since for each 
, the integer p is a multiple of 
, the language L does not contain any word of the form 
. Therefore, the word 
belongs to S(L) and by assumption, an accepting path for this word in 
must contain a loop of some length 
. But then 
is accepted by 
, too. However, since 
, there exists some 
such that 
does not divide 
. This means that 
also does not divide 
. Thus, 
, contradicting the fact that 
belongs to S(L). 
Combining the previous two theorems, we obtain the following corollary.
Corollary 1
Let L be a language that is recognized by a DFA with n states. Then, in general, 
states are necessary and sufficient for a DFA or NFA to recognize S(L).
By reversing the alphabet ordering, we immediately obtain similar results for largest words.
Corollary 2
Let L be a language that is recognized by a DFA with n states. Then, in general, 
states are necessary and sufficient for a DFA or NFA to recognize B(L).
The State Complexity of Computing Successors
One approach to efficient enumeration of a regular language L is constructing a transducer that reads a word and outputs its L-successor [3, 7]. We consider transducers that operate from left to right. Since the output letter in each step might depend on letters that have not yet been read, this transducer needs to be nondeterministic. However, the construction can be made unambiguous, meaning that for any given input, at most one computation path is accepting and yields the desired output word. In this paper, we prove that, in general, 
states are necessary and sufficient for a transducer that performs this computation.
Our proof is split into two parts. First, we construct a transducer that only maps L-length-preserving words to their corresponding L-successors. All other words are rejected. This construction heavily relies on results from the previous section. Then we extend this transducer to L-length-increasing words by using a technique called padding. For the first part, we also need the following result.
Theorem 3
Let 
be a thin language that is recognized by a DFA with n states. Then the languages
 |
are recognized by UFA with 2n states.
Proof
Let 
be a DFA for L and let 
. We construct a UFA with 2n states for 
. The statement for 
follows by symmetry.
The state set of the UFA is 
, the initial state is 
and the set of final states is 
. The transitions are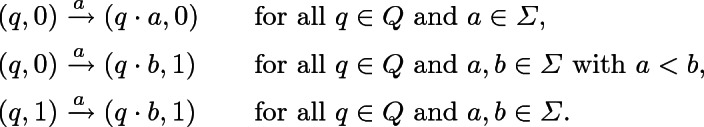 
It is easy to verify that this automaton indeed recognizes 
. To see that this automaton is unambiguous, consider an accepting run of a word w of length 
. Note that the sequence of first components of the states in this run yield an accepting path of length 
in 
. Since 
is thin, this path is unique. Therefore, the sequence of first components is uniquely defined. The second components are then uniquely defined, too: they are 0 up to the first position where w differs from the unique word of length 
in L, and 1 afterwards. 
For a language 
, we denote by 
the language of all words from 
such that there exists no strictly larger word of the same length in L. Combining Theorem 1 and Theorem 3, the following corollary is immediate.
Corollary 3
Let L be a language that is recognized by a DFA with n states. Then there exists a UFA with 
states that recognizes the language 
.
For a language 
, we define
 |
If L is regular, it is easy to construct an NFA for the complement of X(L), henceforth denoted as 
. To this end, we take a DFA for L and replace the label of each transition with all letters from 
. This NFA can also be viewed as an NFA over the unary alphabet 
; here, 
is interpreted as a letter, not a set. It can be converted to a DFA for 
by using Chrobak’s efficient determinization procedure for unary NFA [6]. The resulting DFA can then be complemented to obtain a DFA for X(L):
Corollary 4
Let L be a language that is recognized by a DFA with n states. Then there exists a DFA with 
states that recognizes the language X(L).
We now use the previous results to prove an upper bound on the size of a transducer performing a variant of the L-successor computation that only works for L-length-preserving words.
Theorem 4
Let L be a language that is recognized by a DFA with n states. Then there exists an unambiguous finite-state transducer with 
states that rejects all L-length-increasing words and maps every L-length-preserving word to its L-successor.
Proof
Let 
be a DFA for L and let 
. For every 
, we denote by 
the DFA that is obtained by making q the new initial state of 
. We use 
to denote DFA with 
states that recognizes the language 
. These DFA exist by Theorem 1. Moreover, by Corollary 3, there exist UFA with 
states that recognize the languages 
. We denote these UFA by 
. Similarly, we use 
to denote DFA with 
states that recognize 
. These DFA exist by Corollary 4.
In the finite-state transducer, we first simulate 
on a prefix u of the input, copying the input letters in each step, i.e., producing the output u. At some position, after having read a prefix u leading up to the state 
, we nondeterministically decide to output a letter b that is strictly larger than the current input letter a. From then on, we guess an output letter in each step and start simulating multiple automata in different components. In one component, we simulate 
on the remaining input. In another component, we simulate 
on the guessed output. In additional components, for each 
with 
, we simulate 
on the input. The automata in all components must accept in order for the transducer to accept the input.
The automaton 
verifies that there is no word in L that starts with the prefix ua, has the same length as the input word and is strictly larger than the input word. The automaton 
verifies that there is no word in L that starts with the prefix ub, has the same length as the input word and is strictly smaller than the output word. It also certifies that the output word belongs to L. For each letter c, the automaton 
verifies that there is no word in L that starts with the prefix uc and has the same length as the input word.
Together, the components ensure that the guessed output is the unique successor of the input word, given that it is L-length-preserving. It is also clear that L-length-increasing words are rejected, since the 
-component does not accept for any sequence of nondeterministic choices. 
The construction given in the previous proof can be extended to also compute L-successors of L-length-increasing words. However, this requires some quite technical adjustments to the transducer. Instead, we use a technique called padding. A very similar approach appears in [3, Prop. 5.1].
We call the smallest letter of an ordered alphabet 
the padding symbol of 
. A language 
is 
-padded if 
is the padding symbol of 
and 
for some 
. The key property of padded languages is that all words prefixed by a sufficiently long block of padding symbols are L-length-preserving.
Lemma 7
Let 
be a DFA over 
with n states such that 
is a 
-padded language. Let 
and let 
. Let 
be a word that is not K-maximal. Then the 
-successor of 
has length 
.
Proof
Let v be the K-successor of u. By a standard pumping argument, we have 
. This means that 
is well-defined and belongs to 
. Note that this word is strictly greater than 
and has length 
. Thus, the 
-successor of 
has length 
, too. 
We now state the main result of this section.
Theorem 5
Let 
be a deterministic finite automaton over 
with n states. Then there exists an unambiguous finite-state transducer with 
states that maps every word to its 
-successor.
Proof
We extend the alphabet by adding a new padding symbol 
and convert 
to a DFA for 
by adding a new initial state. The language 
accepted by this new DFA is 
-padded. By Theorem 4 and Lemma 7, there exists an unambiguous transducer of the desired size that maps every word from 
to its successor in 
. It is easy to modify this transducer such that all words that do not belong to 
are rejected. We then replace every transition that reads a 
by a corresponding transition that reads the empty word instead. Similarly, we replace every transition that outputs a 
by a transition that outputs the empty word instead. Clearly, this yields the desired construction for the original language L. A careful analysis of the construction shows that the transducer remains unambiguous after each step. 
We now show that this construction is optimal up to constants in the exponent. The idea is similar to the construction used in Theorem 2.
Theorem 6
There exists a family of deterministic finite automata 
such that 
has n states whereas the smallest unambiguous transducer that maps every word to its 
-successor has 
states.
Proof
Let 
. Let 
be the k smallest prime numbers such that 
and let 
. We construct a deterministic finite automaton 
with 
states such that the smallest transducer computing the desired mapping has at least p states. From known estimates on the prime numbers (e.g., [4, Sec. 2.7]), this suffices to prove our claim.
The automaton is defined over the alphabet 
. It consists of an initial state 
, an error state 
, and states (i, j) for 
and 
with transitions defined as follows:
 |
The set of accepting states is 
. The language 
is the set of all words of the form 
with 
such that j is a multiple of 
.
Assume, to get a contradiction, that there exists an unambiguous transducer with less than p states that maps w to the smallest word in 
strictly greater than w. Consider an accepting run of this transducer on some input of the form 
with 
large enough such that the run contains a cycle. Clearly, since 
and p are coprime, the output of the transducer has to be 
. We fix one cycle in this run.
If the number of 
read in this cycle does not equal the number of 
output in this cycle, by using a pumping argument, we can construct a word of the form 
that is mapped to a word or the form 
with 
. This contradicts the fact that 
is a subset of 
. Therefore, we may assume that both the number of letters read and output on the cycle is 
.
Again, by a pumping argument, this implies that 
is mapped to 
for every 
. Since 
, at least one of the prime numbers 
is coprime to r. Therefore, we can choose j such that 
. However, this means that 
belongs to 
, contradicting the fact that the transducer maps 
to 
. 
Combining the two previous theorems, we obtain the following corollary.
Corollary 5
Let L be a language that is recognized by a DFA with n states. Then, in general, 
states are necessary and sufficient for an unambiguous finite-state transducer that maps words to their L-successors.
Contributor Information
Nataša Jonoska, Email: jonoska@mail.usf.edu.
Dmytro Savchuk, Email: savchuk@usf.edu.
Lukas Fleischer, Email: lukas.fleischer@uwaterloo.ca.
Jeffrey Shallit, Email: shallit@uwaterloo.ca.
References
- 1.Ackerman M, Mäkinen E. Three new algorithms for regular language enumeration. In: Ngo HQ, editor. Computing and Combinatorics; Heidelberg: Springer; 2009. pp. 178–191. [Google Scholar]
- 2.Ackerman M, Shallit J. Efficient enumeration of words in regular languages. Theoret. Comput. Sci. 2009;410(37):3461–3470. doi: 10.1016/j.tcs.2009.03.018. [DOI] [Google Scholar]
- 3.Angrand P-Y, Sakarovitch J. Radix enumeration of rational languages. RAIRO - Theoret. Inform. Appl. 2010;44(1):19–36. doi: 10.1051/ita/2010003. [DOI] [Google Scholar]
- 4.Bach E, Shallit J. Algorithmic Number Theory. Cambridge: MIT Press; 1996. [Google Scholar]
- 5.Berthé, V., Frougny, C., Rigo, M., Sakarovitch, J.: On the cost and complexity of the successor function. In: Arnoux, P., Bédaride, N., Cassaigne, J. (eds.) Proceedings of WORDS 2007, Technical Report, Institut de mathématiques de Luminy, pp. 43–56 (2007)
- 6.Chrobak M. Finite automata and unary languages. Theoret. Comput. Sci. 1986;47:149–158. doi: 10.1016/0304-3975(86)90142-8. [DOI] [Google Scholar]
- 7.Frougny C. On the sequentiality of the successor function. Inf. Comput. 1997;139(1):17–38. doi: 10.1006/inco.1997.2650. [DOI] [Google Scholar]
- 8.Hopcroft JE, Motwani R, Ullman JD. Introduction to Automata Theory, Languages, and Computation. 3. New York: Addison-Wesley Longman Publishing Co., Inc.; 2006. [Google Scholar]
- 9.Mäkinen E. On lexicographic enumeration of regular and context-free languages. Acta Cybern. 1997;13(1):55–61. [Google Scholar]
- 10.Okhotin AS. On the complexity of the string generation problem. Discret. Math. Appl. 2003;13:467–482. doi: 10.1515/156939203322694745. [DOI] [Google Scholar]
- 11.Sakarovitch J. Deux remarques sur un théorème de S. Eilenberg. RAIRO - Theoret. Inform. Appl. 1983;17(1):23–48. doi: 10.1051/ita/1983170100231. [DOI] [Google Scholar]
- 12.Shallit J. Numeration systems, linear recurrences, and regular sets. Inf. Comput. 1994;113(2):331–347. doi: 10.1006/inco.1994.1076. [DOI] [Google Scholar]
- 13.Shallit J. A Second Course in Formal Languages and Automata Theory. Cambridge: Cambridge University Press; 2008. [Google Scholar]