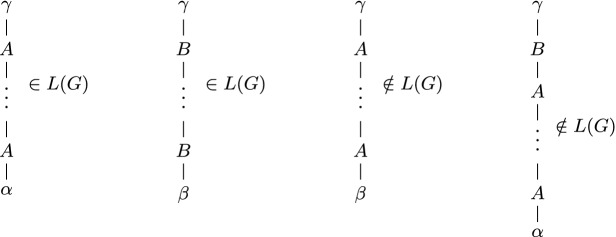Abstract
Tree substitution grammars are formal models that are used extensively in natural language processing. It is demonstrated that their expressive power is located strictly between the local tree grammars and the regular tree grammars. A decision procedure for the problem of determining whether a tree substitution grammar generates a local tree language is provided. Unfortunately, the class of tree substitution languages is neither closed under union, nor intersection, nor complements. Indeed unions of tree substitution languages even generate an infinite hierarchy. However, all finite and all co-finite tree languages are tree substitution languages.
Introduction
Trees are a fundamental data structure in computer science and are used in many application areas like natural language processing [12], database theory [1], and compiler construction [17]. All the mentioned applications as well as others [6, 7] require effective representations of sets of trees, also called tree languages. These requirements triggered detailed investigations of various classes of tree languages since the 1960s and by now there exists an abundance of models [5].
The most robust of those classes of tree languages are the regular tree languages [6, 7], which are generated by finite-state tree automata, which are a natural extension of the finite-state string automata that generate the regular string languages [18]. Most standard problems are decidable for the regular tree languages and they generally enjoy the same nice algorithmic properties as the regular string languages. The main feature of those automata are their finitely many states, which enable most of the positive properties. However, these states are not exhibited directly in the trees generated. In application areas like natural language processing, in which representations of tree languages have to be inferred from finite sets of trees, practitioners often resorted to simpler models, in which the representation can more readily be induced from the sample.
Tree substitution grammars were originally introduced as a special case of tree-adjoining grammars [9, 11], in which no adjunction is allowed. This restriction proved useful in the lexicalization of context-free grammars [10]. However, tree substitution grammar soon became popular in the parsing community [15] under the approach called data-oriented parsing [3] and were the formal model of many state-of-the-art parsers [16]. Similarly, synchronous tree substitution grammars, which are the same as the syntax-directed translation schemes of [2], are used in many statistical machine translation models [4, 8, 13, 14]. Despite the multitude of applications, a fundamental study of their expressive power is missing. Rather they are attributed properties like “extended domain of locality”, which provides some intuition, but has no formal definition.
A tree substitution grammar G is essentially a finite set F of tree fragments together with a set R of permissible root labels. Those tree fragments can be arbitrarily tall or large, which distinguishes tree substitution grammars from local tree grammars [6, 7]. In addition, the fragments can contain leaves that are labeled by internal symbols. Leaves with such labels are called open and can be expanded further by fragments of F that have the same symbol as root label. Indeed G generates trees from a permissible root label of R by successively expanding open leaves with fragments of F until no open leaves remain. The set of all trees derivable in this manner is called the tree language generated by G. The tree languages that can be generated by some tree substitution grammar are called the tree substitution languages.
In this contribution we start a fundamental study of the expressive power of tree substitution grammars. We show that tree substitution grammars are strictly more expressive than local tree grammars [6, 7], but strictly less expressive than finite-state tree automata (see Corollary 10). This, in particular, yields that most standard decision problems are also decidable for tree substitution languages because they are regular. In addition, it is decidable to determine whether a given tree substitution language is local (see Theorem 8). The decidability status of the related question whether a given regular tree language is a tree substitution language remains open. It is interesting to note that all finite and co-finite tree languages are tree substitution languages (see Theorem 6), which makes them much more useful for the approximation of finite samples of trees than the local tree languages, which do not contain all finite tree languages.
We also investigate the closure properties of the tree substitution languages. Unfortunately, they are neither closed under union (see Theorem 9), nor under intersection (see Theorem 13), nor under complement (see Theorem 14). In fact, unions of tree substitution languages even form a strict hierarchy (see Theorem 11), so unions of k tree substitution languages are strictly less expressive than unions of  tree substitution languages. A similar hierarchy is significantly more difficult to prove for intersections and remains an open problem because intersections break the “extended domain of locality” (as shown in the proof of Theorem 13) and can manage a non-explicit information transport over unbounded distances in the trees. Indeed the trivial union construction, which just takes the union of the fragments of the individual tree substitution grammars
tree substitution languages. A similar hierarchy is significantly more difficult to prove for intersections and remains an open problem because intersections break the “extended domain of locality” (as shown in the proof of Theorem 13) and can manage a non-explicit information transport over unbounded distances in the trees. Indeed the trivial union construction, which just takes the union of the fragments of the individual tree substitution grammars  , does yield a tree substitution grammar G that can generate each tree that can be generated by some
, does yield a tree substitution grammar G that can generate each tree that can be generated by some  . However, G might over-generalize in the sense that it may also generate trees that cannot be generated by any
. However, G might over-generalize in the sense that it may also generate trees that cannot be generated by any  . This property is utilized in grammar induction to generalize beyond the seen data. Overall, the expressive power of tree substitution grammars is interesting and offers new challenging problems because they are used extensively in real-world applications despite their brittle expressive power. It is exactly this absence of good closure properties, which requires separate arguments for each individual problem and thus makes several problems challenging as outlined in the open problems section.
. This property is utilized in grammar induction to generalize beyond the seen data. Overall, the expressive power of tree substitution grammars is interesting and offers new challenging problems because they are used extensively in real-world applications despite their brittle expressive power. It is exactly this absence of good closure properties, which requires separate arguments for each individual problem and thus makes several problems challenging as outlined in the open problems section.
Preliminaries
We denote the set of nonnegative integers (including 0) by  . For every
. For every  , we use the subset
, we use the subset  . An alphabet A is simply a finite set and
. An alphabet A is simply a finite set and  is the set of all finite words over A, where
is the set of all finite words over A, where 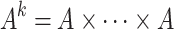 containing k factors A and
containing k factors A and 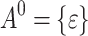 , of which
, of which  is called the empty word. The length
is called the empty word. The length  of a word
of a word  with
with 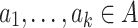 is
is  ; i.e. the number of symbols making up w. Given words
; i.e. the number of symbols making up w. Given words  , their concatenation is written v.w or simply vw. We write
, their concatenation is written v.w or simply vw. We write  provided that there exists
provided that there exists 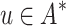 such that
such that 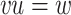 . The relation
. The relation  is actually a partial order, called the prefix order.
is actually a partial order, called the prefix order.
Let S be a set and  be a relation. The identity on S is the relation
be a relation. The identity on S is the relation  . Given another relation
. Given another relation  , the composition
, the composition  is given by
is given by  . The relation R is reflexive if
. The relation R is reflexive if  , and it is transitive if
, and it is transitive if  . The reflexive, transitive closure of R is
. The reflexive, transitive closure of R is  and the transitive closure of R is
and the transitive closure of R is 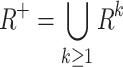 , where
, where  and
and  containing k times the relation R.
containing k times the relation R.
A ranked alphabet  is a pair consisting of an alphabet
is a pair consisting of an alphabet 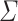 and a mapping
and a mapping  that assigns a rank to each symbol of
that assigns a rank to each symbol of 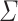 . We usually denote a ranked alphabet
. We usually denote a ranked alphabet  by just
by just  alone when the ranks are clear. We also write
alone when the ranks are clear. We also write  to indicate that
to indicate that 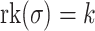 . Moreover, for every
. Moreover, for every 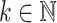 , we let
, we let 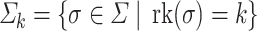 . Given a ranked alphabet
. Given a ranked alphabet  and a set Z, the set
and a set Z, the set  of
of  " trees indexed by Z is the smallest set T such that
" trees indexed by Z is the smallest set T such that  and
and  for every
for every  ,
, 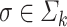 , and
, and  . We abbreviate
. We abbreviate  simply to
simply to  , and any subset
, and any subset  is called tree language. It is co-finite if
is called tree language. It is co-finite if  is finite.
is finite.
Next, we recall some common notions and notations for trees. In the following, let  be a tree for a ranked alphabet
be a tree for a ranked alphabet  and a set Z. The set
and a set Z. The set  of positions of t is inductively defined by
of positions of t is inductively defined by  for all
for all  , and
, and  for every
for every  ,
,  , and
, and  . The height of t is defined by
. The height of t is defined by  , and the size of t is defined by
, and the size of t is defined by  . A leaf is a position
. A leaf is a position 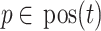 such that
such that 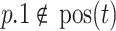 . We denote the subset of leaves of
. We denote the subset of leaves of  by
by  . Given a position
. Given a position  , the label t(p) of t at p and the subtree
, the label t(p) of t at p and the subtree  of t at p are defined by
of t at p are defined by  for all
for all  , and
, and
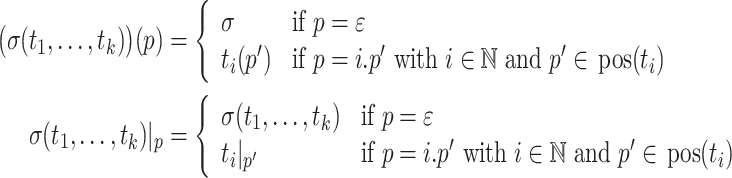 |
for all  ,
, 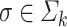 , and
, and 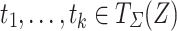 . Finally, the replacement
. Finally, the replacement 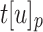 of the leaf
of the leaf  by another tree
by another tree  is given by
is given by  for every
for every  , and
, and  for every
for every 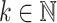 ,
, 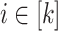 ,
,  ,
,  , and
, and 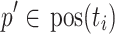 .
.
We reserve the use of the special symbol 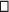 . A tree
. A tree  is a context, if there exists exactly one
is a context, if there exists exactly one  with
with  ; i.e., there is exactly one occurrence of
; i.e., there is exactly one occurrence of  in t. The set of all such contexts is denoted by
in t. The set of all such contexts is denoted by  . Given a context
. Given a context  and a tree
and a tree 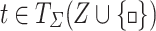 , the substitution c[t] of t into c yields the tree
, the substitution c[t] of t into c yields the tree 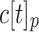 , where p is the unique position
, where p is the unique position  with
with  . Note that given
. Note that given  , also
, also  . Similarly, we write
. Similarly, we write  for
for 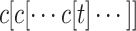 containing the context c a total of k times.
containing the context c a total of k times.
Finally, let us recall regular tree grammars (RTGs) [6, 7]. An RTG is a tuple  , where Q is a finite set of states such that
, where Q is a finite set of states such that 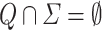 ,
,  is a ranked alphabet of input symbols,
is a ranked alphabet of input symbols, 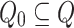 is a set of initial states, and
is a set of initial states, and  is a finite set of productions. We also write productions (q, t) as
is a finite set of productions. We also write productions (q, t) as  . The derivation relation for
. The derivation relation for  is defined for every
is defined for every  by
by 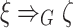 if and only if there exists a production
if and only if there exists a production  and a context
and a context 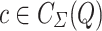 such that
such that  and
and  . The tree language generated by G is
. The tree language generated by G is 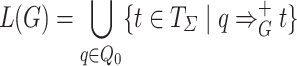 . A tree language L is regular if there exists an RTG G such that
. A tree language L is regular if there exists an RTG G such that 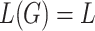 . The class of regular tree languages is denoted by
. The class of regular tree languages is denoted by 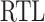 . We note that
. We note that  coincides with the class of tree languages generated by tree automata [6, 7].
coincides with the class of tree languages generated by tree automata [6, 7].
Tree Substitution Grammars
Let us start with the formal definition of tree substitution grammars (TSGs) taken essentially from the natural language processing community [10, 11]. TSGs have been applied to various tasks including parsing [16] and machine translation [19]. Consequently, the definitions of TSGs vary, but our definition captures the essence of the notion, while still being convenient to work with.
Definition 1
A tree substitution grammar (TSG) is a tuple 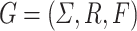 , in which
, in which 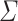 is a ranked alphabet of input symbols,
is a ranked alphabet of input symbols,  is a set of root labels, and
is a set of root labels, and  is a finite set of fragments. The TSG G is a local tree grammar (LTG) if
is a finite set of fragments. The TSG G is a local tree grammar (LTG) if  for all
for all 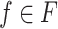 .
.
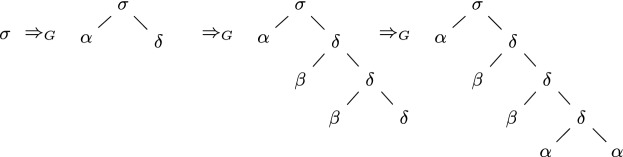
Example 2
Consider the ranked alphabet  and the TSG
and the TSG 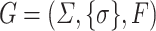 with the fragments displayed in Fig. 1. Clearly, this TSG is not an LTG due to the third and fourth fragment.
with the fragments displayed in Fig. 1. Clearly, this TSG is not an LTG due to the third and fourth fragment.
Fig. 1.
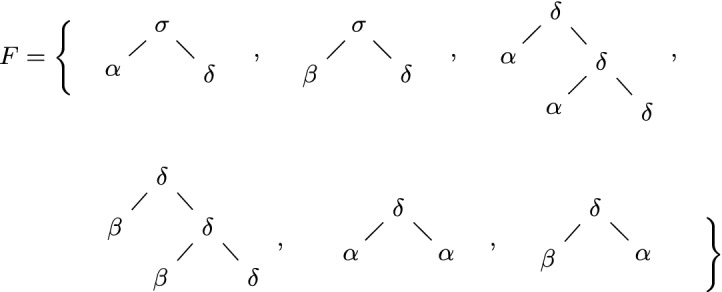
Fragments of the TSG of Example 2.
Next we present the derivation semantics for a TSG  . Essentially we start the derivation process with a tree consisting solely of a root label of R and then iteratively replace a leaf by a fragment of F with the same root label. This process can be repeated until no replacements are possible anymore. If the such obtained tree t contains only leaves that are labeled by nullary symbols, then t is part of the tree language generated by G.
. Essentially we start the derivation process with a tree consisting solely of a root label of R and then iteratively replace a leaf by a fragment of F with the same root label. This process can be repeated until no replacements are possible anymore. If the such obtained tree t contains only leaves that are labeled by nullary symbols, then t is part of the tree language generated by G.
Definition 3
Let  be a TSG. For any two trees
be a TSG. For any two trees  , we write
, we write  if there exists a fragment
if there exists a fragment  and a context
and a context 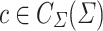 such that
such that 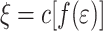 and
and  . The TSG G generates the tree language
. The TSG G generates the tree language  .
.
Example 4
Let  and consider the TSG
and consider the TSG 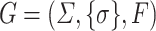 with the fragments displayed in Fig. 3. The derivation presented in Fig. 3 illustrates that a derived tree can contain several leaves that still need to be independently replaced. More precisely, both occurrences of
with the fragments displayed in Fig. 3. The derivation presented in Fig. 3 illustrates that a derived tree can contain several leaves that still need to be independently replaced. More precisely, both occurrences of  in the tree
in the tree 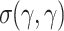 are independently replaced in the displayed derivation.
are independently replaced in the displayed derivation.
Fig. 3.
Fragments of the TSG G of Example 4 and example derivation steps.
Example 5
Consider the TSG G from Example 2. A few derivation steps are displayed in Fig. 2. Let 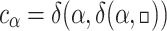 and
and 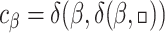 . Overall, this TSG generates the tree language
. Overall, this TSG generates the tree language
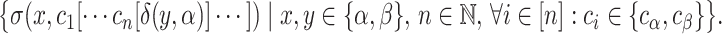 |
Fig. 2.
Example derivation steps using the TSG G of Example 2.
Two TSGs G and  are equivalent if
are equivalent if 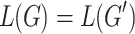 . A tree language L is a tree substitution language if there exists a TSG G such that
. A tree language L is a tree substitution language if there exists a TSG G such that 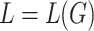 , and it is local [6, 7] if there exists a local tree grammar G such that
, and it is local [6, 7] if there exists a local tree grammar G such that 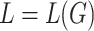 . The classes of all tree substitution languages and all local tree languages are denoted by
. The classes of all tree substitution languages and all local tree languages are denoted by 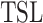 and
and  , respectively.
, respectively.
Expressive Power
In this section, we investigate the expressive power of tree substitution grammars and start with some simple tree languages that are contained in 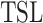 . To this end, let
. To this end, let  and
and  be the classes of all finite and all co-finite tree languages, respectively.
be the classes of all finite and all co-finite tree languages, respectively.
Theorem 6
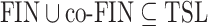 .
.
Proof
Every finite tree language  is trivially a tree substitution language via the TSG
is trivially a tree substitution language via the TSG 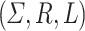 with
with 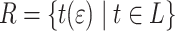 .
.
Now, let  be a co-finite tree language and
be a co-finite tree language and  be the finitely many trees outside L. Moreover, let
be the finitely many trees outside L. Moreover, let 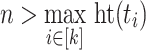 be larger than the height of the tallest tree from
be larger than the height of the tallest tree from  . We construct the TSG
. We construct the TSG 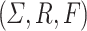 with
with
 and
and .
.
Clearly, F is finite. Now we prove  . For
. For  it is sufficient to show that
it is sufficient to show that  for every
for every  . Obviously, the fragments of F are either in L or have height at least n, which proves
. Obviously, the fragments of F are either in L or have height at least n, which proves 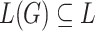 . We prove the converse
. We prove the converse  by contradiction, so suppose that there exists
by contradiction, so suppose that there exists 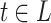 with
with  . Then there also exists a smallest
. Then there also exists a smallest  with
with 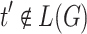 . Since all trees
. Since all trees 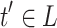 with
with  can be generated directly using a single fragment from F, we must have
can be generated directly using a single fragment from F, we must have 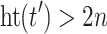 . Let
. Let
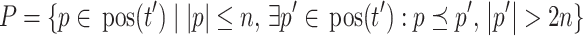 |
be the short positions that are prefixes to long positions, and let  be the maximal (with respect to
be the maximal (with respect to  ) elements of P. We construct the unique tree
) elements of P. We construct the unique tree  with positions
with positions
 |
and labels 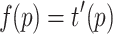 for all
for all  . In other words, we obtain f by cutting all paths in
. In other words, we obtain f by cutting all paths in  that have length more than 2n at length n. Obviously,
that have length more than 2n at length n. Obviously, 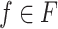 . In addition, we observe that
. In addition, we observe that 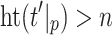 for all
for all  . For every
. For every 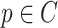 , we thus obtain
, we thus obtain 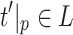 and
and 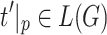 since
since  and
and  is the smallest counterexample. However, this yields that
is the smallest counterexample. However, this yields that  as well as
as well as 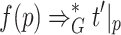 for all
for all  . Altogether
. Altogether  , which proves that
, which proves that  contradicting the assumption.
contradicting the assumption. 
Next we relate the class of tree substitution languages to the well-known classes of local and regular tree languages, respectively. Unsurprisingly, they are situated strictly between them, but the second strictness will be established later (see Corollary 10).
Theorem 7
 .
.
Proof
The first inclusion holds by definition. For the latter, let  be a TSG and
be a TSG and  a new symbol. We construct an RTG
a new symbol. We construct an RTG  such that
such that 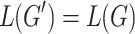 . To this end, we use copies
. To this end, we use copies  of the input symbols of
of the input symbols of  as states. The productions are given by
as states. The productions are given by  with
with
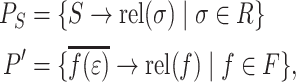 |
where 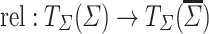 is inductively defined by
is inductively defined by
 |
for every 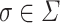 and
and  for all
for all 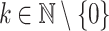 ,
,  , and
, and  . Clearly any derivation
. Clearly any derivation 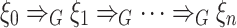 of G yields a corresponding derivation
of G yields a corresponding derivation  of
of  . Together with
. Together with  for all
for all  and the new initial states, we obtain
and the new initial states, we obtain  . The converse is proved similarly.
. The converse is proved similarly.
The first inclusion is strict because  by Theorem 6, but it is well-known [6, 7] that
by Theorem 6, but it is well-known [6, 7] that 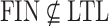 .
. 
The inclusion 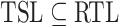 immediately yields that most interesting problems are decidable for tree substitution languages. For example, the emptiness, finiteness, inclusion, and equivalence problems are all decidable because they are decidable for regular tree languages [6, 7]. We proceed with a subclass definability problem: Is it decidable whether an effectively presented tree substitution language is local? Whenever we speak about an effectively presented tree substitution language L, we assume that we are actually given a tree substitution grammar G such that
immediately yields that most interesting problems are decidable for tree substitution languages. For example, the emptiness, finiteness, inclusion, and equivalence problems are all decidable because they are decidable for regular tree languages [6, 7]. We proceed with a subclass definability problem: Is it decidable whether an effectively presented tree substitution language is local? Whenever we speak about an effectively presented tree substitution language L, we assume that we are actually given a tree substitution grammar G such that  . Let
. Let 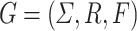 be a TSG. A fragment
be a TSG. A fragment  is useless if G and
is useless if G and  are equivalent. The TSG G is reduced if no fragment
are equivalent. The TSG G is reduced if no fragment  is useless. Clearly, for every TSG we can construct an equivalent reduced TSG.
is useless. Clearly, for every TSG we can construct an equivalent reduced TSG.
Theorem 8
For every effectively presented 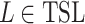 , it is decidable whether
, it is decidable whether  .
.
Proof
Let  be a reduced tree substitution grammar such that
be a reduced tree substitution grammar such that  . We construct the local tree grammar
. We construct the local tree grammar  with
with
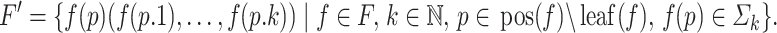 |
Obviously,  and all fragments of
and all fragments of 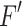 are essential for this property. Consequently, L is local if and only if
are essential for this property. Consequently, L is local if and only if  . Since both
. Since both 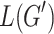 and L are regular by Theorem 7 and inclusion is decidable for regular tree languages [6, 7], we obtain the desired statement.
and L are regular by Theorem 7 and inclusion is decidable for regular tree languages [6, 7], we obtain the desired statement. 
Closure Properties
In this section, we investigate the closure properties of the class of tree substitution languages. More specifically, we investigate the Boolean operations and the hierarchy for union. Unfortunately, the results are all negative, but they and, in particular, their proofs shed additional light on the expressive power of tree substitution languages. Let us start with union.
Theorem 9
 is not closed under union.
is not closed under union.
Proof
Consider the ranked alphabet  and the LTGs
and the LTGs
 |
which generate the local tree languages (see Fig. 4)
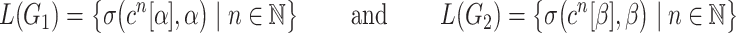 |
with  . Now suppose that their union
. Now suppose that their union 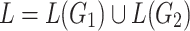 is a tree substitution language; i.e.,
is a tree substitution language; i.e., 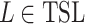 . Hence there exists a TSG
. Hence there exists a TSG  such that
such that  . Let
. Let 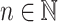 be such that
be such that  . Since
. Since  , there must exist a derivation
, there must exist a derivation  and
and  . Since
. Since  at least two derivation steps are required, so
at least two derivation steps are required, so 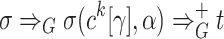 for some
for some  , which yields the subderivation
, which yields the subderivation  . In the same manner we consider the tree
. In the same manner we consider the tree 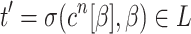 , for which the derivation
, for which the derivation 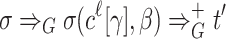 for some
for some 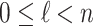 and the subderivation
and the subderivation  must exist. However, exchanging the subderivations yields the derivation
must exist. However, exchanging the subderivations yields the derivation
 |
which shows 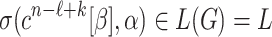 contradicting
contradicting 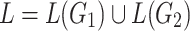 .
. 
Fig. 4.

The tree languages 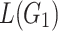 and
and 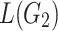 used in the proof of Theorem 9.
used in the proof of Theorem 9.
Since the class of regular tree languages is closed under union [6, 7], we obtain the following corollary from Theorems 7 and 9.
Corollary 10
 .
.
We demonstrated that the union of two tree substitution languages need not be a tree substitution language. Next, we ask ourselves whether additional unions increase the expressive power even further. For every  let
let
 |
be the class of those tree languages that can be presented as unions of k tree substitution languages. Since 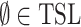 (see Theorem 6), we obtain
(see Theorem 6), we obtain  ,
,  , and
, and  for every
for every 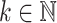 . Next, we show that the mentioned inclusion is actually strict, so that we obtain an infinite hierarchy.
. Next, we show that the mentioned inclusion is actually strict, so that we obtain an infinite hierarchy.
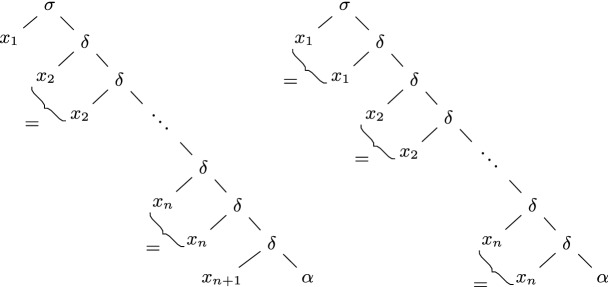
Theorem 11
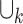 -TSL
-TSL  -TSL for all
-TSL for all 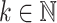 .
.
Proof
The statement is clear for  , so let
, so let  . Consider the ranked alphabet
. Consider the ranked alphabet 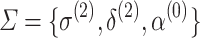 and the TSG
and the TSG  for every
for every  , where
, where
 |
and 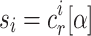 with
with 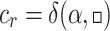 . Clearly,
. Clearly,  with
with  . The tree substitution language
. The tree substitution language  and the tree
and the tree  are illustrated in Fig. 5.
are illustrated in Fig. 5.
Fig. 5.
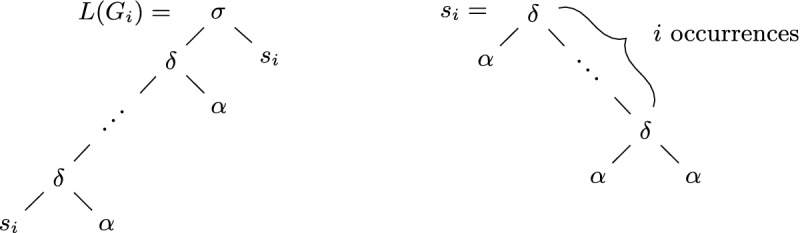
Illustration of the tree substitution languages used in the proof of Theorem 11.
Obviously,  -TSL and those individual tree languages are infinite and pairwise disjoint. For the sake of a contradiction, assume that
-TSL and those individual tree languages are infinite and pairwise disjoint. For the sake of a contradiction, assume that  -TSL; i. e. there exist
-TSL; i. e. there exist 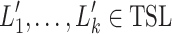 such that
such that  . The pigeonhole principle establishes that there exist
. The pigeonhole principle establishes that there exist 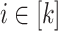 and
and 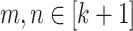 with
with  such that
such that 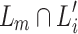 and
and  are infinite. Let
are infinite. Let  be a TSG such that
be a TSG such that  . Let
. Let  . Since
. Since 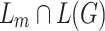 is infinite, there exists
is infinite, there exists  such that
such that 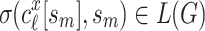 . Similarly, there exists
. Similarly, there exists 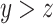 such that
such that  because
because  is infinite. Inspecting the derivations for those trees there exist
is infinite. Inspecting the derivations for those trees there exist  such that
such that
 |
Exchanging the subderivations we obtain
 |
and thus  , which is a contradiction because
, which is a contradiction because 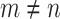 .
. 
Corollary 12
(of Theorem 11).
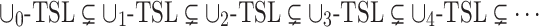 |
Let us move on to intersection. Unfortunately, 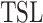 is not closed under intersection, but intersections of
is not closed under intersection, but intersections of  become quite powerful. In particular, they allow information to be transported over unbounded distances, which can be observed from the proof.
become quite powerful. In particular, they allow information to be transported over unbounded distances, which can be observed from the proof.
Theorem 13
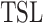 is not closed under intersection.
is not closed under intersection.
Proof
Recall the ranked alphabet  and the TSG G of Example 2 as well as the contexts
and the TSG G of Example 2 as well as the contexts  and
and  from Example 5. Additionally, let
from Example 5. Additionally, let  with
with  displayed in Fig. 6. The generated tree substitution languages L(G) and
displayed in Fig. 6. The generated tree substitution languages L(G) and  are
are
 |
respectively, which are also illustrated in Fig. 7. Their intersection
contains only trees, in which all left children along the spine carry the same label. This tree language is not a tree substitution language, which can be proved using the subderivation exchange technique used in the proof of Theorem 9. 
Fig. 6.
Fragments of the TSG  used in the proof of Theorem 13.
used in the proof of Theorem 13.
Fig. 7.
Tree substitution languages L(G) and  used in the proof of Theorem 13.
used in the proof of Theorem 13.
Note how the intersection achieves a global synchronization in the proof of Theorem 13. This power makes the investigation of the intersection hierarchy difficult. We leave the strictness of the intersection hierarchy as an open problem and conclude by considering the complement.
Theorem 14
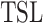 is not closed under complements.
is not closed under complements.
Proof
Consider the ranked alphabet  and the LTG
and the LTG 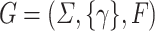 with fragments
with fragments
 |
The generated tree language is illustrated in Fig. 8. Now suppose that its complement 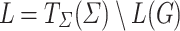 is a tree substitution language; i.e.,
is a tree substitution language; i.e.,  . Hence there exists a TSG
. Hence there exists a TSG  such that
such that  . Let
. Let  be such that
be such that 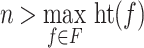 . Since
. Since 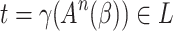 (see Fig. 8) there must exist a derivation
(see Fig. 8) there must exist a derivation  and
and 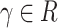 . Since
. Since  at least two derivation steps are required, so
at least two derivation steps are required, so 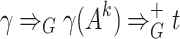 for some
for some  , which yields the subderivation
, which yields the subderivation  . Similarly, we consider the tree
. Similarly, we consider the tree  (see Fig. 8), for which the derivation
(see Fig. 8), for which the derivation 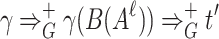 for some
for some  and the subderivation
and the subderivation 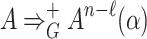 must exist. However, exchanging the subderivations yields the derivation
must exist. However, exchanging the subderivations yields the derivation
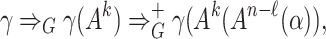 |
which shows  contradicting
contradicting 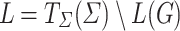 .
. 
Fig. 8.
Trees used in the proof of Theorem 14.
Open Problems
We showed that it is decidable whether a given tree substitution language is local. It remains open if we can also decide whether a given regular tree language is a tree substitution language. Progress on this problem will probably provide additional fine-grained insight into the expressive power of tree substitution grammars in comparison to the regular tree grammars.
Another open problem concerns the intersection hierarchy. We showed that unions of tree substitution languages can progressively express more and more tree languages. A similar hierarchy also exists for intersections of tree substitution languages and we showed that the intersection of two tree substitution languages is not necessarily a tree substitution languages. However, it remains open whether there is an infinite intersection hierarchy or whether it collapses at some level.
Acknowledgements
The authors gratefully acknowledge the financial support of the Research Training Group 1763 (QuantLA: Quantitative Logics and Automata), which is funded by the German Research Foundation (DFG). In addition, the authors would like to thank the anonymous reviewers for the careful reading of the manuscript and their valuable feedback.
Footnotes
K. Stier—Supported by DFG Research Training Group 1763 (QuantLA).
Contributor Information
Nataša Jonoska, Email: jonoska@mail.usf.edu.
Dmytro Savchuk, Email: savchuk@usf.edu.
Andreas Maletti, Email: maletti@informatik.uni-leipzig.de.
Kevin Stier, Email: stier@informatik.uni-leipzig.de.
References
- 1.Abiteboul S, Hull R, Vianu V. Foundations of Databases. Boston: Addison Wesley; 1994. [Google Scholar]
- 2.Aho AV, Ullman JD. The Theory of Parsing, Translation, and Compiling. Upper Saddle River: Prentice Hall; 1972. [Google Scholar]
- 3.Bod R. The data-oriented parsing approach: theory and application. In: Fulcher J, Jain LC, editors. Computational Intelligence: A Compendium. Heidelberg: Springer; 2008. pp. 307–348. [Google Scholar]
- 4.Chiang, D., Knight, K.: An introduction to synchronous grammars (2006). Tutorial at 44th ACL. https://www3.nd.edu/~dchiang/papers/synchtut.pdf
- 5.Comon, H., et al.: Tree automata techniques and applications (2007). http://tata.gforge.inria.fr
- 6.Gécseg F, Steinby M. Tree languages. In: Rozenberg G, Salomaa A, editors. Handbook of Formal Languages. Heidelberg: Springer; 1997. pp. 1–68. [Google Scholar]
- 7.Gécseg, F., Steinby, M.: Tree Automata. arXiv, 2nd edn. (2015). https://arxiv.org/abs/1509.06233
- 8.Howcroft, D.M., Klakow, D., Demberg, V.: Toward Bayesian synchronous tree substitution grammars for sentence planning. In: Proceedings of the 11th NLG, pp. 391–396. ACL (2018)
- 9.Joshi AK, Levy LS, Takahashi M. Tree adjunct grammars. J. Comput. Syst. Sci. 1975;10(1):136–163. doi: 10.1016/S0022-0000(75)80019-5. [DOI] [Google Scholar]
- 10.Joshi, A.K., Schabes, Y.: Tree-adjoining grammars and lexicalized grammars. Technical report, MS-CIS-91-22, University of Pennsylvania (1991)
- 11.Joshi AK, Schabes Y. Tree-adjoining grammars. In: Rozenberg G, Salomaa A, editors. Handbook of Formal Languages. Heidelberg: Springer; 1997. pp. 69–123. [Google Scholar]
- 12.Jurafsky D, Martin JH. Speech and Language Processing. 2. Upper Saddle River: Prentice Hall; 2008. [Google Scholar]
- 13.Maletti, A.: Why synchronous tree substitution grammars? In: Proceedings of the 2010 NAACL, pp. 876–884. ACL (2010)
- 14.Maletti A. An alternative to synchronous tree substitution grammars. J. Nat. Lang. Eng. 2011;17(2):221–242. doi: 10.1017/S1351324911000027. [DOI] [Google Scholar]
- 15.Sangati F, Keller F. Incremental tree substitution grammar for parsing and sentence prediction. Trans. ACL. 2013;1:111–124. [Google Scholar]
- 16.Shindo, H., Miyao, Y., Fujino, A., Nagata, M.: Bayesian symbol-refined tree substitution grammars for syntactic parsing. In: Proceedings of the 50th ACL, pp. 440–448. ACL (2012)
- 17.Wilhelm R, Seidl H, Hack S. Compiler Design. Heidelberg: Springer; 2013. [Google Scholar]
- 18.Yu S. Regular languages. In: Rozenberg G, Salomaa A, editors. Handbook of Formal Languages. Heidelberg: Springer; 1997. pp. 41–110. [Google Scholar]
- 19.Zhang J, Zhai F, Zong C. Syntax-based translation with bilingually lexicalized synchronous tree substitution grammars. IEEE Trans. Audio Speech Lang. Proc. 2013;21(8):1586–1597. doi: 10.1109/TASL.2013.2255283. [DOI] [Google Scholar]