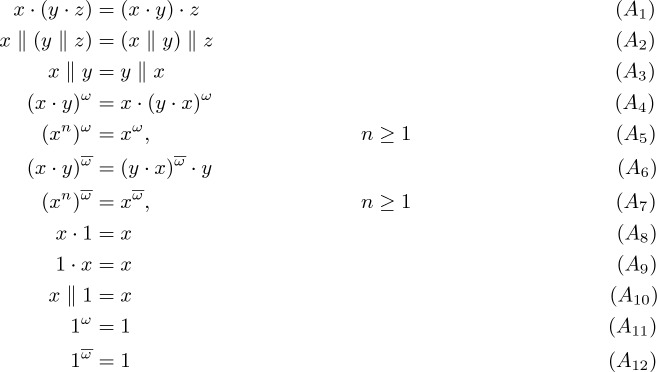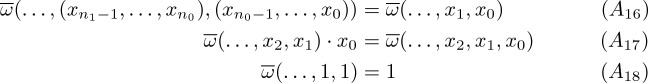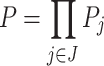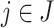Abstract
In this paper we consider two classes of posets labeled over an alphabet A. The class  is built from the letters and closed under the operations of series finite,
is built from the letters and closed under the operations of series finite,  and
and  products, and finite parallel product. In the class
products, and finite parallel product. In the class  ,
, 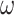 and
and 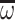 products are replaced by
products are replaced by  and
and  powers. We prove that
powers. We prove that 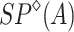 and
and  are freely generated in their respective natural varieties of algebras
are freely generated in their respective natural varieties of algebras 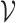 and
and  , and that the equational theory of
, and that the equational theory of  is decidable.
is decidable.
Keywords: Transfinite N-free posets, Series-parallel posets, Variety, Free algebra, Series product, Parallel product,  -power,
-power,  -power, Decidability
-power, Decidability
Introduction
In his generalization of the algebraic approach of recognizable languages from finite words to  -words, Wilke [22] introduced right binoids, that are two-sorted algebras equipped with a binary product and an
-words, Wilke [22] introduced right binoids, that are two-sorted algebras equipped with a binary product and an 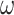 -power. The operations are linked together by equalities reflecting their properties. These equalities define a variety of algebras. This algebraic study of
-power. The operations are linked together by equalities reflecting their properties. These equalities define a variety of algebras. This algebraic study of  -words have since been extended to more general structures, such as for example partial words (or equivalently, labeled posets) or transfinite strings (long words). In [8], shuffle binoids are right binoids equipped with a shuffle operation that enables to take into consideration N-free posets with finite antichains and
-words have since been extended to more general structures, such as for example partial words (or equivalently, labeled posets) or transfinite strings (long words). In [8], shuffle binoids are right binoids equipped with a shuffle operation that enables to take into consideration N-free posets with finite antichains and  -chains instead of
-chains instead of 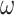 -words. In [3, 5], the structure of right binoids in two parts is modified in order to enable products to extend over
-words. In [3, 5], the structure of right binoids in two parts is modified in order to enable products to extend over 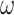 , ie. small ordinals (
, ie. small ordinals ( ,
,  ) and countable ordinals. The latter algebras are enriched in [10, 11] with operations such as for example reverse
) and countable ordinals. The latter algebras are enriched in [10, 11] with operations such as for example reverse 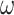 -power in order to take into account countable linear orderings (scattered in some cases). Some of the previous algebraic enrichments were also applied to shuffle binoids [4, 12]. The motivations in [3–5, 10, 11, 17, 22] are mainly the study of the links between automata, rational expressions, algebraic recognition and monadic second-order logic. In [7–9, 12, 22] the authors focus essentially on varieties of algebras; for example, free algebras are characterized in the corresponding varieties, and decisions algorithms for equivalence of terms are provided.
-power in order to take into account countable linear orderings (scattered in some cases). Some of the previous algebraic enrichments were also applied to shuffle binoids [4, 12]. The motivations in [3–5, 10, 11, 17, 22] are mainly the study of the links between automata, rational expressions, algebraic recognition and monadic second-order logic. In [7–9, 12, 22] the authors focus essentially on varieties of algebras; for example, free algebras are characterized in the corresponding varieties, and decisions algorithms for equivalence of terms are provided.
Let us denote by  the reverse ordering of
the reverse ordering of 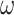 . In this paper we focus on algebras equipped with a parallel product, series product, and either
. In this paper we focus on algebras equipped with a parallel product, series product, and either 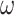 and
and 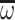 products or
products or  and
and  powers. For example, the class
powers. For example, the class 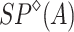 of N-free posets in which antichains are finite and chains are scattered and countable orderings lies in this framework. In [2, 6] this class has been studied from the point of view of automata, rational expression and logic. We prove here that
of N-free posets in which antichains are finite and chains are scattered and countable orderings lies in this framework. In [2, 6] this class has been studied from the point of view of automata, rational expression and logic. We prove here that 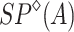 is the free algebra in a variety
is the free algebra in a variety  of algebras equipped with a parallel product, series product, and
of algebras equipped with a parallel product, series product, and  and
and 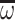 products. By removing the parallel product, it follows that
products. By removing the parallel product, it follows that  , the class of scattered and countable words over A, is also a free algebra in the corresponding variety. We also consider the class
, the class of scattered and countable words over A, is also a free algebra in the corresponding variety. We also consider the class  where the
where the  and
and 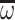 products are replaced by
products are replaced by  and
and  powers, and show that it is freely generated in the corresponding variety
powers, and show that it is freely generated in the corresponding variety  . Relying of decision results of [2] we prove that the equality of terms of
. Relying of decision results of [2] we prove that the equality of terms of  is decidable.
is decidable.
Linear Orderings and Posets
We let  denote the cardinality of a set E, and [n] the set
denote the cardinality of a set E, and [n] the set  , for any non-negative integer
, for any non-negative integer  .
.
Let J be a set equipped with a strict order <. The ordering J is linear if either  or
or  for any distinct
for any distinct  . We denote by
. We denote by 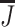 the backward linear ordering obtained from the set J with the reverse ordering. A linear ordering J is dense if for any
the backward linear ordering obtained from the set J with the reverse ordering. A linear ordering J is dense if for any  such that
such that  , there exists an element i of J such that
, there exists an element i of J such that  . It is scattered if it contains no infinite dense sub-ordering. The ordering
. It is scattered if it contains no infinite dense sub-ordering. The ordering  of natural integers is scattered as well as the ordering
of natural integers is scattered as well as the ordering  of all integers (negative, 0 and positive). Ordinals are also scattered orderings. We let
of all integers (negative, 0 and positive). Ordinals are also scattered orderings. We let  ,
,  and
and  denote respectively the class of finite linear orderings, the class of countable ordinals and the class of countable scattered linear orderings. We also let 0 and 1 denote respectively the empty and the singleton linear ordering. We refer to [20] for more details on linear orderings and ordinals.
denote respectively the class of finite linear orderings, the class of countable ordinals and the class of countable scattered linear orderings. We also let 0 and 1 denote respectively the empty and the singleton linear ordering. We refer to [20] for more details on linear orderings and ordinals.
A poset
 is a set P partially ordered by <. For short we often denote the poset
is a set P partially ordered by <. For short we often denote the poset  by P. The width of P is
by P. The width of P is  where
where 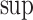 denotes the least upper bound of the set. In this paper, we restrict to posets with finite antichains and countable and scattered chains.
denotes the least upper bound of the set. In this paper, we restrict to posets with finite antichains and countable and scattered chains.
Let  and
and  be two disjoint posets. The union (or parallel composition)
be two disjoint posets. The union (or parallel composition)  of
of  and
and  is the poset
is the poset  . The sum (or sequential composition)
. The sum (or sequential composition) 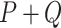 is the poset
is the poset  . The sum of two posets can be generalized to a J-sum of any linearly ordered sequence
. The sum of two posets can be generalized to a J-sum of any linearly ordered sequence 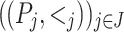 of pairwise disjoint posets by
of pairwise disjoint posets by 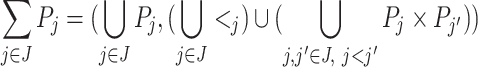 . The sequence
. The sequence 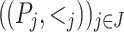 is called a J-factorization, or (sequential) factorization for short, of the poset
is called a J-factorization, or (sequential) factorization for short, of the poset 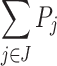 . A poset P is sequential if it admits a J-factorization where J contains at least two elements
. A poset P is sequential if it admits a J-factorization where J contains at least two elements  with
with  , or P is a singleton. It is parallel when
, or P is a singleton. It is parallel when  for some
for some  . A poset is sequentially irreducible (resp. parallelly irreducible) when P is either a singleton or a parallel poset (resp. a singleton or a sequential poset). A sequential factorization
. A poset is sequentially irreducible (resp. parallelly irreducible) when P is either a singleton or a parallel poset (resp. a singleton or a sequential poset). A sequential factorization 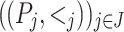 of
of  is irreducible when all the
is irreducible when all the 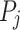 are sequentially irreducible. It is non-trivial if all the
are sequentially irreducible. It is non-trivial if all the 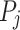 are non-empty. The notions of irreducible and non-trivial parallel factorization are defined similarly. A poset is scattered if all its chains are scattered. The class
are non-empty. The notions of irreducible and non-trivial parallel factorization are defined similarly. A poset is scattered if all its chains are scattered. The class  of series-parallel scattered and countable posets is the smallest class of posets containing 0, the singleton, and closed under finite parallel composition and sum indexed by countable scattered linear orderings. By extension of a well-known result on finite posets [18, 21], it has a nice characterization in terms of graph properties:
of series-parallel scattered and countable posets is the smallest class of posets containing 0, the singleton, and closed under finite parallel composition and sum indexed by countable scattered linear orderings. By extension of a well-known result on finite posets [18, 21], it has a nice characterization in terms of graph properties:  coincides with the class of scattered countable N-free posets without infinite antichains [6]. Recall that
coincides with the class of scattered countable N-free posets without infinite antichains [6]. Recall that  is N-free if there is no
is N-free if there is no  such that
such that 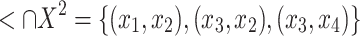 .
.
When  and
and  or
or  for some
for some  then
then  is a factor of P; the factors of
is a factor of P; the factors of  and S are also factors of P.
and S are also factors of P.
F. Hausdorff proposed in [16] an inductive definition of scattered linear orderings. In fact, each countable and scattered linear ordering is obtained using sums indexed by finite linear orderings,  and
and  . This has been adapted in [6] to
. This has been adapted in [6] to  .
.
We let  denote the closure of a set E of posets under finite disjoint union and finite disjoint sum.
denote the closure of a set E of posets under finite disjoint union and finite disjoint sum.
Definition 1
The classes of countable and scattered posets (equivalent up to isomorphism)  and
and  are defined inductively as follows:
are defined inductively as follows:
and the class  of countable and scattered posets by
of countable and scattered posets by 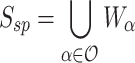 .
.
The following theorem extends a result of Hausdorff on linear orderings [16].
Theorem 1
([6]). .
.
For every  ,
,  can be decomposed as the closure of
can be decomposed as the closure of 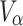 by finite disjoint union and finite disjoint sum:
by finite disjoint union and finite disjoint sum:
Theorem 2
([6]). For all  ,
,  , let
, let
Then  .
.
Example 1
 is the set of all finite N-free posets. Its subset
is the set of all finite N-free posets. Its subset  is the set of all finite linear orderings. The linear orderings
is the set of all finite linear orderings. The linear orderings 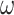 and
and 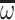 are contained in
are contained in  . Each poset of
. Each poset of  has some chain isomorphic to either
has some chain isomorphic to either  or
or  , but can not have a chain isomorphic to
, but can not have a chain isomorphic to 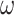 and another isomorphic to
and another isomorphic to  . The ordering
. The ordering  of all integers is in
of all integers is in  . For all
. For all  ,
,  .
.
Define a well-ordering on  by
by  if and only if
if and only if  or
or 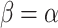 and
and  . As a consequence of Theorems 1 and 2, for any
. As a consequence of Theorems 1 and 2, for any  there exists a unique pair
there exists a unique pair  as small as possible such that
as small as possible such that  .
.
Definition 2
The rank
r(P) of  is the smallest pair
is the smallest pair  such that
such that  .
.
Example 2
The linear ordering  has rank
has rank  . Each linear ordering I of
. Each linear ordering I of 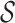 has rank
has rank  for some
for some  . For all
. For all  ,
,  .
.
Remark 1
Let  with
with  ,
,  . Assume that
. Assume that  is a non-trivial J-factorization of P for some
is a non-trivial J-factorization of P for some  . If
. If  (resp.
(resp.  ), then, for all
), then, for all  ,
, 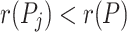 . In addition, for all
. In addition, for all  such that
such that  , for all
, for all 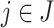 there exists
there exists  such that
such that  (resp.
(resp.  ) and
) and
 |
This implies that, for all  ,
,  (resp.
(resp. 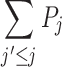 ) is of rank
) is of rank  .
.
Lemma 1
Let  be a sequential poset such that
be a sequential poset such that  ,
,  . Let
. Let  and
and 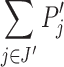 be some non-trivial J- and
be some non-trivial J- and  -factorizations of P where
-factorizations of P where  . Then
. Then  .
.
Proof
Assume by contradiction that 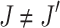 . Assume wlog that
. Assume wlog that  and
and  . Let
. Let  and
and  for some
for some  . Then
. Then  . As a consequence of Remark 1,
. As a consequence of Remark 1,  . Observe that there exists
. Observe that there exists  such that R is a sequential factor of
such that R is a sequential factor of  . Let
. Let  . As a consequence of Remark 1,
. As a consequence of Remark 1,  . Furthermore,
. Furthermore,  . Thus
. Thus 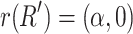 too. We have
too. We have  , and by Theorem 2,
, and by Theorem 2,  , which is a contradiction.
, which is a contradiction.
In [6] an equivalence relation  over the elements of a poset of
over the elements of a poset of  is given, such that
is given, such that  is isomorphic to a countable and scattered linear ordering (Lemma 9), and such that each equivalence class is a sequentially irreducible factor of P (Lemma 10). This leads to the following proposition.
is isomorphic to a countable and scattered linear ordering (Lemma 9), and such that each equivalence class is a sequentially irreducible factor of P (Lemma 10). This leads to the following proposition.
Proposition 1
([6]). Each poset of 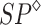 admits a unique irreducible sequential factorization.
admits a unique irreducible sequential factorization.
Definition 1 and Theorem 1 provide a well-founded definition of  which we consider from now as a set, although originally defined as a class.
which we consider from now as a set, although originally defined as a class.
Labeled Posets
An alphabet A is a non-empty set (not necessarily finite) whose elements are called letters or labels. In the literature a word over A is a totally ordered sequence of elements of A. The sequence may have properties depending on the context, for example it can be finite, an ordinal, or a countable scattered linear ordering. The notion of a finite word has early been extended to partial orderings (finite partial words or pomsets [14, 15, 23]). In this paper we consider a mixture between the notions of finite partial words and words indexed by scattered and countable linear orderings.
A poset P is labeled by A when it is equipped with a labeling total map  . Also, the finite labeled posets of width at most 1 correspond to the usual notion of words. We let
. Also, the finite labeled posets of width at most 1 correspond to the usual notion of words. We let  denote the empty labeled poset. For short, the singleton poset labeled by
denote the empty labeled poset. For short, the singleton poset labeled by  is denoted by a, and we often make no distinction between a poset and a labeled poset, except for operations.
is denoted by a, and we often make no distinction between a poset and a labeled poset, except for operations.
The sequential product (or concatenation, denoted by  or
or  for short) and the parallel product
for short) and the parallel product
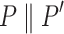 of two labeled posets are respectively obtained by the sequential and parallel compositions of the corresponding (unlabeled) posets. By extension, the sequential product
of two labeled posets are respectively obtained by the sequential and parallel compositions of the corresponding (unlabeled) posets. By extension, the sequential product  of a linearly ordered sequence of labeled posets is the poset
of a linearly ordered sequence of labeled posets is the poset  in which the label of the elements is kept. In particular, the
in which the label of the elements is kept. In particular, the 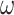 -product (resp.
-product (resp. 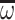 -product) of an
-product) of an 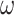 -sequence (resp.
-sequence (resp. 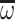 -sequence) of labeled posets
-sequence) of labeled posets  (resp.
(resp.  ) is denoted by
) is denoted by  (resp.
(resp.  ). The
). The 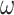 -power (resp.
-power (resp.  -power)
-power)  (resp.
(resp.  ) of the poset P is the
) of the poset P is the 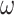 -product (resp.
-product (resp.  -product) of an
-product) of an  -sequence (resp.
-sequence (resp.  -sequence) of posets that are all isomorphic to P. As usual, in this paper we consider two labeled posets to be identical if they are isomorphic. By extension, the rank r(P) of a labeled poset P is the rank of its underlying unlabeled poset.
-sequence) of posets that are all isomorphic to P. As usual, in this paper we consider two labeled posets to be identical if they are isomorphic. By extension, the rank r(P) of a labeled poset P is the rank of its underlying unlabeled poset.
Let A and B be two alphabets and let P be a poset labeled by A. For all  , let
, let 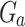 be some poset labeled by B, and let
be some poset labeled by B, and let  . The poset labeled by B consisting of P in which each element labeled by the letter a is replaced by
. The poset labeled by B consisting of P in which each element labeled by the letter a is replaced by  , for all
, for all  , is denoted by
, is denoted by  . If the underlying posets of P and of all the
. If the underlying posets of P and of all the  are in
are in  , then so is
, then so is  .
.
Definition 3
Let A be an alphabet. We define:
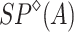 , the smallest set of posets labeled by A containing
, the smallest set of posets labeled by A containing 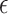 , a for all
, a for all  , and closed under operations of sequential, parallel,
, and closed under operations of sequential, parallel, 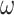 and
and 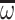 -products. According to Theorem 1, the underlying posets are precisely those of
-products. According to Theorem 1, the underlying posets are precisely those of  ;
; , the smallest subset of
, the smallest subset of 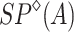 containing
containing  , a for all
, a for all  , and closed under operations of sequential product,
, and closed under operations of sequential product, 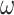 -power and
-power and  -power;
-power; , the smallest subset of
, the smallest subset of  containing
containing  , a for all
, a for all 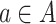 , and closed under operations of sequential product,
, and closed under operations of sequential product, 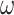 -product and
-product and  -product;
-product; , the smallest subset of
, the smallest subset of  containing
containing  , a for all
, a for all  , and closed under operations of sequential and parallel product,
, and closed under operations of sequential and parallel product,  -power and
-power and 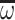 -power;
-power; , the smallest subset of
, the smallest subset of  containing
containing  , a for all
, a for all  , and closed under operations of sequential product, parallel product and
, and closed under operations of sequential product, parallel product and 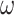 -product (note that there is no
-product (note that there is no 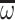 -product here).
-product here).
Note that 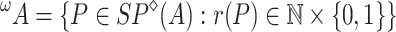 and
and  .
.
Varieties
In this section we define the different varieties studied throughout this paper by listing the axioms they satisfy. The usual notions and results of universal algebra apply to our case, even if we use here for example operations of infinite arity. For more details about universal algebra, we refer the reader to [1]. In the following 1 is considered as a neutral element (the interpretation of a constant).
for all 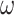 -sequences
-sequences 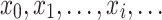 and all decompositions
and all decompositions
for all  -sequences
-sequences  and all decompositions
and all decompositions
Definition 4
We define
 , the collection of algebras
, the collection of algebras  satisfying the axioms ()–(), ()–() and ()–();
satisfying the axioms ()–(), ()–() and ()–(); , the collection of algebras
, the collection of algebras  satisfying the axioms (), (), () and ()–();
satisfying the axioms (), (), () and ()–(); , the collection of algebras
, the collection of algebras  satisfying the axioms ()–(), ()–() and ()–();
satisfying the axioms ()–(), ()–() and ()–(); , the collection of algebras
, the collection of algebras  satisfying the axioms ()–();
satisfying the axioms ()–();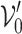 , the collection of algebras
, the collection of algebras  satisfying the axioms (), ()–() and (),().
satisfying the axioms (), ()–() and (),().
In order to simplify the notation, an algebra whose set of elements is S is sometimes denoted by S when there is no ambiguity.
Freeness
Throughout this section, A denotes an alphabet. We start by proving the freeness of  .
.
Theorem 3
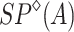 is freely generated by A in
is freely generated by A in  .
.
Proof
For all  , let
, let  denote the set of posets of
denote the set of posets of 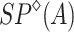 of rank
of rank  or less. Let
or less. Let 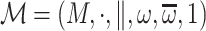 be any algebra of
be any algebra of  and let
and let  be any function. We show that h can be extended into a homomorphism of
be any function. We show that h can be extended into a homomorphism of  -algebras
-algebras  in a unique way. Define
in a unique way. Define  as
as  where each
where each  is defined by induction over
is defined by induction over  as follows. Let us denote by
as follows. Let us denote by  . Let
. Let  . If
. If  then
then  . Otherwise
. Otherwise
if
 and
and 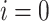 then
then  ;
;- if
 :
:- if P is a sequential poset then it has a factorization
where each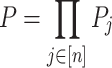
20 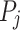 is a non-empty poset of rank lower than
is a non-empty poset of rank lower than  and
and  . Define
. Define  by
by 
- otherwise, P is a parallel poset. Write
where each
 is a sequential poset and
is a sequential poset and  . Then, define
. Then, define  by
by 
By Theorem 2, the factorizations used in the definition of 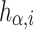 exist. However, observe that the sequential ones ((19) and (20)) are not unique. This would question the fact that
exist. However, observe that the sequential ones ((19) and (20)) are not unique. This would question the fact that  is a well-defined function. For all
is a well-defined function. For all  of rank
of rank  , we show that:
, we show that:
 does not depend on the factorization of P and thus is well-defined;
does not depend on the factorization of P and thus is well-defined; commutes with all the operations of
commutes with all the operations of 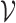 :
:  , for some
, for some  ;
; , for some
, for some  .
.
We proceed by induction on  . Let us start by proving that
. Let us start by proving that  maps
maps  to the same element of M regardless of the factorization of P. If
to the same element of M regardless of the factorization of P. If  the theorem follows immediately. Otherwise, assume first that
the theorem follows immediately. Otherwise, assume first that  . By Lemma 1, all the possible factorizations of P as in (19) are either all
. By Lemma 1, all the possible factorizations of P as in (19) are either all 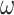 -factorizations or all
-factorizations or all  -factorizations. Assume wlog that P admits only
-factorizations. Assume wlog that P admits only  -factorizations as in (19). Let
-factorizations as in (19). Let 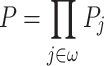 and
and  be two different such
be two different such  -factorizations. By definition of
-factorizations. By definition of 
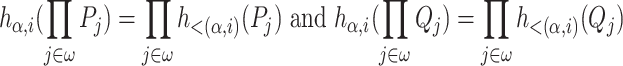 |
There exists a sequence 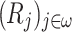 of non-empty posets such that
of non-empty posets such that  and for all
and for all  there exist
there exist  such that
such that
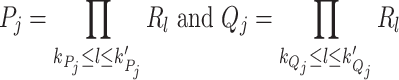 |
By induction hypothesis  commutes with all the operations of
commutes with all the operations of  . Then, we have for all
. Then, we have for all  :
:
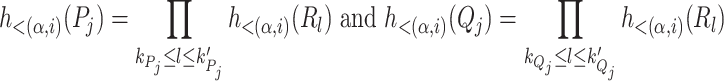 |
Thus  can be written as
can be written as
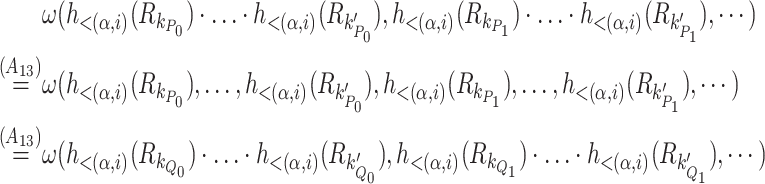 |
We have  . The case where P admits only
. The case where P admits only  -factorizations as in (19) is proved symmetrically using () instead of (). In addition, using () instead of () and arguments similar to those of the previous case, we prove that when P is sequential and
-factorizations as in (19) is proved symmetrically using () instead of (). In addition, using () instead of () and arguments similar to those of the previous case, we prove that when P is sequential and  ,
,  does not depend on the factorization of P.
does not depend on the factorization of P.
Thus, we have proved that 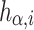 is well-defined for sequential posets of rank
is well-defined for sequential posets of rank  . In addition, the irreducible parallel factorization is unique modulo the commutativity of
. In addition, the irreducible parallel factorization is unique modulo the commutativity of  . Thus
. Thus 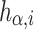 is well-defined for all posets of rank
is well-defined for all posets of rank  , for all
, for all  . Furthermore, proving that
. Furthermore, proving that  commutes with all the operations in
commutes with all the operations in  can be done by induction on r(P) too. The arguments are very similar to those used to prove that
can be done by induction on r(P) too. The arguments are very similar to those used to prove that  is well-defined. It follows that
is well-defined. It follows that  is a homomorphism of
is a homomorphism of  -algebras. In addition, since
-algebras. In addition, since  relies on h then
relies on h then  is unique.
is unique.
The proofs of the following theorems rely on the same arguments. It suffices to restrict  to the operations of the corresponding variety. In particular, this provides a new proof of Theorem 5.
to the operations of the corresponding variety. In particular, this provides a new proof of Theorem 5.
Theorem 4
 is freely generated by A in
is freely generated by A in  .
.
Theorem 5
([12]).
 is freely generated by A in
is freely generated by A in 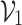 .
.
In the remainder of this section, we prove the freeness of  in
in  . The arguments are similar to those of the proof of Theorem 6.1 in [12] in which the variety considered is
. The arguments are similar to those of the proof of Theorem 6.1 in [12] in which the variety considered is  without
without  -power. We need the following result.
-power. We need the following result.
Theorem 6
([9]).
 is freely generated by A in
is freely generated by A in  .
.
Lemma 2
Let A and B be two alphabets. Let  such that S is closed under sequential product,
such that S is closed under sequential product,  -power and
-power and  -power. Let
-power. Let  be some function defined by
be some function defined by 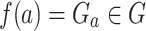 for some
for some  . Then, the function
. Then, the function  extending f defined by
extending f defined by 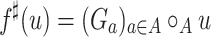 , for all
, for all  , is a homomorphism from
, is a homomorphism from 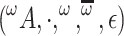 to
to  .
.
Furthermore, if  is bijective, S is generated by G, and G contains only sequentially irreducible posets then
is bijective, S is generated by G, and G contains only sequentially irreducible posets then  is bijective.
is bijective.
Proof
Let  whose irreducible sequential factorization is
whose irreducible sequential factorization is  for some
for some  , where each
, where each 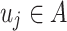 . Note that
. Note that
 |
Let  and
and 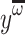 be some sequential factorizations of u. Then, one can prove easily that
be some sequential factorizations of u. Then, one can prove easily that
 |
relying on the uniqueness of the irreducible sequential factorization of u (Proposition 1).
Let us prove now that when f is bijective and S is generated by a set of sequentially irreducible posets then  is bijective. Let
is bijective. Let  and assume that
and assume that  and
and  . Let
. Let  and
and  be the irreducible sequential factorizations of respectively u and v, for some
be the irreducible sequential factorizations of respectively u and v, for some 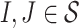 , where each
, where each  and
and  are in A. By definition of
are in A. By definition of  ,
, 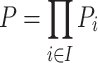 and
and 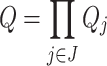 where each
where each  and
and  . Then, for all
. Then, for all 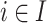 and for all
and for all 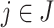 ,
,  and
and  are sequentially irreducible posets of G. Assume that
are sequentially irreducible posets of G. Assume that  . Then
. Then  and, for all
and, for all  ,
,  . We have, for all
. We have, for all 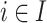 ,
,  since
since  is injective by hypothesis. In addition, as G generates S, each element P of S can be written as
is injective by hypothesis. In addition, as G generates S, each element P of S can be written as  where each
where each  , for some
, for some  . Since
. Since  is surjective by hypothesis, for all
is surjective by hypothesis, for all  there exists
there exists  such that
such that  . Then
. Then  .
.
As a consequence of HSP Birkhoff’s Theorem (see eg. [1, Theorem 1.3.8]) and Lemma 2:
Corollary 1
For all  closed under sequential product,
closed under sequential product,  -power and
-power and 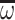 -power and generated by a set of sequentially irreducible posets of
-power and generated by a set of sequentially irreducible posets of  ,
,  is a
is a  -algebra.
-algebra.
Corollary 2
For all  closed under sequential product,
closed under sequential product, 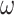 -power and
-power and 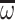 -power and generated by a set G of sequentially irreducible posets of
-power and generated by a set G of sequentially irreducible posets of  ,
,  is freely generated by G in
is freely generated by G in  .
.
We are now ready to prove the following theorem.
Theorem 7
 is freely generated by A in
is freely generated by A in  .
.
Proof
For all  , let
, let 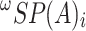 be the subset of
be the subset of  consisting all its posets of width lower or equal to i. Then
consisting all its posets of width lower or equal to i. Then  . Note that
. Note that  and
and 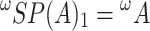 . Observe that for all
. Observe that for all  ,
,  is closed under sequential product,
is closed under sequential product, 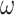 -power and
-power and  -power. In addition, for all
-power. In addition, for all 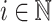 ,
,  is generated by its sequentially irreducible posets. By Corollary 1, for all
is generated by its sequentially irreducible posets. By Corollary 1, for all  ,
,  can be considered as a
can be considered as a  -algebra. In addition, by Corollary 2, for all
-algebra. In addition, by Corollary 2, for all  ,
,  is freely generated by its sequentially irreducible posets in
is freely generated by its sequentially irreducible posets in  . Then, for all
. Then, for all  and
and  , a function
, a function  can be extended in a unique homomorphism of
can be extended in a unique homomorphism of  -algebras
-algebras 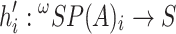 .
.
Let S be some  -algebra and let
-algebra and let  be some function. We show that h can be extended into a homomorphism of
be some function. We show that h can be extended into a homomorphism of  -algebras
-algebras  in a unique way. Indeed, we define
in a unique way. Indeed, we define  as
as  where each
where each 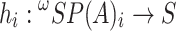 is defined, by induction on i, as follows:
is defined, by induction on i, as follows:
when
 ,
,  is defined by
is defined by  ;
;when
 ,
, 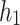 is the unique homomorphism of
is the unique homomorphism of  -algebras
-algebras  extending h (Theorem 6);
extending h (Theorem 6);- when
 ,
,  is defined as follows:
is defined as follows:- on posets P of width lower than i,
 is
is  ;
; - on sequential posets P of width i,
 is
is  ;
; - on parallel posets P of width i,
 is defined relying on the irreducible parallel factorization
is defined relying on the irreducible parallel factorization  of P, for some
of P, for some 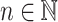 , by:
, by: 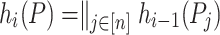
Proving that  is a homomorphism of
is a homomorphism of  -algebras is routine. Furthermore, the uniqueness of
-algebras is routine. Furthermore, the uniqueness of  comes from the facts that
comes from the facts that 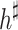 extends h and that A is a generating set of
extends h and that A is a generating set of  .
.
Decidability
Throughout this section, A denotes an alphabet. The set of terms of some signature over A is the smallest set of finite words built from A using the operations of the corresponding signature. In this section we prove the decidability of the equational theory of  .
.
Let 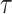 be the signature of
be the signature of  -algebras. We start by defining the set of terms in which we are interested.
-algebras. We start by defining the set of terms in which we are interested.
Definition 5
The set of terms  over A is the smallest set satisfying the following conditions:
over A is the smallest set satisfying the following conditions:
 ;
;if
 then
then  ;
;if
 then
then 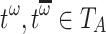 .
.
By equipping  with the operations of
with the operations of  , we define a structure called the term algebra
, we define a structure called the term algebra  over A. Note that
over A. Note that  can be considered also as the set of trees whose leaves are labeled by
can be considered also as the set of trees whose leaves are labeled by  and whose internal nodes are labeled by the operations of
and whose internal nodes are labeled by the operations of  where the out-degree of each internal node coincides with the arity of the corresponding operation.
where the out-degree of each internal node coincides with the arity of the corresponding operation.
Two terms  are equivalent if
are equivalent if 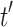 can be derived from t using the axioms which
can be derived from t using the axioms which  satisfy (denoted
satisfy (denoted  ). This equivalence relation is actually a congruence. It is well-known that
). This equivalence relation is actually a congruence. It is well-known that  is absolutely free i.e. it is freely generated by A in the class containing all the algebras of signature
is absolutely free i.e. it is freely generated by A in the class containing all the algebras of signature 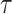 . In addition, as a consequence of Theorem 7,
. In addition, as a consequence of Theorem 7, 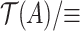 is isomorphic to
is isomorphic to  (see eg. [1, Theorem 1.3.2]). This isomorphism can be defined by
(see eg. [1, Theorem 1.3.2]). This isomorphism can be defined by 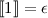 and
and  for all
for all  .
.
Then we have:
Proposition 2
Let  . Then
. Then  if and only if
if and only if  holds in
holds in  .
.
As a consequence, proving the decidability of the equational theory of  can be reduced to decide whether
can be reduced to decide whether  .
.
Theorem 8
Let 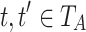 . It is decidable whether
. It is decidable whether  .
.
We now give a quick outline of the proof. The terms t and 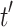 can be interpreted as particular forms of rational expressions over languages of
can be interpreted as particular forms of rational expressions over languages of  , see [6]. By extension of a well-known result of Büchi on ordinals, it is known from [2] that a language of
, see [6]. By extension of a well-known result of Büchi on ordinals, it is known from [2] that a language of 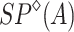 is rational if and only if it is definable in an extension, named P-MSO, of the so-called monadic second-order logic. Two P-MSO formulæ
is rational if and only if it is definable in an extension, named P-MSO, of the so-called monadic second-order logic. Two P-MSO formulæ  and
and  such that
such that 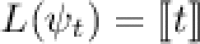 and
and  can effectively be built from t and
can effectively be built from t and 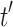 . We have
. We have  if and only if
if and only if  . Theorem 8 follows from the decidability of the P-MSO theory of
. Theorem 8 follows from the decidability of the P-MSO theory of  [2, Theorem 6].
[2, Theorem 6].
This decision procedure has a non-elementary complexity. Another proof with an exponential complexity (in the size of 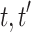 ) can be derived from the proof of [12, Theorem 7.6], in which the
) can be derived from the proof of [12, Theorem 7.6], in which the  -power is not considered, by replacing the use of [12, Theorem 7.3] by [9, Corollary 3.19].
-power is not considered, by replacing the use of [12, Theorem 7.3] by [9, Corollary 3.19].
Acknowledgements
We would like to thank the anonymous referees for their comments on this work. One of them pointed out that Theorem 3 can be deduced from Theorem 1 using the theory of categories, and in particular works by Fiore and Hur [13], Robinson [19], Adámek, Rosicky, Velbil et al.
Contributor Information
Nataša Jonoska, Email: jonoska@mail.usf.edu.
Dmytro Savchuk, Email: savchuk@usf.edu.
Amrane Amazigh, Email: Amazigh.Amrane@etu.univ-rouen.fr.
Nicolas Bedon, Email: Nicolas.Bedon@univ-rouen.fr.
References
- 1.Almeida J. Finite Semigroups and Universal Algebra. Singapore: World Scientific; 1994. [Google Scholar]
- 2.Amrane A, Bedon N. Logic and rational languages of scattered and countable series-parallel posets. Theor. Comput. Sci. 2020;809:538–562. doi: 10.1016/j.tcs.2020.01.015. [DOI] [Google Scholar]
- 3.Bedon N. Automata, semigroups and recognizability of words on ordinals. Int. J. Algebra Comput. 1998;8(1):1–21. doi: 10.1142/S0218196798000028. [DOI] [Google Scholar]
- 4.Bedon N. Complementation of branching automata for scattered and countable N-free posets. Int. J. Found. Comput. Sci. 2018;19(25):769–799. doi: 10.1142/S0129054118420042. [DOI] [Google Scholar]
- 5.Bedon N, Carton O. An Eilenberg theorem for words on countable ordinals. In: Lucchesi CL, Moura AV, editors. LATIN’98: Theoretical Informatics; Heidelberg: Springer; 1998. pp. 53–64. [Google Scholar]
- 6.Bedon N, Rispal C. Series-parallel languages on scattered and countable posets. Theor. Comput. Sci. 2011;412(22):2356–2369. doi: 10.1016/j.tcs.2011.01.016. [DOI] [Google Scholar]
-
7.Bloom S, Choffrut C. Long words: the theory of concatenation and
 -power. Theor. Comput. Sci. 2001;259(1–2):533–548. doi: 10.1016/S0304-3975(00)00040-2. [DOI] [Google Scholar]
-power. Theor. Comput. Sci. 2001;259(1–2):533–548. doi: 10.1016/S0304-3975(00)00040-2. [DOI] [Google Scholar] - 8.Bloom S, Ésik Z. Shuffle binoids. RAIRO-Theor. Inform. Appl. 1998;32(4–6):175–198. doi: 10.1051/ita/1998324-601751. [DOI] [Google Scholar]
- 9.Bloom S, Ésik Z. Axiomatizing omega and omega-op powers of words. RAIRO-Theor. Inform. Appl. 2004;38(1):3–17. doi: 10.1051/ita:2004005. [DOI] [Google Scholar]
- 10.Carton, O., Colcombet, T., Puppis, G.: Regular languages of words over countable linear orderings. CoRR abs/1702.05342 (2017). http://arxiv.org/abs/1702.05342
- 11.Carton O, Rispal C. Complementation of rational sets on countable scattered linear orderings. Int. J. Found. Comput. Sci. 2005;16(4):767–786. doi: 10.1142/S0129054105003285. [DOI] [Google Scholar]
- 12.Choffrut C, Ésik Z. Two equational theories of partial words. Theor. Comput. Sci. 2018;737:19–39. doi: 10.1016/j.tcs.2018.04.010. [DOI] [Google Scholar]
- 13.Fiore M, Hur CK. On the construction of free algebras for equational systems. Theor. Comput. Sci. 2009;410(18):1704–1729. doi: 10.1016/j.tcs.2008.12.052. [DOI] [Google Scholar]
- 14.Gischer J. The equational theory of pomsets. Theor. Comput. Sci. 1988;61(2–3):199–224. doi: 10.1016/0304-3975(88)90124-7. [DOI] [Google Scholar]
- 15.Grabowski J. On partial languages. Fundam. Inform. 1981;4(1):427–498. [Google Scholar]
- 16.Hausdorff F. Grundzüge einer theorie der geordneten mengen. Mathematische Annalen. 1908;65(4):435–505. doi: 10.1007/BF01451165. [DOI] [Google Scholar]
- 17.Kuske D. Towards a language theory for infinite N-free pomsets. Theor. Comput. Sci. 2003;299:347–386. doi: 10.1016/S0304-3975(02)00370-5. [DOI] [Google Scholar]
- 18.Rival I. Optimal linear extension by interchanging chains. Proc. AMS. 1983;89(3):387–394. doi: 10.1090/S0002-9939-1983-0715851-3. [DOI] [Google Scholar]
- 19.Robinson E. Variations on algebra: monadicity and generalisations of equational theories. Formal Aspects Comput. 2002;13(3–5):308–326. doi: 10.1007/s001650200014. [DOI] [Google Scholar]
- 20.Rosenstein JG. Linear Orderings. Cambridge: Academic Press; 1982. [Google Scholar]
- 21.Valdes J, Tarjan RE, Lawler EL. The recognition of series parallel digraphs. SIAM J. Comput. 1982;11:298–313. doi: 10.1137/0211023. [DOI] [Google Scholar]
- 22.Wilke T. An algebraic theory for regular languages of finite and infinite words. Int. J. Algebra Comput. 1993;3(4):447–489. doi: 10.1142/S0218196793000287. [DOI] [Google Scholar]
- 23.Winkowski J. An algebraic approach to concurrence. In: Bečvář J, editor. Mathematical Foundations of Computer Science 1979; Heidelberg: Springer; 1979. pp. 523–532. [Google Scholar]