Abstract
The World Health Organization (WHO) upgraded the status of the coronavirus disease 2019 (COVID-19) outbreak from epidemic to global pandemic on March 11, 2020. Various mathematical and statistical models have been proposed to predict the spread of COVID-2019 [1]. We collated data on daily new confirmed cases of the COVID-19 outbreaks in Japan and South Korea from January 20, 2020 to April 26, 2020. Auto Regressive Integrated Moving Average (ARIMA) model were introduced to analyze two data sets and predict the daily new confirmed cases for the 7-day period from April 27, 2020 to May 3, 2020. Also, the forecasting results and both data sets are provided.
Keywords: Daily new cases, Statistical analysis, stationarity, Dynamic prediction
Specifications Table
| Subject | Infectious Diseases |
| Specific subject area | ARIMA model applied to predict COVID-19 outbreaks |
| Type of data | Table Image |
| How data were acquired | The data on daily new confirmed cases of COVID-19 were taken from Wind Database. The data ware built as a time-series database by excel 2017 and ARIMA model was established for analysis using R software. |
| Data format | Raw |
| Parameters for data collection | Under the framework of Box-Jenkins method, model identification, estimation, diagnostic checking, and forecasting for ARIMA model was applied to the daily new confirmed cases data in Japan and South Korea. |
| Description of data collection | The daily new confirmed cases data of the COVID-19 outbreaks in Japan and South Korea from January 20, 2020 to April 26, 2020 are available from the Wind Database(https://www.wind.com.cn/newsite/edb.html). Also, there are no missing values and the Excel file of the daily data are presented in Supplementary data. |
| Data source location | Japan and Korea |
| Data accessibility | With the article The raw data is in Appendix A. |
Value of the Data
-
•
These data are easy to collect, and countries are beginning to collect and collate the data and release it publicly for study and analysis.
-
•
These data can be updated through news and websites to facilitate tracking and analysis during the development of the epidemic. In particular, data on daily new cases are useful because they can be used to predict covid-19 outbreaks. The data from these two typical Asian countries have practical implications for the analysis and intervention of covid-19.
-
•
The analysis of new data with ARIMA model can timely analyse and predict the changes of COVID-19, and provide dynamic information to relevant departments.
-
•
At the same time, other research institutions and management departments can also use these data to timely track and study the development and changes of the epidemic.
1. Data Description
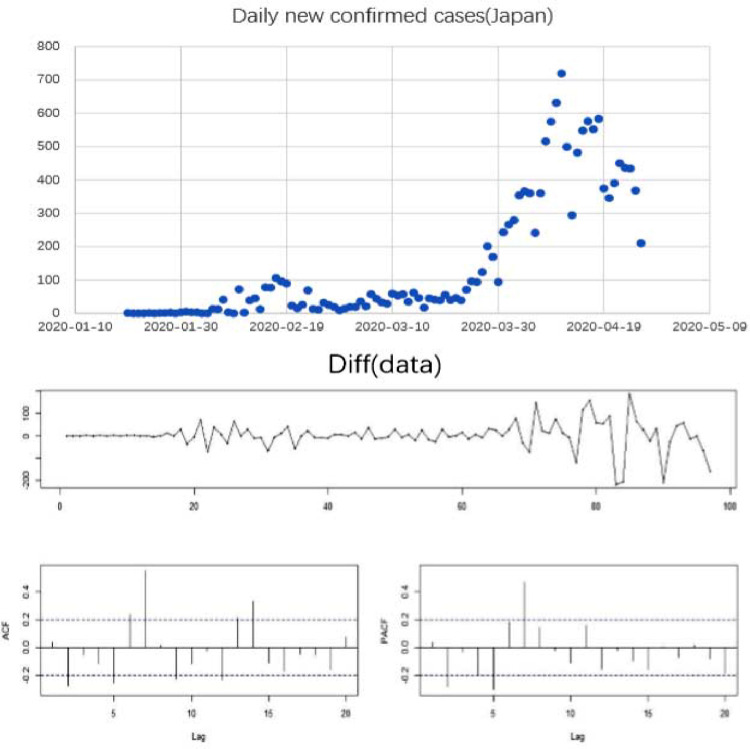
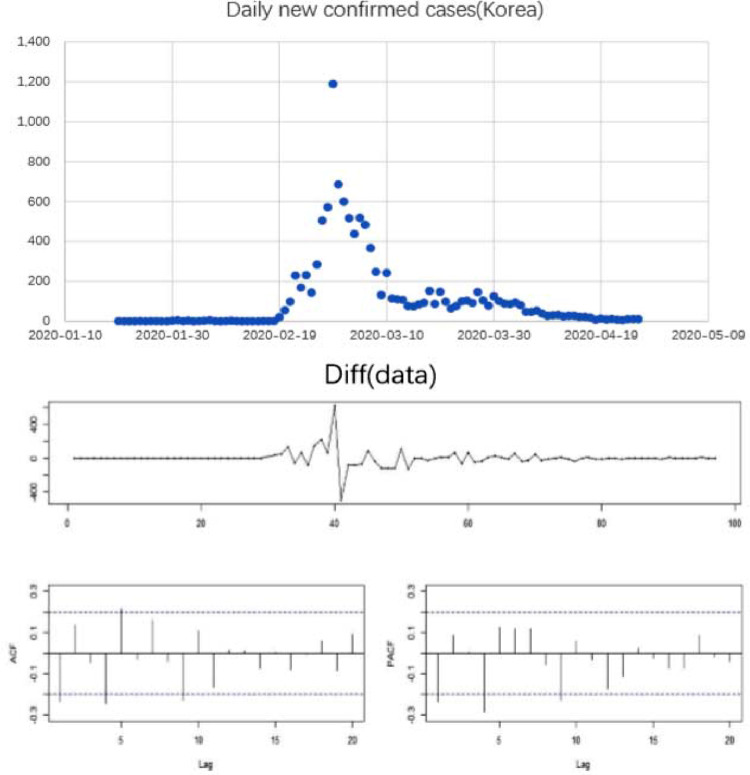
The daily new confirmed cases data of the COVID-19 outbreaks in Japan and South Korea from January 20, 2020 to April 26, 2020 are available from the Wind Database[2]. Also, there are no missing values and the Excel file of the daily data are presented in Supplementary data. The data were analysed using the statistical software R. To visualize the data time series plots of the daily new confirmed cases data in Japan and South Korea for the 98-day period from January 20, 2020 to April 26, 2020, are displayed in Figure 1, Figure 2; respectively. It can be seen from Figure 1 and 2 that both original time series look much more nonstationary and present irregular pattern; therefore, the differencing transformation was incorporated as a useful approach to stabilize the original time series. In addition, the first- difference time series look stationary when compared with the original time series shown in Figure 1 and 2.
Figure 1.
Daily new confirmed cases in Japan,first- difference of the original data ,ACF and PACF PLOT.
Figure 2.
Daily new confirmed cases in South Korea,first- difference of the original data ,ACF and PACF PLOT.
2. Experimental Design, Materials, and Methods
Auto Regressive Integrated Moving Average model, referred as ARIMA model, is employed to analyse the daily new confirmed cases data in Japan and South Korea; respectively. Under the framework of Box-Jenkins method, model identification, estimation, diagnostic checking, and forecasting for ARIMA model was applied to the two original time series [3,4]. The differencing transformation was used to achieve stationarity on certain nonstationary time series. The Augmented Dickey-Fuller (ADF) unit-root test was also introduced to identify whether the time series is stationary [3]. In addition, the R package “tseries” and “forecast” were implemented to produce the numerical output for ARIMA [5].
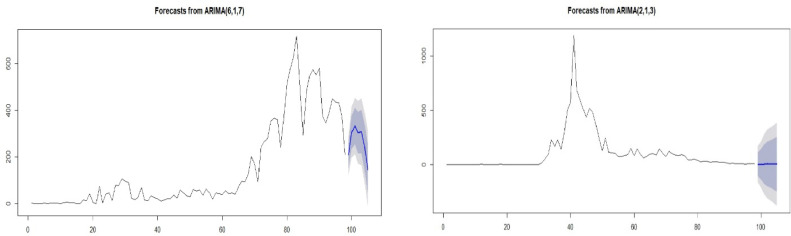
The first difference of two original series and their ADF unit-root test appear to support stationary ARMA model; therefore, we consider a class of stationary ARMA model as appropriate. Combinating parsimonious parameter models, auto-selection of model order based on R package “tseries” and correlogram of the sample autocorrelation function (ACF) and partial autocorrelation function (PACF) shown in Figure 1 and 2, we chose the orders for ARIMA model as ARIMA (6,1,7) in Japan and ARIMA (2,1,3) in South Korea; respectively. Furthermore, we adopted the following moment method and unconditional least squares to estimate the parameters for the stationary ARMA model. To save space, these estimated results were not reported. To check on the independence of the noise terms from the above ARMA model, we implemented the following diagnostic checking tools: a sequence plot of the residuals, the sample ACF of the residuals, and p-values for the Ljung-Box test statistic for a whole range of the residuals; which indicate the residuals from these ARIMA follow the white noise process. Therefore, the estimated ARIMA model can capture the dependent structure of the daily new confirmed cases time series very well. Finally, based on the above ARIMA model, the predicted value and the upper and lower limits of the predicted value under the 95% confidence level of the daily new confirmed cases for the 7-day period from April 27, 2020 to May 3, 2020 were reported in Table 1 and displayed in Figure 3.
Table 1.
Predicted value under the 95% confidence level of the daily new confirmed cases for the 7-day period
| Japan | date | lowwer | mean | upper | Korea | date | lowwer | mean | upper |
| 2020-04-27 | 122.68342 | 207.5012 | 292.319 | 2020-04-27 | -161.9685 | 6.36643 | 174.7014 | ||
| 2020-04-28 | 194.68068 | 303.4768 | 412.2729 | 2020-04-28 | -210.9135 | 2.035784 | 214.9851 | ||
| 2020-04-29 | 211.76786 | 333.6616 | 455.5554 | 2020-04-29 | -272.6349 | 4.635792 | 281.9065 | ||
| 2020-04-30 | 170.06375 | 304.8661 | 439.6684 | 2020-04-30 | -308.2444 | 7.649637 | 323.5437 | ||
| 2020-05-01 | 164.28963 | 308.5206 | 452.7516 | 2020-05-01 | -330.465 | 7.153191 | 344.7714 | ||
| 2020-05-02 | 93.39579 | 244.7979 | 396.1999 | 2020-05-02 | -354.1099 | 5.432586 | 364.975 | ||
| 2020-05-03 | -22.66019 | 143.4524 | 309.565 | 2020-05-03 | -381.2896 | 5.198718 | 391.687 |
Figure 3.
7-day period prediction of the daily new confirmed cases for Japan and Korea plot.
Appendix A. Supplementary data
Appendix A.xlsx
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships which have, or could be perceived to have, influenced the work reported in this article.
Acknowledgments
We are grateful to Professor Renjun Ma for constructive suggestions during the preparation of the manuscription. XD was supported in part by the Science and Technology Foundation of Guizhou Province ([2020]1Y009) and the talents for scientific research project of Guizhou University of Finance and Economics (2018YJ104) and XZ was supported in part by the Yunnan Philosophy and Social Science Planning Project Fund (HX2019082760).
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.dib.2020.105779.
Appendix. Supplementary materials
References
- 1.X. L. Zhang, R. J. Ma, L. Wang, Predicting turning point, duration and attack rate of COVID-19 outbreaks in major Western countries, Chaos, Solitons & Fractals (2020). 10.1016/j.chaos.2020.109829. [DOI] [PMC free article] [PubMed]
- 2.The Wind Database. https://www.wind.com.cn/newsite/edb.html.
- 3.G. E. P. Box, G. M. Jenkins, Time Series Analysis, Forecasting and Control, San Francisco: Holden-Day (1976).
- 4.Haines L.M., Munoz W.P., Van Gelderen C.J. ARIMA modelling of birth data. Journal of Applied Statistics. 1989;16:55–67. [Google Scholar]
- 5.J. D. Cryer, K. S. Chan, Time Series Analysis with Applications in R, Second ed, Springer (2010).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.