Integration of Heterogeneous Experimental Data Improves Global Map of Human Protein Complexes

Abstract

Protein complexes play a significant role in the core functionality of cells. These complexes are typically identified by detecting densely connected subgraphs in protein-protein interaction (PPI) networks. Recently, multiple large-scale mass spectrometry-based experiments have significantly increased the availability of PPI data in order to further expand the set of known complexes. However, high-throughput experimental data generally are incomplete, show limited agreement between experiments, and show frequent false positive interactions. There is a need for computational approaches that can address these limitations in order to improve the coverage and accuracy of human protein complexes. Here, we present a new method that integrates data from multiple heterogeneous experiments and sources in order to increase the reliability and coverage of predicted protein complexes. We first fused the heterogeneous data into a feature matrix and trained classifiers to score pairwise protein interactions. We next used graph based methods to combine pairwise interactions into predicted protein complexes. Our approach improves the accuracy and coverage of protein pairwise interactions, accurately identifies known complexes, and suggests both novel additions to known complexes and entirely new complexes. Our results suggest that integration of heterogeneous experimental data helps improve the reliability and coverage of diverse high-throughput mass-spectrometry experiments, leading to an improved global map of human protein complexes.

1. INTRODUCTION

Protein interactions and complexes play a central role in the functionality of cellular organisms. A critical task in the analysis of biological systems at the molecular level is the systematic study of the protein-protein interaction (PPI) networks underlying all cell functions.

PPIs can be divided into two types (i) direct physical interactions between protein pairs, and (ii) indirect interactions through other proteins in a complex typically referred to as complex co-membership. The former interaction type is commonly detected experimentally by a yeast two-hybrid (Y2H) assay, whereas the latter interaction type is frequently determined by co-immunoprecipitation (coIP) coupled with mass-spectrometry (MS) [5, 32]. Despite several years of experimental work, the coverage of PPI networks for most organisms is largely incomplete [9, 20]. For instance, the comprehensive resource of mammalian protein complex (CORUM) database is one of the most widely used databases of manually annotated protein complexes from mammalian organisms [11]. However, the latest release of CORUM (version 3.0) only lists 4, 274 mammalian protein complexes across 4, 473 different genes. Thus, close to 80% of the human proteins are not included in CORUM while Berggård et al [5] estimate that over 80% of proteins participate in complexes. Hence, experimental and computational efforts are still required to establish a more comprehensive set of protein complexes.

Recently, three large-scale MS-based experimental studies have published protein interaction maps [14, 16, 38]. While these studies significantly increase the set of known human co-membership interactions, several are still likely missing [7, 9]. The data of Huttlin et al [16] (BioPlex) and Hein et al [14] is derived from affinity purification/mass-spectrometry (AP-MS), where interactions with a tagged subset of human proteins referred to as baits are surveyed; this restricts the set of observable co-membership interactions to those revealed by co-precipitation with a bait protein (often termed preys). The resulting interaction sets are comprised of 23, 744 bait-prey pairs over 7, 668 proteins (2, 594 baits) in Bioplex, and 26, 642 bait-prey pairs over 5, 462 proteins (1, 125 baits) in Hein et al. While the two data sets overlap in 47% and 69% of the proteins studied, only 3–4% of the identified pairwise interactions overlap [7]. This partially results from the different cell lines used by each study, but also indicates that both are likely far from complete. In the case of Wan et al [38], the interaction data is determined from co-fractionation/mass-spectrometry (CF-MS) experiments, which measures whether untagged proteins fractionate together. In this experiment, protein interactions are inferred from repeated observation of co-eluting proteins across samples and separations. This data set contains 16, 665 protein interactions out of 3, 466 proteins from fractionated soluble complexes across nine metazoan species such that each interaction is supported by at least two species. As a result, this interaction data is biased towards evolutionarily conserved complexes from abundant and soluble human proteins.

Although complementary, as mentioned above these independent experiments typically show limited overlap, are incomplete, and contain large fractions of false positive interactions [4, 7–9, 12, 37, 40]. Therefore, there is a need for systematic studies which integrate MS-based experiments as a means of creating a unified and full view of the set of human protein complexes.

Toward this goal, several methods have been developed to integrate molecular information for improving prediction of protein interactions and complexes [1–3, 15, 17–19, 21–26, 28–30, 39]. At the core, these methods predict complexes via a multi-step process: (i) assign confidence scores to pairwise interactions, (ii) identify densely connected clusters (iii) refine clusters into protein complexes, and (iv) evaluate complexes against a set known from previous work. Recently, Drew et al [7] integrated and re-analyzed 9, 063 MS experiments comprising the BioPlex, Hein et al and Wan et al data sets in order to provide a more global map of human protein complexes. They developed a two-stage machine learning pipeline for building protein complexes that first integrates protein pair features from the three data sets using a Support Vector Machine and then clusters the resulting pairs to obtain protein complexes. A key component utilized by this framework is a weighted matrix model based on prior work by Hart et al [13]; it produces estimated weights for prey-prey interactions under a common bait when re-analyzing data from AP-MS experiments. This integrative approach resulted in improved coverage of the map of human complexes, which the authors incorporated into a database referred to as hu.MAP.

While hu.MAP identifies previously uncharacterized protein interactions, it is still restricted since it can only predict interactions between observed prey proteins that share an underlying bait. Thus, it cannot be generalized to identify potentially novel protein interactions or complexes in the absence of an anchoring bait. Furthermore, as previously mentioned, most of the existing high-throughput protein interaction data is noisy and likely missing interactions; these will also be absent from hu.MAP. To mitigate these challenges, several methods combine different types of auxiliary information such as gene expression data [17], protein domains [18, 28] and functional annotation [22]. However, most of these methods were applied to older mass spec data and do not use additional recent complementary data. In particular, these prior methods do not use protein sub-cellular localization annotations from large scale bioimage databases (e.g., Human Protein Atlas [34, 35]) and so the utility of this complementary source remains largely unexplored.

To increase the reliability and coverage of predicted complexes we developed a new method that integrates data from multiple recent heterogeneous experiments and sources (mass spec experiments, gene expression measurements and sub-cellular localization annotations). In particular, we first fused the heterogeneous data into features and then trained a random forest classifier for pairwise protein interactions. We next developed graph based methods to combine pairwise interactions into protein complexes of varying sizes which are optimized and refined using a validation set derived from an earlier version of CORUM. We present results showing that our approach improves prediction of pairwise interactions, accurately identifies known complexes, and predicts novel complexes and additions to known complexes that are supported by other data sources.

2. METHODS

We developed an integrated approach for predicting protein complexes by fusing heterogeneous data from different experiments and sources. The key insight is that by combining orthogonal data sources, we can increase coverage of the protein space, compensate for missing or incomplete information, and reduce false positives and negatives.

Our approach involves multiple steps: (i) creating a fused heterogeneous set of protein interactions features, (2) learning an accurate classifier of pairwise protein interactions and (3) combining clusters of densely interacting protein pairs to form protein complexes.

2.1. Data sets

We used the training and test data sets compiled by Drew et al [7] which were generated from the literature-curated complexes in the CORUM core set (version 2.0 released on February 2012). These sets are comprised of 27, 665 and 15, 575 positive interactions defined as pairs of proteins in the same protein complex, and 2, 543, 855 and 2, 867, 914 negative interactions defined as pairs of proteins in known complexes but not part of the same complex. Additionally, we downloaded the latest version of the CORUM core set (version 3.0 released on July 2018), as well as the hu.MAP database which was trained on CORUM 2.0 [7]. These data sets were used for performance evaluation and identification of previously uncharacterized protein pairwise interactions and complexes. Interestingly, CORUM 3.0 and hu.MAP share only 29 identical protein complexes [11]. Table 1 summarizes the protein complex data sets used in this study.

Table 1:

Summary of protein complex data sets. For each data set, we show the number of distinct proteins P, number of complexes C, average number of proteins per complex P_C and average number of complexes per protein C_P.

Data set name	P	C	PC	CP
CORUM core set (v2.0)	3, 189	2, 083	4.53	2.41
CORUM core set (v3.0)	4, 473	3, 512	4.11	2.63
hu.MAP	7, 777	4, 659	3.99	2.39

2.2. Integrating heterogeneous experimental data into protein interaction features

We use several different types of features for predicting pairwise complexes. We first followed Drew et al [7], and collected all raw protein pair features from the mass-spectrometry experiments in BioPlex [16], Hein et al [14] and Wan et al [38], as well as the additional features introduced in [7] for bait-prey or prey-prey pairs from the two AP-MS experiments. In addition, we generated 15 new features. These included four additional features based on mass spec data (two for each AP-MS data sets) defined as the Pearson correlation coefficient between (i) prey-prey profiles across all baits, and (ii) bait-bait profiles across all preys. The remaining eleven features were computed between all pairs of proteins. Three features were computed from the NCI-60 human tumor cell lines panel [10]: the Pearson correlation coefficients between (i) co-expression profiles at the RNA-level across all cell lines, (ii) co-expression profiles at the protein-level across all cell lines, and (iii) co-expression profiles at the protein-level across all tissues. Four additional location-based features were calculated using data from either the Human Protein Atlas or Swiss-Prot [36], respectively. Specifically, let S_pi and S_pj be the sets of sub-cellular localization annotations for a protein pair (p_i, p_j )i ≠ j, then these location features are defined as

$$\left(1\right)\hspace{0.17em}\text{overlap}:=\left|S_{pi}\cap S_{pj}\right|$$

$$\left(2\right)\hspace{1em}\text{set}\hspace{0.17em}\text{equality}:=\{\begin{array}{ll}1\hfill & \text{if}\hspace{0.17em}{S}_{pi}=S_{pj}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

$$\left(3\right)\hspace{0.17em}\text{Jaccard}\hspace{0.17em}\text{similarity}:=\left|\frac{S_{pi}\cap S_{pj}}{S_{pi}\cup S_{pj}}\right|$$

$$\left(4\right)\hspace{0.17em}\text{set}\hspace{0.17em}\text{inclusion}:=\{\begin{array}{ll}1\hfill & \text{if}\hspace{0.17em}{S}_{pi}\subseteq S_{pj}\hspace{0.17em}\text{or}\hspace{0.17em}{S}_{pj}\subseteq S_{pi}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

2.3. Learning a classifier for pairwise protein interactions

We trained and evaluated predictors of pairwise interactions for different data sets and combinations of features. For a given feature matrix, we trained a random forest classifier using the TreeBagger function in Matlab (version R2017b). We performed a parameter sweep on the number of trees over the set {100, 200, 300, 400, 500} using cross-validation over the training set. Prediction scores were computed using the predict function with the default setting which reports an average vote from all trees in the ensemble. For each classifier, the result was a protein interaction network graph such that each edge (pairwise interaction) was weighted according to the predicted score from all trees in the random forest. After the evaluations were completed, we merged the training and test sets to learn a final random forest classifier and applied this classifier to all pairs of proteins for which we had data. This final set was comprised of 6, 543 proteins and 21, 533, 203 interactions.

2.4. Building protein complexes from predicted pairwise protein interactions

We applied a two-stage approach for building protein complexes from pairwise protein interactions. First, we defined a weighted undirected graph G_t = (V, E, w), where V represents the set of proteins, E = {(v_i,v_j) | w(v_i,v_j) ≥ t and v_i,v_j ∈ V} set of protein pairs with interaction probability above a pre-defined threshold t, and $\text{w}\hspace{0.17em}:\hspace{0.17em}E\to ℝ$ is the classifier’s estimate of the probability of interaction for all protein pairs (v_i, v_j). The threshold t was chosen to select a given percentage of high-scoring protein pairs in the range of {0.001, 0.002, 0.005, 0.01, 0.02, 0.05}. For each t, we applied Algorithm 1 which returns all maximal cliques in G_t as the set of predicted protein complexes C_t. Furthermore, each complex c ∈ C_t is assigned a complex score defined as the minimum edge weight between all interactions in the complex. While Algorithm 1 is able to identify strongly connected sets, we noticed that it often generates several largely overlapping sets that differ in one protein which are all annotated as part of a larger complex in CORUM (see Figure 3A). To improve the ability of our methods to identify large complexes we further developed Algorithm 2 which is applied to refine the initial set of cliques. Algorithm 2 works on the set of complexes predicted by Algorithm 1, C_t, and the interaction network G_t′ = V_t′, E_t′ to refine the set of complexes by adding new protein members from V_t′, thereby effectively expanding and possibly merging complexes. Parameter t′ is selected from the set {0.65, …, t} which was determined by a parameter sweep. The main idea behind Algorithm 2 is to relax the strict threshold t′ when we observe a large overlap between two strongly connected components. Biologically, this corresponds to larger complexes where not all proteins are expected to physically interact. In such cases our pairwise score may be lower for some of the pairs even if they are in the same complex.

Figure 3:

Comparison of predicted complexes against gold standard CORUM (version 2.0). Figure shows all predicted complexes (blue) across three different categories as a function of complex size. The categories are (1) identical match to complex in CORUM (gray), (2) strict subset to a complex in CORUM (yellow), and (3) potentially novel complex (orange). (A) Figure shows predicted complexes using Algorithm 1 for threshold t = 0.87 selected from top 0.02% of high-scoring proteins pairs. (B) Figure shows predicted refined complexes using Algorithm 2 with t′ = 0.85 on top 0.02% high-scoring proteins pairs shown in (A).

$$\overline{\begin{array}{l}\mathbf{\text{Algorithm}}\hspace{0.17em}\mathbf{1}\hspace{0.17em}\text{Protein}\hspace{0.17em}\text{Complexes}\hspace{0.17em}\text{Identification}\hspace{0.17em}\text{Algorithm}\\ \overline{\underset{\_}{\begin{array}{l}\hspace{0.17em}\hspace{0.17em}1:\hspace{0.17em}\mathbf{\text{function}}\hspace{0.17em}\text{IDENTIFY-CANONICAL-COMPLEXES}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{Input}}\mathbf{:}\hspace{0.17em}{G}_t:=\hspace{0.17em}\text{weighted}\hspace{0.17em}\text{interaction}\hspace{0.17em}\text{network}\hspace{0.17em}\text{of}\hspace{0.17em}\text{protein}\hspace{0.17em}\text{pairs}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{above}\hspace{0.17em}\text{threshold}\hspace{0.17em}t\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{Output}}\mathbf{:}\hspace{0.17em}{C}_t:=\hspace{0.17em}\text{set}\hspace{0.17em}\text{of}\hspace{0.17em}\text{protein}\hspace{0.17em}\text{complexes}\\ \hspace{0.17em}\hspace{0.17em}2:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}_t=\hspace{0.17em}\text{Compute}\hspace{0.17em}\text{all}\hspace{0.17em}\text{maximal}\hspace{0.17em}\text{cliques}\hspace{0.17em}\text{in}\hspace{0.17em}{G}_t\\ \hspace{0.17em}\hspace{0.17em}3:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}c\in C_{t\hspace{0.17em}}\mathbf{\text{do}}\\ \hspace{0.17em}\hspace{0.17em}4:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}c.score\hspace{0.17em}=\hspace{0.17em}\min \left\{w\left(v_i,v_j\right)|\forall \hspace{0.17em}{v}_i,v_j\in c\right\}\\ \hspace{0.17em}\hspace{0.17em}5:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{return}}\hspace{0.17em}{C}_t\end{array}}}\end{array}}$$

2.5. Evaluation methodology

To enable comparisons on new sets of proteins we evaluated our approach by comparing it to our implementation of the method proposed by Drew et al [7]. We determined that our implementation was able to generate the same results on the set of proteins originally considered in that paper as shown in Figure S1 (compare to Figure 2A in Drew et al [7]).

Figure 2:

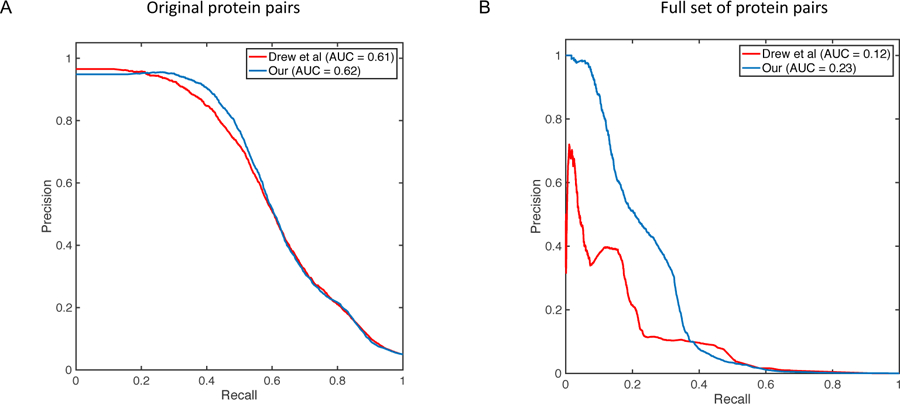
Performance comparison of pairwise protein interactions prediction. Figure shows precision-recall curve and area under the curve (AUC) of our proposed method (blue) compared against a previously published approach by Drew et al [7] (red). (A) Figure shows the comparison results for the original test set of protein pairs in [7]. (B) Figure shows the comparison results on the full set of protein pairs for which we had data.

Performance assessment on pairwise interaction prediction.

The performance of each method was evaluated through a 10-fold cross-validation. In each iteration, 10% of pairwise interactions in the network are selected for the test set, whereas the remaining 90%

$$\overline{\begin{array}{l}\mathbf{\text{Algorithm}}\hspace{0.17em}\mathbf{2}\hspace{0.17em}\text{Protein}\hspace{0.17em}\text{Complexes}\hspace{0.17em}\text{Refinement}\hspace{0.17em}\text{Algorithm}\\ \overline{\underset{\_}{\begin{array}{l}\hspace{0.17em}\hspace{0.17em}1:\hspace{0.17em}\mathbf{\text{function}}\hspace{0.17em}\text{REFINE-CANONICAL-COMPLEXES}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{Input}\mathbf{:}\hspace{0.17em}{C}_t:=\hspace{0.17em}\text{set}\hspace{0.17em}\text{of}\hspace{0.17em}\text{protien}\hspace{0.17em}\text{complexes}\hspace{0.17em}\text{and}\hspace{0.17em}{G}_{t^{\prime }}=\left(V_{t^{\prime }},E_{t^{\prime }},w\right):=\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{weighted}\hspace{0.17em}\text{interaction}\hspace{0.17em}\text{network}\hspace{0.17em}\text{of}\hspace{0.17em}\text{protien}\hspace{0.17em}\text{pairs}\hspace{0.17em}\text{above}\hspace{0.17em}\text{refinment}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{threshold}\hspace{0.17em}{t}^{\prime }\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{Output}}\mathbf{:}\hspace{0.17em}{C}_{t^{\prime }}:=\hspace{0.17em}\text{set}\hspace{0.17em}\text{of}\hspace{0.17em}\text{refined}\hspace{0.17em}\text{protein}\hspace{0.17em}\text{complexes}\\ \hspace{0.17em}\hspace{0.17em}2:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}c\in C_{\hspace{0.17em}}\mathbf{\text{do}}\\ \hspace{0.17em}\hspace{0.17em}3:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{for}}\hspace{0.17em}v\in V_{t^{\prime }\hspace{0.17em}}\mathbf{\text{do}}\\ \hspace{0.17em}\hspace{0.17em}4:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Add}\hspace{0.17em}v\hspace{0.17em}\text{to}\hspace{0.17em}c\hspace{0.17em}\text{if}\hspace{0.17em}\text{and}\hspace{0.17em}\text{only}\hspace{0.17em}\text{if}\hspace{0.17em}w\left(v,v_i\right)\ge t^{\prime }\hspace{0.17em}\forall \hspace{0.17em}{v}_i\in c\\ \hspace{0.17em}\hspace{0.17em}5:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{if}}\hspace{0.17em}c\hspace{0.17em}\notin \hspace{0.17em}{C}_{t^{\prime }}\hspace{0.17em}\mathbf{\text{then}}\\ \hspace{0.17em}\hspace{0.17em}6:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{Update}\hspace{0.17em}c.score\hspace{0.17em}=\hspace{0.17em}\min \left\{w\left(v_i,v_j\right)|\forall \hspace{0.17em}{v}_i,v_j\in c\right\}\\ \hspace{0.17em}\hspace{0.17em}7:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{C}_{t^{\prime }}=C_{t^{\prime }}\cup \left\{c\right\}\\ \hspace{0.17em}\hspace{0.17em}8:\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{\text{return}}\hspace{0.17em}C\end{array}}}\end{array}}$$

are used for training. Random forest classifiers were used to construct all predictors and perform comparative evaluation. Finally, we estimated the area under the precision-recall curve (AUC-PR), which plots precision as a function of recall.

Performance assessment on predicted protein complexes.

To evaluate the predicted set of complexes we used k-cliques [7], a new class of similarity metrics for comparing sets of complexes in a formal precision-recall framework. Additionally, this k-clique metric can be used to evaluate different protein complex scoring schemes in order to effectively rank candidate complexes.

2.6. Identification of potentially novel protein complexes

In order to identify potentially novel complexes, we took all candidate complexes that did not overlap with CORUM and ranked them by their score. The resulting set of potential complexes was further evaluated by traditional enrichment analysis of functional annotations, as well as other protein-protein interaction tests to eliminate potential artifacts. For instance, we computed Gene Ontology (GO) functional annotation enrichment (excluding electronic annotations) for each complex via g:Profiler [31] with g:SCS method for multiple testing correction of p-values. Additionally, we restricted the gene list in the statistical background to the set of proteins V in the corresponding interaction graph G_t for a given threshold t. Furthermore, for each predicted complex size, we generated a random set of 10, 000 complexes of same size using the proteins in V and computed GO annotation enrichment for each random complex as described above. Finally, for each complex size l, the resulting set of l -specific p-values from random complexes is used to assigned a final p-value, GO_P-value, on each candidate complex of equal size, where ${\text{GO}}_{\text{P-value}}\in \left[\frac{1}{10,000},1\right]$.

In the context of interaction-level analysis, we exploited two independent annotation sources. First, we used the protein-protein interaction scores from STRING database [33], which are derived by integrating multiple data sources (e.g., high-throughput experiments and automated literature mining) into a single confidence score for each pairwise interaction in the database. For each predicted complex, we computed the average STRING score (experimentally-derived only) across all pairwise interactions between members of the complex. Second, we downloaded protein abundance profiles for CaCo-2 cells expressing wild-type BRAF compiled by Diedrich et al [6]. They applied size-exclusion chromatography (SEC) combined with protein correlation profiling-stable isotope labeling by amino acids in cell culture (PCP-SILAC) as a means to characterize the protein-protein interactions indirectly via cofractionation. The resulting protein-level data set contains normalized SEC-PCP-SILAC ratios of 54 SEC fractions for three biological replicates. For each possible protein pair in the complex, we computed the Pearson’s correlation coefficient of the normalized ratios across the 54 fractions. Finally, for each candidate complex, the minimum correlation coefficient is reported.

3. RESULTS

Figure 1 presents the computational pipeline we developed for identifying protein complexes from heterogeneous experimental data. We start by combining multiple experiments and sources into protein pair features (Figure 1A–B). Of particular note here is that some of our new features can be calculated between all possible pairs of proteins, even for those proteins that have not been detected in previous MS experiments. Next, we use the fused features to train a classifier for pairwise protein interactions (Figure 1C). We then generated a protein-protein interaction network based on the classifier’s estimate of the probability of pairwise interaction. Finally, we employ a two-step graph-based approach for integrating pairwise interactions into protein complexes (Figure 1D–E).

Figure 1:

Schematic diagram illustrating the whole computational pipeline proposed in this work. Figure shows step in the pipeline. (A) Collecting heterogeneous experimental data sources derived from mass spectrometry (MS) experiments, gene expression measurements and sub-cellular localization annotations, (B) Integrating heterogeneous data into a fused feature matrix, (C) Training a random forest classifier for predicting pairwise interactions, (D) Identifying protein complexes as strongly connected protein clusters from high-scoring pairwise interactions, and (E) Refining protein complexes by adding weaker pairwise interactions and merging highly overlapping complexes.

We applied our pipeline to identify protein complexes from distinct mass-spectrometry experiments combined with gene expression data and sub-cellular localization annotations (see Methods for detailed descriptions). These experiments vary in the type of method employed (AP-MS vs. CF-MS) and the number and composition of samples used, as well as number of baits surveyed in the case of AP-MS experiments. Therefore, these heterogeneous data sets provide a good opportunity to test the generality of our approach for identifying previously uncharacterized pairwise interactions and protein complexes.

3.1. Heterogeneous data improves performance and coverage of pairwise interactions

To evaluate our method and compare it to prior methods, we tested predictive performance against each individual mass spectrometry data set (using positive and negative pairwise interactions derived from known complexes in CORUM). Figures S2 and S3 show precision-recall curves and area under the curve (AUC-PR) on the AP-MS data sets for three different protein pair models (bait-prey, bait-prey and prey-prey, and all protein pairs) using (i) only data set specific features, (ii) adding weighted matrix model features (denoted by MM) as was done by Drew et al [7] and (iii) our approach which adds several heterogeneous features. As can be seen, for data from BioPlex (Figure S2), the addition of co-expression (denoted by coExp) and co-localization (denoted by coLoc) features provided a boost in performance (AUC) when compared against previous methods for all protein pair models: the bait-prey model showed AUC gains between 0.03–0.19, the bait-prey and prey-prey model showed AUC improvements between to 0.05–0.17, and the all pairs model displayed AUC gains between 0.15–0.26. Similarly, using data from Hein et al (Figure S3) we observed gains in performance when compared to prior methods over the different protein pair models. These AUC performance improvements ranged between 0.01–0.04 for the bait-prey model, 0.02–0.11 for the bait-prey and prey-prey model, and 0.09–0.20 for the all pairs model. Interestingly, heterogeneous features improved protein interaction discovery on the AP-MS data sets even in the stringent bait-prey model (i.e., protein pairs with direct evidence in the AP-MS data), highlighting the usefulness of non-physical orthogonal interaction information. In the context of CF-MS data, Figure S4 shows the precision-recall curve and AUC on the Wan et al data set using (i) only data set specific features, and (ii) adding proposed heterogeneous features. Again, our method exhibited a 6% boost in AUC performance (0.73 vs. 0.69) for the all pairs model. Overall, as shown by all three figures, our method outperforms all other feature combinations across multiple protein pair models. As expected, the use of co-expression and co-localization features showed the largest performance gains on the all protein pairs model since it includes pairs without direct evidence in the co-precipitated or co-fractionated data. These results are consistent with previous studies (e.g., Wan et al [38]) which reported performance gains when auxiliary data (e.g., co-expression and co-citation) is combined with MS-based features for identifying pairwise interactions.

Next, for performance comparisons on the pairwise protein interaction prediction task across the fully integrated mass spec data, we trained a random forest classifier using the features described in Methods and compared our proposed method against the method proposed by Drew et al [7]. Figure 2A shows the precision-recall curve and AUC for each method on the original pairwise interaction test set, whereas Figure 2B shows the precision-recall curve and AUC for both methods on the the full set of pairwise interactions. As shown in Figure 2A, both methods perform comparably on the original data which is unsurprising as this set is solely comprised of protein pairs derived from MS experiments. However, our method strongly outperforms the method by Drew et al when evaluated using all protein pairs (Figure 2B). Specifically, our method led to almost double AUC score when compared to Drew et al (0.23 vs. 0.12). The AUC improvement is even larger (0.30 vs. 0.13) when focusing on the top 10% of the scores (not shown). These results highlight the critical role of auxiliary data sources (i.e., co-expression and co-localization) not only for improving performance in the identification of pairwise interactions but also for increasing coverage across protein pairs for which there is no evidence in the MS-based data.

3.2. Identification of human protein complexes

Given the results regarding accurate prediction of pairwise interactions, we next looked at the ability of our method to predict known and novel complexes. A well-known signature of protein complexes is that co-membership proteins tend to exhibit a dense connectivity in the underlying interaction network. To this end, we applied Algorithm 1 (Methods) to the interaction network G_t derived from high-scoring protein pairs across different thresholds t (Methods). We denote the set of protein complexes identified when using G_t as C_t. To further improve the set of complexes from Algorithm 1 (i.e., C_t ), we applied Algorithm 2 to merge complexes in C_t using a lower threshold network Gt′. This further refines the set of complexes by effectively adding new protein members and possibly merging complexes. Figure 3A–B shows the number of predicted complexes from Algorithm 1 (A) and Algorithm 2 (B) when using the top 0.02% of high-scoring pairs (t = 0.87; t′ = 0.85) as a function of complex size (shown in blue). In particular, the total number of predicted complexes is reduced from the initial set of 1, 340 in Algorithm 1 to 1, 182 in Algorithm 2. To evaluate the accuracy of both algorithms, we computed the number of predicted complexes that are identical to those found in CORUM (gray), as well as those complexes that are a strict subset of a CORUM complex (yellow). The remaining predictions are labeled as novel predicted complexes (orange). As shown in Figure 3, our method produces accurate complexes even when lowering the threshold to allow merging (Methods and Figure 3B). Comparing these complexes to the hu.MAP complexes proposed by Drew et al [7], we observe that our approach produces more complete complexes (Figure S5) while hu.MAP generally tends to predict a larger number of new complexes. Specifically, our approach predicts a total of 1, 182 complexes after merging (Figure 3B) whereas hu.MAP predicts 3, 095 complexes (Figure S5). Among these predicted complexes, our approach produces 1.8% complexes with identical matches in CORUM as opposed to 0.7% of the total complexes in hu.MAP. Similarly, 21.6% of the complexes identified by our method are strict subsets of known complexes in CORUM compared to just 3.0% of the predicted complexes in hu.MAP.

To further analyze the effects of the refinement threshold on the set of complexes C_t, Figure S6 shows the number of predicted complexes for six different values of t as a function of threshold t′. In all cases, the number of predicted complex decreases as threshold t′ decreases. For example, for t = 0.87 (i.e, top 0.02% of high-scoring pairs) the initial set of complex is 1, 340 whereas the number of refined complexes is 550 at t′ = 0.65. As expected, we observe the large increase of initial complexes between thresholds t = 0.87 (C_t = 1, 340) and t = 0.77 (C_t = 7, 917).

3.3. Evaluation of predicted protein complexes

To further evaluate our predictions we compared them to complexes in CORUM and hu.MAP, as well as to complexes generated by using hu.MAP pairwise scores as input to Algorithms 1 and 2. To systematically evaluate the accuracy of the predicted complexes, we use the k-cliques metrics proposed by Drew et al [7] for comparing sets of complexes in a formal precision-recall frame-work. Figure 4 and Figure S7 show F-weighted k-clique score as a function of average complex size for each threshold t. As can be seen, our method (circles) performs favorably when compared to hu.MAP database (square). For instance, hu.MAP exhibits a F-weighted k-clique score of 0.31 whereas our complex maps show higher F-weighted k-clique scores (ranging from 0.37 for top 0.05% to 0.48 for top 0.002%). In addition, our methods produced larger complex sizes irrespective of the value of threshold t (average complex sizes range between 15.9 for top 0.05% and 24.9 for top 0.002% compared to 4 for hu.MAP). Interestingly, we observe that if we use hu.MAP pairwise scores in the top 0.02% as input to Algorithms 1 and 2, the resulting set of predicted complexes (green dotted line with triangles) outperforms those obtained by hu.MAP itself in terms of both F-weighted k-clique score (0.33 vs. 0.31) and average complex size (7.6 vs. 4.0). Regardless of the initial set of pairwise scores, our method produces larger complexes to those obtained by hu.MAP which suggests hu.MAP tends to predict sparser interaction networks.

Figure 4:

Comparison between predicted and hu.MAP complexes. Figure shows F-weighted k-clique score [7] of our method (solid lines with circles) for two representative thresholds t as a function of average complex size for each t′ threshold. Figure also shows corresponding scores for hu.MAP (square) and an in-house implementation that uses hu.MAP pairwise scores as input to Algorithms 1 and 2 (dotted lines with triangles).

Next, we assessed the quality of the set of predicted complexes via traditional enrichment analysis of functional annotations, as well as other complementary data sets for three classes of predicted complexes with varying degrees of overlap with CORUM: (i) full overlap with a CORUM complex (orange circles), (ii) at least half the member proteins overlap with CORUM complex (gray diamonds), and (iii) less than half of co-member proteins overlap with CORUM complex (blue triangles). Figure S8 evaluates the distribution of the largest p-value from enriched functional annotations (plotted as -log₁₀(GO_P-value)) for each complex using g:Profiler and further adjusted using randomization analysis. As can be seen, over 97% (384 out of 394) of predicted complexes in CORUM (orange circles) had at least one significantly enriched functional annotation at the 0.05 (i.e., -log₁₀ (0.05) = 1.30) significance threshold. In the case of the class of complexes for which at least half the member proteins overlap with a CORUM complex (gray diamonds), the majority of complexes (> 98%; 737 out of 755) also had at least one significantly enriched functional annotation; for complexes with less than half of co-member proteins overlapping with CORUM this value was 77% (148 out of 191) (blue triangles). These results provide strong evidence of the ability of our method to identify biologically relevant protein complexes.

As an additional metric, Figure S9 shows the distribution of average STRING score for each complex as a function of complex score across the three complex classes. In this case, we find significantly high STRING scores (> 0.9) for 86.3% (340 out of 394) of those complexes already found in CORUM, 32.7% (247 out of 755) of complexes with at least half the member proteins overlap with a CORUM complex, and 26.2% (50 out of 191) of the predicted complexes with at most half the member proteins overlap with a CORUM complex. As expected, the majority of protein pairs in CORUM are generally characterized by high STRING scores, whereas other pairwise interactions show a more disperse pattern of STRING score values. Additionally, Figure S10 shows the distribution of the most significant p-value from enriched functional annotations (plotted as -log₁₀ (GO_P-value)) for each complex as a function of the average STRING score for the same complex across the three complex classes. In summary, these results demonstrate the ability of our method to identify high-scoring and potentially novel candidate complexes.

We also downloaded protein abundance profiles from Diedrich et al [6] and computed the Pearson’s correlation coefficient between each protein pair in the predicted complex from the expression profiles across the 54 fractions. Figure S11 reports the distribution of this coefficient for each complex as a function of complex score across the three complex classes. Only complexes for which at least 50% of its protein members had values in the expression profiles were considered. Remarkably, more than 27% (12 out of 43) of the class of predicted complexes with at least half the member proteins in CORUM show a strong correlation coefficient (> 0.6) as opposed to just 10.3% (27 out of 263) for complexes in CORUM and 3.1% (19 out of 618) for complexes where at least half of the co-member proteins overlap with a CORUM complex.

3.4. Identification of previously uncharacterized protein complexes

In order to identify new protein complexes, we first downloaded version 3.0 of CORUM and searched for protein complexes that were not included in the earlier version used for training and testing. We found three protein complexes that were predicted by our method based on CORUM version 2.0 that were subsequently added to version 3; these are summarized in Table 2. Figure 5A illustrates these complexes along with corresponding pairwise score. For example, we predicted the CCT complex comprised of seven proteins (CCT2, CCT3, CCT4, CCT5, CCT7, CCT8, CCT6A) which belongs to a family of molecular chaperones involved in protein folding, assembly and transport. As shown in Table 2, the CCT complex is assigned a complex score of 0.94 for which the most significantly enriched functional annotations include regulation of protein localization and chaperonin-containing T-complex both of which are biologically consistent with the role of this complex. Interestingly, this complex was only partially predicted (4 out of 7 protein members) in the hu.MAP database. Similarly, the mitochondrial membrane respiratory chain NADH dehydrogenase (Complex I) is correctly predicted by our method (15 out of 15 protein members) with a complex score of 0.60 while only a partial complex (5 out of 15) is found in hu.MAP. Another complex correctly predicted is the ILK-LIMS1-PARVA complex which is a complex known to play important roles in the regulation of glomerular cell behavior (complex score 0.87). It is noting that our method predicted an additional protein (RSU1) as a member of the ILK-LIMS1-PARVA complex. We next computed the average STRING score between RSU1 and the three complex members restricted to experimental sources only; the resulting score of 0.899 indicates strong support that RSU1 plays a role in this complex. In addition to finding these correct predictions for new protein complexes, we also searched the latest version of CORUM for protein members that were not listed in the earlier version. For instance, Figure 5B shows the anaphase-promoting complex, a multi-subunit ubiquitination complex involved in initiation of anaphase and exit from mitosis. In this case our method was able to capture two additional proteins (ANAPC16 and CDC26) that were not originally included in CORUM version 2.0. We also computed the experimental-derived average STRING score between ANAPC16 and CDC26 against the other members of the complex; the resulting score of 0.995 (ANAPC16) and 0.990 (CDC26) provides compelling support of the role of both proteins within this complex. Overall, these results provide evidence of the importance of incorporating orthogonal data sources such as co-expression and co-localization as means to accurately predict protein complexes.

Table 2:

Summary of predicted protein complexes that are present in the latest CORUM release (version 3.0) but were not used for training. For each predicted complex, we provide the complex name, predicted member proteins, complex score and top 3 GO functional annotations from g:Profiler along with corresponding p-value.

Complex name	Predicted complex members	Complex score	Top 3 GO annotations (p-value)
CCT complex	CCT2, CCT3, CCT4, CCT5, CCT7, CT8, CCT6A	0.94	Chaperonin-containing T-complex (2.2E-22) Regulation of protein localization to Cajal body (8.4E-22) Positive regulation of protein localization to Cajal body (8.4E-22)
ILK-LIMS1-PARVA complex	ILK, LIMS1, PARVA, RSU1	0.87	Focal adhesion (5.1E-5) Cell-substrate adhesion (5.1E-5) Cell-substrate adherens junction (5.2E-5)
Respiratory chain complex I	NDUFA7, NDUFA8, NDUFA9, NDUFA10, NDUFB1, NDUFB4, NDUFB8, NDUFS1, NDUFS2, NDUFS3, NDUFV1, NDUFS4, NDUFS8, NDUFV2, NDUFA12	0.60	NADH dehydrogenase (ubiquinone) activity (1.4E-39) NADH dehydrogenase (quinone) activity (1.4E-39) NADH dehydrogenase activity (2.3E-39)

Figure 5:

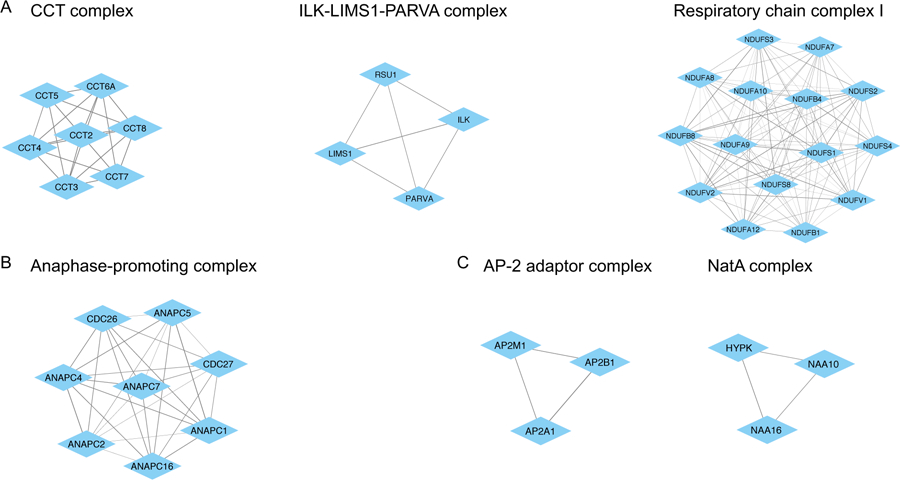
Examples of known and new complexes identified by our method. Complexes are illustrated using Cytoscape (version 3.7.1); diamond nodes represent a protein in the complex and edges represent predicted interactions (all edges presented had probability > 0.6). (A) Correctly identified protein complexes from the latest CORUM release that were not part of the earlier version of CORUM used for training. (B) Our method correctly adds novel proteins, ANAPC16 and CDC26, to a known protein complex. (C) Two new complexes identified by our method. Both are strongly supported by complementary data from GO and STRING.

Table 3 presents a subset of the top predictions by our method that are still not present in the latest version of CORUM. For example, Figure 5C shows two predicted complexes: AP2A1, AP2B1, AP2M1 with complex score of 0.88, STRING score of 0.911 and top GO annotation of AP-2 adaptor complex, and HYPK, NAA10, NAA16 with complex score of 0.80, STRING score of 0.535 and top GO term of NatA complex. Additionally, the complex comprised of proteins ARCN1, COPA, COPB1, COPB2 and COPG1 is listed in STRING as the coatomer protein complex which is a cytosolic protein complex that binds to dilysine motifs and reversibly associates with Golgi non clathrin-coated vesicles (complex score of 0.90). In addition to a significantly high average STRING score from experimental sources (0.943), this complex also shows a large minimum Pearson’s correlation coefficient (0.736) with the CaCo-2 co-fractionation data. Similarly, POLR3A, POLR3B, POLR3C, POLR3F, POLR3G and POLR3H are listed as members of the RNA polymerase III complex which is also missing from CORUM. These and other predicted complexes are strongly supported by functional enrichment analysis and STRING scores, thus, demonstrating the ability of our method to identify new complexes. A full list of predicted complexes with their scores, enrichment value, STRING scores and co-location measures is available in Supporting File 1.

Table 3:

Summary of top 25 potentially novel candidate protein complexes. For each candidate predicted complex, we list the complex members, complex score, top GO annotations from g:Profiler and their p-value, STRING score (experimental only) and minimum Pearson correlation coefficient.

Predicted complex	Complex score	Top GO annotation (p-value)	STRING score	Pearson corr. coeff. (min)
ACTR1A, DCTN4, ACTR10	0.93	Dynactin complex (3.1E-5)	0.879	-
DLAT, DLD, PDHA1	0.92	Pyruvate dehydrogenase complex (3.7E-9)	0.839	−0.199
DLAT, PDHA1, PDHB	0.92	Pyruvate dehydrogenase complex (3.7E-9)	0.895	-
ACTR1B, ACTR10, DCTN4	0.92	Dynactin complex (3.1E-5)	0.862	-
ACTR1B, DCTN1, DCTN2, DCTN4	0.91	Dynactin complex (1.1E-8)	0.855	-
ARCN1, COPA, COPB1, COPB2, COPG1	0.90	COPI vesicle coat (2.1E-14)	0.943	0.736
NUP62, NUP88, NU214	0.90	Nuclear pore (1.3E-5)	0.867	-
NSMCE1, NSMCE2, SMC5, SMC6	0.90	Smc5-Smc6 complex (2.4E-12)	0.956	-
NSMCE1, NDNL2, SMC5, SMC6	0.89	Smc5-Smc6 complex (2.4E-12)	0.957	-
POLR3A, POLR3C, POLR3F, CRCP	0.89	RNA polymerase III complex (2.1E-10)	0.856	-
ACTR1A, DCTN1, DCTN2, DCTN4, CAPZA2	0.88	Antigen processing and presentation (8.8E-8)	0.809	−0.347
POLR3A, POLR3B, POLR3C, POLR3F, POLR3G, POLR3H	0.88	RNA polymerase III complex (9.4E-17)	0.872	-
TMED2, TMED3, TMED10	0.88	COPI-coated vesicle (1.5E-7)	0.858	-
KPNA3, KPNA4, RANGAP1	0.88	Protein localization to nucleus (9.4E-4)	0.282	0.294
AP2A1, AP2B1, AP2M1	0.88	AP-2 adaptor complex (4.1E-8)	0.911	-
DCTN2, DCTN4, DCTN5	0.87	Dynactin complex (3.1E-5)	0.936	-
DCTN4, DCTN5, DCTN6	0.87	Antigen processing and presentation (5.7E-4)	0.924	-
COPA, COPB1, COPE, COPG1	0.87	COPI vesicle coat (4.9E-11)	0.943	0.857
NDNL2, NSMCE1, NSMCE2, SMC5, SMC6	0.86	Smc5-Smc6 complex (3.5E-16)	0.964	-
ARCN1, COPA, COPB1, COPB2, COPE, COPG1	0.84	COPI vesicle coat (8.7E-18)	0.944	0.736
SEC23B, SEC24A, SEC24C	0.80	6-phosphofructokinase activity (2.8E-5)	0.900	-
HYPK, NAA10, NAA16	0.80	NatA complex (3.05E-5)	0.535	0.988
CYC1, UQCRQ, UQCRQ2, UQCRFS1	0.79	Mitochondrial respiratory chain complex III (3.3E-11)	0.851	-
NHP2, NOP10, RIOK1	0.78	snRNA pseudouridine synthesis (3.9E-5)	0.222	-
COPB, PC, PFKL, PFKM	0.78	6-phosphofructokinase activity (2.8E-5)	0.292	-

4. CONCLUSIONS

We presented an approach which integrates multiple heterogeneous experiments and sources to identify potential protein complexes. In addition to using mass spectrometry experiments, gene expression measurements and protein abundance levels, we have also included sub-cellular localization annotations in our feature set. This allowed us to increase the set of potential interactions that the method can predict so that it includes all protein pairs. We next used methods for max clique discovery to combine pairs into complexes and developed new methods for further refining these complexes to avoid local minima.

Evaluation of our method on the task of predicting protein pairwise interactions improves predictive performance by close to 100% over previous methods when evaluated using all protein pairs. Additionally, we show that our two-stage method for combining pairwise interactions into protein complexes leads to a performance improvement between 19% and 50% over a recently published method. We provide multiple examples where our method correctly identifies novel additions to known complexes as well as new complexes.

In addition to validation of our method on known complexes we have also compiled a set of novel predictions. These predicted complexes do not fully overlap with known CORUM complexes, yet display many similar characteristics. In particular, several are strongly supported by significantly enriched functional annotations, as well as significant interaction-level scores derived from the STRING database or independent co-fractionation experiments on CaCo-2 cells.

While our work improved coverage and the identification of known complexes, we believe that there is still a lot of room for further improvements for protein complex prediction methods by making use of additional data sources. For example, Orre et al [27] recently performed sub-cellular fraction on more than 12, 000 proteins across multiple cell lines and conditions. We hope to use these and additional new data sources to further improve our predicted set in the future.

CCS CONCEPTS.

• Applied computing → Biological networks; Computational proteomics; Bioinformatics