Unsupervised Machine Learning Reveals Novel Traumatic Brain Injury Patient Phenotypes with Distinct Acute Injury Profiles and Long-Term Outcomes

Abstract

The heterogeneity of traumatic brain injury (TBI) remains a core challenge for the success of interventional clinical trials. Data-driven approaches for patient stratification may help to identify TBI patient phenotypes during the acute injury period as well as facilitate targeted trial patient enrollment and analysis of treatment efficacy. In this study, we implemented an unsupervised machine learning approach to identify TBI subpopulations at injury baseline using data from 1213 TBI patients who participated in the Citicoline Brain Injury Treatment Trial (COBRIT) Trial. A wrapper framework utilizing generalized low-rank models automatically selected relevant clinical features that were subsequently used to cluster patients using a partitioning around medoids clustering algorithm. Using this approach, we identified three patient phenotypes with unique clinical injury profiles based on a subset of acute injury features. Phenotype-specific differences in long-term functional outcome trajectories were respectively observed at 3 and 6 months after injury. In comparison, when patients were grouped by baseline Glasgow Coma Scale (GCS), no differences in baseline clinical feature profiles or long-term outcomes were observed. To test phenotype reproducibility in an external validation data set, we used a K-nearest neighbors algorithm to classify subjects in the Transforming Research and Clinical Knowledge in Traumatic Brain Injury (TRACK-TBI) Pilot data set into corresponding phenotypes, then measured the Gower's dissimilarities between TRACK-TBI and COBRIT subjects in each phenotype. No significant differences were found between trial subjects within two phenotypes, suggesting that these phenotypes may be generalizable within a broad range of TBI severity. Further, Extended Glasgow Outcome Scale (GOS-E) outcomes in the TRACK-TBI data set similarly demonstrated phenotype-specific differences in long-term outcomes. Our results suggest that unsupervised machine learning is a promising and effective approach for discovery of novel injury subpopulations over the conventional GCS-based method, and may improve patient selection in future TBI clinical trials.

Introduction

Traumatic brain injury (TBI) is a leading cause of death and disability in the United States, with an estimated 2,800,000 new cases annually.¹ Within the past 30 years, several promising, high-profile TBI treatments have entered late-stage clinical trials, yet none were proven to show patient benefit.^2–6 A core challenge for TBI clinical trials is the identification of patients most likely to respond to treatment, which is difficult because of the heterogeneity of TBI with respect to cause, severity, pathology, and prognosis. Currently, TBI is predominantly classified based on acute clinical symptoms. The Glasgow Coma Scale (GCS), one of the most widely used schemas to score the severity of acute brain injury, is the primary selection criteria for inclusion in most TBI trials.⁷ Based on a patient's GCS score, one may be classified as having a mild (GCS 13–15), moderate (GCS 9–12), or severe (GCS <8) injury. Although symptom scoring does play an important role in clinical management of TBI, there is consensus among TBI researchers that the GCS is not granular enough to capture the complexity of brain injury.^6,7 The limitations of the current TBI classification system imply a need for a more accurate and comprehensive schema to better stratify TBI patient subpopulations for clinical trial development and treatment.

Unsupervised machine learning is a promising method for discovery of patient phenotypes, and has previously improved classification and identification of patient subpopulations for several diseases.^8–11 Recently, unsupervised algorithms have also been applied within the context of TBI.^12–16 In this study, we employed an unsupervised machine learning approach to identify both relevant clinical variables and patient phenotypes at injury baseline using data from 1213 TBI patients who participated in the Citicoline Brain Injury Treatment Trial (COBRIT).¹⁷ Our unsupervised approach consisted of two stages within a wrapper framework wherein the first stage, generalized low-rank models (GLRMs), was used to automatically select important clinical features that were used in the second stage to cluster patients into phenotypes using a partitional clustering algorithm. To understand the clinical significance of the resulting phenotypes, patients were examined for differences in acute injury profile and long-term neurofunctional outcomes. To demonstrate reproducibility of the phenotypes, we trained a supervised K-nearest neighbors (K-NN) classifier model on the COBRIT data to predict cluster membership for subjects in the Transforming Research and Clinical Knowledge in Traumatic Brain Injury (TRACK-TBI) Pilot data set, and then examined the similarity of subjects assigned to the same cluster from each trial cohort. This study supports the use of machine learning in the development of a more comprehensive approach to TBI clinical stratification and analysis of clinical trial outcomes.

Methods

Study design

This study was approved by the Children's Hospital of Philadelphia Institutional Review Board. Analysis was conducted on data from the interventional COBRIT (NCT00545662; n = 1213 subjects) trial and the observational TRACK-TBI (NCT01565551; n = 599 subjects) study.^17–19 The data sets were sourced from the Federal Interagency Traumatic Brain Injury Research Informatics Systems.²⁰ Because experimental treatment was concluded to be ineffective over placebo in the COBRIT trial, subjects from both treatment and placebo study arms were pooled into one cohort for our study. Inclusion criteria for the COBRIT study specified that all patients be between the ages of 18 and 70 years old, been diagnosed with a non-penetrating TBI, and have a positive baseline computed tomography (CT) scan. Subjects enrolled in the TRACK-TBI Pilot study were ≥16 years of age, with an external force head trauma, and a positive baseline CT scan taken within 24 h of injury.

Data cleaning

COBRIT baseline data were acquired prior to injury or within 24 h of injury. All available baseline data were included for analysis unless otherwise indicated (Table S1). Baseline data consisted of both numerical and categorical variables (i.e., features) and included pre-injury data such as subject demographics and medical history 3 months prior to injury, and acute (< 24 h after injury) data such as mechanism of injury, CT radiology assessments, laboratory tests, physiological measurements, physician intervention, and toxicology screens. Where only the highest and lowest values were reported for physiological measurements (e.g., heart rate and blood pressure) within 24 h of injury, values were averaged into a single baseline value. All categorical features were consolidated into a maximum of three categories, based on frequency to reduce data sparsity. These categorical variables were then dummy coded into binary representations (i.e., assigned “1” if feature was present or “0” if it was absent) to allow input into the categorical hinge loss functions used in training our generalized low-rank model. The cleaned baseline data set consisted of 156 features.

Missing data were handled according to the mechanism of missingness: missing at random (MAR), missing completely at random (MCAR), or missing not at random (MNAR).^21,22 The values of data that are MCAR are independent of observed and unobserved features. Values are considered MAR if their missingness is conditional on the value of another observed feature (e.g., CT lesion volumes are conditionally reported based on the reported presence of a lesion). Features were considered MNAR if their values are suspected as missing in a biased manner because of unobserved data, as determined from the original trial case report form and trial metadata. Data considered to be MNAR were excluded from further analysis. For the remaining MAR and MCAR data, features that were missing <10% of values were imputed and used as input features for clustering analysis. Features missing 10–30% of values were imputed but not used as clustering input features. Lastly, MAR and MCAR features missing >30% of values were excluded. Number of missing values per feature is provided in Table S1. For features where missing values were imputed, we used multiple imputation with random forest completion method (multivariate imputation by chained equations [MICE] algorithm implemented in “mice” R package version 3.6).²³ For each feature with missing values, we generated five completed data sets (m = 5), each with slightly different missing value estimates. Each imputed data set was individually run through the unsupervised GLRM framework for feature selection (described subsequently), leading to m = 5 sets of selected features. In the final clustering schema, the intersection of the m feature sets was used for the final clustering analysis performed on a single data set pooled by averaging the m point estimates for each missing value.

To calculate the baseline GCS scores for subjects in the COBRIT study, we averaged the best and worst GCS values reported during the acute injury period, as these were the only GCS values reported in the raw data. GCS scores were then used to assign injury severity groups: complicated mild (GCS 13–15 with positive CT scan), moderate (GCS 8–12), and severe (GCS <8). Only one subject was missing baseline GCS scores and was dropped from the analysis. Patient outcomes were assessed using the Extended Glasgow Outcome Scale (GOS-E) primary study outcome measure, collected at 90 and 180 days after injury. The COBRIT study primary outcomes data contained missing GOS-E values at 90 (n = 263) and 180 days (n = 383) because of subjects lost to follow-up, missed follow-up visits, and death.¹⁸ Subjects whose study termination was the result of death (n = 67 at 90 days, n = 73 at 180 days, cumulatively) were assigned the GOS-E score of 1, according to the GOS-E scale.²⁴ There was no difference in the baseline GCS scores of subjects with missing and non-missing GOS-E scores (χ² = 8.11, df = 6, p = 0.43).

Feature selection and unsupervised clustering

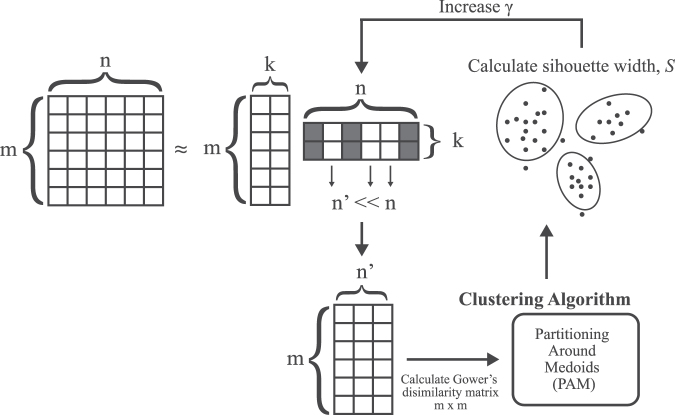
Baseline data were run through an unsupervised learning framework to simultaneously select the subset of features and tuning parameters that produced the best clusters in an iterative process (Fig. 1). To avoid overfitting, we utilized a sparse GLRM framework to select the most relevant features during our clustering analysis (GLRM implemented using R package h2o version 3.26). GLRMs can represent high-dimensional data of mixed data types (e.g., numerical and categorical) in a transformed lower-dimensional space (i.e., low-rank).²⁵ Essentially, the GLRM decomposes an m x n matrix, A, into matrices X and Y such that XY is approximately equal to A under the constraint that the number of linearly independent columns (i.e., the rank), k, in XY ≤ n. In our approach, we used a GLRM to decompose our baseline data matrix, A, composed of m rows of patients and n columns of clinical features, into matrices X and Y. The Y matrix can be viewed as a set of new features derived from the original n. The X matrix can be viewed as a lower dimensional representation of the patients composed of features represented by columns in Y. Hyperparameter k was selected to be the minimum k that captured the majority of variance in A (i.e., >50% of the total variance), balancing the sparsity of matrix Y—and in turn reducing the number of selected features to create a more parsimonious model—against fidelity. Quadratic and hinge loss functions were used to approximate numerical and binary features, respectively.²⁵ We applied an L1-norm regularization parameter to Y to reduce the size of the feature set contributing to the low rank decomposition of our data. Thus, the GLRM approximated the input data matrix A, with the following loss functions:

FIG. 1.

Diagram of the hybrid generalized low-rank model and clustering approach implemented for unsupervised learning. The full feature set with n features and m observations (i.e., traumatic brain injury [TBI] patients) is decomposed into two matrices of lower rank (i.e., dimensions), k. An L1-regularization parameter, γ, is applied to the second low-rank matrix to create a feature subset n’, of the original matrix. The n’ x m feature subset is used to calculate an m x m dissimilarity matrix of the observations and clustered using the partitioning around medoids (PAM) algorithm. The average silhouette width of the clusters is calculated for a range of 3–10 clusters in PAM. The γ parameter is increased if the average silhouette width is higher than the previous iteration and stopped when n’ is zero. The final feature subset n’ and clustering schema is selected using the γ value that yields the highest cluster silhouette width.

$$L\left(A,XY\right)=minimize\left\{\begin{array}{c}{\Sigma }_{i=1}^m{\Sigma }_{j=1}^n{\left(A_{ij}-X_i{Y}_j\right)}^2∕{\sigma }_j^2+\gamma {\Sigma }_{j=1}^n\parallel Y_j{\parallel }_1,if{A}_{ij}\in R\\ {\Sigma }_{i=1}^m{\Sigma }_{j=1}^{n}max{\left(1-A_{ij}\cdot X_i{Y}_j\right)}^2+\gamma {\Sigma }_{j=1}^n\parallel Y_j{\parallel }_1,if{A}_{ij}\in \left(0,1\right)\\ \end{array}\right..$$

where the L1-regularization parameter γ > zero. Instead of scaling the numeric features prior to the GLRM, the quadratic loss function was scaled by dividing by e variance, ${\sigma }_j^2,$ of each feature j, to compensate for unequal feature scaling. The regularization parameter, γ, produces a column-sparse matrix, Y, where the number of non-zero columns, d, is small relative to the total column number, n. A column, y_j of Y, which is all zero, signifies that feature j was uninformative in approximating matrix A, and therefore not selected for clustering analysis.^26–28

To select the smallest feature subset capable of generating well-defined patient clusters, we utilized a wrapper approach wherein features were selected by optimizing the GLRM regularization parameter, γ, based on the performance of the clustering algorithm. For a given value of γ, matrix Y in the GLRM contained d non-zero feature columns. The d features found in the GLRM, were then used to cluster patient observations. Clustering performance was assessed by calculating the average silhouette width for a given number of clusters.²⁹ The value of γ was increased until maximal silhouette width was achieved for which d > 0. For each GLRM-produced feature subset, the pairwise dissimilarities (i.e., distances) between observations in the data set were computed in a Gower's dissimilarity matrix.³⁰ Gower's dissimilarity was chosen because it can accommodate mixed feature types (i.e., continuous and categorical). The resulting dissimilarity matrix was clustered using the partitioning around medoids (PAM) clustering algorithm (PAM implemented using R package cluster, version 2.0.6).^31,32 Optimal number of clusters, k, was determined by selecting the average cluster silhouette width for k between 3 and 10. The range of values for k was chosen to consider both clinical utility and capture the maximum average silhouette width between the clusters. Specifically, we set the lower limit of k to three clusters, because that would be at least as granular as the number of injury severity groups based on GCS score (i.e., mild, moderate, severe). The upper limit was set to k = 10 from empirical demonstration that cluster silhouette width scores reached a minimum by this point. Clusters were visualized in two-dimensional space using t-distributed stochastic neighbor embedding (T-SNE) with a perplexity set at 50.³³

To ensure the reproducibility of the feature selection and stability of the clustering result, we ran a fivefold cross-validation of the data. Each fold, consisting of ∼20% of the total number of samples, was left out as a test set while the remaining observations comprised a training set used to select γ and subsequently determine the selected feature subset for each fold. The training feature subset was then used to cluster the observations in the test set, and the maximum average silhouette width score and optimal k clusters were recorded. The intersection of the features identified in each fold was used to cluster the full data set. Stability of both the training and test clusters was assessed by comparing the similarity of cluster membership between pairs of observations in the training and test sets, respectively, with their cluster membership in the full data set using the Pairwise Similarity Index (PSI). PSI was defined for two sets of clustering labels of equal length—Set A and Set B—as the number of observation pairs that belong to the same cluster in both Set A and Set B divided by the total number of observation pairs:

$$\text{Pairwise\hspace{0.17em}Similarity\hspace{0.17em}Index\hspace{0.17em}}\left(\%\right)=\frac{(\text{Same Cluster in Set A }\cap \text{Same Cluster in Set B})}{\text{Total numer of observation pairs}}*\text{\hspace{0.17em}1}00$$

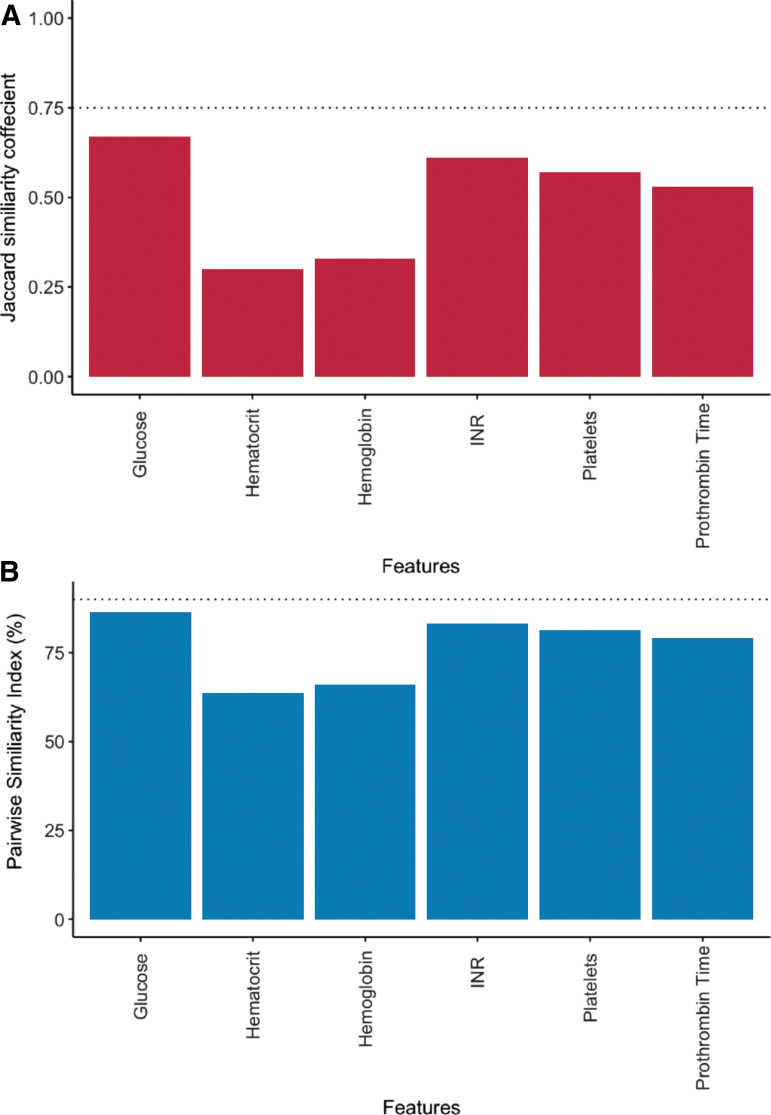
In determining the necessity of the final feature subset, both the PSI and the Jaccard similarity coefficient were calculated.³⁴ Two clustering results were considered similar if the PSI was >90%, such that 90% of observation pairs had the same relationship (i.e., belonged to the same cluster in both cluster schemas, or belonged to different clusters in both cluster schemas) and had a Jaccard coefficient >0.75, indicating that 75% of each cluster was recovered in the alternate cluster schema.³⁵ To ensure none of the selected features were redundant or non-informative to cluster formation, we tested the necessity of each feature in achieving the same clustering result. Individual features were “nullified” by randomly shuffling values among patients, essentially transforming that feature into noise. This shuffling procedure was repeated 500 times to generate a series of null feature distributions. Clustering was performed on the feature subset with the null-shuffled feature, and the likeness of the new clusters to the clusters of the full feature set was compared by measuring the mean Jaccard similarity coefficients and pairwise similarity indices, respectively (Fig. 2A, B). Features that exceeded the PSI and Jaccard similarity thresholds were excluded from the final feature set used to generate clusters.

FIG. 2.

Determining the necessity of each feature in contributing to the final cluster assignment. Feature necessity: Each feature was individually replaced with a null distribution of randomly shuffled values. The remaining features plus the null feature were then clustered upon and the similarity of the clustering result was compared with the original feature set clustering solution using two different measures: (A) the Jaccard similarity coefficient and (B) the pairwise similarity index. Any feature with a Jaccard similarity coefficient >0.75 and pairwise similarity index >90% (dotted lines) when nullified was considered unnecessary. Color image is available online.

Reproducibility of clusters in external validation data set

To assess cluster generalizability in an external validation data set, we developed a supervised K-NN classifier to determine the cluster assignments of subjects in the TRACK-TBI Pilot data set using the GLRM-selected features. Briefly, K-NN is a nonparametric algorithm in which the target class of a new observation is determined by the majority target class of the K neighboring observations used to train the model. COBRIT data were split into a training data set (80%, n = 970 subjects) and a holdout data set (20%, n = 243 subjects). Model hyperparameter K was tuned using 10-fold cross-validation on the training data for values of K between 1 and 20 (K-NN implemented using caret package in R, version 6.0-78).³⁶ The performance of the trained K-NN model was evaluated by measuring the accuracy of labeling the correct cluster in the holdout data set. The trained K-NN model was then used to predict the subtypes (i.e., cluster membership) of TRACK-TBI Pilot subjects with predictor feature data available (n = 385). To determine the resemblance of TRACK-TBI-predicted clusters to the original COBRIT-derived clusters, the pairwise Gower's dissimilarities between TRACK-TBI and COBRIT patients in the same clusters were calculated and compared between the two data sets using the cross-match test.³⁷ The cross-match statistical test is a distribution-free permutation test that compares two multivariate distributions of different sample sizes by using distances between observations. Observations are divided into pairs with the goal of minimizing the distance between observations. The cross-match statistic is defined as the number of times a subject from one group was paired with a subject from another group; small values of the statistic (i.e., fewer pairs with observations from both groups) reject the hypothesis that the observations come from the same distribution. Lastly, to determine if TRACK-TBI clusters had similar long-term recovery outcomes to COBRIT clusters, 90- and 180-day GOS-E scores for TRACK-TBI subjects were examined for inter-phenotype differences.

Statistical analysis

We assessed differences in the multivariate predictors (i.e., the GLRM-selected baseline features) of cluster membership and GCS severity group by conducting multinomial logistical regression analyses in which cluster membership was modeled as the dependent variable. The adjusted odds ratios with associated 95% confidence intervals (CI) and p values calculated from Wald tests are reported to demonstrate the magnitude of influence that each predictor feature had on cluster membership. Non-predictor numerical variables were univariately assessed for differences between clusters using the Kruskal–Wallis test with Holm's correction for multiple comparisons. Pearson's χ² test was used to compare the distribution of categorical variables by cluster. Numerical data are presented as the median and interquartile range (IQR). Statistical comparisons were considered significant when corresponding p values were <0.05 or as determined by the Holm's test statistic after correcting for multiple comparisons. All data were processed and analyzed using the R statistical programming language (R version 3.4.0) and RStudio software (version 1.0.143). The code repository used to generate study results is provided at: https://github.com/masino-lab/tbi-clusters.

Results

Unsupervised machine learning identified relevant baseline clinical features

Fivefold cross-validation of the COBRIT study baseline data identified an intersection of six features (Table 1).³⁸ The feature subset included: hematology measures such as platelet count, hematocrit, and hemoglobin levels; coagulation measures such as prothrombin time (PT) and PT international normalized ratio (INR); and blood glucose levels. Other features in the union, but not the intersection, of training sets, included partial thromboplastin time, blood pressure, heart rate, and midline shift measurement as observed in CT findings. Study treatment arm (i.e., citicoline or placebo) was not selected by the model as an important feature. Permutation shuffling of individual features demonstrated no redundancy in the selected feature subset and that each feature selected in the GLRM was necessary in generating the final clustering result (Fig. 2).

Table 1.

Fivefold Cross-Validation Results of GLRM-Wrapper Feature Selection and Clustering

	Training γ	Number of selected features d	Training k	Training SW	Training similarity index (%)	Testing SW	Testing similarity index (%)
CV Fold 1	325	7	3	0.15	70.71	0.15	69.10
CV Fold 2	331	7	3	0.14	67.36	0.14	79.80
CV Fold 3	336	6	3	0.18	71.30	0.18	69.08
CV Fold 4	340	6	4	0.14	96.69	0.14	69.92
CV Fold 5	333	6	3	0.16	66.20	0.16	76.26

For each of the m imputed data set of baseline features, observations were split into five cross-validation (CV) folds, where the observations in each fold were separately used as a test set and the remainder comprised the training set. The table reports the averaged parameter values for each CV fold across the m imputed data sets. Training observations were used to train the generalized low-rank models (GLRM) wrapper for the L1-regularization hyperparameter γ (Column 1), and consequently the number of non-zero weighted features, d (Column 2). Training and test sets with d features were individually clustered using the partitioning around medoids (PAM) algorithm and the number of clusters that yielded the maximum average silhouette width (SW) was recorded for the training set and testing sets, (training, Columns 3 and 4; test, Column 6). To assess how well pairs of observations were clustered together in each training or test set versus the full set of observations, the pairwise similarity index was calculated for all training and test sets (training, Column 5; testing, column 7).

Novel TBI phenotypes have unique clinical feature profiles

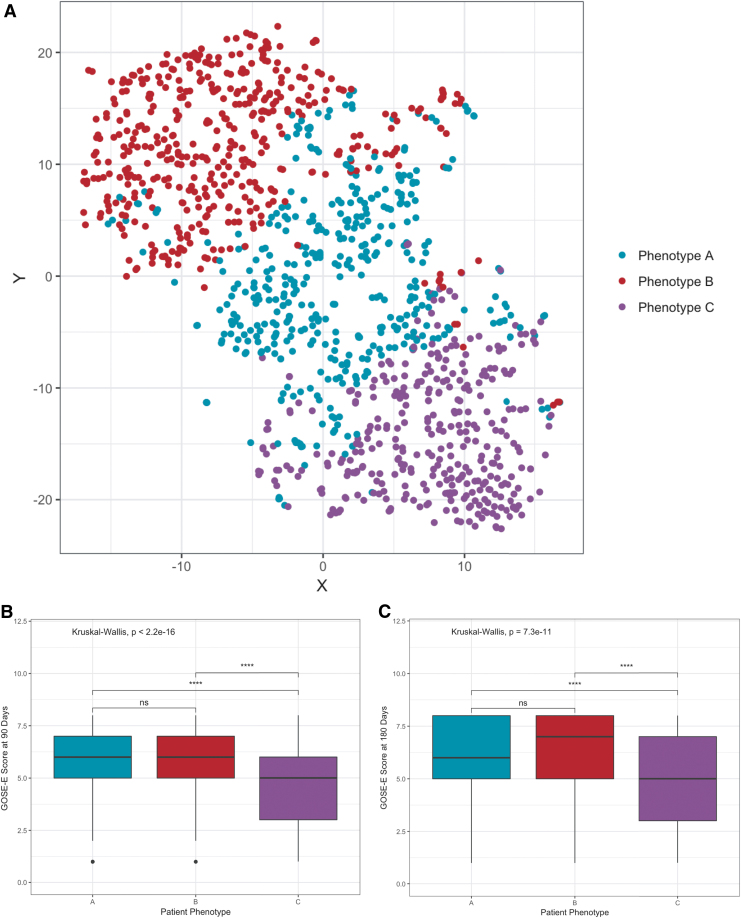
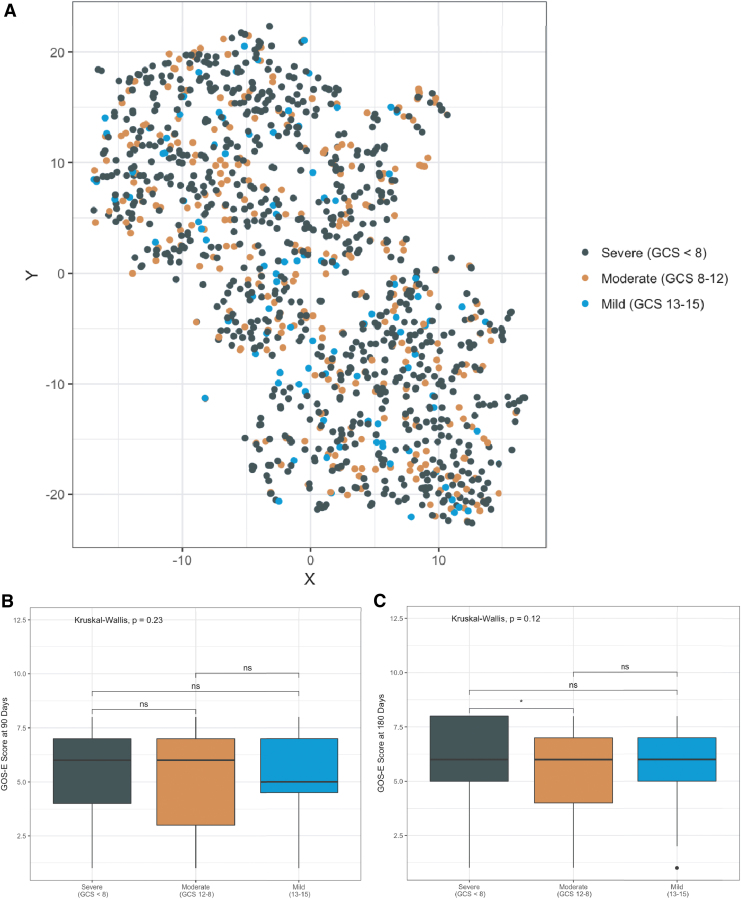
Using the six features selected from the baseline COBRIT data, three subject clusters, or phenotypes, were readily identified (Fig. 3A, maximum average cluster silhouette width = 0.193). Subjects belonged to one of three groups identified as phenotype A (n = 420), phenotype B (n = 446), and phenotype C (n = 347). Demographically, there were no differences in phenotype age, race, ethnicity, and education level distributions; however, there was a significant difference in phenotype gender distribution (p < 0.001, Table 2). To test if the original study treatment group influenced cluster membership, we examined the distribution of treatment groups in each phenotype. Here we found no association between treatment arm and cluster membership (χ² test, p = 0.79, χ² = 0.48, df = 2). Additionally, there was no significant enrichment of GCS injury severity groups (i.e., complicated mild, moderate, severe) in any of the clusters (Fig. 4A; χ² test, p = 0.76, χ² = 1.84, df = 4).

FIG. 3.

Partitional clustering reveals distinct traumatic brain injury phenotypes. (A) T-distributed stochastic neighbor embedding (T-SNE) projection of 1213 traumatic brain injury (TBI) patients from the Citicoline Brain Injury Treatment Trial (COBRIT) study, each dot representing one patient. The partitioning around medoids (PAM) clustering solution, which yielded the maximum average silhouette width, resulted in three clusters labeled phenotype A (teal, n = 420), phenotype B (red, n = 446), and phenotype C (purple, n = 347). X and Y axes denote two-dimensional (2-D) representation of six-dimensional feature space. Novel TBI phenotypes have different recovery outcome trajectories based on the Extended Glasgow Outcome Scale (GOS-E) scores at (B) 90 days and (C) 180 days post-injury. Statistical significance was computed using the Kruskal–Wallis test with Holm's correction for multiple comparisons (asterisks represent p values: ****p < 0.0001, p > 0.05 n.s.). Color image is available online.

Table 2.

Patient Demographics by TBI Phenotype

	Phenotype A	Phenotype B	Phenotype C	p value
Age (years)a
Median (IQR)	42 (29)	35 (28)	40 (31)	0.116
Subject Count (%)
18–30	144 (34%)	184 (41%)	124 (36%)
>30–45	98 (23%)	97 (22%)	76 (22%)
>45–60	124 (30%)	118 (26%)	101 (29%)
>60	54 (13%)	47 (11%)	46 (13%)
Genderb
Male	281 (67%)	403 (90%)	219 (63%)	p < 0.0001
Female	139 (33%)	43 (10%)	128 (37%)
Raceb
White	347 (83%)	369 (83%)	282 (81%)	p = 0.863
Black or African-American	61 (14%)	60 (13%)	54 (16%)
Another race	12 (3%)	17 (4%)	11 (3%)
Ethnicityb				p = 0.240
Hispanic	18 (4%)	22 (5%)	9 (3%)
Non-Hispanic	402 (96%)	424 (95%)	338 (97%)
Educationb
High school or less	203 (48%)	211 (47%)	182 (52%)	p = 0.604
Some college or trade school	142 (34%)	161 (36%)	110 (32%)
College graduate or more	75 (18%)	74 (17%)	55 (16%)

The demographic distribution of patients in each phenotype. Number of subjects in each demographic group is listed under phenotype columns as well as the percentage of the total number of patients in that phenotype group. Superscripts denote statistical test used to compute p values displayed in Column 6.

^aKruskal–Wallis test with Holm's correction for multiple comparisons used to compute p values, significance is p < 0.05.

^bPearson's χ² test used to compute p-values, significance is p < 0.05.

TBI, traumatic brain injury; IQR, interquartile range.

FIG. 4.

Baseline Glasgow Coma Scale (GCS) scores do not overlap with traumatic brain injury patient phenotypes and do not correlate with long-term outcome. (A) T-distributed stochastic neighbor embedding (T-SNE) projection of patients within a reduced feature space (same as Fig. 3) labeled by injury severity based on patients' acute GCS score. Injury severity was classified as severe (GCS <8, n = 834; dark green), moderate (GCS 9–12, n = 304; orange), and mild (defined as GCS 13–15 with an abnormal computed tomography [CT] scan, n = 75; blue). Extended Glasgow Outcome Scale (GOS-E) scores at (B) 90 days and (C) 180 days post-injury by injury severity. Statistical significance was computed using the Kruskal–Wallis test with Holm's correction for multiple comparisons (asterisks represent p values: *p < 0.05, p > 0.05 n.s.). Color image is available online.

When assessing the values of the features used to identify the phenotypes, we found that each phenotype had a unique clinical profile (Table 3). Phenotype A was predominantly characterized by mild anemia indicated by low hematocrit (median [IQR] = 37 [3], %) and hemoglobin levels (median [IQR] = 12.4 [1.2], g/dL). Phenotype B contained subjects with relatively normal hematological values, but a lower platelet count (216 [87], 1000/μL) and an elevated prothrombin time (median [IQR] = 13 [2.8] sec) compared with phenotype A. Phenotype C had the most severe clinical profile, with abnormal feature values indicative of thrombocytopenia, anemia, and coagulopathy. To understand feature differences among phenotypes, we performed a multinomial logistical regression analysis (Table 3). In comparison with phenotype C, phenotype A was more likely to have higher hematological values (platelets, hemoglobin, hematocrit) but shorter prothrombin time and lower glucose levels. Additionally, no difference in INR was demonstrated (adjusted odds ratio [95% CI]: 0.72 (0.44–1.18), p = 0.19). Likewise, compared with phenotype C, phenotype B was significantly likely to have higher hematological values, lower coagulation measurements, and no difference in blood glucose (Adjusted odds ratio [95% CI]: 0.99 [0.98–1.0], p = 0.13). For comparison, we examined the same feature profiles when patients were grouped by their GCS score (Table 4). Interestingly, no significant differences were detected between the severe and the complicated mild severity groups, except that the complicated mild group had lower INRs (adjusted odds ratio [95% CI]: 4.37 [1.101–7.42], p = 0.04). Platelet count was also higher in the moderate group than in the complicated mild group (adjusted odds ratio [95% CI]: 1.00 [1.00–1.01], p = 0.03). Overall, this suggests that GCS scoring cannot detect differences in these baseline clinical feature profiles.

Table 3.

Baseline Feature Values by TBI Phenotype

	Phenotype A	Phenotype B	Phenotype C	Phenotype A vs. phenotype C adjusted OR (95% CI)		Phenotype B vs. phenotype C adjusted OR (95% CI)
Clinical feature	Median (IQR)	Median (IQR)	Median (IQR)		p value		p value
Platelet count (1000/μL)	226 (74)	216 (87)	163 (76)	1.02 (1.01–1.03)	< 0.0001	1.02 (1.01–1.03)	< 0.0001
Hemoglobin (g/dL)	12.4 (1.2)	14.4 (1.4)	10.1 (2.0)	5.76 (4.61–7.19)	< 0.0001	6.48 (4.38–9.58)	< 0.0001
Prothrombin time (sec)	11 (3.0)	13 (2.8)	14.6 (3.1)	0.48 (0.4–0.56)	< 0.0001	1.58 (1.26–1.97)	< 0.0001
INR	1.1 (0.1)	1.1 (0.1)	1.2 (0.2)	0.72 (0.44–1.18)	0.19	0.001 (0.0002–0.02)	< 0.0001
Hematocrit (%)	37 (3)	42.5 (3)	32 (4.5)	1.73 (1.62–1.85)	< 0.0001	6.75 (5.94–7.67)	< 0.0001
Glucose (mg/dL)	127 (36)	128 (36)	145 (43)	0.99 (0.98–0.99)	0.0004	0.99 (0.98–1.0)	0.13

(Columns 1–3) The median and interquartile range (IQR) of GLRM-selected baseline features in each phenotype, respectively. (Columns 4, 6) Multinomial logistical regression was used to calculate the adjusted odds ratio (OR) and 95% confidence intervals (CI) for the likelihood of phenotype membership based on the GLRM-selected predictor features, where phenotype C is the reference outcome variable. (Columns 5,7) Wald tests were used to calculate p values for each regression coefficient (p < 0.05 considered significant, bold font).

TBI, traumatic brain injury; INR, international normalized ratio; GLRM, generalized low-rank models.

Table 4.

Baseline Feature Values by Baseline GCS Injury Severity Category

	Severe (GCS score ≤8)	Moderate (GCS score 9–12)	Complicated mild (GCS score 13–15)	Severe vs. complicated mild adjusted OR (95% CI)		Moderate vs. complicated mild adjusted OR (95% CI)
Clinical feature	Median (IQR)	Median (IQR)	Median (IQR)		p value		p value
Platelet count (1000/μL)	206 (93)	209 (83)	206 (82)	1.00 (0.99–1.08)	0.07	1.00 (1.00–1.01)	0.03
Hemoglobin (g/dL)	12.6 (3)	12.5 (3.1)	12.7 (3.2)	0.94 (0.82–1.08)	0.37	0.94 (0.81–1.10)	0.43
Prothrombin time (sec)	13.1 (3.8)	13.1 (3.3)	12.4 (3.3)	1.00 (0.89–1.13)	0.92	1.06 (0.93–1.20)	0.40
INR	1.1 (0.20)	1.1 (0.15)	1.05 (0.12)	4.37 (1.10–17.42)	0.04	1.15 (0.26–5.01)	0.85
Hematocrit (%)	38 (7)	38 (6.5)	38 (6.5)	1.05 (1.00–1.11)	0.05	1.03 (0.98–1.09)	0.24
Glucose (mg/dL)	132 (41)	136 (40)	132 (30)	1.00 (0.99–1.01)	0.65	1.00 (0.99–1.01)	0.24

Patients were divided into the injury severity groups complicated mild, moderate, and severe based on average acute Glasgow Coma Scale (GCS) score (< 24 h after injury). (Columns 1–3) The median and interquartile range (IQR) of GLRM-selected baseline features in each phenotype, respectively. (Columns 4, 6) Multinomial logistical regression was used to calculate the adjusted odds ratio (OR) and 95% confidence intervals (CI) for the likelihood of phenotype membership based on the GLRM-selected predictor features, where the complicated mild injury severity group is the reference outcome variable. (Columns 5, 7) Wald tests were used to calculate p values for each regression coefficient (p < 0.05 considered significant, bold font).

INR, international normalized ratio; GLRM, generalized low-rank models.

Although the GLRM-selected features hold clinical relevance for classifying new patients into a phenotype, we wanted to investigate whether baseline phenotypes also held information on TBI explicitly. To explore this, we looked at the subset of baseline features specific to TBI, including CT scan findings and injury event information (mechanism, time of injury). Several TBI features demonstrated phenotypic differences (Table 5). These features included several CT findings including hemorrhage, midline shift, lesions, and cistern abnormalities, as well as mechanism of injury. Of these features, phenotype A was primarily characterized by a high incidence of abnormal mesencephalic cisterns (30% of subjects) but a low incidence of intraventricular hemorrhage (IVH) (11%.). Phenotype B had a similar incidence rate of IVH (11%) and abnormal cisterns (23%), but had a higher prevalence of subdural lesions present in the supratentorial region (16%). The most severe TBI signature was seen in phenotype C, which had high rates of IVH (24%), abnormal mesencephalic cisterns (47%), and midline shift measurements >5 mm (15%). In summary, hemorrhage and subcortical/cisternal abnormalities, as well as injury mechanism, defined the TBI-specific differences among baseline phenotypes.

Table 5.

Differences in the Occurrence of TBI-Specific Features among Baseline Phenotypes

TBI specific feature	Phenotype A	Phenotype B	Phenotype C	p value
Intraventricular hemorrhage	11% (48)	11% (50)	24% (84)	< 0.0001
Lesion anatomical sites
Intraparietal lesion in brainstem/diencephalon/corpus callosum	4% (18)	2% (11)	6% (22)	0.026
Subdural lesion in left supratentorial region	9% (39)	16% (73)	17% (58)	0.002
Abnormal mesencephalic cisterns	30% (127)	23% (102)	47% (162)	< 0.0001
Mechanism of injury
Motor vehicle	56% (236)	44% (195)	68% (235)	< 0.0001
Fall	31% (129)	35% (158)	26% (91)
Other	13% (55)	21% (93)	6% (21)
Midline shift
No shift	79% (330)	81% (362)	73% (252)	< 0.0001
0–5 mm shift	16% (67)	16% (70)	12% (43)
6–10 mm shift	4% (18)	2% (11)	10% (36)
> 10 mm shift	1% (5)	0.6% (3)	5% (16)

(Column 1) The subset of TBI-specific features that demonstrated significant differences in the frequency of patients in each phenotype presenting with these features. Radiology assessment findings on CT scan: presence of intraventricular hemorrhage, anatomical locations of lesions, and abnormal status of mesencephalic cisterns (abnormal status defined as blood-filled, compressed, or obliterated cisterns). Injury information: mechanisms of injury including motor vehicle accidents, falls, and other mechanisms, including assault and sports-related injuries. (Columns 2–5) The percentage and number of patients (expressed in parentheses) in each phenotype who presented with the selected TBI-related features. (Column 6) Statistically significant p values (p < 0.05) determined using Pearson's χ² test.

TBI, traumatic brain injury; CT, computed tomography.

TBI phenotypes have different long-term outcome trajectories

To determine the clinical utility of our patient phenotypes, we compared long-term functional outcomes at 90 and 180 days after injury using the GOS-E, the primary outcome measure chosen in the original COBRIT study. At 90 days, there were significant differences in phenotype GOS-E scores (Kruskal–Wallis χ² = 84.08, p < 0.0001, and Fig. 3B). Patients in phenotypes A and B exhibited the best overall GOS-E scores (phenotype A: median [IQR] = 6 [2]; phenotype B: median [IQR] = 6 [2], p = 0.13). Conversely, patients in phenotype C had the poorest 90-day GOS-E scores (median [IQR] = 5 [3]). Additionally, we measured the effect size of 90-day GOS-E scores to assess the magnitude of outcome differences among phenotypes. Between phenotypes A and B, the effect size was negligible (Cohen's d: −0.149, 95% CI: −0.297– −0.0004). There was a medium effect size between phenotypes A and C (Cohen's d: 0.533, 95% CI: 0.378–0.687) and phenotypes B and C (Cohen's d: 0.719, 95% CI: 0.561–0.877). Respectively, these effect sizes correspond to a 65% chance that a subject in phenotype A, and a 69% chance that a subject in phenotype B will have a more favorable 90-day GOS-E score than a randomly selected subject in phenotype C.

This phenotypic trend in outcomes persisted at 180 days after TBI (Kruskal–Wallis χ² = 46.69, p < 0.0001). At 180 days after injury baseline, the effect size between phenotypes A and B remained negligible (Cohen's d: −0.175, 95% CI: −0.331 – −0.018). Interestingly, the effect size between phenotypes B and C remained of medium magnitude (Cohen's d: 0.572, 95% CI: 0.404–0.739), whereas the effect size between phenotypes A and C was reduced at this time point (Cohen's d: 0.380, 95% CI: 0.217–0.543). This signifies that there is a smaller chance (60%) that a subject in phenotype A will have more favorable outcome (i.e., higher GOS-E score) than a subject in phenotype C at 180 days after injury. No significant differences in GOS-E scores at either 90 or 180 days after injury were observed when subjects were grouped by baseline GCS scores (90 days: Kruskal–Wallis χ² = 0.93, p = 0.63 [Fig. 4B]; 180 days: Kruskal–Wallis χ² = 0.93, p = 0.65).

COBRIT phenotypes demonstrate generalizability in the TRACK-TBI Pilot data set

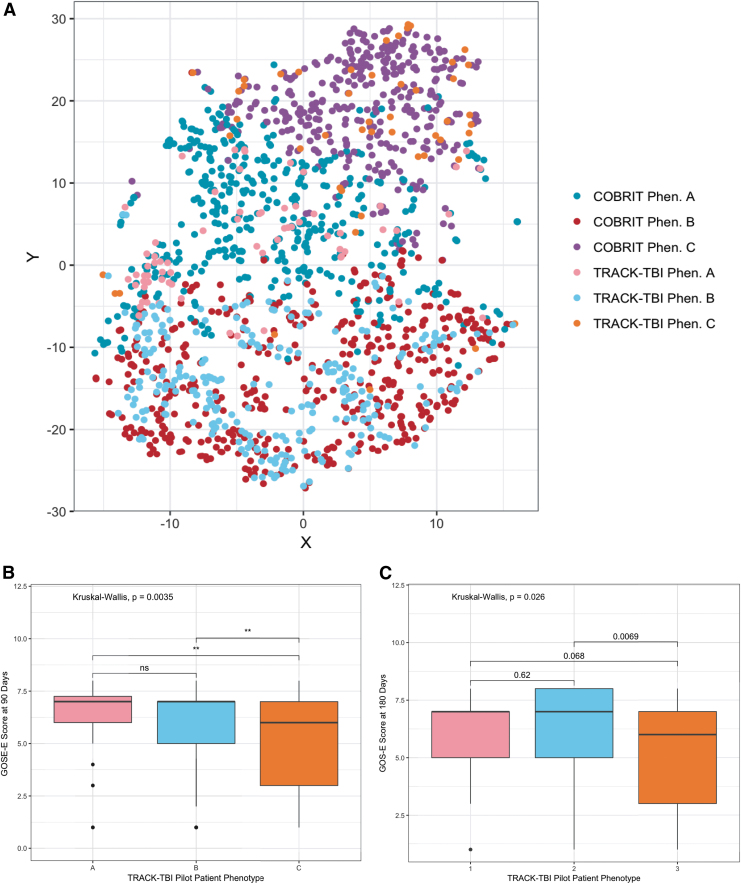
In order to test the reproducibility of the patient phenotypes found using the COBRIT study data, we performed a supervised learning analysis to classify subjects in the TRACK-TBI data set into phenotypes and examined their similarity with subjects in each COBRIT phenotype. A K-NN multi-class classifier was trained on 80% of the COBRIT data (n = 971) to predict the phenotype of each observation. Tenfold cross-validation determined the optimal number of nearest neighbors to be K = 19. Accuracy on the remaining 20% of the COBRIT data in the holdout set was 92.2% overall (95% CI: 88–95.2%; Accuracy for individual phenotypes: A = 89.3%, B = 96.6%, C = 90%). The resulting K-NN model was then utilized to predict the cluster assignments of TRACK-TBI Pilot subjects (n = 385) based on the six GLRM-selected features originally used to generate the clusters. As a result, 68 subjects were assigned to phenotype A, 268 subjects to phenotype B, and 49 subjects to phenotype C. To examine the similarity of TRACK-TBI subjects and COBRIT subjects assigned to each phenotype, Gower's pairwise dissimilarity matrices were calculated for subjects in each phenotype (i.e., measurement of how similar subjects within a given phenotype are to each other, Fig. 5A) and subsequently compared using a cross-match permutation test to determine if TRACK-TBI and COBRIT subjects in each phenotype belonged to the same distribution based on the Gower's distance between observations. TRACK-TBI Pilot subjects in phenotypes B and C were not significantly different from COBRIT subjects in each respective phenotype (phenotype B: cross-match statistic = 164, p = 0.34; phenotype C: cross-match statistic = 41, p = 0.25). However, TRACK-TBI Pilot subjects were significantly different from COBRIT subjects in phenotype A (cross-match statistic = 52, p = 0.03), suggesting that phenotype A may not generalize to an external data set.

FIG. 5.

Transforming Research and Clinical Knowledge in Traumatic Brain Injury (TRACK-TBI) Pilot subjects classified into phenotypes demonstrate similar injury profiles and Extended Glasgow Outcome Scale (GOS-E) outcomes as Citicoline Brain Injury Treatment Trial (COBRIT) phenotype subjects. (A) T-distributed stochastic neighbor embedding (T-SNE) projection of the original COBRIT subject phenotypes (COBRIT Phen. A, Phen. B, Phen. C) with the addition of TRACK-TBI Pilot subjects given phenotype assignments by a K-nearest neighbors (K-NN) classifier (TRACK-TBI Phen. A, Phen. B, Phen. C). TRACK-TBI phenotype extended GOS-E scores at (B) 90 days and (C) 180 days post-injury significance was computed using the Kruskal–Wallis test with Holm's correction for multiple comparisons (asterisks represent p values: **p < 0.01, p > 0.05 n.s.). Color image is available online.

Further, TRACK-TBI phenotypes also demonstrated similar correlations with 90- and 180-day GOS-E scores. At 90 days after injury, phenotypes A and B exhibited the highest GOS-E scores (Fig. 5B; phenotype A median [IQR] = 7 [1.25], phenotype B median [IQR] = 7 [2]) with phenotype C demonstrating significantly poorer GOS-E scores (median [IQR] = 6 [4], Kruskal–Wallis, p = 0.0035). Although the effect size was negligible between TRACK-TBI subjects in phenotypes A and B (Cohen's d: 0.069, 95% CI: −0.228–0.365), there was a medium effect size between phenotypes A and C (Cohen's d: 0.617, 95% CI: 0.193–1.040) and phenotypes B and C (Cohen's d: 0.575, 95% CI: 0.227–0.923). Like COBRIT phenotypes, TRACK-TBI phenotypic differences in GOS-E scores persisted at 180 days post-injury (p = 0.023). The effect size decreased slightly between phenotypes A and C (Cohen's d: 0.310, 95% CI: −0.133–0.754); however, a medium effect size between phenotypes B and C remained at 6 months post-injury (Cohen's d: 0.520, 95% CI: 0.160–0.881). This suggests that TRACK-TBI phenotypes A and B also have a similar likelihood of favorable GOS-E outcome scores as COBRIT subjects. In all, these findings demonstrate the generalizability of the TBI baseline phenotypes discovered using an unsupervised learning approach to an external data set.

Discussion

The heterogeneity of TBI has been a core challenge for clinical trials. Classifying TBI patients by symptom scoring, such as GCS, does not fully capture the spectrum of injury heterogeneity and leaves a critical need for more precise methods of patient stratification. In this study, we identified three TBI patient phenotypes using unsupervised machine learning. Each patient phenotype was found to possess a unique baseline feature profile that corresponded to phenotype-specific differences in long-term functional outcome. Comparatively, when patients were categorized by their baseline GCS score, these groups did not demonstrate distinct feature profiles and did not correlate with long-term patient outcomes. Further, when new subjects in the TRACK-TBI Pilot data set were classified into the phenotypes, there was no difference in the injury profiles of TRACK-TBI subjects and COBRIT subjects within phenotypes B and C. These results suggest that the novel patient phenotypes discovered using our unsupervised clustering approach are largely reproducible in an external data set and may significantly improve the precision and value of TBI classification over the current GCS-based standard.

Generalized low-rank models have demonstrated broad utility in identifying patient subpopulations based on electronic health record data.³⁹ Instead of clustering on latent features (e.g., principal components), which adds a layer of abstraction to the original features, we used a regularized GLRM to identify features with non-zero weights in the low-rank representation, and then clustered patients on the original values of these features. This methodology is novel for its implementation of a GLRM for feature selection within a wrapper framework, and facilitates simultaneous unsupervised dimensionality reduction and clustering. By clustering on the original features and not latent feature representations, the results of our model have clinical interpretability, as well. GLRM feature selection demonstrated robustness in selecting non-redundant features as the cluster schema, and membership did not change significantly when individual features were randomly shuffled during permutation testing. Lastly, two phenotype groups determined by PAM clustering were reproducible such that when new observations from the TRACK-TBI Pilot data set were classified into phenotypes using K-NN, they did not differ significantly from COBRIT observations in the corresponding phenotype. Reproducibility of phenotype membership in the TRACK-TBI data set is a significant finding, because the TRACK-TBI Pilot study is observational and also contains a higher proportion of subjects with mild TBI than is present in the COBRIT cohort.¹⁹ This demonstrates that the phenotypes found using our GLRM-clustering approach can generalize to a wider TBI severity range more indicative of the broader TBI population.

It is promising that the GLRM-selected features used in unsupervised clustering support clinical intuition and are associated with phenotypic TBI signatures. For example, several coagulation and hematological features were identified as important for clustering. Coagulopathy is common in TBI patients and can occur from blood loss and hemodilution secondary to fluid resuscitation and is also associated with poor outcomes.^40–42 Phenotype C had the lowest median values of hematocrit, hemoglobin, and platelet counts, as well as elevated prothrombin time and INR. This suggests that this group contains patients with severe coagulopathy or bleeding abnormalities associated with their TBI, and may also indicate additional extracranial injuries.⁴³ This was corroborated by phenotype C's TBI signature of intraventricular hemorrhage, cisternal damage and severe midline shift. Likewise, hyperglycemia in this phenotype is indicative of activation of the sympathetic stress response that commonly occurs following TBI. Hyperglycemia can also signify a reactive response to cellular metabolic dysfunction and has been linked to coagulopathy in some TBI patients.⁴⁴ Phenotype A had relatively normal coagulation measures, which also corresponds with its low rates of hemorrhage. Additionally, subjects in phenotype A had injuries characterized by mild anemia and a high prevalence of abnormal mesencephalic cisterns from CT findings. Phenotype B similarly had normal hematological laboratory values, but had abnormal coagulation as evidenced by the elevated prothrombin time, and higher incidence of subdural lesions. The clinical feature characteristics of both phenotypes A and B indicate that subjects in these phenotypes presented with milder injury severity than phenotype C, but are separated by signs of anemia and coagulation, respectively.

Not surprisingly, based on their baseline clinical profiles, patients in phenotype A and B had the best long-term functional outcomes, and phenotype C had the worst outcomes at 90 and 180 days after injury. These outcomes correlate with the inferred level of severity given feature values indicative of coagulopathy and hemorrhage. Phenotypes A and B had similar GOS-E outcomes, which were significantly higher than phenotype C. This suggests that subjects in phenotypes A and B have a milder injury severity profile that can achieve similar neurorecovery, regardless of presenting with different pathophysiological feature values at baseline.

In contrast, grouping by GCS score provided no correlation with long-term outcome recovery or baseline feature profiles. This suggests that the novel phenotypes discovered here may possess greater clinical utility for stratifying TBI patients and selecting appropriate clinical trial cohorts than GCS scores.⁷ Although the GCS remains important for assessing neurological state, our results suggest that it is not a useful measure for TBI stratification, especially when used as the primary measure for trial inclusion/exclusion criteria. Here, we provide a viable alternative classification approach that can be further developed for practical use.

The recovery of subjects with similar feature values in the TRACK-TBI Pilot data set, as demonstrated by Gower's distance, demonstrates that phenotypes B and C defined by unsupervised clustering analysis can generalize to the wider TBI population. We were surprised to find that phenotype A was irreproducible in the TRACK-TBI data set. By examining the overlay of cluster assignments in the T-SNE plot in Figure 5A, it seems that there is a subset of TRACK-TBI subjects assigned to phenotype A (pink points, left side of plot) which are closer to phenotype B, suggesting that a subset of subjects assigned to phenotype A in TRACK-TBI perhaps would be more appropriately grouped with phenotype B. This could occur as a result of phenotype misclassification by the K-NN classifier for these subjects, possibly because phenotype A shares many commonalities with phenotype B in baseline feature values (e.g., INR and glucose) and as demonstrated by similar GOS-E outcome scores. Follow-up analysis in additional external data sets may provide understanding of whether phenotype A is a “true” phenotype present in the population or if subjects from phenotype A would be more appropriately consolidated into phenotype B.

Our study has two major limitations. First, both the COBRIT and TRACK-TBI Pilot subjects had a TBI-positive CT scan, as this was an inclusion criterion set in both studies. Therefore, we do not know how the phenotypes here will generalize to patients experiencing TBI symptoms who did not have a CT scan positive for brain injury. However, the use of clinical trial data aligns with our objective to facilitate future clinical trial enrollment and the types of TBI cases seen in a critical care setting. Additionally, the relationship between phenotype feature profiles and long-term patient outcomes is only correlative in this study. In future studies, we plan to investigate the causal relationship between phenotype features and long-term outcomes as well as integrate these findings into a supervised machine learning model to predict TBI prognosis.

Conclusion

In summary, our results demonstrate that unsupervised machine learning holds significant value in identifying novel TBI phenotypes and important clinical features. With further development, we anticipate that data-derived patient phenotypes will enhance TBI patient stratification in clinical trials beyond the GCS-based gold standard, and ultimately provide clinicians with more detailed information to acutely manage TBI cases.

Data and Materials Availability

Data used in the preparation of this manuscript were obtained and analyzed from the controlled access data sets distributed from the Department of Defense (DOD)- and NIH-supported Federal Interagency Traumatic Brain Injury (FITBIR) Informatics Systems. FITBIR is a collaborative biomedical informatics system created by the DOD and the NIH to provide a national resource to support and accelerate research in TBI. Dataset Identifier: FITBIR-STUDY0000240. This manuscript reflects the views of the authors and may not reflect the opinions or views of the DOD, NIH, or those submitting the original data to FITBIR Informatics System.

Funding Information

This project was funded by the Department of Anesthesiology and Critical Care at the Children's Hospital of Philadelphia and the Children's Hospital of Philadelphia Research Institute (A.J.M) as well as by National Institutes of Health (NIH) R37 HD059288 (A.S.C).

Author Disclosure Statement

No competing financial interests exist.

Supplementary Material

Supplementary Table S1