Effect of ceramic infrastructure on the failure behavior and stress distribution of fixed partial dentures

Abstract

Objectives

the effect of the ceramic infrastructure (IS) on the failure behavior and stress distribution of fixed partial dentures (FPDs) was evaluated.

Methods

Twenty FPDs with a connector cross-section of 16 mm² were produced for each IS and veneered with porcelain: (YZ) Vita In-Ceram YZ/Vita VM9 porcelain; (IZ) Vita In-Ceram Zirconia/Vita VM7 porcelain; (AL) Vita In-Ceram AL/Vita VM7 porcelain. Two experimental conditions were evaluated (n=10). For control specimens, load was applied in the center of the pontic at 0.5 mm/min until failure, using a universal testing machine, in 37°C deionized water. For mechanical cycling (MC) specimens, FPDs were subjected to MC (2 Hz, 140 N, 10⁶ cycles) and subsequently tested as described for the control group. For YZ, an extra group of 10 FPDs were built with a connector cross-section of 9 mm² and tested until failure. Fractography and FEA were performed. Data were analyzed by ANOVA and Tukey’s test (α=0.05).

Results

YZ16 showed the greatest fracture load mean value, followed by YZ16-MC. Specimens from groups YZ9, IZ16, IZ16-MC, AL16 and AL16-MC showed no significant difference for the fracture load.

Significance

The failure behavior and stress distribution of FPDs was influenced by the type of IS. AL and IZ FPDs showed similar fracture load values but different failure modes and stress distribution. YZ showed the best mechanical behavior and may be considered the material of choice to produce posterior FPDs as it was possible to obtain a good mechanical performance even with a smaller connector dimension (9 mm²).

Introduction

The introduction of CAD/CAM (computer-aided design/computer-aided machining) technology in dentistry and the development of ceramics with high crystalline content increased the range of application of all-ceramic restorations [1, 2]. High-crystalline content ceramics, such as yttria stabilized tetragonal zirconia polycrystal (Y-TZP), alumina-based zirconia-reinforced glass-infiltrated ceramic (IZ) and polycrystalline alumina (AL), show higher fracture toughness values than those reported for glass-based materials [3], justifying their indication to produce all-ceramic fixed partial dentures (FPDs) [1, 2].

On the other hand, as these ceramics show different chemical compositions and microstructure, different physical and mechanical properties are expected [3–5], which could influence the long-term clinical behavior of the restorations [2]. Clinical trials on zirconia-based all-ceramic FPDs reported infrastructure failure rates as low as 6%. In these studies, most clinical failures were related to chipping of the porcelain veneer and secondary caries, which are not infrastructural failures. Yet, the follow-up periods for these clinical studies are still relatively short, varying from 2 to 5 years [6–10]. One study successfully followed up three to five-unit Y-TZP FPDs for 10 years and reported a survival rate of 91.5% for the zirconia infrastructures [11]. For all-ceramic FPDs, the probability of failure is related to the properties of the ceramic systems, the size and shape of the connectors, the span of the pontic and to the position in the oral cavity [11–15]. FPDs most commonly fail from flaws located in the connector cervical area, where a higher stress concentration is produced during chewing [12, 16, 17].

Clinical studies provide reliable information on the longevity and failure behavior of dental restorations; however they are not easily carried out. On the other hand, laboratory tests and computer modeling represent more efficient research tools to obtain data on the stress distribution and failure behavior of dental prostheses [12, 16]. Caution should be taken to guarantee that in vitro experiment properly simulates the clinical situation in all of its complexity [18]. The influence of the restoration configuration (multi-layer system) and its geometry in the stress distribution needs to be determined in order to better understand the long term behavior of all-ceramic prostheses. In vitro set-ups should take into account the processing steps used to produce dental restorations as to obtain the same flaw population leading to clinical failures [12, 19]. Therefore, a more reliable prediction of the failure behavior of ceramic restorations could be obtained through in vitro evaluation of specimens that reproduce the shape of dental restorations, such as crowns and fixed partial dentures (FPDs).

In vitro tests should also simulate the loading and environmental conditions observed in the oral cavity [18]. Cyclic loading, as observed during chewing, contributes to the subcritical crack growth (SCG) of ceramic materials [20]. Ceramic lifetime may be overestimated when predictions are based only on static load and fracture toughness data, without considering the effect of cyclic loading [20–22]. When a ceramic material is subjected to a long period of intermittent stresses in a humid environment, below the critical stress level (<K_Ic) but above a threshold stress level (≥K_I0), pre-existing flaws may grow slowly in areas of stress concentration or near the surface. When these pre-existing flaws reach a critical size due to continue loading, the mechanical capacity of the material is exceeded, resulting in catastrophic failure [23]. Under subcritical conditions, the initial flaw size distribution changes as a function of time, according to each material susceptibility to SCG. Thus, a different failure mode may occur for a prosthesis subjected to mechanical cycling in comparison to fast fracture [15].

The purpose of this study was to evaluate the effect of the ceramic infrastructure on the fracture load, failure mode and stress distribution of three-unit FPDs. This study tested the hypotheses that (1) the infrastructural material influences the failure behavior and stress distribution of FPDs and (2) the mechanical cycling effect on the fracture load of FPDs varies with the type of ceramic infrastructure.

Materials and Methods

Specimen Fabrication

FPDs were produced using three high crystalline-content infrastructure ceramics veneered with the recommended porcelain, as follows:

• YZ- An yttria partially stabilized tetragonal zirconia polycrystal (Y-TZP) infrastructure (IS) (Vita In-Ceram YZ, Vita Zahnfabrik, Bad Sackingen, Germany) veneered with a porcelain (Vita VM9, Vita Zahnfabrik, Bad Sackingen, Germany);

• IZ- A glass infiltrated zirconia-reinforced alumina-based ceramic IS (Vita In-Ceram Zirconia, Vita Zahnfabrik, Bad Sackingen, Germany) veneered with a porcelain (Vita VM7, Vita Zahnfabrik, Bad Sackingen, Germany);

• AL- An alumina polycrystal IS (Vita In-Ceram AL, Vita Zahnfabrik, Bad Sackingen, Germany) veneered with a porcelain (Vita VM7, Vita Zahnfabrik, Bad Sackingen, Germany).

Stainless steel models simulating prepared abutment teeth were constructed with 4.5 mm height, 6° of taper and 120° chamfer as finish line [24]. The distance between the centers of the dies was 16 mm, corresponding to the distance between a lower second premolar and a lower second molar (span of 10 mm). An artificial gingiva was produced with acrylic resin (JET, Classico, Sao Paulo, SP, Brazil). Polyvinyl siloxane impressions of the model were taken (Aquasil^™, Dentsply, Petropolis, RJ, Brazil) and a working cast was made using type IV special CAD/CAM stone (CAM-base, Dentona AG, Dortmund, Germany).

The stone cast was digitized by the internal laser scanner component of CEREC inLab unit (Sirona Dental Systems, Charlote, NC, USA) to generate a tridimensional image that was used to design the FPDs infrastructures from YZ, IZ and AL ceramic systems. After the milling process, YZ and AL infrastructures were sintered using the Zyrcomat furnace (Vita Zahnfabrik, Bad Sackingen, Germany), and IZ infrastructures were glass infiltrated (Z21N Zirconia Glass Powder, Vita Zahnfabrik, Germany) using the Inceramat 3 furnace (Vita Zahnfabrik, Bad Sackingen, Germany), according to the manufacturer’s instruction. The excess glass was removed with airborne particle abrasion using 50-μm aluminum oxide particles. Only the external surface of the infrastructures was air abraded.

The infrastructures were veneered with the recommended porcelain, which were sintered using a Keramat I furnace (Knebel, Porto Alegre, Brazil) according to the cycle provided by the manufacturer. Before veneering, a bonding agent (Effect Bonder, Vita Zahnfabrik, Bad Sackingen, Germany) was applied on the YZ infrastructures and sintered according to the manufacturer instructions. Three porcelain applications were performed and a polishing bur was used to obtain a uniform thickness of, approximately, 1.2 mm around the crowns and pontic and 0.6 mm around the connectors. The porcelain thickness was measured at six different points as proposed by Sundh et al. (2005) [24]. Finally, all FPDs were subjected to a glaze cycle using Keramat I furnace at 900°C for 1 min with a rate of 80°C/min and slow cooling (~6 min).

The FPDs were cleaned in a sonic bath with distilled water for 15 min and cemented in the metal dies with zinc phosphate cement (Cimento de Zinco, SS White, RJ, Brazil), following the manufacturer’s instructions. A cementation device was used to apply a uniform pressure of 15 N for 10 min in the FPD occlusal surface aiming to guarantee an adequate fit in the dies.

Twenty FPDs with a connector cross-section area of 16 mm² (5.0 mm high × 4.2 mm thickness) were produced for each IS material. This connector dimension was chosen based on the manufacturer indication for an IZ FPD with 16 mm span. In addition, for YZ, an extra group of 10 FPDs were built with a connector cross-section area of 9 mm² (3.6 mm high × 3.1 mm thickness), following the manufacturer’s recommendation for a YZ FPD with 16 mm² span. The experimental groups are described in Table 1.

Table 1.

Description of the experimental groups (n=10).

Connector	Mechanical Cycling	Materials
		YZ	IZ	AL
9 mm2	no	YZ9	-	-
16 mm2	no	YZ16	IZ16	AL16
	yes	YZ16-MC	IZ16-MC	AL16-MC

Fracture Load and Fractography

The fracture load of 16 mm² connector FPDs was evaluated in two experimental conditions (n=10):

1. Control: the fracture load was evaluated using a universal testing machine (MTS, MTS Systems Corporation, MN, USA) in 37°C deionized water. The load was applied in the center of the pontic with a 6 mm diameter stainless steel sphere at 0.5 mm/min until failure.

2. Mechanical cycling (MC): FPDs were subjected to MC using a chewing simulator composed of 10 pneumatic cylinders with a load of 140 N and frequency of 2 Hz for 10⁶ cycles in distilled water. Load was applied using a stainless steel sphere with 6 mm diameter. After aging, FPDs were tested until failure as previously described for the control group.

Fracture surfaces were examined using a stereomicroscope to determine the mode of failure based on the fracture origin and fractographic principles [25–27]. Subsequently, specimens were sputter-coated with gold-palladium and examined using a scanning electron microscope (SEM) to locate and measure the critical flaw dimensions (c). The size of a semicircular flaw, with equal stress intensity factor, was determined using the following equation 1 [28, 29]:

$$c=\sqrt{ab}$$ (1)

where, a is the crack depth and b is half of the crack width.

Fracture toughness (K_Ic) was calculated through fractographic analysis of bar-shaped specimens subjected to three-point flexural test. Fracture mechanics was used to estimate the fracture stress (σ_f) of FPDs, following Griffin-Irwin equation (Equation 2) [30–32]:

$$K_{IC}=Y{\sigma }_f\sqrt{c}$$ (2)

where Y is a geometric factor, which accounts for the shape and location of the fracture-initiation crack and loading condition, and also depends on the ratio a/b. Y was assumed to be 1.24 for semicircular cracks and 1.4 for corner cracks.

Fracture load, fracture stress and c-values were statistically analyzed by one-way ANOVA and Tukey’s test (α=0.05). The relation between the experimental group and failure origin was analyzed using Chi-square test (α=0.05).

Finite Element Analysis

A SkyScan 1172 micro-CT scanner (Microphotonics, Allentown, PA, USA) was used to produce the FPD models. Two parts were scanned separately: (1) the stainless steel dies simulating the prepared teeth and (2) the three-unit all-ceramic FPD (9 mm² and 16 mm² connector cross-section).

The scanning parameters were: accelerating voltage of 100 kV, current of 100 μA, exposure time of 2950 ms per frame, Al+Cu filter, and rotation step at 0.4° (180° rotation). For the metal dies, the x-ray beam was irradiated perpendicularly to the preparation long axis, and for the FPDs, the beam was parallel to their long axis. The image pixel size was 6.97 μm. The x-ray projections were reconstructed to form a 3D model, which was saved as a stack of bmp-type files using NRecon software (Microphotonics, Allentown, PA, USA). Beam hardening correction of 80% and ring artifact correction of 7 were used for the reconstruction. Tomography images of the structures were generated at each 0.034 mm and processed by an interactive medical image control system (Mimics 13.0, Materialise, Belgium) [33].

The micro-CT files corresponding to the metal dies and the FPD were processed separately to reduce the amount of manual work necessary to build three different masks with Mimics software. A mask of the dies was obtained though brightness and contrast adjustment, and a 3D object was produced and converted into a STL file (stereolithography, bilinear and interplane interpolation algorithm). For the FPD, segmentation based on image density thresholding of different value scale intensity levels was used to generate two masks, corresponding to the infrastructure and the veneering layer. 3D objects were obtained for the infrastructure and the veneer. The metal dies STL file was imported to the FPD file, making for a three-part final file: metal dies, infrastructure and veneer.

The masks of each part of the models were separately converted into STL files, which are improper for FEA because of the amount and shape of the triangles. Thus, the files of different parts were incorporated into non-manifold assembly in Mimics, and edited simultaneously. The parts were remeshed with a maximum geometrical error of 0.05%, maintaining the original geometry. Wrapping and smoothing operations were used to remove undesired sharp edges. The mesh quality was defined by controlling triangle edge length, the ratio between height and base of the triangles and removing sharp triangles using a triangle filter, so that the file could be imported into the FEA software without generating errors. Subsequently, the objects were separated according to the original parts and volumetric meshes were generated and imported by the FEA software (ABAQUS V6.8, Simulia, USA).

The final FPD model was composed of tetrahedral elements and three layers: (1) metal dies, (2) ceramic infrastructure and (3) porcelain layer. Two interfaces were created, between the metal dies and the infrastructure and between the infrastructure and the porcelain layer. The cement layer was neglected.

Nodes in the bottom surface of the dies were fixed in all directions; no rotation or translation was allowed. A compressive load, perpendicular to the restoration long axis, was applied in the center of the occlusal surface of the pontic. A load of 200 N was distributed uniformly over 20 nodes located in a circular area with 3 mm diameter.

The following considerations were made: (1) the materials were considered to be isotropic and homogeneous and to have a linear elastic behavior; (2) the effects of the periodontal ligament and pulp chamber were not considered; (3) elastic modulus (E) and Poisson’s ratio (v) were maintained constant. The values of the material properties used to perform the analysis are presented in Table 2 [34–36].

Table 2.

Mean values of elastic modulus (E) and Poisson’s ratio (ν) for the studied materials.

	Materials
	YZ	IZ	AL	VM7	VM9	Stainless Steel
E (GPa)	209	247	390	67	67	190
ν	0.32	0.26	0.24	0.23	0.21	0.27

The stress distributions from the linear finite element analyses were evaluated according to the location and magnitude of the maximum first principal stress.

Results

Fracture Load and Fractography

The mean fracture load (N) and standard deviation values for the experimental groups are presented in Table 3. YZ16 showed the greatest mean value of fracture load, followed by YZ16-MC. Specimens from groups YZ9, IZ16, IZ16-MC, AL16 and AL16-MC showed no significant difference for the fracture load (p>0.05). Mechanical cycling had no influence on the fracture load values of IZ and AL FPDs.

Table 3.

Mean fracture load (N), fracture stress (MPa) and crack size (c in μm) values for the experimental groups, followed by standard deviation (SD) and coefficient of variation (CV).

	Fracture Load (N)		c (μm)	Fracture Stress (MPa)
Groups	Mean (SD)	CV (%)	Mean (SD)	Mean (SD)
YZ16	4526 (406)a	9	25 (5)b	1100 (115)a
YZ16-CM	3992 (653)b	16	31 (4)a	940 (49)b
IZ16	2310 (134)c	6	38 (6)a	470 (41)c
IZ16-MC	2220 (244)c	11	34 (5)a	500 (38)c
AL16	1973 (238)c	12	38 (5)a	460 (27)c
AL16-MC	2021 (253)c	13	37 (6)a	480 (37)c
YZ9	2205 (186)c	8	32 (6)ab	940 (82)b

^*Values followed by the same letter in the column are statistically similar (p>0.05).

Macroscopic analysis of the FPDs after the mechanical test showed three possible sites of fracture initiation: (1) connector, (2) pontic and (3) crown. In general, fracture started in the FPD cervical area and propagated obliquely in the direction of the occlusal surface. YZ9 specimens showed the highest number of connector fractures (7). All fractures from IZ16 group initiated at the pontic area.

It was possible to identify different flaw origins through the analysis of the FPDs fracture surfaces using stereomicroscope and SEM. In the cervical area of the pontic and connectors, the critical flaw was located either on the porcelain surface and the IS surface (two critical flaws) or only at the IS surface (only one critical flaw). When failure of the crown was observed, the critical flaw was located in the IS, in the internal surface of the margin adjacent to the connector (Figure 1).

Figure 1.

Fracture surface of a FPD from YZ16 group that showed failure of the crown with the flaw origin located in the internal surface of the margin. A) Stereomicroscope image of the critical flaw. B) Stereomicroscope image of the crown fracture surface. It is possible to observe markings such as compression curl (CC) and twist hackles lines (HL). C) SEM image of the critical flaw. White arrows (images A and C) point to the flaw origin.

There was a significant relation between the experimental group and the flaw origin (p≤0.05) (Table 4), which means that the failure mode was influenced by the type of IS material. When two critical flaws were observed, one in the porcelain layer and another in the infrastructure (Figure 2), the fracture plane of the porcelain layer was, usually, different from the plane observed for the infrastructure. This behavior was evidenced by delamination of the porcelain.

Table 4.

Distribution flaw origin location per experimental group^*.

Groups	Porcelain and IS	Margin	IS
YZ16	6	3	0
YZ16-MC	6	2	0
IZ	6	0	2
IZ-MC	4	1	0
AL	4	0	6
AL-MC	0	0	6
YZ9	8	0	0

^*It was not possible to locate the flaw origin of some FPDs

Figure 2.

SEM image of the fracture surface of a FPD from YZ16 group that had fracture of the pontic. A) Cervical area of the pontic showing the ceramic IS and the porcelain layer (P). Two critical flaws were located, one on the porcelain surface and another on the IS surface. Critical flaws are evidenced in black boxes and white arrows indicate wake hackles that show the direction of crack propagation B) Infrastructure critical flaw. C) Porcelain critical flaw. White arrows (images B and C) point to the flaw origin.

For AL16 and AL16-MC specimens, more frequently, only one critical flaw was identified. The critical flaw was located on the surface of the IS material and the same fracture plane was observed for the porcelain and infrastructure layers, suggesting no delamination. This fracture pattern can be observed in Figure 3, in which a map of the specimen fracture surface was created showing that wake hackles in the porcelain layer point to the IS, where a critical flaw can be located. There is no evidence of a critical flaw on the porcelain.

Figure 3.

SEM image of the fracture surface of a FPD from AL16 group that presented failure of the pontic. It is possible to observe in the porcelain layer (P) wake hackles (identified by white arrows) pointing to the IS surface, where a critical flaw was located (identified by the black arrow). Only one critical flaw was observed, there was no evidence of flaw origin in the porcelain layer. Compression curl (CC) and hackle lines (HL) also show the direction of flaw propagation.

Table 3 also shows the mean values of the critical flaw (c) and fracture stress (σ_f) for the FPDs infrastructures. YZ16 had the smallest c value and the highest fracture stress. IZ and AL infrastructures showed similar crack sizes before and after mechanical cycling. The fracture stress for the porcelain was not estimated since this layer was damaged for most FPDs, and it was not possible to measure the critical flaw.

Finite Element Analysis

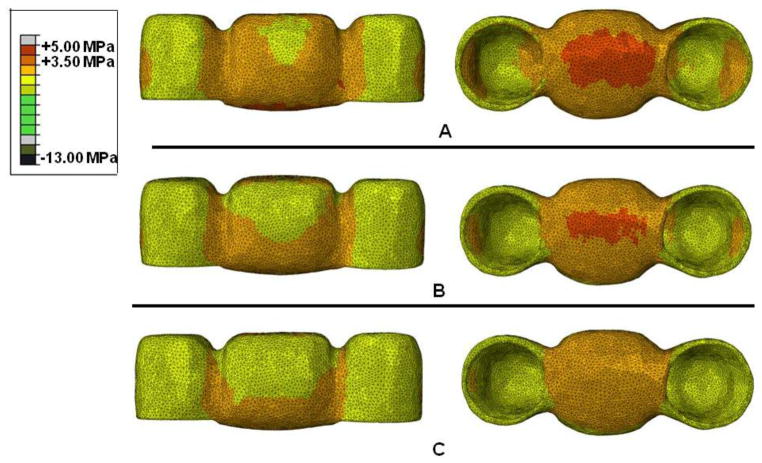
It was possible to notice, when YZ9 and YZ16 groups were compared, that the stress distribution for YZ16 was more uniform and the maximum tensile stress was located just underneath the pontic (Figure 4). In addition, for YZ9, tensile stresses were concentrated in a smaller area near the connectors. Higher stress concentration was observed in the internal surface of the crowns for YZ16 than for YZ9. A similar behavior was observed in the veneer layer.

Figure 4.

Stress distribution in the infrastructure cervical area for YZ16 (A) and YZ9 specimens (B).

For AL, a higher tensile stress concentration was found in the cervical area of the pontic when compared to other ceramic systems (YZ and IZ) (Figure 5). Considering the porcelain layer, an increase in the tensile stress concentration was observed with a decrease in the framework material elastic modulus value (Figure 6). The same behavior was observed for the crowns.

Figure 5.

Stress distribution in the infrastructure for IZ16 (A) and AL16 groups (B).

Figure 6.

Stress distribution in the porcelain layer for YZ16 (A), IZ16 (B) and AL16 groups (B).

Discussion

Ceramics with different compositions and microstructures are available to produce all-ceramic restorations using the CAD/CAM technology [1, 3]. The present investigation showed that the type of ceramic material used as infrastructure influences the failure mode and stress distribution of fixed partial dentures, partially accepting the first study hypothesis, as the fracture load values were similar among groups. YZ showed the best mechanical behavior, which is in agreement with the current literature on this ceramic material [37–40].

YZ FPDs with 16 mm² connector cross-section showed the highest fracture load value. In addition, the YZ FPDs with the recommended connector dimension (9 mm²) showed similar mechanical behavior to IZ and AL FPDs with 16 mm² connectors. Based on the materials mechanical properties, the manufacturer suggests a larger connector cross-section for posterior FPDs (10-mm span) when IZ system (16 mm²) is used in comparison to YZ (9 mm²). Clinically, a small connector cross-section is often desired, especially in posterior restorations, where the connector height is usually limited by short clinical molar crowns. Thus, YZ may be considered the best material to produce posterior FPDs as it is possible to obtain good mechanical performance even with a smaller connector dimension.

The influence of connector dimension and shape on the fracture load of FPDs has been previously studied. FPDs fracture load values increase with an increase in the dimension and in the radius of curvature of the connectors [13, 14, 41]. In the present study, different failure modes and stress distribution were observed for YZ FPDs with different connector dimensions. For YZ9, FEA showed that the highest tensile stresses were near the connectors. For YZ16, higher stress concentration was found in the pontic and the crowns. These findings are in agreement with the in-vitro tests carried out, in which 70% of the 16 mm² FPDs showed fracture of the pontic and 70% of the 9 mm² FPDs showed fracture at the connectors. In addition, YZ16 and YZ16-MC groups presented the largest number of crown failures. Furthermore, FPDs with 16 mm² connector cross-section show higher radius of curvature at the gingival embrasure than 9 mm² connector FPDs, which influences the stress distribution [13].

Due to the FPD geometry and the type of loading, the stress distribution observed was similar to a three-point flexure bar, in which a non-uniform stress distribution is created. Thus, the maximum tensile stress was located on the surface under tension directly below the applied load (cervical area of the pontic). Although, clinically, the load is usually distributed on all occlusal surfaces, it was previously reported that when the load is applied on the center of the pontic, the values of maximum tensile stress are higher, but the stress distribution is similar to physiologic loading [42]. In the present study, a stiff metal abutment was chosen because high loads applied during the mechanical test could lead to abutment failure before the FPD, as previously reported [43]. There is also lack of scientific evidence that the materials used to simulate the periodontal ligament in previous studies properly simulate its resilience. When abutments are allowed to rotate, stresses are likely to concentrate in the connectors but overall no major changes in the stress distribution are observed [12]. Yet, even with rigid abutments, FEA showed that the highest tensile stresses were in the 9 mm² connectors of the modeled FPDs.

Macroscopically, the specimens from all experimental groups showed similar fracture mode. The fracture initiated in the cervical area of the connector or pontic (area under tension) and propagated obliquely through the pontic occlusal surface, near the area of load application. The failure initiation site was observed on one of the crowns for 9% of the FPDs. In these cases, the critical flaw was located on the internal surface of the margin of the crown, in the infrastructure material. The crown margin is thinner and sharper than the pontic and connectors. Therefore, the margin is a site of stress concentration and is susceptible to failure, especially when large connector cross-sections (16 mm²) and high toughness materials are used, such as YZ. In addition, YZ has higher deformation (higher Poisson ratio) than other ceramics, leading to greater stress concentration in the crowns during bending.

In approximately 60% of the connector and pontic failures, two critical flaws were identified, one at the porcelain surface and another at the infrastructure surface, both located in the cervical area. Fractographic analysis suggests that the initial flaw propagated through the porcelain layer and deflected at the interface. When the stress magnitude exceeded the fracture toughness of the infrastructure material, another flaw initiated in the infrastructure surface and propagated resulting in catastrophic failure of the FPD. Crack arresting was also observed by the difference between the fracture surface planes of the porcelain and the infrastructure. Similar failure behavior was observed in a fractographic study of clinically failed YZ FPDs [17].

AL and IZ FPDs showed similar fracture load and fracture stress values but different failure modes and stress distribution. For AL specimens, 60–75% of the failures started in the materials interface with the critical flaw located at the IS surface. Flaw propagated through the structure as if it was a homogeneous material, with no deflection at the interface. Only one critical flaw was identified, with no fractographic evidence of flaw origin located at the porcelain layer. This behavior could be related to the great mismatch between the elastic modulus of AL (390 GPa) and VM7 porcelain (67 GPa), inducing higher stress concentration on the IS, also showed by the FEA models. FEA also showed that the tensile stress concentration in the porcelain layer increased with a decrease in the infrastructure material elastic modulus. This behavior could be explained by the fact that a material with higher elastic modulus has less strain and lower stresses are induced in the porcelain layer. In addition, the interface is a local of unique flaws, phase boundaries and residual stresses induced by thermal mismatches. This findings are in agreement with an investigation with alumina-based (In-Ceram Alumina) FPDs that failed in vitro and in vivo[12].

The effect of mechanical cycling on the fracture load of FPDs varies with the type of ceramic infrastructure. Thus, the study second hypothesis was accepted. Mechanical aging simulating one-year of in-vivo chewing [23, 44] had no influence on the fracture load and failure behavior of the AL16 and IZ16 FPDs. Similar critical flaw sizes were observed for aged and control specimens. On the other hand, an increase in the fracture load coefficient of variability was observed for zirconia-based FPDs after cycling (YZ16-MC and IZ16-MC). It was also observed that mechanical aging decreased the fracture load values of YZ16 FPDs. The critical flaw size was greater for YZ16-MC specimens compared to YZ16 specimens, suggesting that aging induced slow crack growth for this material.

Cyclic loading of ceramic materials involves intrinsic and extrinsic fatigue mechanisms. Intrinsic mechanisms include accumulated damage in material ahead of the crack tip in the form of localized microplasticity, or microcraking. Extrinsic mechanisms act to diminish the effect of a crack-tip shielding process, increasing the stress intensity factor compared to equivalent monotonic loading conditions [21]. In transforming ceramics, such as Y-TZP, an extrinsic mechanism could result from a reduction of the degree of transformation toughening [20, 45]. The temperature and humidity present in the aging simulation could also contribute to the low temperature degradation (LTD) of zirconia crystals, although YZ infrastructure was completely veneered and was not directly exposed to the humidity [46]. However, even after mechanical cycling, the estimated stress in the infrastructure ceramic at failure for all specimens (480–940 MPa) was well above the stresses estimated for the posterior areas of the mouth (27 to 31 MPa) [44], which suggests that these materials have been properly indicated as infrastructure for three-unit all-ceramic FPDs. Yet, extrapolation of the results to the clinical situation should be performed with caution since the effect of other factors, such as the lateral component of load, R-curve behavior, and the presence of the periodontal ligament, were not considered.

Conclusion

The failure mode and stress distribution of FPDs was influenced by the type of infrastructure ceramic. Polycrystalline alumina and In-Ceram Zirconia FPDs showed similar fracture load values but different failure modes and stress distribution. Y-TZP showed the best mechanical behavior and may be considered the material of choice to produce posterior FPDs as it was possible to obtain a good mechanical performance even with smaller connector dimension (9 mm²).

The effect of mechanical cycling on the fracture load of FPDs varies with the type of ceramic infrastructure. YZ FPDs were more susceptible to mechanical properties degradation after one-year aging simulation.