Compact off-axis holographic slide microscope: design guidelines

Abstract

Holographic microscopes are emerging as suitable tools for in situ diagnostics and environmental monitoring, providing high-throughput, label-free, quantitative imaging capabilities through small and compact devices. In-line holographic microscopes can be realized at contained costs, trading off complexity in the phase retrieval process and being limited to sparse samples. Here we present a 3D printed, cost effective and field portable off-axis holographic microscope based on the concept of holographic microfluidic slide. Our scheme removes complexity from the reconstruction process, as phase retrieval is non iterative and obtainable by hologram demodulation. The configuration we introduce ensures flexibility in the definition of the optical scheme, exploitable to realize modular devices with different features. We discuss trade-offs and design rules of thumb to follow for developing DH microscopes based on the proposed solution. Using our prototype, we image flowing marine microalgae, polystyrene beads, E.coli bacteria and microplastics. We detail the effect on the performance and costs of each parameter, design, and hardware choice, guiding readers toward the realization of optimized devices that can be employed out of the lab by non-expert users for point of care testing.

1. Introduction

The latest advances in the fields of Microscopy, Optical systems engineering, Materials science, Computer science, Physics, Chemistry and Bioinformatics have pushed the exponential growth in the last decade of the new paradigm of “point of care diagnostics” [1–3]. While more and more companies are entering the imaging market, they are mostly offering bulky microscopes providing quantitative phase imaging capabilities. Ptychographic imaging, optical diffraction tomography and Spatial Light Interference Microscopy (SLIM) are good examples in this sense [4–7]. Introducing new methods and technologies to develop further field-portable analysis systems is undoubtedly a research topic of broad interest, connected to the trend of Lab-on-Chip (LoC) platforms. The latter are characterized by an outstanding compactness, resulting ideal for in situ analysis. Moreover, they typically exploit microfluidic channels to handle extremely reduced volumes of liquid samples and reagents, which is a major advantage in terms of resources optimization.

The progress of LoC technology has stimulated research in complementary fields, leading to advances in microfluidics, micromanipulation and fabrication techniques. Optical microscopy is one of the areas invested by the interest toward miniaturization, and a growing number of compact optical systems are being developed, often embedding optical components directly onboard microfluidic platforms [8,9]. Among the huge variety of imaging solutions proposed in literature, Digital Holography (DH) in transmission microscopy configuration emerges as one of the most convenient in the framework of coherent approaches [10–15]. DH is non-invasive and marker-free, thus avoiding procedures of sample pre-treatments or labelling. Above all, DH gives access to the complex amplitude of the sample, which can be imaged in amplitude as well as quantitative phase-contrast. Numerical backpropagation of the hologram allows flexible refocusing of objects captured out of focus. Thus, a digital hologram can code on a 2D support, in the form of a modulated fringe pattern, information from objects moving in a volume [14]. This makes DH a very high-throughput imaging solution, well suited for microfluidics [16]. DH microscopy has been deeply employed to study cell mechanics, classify and sort samples in LoC environment, track in 3D particles and flowing specimens (e.g. for sperm motility assays), pre-screen inherited anemias in blood testing, detect pathogens and parasites in bodily fluids, investigate morphology, biovolume, and refractive index distribution of samples in microfluidic streams, study the collective movement of bacteria biofilms, detect, count and classify bacteria species on solid food or liquid environment, image micro-plankton for taxonomy purposes, recognize micro-plastics and other pollutants in heterogeneous mixtures [10–18,19,20]. In off-axis DH, a tilt is introduced between the object beam and the reference beam. This introduces a spatial carrier on the hologram, so that the object can be separated from the so called twin image by trivial demodulation in the Fourier domain [11,15,21].

However, off-axis DH setups are typically non-portable and costly, due to the need of temporally and spatially coherent laser sources. Optimized commercial solutions exist on the market that make use of bulky configurations based on off-axis DH [22–25]. In order to bring DH functions out of the lab, lensless inline DH solutions have been implemented as field portable devices. These make use of compact low coherence sources and a single beam scheme to contain costs and encumbrance and to avoid the use of bulky lasers [14,16,18,26,27]. Accordingly, a remarkably wide commercial market has grown in the last decade based on inline setups as well [28–30]. Although they promote field portability and cost-effectiveness, object recovery in inline DH involves a phase retrieval process, mostly based on modified versions of the Gerchberg-Saxton algorithm [26]. Convergence is not always guaranteed, e.g. in the presence of non sparse samples. This can be a binding constraint in the case of very dense liquid samples (e.g. slightly diluted blood). Although very high throughput holographic flow cytometers have been reported so far based on inline schemes, restrictions on the sample densities can severely limit the throughput of these systems in terms of cells imaged per hour [16]. To cope with the phase retrieval problem, Convolutional Neural Networks (CNNs) have been used to reconstruct inline holograms in quasi real-time [16,31], but CNNs require a large ground truth training dataset. Similarly, microscopes based on the Transport of Intensity Equation (TIE) concept have been introduced, where phase is obtained by intensity measures by solving the TIE. However, performance depend on the knowledge of prior information on the boundary conditions, and the sample density can impair a correct phase estimation [32,33].

Recently, we introduced a different optical design based on off-axis DH. We equipped a plain commercially available microfluidic chip with polymeric lenses and a polymer diffraction grating to create a cost effective holographic microscope slide, i.e. a pocket optical module that serves as a common-path wavefront division interferometer [9]. Thanks to the common path scheme, vibration isolation systems (e.g. optical tables) are not required, while the off-axis configuration allows removing the twin image avoiding iterative approaches. We demonstrated the effective use of the slide by imaging not sparse samples, e.g. adult C. Elegans and by counting Red Blood Cells (RBCs) in high density flow [9,34]. However, a bulky high coherent laser source was used in lab conditions and the optimal configuration of the setup parameters minimizing encumbrance was not yet investigated. A similar scheme makes use of a He-Ne laser and a grating to obtain a resolution gain in a shearing DH setup [35]. Solutions embedding Light Emitting Diode (LED) sources have been introduced [36–39]. These exploit additional optical components to increase the source temporal and spatial coherence, trading off compactness and simplicity of the optical setup [36,37]. LED based field portable configurations have been also proposed to yield ptychographic imaging capabilities at the cost of the accessible depth of field [38] or optical tomography exploiting the object flow [39]. The abovementioned advantages offered by DH imaging has pushed efforts toward the realization of compact and simple DH setups in off-axis configuration making use of low coherence sources. In [40], two pinholes and embedded microlenses are exploited in a common path scheme. As in the case of the holographic slide, the wavefront division configuration assures tolerance against vibrations. Although fringe spacing cannot be adjusted and optimized to efficiently demodulate the hologram in the Fourier domain, this solution is an effective way of relaxing the phase reconstruction process through an efficient use of embedded optical elements [40].

In this work we present and test a 3D printed implementation, shown in Figs. 1(a,b), of compact, light in weight, cost effective and field portable off-axis DH microscope . The aim of this work is to discuss the trade-offs and design rules of thumb that have to be followed to develop off-axis DH microscopes based on the holographic slide principle. We will hereafter refer to these compact devices as Holographic Slide Microscopes (HSMs). A HSM allows some flexibility in the definition of the optical scheme, which can be exploited to obtain devices with different, modular, or even changeable features. We detail the effect on the optical system performance of each parameter and design choice, stressing their relation to the selection of appropriate hardware components. Two different configurations will be hereafter compared for the scope, highlighting differences in performance and possible applications. Compactness, scalability and cost effectiveness will be analysed in both cases.

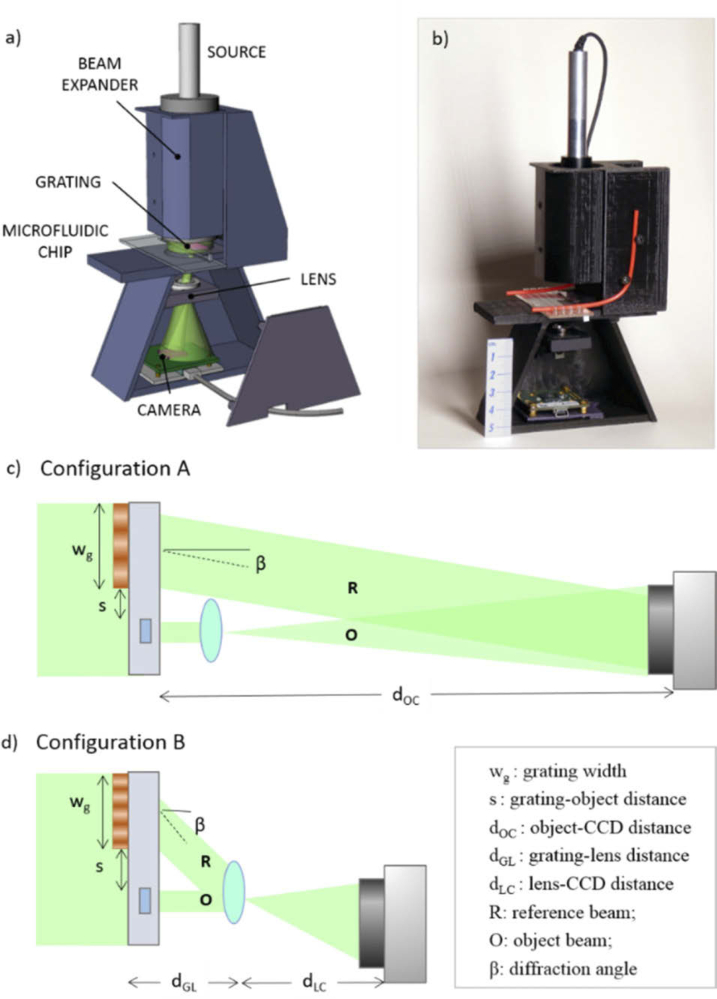
Fig. 1.

Compact HSM (a) 3D model and (b) corresponding 3D printed prototype, realized as per configuration in panel d. (c) Schematic representations of the setup “Configuration A” and (d) “Configuration B”. R: reference beam; O: object beam; w_g: grating width; s: separation between grating and microchannel; d_GL: distance grating-lens; d_LC: distance lens-camera.

2. Field portable HSM: parameters and components

We propose a wavefront division interferometric configuration, which uses a single beam to obtain off-axis recording of the hologram. According to the HSM principle, the reference wave is obtained using a diffraction grating, printed onto a microscope slide or directly on a plastic microfluidic chip. Light is collected through a single lens to control the magnification or to satisfy the sampling constraints. In particular, we will analyse two different device configurations. In the first one (sketched in Fig. 1(c)), the lens collects only the object light, while the reference beam travels unperturbed; then, the two waves recombine on the camera. This configuration provides a certain flexibility in setting the magnification by changing the objective lens. Moreover, it can be also used as a lensless setup. The second configuration renounces some flexibility in exchange to enhanced compactness: the interference is formed on a relay lens, whose characteristics are fixed by the need to achieve optimal fringe sampling on the camera (Fig. 1(d)). In the following sections, the two setups will be considered in detail and compared, stressing similarities and design-specific features. For each configuration, an interplay exists between the hardware and design choices and the subsequent characteristics of the system. Thus, before proceeding, it is useful to offer a brief description of the main hardware components, highlighting their key parameters and their role in the design and realization of a portable HSM.

Light Source. DH is based on the recording of an interference pattern obtained from the superposition of an object and a reference wave. Thus, the coherence length of the light source is a fundamental parameter to consider. Typical laser sources satisfy the coherence requirement, but are detrimental in terms of compactness, portability and cost-effectiveness. Moreover, a high degree of coherence results in deleterious effects such as speckles, which degrades the image quality [41]. Partially coherent sources such as diode lasers or LEDs offer an affordable alternative. However, to employ them in off-axis DH it is necessary to overcome hurdles represented by the degraded light beam quality and stability, increased chromatic dispersion and limited coherence length. In addition, in our wavefront splitting configuration the illuminating beam should also present adequate spatial coherence.

Here we use a DPSS laser diode (CPS532, Thorlabs). This instrument offers a good compromise between cost and beam quality. It is highly portable (the housing has length of $701mm$ and diameter of $11mm$) and provides a collimated beam (diameter of $3.5mm$) at $\mathit{\lambda }=532nm$, with a coherence length $l_c=140$µm. Before impinging the chip, the light passes through a fixed magnification beam expander providing a 5X enlargement of the beam diameter.

Grating. In our devices, we let part of the wavefront impinge orthogonally over a sinusoidal one-dimensional transmission grating. The grating produces diffracted plane waves that propagate at different angles ${\beta }_i={\sin }^{-1}(i\lambda /g)$, where g is the grating period. In our systems, we use the first diffraction order ($i=1$) as reference wave. It is worth to point out that the choice of the grating period is the most critical step of the overall system design. Indeed, the diffraction angle β regulates the interference fringes period p_f, which is related to both the sampling of the signal over the sensor surface and the separation of the diffraction orders in the Fourier domain [21]. In fact, if the fringes period is too small, the recording media resolution could not be sufficient to sample it correctly (see Appendix 1). On the other hand, increasing the period p_f corresponds to a lower carrier frequency for the hologram, which could impede an efficient Fourier filtering during the holographic reconstruction process with subsequent loss of resolution (see Methods). In addition, the grating period introduces some geometrical constraints on the distance at which the object and reference waves superpose and the interference pattern is observed, affecting the device compactness.

Lenses. Conventional DH microscopy systems use a microscope objective to magnify the object image. Depending on their grade, microscope objectives correct less or more efficiently the different types of aberrations (e.g. spherical aberration, chromatic aberration, and field curvature) and can provide outstanding quality imaging. However, they are usually expensive and have considerably large transversal and longitudinal dimensions. Recently, ultra-compact objectives have been introduced on the market. However, their case diameter and the usually small NA made them still unsuited for use in our setup. In our work, we use instead a single relay lens to collect and magnify the object image. While the image quality is lower, in particular far from the optical axis, a relay lens provides minimum encumbrance and high NA.

Digital Camera. Different factors influence the selection of a digital camera for DH, such as the bit depth, acquisition framerate, dimension and number of pixels. The last two are especially significant in our setup. The pixel size affects the image resolution and determines the spatial sampling frequency of the intensity pattern in the hologram plane. According to Nyquist’s sampling criterion, one interference fringe should be sampled by at least two pixels. This translates into a limit on the maximum acceptable angle between the reference and object wave, namely ${\theta }_{Nyq}={\sin }^{-1}(\lambda /2\mathrm{\Delta }p)$, where $\mathrm{\Delta }p$ is the pixel pitch. Thus, the pixel size directly affects the choice of the grating period and the system design. As for the number of pixels, this governs the maximum observable Field-of-View (FoV). Generally, a small pixel size and a large active area are desirable. We have selected a CCD camera (UI-2280SE-M-GL) with $\mathrm{\Delta }p=3.45$µm and $2048\times 2448$ pixels.

Masks. Customized masks are placed in the object plane to block unwanted light coming directly from the illumination source. In fact, the latter would cause saturation of camera pixels, leading to a weaker signal and information loss. Note however that it is important to verify during the setup assembly that diffraction from the mask borders does not overlap with the object signal. When it happens, one can introduce a small gap between object and mask edge.

3. Results

As described in the previous section, the system components define various constraints that will influence the final design. In this section, we present two different setups, herein referred to as “Configuration A” and “Configuration B”: they offer the insight necessary to plan and fabricate a system, whose features are adapted to specific applications. In both cases, we maintain as the core element of our proposal the introduction of a grating inscribed on a commercial plastic chip that serves as a holographic slide. In this way, we achieve a wavefront separation architecture that optimizes the fringes’ stability and is thus tolerant to vibrations. Moreover, we use the same source and camera. We change instead the grating step and the way we collect the object and reference waves after the chip. The key elements, the design procedure and relevant experimental results are illustrated for the two proposed configurations.

3.1. Configuration A

The first device we present is outlined in Fig. 1(c). The reference beam is steered by the grating directly on the camera sensor, while the object is collected by a lens. In this setup the fringe formation is independent of the magnification of the object: different lenses and even a lensless approach could be used, without modifying the object, grating and camera relative positions. Thus, this configuration offers a high degree of flexibility.

The choice of the parameters and distances involved can be performed according to this outline:

• 1.fix the laser wavelength and the camera parameters, calculate the maximum acceptable angle according to Nyquist theorem and select an adequate grating period;
• 2.position the chip to keep camera, lens and object on axis;
• 3.guarantee that the diffraction orders are separated on the camera, by masking the grating and selecting an opportune distance between chip and camera.

With a light source at $\lambda =532nm$ and a CCD pixel size of $3.45$µm, the Nyquist condition imposes a maximum accepted angle between object and reference wave ${\theta }_{Nyq}=4.4°$. However, in practice, it is common to sample a fringe over more than two pixels. In this way, one can account for any deviation of the real waves from the perfect plane wave model employed in the calculation of ${\theta }_{Nyq}$. We set our desired sampling over 5 pixels, which then requires a maximum angle ${\theta }_{MAX}=1.7°$. We can consider that the angle between O and R is equal to the reference inclination angle $\beta$. This estimation is possible as the objects that we consider have small lateral dimensions and are placed far away from the camera. Thus, the Nyquist condition is transferred to the grating parameters: the minimum accepted period is $g_{min}=\lambda /\text{sin}({\theta }_{MAX})\cong 17$µm. We realized a grating with period $19.2$µm, which corresponds to an angle of the first diffraction order of $1.6°$. For a faster rule of thumb, one can introduce in the sampling condition the explicit expression for the reference inclination (see sections “Digital Camera” and “Grating”). The result is the condition $g\ge n\mathrm{\Delta }p$ (where n is the number of pixel to be used for the sampling), which is remarkably independent on the wavelength. Note that the introduction of lenses on the object path has the effect of modifying the angle between O and R. Thus, by selecting a grating period bigger than the strictly required one, one can buffer the changes in the object wave, keeping in the limits of the Nyquist condition. A detailed description of the optical system corresponding to the Configuration A can be found in the Appendix 1.

Once the grating with the selected period is printed on the chip, the latter is positioned so that it is aligned to the camera. At this stage, it is also possible to insert the lens, having care to keep object and camera along the optical axis to minimize the effect of the aberrations on the object wave. Note that the introduction of a lens should leave the reference wave path unobstructed. This is possible by selecting an optical element with a small diameter and a thin lens holder, and by placing the lens in the proximity of the object (see Fig. 1(c)). We have selected a lens with outer diameter of $9.2mm$ and focal length equal to $4.51mm$ (Thorlabs, C230TMD-A), placed at distance $d\cong 6mm$ from the object. As for the reference beam, the small diffraction angle elicits some geometrical considerations. The first one steams from the necessity to separate the zeroth, first and second diffraction orders coming from the grating. Then, the desired order should impinge on the camera. These two issues are solved by introducing a $5mm$ wide mask for the grating: the mask permits to control the distance between grating and microchannel and the position of the intersection between optical axis and the first order. Then, separation of the orders is simply obtained by free-space propagation, namely by moving the camera further away from the object. In our final design, we have a distance $d_{OC}=19cm$ and a separation between the channel and the selected grating slide $s=2mm$ (see Fig. 1(c)).

Initially, we test the setup using as sample polystyrene beads dispersed in water. In particular, we mix different monodispersed polystyrene microparticles with nominal diameter of 2, 5, 10 and 15 µm. The sample is inserted into a straight microfluidic PMMA chip with height of 200 µm and width of 1 mm. We selected an area containing multiple beads and acquired the hologram. Details and the results of this first assessment test can be found in the Appendix 1 section (Fig. 8). The results reported in Fig. 8 provide an evidence of the possibility to scan the optical axis by wavefront propagation starting from out of focus DHs acquired with the DH microscope Configuration A. Moreover, we used these experiments carried out using well-known tester samples to estimate the system resolution. Accordingly, in the case of objects flowing inside the chip, Configuration A provides a spatial resolution equal to 0.58 µm in both directions. Details about the process of DH reconstruction, automatic focusing [42] and phase estimation in off-axis DH are provided in the Methods section. After having tested the setup with polystyrene microparticles, i.e. a regular shaped sample of homogeneous composition, we switch to two different cases of biological material. Diatoms are a first significant example of biological material worth to be tested using a field portable DH microscope. Diatoms are eukaryotic microalgae that can be found worldwide in waters. They have a crucial role in the global carbon cycle and in the production of the organic matter necessary for life in waters [43]. Because of their sensitivity to the ecological conditions, they are considered in studies related to climate changes and are used as bio-indicators of environmental conditions for water quality assessment. Hence, mapping diatoms distribution and taxonomy using compact DH imaging devices is highly demanded [16]. Diatoms are present in waters in the form of thousands different species, with dimensions ranging from 1 µm to 500 µm in length. All diatom species are characterized by a siliceous cell wall called a ‘frustule’, whose surface present an ultrastructure, or ornamentation, reproducing a strict pattern.

In our first experiment, we use as object a target made of different diatoms, fixed between two glass slides (see the sample preparation section). The glass slide we used contains 50 different diatom species, with diameter ranging from 50 µm to 200 µm. This is a very heterogeneous tester, as the selected diatoms have tiny inner structures at different scales and span over a wide FoV. We use this fixed sample to test and compare the two different configurations shown in Figs. 1(c,d). Note that in this case we cannot print the grating over the tester, so we instead prepare it over a microscope coverslip, which is then positioned directly over the plate. In the case of the microscope Configuration A (Fig. 1(c)), the accessible FoV ($\text{Fo}{\text{V}}_{\text{A}}=0.023m{m}^2$) is such that a single holographic acquisition can record at maximum two diatoms. In our experiments, we imaged different diatoms by scanning the object holder with respect to the imaging system.

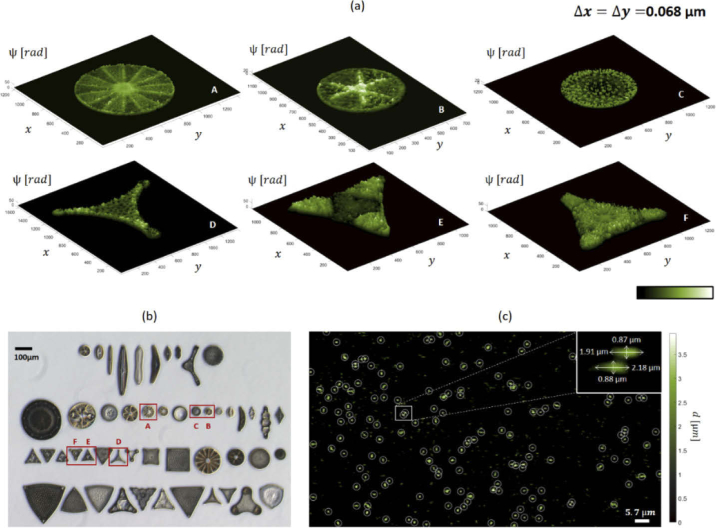
Figure 2(a) shows pseudo-3D views of phase-contrast reconstructions, $\psi$, of some of the diatoms contained in the glass slide. For the sake of comparison, Fig. 2(b) shows a bright field microscope image of the glass slide, captured under a 5x magnification microscope objective. Red square boxes and capital letters identify each of the selected diatoms shown in Fig. 2(a). Testing this configuration using a known sample allowed us to evaluate the magnification of the optical system in Configuration A, $M_A$. Although this is estimated to provide ${\text{M}}_{\text{A}}=50.5\times$ magnification of the sample, the tiniest inner structures of the diatoms can be barely appreciated. Nevertheless, diatoms are shown with sharp phase contrast and the retrieved morphology is in good agreement with the morphology inferable from the bright field image of Fig. 2(b). Noteworthy, in the case of diatoms, the large variability of refractive index within the same sample and among different species prevents us from converting phase values ($\psi$, expressed in radians) into thickness distributions. This limitation can be overcome whenever it is possible to assume uniform refractive index within a sample.

Fig. 2.

Phase contrast mapping using the proposed configuration A. (a,b) Marine algae (diatoms) fixed on a glass slide. (a) Pseudo 3D view of the diatoms inside the red rectangles in (b) after DH reconstruction. $\mathrm{\Delta }x$ and $\mathrm{\Delta }y$ denote the pixel size in the image plane. (b) Bright-field 5x microscope image of the slide containing the set of imaged diatoms. (c) Thickness of E-coli bacteria inside a microfluidic channel is measured. White circles indicate the positions where bacteria are automatically detected.

Then we test the setup for the detection and counting of Escherichia coli bacteria. E.coli is a prokaryotic organism known to cause a variety of disease syndromes, making it an important indicator in environmental water quality monitoring and food security [44,45]. The E.coli cells are rod shaped, with typical lengths of $2-3$µm and a diameter of $0.5-1$µm [44,46,47], with an almost uniform refractive index $n=1.384$. Their small dimensions challenge the resolution of conventional microscopes. Moreover, the small difference between the refractive indexes of E.coli, n, and the surrounding medium, ${\text{n}}_m=1.339$, often results in poor phase contrast with respect to the noise level, which makes them hard to detect by coherent imaging techniques. Thus, they represent an interesting tester for the setup we propose. Bacteria are inserted with their broth medium in the microfluidic channel, which is then sealed, and a hologram of the static sample is recorded. In this case, due the slightly different position of the sample plane with respect to the case of the glass slide, we have a smaller FoV, $\text{Fo}{\text{V}}_{A-chip}=0.019m{m}^2$, and in turn a larger magnification of the samples inside the channel, $M_{A-chip}=55.64\times$. After DH reconstruction, the phase-contrast map is obtained from Eq. (2) (see the Methods section), from which the thickness map is estimated as $d=(\lambda \psi )/[2\pi (n-n_m)]$. Figure 2(c) shows the thickness map for one of the reconstructed layers. Since the average level of the background is $d_a=1.365$µm, values of d estimated to be approximately $3.5$µm in the centroid locations result in thickness differences approaching $2$µm, as expected. White circles and crosses in Fig. 2(c) point the centroid of each element, which has been estimated applying a detection criterion based on thresholding the thickness map and filtering on area basis the detected spots. The white box in Fig. 2(c) shows the zoom in detail of two detected bacteria along with their estimated sizes, in good agreement with the expected values reported in literature. Despite the poor phase contrast and the reduced size of the test samples, the setup Configuration A is shown to be suitable for automatic detection and counting the E.coli population.

3.2. Configuration B

In Configuration A, the grating period is determined by the Nyquist criterion, and the subsequent geometrical and physical constraints heavily influence the final geometry. In the second design that we present, we show how the compactness of the device can be improved without sacrificing resolution and extending at the same time the FoV. To obtain this result, we select a grating with smaller period, which corresponds to larger diffraction angles (see Fig. 1(d)). Indeed, in this case shorter propagation distances are required to separate the different orders. At the same time, however, the more pronounced inclination could exceed the limit on the maximum acceptable angle imposed by the Nyquist condition. When this happens, we can collect both the object and reference waves with a single relay lens that magnifies the hologram.

With respect to the Configuration A, the selection of the appropriate distances and hardware components follows a different process. A detailed description of the design procedure is presented in the Appendix 1, where the mathematical expressions used to calculate the minimum acceptable distances, d_GL and d_LC, and the magnification are derived. A synthetic outline of the principal steps is the following:

• 1)Fix the source and the camera
• 2)Fix the grating period and select the lens
• 3)Calculate minimum required fringes magnification
• 4)Calculate the minimum distance grating-lens
• 5)Calculate minimum required distance lens-camera
• 6)Estimate object magnification
• 7)Adjust distances and camera position in the x-y plane

The hardware choices and the design parameters are strongly interlinked. It is reasonable to establish in the first place the source and camera to be used: in our case, they are unchanged with respect to Configuration A and so is the Nyquist condition. Regarding the grating period and the lens, they should be optimized in order to have the desired combination of distances and magnification. In practical situations, we expect the designer to work with commercially available products so that we cannot access a continuous range of grating and lens parameters. In this case, it can be helpful to calculate some tables (see Table 2 in Appendix) where the characteristics of the available gratings and lenses are given, and the values from points 4) to 6) are calculated accordingly. In this way it is possible to select the best combination in accord to the desired system features. In our case, we adopt a grating with period $g_p=3$µm and a lens with f = 6.24 and NA = 0.4 (Thorlabs, C110TMD-A). The first diffraction order, i.e. the reference wave, is inclined at an angle $\beta =10.2°$, which is largely above the Nyquist condition ${\theta }_{Nyq}=4.4°$. We estimate that a fringes magnification $M_f=4.6\times$ assures that a single fringe will be sampled over 4 pixels. Then we evaluate the minimum distances to be used, i.e. $d_{GLmin}=8.9mm$ and $d_{LCmin}=3.5cm$, and an estimated magnification of the object $M_{obj}=5.5\times$. In the final implementation of the setup, we have used slightly larger distances with respect to the calculated ones. In the case of the distance between grating and camera, we have increased the distance to $d_{GL}\cong 9.2mm$ in order to achieve a better separation of the diffraction orders. Although it is easy to experimentally verify this condition, a rule of thumb to aid in the design can be extracted. As we know that the first order experiences a shift $ksin\beta$, the condition for separation is $k>3\mathrm{\Delta }k/2$, where $\mathrm{\Delta }k=\frac{2\pi }{M_{obj}\lambda }NA$ is the signal bandwidth [48]. Thus, we obtain the condition $\frac{g}{\lambda }<\frac{2M_{obj}}{3NA}$. For the lens-camera distance, we have instead selected $d_{LC}\cong 4cm$ to record the interference region over the whole active area of the CCD. Using these values, we estimate for the object in the chip a magnification $M_{obj}=4.3\times$. It is worth to note that, since the reference beam propagation direction is inclined with respect to the lens optical axis, the interference region after the lens will be deviated on the side: thus, it is necessary to adjust the sensor position in the x-y plane to record the hologram.

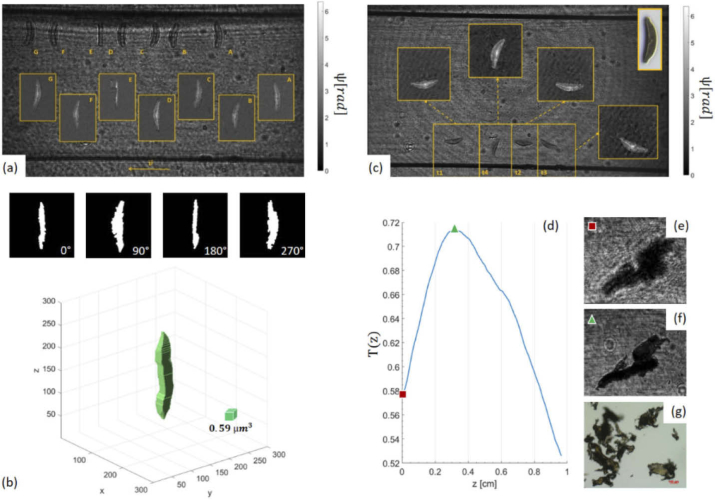
We test the setup Configuration B using the glass slide containing fixed diatoms presented in the previous section. The captured hologram (Fig. 3(a)) records the target largely out of focus. Then, we performed numerical refocusing to recover the image in its best focal plane (Fig. 3(b)). The first and more obvious difference with respect to the previous configuration concerns the recorded FoV. In this case, the system magnification is reduced at ${\text{M}}_{\text{B}}=4.9\times$, and the imaged FoV is $\text{Fo}{\text{V}}_{\text{B}}=2.49m{m}^2$, allowing us to observe all the algae in the glass slide by a single DH shot. At the same time, the internal features of all the algae can be resolved. The improved resolution depends mainly on the position of the camera in this configuration: placing it closer to the lens allows accepting higher spatial frequencies, which is a remarkable advantage of this configuration. Figure 3(b) shows an amplitude reconstruction where all diatoms are retrieved in sharp focus and tiny details of their inner structures can be appreciated as well. The $5\times$ bright field microscope image of the glass slide is shown in Fig. 3(c), thus providing readers with a side by side comparison between the DH reconstructions achieved using the setup Configuration A and the result obtainable by white light imaging. Figures 3(b,c) show a very good agreement between the two imaging modalities in terms of object morphology. However, the DH reconstruction is restored from a largely defocused image of the target. Although the image quality is still affected by speckle artefacts [41], the effect is strongly reduced respect to previous uses of the holographic slide concept [9,34], thanks to the lower coherence of the DPSS laser with respect to the He-Ne laser. It is also possible to observe ringing artefacts arising from dust and imperfections on the plastic chip, which can be reduced by closing the device in a sealed box. A better noise rejection is a further advantage deriving from the minimization of the optical path difference between the object and the reference waves. The larger FoV provided by the setup Configuration B is particularly advantageous in the case of microfluidics DH imaging, as it enables the observation of the whole channel (Fig. 4). We test the use of the device as a holographic flow cytometer by acquiring holographic sequences during sample flow inside the chip. As test samples we imaged diatoms and microplastics dispersed in water, which are both objects of interest for in situ environmental monitoring. In the case of diatoms, we use a sample containing in particular one species present on the glass slide, as marked by the red arrow in Fig. 3(c). The sample is withdrawn into a syringe that is then connected to the microchannel inlet, while the outlet is coupled to a waste reservoir. The sample is pushed through the channel, while a holographic video is recorded with a framerate $F_R=5s^{-1}$. In this set of experiments, due to the different position of the sample plane with respect to the case of the glass slide of Fig. 3, the system provides a slightly lower magnification ${\text{M}}_{B-chip}=4.11\times$ and a larger FoV, $\text{Fo}{\text{V}}_{B-chip}=3.02m{m}^2$. In Figs. 4(a-c) we report the results obtained from two different DH sequences of diatoms flowing along the channel. In particular, Fig. 4(a) is a hologram showing some of the frames of the first sequence (Visualization 1 ^{(1.2MB, avi)} ), where a diatom is largely out of focus and rotates while flowing along the channel. Capital letters in Fig. 4(a) denote subsequent frames extracted from the video and allow tracking the object motion. The corresponding phase contrast maps obtained by numerical refocusing are reported in the insets. Sample rotation due to the microfluidic flow can be exploited to obtain a 3D rendering of the object shape using a Shape From Silhouette (SFS) algorithm [49], or to estimate its refractive index distribution through in-flow diffraction tomography approaches [17]. In this set of experiments the frame rate of the camera was not high enough to estimate accurately the object tomogram. However, the object is retrieved in sharp focus in each frame, with a phase-contrast large enough to estimate its support. The 3D shape of the diatom reported in Fig. 4(b) results from the application of the SFS algorithm to 13 silhouettes extracted by binarization of the phase contrast map. Some of the silhouettes we used, corresponding to the subset of angles $\gamma =[0°,90°,180°,270°]$, are reported in the uppermost part of Fig. 4(b). Although only 13 projections have been used with non-uniform sampling (we did not engineer the flux to control the rotation), the object 3D morphology looks in good agreement with the shape expected for the diatom species selected. This suggests that the proposed DH microscope configuration could be coupled to a higher frame rate sensor to obtain tomograms of samples flowing inside the channel. Investigating this possibility will be object of future work from our group.

Fig. 3.

DH imaging of diatoms fixed on a glass slide using the proposed Configuration B. (a) Digital hologram shows the test sample largely out of focus. (b) Amplitude reconstruction of the samples after DH numerical refocusing. (c) Bright-field microscope image (5x magnification) of the glass slide.

Fig. 4.

(Visualization 1 ^{(1.2MB, avi)} ) The HSM device shown in Fig. 1 was used to image objects of interest for environmental monitoring. (a-b) Diatoms flowing inside a microfluidic channel. (a) Out of focus DHs of a flowing and rotating diatom are superposed on the same image to show the movement. The corresponding phase-contrast maps after refocusing each DH are shown in the insets. (b) 3D rendering of the rotating diatom in (a), obtained as a result of the SFS algorithm. (c) Amplitude reconstructions of a flowing diatom in different time instants show the movement of the alga due to the flow. The corresponding phase contrast maps are shown in the insets. The bright-field microscope image of the same diatom class is shown for the sake of comparison in the top-right corner of (c). (d-g) Imaging microplastics using the proposed field portable DH microscope of Fig. 1. (d) T(z) vs. z. (e). Out of focus DH of a PVC plastic item. (f) Amplitude DH reconstruction at z maximizing T(z). (g) Bright-field microscope image of PVC plastics.

Figure 4(c) shows in focus reconstructions of a flowing diatom that did not undergo any rotation around its main axis of symmetry and rotated in the sole (x,y) plane. In particular, four different object positions are selected from the reconstructed sequence, marked with $t_1,\dots ,t_4.$ In Fig. 4(c), amplitude DH reconstructions are shown in focus for each time instant along with the corresponding phase-contrast maps. The bright field microscope image of a diatom belonging to the same species of the samples imaged in Figs. 4(a-c) is reported in the top-right corner of (c). The same configuration is tested with microplastics dispersed in water. Microplastics can be found in high abundance in marine as well as freshwater, and raise major concerns due to their potential to provoke toxicological injuries to marine life and to affect the food chain due to ingestion by marine organisms. Thus, field-portable DH microscopes could be used in a next future to measure the density of plastic pollutants in water in field sampling campaigns [50,51,19]. Here we made a first imaging test using a PVC plastic fragment (see sample preparation for details). As in the previous case, the sample is inserted in the channel using a syringe. Figures 4(d-g) report the results of the automatic refocusing of the plastic item. In particular, the Tamura coefficient is plotted in Fig. 4(d) as a function of the propagation distance, z. The demodulated hologram, corresponding to $z=0$, is shown in Fig. 4(e) and the corresponding Tamura value is marked with a red square in the plot of $T(z)$. Differently from the case of pure phase objects, e.g. cells, in the case of PVC plastics the best focus DH amplitude reconstruction maximizes $T(z)$. This is shown in Fig. 4(f) in sharp focus and the corresponding Tamura value is marked with a green triangle in Fig. 4(d). The irregular shape of the object is a typical feature of microplastics, likely due to the fragmentation process it underwent, since these pollutants mostly derive from breakup of larger plastic items. A bright field microscope image of PVC micro-plastics is shown in Fig. 4(g).

4. Discussion and conclusions

The development of portable systems for the optical inspection of samples in a microfluidic environment is undergoing intense study. In fact, it has potential applications in fields of broad interest, such as in situ diagnostics and environmental monitoring. Portable DH offers label-free recording of the sample amplitude and quantitative phase information. It also yields flexible focusing capabilities, so that objects flowing at different positions in the channel volume can be imaged without any mechanical movement. Moreover, DH is extremely compatible with high throughput microfluidic systems and dynamic imaging, as the acquisition rate is ultimately limited only by the camera performance.

However, this interferometric technique requires special care to be implemented in a portable configuration. Here, we have presented a compact, off-axis device, which we refer to as holographic slide microscope. Its core element, the holographic slide [9], is a commercial plastic microfluidic chip, functionalized with embedded optical elements. Specifically, in the configurations shown in this work a diffraction grating is written onto the microfluidic chip. Thus, a single beam impinging on the chip is split into an object wave (passing through the microchannel) and a reference wave (generated after the grating as the first diffraction order). This wavefront division configuration offers the fringe stability necessary for correctly acquiring holograms outside laboratory conditions.

Maintaining this concept at the core of the HSM architecture, we have proposed two configurations. They differ in the grating step and in the way the light is steered and collected after the chip. We have described and analysed the design procedure and the resulting devices performances, using as a starting point the selection of the light wavelength and of the imaging sensor. Apart from the specific solutions that we adopt, the two configurations outline the approach to be used in two circumstances: if the reference beam inclination permits an adequate sampling of the hologram on the camera, we fall into the case study of Configuration A. Instead, if the inclination angle exceeds the maximum acceptable, we refer to the procedure assumed in Configuration B. Thus, we provided two routes to produce a field portable HSM, exhausting all the possibilities related to the hologram sampling.

In Configuration A (Fig. 1(c)), the reference wave impinges directly on the camera, while the object wave is collected by a lens. This configuration offers the biggest flexibility regarding the collection of the object wave. In fact, without changing the grating and the relative positions of chip and camera, it is possible to introduce on the object path different lenses (as long as the reference wave is not obstructed) or even to implement a lensless configuration. This makes this solution modular and changeable. For example, polymer micro-lenses could be delivered onto the chip by forward inkjet printing to tune sample magnification further [9,52]. On the other hand, the separation of the diffraction orders by free-space propagation requires a positioning of the camera at a relatively high distance from the chip. This results in a reduced FoV ($\text{Fo}{\text{V}}_{A-chip}=0.019m{m}^2\ll \text{Fo}{\text{V}}_{B-chip}=3.02m{m}^2$) and potentially in a loss of resolution, as light carrying the higher frequencies information from the object is not collected by the camera. Note however that these disadvantages would be mitigated when using a camera with smaller pixel size – and consequently a grating with lower period.

The Configuration B (Fig. 1(d)) is developed so that the FoV covers the width of the microchannel and it offers improved resolution. This solution results overall more compact, increasing its portability. In this architecture, both the object and the reference wave are collected by a lens. The lens modifies the angles between reference and object wave, relaxing the requirement on the maximum first-order diffraction angle. The possibility to use a largely tilted reference wave helps to promptly separate the diffraction orders. Moreover, the requirements on the minimum distances between the functionalized chip and the camera are vastly reduced: we have an overall distance of about 7 cm, against the 21 cm of the Configuration A. At the same time, by lessening the separation between the camera and the lens, we collect higher spatial frequencies from the object, thus improving resolution. Although providing better performance in a more compact device, this configuration sacrifices the flexibility of the setup, as any change in one of the components will likely require a reconsideration of all the distances involved. Moreover, the alignment of the system results more challenging.

Apart from their specific features, the two configurations share some common traits. Both exploit a wavefront-splitting architecture, which increases the stability of the optical system, enabling a portable off-axis DH device. This is in contrast with conventional off-axis DH setups, which are susceptible to mechanical vibrations and require a controlled environment, such as vibration isolation through optical tables. At the same time, the proposed design benefits from all the advantages and features of conventional off-axis DH. Imaging is non-invasive and label-free. The numerical focusing capabilities can be exploited to image out-of-focus objects, and still recover the complex amplitude of the sample. Above all, the reconstruction procedure is a non-iterative, closed form solution of the diffraction integral and is not hampered by the sample density. This makes HSM solutions substantially different from inline DH approaches to the realization of field portable microscopes.

Phase reconstruction is operated in real time, without requiring multiple measures or prior knowledge of the object support, and the accuracy in phase estimation is not affected by the sparsity of the samples inside the liquid volume. These advantages are obtained at the cost of a smaller available bandwidth (due to the need of allocating the twin image and the zeroth order in the Fourier spectrum), but make the proposed configurations applicable to a larger variety of cases. Moreover, recording dynamic processes is possible, with a temporal resolution limited only by the camera performance. This characteristic makes our system suited for high-throughput microfluidic implementations [34]. The two configurations are also similar in terms of production costs. With respect to conventional off-axis DH, our system designs drastically reduce the optical elements involved, making HSMs particularly cost effective. In Table 1 we report a rough estimate of the main components price, based on the specific elements selected in this work and their retail value. The total cost of the HSM is estimated to be lower than 800€. Our appraisal leaves ample room to further cost reductions, considering that the most expensive element is the CCD camera. For example, it is possible to switch to CMOS imaging sensors, which are advancing into high-performance applications while also offering competitive camera prices. Moreover, the overall costs reported in Table 1 refer to the realization of one single device. A significant cost reduction is to be expected in the case large volumes of components are purchased. For large volume productions, a 65% reduction of the overall costs are expected [16], making each single microscope obtainable for less than 300 €. It is worth to point out that this analysis does not include the cost of the grating and of the 3D printed device case, which are both strongly dependent of the fabrication procedure. However, we would like to remark that low cost options for both are available and becoming increasingly accessible with the development of novel 3D printing and photolithography technologies [53–55].

Table 1. Retail price in Euro for the main hardware components of the HSM. The total cost of the 3D printed microscope in Fig. 1 is estimated to be lower than 800€ for the production of one single device, and lower than 300€ for large production volumes.

Components	Retail Price [ € ]
Source CPS532, Thorlabs	147
Beam Expander 160-0051, Eksma Optics	252
Lens Molded aspheric, Thorlabs	73
PMMA straight channel chip 01-0174-0138-01, microfluidic ChipShop	18
Camera UI-2280SE-M-GL, uEye	300

In conclusion, we have introduced and discussed a 3D printed prototype of a compact field-portable imaging system for off-axis DH microscopy, named here HSM. The use of different grating periods introduces the opportunity to modify the optical scheme to obtain devices with different features. We have described here two different configurations, clarifying for each the key parameters and the design procedure. We have addressed with particular care the interplay of the different hardware components, providing the reader with guidelines for the assembly of HSMs with performances tunable to address specific application needs. Successful off-axis DH acquisitions and reconstructions have been experimentally demonstrated for both configurations, using samples relevant to the field of environmental monitoring. The two configurations have been compared in terms of optical performance, compactness, alignment and use simplicity, flexibility and costs, underlining specific advantages and drawbacks. Future work from our group will be devoted to add an accurate flow engineering module to the device, with the aim to induce controlled rotations to the sample for inflow tomography purposes. Also, the design of a new version of the microscope providing RGB phase-contrast holographic imaging is currently subject of study. We believe the configurations presented in this work will provide readers with guidelines to design cheap, field portable off-axis DH microscopes with modular of changeable features, easy to reproduce, and requiring minor data processing steps, with the hope this will help in pushing further the ongoing processes of healthcare and field testing democratization.

5. Methods

5.1. Off-axis digital holography

Digital holography (DH) is a technique based on the digital recording of the interference pattern that results from the superposition of an object wave O(x,y) and a reference wave R(x,y). The intensity distribution that results in the hologram plane is given by $h={|O|}^2+{|R|}^2+O{R}^{\ast }+O^{\ast }R=H_0+H_{+1}+H_{-1}$. The intensities of the object and reference waves are grouped in H₀, which is known as the autocorrelation term. The last two are the interference terms; they contain the real and twin images of the complex object. The former is the image that needs to be retrieved. This problem is easily solved with the off-axis configuration, as the three orders can be separated in the Fourier domain. This is evident using as an example a plane reference wave, traveling in the x-z plane, at angle θ respect to the object wave. Then, h can be rewritten as:

$$h={|O(x,y)|}^2+{|R(x,y)|}^2+O(x,y)|R(x,y)|e^{-j{k}_{0}sin\theta x}+O{(x,y)}^{\ast }|R(x,y)|e^{j{k}_{0}sin\theta x}$$ (1)

If we calculate the Fourier transform of this hologram, the zeroth diffraction order is placed at the center of the spectrum, while the terms H_-1 and H₊₁ are shifted to the opposite sides with a displacement $k_{0}sin\theta$. If the shifting is sufficient to separate the different orders, it is possible to isolate the spatial frequencies with the information on the object by Fourier filtering. Thus, the off-axis DH setup allows extracting the object by trivially demodulating the hologram. After accessing the complex object wavefront, this can be back-propagated along the optical axis by solving the Rayleigh-Sommerfeld diffraction integral [21]. The object of interest can be then refocused by solving the integral using the proper reconstruction distance. In order to find the best focus position for each object, we optimized the Tamura coefficient, $T(z)$, i.e. a suitable contrast metric measured over the amplitude DH reconstruction in the area containing the object to be refocused [42]:

$$T(z)=\sqrt{\frac{\sigma [|P\{H_{+1};z\}|]}{\mu [|P\{H_{+1};z\}|]}}$$ (2)

where σ and µ are the standard deviation and the mean value of the grey level distribution over the region of interest, and $P\{\dots \}$ is the propagation operator. Once refocused, the object wavefront yields both the amplitude and the phase-contrast map. The latter is obtained as $\psi =\text{Unw}\{\mathrm{\angle }[P\{H_{+1};z_F\}]\},$ where $\mathrm{\angle }[\dots ]$ extracts the modulus 2π phase, $Unw\{\dots \}$ is the phase unwrapping operator and $z_F$ is the estimated best focus distance.

5.2. Photolithographic process

Standard $76mm\times 26mm$ glass substrates were cleaned in acetone and $5min$ in ultrasound bath. After that, a positive photoresist (Microresist mp-1210) was spin coated on the surface obtaining a resist thickness of about $1$µm. The two different gratings were patterned with different methods. In the case of setup Configuration A ($g=19.2$µm) standard photolithography with mask was used. In the case of the setup Configuration B ($g=3$µm ) the grating was inscribed by means of interference lithography. In both cases, after the exposition to the light (HeCd laser light with a writing wavelength of $442nm$) the samples were developed with specific solution. The same procedure can be applied directly on the PMMA chip surface in the case of chip functionalization.

5.3. Sample preparation

Diatoms: diatoms cultures were diluted with filtered sterile seawater and maintained at room temperature until the experiments were performed. Diatoms in the glass slide were prepared by Stefano Barone - Diatom Lab, and purchased from www.diatomshop.com.

Bacteria: bacteria were cultured on Luria-Bertani (LB) agar plates (10 g/L NaCl, 10 g/L tryptone, 5 g/L yeast extract, and 15 g/L agar, Thermo Fisher Scientific, provided by Life Technologies Italia), and incubated at 37 °C. Before the experiments, a single bacterial colony was transferred in LB broth medium and incubated at 37 °C and at 100 rpm for about 18/20 h before being used in experiments.

Microplastics: microplastics were provided by Dr. Rastelli (Stazione Zoologica “Anton Dohrn”) and were manufactured in the laboratory of the “Università Politecnica delle Marche”. The plastic material used in the experiments was polyvinylchloride (PVC), with density in the range 1.16-1.41 gcm-3). Large pieces of plastic were finely grinded to obtain items ranging between 20 µm and 1000 µm and then suspended in sterile seawater.

3D printing: The 3D printing project was developed using the Rhinoceros CAD software. A Kloner3D 240 model was used as a 3D printer. The model in Fig. 1(b) was printed using Polylactic acid (PLA) material. The model is constituted by three different parts separately printed, namely the base, the top cover (used to contain the diode laser and the beam expander), and the base side cover. Each part is printed with 0.1 mm vertical resolution. A 25 mm/sec printing speed was set in order to minimize vibrations and, in turn, surface roughness. These settings constitute, for the 3D printer we used, a good compromise between printing speed and quality. The parts constituting the prototype in Fig. 1(b) required about 13 hours to be printed using the abovementioned settings.

APPENDIX 1

CONFIGURATION A

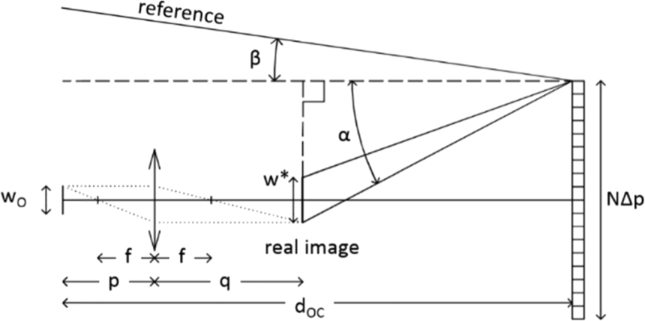
In off-axis DH, a meaningful sampling of the intensity distribution that characterizes the hologram is guaranteed by the Nyquist condition. It states that the period of the interference fringes should be sampled by at least two pixels. Thus, it relates the pixel size Δp of the recording device and the wavelength of light λ to the maximum acceptable angle ${\theta }_{Nyq}$ between the reference (R) and object (O) waves. Using a small angle approximation, the relation is expressed by ${\theta }_{Nyq}\cong \lambda /2\mathrm{\Delta }p$. However, sampling of interference fringes by 3-5 pixels is usually adopted for practical purposes, related also to the difficulties in obtaining perfect plane waves. In this case, the required angle is $\theta <{\theta }_{Nyq}$.

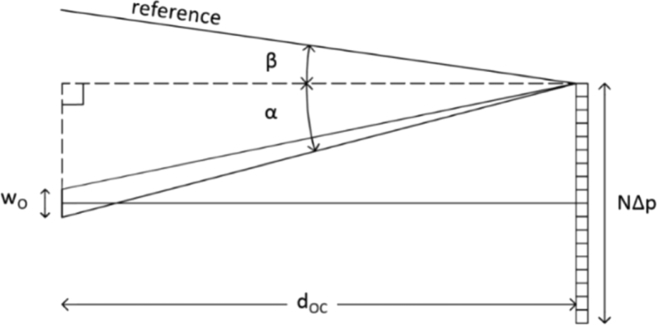
The basic geometry for the Configuration A is reported in Fig. 5. For the sake of simplicity, let us start by considering a lensless configuration and let us perform our analysis in the x-z plane only. We consider a CCD array composed of N pixels of size Δp. To determine the angle between O and R, we follow the procedure outlined by Kreis (T.Krais, (2005) “Handbook of Holographic Interferometry”, Wiley-Vch, pp.81-89). According to the figure, the maximum possible angle between O and R is given by $\theta =\alpha +\beta$, with:

$$\{\begin{array}{l}\alpha \cong \tan \alpha =\left(\frac{N\mathrm{\Delta }p}{2}+\frac{w_O}{2}\right)\frac{1}{d_{OC}},\\ \beta =a\sin \left(\frac{\lambda }{g}\right)\end{array}$$ (3)

where NΔp and w_o are the CCD and the object lateral dimensions, d_OC is the distance object-camera and g is the period of the grating originating R. The Nyquist condition is then verified when:

$$\alpha +\beta <{\theta }_{Nyq}\Rightarrow \beta <\frac{\lambda }{2\mathrm{\Delta }p}-\left(\frac{N\mathrm{\Delta }p}{2}+\frac{w_O}{2}\right)\frac{1}{d_{OC}}$$ (4)

Fig. 5.

Recording geometry for the setup Configuration A, in lensless modality.

When d_OC is much larger than the transversal dimension of the CCD array and object, we can consider $\alpha \approx 0$, which is the approximation used to determine the lower bound on the grating period in the main text. Note that, with respect to Eq. (4), the maximum acceptable angle is overestimated. Nevertheless, by planning to sample an interference fringe over more than two pixels (${\theta }_{MAX}<{\theta }_{Nyq}$), we assure that the sampling condition will be verified. Moreover, this choice offers a buffer to the changes in the inclination of the object angle due to the introduction of a lens. Figure 6 reports the geometry of recording when a lens is added on the object path. The angle $\alpha$ is modified to:

$${\alpha }^{\ast }=\left(\frac{N\mathrm{\Delta }p}{2}+\frac{w^{\ast }}{2}\right)\frac{1}{{d^{\ast }}_{}}$$ (5)

Where $w^{\ast }=w_o{M}_T$ and $d^{\ast }=d_{OC}-p-q=d_{OC}-p-pf/(p-f)$.

Fig. 6.

Changes in the recording geometry for the setup Configuration A by adding a lens.

Distance between object and camera

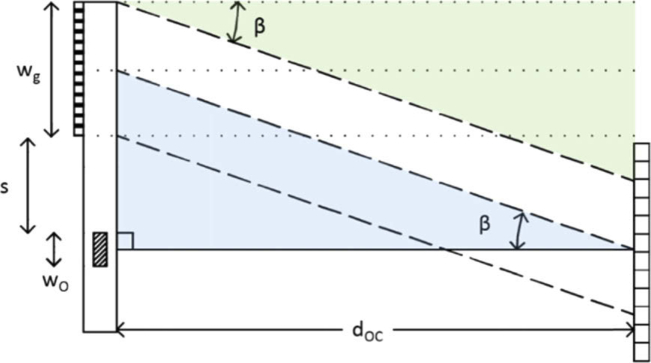
The selection of the proper distance d_OC between camera and object plane depends on the grating characteristics. It should be high enough to enable the separation of the various diffraction orders; moreover we need the first diffraction order to impinge on the camera sensor. Masking the grating to select a specific working zone helps in this process; at the same time, the mask can be designed to block unwanted light from the source. Referring to Fig. 7, the conditions on the d_OC are:

$$\{\begin{array}{l}{d}_{OC}\tan \beta -w_g\ge 0\\ d_{OC}\ge \left(\frac{w_o}{2}+s+\frac{w_g}{2}\right)\cot \beta \end{array}$$ (6)

Where w_O and w_g are the lateral dimensions of the object and grating, and s is the separation between the two of them. We neglect the thickness of the chip, since this is much smaller than d_OC. The first condition in Eq. 6 corresponds to the separation of first and zeroth diffraction orders, while the second corresponds to the intersection on the sensor of reference and object wave.

Fig. 7.

Selection of distance d_OC in setup Configuration A.

Given the microchannel width w_O=1 mm, we prepare a mask that gives s = 2 mm and w_g=5 mm, so that the two conditions become equivalent: the calculated minumum distance is then of 18 cm. Of course, any other combination that satifies the conditions in Eq. 6 would be equally acceptable.

Hologram refocusing: a test with sample polystyrene beads

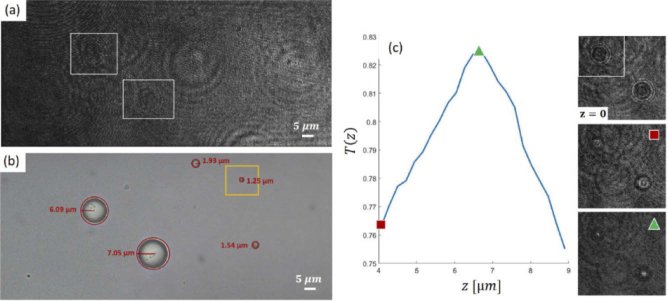
We mix different monodispersed polystyrene microparticles (Sigma Aldrich), with nominal diameter of 2 µm, 5 µm, 10 µm and 15 µm. The sample is inserted into a straight microfluidic PMMA chip with height of 200 µm and width of 1 mm. Flow is stopped and the inlet and outlet are sealed. Then, we select an area that contains multiple beads and acquire the hologram. The hologram and the corresponding bright field image are respectively presented in Figs. S4(a-b). As the camera position does not correspond to the image plane of the lens, the objects are initially out-of-focus (Fig. 8(a)). The best focus position is estimated by optimizing the Tamura coefficient, $T(z)$, over the region in the white box of Fig. 8(a). The plot of $T(z)$ vs. z, is reported in Fig. 8(c), along with the demodulated hologram, $H_{+1}$, an amplitude reconstruction of the bead out of its focus plane (marked with a red square), and the focused amplitude image of the object (marked with a green triangle). From the insets in Fig. 8(c), it is apparent that the best focus position for the bead of interest maximizes $T(z)$ and corresponds to a sharp spot, while the other bead in the same FoV is not in sharp focus in the same plane. The same set of holograms has been used to estimate the system resolution. Considering beads with diameter nominal radius equal to 1 µm as tester samples, such as the object shown in the yellow box in Fig. 8(b), we determined the 2D Gaussian curve that best fits the shape of the spots corresponding to the beads in focus, thus obtaining an estimate of the system Point Spread Function (PSF). We determined the Full Width at Half Maximum (FWHM) of the PSF, namely $\text{FWHM}=0.58$µm, which is an estimate of the system spatial resolution in both directions for objects flowing inside the chip.

Fig. 8.

Refocusing holograms of polystyrene micro-beads captured using configuration A. (a) Digital hologram. (b) Bright-field microscope image of the same beads. (c) Tamura coefficient, $T(z)$ vs. z. DH amplitude reconstructions at different z are shown in the insets.

Configuration B

In Configuration B, we employ a grating with smaller step and thus larger diffraction angle to drastically reduce the overall system length. However, the resulting denser pattern of fringes would not be correctly sampled with this choice. Hence, we use a single relay lens to collect the under-sampled hologram and magnify it on the recorder plane. We start by assuming the grating period g fixed, and we check the distance over which the various diffraction orders will separate (Fig. 7). The condition for the separation of the diffraction orders is $d_{GL}\ge \frac{w_g}{\text{tan}\beta }$. Increasing the angle β reduces the minimum acceptable distance between grating and lens, d_GL. In our case, we have selected $g=3$µm and $w_g=1.6\text{mm}$, corrensponding to an angle $\beta =7.6°$ and a minimum distance $d_{GL}=8.9\text{mm}$.

Also the selection of the lens and the distance between lens and camera affect the hologram sampling. A rigourous analysis of this issue can be performed following the same procedure described for the Configuration A. In this case, the propagation of the beams O and R through the lens should be considered independently, while focusing on the subsequent changes in the angle between them. It is expected that propagation through the lens modifies the reference wavefront from plane to spherical. Thus, after the lens we will have two spherical waves interference, which is know to relax the sampling requirements with respect to the case of spherical-plane waves interference (W.Zhang et al., AIP Advances 8, 055304 (2018)).

We propose here a different approach, more suited to extrapolate a set of straightforward rule of thumbs, by regarding the lens as a relay element that provides a magnified image of the hologram. Before the lens a single hologram fringe is too small to be properly sampled. Thus, on the camera plane after the lens, the magnified hologram must respect the Nyquist sampling requirement, expressed as $p_{f}M\ge 2\mathrm{\Delta }\xi$, where p_f is the fringes period and M is the necessary magnification. We can rewrite this expression as :$\frac{\lambda }{\text{sin}(\theta )}M\ge n\mathrm{\Delta }p$, where we have furthermore introduced n as the number of pixels over which we desire to sample one fringe. By approximating the angle between object and reference wave as $\theta =\alpha +\beta \approx \beta$, we can obtain a simple axpression for the necessary hologram magnification:

$$M_f\ge \frac{n\mathrm{\Delta }p\text{sin}(\beta )}{\lambda }$$ (7)

This value is connected to the position of the recording plane with respect to the lens. We introduce a thin lens approximation to recover an approximate value also for the minimum distance necessary between lens and camera:

$$d_{LC\text{min}}=f(M_f+1)$$ (8)

In practice, we sample a fringe over 4 pixels, to account for any discrepancy from the approximations employed, and we select a lens with focal length $f=6.41mm$. Thus, we obtain from the Eqs. (7) and (8) the values $M_{f\text{min}}=4.6\text{x}$ and $d_{LC\text{min}}=3.5cm$. Note that in the previous discussion, the value of the magnification does not reflect exactly the magnification of the object after reconstruction. To account for it, we must consider the exact position of the object inside the chip (Fig. 9). Then, using the thin lens approximation, it follows that:

$$M_{obj}=-\frac{f}{f-p_{obj}},$$ (9)

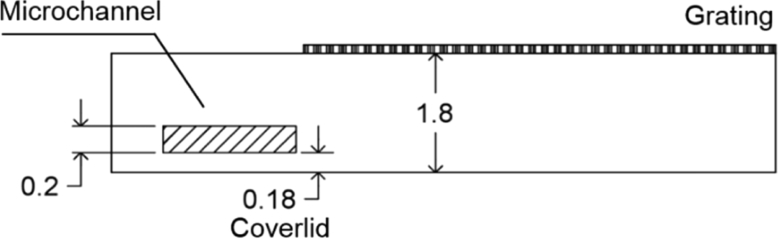
where the minus sign accounts only for the inversion of the real image respect to the object. An accurate estimation of the distance p_obj and the magnification can be obtained if detailed information on the sample platform are known. In the case of the chip, we can refer to Fig. 9. Thus, we can determine the object position as $p_{obj}=d_{GL}-(h_{chip}-h_{coverlid}-h_{channel}/2)$.

Fig. 9.

Details of the PMMA chip structure. Dimensions are expressed in mm.

In conclusion, by using the Eqs. 7–9 we can obtain the guideline values for the realization of the holographic slide microscope in Configuration B.

As a final remark, note that in the previous considerations we have assumed the grating period and the lens focal length as fixed, while their choice should be optimized based on the desired system performance. However, in practice we expect these two elements to be selected from a limited subset of commercially available products or to be subjected to different constraints related to the fabrication process. In this case, it can be helpful to calculate a table of values, where the characteristics of the available gratings and lenses are given, and some subsequent system features are calculated. In this way it is possible to select the best combination in accord to the desired system features. An example is given in Table 2. We examine the combinations of grating and lens, assuming for each two different values. For the latter, we use two lenses from the Thorlabs glass aspheric series, with focal length respectively f = 6.42 and f = 4.51 mm (the second lens is the one employed in Configuration 1). For the grating, we check two possible periods, g = 3um and g = 1.5um. Starting from these values, we calculate the first order inclination angle β, the expected object magnification M_obj and a rough estimate of the minimum value of the system total length, d_TOT=d_GL+d_LC.

Table 2. Relation between the main optical and geometrical parameters in Configuration B. The combination selected in our work is highlighted in blue.

g (μm)	3	3	1.5	1.5
f (mm)	6.24	4.51	6.24	4.51
β (°)	10.2	10.2	20.7	20.7
Mobj	5.5	1.5	1.8	2.5
dTOT(cm)	4.4	3.4	6.9	5.1

Note that, while the smaller grating period offers a wider diffraction angle (and thus a larger separation of the diffraction orders), the overall system length increases. This is caused by the necessity to obtain a higher fringes magnification, $M_{f\text{min}}=9.3\text{x}$ . The first column in Table 2 (highlighted in blue) reflects our final choice, which offers the best compromise between object magnification and system dimensions.

Funding

Ministero dell’Istruzione, dell’Università e della Ricerca10.13039/501100003407 (PON ARS01_01183).

Disclosures

The authors declare no conflicts of interest.