Abstract
Diffusive correlation spectroscopy (DCS) is an emerging optical technique that measures blood perfusion in deep tissue. In a DCS measurement, temporal changes in the interference pattern of light, which has passed through tissue, are quantified by an autocorrelation function. This autocorrelation function is further parameterized through a non-linear curve fit to a solution to the diffusion equation for coherence transport. The computational load for this non-linear curve fitting is a barrier for deployment of DCS for clinical use, where real-time results, as well as instrument size and simplicity, are important considerations. We have mitigated this computational bottleneck through development of a hardware analyzer for DCS. This analyzer implements the DCS curving fitting algorithm on digital logic circuit using Field Programmable Gate Array (FPGA) technology. The FPGA analyzer is more efficient than a typical software analysis solution. The analyzer module can be easily duplicated for processing multiple channels of DCS data in real-time. We have demonstrated the utility of this analyzer in pre-clinical large animal studies of spinal cord ischemia. In combination with previously described FPGA implementations of auto-correlators, this hardware analyzer can provide a complete device-on-a-chip solution for DCS signal processing. Such a component will enable new DCS applications demanding mobility and real-time processing.
Keywords: High Performance Computing, Field Programmable Gate Array, Diffuse Correlation Spectroscopy
I. INTRODUCTION
DCS is a relatively new optical technology to probe microvascular blood flow [1]. In the typical implementation, the tissue of interest is illuminated with a long-coherence length near infra-red (NIR) laser and the temporal fluctuation of interference patterns formed on the tissue surface are detected. This interference (‘speckle’) pattern fluctuates on a time scale dependent on the motion of scatterers in tissue dominated by red blood cells. Such temporal fluctuations can be quantified with an autocorrelation function. A correlation diffusion equation [2] relates tissue optical properties and motion of scatterers to the correlation decay. By fitting the measured autocorrelation curve using the theoretical model to the diffusion correlation function, a blood flow index (BFI) can be derived. This technology has been validated against various techniques, including MRI [3-5], microspheres [6], and Doppler ultrasound [7]. It is fundamentally different from measurements of blood volume and/or saturation with Diffuse Optical Spectroscopy (DOS) or Near Infrared Spectroscopy (NIRS) devices. DCS probes the motion of scatterers (including red blood cells) in tissue on scales of ~ 1 μs, quantifying this motion every 10-1000 ms, while DOS/NIRS measures tissue absorption and scattering at ≫1 ms time scales [1].
DCS has been widely used to assess blood flow in tissues more than 1 cm below the tissue surface, permitting non-invasive assessment of blood flow. This technique is particularly useful to measure microvascular cerebral blood flow and offers some unique advantages over other techniques. For example, DCS has been widely applied to measure cerebral blood flow in the critically and chronically ill, including adults with ischemic stroke [8-10] or during neuro-critical care [11, 12] and pediatric patients [13, 14]. This technology has also been applied to cancer monitoring, as many tumors have abnormal microvasculature and enhanced blood flow [15]. Recently, minimally invasive DCS probes have been developed to allow for measurement of spinal cord blood flow. These probes can be placed into the spinal canal within the epidural space through a laminotomy or percutaneously via an epidural needle to monitor spinal cord blood flow. Extensive studies in large animal models have demonstrated the feasibility of these measurements during a variety of surgical interventions [16-18]. Monitoring spinal cord ischemia may have utility during aortic surgery, spine reconstruction procedures, and in the management of patients after spinal cord injury to prevent secondary ischemia. Recently, so-called “Fast DCS” has been developed by Wang [19], which measures blood flow dynamics at up to 100 Hz utilizing a software correlator. This higher temporal resolution enables resolution of blood flow pulsation due to the cardiac cycle [20, 21].
The DCS data analysis typically requires two steps: (1) calculating a temporal autocorrelation function of the scattered light intensity and (2) fitting the measured autocorrelation to a theoretical model, i.e. a solution of the correlation diffusion equation, to extract a blood flow index. The autocorrelation function measured in DCS requires a large range of correlation delay times (τ:200 ns-1 ms). In calculating the temporal autocorrelation function in DCS, a ‘multi-tau’ approach, which adjusts integration times as τ increases, is generally used to improve computational efficiency by significantly reducing the number of correlation values to be calculated. Multi-tau correlation was first invented by Schatzel et al [22] and has been implemented in software [23, 24] and in hardware using FPGA technology [25]. Both traditional and fast DCS measurements require a non-linear fit of the auto-correlation curve at each time point of measurement to a solution of the correlation diffusion equation. This forms a computational bottleneck, as these fitting algorithms require significant computation resources. This fit is frequently performed in postprocessing, reducing the utility of DCS measurements, e.g., in guiding surgical interventions in real time. We have developed a hardware analyzer that implements the DCS curve-fitting algorithm on a Xilinx FPGA with a significantly increased processing efficiency. Coupled with previous work utilizing FPGAs to calculate the correlation function, this has opened the path to integrate the entire data processing necessary for DCS on a single silicon chip.
II. METHODS
A. Theoretic DCS Model
We apply the simplest (infinite homogeneous medium, eqn. 1) and most common (semi-infinite half-space, eqn. 2) analytical solutions to the diffuse correlation equation. In the semi-infinite half-space (eqn. 2), there is a planar boundary between a homogenous diffuse media and a non-diffuse medium (e.g., tissue-air) at z=0 in the solutions described in Durduran et al [1]. For the purposes of these calculations, tissue optical properties (index of refraction, absorption, and scattering) and experimental geometry (source-detector separation) are assumed constants in the fitting procedure. Combinations of these constants are designated as A, B, F and H in equations (1) and (2) and defined in Appendix 1. The resulting simplified equations have only two free parameters: β and αDB.
| (1) |
| (2) |
β is the inverse of the number of detected modes. In our work, β ≤ 1/2 because we detect unpolarized light through a single mode fiber. In an ideal experiment in which there is only a single spatial and polarization mode detected, β = 1. As our device does not select the polarization of the highly scattered detected light with two polarization modes, β is 1/2. Any additional modes, background light, etc., will further reduce this value. Clinical experiments often take place under non-ideal circumstances and β may change with time and is a parameter in experimental data fitting. The product αDB is often termed the “blood flow index” (BFI).
The DCS analysis computes αDB and β values through the best fit of the theoretical autocorrelation function from equation (1) or (2) to the acquired experimental intensity autocorrelation g2e (τ). The Mean Square Error (MSE) of the fit is defined using equation 3 where N is the number of values in g2e(τ). The best fit criteria is defined as the minimum of the MSE.
| (3) |
We use an iterative, non-linear Nelder-Mead method to search the minimum value of MSE without the need to calculate its derivative [26]. We have implemented the algorithm using FPGA for true hardware computing.
B. FPGA Computation
FPGA was first developed in 1985 by Xilinx and later expanded by Altera, Actel, Lattice and other semiconductor companies. An FPGA chip has a huge number of configurable logic blocks (CLB), digital signal processing (DSP) slices and distributed memory on one silicon chip. FPGA hardware computing employs the parallel processing technology and implements algorithms as digital logic circuits using the CLBs, DSP slices and memory blocks on a FPGA chip. Compared with software solutions for the same computation, it eliminates the necessity for an operating system and guarantees high throughput. Algorithms implemented on an FPGA can be much faster than those programs in a typical computer language because the performance of the FPGA is not compromised by the overhead of operating systems and other unrelated processes running in the background.
Numeric representation is the key factor that determines the complexity of the computing logic. Fixed-point representation was popular in the past when the FPGA resources were not abundant. Its limited resolution can introduce significant computing error that could alter the convergence of the algorithm. Furthermore, the dynamic range of fixed-point value is also limited and can easily cause overflow during computation. αDB is roughly 10−8 smaller than β in the DCS model and thus floating point representation is a better choice than the fixed point. As the FPGA resources grow exponentially with the technology development, it becomes affordable to adopt floating-point representation in FPGA to address the issues in fixed-point representation. There are two floating-point representations: single floating-point representation that uses 32-bit binary and double precision representation that uses 64-bit binary. Both are defined by the IEEE Standard for Binary Floating Point Arithmetic (IEEE 754) [27]. We adopted single floating-point representation in our DCS analyzer because it consumes moderate amount of DSP slices and logic cells and offers reasonable resolution and dynamic range. Double precision can also be considered if the FPGA resources are sufficient to hold the computation logic of the double precision operations of the algorithm. The FPGA can also accommodate the customized floating point data type for the optimal use of the FPGA resources [28]. However, it needs an extra step of conversion to either single precision or double precision data type for subsequent processing off the FPGA.
It is challenging to build the computing circuits of arithmetic operations and math functions from scratch. Fortunately, FPGA manufacturers have provided the solution by offering FPGA IP cores for the hardware computation. Xilinx (Xilinx, Inc., San Jose, CA 95124) has IP cores [28] that adopted the Coordinate Rotation Digital Computer (CORDIC) algorithm [29, 30] and expanded the support to cover the basic math functions of trigonometric, exponential and logarithmic functions. Those IP cores support the computation in both single precision and double precision format as well as customized floating-point representation.
A “pipeline” is the primary structure for high throughput parallel processing in FPGA. It divides an algorithm into multiple steps and each step is implemented as a digital module in FPGA, which completes its operation within one FPGA clock cycle. The modules in the pipeline work simultaneously under the same FPGA clock signal, which is a series of digital pulses of fixed frequency. The signal edge (e.g. the rising edge) moves the data a step forward in the pipeline. Therefore, the pipeline inputs data one per FPGA clock and outputs the processed data one per FPGA clock after a fixed latency (Equ.4). Computing cores are designed as the pipelines and can be connected in serial to form a larger pipeline. If M is the number of clocks to process the first data point through the pipeline and ΔT is the clock cycle, MΔT will be the time delay or latency of the FPGA computation pipeline. The total time needed for the processing N data points in a pipeline can be determined using the following equation.
| (4) |
Data synchronization is the essential mechanism to ensure the correct data flow in pipeline. If the operands at the inputs of a core are from different data paths, they must be synchronized to guarantee the correct output. This is achievable by adjusting the delays in the data flow paths to synchronize the input data.
C. FPGA DCS Analyzer
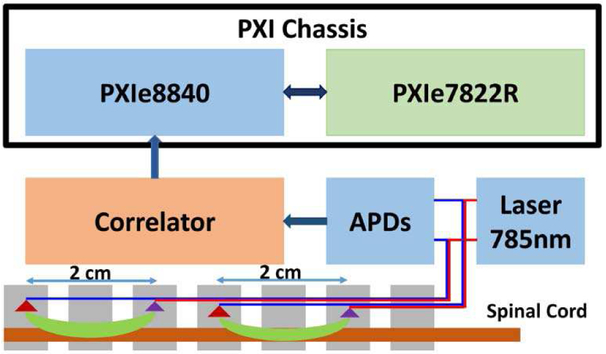
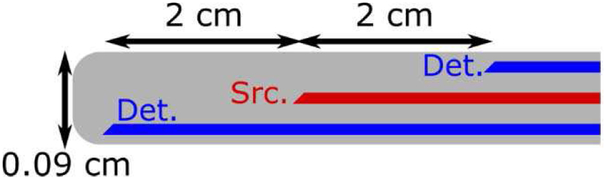
Figure 1 illustrated the composition of the DCS system with an FPGA analyzer. The computer is a PXI embedded computer system running Windows 7 (PXIe 8840, National Instruments, Austin, TX) with a reconfigurable digital I/O PXIe module powered by Xilinx Kintex 325 (PXIe 7822R, National Instruments, Austin, TX). The probe consisted of a pair of single mode detector fibers placed symmetrically about a source fiber inside a cylindrical sheath of milky plastic (Fig. 2). A long coherence laser (Crystalaser, Reno NV, 785nm) light was coupled into the source fiber and attenuated to ~25 mW. Each detector fiber was connected to an individual avalanche photodetector (APD). The scattered light from tissue is collect by a fiber optic probe and a Silicon APD (Model SPCM-AQ4C, Excelitus Technologies, Watertown, MA) converts the photons into a series of electronic pulses. The correlator (correlator.com, NJ) counts the pulses and outputs an autocorrelation function. The correlation data are transferred to the embedded computer through a USB connection. LabVIEW FPGA (National Instruments, Austin, TX) was used to program the FPGA chip on the reconfig-urable digital module. It has the convenience of the graphic programming tool of LabVIEW and removes the challenge of using hardware descriptive languages to program the FPGA chip. The system software is also programmed in LabVIEW.
Fig. 1.
The functional diagram of a DCS system. Only one detector is shown for each probe.
Fig. 2.
DCS probe used in the measurement of microvascular blood flow in the spinal cord. Source (Src.) and detector (Det.) fibers are described in the text.
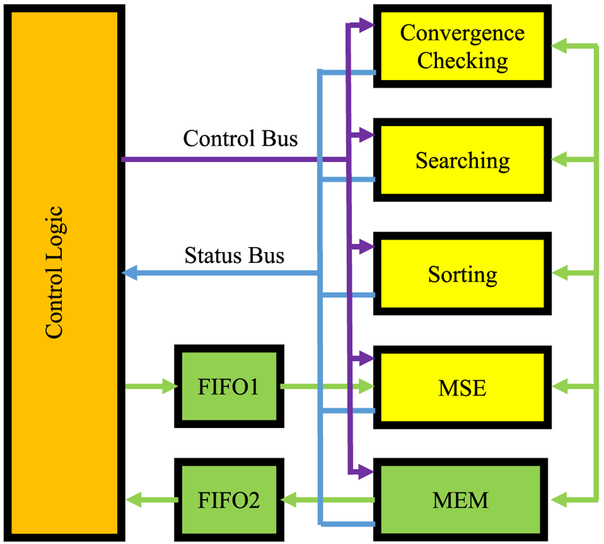
We utilized the semi-infinite solution to the correlation diffusion equation to derive the BFI at each time point. In a preparatory step, some constant values are combined to avoid redundant computation and save FPGA resources. The values 1/(r1*H) and 1/(rb*H) are calculated so that multiplication replaces division in equation 2. The product of B* τ is also calculated in advance where τ is a series of time delays corresponding to the correlation values. In addition, one is subtracted from the acquired correlation values so that there is no need to implement the “plus one” operation in equation 2 for the MSE calculation in equation 3. The modified correlation values and the corresponding product of B* τ are sent to FPGA via a first-in-first-out buffer (FIFO1) and stored in two memory blocks in FPGA memory (MEM). The initial values of αDB and β and the model constants are sent to FPGA and stored in registers in MEM for easy access. Figure 3 illustrated the system diagram of the FPGA analyzer. The computations in the Nelder-Mead algorithm are divided into four sections that can be implemented as four pipelines: an MSE pipeline to calculate the MSE of each αDB and β pair, a sorting pipeline to find the sequence of the latest three MSEs, a search pipeline to find new pair of αDB and β values that have a smaller MSE, and a convergence pipeline to determine when to terminate the curve fitting. The control logic module receives the status of pipelines from the status bus and use the rules in the Nelder-Mead algorithm to determine the operation sequence of the pipelines. The following is the description of the general flow of the sequence control.
Fig. 3.
The computing logic of multi pipelines for the Nelder-Mead method for numerical modeling. Four pipelines are used for MSE computing, MSE sorting, Parameters searching and convergence checking. The execution sequence is controlled by the control logic module based on the outputs from the pipelines. The paths between MEM and the four pipelines are bidirectional for data transmission.
First, the control logic starts the MSE pipeline to calculate the MSE of three pairs of αDB and β values. The MSEs are then stored in MEM for future use. Second, the control logic sends the three MSEs to the sorting pipeline to rank the MSEs. The output data of the pipeline are the indexes of αDB and β pairs corresponding to the sorted MSEs and are stored in registers for the convergence pipeline and the searching pipeline. Third, the control logic picks the smallest and largest MSE and sends them to the convergence pipeline to test if the difference is within the preset range. If the convergence criterion is met, the control logic outputs αDB and β values of the smallest MSE via FIFO2. Otherwise, it starts the searching pipeline using αDB and β pairs of the two smallest MSEs to find candidates of the new pairs with the reflection, extension and contraction formulae defined in the algorithm. The MSEs of those candidates of αDB and β pairs are computed using the MSE computing pipeline again and the new αDB and β pair is selected by the control logic so that its MSE is at least smaller than the largest MSE calculated in the previous step. The new αDB and β pair will replace that of the largest MSE. If it fails to find the new αDB and β pair, the search pipeline will generate two pairs of αDB and β values using the shrink formula in the algorithm. The control logic replaces the αDB and β pairs of two largest MSEs with the two new αDB and β pairs and computes their MSEs using the MSE pipeline. The iteration repeats from the second step until the convergence criteria are satisfied.
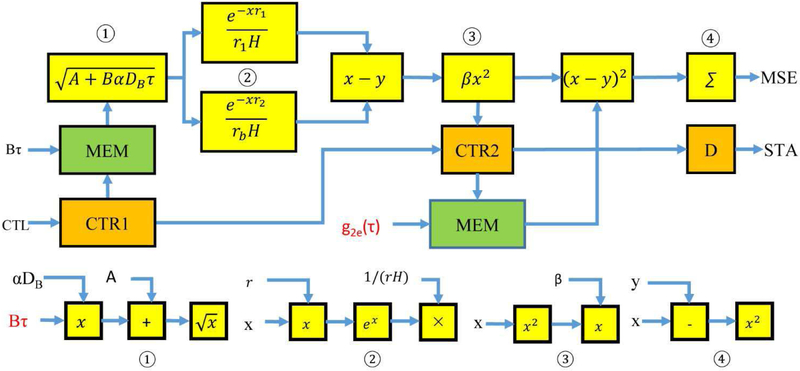
The MSE pipeline using equations 2 and 3 is the most complicated pipeline in the analyzer (Fig. 4). The inputs to the pipeline are the acquired correlation data g2e(τ) and B*τ. The two terms inside the parenthesis in equation 2 are identical operations and therefore two instances of the same module ② are used in parallel. The latencies of the computing cores in the pipeline are set to one FPGA clock cycle except for the square root core in ① and exponent core in ③. The square root core has the latency of four FPGA clock cycles and the exponent core has the latency of ten FPGA clock cycles. Based on those settings, module ① has latency of 6 FPGA clock cycles, module ② has latency of 13 FPGA clock cycles including the following subtraction, module ③ has the latency of 2 FPGA clock cycles and module ④ has latency of 3 FPGA clock cycles including the following accumulator (Σ). Thus, the entire pipeline has the latency of 24 FPGA clock cycles. Counters (CTR1 and CTR2) are incremental counters driven by the FPGA clock and the number of correlation time values N is their overflow values. The control module resets both counters to zero as the initial addresses of the two memory blocks holding the input data through the CTL signal from the control bus. It also starts the pipeline by enabling CTR1 to read the B* τ, and sends them to module ① one value per clock. The output data of module ③ are the theoretical correlation values from the numerical model. The CTR2 is not enabled until the valid signal from module ③ is active. This synchronizes the theoretical correlation values with the acquired correlation values at the same time delay for the following MSE computation. When the CTR1 overflows, the valid signal to module ① becomes inactive indicating the end of data input to the pipeline. When CTR2 reaches the overflow value, the overflow signal enters a delay module (D) with the latency of 3 FPGA clock cycles, which is the total latency of the module ④ and the accumulation core. The output of the delay module is the active completion signal STA and ensures that the output MSE including the sum of squared errors of all data points. Since N is a constant during the fitting, there is no need to divide the MSE by N for the following sorting step. When the control module receives the STA signal from the MSE pipeline, it deactivates the CTL signal to put the MSE pipeline on hold.
Fig. 4.
The pipeline implementation of the MSE calculation in the DCS analysis. Each block in yellow is an IP core or modular combinations of IP cores (①, ②, ③ and ④). ∑ is the accumulator core. CTR1 and CTR2 are counters. D is the delay unit of three clock cycles that turns the counter overflow signal into the STA signal of the pipeline. MEM is the memory storing the correlation delay and experiment data. Bτ and g2e(τ) (labeled in red) are inputs to the pipeline. Constants A, r1, rb and H are stored in FPGA memory. αDB and β are iteration parameters. x and y represent the input data of the cores.
D. Phantom Study
The FPGA analyzer was also tested against a software analysis scheme in phantoms. Phantoms with a range of viscosities (and therefore effective diffusion constants DB) were produced utilizing glycerol, 20% Intralipid (Baxter Healthcare, Deerfield, IL), and water, following recipes from Cortese [31] to maintain a constant . We produced four phantoms with four different flow levels. We measured the flow levels using the DCS system with the FPGA analyzer and an independent DCS system with offline DCS analysis in a semi-infinite geometry for ~5 minutes for each phantom. BFI of the lowest viscosity phantom (no glycerol) was set as baseline. BFI is normalized to baseline using equation 5 as the relative BFI or rBFI. The phantom test was conducted in the room temperature of 25 °C. The rBFI of each phantom was measured by both DCS systems. Bland Altman plot was used to compare the consistency of the BFI measurement with 50 pairs of measurements for each phantom.
| (5) |
E. PRE-Clinical Study
We tested the DCS analyzer in the preclinical study of ischemia of spinal cord during spinal cord distraction in an adult sheep model. Details of the study will be reported separately. The protocol was approved by the IACUC at Stony Brook University. The sheep was pretreated with glycopyrrolate (0.02 mg/kg, IM). Anesthesia was induced with ketamine 10 to 20 mg/kg IM, animals were intubated, and anesthesia was maintained with isoflurane (1.5 to 3.0%). The spine was exposed sub-periosteally from T11 to L2. Fiber-optic probes were inserted into the epidural space through a laminotomy at the L1/L2 level and advanced to the planned distraction site under fluoroscopic imaging. Pedicle screws (5.5×30mm) were placed at the lowest two thoracic levels and connected to 5.5mm bilateral rods. Baseline flow data was obtained at the start of distraction and the spine was distracted at 2 mm intervals until a 50% drop in optically measured blood flow was observed or maximum distraction distance was reached. The DCS analyzer performed the real-time analysis of DCS data and presented the real-time rBFI.
III. REULTS
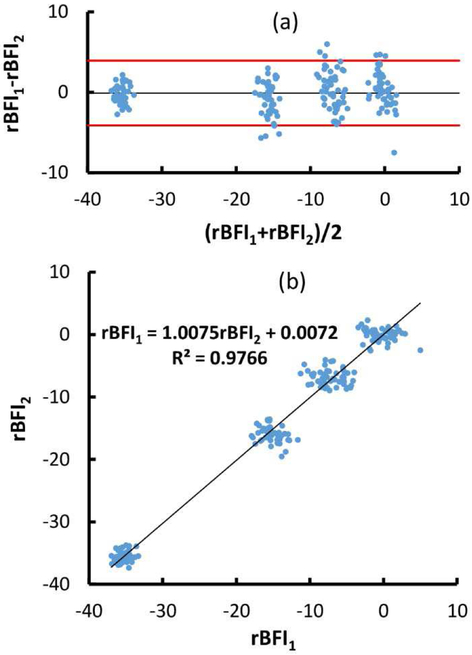
The Bland Altman plot (Fig. 5) demonstrated that the rBFI differences between the measurements by the FPGA analyzer and those by the software analysis were within the 95% of confidence level. This suggested that both measurements were consistent. The linear correlation showed high correlation with r2 value of 98% and the slope of 1.01.
Fig. 5.
rBFI1 is from FPAG analyzer and rBFI2 is from software analysis. (a) Bland Altman plot of the BFI measurements on four phantoms by two independent DCS systems. The black line indicated the difference mean and the red lines define 95% confidence interval (1.96 standard deviation of the rBFI difference) from the difference mean. (b) Linear correlation between the rBFIs.
We have compared the performance of the FPGA implementation of the Nelder-Mead method with the software approach to fit the measured autocorrelation function to the theoretical model. We added a counter in the FPGA to measure the total number of clocks used for the curve fitting of one data set. The computation time of FPGA was the product of the total number of clocks and the FPGA clock cycle, which is 25ns at the FPGA frequency of 40MHz. In addition to the FPGA-based algorithm, we utilized the MATLAB function fminsearch (Mathworks, Natick, MA), which also uses Nelder-Mead algorithm to derive BFI from the same correlation data. We used the MATLAB profiling tool to measure the CPU time for the fminsearch function to process the same data set. The MATLAB code was executed on the Dell Optiplex 9010 (Dell, Round Rock, TX) with a CPU of i7-3770 quad cores running at 3.4GHz. Twenty-seven autocorrelation curves were used in the test. Each containing approximately 60 paired values of tau and g2 were used in the test. The FPGA implementation used the single precision float point as the data representation. The initial values of αDB and β were set the same for both FPGA and MATLAB computation. The averaged time was 539±127 μs for the FPGA processing and 51 ±8 ms for the fminseach function of MATLAB. The BFI values of the same correlation data set from both methods were also compared. The relative error, defined as the ratio of the absolute difference between the FPGA BFI and the software BFI to the software BFI, is within 0.1%. The difference could be attributed to the data precision and the convergence criteria used in the two methods.
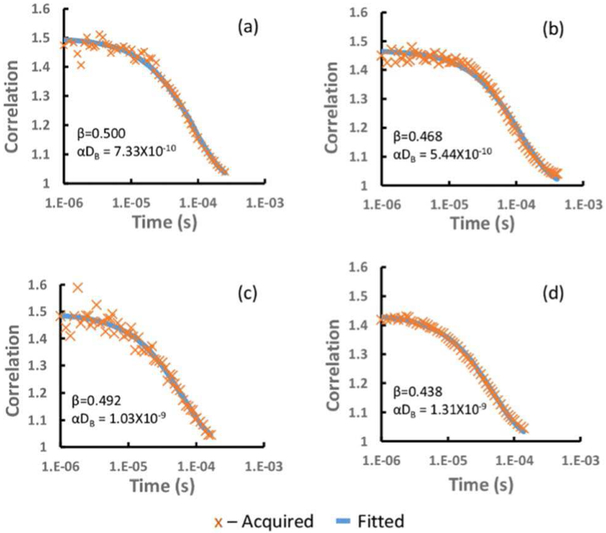
We utilized this DCS analysis system in a large-animal pre-clinical monitor of spinal cord ischemia to demonstrate the potential utility of real-time DCS analysis. Figure 6 showed four correlation fitting curves from the FPGA DCS analyzer. They were from two detector acquired at the beginning of the stretch (baseline) and the end of stretch in the animal study.
Fig. 6.
The fitted vs. acquired correlation. (a) at site, baseline (b) at site, end stretch (c) above site, baseline (d) above site, end stretch.
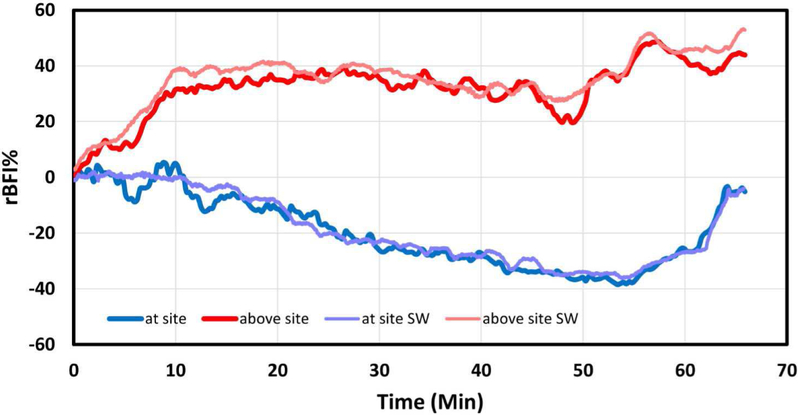
Figure 7 demonstrates a typical time course, in which the rBFI at and above the distraction levels. It can be seen that flow falls at the site of distraction and increases above the site. The distraction started at 0 minutes, defining a baseline BFI for each site. The rBFI at the distraction site decreased progressively with increasing distraction to a nadir of ~−40% of baseline at 50 minutes. Following release of the distraction hardware at around 57 minutes, blood flow at the site of injury recovered slowly to nearly the baseline level. During this period, rBFI at the site superior to the distraction site continue to increase up to 50%. This increase in blood flow may be due to a redirection of blood flow from the distraction site into alternate paths in the spinal cord vasculature. The results of the full parametric fit were displayed in the operating room, enabling clinicians to observe the change of spinal cord blood flow in real-time throughout the surgery. The correlation data from animal study were also processed by MATLAB DCS analysis software offline for the system level comparison and both results matched well. The minor difference could be attributed to the difference in the preprocessing of the correlation data and the post-processing of the BFI data in the two methods.
Fig. 7.
Temporal and spatial variations in the relative BFI (rBFI) at two sites on the spinal cord: at and above an injury caused by vertical stretching of the spinal column in a scoliosis surgery model. The “at site SW’ and “above site SW” are the data processed offline by software. The photon count rates were between 100 and 700 k counts/s during the experiment.
IV. DISCUSSION
It is computationally intensive to obtain the BFI from measured autocorrelation of the scattering lights from tissue using the analytical DCS model. Curve fitting of the measured autocorrelation values with the theoretical model is a non-linear process, which requires the repeated computation of the theoretical correlation values from the pair of αDB (BFI) and β parameters in the model until convergence. That process is time consuming and must be repeated for each time point and detector channel. Existing real-time fitting algorithms in software frequently use a simplified fitting procedure, for example, calculating the half time of the decay, to minimize the computational load.
We successfully implemented the DCS analysis algorithm of non-linear fitting on an FPGA chip. We adopted the Nelder-Mead method because it is used in our offline DCS analysis and it involves only simple math computations implementable in FPGA. The phantom study demonstrated that the DCS system with the hardware analyzer produced the consistent data compared to the independent DCS system with offline DCS data analysis. The pre-clinic study has proved that the DCS analyzer enables the real time processing of DCS data and the presentation of rBFI to clinicians intraoperatively. The DCS FPGA analyzer will have a significant impact on the design of DCS systems. To our knowledge, this is the first report of implementing the DCS algorithm on an FPGA chip. Current DCS systems rely on powerful desktop computers for the DCS data processing. Some use hardware correlators to relieve the computation burden of the autocorrelation of the scattered light from the main computer. A high-end desktop computer is a necessity to provide the computation power, but it is not suitable for applications when portability and size of the device is crucial. For example, while high end computers are usually integrated into research DCS systems, DCS clinical monitors which may be routinely deployed at patient’s bedsides during critical care requires significant reductions in device size and cost. The DCS FPGA analyzer has moved the computation task of DCS algorithm to the FPGA hardware. The associated enormous reduction in required computing power significantly reduces the device profile and enables use of computers with limited capacity, e.g., tablets, for user interface, device control and data presentation, as well as integration with multi-device clinical monitors.
Moving forward, a correlator and analyzer may be integrated into the same FPGA chip. This will be the complete device-on-a-chip solution for DCS data processing. The FPGA chip will accept the output from the photo detector, compute the correlation of the scattered light intensity, and derive the BFI as the output. When combined with microcontroller technology, the FPGA can communicate with the computing device through a variety of wired or wireless communication links and make the DCS system both portable and with fast real-time processing capability.
The DCS FPGA analyzer provided a full parametric fit of the DCS theoretical model. It can also be adapted to process correlation curves calculated from photons binned by detector arrival time, i.e. time-domain DCS. Current implementation utilizes a semi-infinite model. This design is modular: multiple analyzer modules can be implemented on one FPGA chip. Our current solution used 12.5% of the total available CLBs, 2.5% of block RAM and 8% of DSP units on a Xilinx Kintex 325 FPGA for one channel. The usage is about 1/8 of the chip capacity, suggesting that at least 6 detector channels may be analyzed with the same FPGA chip.
Our preliminary performance test showed that the DCS FPGA analyzer is at least comparable to a typical software solution. It takes less than 1 ms to finish one curve fitting on FPGA and enables real-time data display, even for ‘fast’ DCS data collected at ~100 Hz. Two main factors affect the performance difference between FPGA and CPU. First, the software runs under the support of an operating system and compete resources with other software threads. The CPU time spent on the DCS analysis is dependent on the number of concurring threads and their priorities. Even though the CPU is running at GHz frequency, the effective running speed of the DCS analysis is much lower. FPGA solution is the digital circuit entirely dedicated to the DCS analysis algorithm and at the full speed of FPGA clock. Second, the software solution processes data in serial. For example, the correlation from the theoretic model is computed one value at a time. That means that the next correlation value will not be processed until the completion of the current correlation value. FPGA solution uses a pipeline for parallel processing so that the computation of the correlation values are handled one value per FPGA clock cycle. Our pipeline takes 21 FPGA clocks cycles out of 24 clock cycles in the MSE pipeline to compute one correlation value. However, during the 21 FPGA clocks, there are other 20 correlation values are also being calculated in the pipeline. Pipeline architecture is efficient in the resources uses and scalable to accommodate any data size without the need of additional computation units. In our analyzer, the pipeline for the computation of one MSE has the latency of 24 clock cycles. To compute an MSE from eqn. 2 and a measured autocorrelation function of 50 time delays (values of τ), it takes 73 FPGA clock cycles (49+24). If the same computation is done in serial processing, it will cost 1200 clock cycles (50*24) for the same data size. The difference will be even greater at larger data sizes (number of τ values). In the DCS analysis, the time saving is significant using the FPGA pipeline solution because most of the processing time is on the repeated computation of the theoretical correlation values in the curve-fitting algorithm. That is major factor that FPGA outperforms CPU in the DCS measurement. Note that the performance test was preliminary and was not intended to accurately measure the performance difference between the DCS measurement algorithm implemented on a FPGA or CPU.
Our solution also has limitations. Like all single-wavelength DCS implementations, this DCS FPGA analyzer assumes knowledge of the tissue optical properties, which can be obtained from simultaneous measurements with time or frequency domain diffuse optical spectroscopy. A more comprehensive solution should also include the optical properties as variables and additional equations from diffuse optical spectroscopy. Our FPGA analyzer can only process two variables using the Nelder-Mead algorithm. This requires major modification in the FPGA logic to accommodate the additional variables and new pipelines for the additional equations.
In conclusion, the DCS hardware analyzer offers a new data processing solution for DCS technology. This advance is a critical step towards developing standardized DCS modules and devices for clinical applications.
ACKNOWLEDGMENT
This work was supported by NIH under the Grant U01NS095761, “Spinal Fiber Optic Monitoring”
Biography

Wei Lin received B.Ss degree in Biomedical Engineering in 1986 and M.S. degree in Mechanical Engineering in 1989 from Shanghai Jiaotong University, Shanghai, China. He received Ph.D. degree in Mechanical Engineering from Stony Brook University in 2001, Stony Brook, NY, U.S.
Dr. Lin joined the Department of Applied Mechanics in Fudan University, Shanghai, China as the assistant professor in 1989 and lecturer in 1993. He joined the Department of Biomedical Engineering as the assistant professor in 2004 and associate professor in 2013. His current research interests include medical instrumentation, wearable medical devices and high performance computing in embedded systems.
Dr. Lin is a member in IEEE and Biomedical Engineering Society.

David R. Busch (M’10) received a B.A. in Physics from St. John’s University, Collegeville, MN, in 2001, a Ph.D. degree in Physics from the University of Pennsylvania, Philadelphia, PA, in 2011, and post-doctoral training at the Children’s Hospital of Philadelphia.
Since 2018, he has been an Assistant Professor of Anesthesiology & Pain Management and Neurology & Neurotherapeutics at the University of Texas Southwestern Medical Center.

Chia Chieh Goh was born in Malaysia in 1979. He received the BE degree in electronic and communication engineering from the University of Nottingham, UK, in 2003 and the Ph.D. degree on research of smart vehicle embedded system for abnormal driver behavior in 2014. He became a Member (M) of IEEE in 2015.
From 2003 to 2017, he was working in both academic and industrial field. Primary research and job focus on embedded hardware/software system, artificial intelligence, parallel processing and cloud computing for academic, multinational companies and industry sectors.
Dr. Chia Chieh Goh is the member of the Institution of Engineering and Technology (MIET) in 2014. He is currently a postdoc researcher in the Department of Biomedical Engineering, Stony Brook University. Research focus on spinal cord injury monitoring system on a FPGA chip.

JAMES BARSI was born in Bronx, New York, NY, USA in 1979. He received a B.S. in chemistry from Fordham University in 2001 and M.D. degree from New York University, in 2005.
From 2005 to 2010, he completed an Orthopaedic Residency at St. Luke’s Roosevelt Hospital in New York. In 2010 to 2011, he completed a fellowship in Pediatric Orthopaedics at Children’s Hospital Colorado. Since 2011, he has been an Assistant Professor with the Department of Orthopaedics, Stony Brook University, Stony Brook. He is the author of numerus articles and has presented nationally on topics related to basic science and clinical orthopaedics. His research interests include scoliosis and pediatric trauma.
Dr. Barsi is a diplomate of the American Academy of Orthopaedic Surgeons and a member of the Pediatric Orthopaedic Society of North America.

Thomas Floyd, M.D. received his medical degree at the University of Pennsylvania, School of Medicine and completed a residency in anesthesiology at the University of Minnesota. He received advanced training through a magnetic resonance fellowship and a cardiovascular and anesthesia fellowship, both at the University of Pennsylvania.
Dr. Floyd is a Professor in the Department of Anesthesiology and Pain Management at UT South-western Medical Center. He has served as principal investigator on several NIH funded research projects focused primarily on the development and application of imaging technologies and strategies for the early diagnosis and management of neurological sequelae associated with surgery. A second major focus for his laboratory is in understanding the role of hypoxia in aging-associated cognitive failure.
APPENDIX
In this appendix, we describe the simplification of the solutions to the diffusion equation solutions for infinite and semi-infinite media, with the assumption that all tissue optical properties and probe geometry are known. The solutions therefore have only αDB and β as free parameters in the fit. Table I is the glossary of variables used in the equations.
TABLE I.
Glossary
| Symbol | Description | |
|---|---|---|
| α | Fraction of scattering events from moving particles. | |
| DB | Effective Brownian diffusion coefficient. | |
| D | Photon diffusion constant | |
| k0 | 2π/λ | Wavenumber of DCS illumination of wavelength λ (785nm) |
| μa | Tissue absorption coefficient at the wavelength of interest (0.1cm−1) | |
| Tissue reduced scattering coefficient at the wavelength of interest (17 cm−1) | ||
| ρ | Radial distance between source and detector in semi-infinite measurement (known) | |
| Position of detector | ||
| Position of source | ||
| Distance between source and detector position (dependent on probe) | ||
| v | Speed of light in the medium | |
| z | Depth into semi-infinite medium; surface is z=0 |
A. Infinite Geometry
The infinite media Green’s function for the non-normalized electric field autocorrelation function for a source of unit power in the diffusion approximation is [1]
| (A1) |
where
| (A2) |
This assumes the mean squared displacement of the scatters is well modeled by a Brownian diffusion coefficient (< Δr2 > = 6DBτ). For the purposes of this calculation, the source and detector positions, tissue optical properties, and fraction of moving scatterers are fixed. Letting , , , and C = v/(4π D) (all constants for this calculation), the above reduces to
| (A3) |
The normalized temporal field autocorrelation function is
| (A4) |
which is related to the intensity autocorrelation function through the Siegert relation [32] under the assumptions of the photon diffusion model,
| (A5) |
The intensity autocorrelation function is much easier to measure experimentally and forms the data input to our fitting model. This reduces to
| (A6) |
where . β and the product αDB are the free parameters in the fit. αDB is often referred to as the ‘blood flow index’ (BFI) and it is sensitive to the number of moving scatterers (α) and their motion DB.
B. Semi-infinite Geometry
The semi-infinite solution utilizes the well-known method of images [1], placing the image source at rb. Evaluated on the tissue-air boundary with an extrapolated boundary condition and separation between the source and detector of ρ, the Green’s function for the field correlation diffusion equation is
| (A7) |
Where
| (A8) |
| (A9) |
and the position of the extrapolated boundary above the surface . Reff is the effective Fresnel reflection coefficient from the interface [33].
| (A10) |
| (A11) |
| (A12) |
where
References
- [1].Durduran T; Choe R; Baker WB; Yodh AG Diffuse optics for tissue monitoring and tomography. Rep. Prog. Phys 2010, 73, 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Boas DA; Yodh AG Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation. J. Opt. Soc. Am. A-Opt. Image Sci. Vis 1997, 14, 192–215. [Google Scholar]
- [3].Buckley EM; Hance D; Pawlowski T; Lynch J; Wilson FB; Mesquita RC; Durduran T; Diaz LK; Putt ME; Licht DJ, et al. Validation of diffuse correlation spectroscopic measurement of cerebral blood flow using phase-encoded velocity mapping magnetic resonance imaging. J. Biomed. Opt 2012, 17, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Carp SA; Dai GP; Boas DA; Franceschini MA; Kim YR Validation of diffuse correlation spectroscopy measurements of rodent cerebral blood flow with simultaneous arterial spin labeling mri; towards mri-optical continuous cerebral metabolic monitoring. Biomed. Opt. Express 2010, 1, 553–565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Yu GQ; Floyd TF; Durduran T; Zhou C; Wang JJ; Detre JA; Yodh AG Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion mri. Opt. Express 2007, 15, 1064–1075. [DOI] [PubMed] [Google Scholar]
- [6].Zhou C; Eucker SA; Durduran T; Yu GQ; Ralston J; Friess SH; Ichord RN; Margulies SS; Yodh AG Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury. J. Biomed. Opt 2009, 14, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Buckley EM; Cook NM; Durduran T; Kim MN; Zhou C; Choe R; Yu GQ; Shultz S; Sehgal CM; Licht DJ, et al. Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial doppler ultrasound. Opt. Express 2009, 17, 12571–12581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Delgado-Mederos R; Gregori-Pla C; Zirak P; Blanco I; Dinia L; Marin R; Durduran T; Marti-Fabregas J Transcranial diffuse optical assessment of the microvascular reperfusion after thrombolysis for acute ischemic stroke. Biomed. Opt. Express 2018, 9, 1262–1271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Durduran T; Zhou C; Edlow BL; Yu GQ; Choe R; Kim MN; Cucchiara BL; Putt ME; Shah Q; Kasner SE, et al. Transcranial optical monitoring of cerebrovascular hemodynamics in acute stroke patients. Opt. Express 2009, 17, 3884–3902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Gregori-Pla CB,I; Camps-Renom P; Zirak P; Serra I; Cotta G; Maruccia F; Prats-Sánchez L,; Martínez-Domeño A; . Early microvascular cerebral blood flow response to head-of-bed elevation is related to outcome in acute ischemic stroke. Journal of Neurology 2019. [DOI] [PubMed] [Google Scholar]
- [11].Busch DR; Balu R; Baker WB; Guo WS; He L; Diop M; Milej D; Kavuri V; Amendolia O; St Lawrence K, et al. Detection of brain hypoxia based on noninvasive optical monitoring of cerebral blood flow with diffuse correlation spectroscopy. Neurocrit. Care 2019, 30, 72–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Selb J; Sutin J; Lin PI; Bechek SC; Boas DA; Franceschini MA; Rosenthal ES Feasibility of diffuse correlation spectroscopy for prolonged monitoring of cerebral autoregulation during neurocritical care. J. Cereb. Blood Flow Metab 2016, 36, 728–729. [Google Scholar]
- [13].Durduran T; Zhou CA; Buckley EM; Kim MN; Yu GQ; Choe R; Gaynor JW; Spray TL; Durning SM; Mason SE, et al. Optical measurement of cerebral hemodynamics and oxygen metabolism in neonates with congenital heart defects. J. Biomed. Opt 2010, 15, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Lynch JM; Buckley EM; Schwab PJ; McCarthy AL; Winters ME; Busch DR; Xiao R; Goff DA; Nicolson SC; Montenegro LM, et al. Time to surgery and preoperative cerebral hemodynamics predict postoperative white matter injury in neonates with hypoplastic left heart syndrome. J. Thorac. Cardiovasc. Surg 2014, 148, 2181–2188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Cochran JM; Chung SH; Leproux A; Baker WB; Busch DR; DeMichele AM; Tchou J; Tromberg BJ; Yodh AG Longitudinal optical monitoring of blood flow in breast tumors during neoadjuvant chemotherapy. Phys. Med. Biol 2017, 62, 4637–4653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [16].Busch DR, Davis J, Kogler A, Galler RM, Parthasarathy AB, Yodh AG, Floyd TF Laser safety in fiber-optic monitoring of spinal cord hemodynamics: A preclinical evaluation. J. of Biomedical Optics 2018, 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Kogler AS; Bilfinger TV; Galler RM; Mesquita RC; Cutrone M; Schenkel SS; Yodh AG; Floyd TF Fiber-optic monitoring of spinal cord hemodynamics in experimental aortic occlusion. Anesthesiology 2015, 123, 1362–1373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Mesquita RC; D’Souza A; Bilfinger TV; Galler RM; Emanuel A; Schenkel SS; Yodh AG; Floyd TF Optical monitoring and detection of spinal cord ischemia. PLoS One 2013, 8,9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Wang DT; Parthasarathy AB; Baker WB; Gannon K; Kavuri V; Ko T; Schenkel S; Li Z; Li ZR; Mullen MT, et al. Fast blood flow monitoring in deep tissues with real-time software correlators. Biomed. Opt. Express 2016, 7, 776–797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Carp SA; Farzam P; Redes N; Hueber DM; Franceschini MA Combined multi-distance frequency domain and diffuse correlation spectroscopy system with simultaneous data acquisition and real-time analysis. Biomed. Opt. Express 2017, 8, 3993–4006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Parthasarathy AB; Gannon KP; Baker WB; Favilla CG; Balu R; Kasner SE; Yodh AG; Detre JA; Mullen MT Dynamic autoregulation of cerebral blood flow measured non-invasively with fast diffuse correlation spectroscopy. J. Cereb. Blood Flow Metab. 2018, 38, 230–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Schatzel K; Drewel M; Stimac S Photon-correlation measurements at large lag times - improving statistical accuracy. Journal of Modern Optics 1988, 35, 711–718. [Google Scholar]
- [23].Magatti D; Ferri F Fast multi-tau real-time software correlator for dynamic light scattering. Applied Optics 2001, 40, 4011–4021. [DOI] [PubMed] [Google Scholar]
- [24].Magatti D; Ferri F 25 ns software correlator for photon and fluorescence correlation spectroscopy. Review of Scientific Instruments 2003, 74, 1135–1144. [DOI] [PubMed] [Google Scholar]
- [25].Kalinin S; Kuhnemuth R; Vardanyan H; Seidel CAM Note: A 4 ns hardware photon correlator based on a general-purpose field-programmable gate array development board implemented in a compact setup for fluorescence correlation spectroscopy. Review of Scientific Instruments 2012, 83. [DOI] [PubMed] [Google Scholar]
- [26].Nelder JA; Mead R A simplex-method for function minimization. Comput. J 1965, 7, 308–313. [Google Scholar]
- [27].IEEE. Ieee standard for binary floating-point arithmetic. 1985.
- [28].Xilinx. Cordic v6.0 logicore ip product guide. 2016.
- [29].Volder JE The cordic trigonometric computing technique. Institute of Radio Engineers Transactions on Electronic Computers 1959, EC-8, 330–334. [Google Scholar]
- [30].Volder JE The birth of cordic. J. VLSI Signal Process. Syst. Signal Image Video Technol 2000, 25, 101–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Cortese L; Lo Presti G; Pagliazzi M; Contini D; Dalla Mora A; Pifferi A; Sekar SKV; Spinelli L; Taroni P; Zanoletti M, et al. Liquid phantoms for near-infrared and diffuse correlation spectroscopies with tunable optical and dynamic properties. Biomed. Opt. Express 2018, 9, 2068–2080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Lemieux PA; Durian DJ Investigating non-gaussian scattering processes by using nth-order intensity correlation functions. J. Opt. Soc. Am. A-Opt. Image Sci. Vis 1999, 16, 1651–1664. [Google Scholar]
- [33].Contini D; Martelli F; Zaccanti G Photon migration through a turbid slab described by a model based on diffusion approximation .2. Theory. Applied Optics 1997, 36, 4587–4599. [DOI] [PubMed] [Google Scholar]