scRCMF: Identification of cell subpopulations and transition states from single cell transcriptomes

Abstract

Single cell technologies provide an unprecedented opportunity to explore the heterogeneity in a biological process at the level of single cells. One major challenge in analyzing single cell data is to identify cell subpopulations, stable cell states, and cells in transition between states. To elucidate the transition mechanisms in cell fate dynamics, it is highly desirable to quantitatively characterize cellular states and intermediate states. Here, we present scRCMF, an unsupervised method that identifies stable cell states and transition cells by adopting a nonlinear optimization model that infers the latent substructures from a gene-cell matrix. We incorporate a random coefficient matrix-based regularization into the standard nonnegative matrix decomposition model to improve the reliability and stability of estimating latent substructures. To quantify the transition capability of each cell, we propose two new measures: single-cell transition entropy (scEntropy) and transition probability (scTP). When applied to two simulated and three published scRNA-seq datasets, scRCMF not only successfully captures multiple subpopulations and transition processes in large-scale data, but also identifies transition states and some known marker genes associated with cell state transitions and subpopulations. Furthermore, the quantity scEntropy is found to be significantly higher for transition cells than other cellular states during the global differentiation, and the scTP predicts the “fate decisions” of transition cells within the transition. The present study provides new insights into transition events during differentiation and development.

I. INTRODUCTION

With the development of new single-cell technologies, a large amount of single-cell data have been collected. Three of the most important challenges in analyzing single-cell RNA-sequencing (scRNA-seq) data are the identification of cell subpopulations (states), the identification of cells in transition between states (i.e., transition cells), and the quantitative characterization of those transition cells because cells often transit from one state (type) to another through a sequence of fate decisions during cell development [1]-[2].

A transition state is an intermediate state during cell fate decisions in which a cell exhibits a mixed identity between two or more states, often representing the state of origin (i.e., the initial state the cell) and the state of destination (i.e., the identity that the cell is adopting) [1]. The transition cells are defined as those cells that are in transition states in cell fate dynamics. Many attempts have been made to understand critical transitions and cell fate decisions in developing organisms and to identify the underlying molecular mechanisms [1]-[4]. However, to the best of our knowledge, only a few studies have sought to quantify the cellular states and transition states based on single cell data [3], [5]-[6]. For example, SLICE and SCENT both quantify cell potency and cellular differentiation processes using entropy-based measures [6]-[7]. [3] proposed a quantitative index to predict critical transitions, which revealed a decrease in the correlation between cells and a concomitant increase in the correlation between genes as cells approach a tipping point [3]. Therefore, identifying the transitional processes and quantitatively characterizing them based on global transcriptome profiles remain largely unanswered at the single-cell level.

Trajectory methods offer an unbiased and transcriptome-wide understanding of a dynamic process, thereby allowing the objective identification of subsets of cells and the delineation of a differentiation tree [8]-[11]. TSCAN using minimum spanning tree (MST) [9], SLICER using local linear embedding [10] and Monocle2 using Reverse Graph Embedding (DDRtree) [11]. Resolving subpopulations is one of the main tasks in the analysis of single cell data [12]. Several approaches have recently been developed to address this task [13]-[15]. Dimension reduction techniques, e.g. principal components analysis (PCA) [13] and t-distributed stochastic neighbor embedding (tSNE) [14] are widely employed to capture the structure of the data for visualization and pattern detection. Based on the transformed low-dimensional space, graph and community detection such as SC3 [15], SNN-Cliq [16] and Seurat [17], can be used to identify the cell clusters. In contrast to these methods, optimization-based algorithms (e.g. SIDEseq [18]) seek to learn a cell-cell similarity matrix to further classify cells into subpopulations based on their similarity. However, none of these methods can identify transition cells simultaneously.

Nonnegative matrix factorization (NMF) is a powerful matrix factorization technique, that typically decomposes a nonnegative data matrix into the product of two low-rank nonnegative matrices [19]. NMF has been shown to be able to generate sparse and part-based representation of data. In other words, the factorization allows us to easily identify meaningful substructures underlying the data [20]. Although it has been widely used for classification [21], it was not used to identify the transition states in cell differentiation and development. In this study, we presented the scRCMF (single-cell Random Constrained Nonnegative Matrix Factorization) algorithm, which incorporates a new regularization term involving the constraint of the decomposed coefficient matrix, to identify cell subpopulations and transition processes from scRNA-seq data. Moreover, two new measures, termed single-cell transition entropy (scTE) and transition probability (scTP), were used to quantify the plasticity of transition cells and predict the dynamic behavior of transition states, respectively. scRCMF also allows us to identify critical subpopulations and transition processes, and to extract significant gene patterns during development processes. Finally, we evaluated the performance of scRCMF by comparison several existing methods using one simulated and three published datasets.

II. METHODS

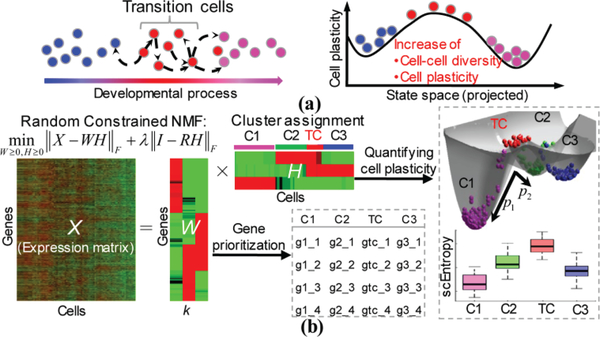
The overview of the analysis workflow that underlies scRCMF is shown in Fig.1. There are some critical cells with multiple functions in the development process. The identification of subpopulations and the transition state can capture distinct functional cell types and better predict the functional capacity of cells. These critical transition states need to be identified with more diversity and plasticity in the projected state space of a single cell, as shown in Fig. 1(a). To address these questions, in Fig. 1(b), we present scRCMF, a random constrained NMF algorithm that enables the simultaneous detection of meaningful subpopulations and identification of transition states from single cell data. scRCMF takes X = (x_ij) as input, where X is an expression matrix in which rows correspond to genes/transcripts and columns correspond to cells. Each element x_ij of X gives the expression of a gene/transcript i in a given cell j. scRCMF consists of three critical steps. First, a nonlinear optimization model is proposed to learn a low-rank representation of the matrix X based on NMF, giving the latent substructures of the data matrix. Second, cell subpopulations and transition states as well as the associated feature genes can be identified based on the learned coefficient matrix H and basis matrix W, respectively. Finally, two measures, scEntropy and scTP, are defined to quantitatively characterize and predict the transition cells (states).

Fig. 1.

The workflow of scRCMF aimed at identifying subpopulation structures and transition cells.

(a) A series of transition cells occurs from initial states (blue circles) to final states (purple circles) during cell development, and each of these transition cells (red circles) exhibits a different probability of transitioning to another state (i.e., making a cell fate decision) and higher diversity and plasticity (compared to the stable initial and final states, these cells have a higher ability to transition to another state, both forward and backwards). (b) Pipeline of the scRCMF algorithm. Random constrained NMF decomposes a gene-cell expression matrix into a coefficient matrix H and a basis matrix W with rank k. H and W are used to identify subpopulations and transition states, and prioritize feature genes associated with each identified cluster, respectively. scEntropy is proposed to quantify the plasticity of cells and scTP (e.g., p₁ and p₂) is proposed to predict the behavior (“cell fate decision”) of these transition cells.

A. Extracting low-rank structures via a nonlinear optimization model

To reveal substructures in the underlying single-cell data, scRCMF decomposes X (m×n) into two low-rank nonnegative matrices W and H with a given cluster number k using the following optimization model:

$$\underset{W\ge 0,H\ge 0}{\min }F(W,H,k)=\Vert X-WH{\Vert }_F+\lambda \Vert I-RH{\Vert }_F,$$ (1)

where W and H are the basis matrix and coefficient matrix with sizes of m×k and k×n respectively, and m and n are the numbers of genes and cells, respectively. Rank k represents the number of subpopulations, and λ is the regularization parameter. I is an n×n identity matrix, and R is an n×k random matrix with R_ij∈[0,1]. The regularization terms or constraints are often required to guarantee more accurate and robust results because of the non-uniqueness and ill-posedness of NMF [22]. motivated by [22], we apply a stochastic constraint to the coefficient matrix H. The regularization parameter λ in model (1) balances stability and the precision of the resulting low-rank structure. We determine the rank k using the Gap statistic [23] and the λ - chosen from 0.001, 0.01, 0.1, 1, 10 - using the BIC principle [24]. The gap statistic is calculated with k-medoid clustering using 1- Pearson’s correlation as the clustering distance metric. The model selection and update rules for this optimization model are shown in Supplementary A.

B. Identifying cell subpopulations and transition cells

The optimization model (1) based on the inferred number of clusters k, and the expression matrix X is projected into low-rank structures to explore meaningful substructures (groups of cells or genes). Typically, the maximal value of each column of coefficient matrix H can be used to determine clusters [21]. In this way, each cell is assigned to a unique cluster. However, transition cells are considered an intermediate state, in which cells exhibit a mixed identity between two or more subpopulations and might be involved in several functional states [1]. Given these facts, we normalized H to make each column unity. The normalized value in each column can be thought of as the probability of the j-th cell belonging to i-th cluster. Formally, we define a probability matrix P of size k×n as follows:

$$P_{ij}=\frac{H_{ij}}{\sum _{i=1}^k{H}_{ij}},$$ (2)

With this probability matrix P, we can define cell clusters and transition cells. Intuitively, a cell j is assigned to a unique cluster i if the probability P_ij highly dominates the cluster i (i.e., P_ij is larger than some threshold c₀) compared to the probabilities in other clusters; otherwise, if the probabilities in all clusters are similar (i.e., P_is < c₀, s = 1,2,…,k), which means that these cells have almost equal probabilities belong to all cell clusters. These cells are therefore defined as transition cells. Thus, the probability matrix P provides a natural way to define transition cells. In addition, the basic matrix W provides a direct, unbiased method to select feature genes associated with each cell cluster. Mathematically, cell cluster C_i and its associated gene cluster G_i were defined as follows.

$$\begin{array}{l}{C}_i=\left\{j|P_{ij}>=P_{sj}\ge c_0,i\ne s,s=1,\cdots ,k\right\}\\ G_i=\left\{l|W_{li}>=W_{lj},j\ne i,j=1,\cdots ,k\right\}\end{array},$$ (3)

where c₀ is a threshold of the probability. Generally, it is set to be 1/k or greater, where k is the number of clusters. The overall results are not sensitive to choices of c₀ within certain ranges, and the specific ranges of c₀ for the six datasets are shown in Supplementary Table I. P_ij means that j-th cells with maximal probability belonged to i-th cluster larger than c₀. We focus on the transition processes consisted of transition cells and cells belonged to two corresponding clusters with first two probability less than c₀. We further define transition cells (TC) as most likely occurring between two cell clusters, C_u and C_v, as follows:

$$TC=\left\{i|c_0>P_{ui}\ge P_{vi}\ge P_{li},l\ne u\ne v,1\le l\le k\right\}.$$

In this study, we consider two types of gene signatures: cluster-specific genes and transition genes that are coexpressed by multiple clusters leading to this transition event. In addition to selecting feature genes based on gene cluster G_i defined in (3), cell-type-specific gene signatures (differentiated genes and coexpressed genes) need to be discovered. For different populations, the gene patterns of differentiated expression and function differences can be analyzed by comparing the fold change and statistical test results of these gene clusters. Considering the mixed states of transition cells, the coexpressed marker genes leading to transition are ranked based on the average expression value in transition cells.

C. Quantification of the transition capability by estimating single-cell transition entropy (scEntropy) and transition probability (scTP)

We observe the chaos of stable states and transition states from the entropy during the differentiation, and further predict the transition behavior of transition states based on fuzzy degree during the transition [25]. To quantitatively assess the cell-to-cell variability in gene expression, we introduce a quantity called single-cell transition entropy (scEntropy) as a measure of cell plasticity, i.e., the ability of cells transitioning to new cell states. Based on the Shannon entropy equation, scEntropy is defined as:

$$E_i=-\sum _{j=1}^k{P}_{ji}\log P_{ji},$$ (4)

where P_ij is defined in Equation (2). Obviously, the transition entropy of a cell indicates the degree of uncertainty of cell fate. Thus transition cells should possess a higher entropy value than other cells in different subpopulations.

Given #e transition cells TC_e = {s₁, s₂,…,s_e} with initial probability P between the u-th and v-th cell subpopulations, we can predict the probability of such a transition state transferring to other cell cluster behavior (scTP): $P^{*}(P_{tr}:s_r\to C_t,r=1,2,\dots ,e;t=u,v)$.. For the e transition process, the initial membership degree P₀ can be obtained by P:

$$P_0=\left(\begin{array}{l}{P}_{u,T{C}_e}\\ P_{v,T{C}_e}\end{array}\right),$$ (5)

where P₀ is the matrix with a size of 2×e and represents transition probability from e transition states to states from the u-th and v-th cell clusters. The objective function of the fuzzy membership degree analysis of n cells is defined as:

$$J(P,Y)=\sum _{i\in u,v}\sum _{j=1}^e{\left(P_{i,s_j}\right)}^2{\Vert Y_i-X_{s_j}\Vert }_2^2,$$ (6)

where _Xs, represents the gene expression of the j-th transition cell in TCe, Y=[Y_u,Y_v] is the gene expression matrix with sizes of 2×m and Y_i (i = u, v) represents the expression of cluster center belonging to the i-th cluster.

Based on the definition and properties (nonnegativity and incompatibilities) of fuzzy membership degree [26], we predict the final transition probability (scTP) for e transition states to u-th or v-th cell clusters as:

$$P^{*}=\underset{P,Y}{\min }J(P,Y),$$ (7)

where the initial value of the above optimization problem is P₀ and the update strategy details in (7) are shown in Supplementary B.

D. Two Simulated datasets

To assess the performance of scRCMF, we generate two simulated datasets using the Splatter package in [27]. The simulated expression levels for cell clusters are based on a Gamma-Poisson distribution. To simulate transition cells, we choose the top five most relevant based on Pearson correlation coefficient pairs of cells from distinct cell clusters and generated the mean values that represent the mixed gene expressions of ‘transition cells’ in one transition. In total, we generated the first simulated dataset of two clusters and one transition with expressions of 10000 genes across 100 cells and 5 transition cells, the second simulated dataset of five clusters and two transitions with expressions of 10000 genes across 1200 cells and 40 transition cells.

E. Data sources

To further demonstrate the performance of scRCMF as well as biological discovery, we adopt the three real scRNA-seq datasets, which capture dynamical processes during mouse/human early embryo development [28]-[31]. The first dataset (MEG, GSE100597) consists of 204 cells collected at E3.5 and E4.5 during the mouse early gastrulation [28]. The second dataset consists of 88 cells from seven stages in human early embryos (HEE, GSE36552) [31]. The third dataset (qPCR, J:140465) consists of 334 cells from mouse late preimplantation development [30]. The scRNA-seq and cell stages of MEG, HEE and qPCR cells were obtained from [28], [30]-[31].

F. Evaluation of the algorithms

To evaluate the performance of clustering algorithms, the adjusted Rand index (ARI) [32] is widely used to evaluate accuracy and similarity between the inferred labels and reference labels.

III. RESULTS

A. scRCMF accurately recovers cell subpopulations and transition cells in the simulated dataset

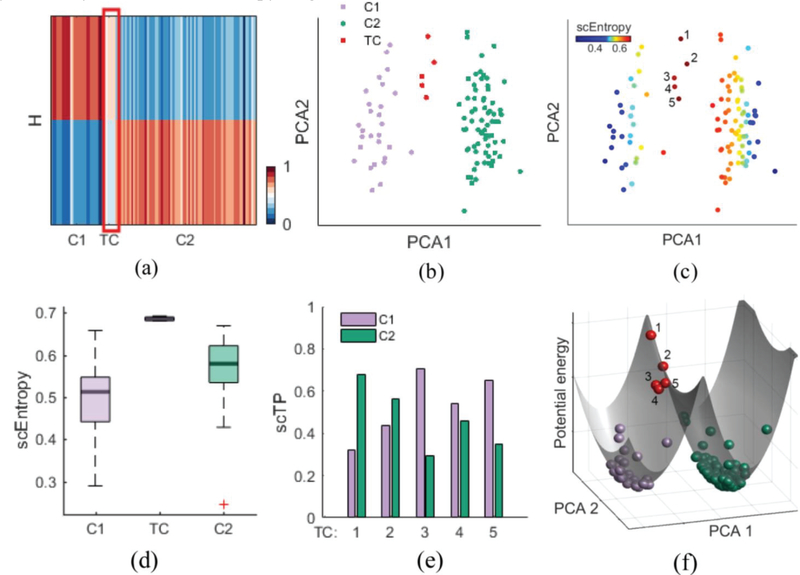
First, we apply scRCMF to two simulated datasets that contain multiple subpopulations and transition processes located close to one another in gene space (See Methods). In first dataset, as shown in Fig. 2(a) and (Fig. S1(a) in Supplementary C), the coefficient matrix H clearly revealed two distinct cell subpopulations (C1, C2) and one transition state between these two subpopulations (λ = 0.01 and c₀ = 0.6). The two cell clusters identified by scRCMF are well separated on the first two principal components (Fig. 2(b)) and characterized by relatively low transition entropy (Fig. 2(c) and 2(d)). As expected, the identified 5 transition cells are located between the two subpopulations in the low-dimensional space, and are characterized by high transition entropy (deep red color in Fig. 2(b)). Furthermore, using fuzzy degree analysis, we observe that these 5 transition cells (TCs) exhibited distinct transition directions: TC 1 likely switches to cluster C2, while TC 3 and TC 5 likely switch to cluster C1; TC 2 and TC 4 are very plastic with approximately 0.5 probability of transitioning to either cluster (Fig. 2(e)). To gain clearer insight into how the different behaviors of these transition cells translate to distinct differentiation propensities of cells, we create a 3D global potential landscape of the single-cell data based on the reduced dimensional space. The landscape topography is characterized by two narrow potential energy wells corresponding to the C1 and C2 states and one barrier corresponding to the transition cells. In terms of the dynamic behaviors of these transition cells, TC 2 likely favors a transition in the C2 direction, while TC 4 is more likely to convert into C1 cells. To further test the performance on multiple cell populations, the second dataset consisted of five populations with two transition processes can be identified by scRCMF (Fig. S2 in Supplementary C). Five distinct cell subpopulations (C1, C2, C3, C4 and C5) with low entropy are clearly identified by scRCMF in the low-dimensional space with the coefficient matrix H in (Fig. S2 in Supplementary C). Two transitions (C1-C5 and C3-C5) consisted of 39 cells are characterized by higher transition entropy and exhibit distinct transition directions (Fig. S2 in Supplementary C). Taken together, scRCMF accurately identifies the multiple subpopulations and transition states. The defined transition entropy significantly distinguishes transition cells from other cells. Fuzzy degree analysis as well as the potential landscape gains us insight into the transition behavior.

Fig. 2.

scRCMF identifies subpopulation structure and transition cells in the simulated data.

(a) The heatmap of coefficient matrix H, signifying two cell subpopulations (C1, C2) and one transition state (TC) denoted by a red frame. (b-c) Cells are visualized on the first two principal components and coloured by the scRCMF-derived states and transition entropy, respectively. 5 red cells with labels represent transition cells. (d) Comparison of scEntropy among C1, C2 and TC. (e) Transition probability (TP) of 5 transition cells to C1 and C2. Cell are colored as in panel (c). (f) Potential landscape of the simulated data. Cells are colored as in panel (b).

B. scRCMF identifies critical lineage commitments and mixed-lineage state during mouse embryo implantation

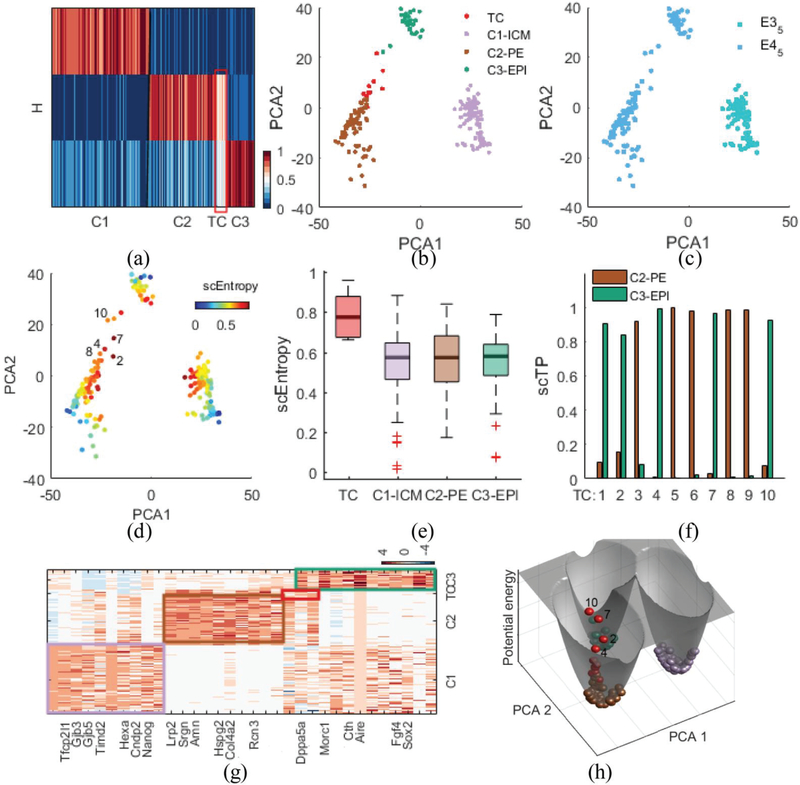
Next, we demonstrate the performance of scRCMF using the MEG dataset [28]. This dataset provides a high-resolution scRNA-seq map of mice from preimplantation to early gastrulation, from E3.5 to E6.5. To gain insights into the critical lineage commitment, i.e., the segregation of mouse inner cell mass (ICM) into the epiblast (EPI) and primitive endoderm (PE) lineages, we focus only on the stages before implantation of the embryo, i.e., E3.5 and E4.5, including 204 cells. We selected potentially informative genes (n =14451) with the variance of log2-transformed FPKM of each gene greater than 0.1. Unsupervised clustering using scRCMF leads to three clusters (Fig.S1(b) in Supplementary C). The heatmap of H describes the low-rank structure of the three cell subpopulations (C1, C2, and C3) and one transition state between C2 and C3 (λ= 0.001 and c₀ = 0.63), as shown in Fig.3(a). By comparing with the known labels and marker genes in the subpopulations identified by scRCMF, our results show that cluster C1 from E3.5 is ICM stage, characterized by high Gata6 and high Nanog (C1-ICM, 97 cells); cells from E4.5 are clustered into two distinct subpopulations: cluster C2 with high Gata6 and low Nanog is the PE state (C2-PE, 67 cells), and cluster C3 with high Nanog and low Gata6 is EPI state (C3-EPI, 28 cells) (Fig. 3(b), Fig. 3(c) and Fig. S2 in Supplementary C). Importantly, we identified 10 transition cells in the E4.5 stage. These cells express a middle level of Nanog or Gata6 (Fig. S2 in Supplementary C) and are located between C2-PE and C3-EPI in the PCA space (Fig. 3(b)), indicating a mixed-lineage state during lineage commitment. Again, higher entropies observed in these transition states than in cells belonged to other clusters (Fig. 3(d) and Fig. 3(e)). The mixed-lineage state was also observed recently in the hematopoietic stem cell differentiation process [33]. Based on fuzzy degree analysis, Fig.3 (f) shows that 5 transition cells (TC 3 and TC 8) appear prepared to convert into the C2-PE state, which are closer to cells from C2-PE in PCA space (Fig. 3(d)), and five cells (e.g., TC 2 and TC 7) are more likely to become the C3-EPI state. We also find several transition states located in the well between C2 and C3 and possess the higher potential energy in Fig. 3(h). Transitions with multiple directions and energies indicate that these transition cells are indeed very plastic during the PE and EPI stages in mouse early gastrulation which is consistent with previous papers, and the overexpression gene of Gata4, a differentiated gene in C2-PE, in embryonic stem cells is sufficient to direct cells toward a PE-like state [34]-[35].

Fig. 3.

scRCMF identifies critical lineage commitments and mixed-lineage state as well as associated marker genes during mouse embryo implantation.

(a) The heatmap of coefficient matrix H, signifying three cell subpopulations (C1, C2, C3) and one transition state (TC) denoted by a red frame in the MEG dataset [28]. (b-c) Cells are visualized on the first two principal components and colored by identified clusters (b) and developmental stages (c). (d) Cells are labeled by transition entropy. 5 red cells with labels are representative transition cells. (e) Comparison of scEntropy among C1, C2, C3 and TC. (f) Transition probability (TP) of 5 transition cells to C1 and C2. Cell labels are consistent with panel (d). (g) Heatmap of the top 33 marker genes for three clusters and one transition state. Genes are ranked by average expression value in three clusters and transition states respectively. (h) Potential landscape of the data. Cells are colored as in panel (b).

To further elaborate whether this critical transition between two lineages is likely to be functional, we performed differential expression and co-expression analysis. We observed significant 172 marker genes and clear gene patterns among the three clusters. Fig. 3(g) shows the top 10 feature genes associated with each cluster, where some signature genes reported in previous studies are also uncovered. Nanog and Gata4 identified pioneering symmetry that primarily represent transcription factors [28]. Gene Gata6 and Aire were marker genes co-expressed in a non-lineage-based random manner at E3.5, exhibiting substantial coexpression before displaying mutually exclusive lineage-specific expression patterns at E4.5 [28], [35]. We further found that Dppa5a expressed in the transition state and is associated with a shift toward the EPI fate and PE cell fate. Therefore, scRCMF captures the critical lineage commitment and mixed-lineage state with meaningful biological function during mouse embryo implantation.

C. scRCMF pinpoints the timing of key transitions of human early embryo development

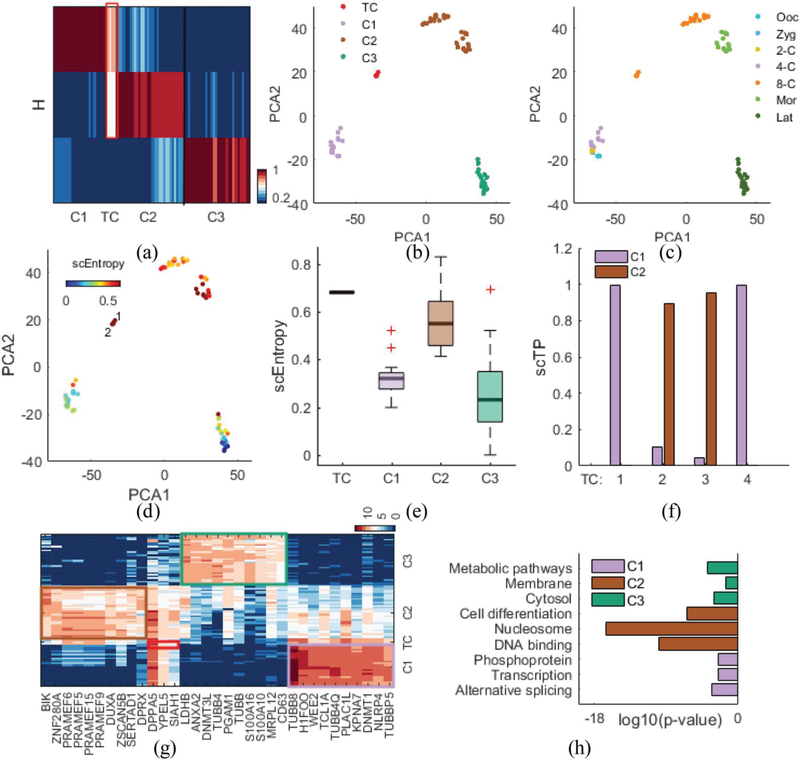
As a third demonstration, we applied scRCMF to scRNA-seq data studying human early embryo (HEE) development [31], which consists of 88 individual cells from seven developmental stages: oocyte, from the 2-cell to 8-cell stages, the morula, and the late blastocyst stage. To perform principal component analysis, we selected potentially informative genes (n = 10,316) with the variance of the log2-transformed FPKM greater than 0.5. We also performed unsupervised clustering, leading to three clusters determined with λ = 1 and c₀ = 0.63 (Fig. S1(c) in Supplementary C). In Fig. 4(a), the heatmap of H indicates three distinct blocks corresponding to three subpopulations (C1, C2 and C3) and one transition state between C1 and C2. scRCMF classifies the oocyte, zygote, 2-cell and 4-cell stages into a single subpopulation (C1, 24 cells), 8-cell and Morula cells together (C2, 30 cells), and the late blastocyst stage as another subpopulation (C3, 30 cells) (Fig. 4(b) and Fig. 4(c)). Interestingly, the most significant transition state, consisting of 4 transition cells, occurs at the 8-cell stage, which is located in the middle between C1 and C2 in the low-dimensional space, and emerged at a higher entropy than other cells (Fig. 4(d) and Fig. 4(e)). These results suggest that a critical transition occurs from the 4-cell to 8-cell in human early embryo development, which is consistent with previous studies [29], [31] showing that the major maternal-zygotic transition occurs at the 8-cell stage and that gene expression signatures first occur between the 4-cell and 8-cell stages during the preimplantation stages of human development. To further describe the dynamic characteristics of the transition state, fuzzy degree analysis shows that two transition cells appear likely to translate into the C1 state (TC1 and TC4), and the other two transition cells appear likely to C2 state (Fig. 4(d) and Fig. 4(f)). These results were consistent the findings that cells reconverged in both timing and function from the 8-cell to the morula stage after the gene expression of cells had achieved significant overlap and spread through the 4-cell and 8-cell stage [29].

Fig. 4.

scRCMF identifies subpopulation structure and pinpoints the timing of key transitions during human early embryo development.

(a) The heatmap of H with three cell subpopulations and four transition cells (TCs) denoted by a red frame in the HEE dataset [31]. (b-c) Cells are visualized on the first two principal components and colored by identified clusters and developmental stages. (d) Cells are labeled by transition entropy. Two red cells with labels are representative transition cells. (e) The distribution of entropy for TC and three clusters. (f) Transition probability (scTP) from the 4 transition cells to relevant two cell subpopulations (C1 and C2). (g) Heatmap of the top 33 marker genes for each cluster and four transition cells in human early embryo development. Genes are ranked by average expression value in three clusters and transition state. (h) Comparison of key functional annotation for enriched genes in the three clusters.

To further elaborate whether this critical transition and these clusters are likely to be functional, we identify the significant feature genes associated with each cell state. We perform a two-sample t-test for any two clusters (Fold Change (FC) > 2, p-value < 0.001) and compute the intersection of these differentially expressed genes with cluster-specific genes given by the basis matrix W. Fig. 4(g) shows the heatmap of the top 33 feature genes, which reveals a clear specific-expression pattern in each cluster as well as a coexpression pattern in transition cells defined by scRCMF. The top 10 differentiated expressed genes from each cluster are ranked by average expression value in each cluster. DAVID functional enrichment analysis [36] of 642 key genes of C1 (p-value < 0.01) revealed that these feature genes relate to mRNA metabolism and transcription (count > 30), e.g., alternative splicing (p-value = 5.55×10–4), transcription (p-value = 0.0035) and phosphoprotein (p-value = 0.0036) in the early stage (4-cell, 2-cell, oocyte and zygote) (Fig. 4(h)). A total of 303 feature genes of C2 are involved in DNA metabolism and the cell nucleus (count >10 and p-value <0.001), such as DNA binding (p-value = 1.18×10–10), nuclosome (p-value = 2.67×10⁻¹⁷) and cell differentiation (p-value = 4.03×10⁻⁷), implying that the epigenetics and cell-cycle regulation are also shifting after the highly expressed genes are activated in the middle stage (4-cell and 8-cell). Similarly, the functional enrichment of 304 important genes in C3 associated with cell metabolism and cytoplasm (count > 30 and p-value < 0.001), including the cytosol, membrane and metabolic pathways in Fig. 4(h). Moreover, we observed 119 significant transition genes in transition cells that are coexpressed by C1, C2 and TC (Fig. 4(g)). The GO terms of these coexpressed genes focused on DNA binding (p-value = 2.46×10–4), Zinc (p-value = 0.0030), Nucleus (p-value = 0.0079) and transcription regulation (p-value = 0.0085), as shown in Supplementary Table II. These findings suggested that scRCMF can be used for the unbiased identification of biologically meaningful subpopulations, critical transition and marker genes during early embryo development.

D. scRCMF identifies multiple transition states during mouse preimplantation development

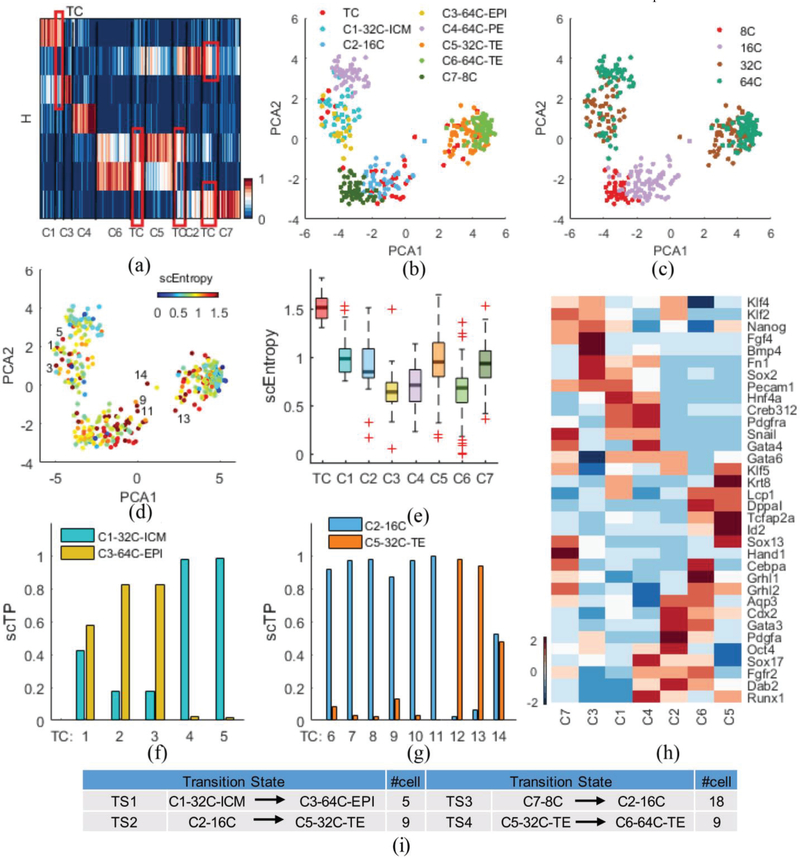
As a third demonstration, we show the performance of scRCMF using qPCR data on mouse embryo development from zygote to blastocyst [30]. Guo et al. ([30]) conducted a qPCR experiment on 48 genes in seven different developmental stages. To understand the critical cell fate decisions in a developing mouse embryo, we used 334 individual cells from the 8-cell, 16-cell, 32-cell and 64-cell stages. The gap statistics predict seven clusters (Fig. S1(d) in Supplementary C). Heatmap of the coefficient matrix H shows the distinct patterns of the seven cell subpopulations and 41 transition cells identified with λ = 0.001 and c₀ = 0.38 (Fig. 5(a)). Our results in Fig. 5(b) and Fig. 5(c), show that scRCMF separates the 32-cell stage into two clusters, C1–32C-ICM with high Sox2/Nanog/Gata6 and C5–32C-TE with high Cdx2 and low Sox2, and the 64-cell stage into three clusters C3–64C EPI with high Nanog and low Gata6, C4–64C-PE with high Gata6/Gata4 and low Nanog, and C6–64C-TE with high Cdx2 and low Sox2 (Fig. 5(h) and Fig. S3 in Supplementary C). The other two clusters are C7 enriched in the 8-cell stage and C2 enriched in the 16-cell stage. We also identify 4 transition states (Fig. 5(a) and Fig. 5(i)). The first transition occurs between C1–32C-ICM and C3–64C-EPI, and 5 transition cells exhibit a mixed location between C1 and C3, while 9 transition cells appear in the second transition state between C2–16cell and C5–32C-TE (Fig. 5(b)). Similarly, 18 transition cells were observed in the third transition state between C7–8cell and C2–16cell, and 9 transition cells were observed in the fourth transition state between C5–32C-TE and C6–64C-TE (Fig.S3 in Supplementary C). The last transition was located between C6–64C-TE and C5–32C-TE, as shown C5 in Fig. 5(b). 41 transition cells in the four transition states possessed higher entropy than the other seven clusters identified by scRCMF in Fig. 5(e). The second and third transitions among C2, C5 and C7 (Fig. 5(g) and Fig. S3) indicated the multiple shift and transition of cell states at 16-cell stages, in agreement with the study reported that mixed lineage expression in 16 cell blastomeres [30]. We further observe that two cells (e.g., TC 5) intend to C1, two cells (e.g., TC 3) are closer to C3, and TC 1 is plastic between C1 and C3 in Fig. 5(d) and Fig. 5(f). We further found that 6 transition cells (e.g, TC 9 and TC 11) are likely to convert into C2, while the plastic TC 14 and two other states (e.g, TC 13) might translate into C5, as shown in Fig. 5(d) and Fig. 5(g). Taken together, the results show that scRCMF captures the transition states in the critical lineage commitment during mouse preimplantation development.

Fig. 5.

scRCMF identifies subpopulation structure and multiple transition states during mouse preimplantation development.

(a) The heatmap of H with seven cell subpopulations and four transition states (TC) denoted by red frames in the qPCR dataset [30]. (b-c) Cells are visualized on the first two principal components and coloured by the identified subpopulations and developmental stages, respectively. (d) Cells are labeled by entropy. 7 red cells with labels represent the representative transition cells. (e) The distribution of entropy for TC and seven clusters. (f-g) Transition probability (scTP) from two transition states between two cell subpopulations (C1 and C3, C2 and C5). (h) Heatmap of thirty four marker genes for each cluster and four transition states. Genes are ranked according to their similarity. (i) Summary of the identified four transition states and the number of cells in each state.

To further elaborate whether the three transitions are likely to be functional, we examined the differential expression and the coexpression patterns in different transitions by gene clusters (W). We observe 34 significant marker genes and multiple clear gene patterns among the seven clusters in Fig.5 (h). We further found that Pecam1 is expressed in the transition between C1 and C3, Apq3 and fgfr2 are expressed in the transition between C2 and C5, Cdx2, Grhl2 and Lcp1 are expressed in the transition between C5 and C6 in late mouse preimplantation development. We further found that the same marker coexpressed genes showed different regulation in the four transition processes, such as the marker gene Klf5 is expressed in C2, C5 and C7. Among these genes, several have been identified as key genes in previous studies.

Cdx2 is a the TE-specific transcription factor coexpressed from the 8-cell stage through to the blastocyst [37]-[38]. Both Gata6 and Gata4 are early markers of the PE [30]. Biological subpopulation structures, multiple transition processes and key gene markers can be identified by scRCMF during mouse preimplantation development.

These three different datasets emphasize different aspects of the dynamic process of the early embryo development, allowing us to comprehensively understand the distribution and trend in gene expression during the transition in Fig. S4 and Fig. S5. In the MEG dataset [28], cells were from mouse preimplantation ICM at E3.5 and the epiblast at E4.5. Therefore, no TE cells existed in these data (TE marker Cdx2 is not expressed, Fig. S4 in Supplementary C), allowing us to focus on the segregation from ICM into EPI and PE. We also identified a transition/intermediate state with the mixed gene signatures of both EPI and PE. The HEE dataset [31] described the whole process from oocyte to late blastocyst during human early embryo development. Due to the excessive expression of PE marker GATA6 in late blastocyst (Fig. S4 in Supplementary C), we were not able to distinguish EPI from PE in an unbiased manner. However, we observed a transition state between the 4-cell and 8-cell stages in agreement with previous studies showing that the major maternal-zygotic transition occurs at the 8-cell stage [29], [31]. The third mouse qPCR dataset [30] allowed us to investigate two critical lineage commitments: the segregation of 16 cells into TE and ICM, and subsequently from ICM into PE and EPI. From Fig. S5, we further observed that the transition state was the extreme point for several marker genes’ expressions, that was, gene expression value was first increasing and then decreasing or first decreasing and then increasing. The gene expression changes of these maker genes may lead to distinct cell fate decisions and various biological functions of different cell types [1]. Moreover, We used the scRCMF to one more dataset with 57951 genes across 379 cells related to immune cell lineage, identify seven clusters and 4 transitions (C1-C3,C1-C7,C4-C7 and C6-C7) in primary breast cancer (PBC) [39]. We labeled C4 belonged to the B cell stage with marker gene CD2D, C1 belonged to the Macrophages stage with marker gene CD68 and C7 contained T cell stage with marker gene CD3D. Fig.S6 in Supplementary C further showed that transition states focused on the BC07 (lymph node metastasis of BC07) and BC09 (Breast cancer cells) with highest entropy. Taken together, our results reveal that multiple transition states occur in both mouse, human early embryo and primary breast cancer development. Such transitions may exhibit very different characteristics when the starting cell state is different, as observed in many biological processes, such as the transition from the hepatocellular carcinoma state to the normal liver state [4], and the epithelial-mesenchymal transition (EMT) [40]-[41].

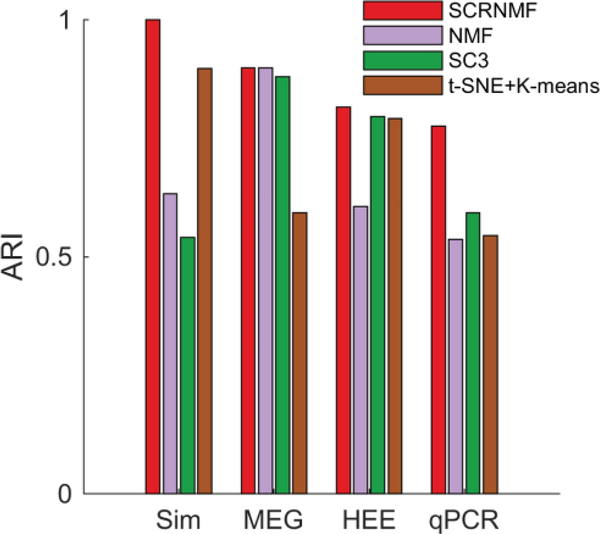
E. Comparison of scRCMF with other clustering methods

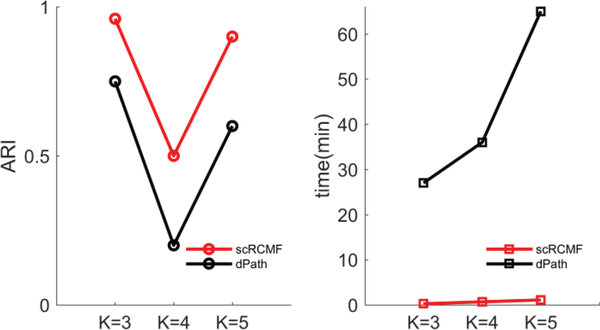
We compare the performance of scRCMF on the one simulated dataset and three real datasets with three other algorithms: t-SNE+K-means [14]-[15], SC3 [15] and the classical NMF [19]. We repeated NMF and scRCMF for 20 times and present the average result. The number of clusters is assured by Gap statistics, and transition states are not considered in the comparison. As a test statistic, we used the adjusted Rand index (ARI) to quantify the consistence between the predicted clusters and real developmental stages. For the real datasets and simulated dataset, scRCMF exhibits a good performance (Fig. 6). We further compared our methods with dPath [42] in terms of the accuracy and time complexity on three simulated datasets produced by splatter [27]. In Fig. 7, the computation time was initially less than two minutes but slowly increased with the number of clusters. scRCMF has better accuracy and is obviously superior to dPath [42] in terms of computation time. Our method and dPath [42] are computed on a dual 3.40 GHz Dell desktop computer with 8 GB of RAM.

Fig. 6.

Comparison of the performance of scRCMF with that of several other clustering methods on one simulated dataset and three real datasets.

Fig. 7.

Comparison of the performance of scRCMF and dPath [42] on three simulated datasets with different clusters in terms of accuracy (ARI) and time complexity (min). K indicates the number of cell subpopulations.

IV. DISCUSSIONS

Compared with typical sequential methods, such as identification of cell populations using clustering methods (e.g. SC3) and then inference of cell transitions using pseudotime analysis, scRCMF enables the simultaneous identification of cell populations and estimation of cell transition probability. On the one hand, our integrative framework can increase accuracy and reduce computational cost. Moreover, it can identify which cell clusters are more likely making transitions to the other states. The pseudotime analysis characterizes continuous cell states, while the clustering analysis usually captures discrete cell states. Such characterization of individual cells might make the identification of transition states less robust and introduce errors in finding the transition states. As shown in our previous studies [43]-[44] on the pseudotime analysis, some cell states might be mixtures of multiple identified cell subpopulations through direct application of clustering methods. Thus, it is a challenging task to identify the cell transitions and transition states connecting the identified subpopulations.

In addition, it is also a challenging task to distinguish different transitions when different cell populations are closely related. In this study, we distinguish them through calculating the transition probabilities of cells. More effective methods that can deal with such case will be explored in the future.

V. CONCLUSION

Here we present scRCMF, a new method for simultaneously identifying cell subpopulations and transition cells, and quantifying transition cells from single-cell gene expression data. The main contributions of this study include three aspects: (1) we proposed a matrix factorization model by introducing a new regularization with random constraints, which is shown to improve accuracy for inferring cell subpopulations; (2) we used the quantity scEntropy to measure the plasticity of cells and found that the entropy of transition state is significantly higher than that of cells belonging to other clusters, which further reveals the instability during transition; (3) a quantity scTP based on fuzzy membership degree was proposed to predict the fate decision and dynamic behavior of transition cells. by calculating their probability of moving from the transition state to other states.

We apply scRCMF to two simulated datasets and four published datasets. Applied to the first three real datasets involved in the early embryo development, scRCMF identifies the biological meaningful subpopulations, and the transition processes. Moreover, we identified maker genes of the associated subpopulations and transition states (Supplementary Table III).

Although we have made significant progress toward identifying transition states and cell subpopulations, much interesting work remains to be done in the future, such as cell trajectory reconstruction, network inference, and stochastic dynamic analysis. We further suggest that the experimental datasets of single cell with batch effects can be removed by matching mutual nearest neighbors [45].

In conclusion, the proposed scRCMF provides a computational framework to quantitatively analyze scRNA-seq data and advance our understanding of single-cell biology. We believe that the proposed scRCMF will help to capture meaningful cell types and transition states and to identify key genes in emergent biological processes and cell fate decisions.