Abstract
The objective of this work is to reduce the user effort required for 2D segmentation when building patient-specific cardiovascular models using the SimVascular cardiovascular modeling software package. The proposed method uses a fully convolutional neural network (FCNN) to generate 2D cardiovascular segmentations. Given vessel pathlines, the neural network generates 2D vessel enhancement images along the pathlines. Thereafter, vessel segmentations are extracted using the marching-squares algorithm, which are then used to construct 3D cardiovascular models. The neural network is trained using a novel loss function, tailored for partially labeled segmentation data. An automated quality control method is also developed, allowing promising segmentations to be selected. Compared with a threshold and level set algorithm, the FCNN method improved 2D segmentation accuracy across several metrics. The proposed quality control approach further improved the average DICE score by 25.8%. In tests with users of SimVascular, when using quality control, users accepted 80% of segmentations produced by the best performing FCNN. The FCNN cardiovascular model building method reduces the amount of manual segmentation effort required for patient-specific model construction, by as much as 73%. This leads to reduced turnaround time for cardiovascular simulations. While the method was used for cardiovascular model building, it is applicable to general tubular structures.
Keywords: Cardiovascular modeling, Convolutional neural networks, SimVascular, Patient-specific modeling, Cardiovascular simulation
1. Introduction
Cardiovascular disease (CVD) is the leading cause of death worldwide [16]. This has motivated the development of new simulation-based technologies to aid the prevention, diagnosis, analysis, and treatment of CVD [10]. With recent advances in cardiac and vascular imaging, patient-specific simulations of cardiovascular hemodynamics are gaining increased clinical utility in relation to CVD [32, 46].
In the clinical workflow, the available time to produce simulation results is typically limited. Furthermore, to translate simulation tools to the clinic, studies and trials on large patient cohorts are required to statistically correlate simulation predictions with clinical outcomes. In both cases, lengthy simulation workflows are a prohibitive bottleneck. For cardiovascular simulation in particular, high-quality three-dimensional patient-specific models must be constructed for each patient, a process that requires substantial user input and delays simulation turnaround time [42, 46].
Patient-specific models typically include a network of vessels in specific anatomical regions of interest. Therefore, a common approach in cardiovascular modeling is to build the models vessel by vessel (Fig. 1). Often, specialized cardiovascular simulation software tools such as SimVascular1 [48, 49], Cardiovascular Integrated Modeling and Simulation (CRIMSON) [20], and the Vascular Modeling Toolkit (VMTK) [1] are used.
Fig. 1.
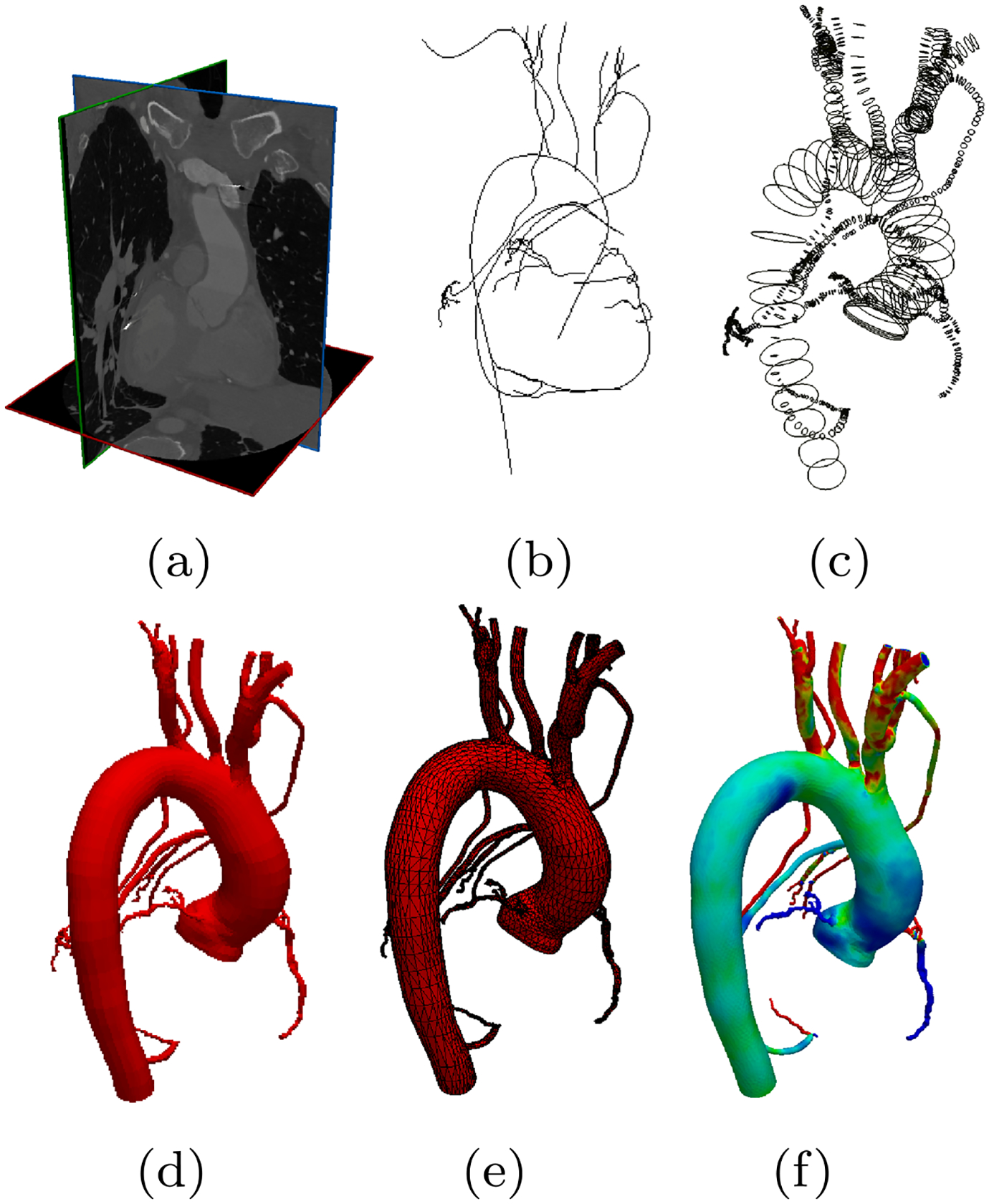
The cardiovascular model construction workflow used in SimVascular [48]. Starting from a image data, b users manually generate pathlines, c use these pathlines to segment 2D cross-sectional contours, d loftsegmented contours into a 3D model, e generate a numerically stable 3D geometric mesh, and finally f computational flow simulations are calculated
While this workflow offers the control and accuracy necessary to segment individual vessels, the segmentation step is particularly time consuming. Due to the importance of precisely identifying cardiovascular geometry, a large and diverse body of existing work has been dedicated to the acceleration of cardiovascular segmentation [27, 41, 43]. Early approaches made use of active contours [36, 50] and filtering techniques [12]. Later methods such as Optimally Oriented Flux [24, 25] and CURVES [30] included curvilinear structure information to improve segmentation accuracy. Other approaches have used stochastic methods [14] for segmentation. Another category of methods developed around modeling tubular structures such as intensity appearance models [23], 4D curves [3], circular and elliptical cross-sections [22, 45, 52], intensity-gradient profiles [35], vessel templates [55], and vessel tracking [13]. Modern methods leverage sophisticated statistical algorithms such as Random Sample Consensus (RANSAC) [19], machine learning techniques [2, 34, 39], or optimization methods tailored towards tubular structure segmentation [38, 47].
Recently, neural networks and deep learning have seen a surge of interest and development [26, 44]. Within medical imaging, numerous groups are making use of neural networks [4, 5, 7, 11, 18, 33]. These studies have shown that neural network-based methods can outperform standard methods in segmentation accuracy. However, to our knowledge, no studies have shown the utility of neural networks for cardiovascular model building on general vascular anatomy. The closest works are the I2I network [33], which did not consider downstream applications and DeepLumen [37] which is closed-source and restricted to CT coronary artery segmentation. In this work, we use FCNNs trained for vessel enhancement to accelerate the cardiovascular model building workflow (Fig. 1). Our main contributions are
A segmentation pipeline, based on fully convolutional neural networks, that produces automated segmentations as required in Fig. 1c.
A novel loss function that can be used to improve vessel enhancement accuracy of neural networks with partially labeled data through the use of a binary dilation of the label image.
An automated quality control system that can be used to identify and reject low quality predicted segmentations.
2. Methods
In this study, we use 2D convolutional neural networks to develop an accelerated cardiovascular model building workflow, implemented within the pathline-based model building pipeline developed for SimVascular [48] (Fig. 1). In particular, given a local 2D image of the vascular anatomy, the neural network should identify the vessel lumen at that location. Here, we outline how the neural network is used for cardiovascular model construction, the neural network architectures we selected, our training process, and the methods we developed for automated quality control of segmentations produced. We investigated the use of 3D convolutional neural networks for cardiovascular model building, but were unable to obtain acceptable performance, similar results were shown in [37]. As such we believe the use of 3D neural networks for cardiovascular model building is still an open avenue for further research.
With the proposed FCNN segmentation pipeline, the first few steps of model building remain the same: users first load medical image volume data and indicate points along the pathline of the vessel of interest (Fig. 2) and 2D images are extracted along pathline at discrete intervals. However, then the extracted 2D images are automatically preprocessed and input to a FCNN that has been trained to output vessel enhancement images. Vessel segmentationss are then automatically computed by applying the Marching-Squares algorithm to each FCNN output image. Using the pathline, the produced contours are reoriented in 3D space and interpolated to form the final vessel surface, after which the vessel models are merged as described above.
Fig. 2.
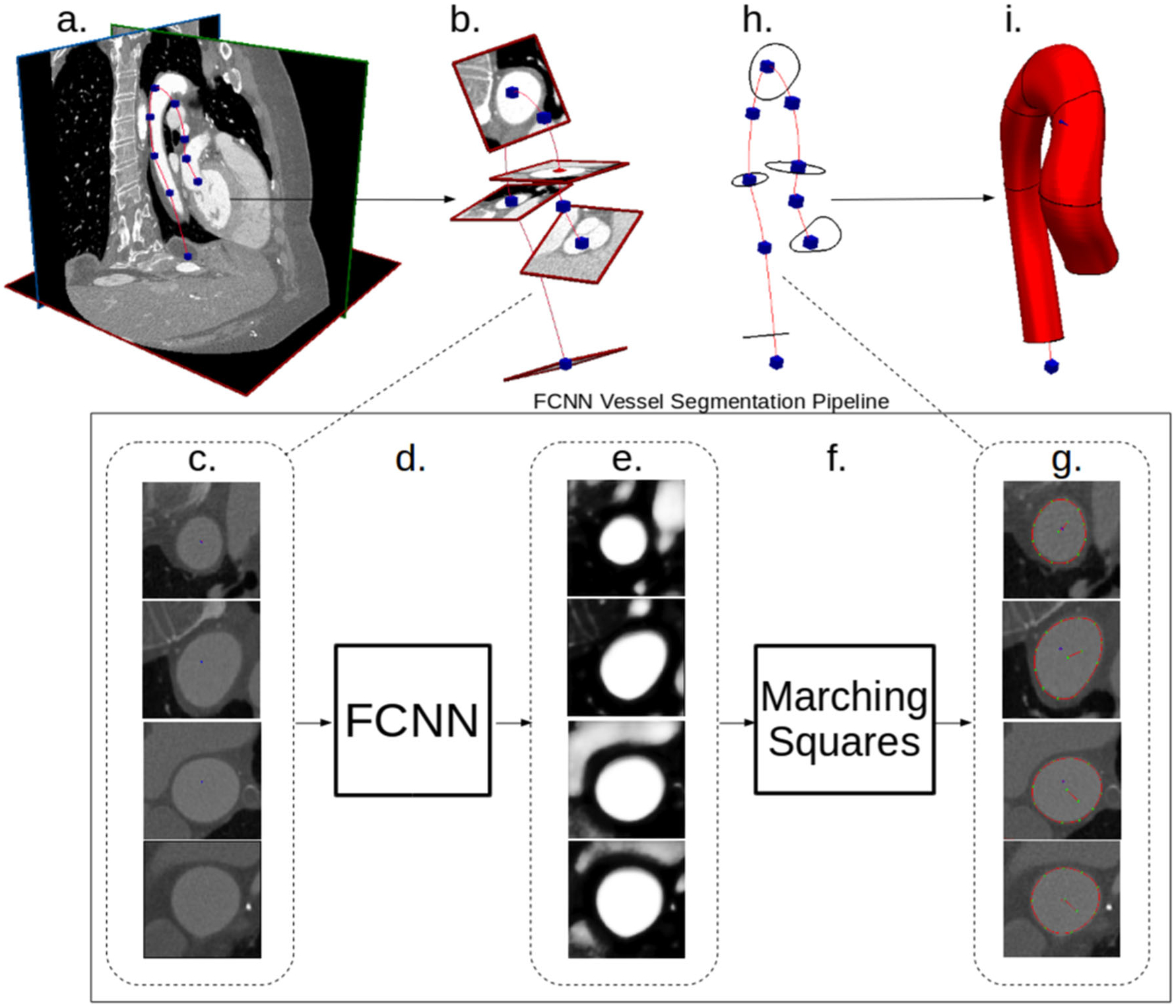
Our proposed FCNN-based cardiovascular model building pipeline. a Image data and vessel pathline supplied by the user. b Path information is used to extract image pixel intensities in plane perpendicular to the vessel path. c 2D images extracted along vessel pathlines are input to the FCNN. d FCNN acts on the input images to compute local vessel enhancement images. e Vessel enhancement images computed by the FCNN, the pixel values are between 0 and 1 indicating vessel tissue likelihood. f The marching-squares algorithm is applied to each enhanced image to extract the central vessel segmentation. g 2D extracted vessel surface points overlayed on original input images. h The 2D vessel surface points are transformed back to 3D space. i 3D cross-sectional vessel surfaces are interpolated along the pathline to form the final vessel model
2.1. Vessel image enhancement with fully convolutional neural networks
The main component of our proposed model building workflow is an FCNN that computes vessel enhancement images from 2D input medical image slices. The main advantage of FCNNs is that they can be trained to directly produce enhanced images, from which vessel segmentations can be extracted with the marching-squares algorithm. Therefore, we can train the FCNN using a labeled dataset and provide the trained network to users such that they can immediately use it to construct cardiovascular models more efficiently.
For our particular use-case, the FCNN operates on the 2D cross-sectional images extracted along the vessel pathlines. In particular, given a grayscale image , first we compute a normalized image by normalizing x to have zero mean and unit variance pixel values, so that
| (1) |
where μx and σx are the mean and standard deviation of the pixel values of x and are given by
| (2) |
and
| (3) |
The output of the neural network is a function of , and is an image where pixels containing vessel tissue have been enhanced. To be precise, the neural network output is denoted by , where , hθ is the neural network function, and θ are the trainable parameters of the neural network. is where binary classification has been applied to each pixel, i.e., each pixel has values between 0 and 1, indicating the probability of that pixel being inside the structure of interest, in this case blood vessels. H and W denote the height and width, in pixels, of the input and output image. As such the FCNN enhances the input images by setting the vessel pixel values close to 1 and the non-vessel pixel values close to 0.
The final vessel segmentation is then extracted by applying the marching-squares algorithm to , and is represented as a set of n points
| (4) |
where is a vector indicating the x- and y-coordinates of the ith point. Finally c is repositioned in 3D space using the supplied pathline point and tangent.
2.2. Neural network architecture
Neural networks are typically constructed by composing so-called neural network layers into a computational graph [26]. Each neural network layer contains parameters with values that are optimized using example input-output pairs from a training dataset and an optimization algorithm to minimize a selected loss function. For image segmentation tasks, feedforward fully convolutional networks [29, 53] have shown promising results and therefore we restrict ourselves to this class of network. In feedforward networks, a series of layers is sequentially applied to a given input, where the output of a given layer is used as input for the next layer. Each layer typically consists of a transformation, e.g., linear transformation or cross-correlation, followed by a nonlinear function referred to as an activation function. Convolutional neural networks are neural networks in which convolutional layers are primarily used and they typically operate on input images or tensors. For the sake of brevity, we do not provide a detailed description of neural network layers here; the interested reader is referred to the Appendix and the reviews in [26, 44].
With fully convolutional neural networks (FCNN), typically both their input and output are images or tensors, whereas convolutional networks typically produce vector-valued outputs such as classification probabilities. In general, the best combination of layers is a-priori unknown. Furthermore, the neural network design can have a large influence on its performance. Here we have selected three existing FCNN architectures that have previously shown good performance in medical imaging and segmentation tasks. The first network is the I2INet architecture [33], which was originally designed to operate on 3D medical image volumes and to detect blood vessel edges. The original motivation for the I2INet architecture was to preserve small scale image features which are often important in medical imaging. For our application, the network has to detect the entire blood vessel and operate on 2D images; therefore, we modified the I2INet for this purpose.
We replicated the I2INet architecture while replacing all 3D convolution and pooling layers with their 2D counterparts. Converting I2INet from vessel edge detection to vessel enhancement was accomplished through using blood vessel labeled training images, described in Section 2.4. The second network selected for comparison is the UNet architecture [40]. UNet was originally designed for 2D image enhancement; therefore, we did not need to modify the network architecture for our application. Both the modified I2INet and UNet architectures are shown in Fig. 3. The final selected network is the DeepLab network with Atrous Spatial Pyramid Pooling (DeepLab-ASPP) [6]. DeepLab-ASPP consists of a 101 layer Residual Network [15] with its fully connected layers replaced by multiple atrous convolution layers with different dilation rates. DeepLab-ASPP was selected due to its exceptional performance on semantic image segmentation tasks and the fact that the atrous spatial pyramid pooling processes features at multiple resolutions. For the sake of brevity, the reader is referred to [6, 15] for a full description of the DeepLab-ASPP architecture.
Fig. 3.
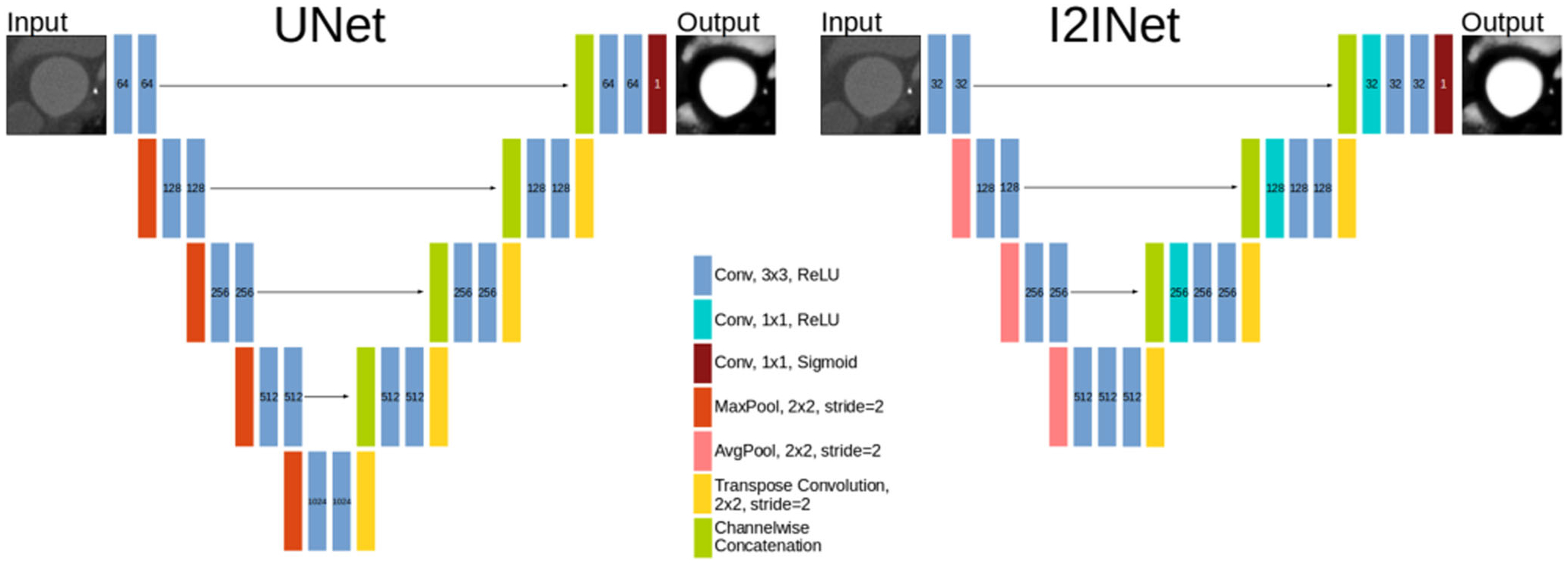
I2INet and UNet networks. Number labels indicate the number of channels in that layer. The input image and output segmentation have the same dimensions
We note the similarities and differences between the I2INet and UNet architecture. Both make extensive use of pooling and transpose convolution layers to operate on multiple resolutions of the network’s hidden state. Applying the downsampling and upsampling layers to the hidden state allows the resolution of the input image to be preserved, while simultaneously enabling processing at multiple resolutions. I2INet makes use of average-pooling layers whereas UNet uses max-pooling. Furthermore, the UNet network downsamples four times whereas I2INet downsamples three times. Following transpose convolutions, I2INet uses 1 × 1 convolutions to compute linear combinations of the upsampled inputs, whereas UNet inputs the upsampled input to a 3 × 3 convolution. Performance of these networks is compared in Section 4.
2.3. Loss function for partially labeled images
Optimal values for the neural network’s parameters are found by minimizing a loss function using example input and output images from a training dataset. The loss function should be chosen such that, when it is minimized using the example dataset, the neural network’s outputs resemble the output examples. For binary pixel classification problems, the pixel values of the output image of the neural network are interpreted as indicating the probability of that pixel being the target structure. A commonly used loss function in this scenario is the sigmoid cross-entropy loss function which indicates the log-likelihood of the neural network output pixels compared with the label pixels. For a neural network output and label image y, the sigmoid cross-entropy loss function is
| (5) |
The distribution of classes in labeled image segmentation data is typically skewed. The sigmoid cross-entropy is not well suited for the unbalanced class case, but can be modified to take the class imbalance into account [53]. A common approach is to use a balanced loss function that re-weighs the contribution of each class, such that all classes contribute equally to the loss. The balanced sigmoid cross-entropy loss is formulated as
| (6) |
with
| (7) |
where β is the fraction of pixels with a positive label and is used in Eq. 6 to compensate for the fact that there are typically many pixels with the negative class. However, balanced loss functions can cause the network to oversegment, leading to an increased false-positive error rate. This is problematic for blood vessel segmentation of small vessels, e.g., coronary arteries, with typical cross sections of only a few pixels.
Furthermore, in our dataset, not all blood vessels in every image volume have been segmented. Therefore, a naive implementation of assigning the positive class to every segmented vessel pixel and negative class to every pixel that was not segmented will increase the error rate of the network. Various methods exist to handle partially labeled data [8]; however, these approaches are not applicable to our use-case where the same tissue may appear labeled and unlabeled in an image.
To resolve the issues of imbalanced classes and partially labeled data, we introduce a new loss function that ignores regions of images that were not labeled during the labeling process. Let be a partially labeled image, a pixel value of 1 indicates that the labeler designated that pixel as the structure of interest and a pixel value of 0 indicates a pixel that was not labeled.
Let be a binary dilation of y by K pixels. Given a predicted image , our new loss function is then
| (8) |
The intuition behind the above loss function is that labelers tend to focus on specific vessels in an image and their surroundings, in regions close to the vessel pathlines. Therefore, other pixels that are far away from all labeled pixels were likely ignored during the labeling process. thus indicates the area of the image that the labeler focused on and only this region is considered in our loss function. For simplicity, we use a binary dilation y to produce . The process of generating from y has been illustrated in Fig. 4.
Fig. 4.

Illustration of the masked loss function generation, note how, in the label image y, some but not all vessel pixels have been labeled. a Example 2D cross-sectional input image x. b Corresponding partially labeled binary image y. c Mask image, , generated through binary dilation of label image y by a set number of pixels
2.4. Neural network training process
During training, the network’s weights are initialized with small random parameter values drawn from a normal distribution. We then find optimized values for the weights using a dataset of medical image volumes and corresponding cardiovascular binary image volumes and vessel pathlines. The weights are optimized using a stochastic gradient-descent algorithm to minimize the selected loss function over the training dataset. We describe the training data collection process for a single-labeled image volume, as it is straightforward to extend to multiple images (Fig. 5).
Fig. 5.
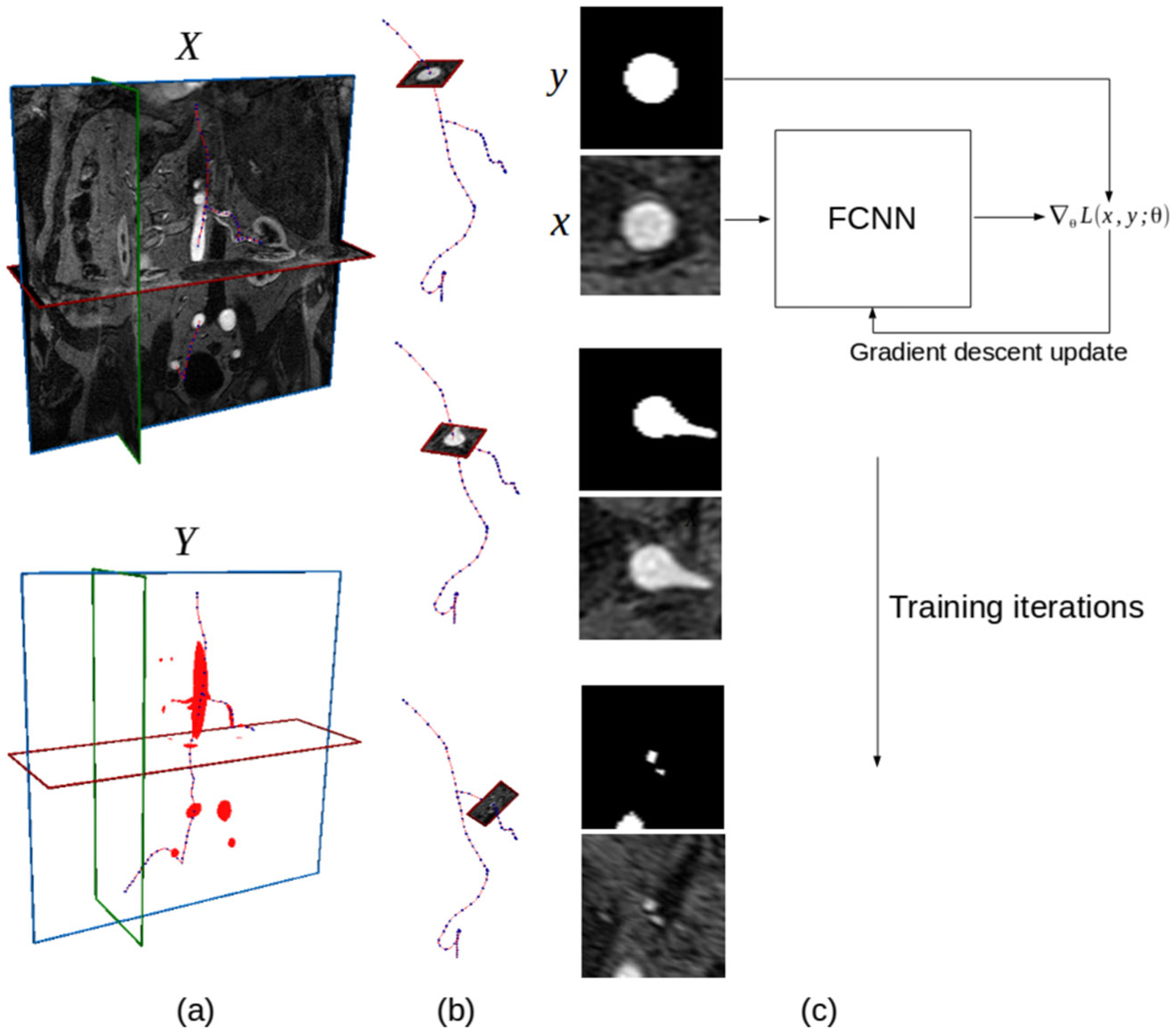
Illustration of the FCNN training process for a single image volume and binary label volume pair (X, Y). a Original 3D medical image volume X, associated 3D binary label image Y with blood vessel pixels labeled and selected vessel pathlines. b Extraction of 2D input and label images along selected centerline points by interpolating pixel values in the plane perpendicular to the pathline at each point. c FCNN training loop, at each iteration several input and label image pairs are used to calculate the gradient of the loss function with respect to the FCNN weights and the gradient is used to update the weights according to a gradient-descent update rule
Let X denote a grayscale medical image volume with Nx, Ny, Nz voxels in the height, width, and depth directions, respectively. Y is a labeled binary image volume, with the same dimensions as X, with pixel values indicating whether that pixel is part of a blood vessel. Finally the vessel pathlines are denoted by a set of Np points, , with each indicating a 3D point in physical space along the pathlines (Fig. 5a).
Given X, Y, and P, we then extract a dataset of Nd pairs of 2D input and label images,
| (9) |
We obtain the image and label pairs by first moving through each point along the vessel pathlines and interpolating the local pixel values in X and Y in the plane perpendicular to the vessel pathline at that point to obtain the local image patches xi and yi (Fig. 5b).
With our training dataset D, we can then optimize the weights of our FCNN using a stochastic gradient-descent algorithm (Fig. 5c). Here we use the ADAM algorithm [21].
2.5. Adaptive segmentation with automated quality control
Due to the black-box nature of neural networks, it is difficult to control the quality of segmentations produced. We implemented an automated method to control segmentation quality by eliminating undesirable segmentations.
Our approach for automated quality control differs from existing methods [54], in that we use the output information from our FCNN as a quality indicator. In particular, we found the center pixel confidence of the FCNN output to be correlated with segmentation accuracy. Furthermore, the segmentations should be approximately centered on the pathline. As a result, we found the distance of the center of the extracted vessel segmentation from the pathline to be an indicator of quality. Finally as blood vessel surfaces are roughly circular, we developed a metric to measure the deviation of the predicted surface (Fig. 6).
Fig. 6.
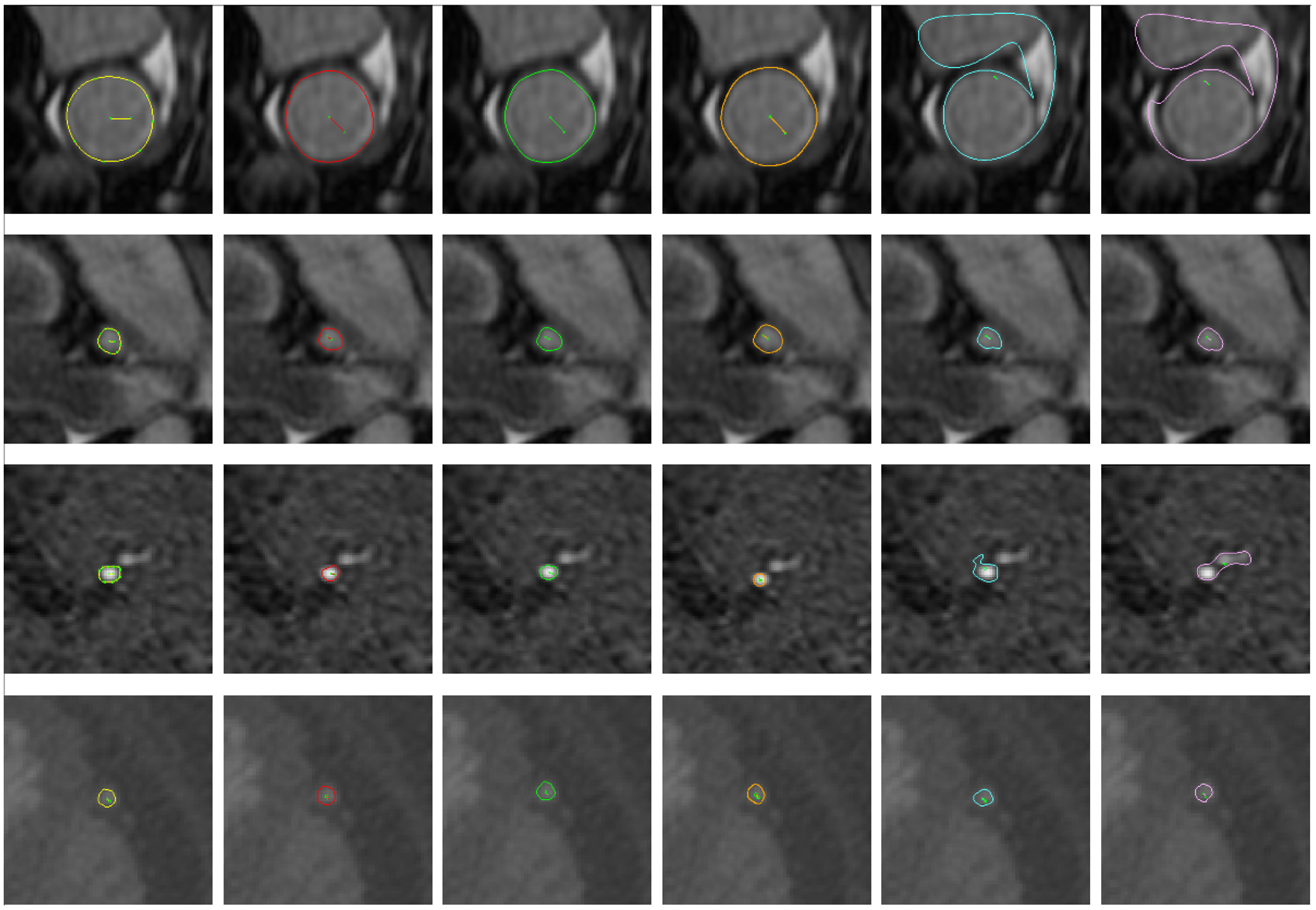
Selected example vessel surfaces detected by each method. From left to right: ground-truth, I2I-M, UNet-M, DeepLab-M, Threshold, and DLRS. From top to bottom: MR aorta, MR left coronary artery, MR posterior cerebral artery, and CT saphenous vein graft
The first metric is defined as
| (10) |
where CP denotes the center pixel value of .
For the second metric, we first compute the center of the vessel lumen
| (11) |
where pi is the ith point on the vessel lumen. If the vessel is exactly centered on the current pathline then . Therefore, the second metric denotes the distance from the center of the image and is
| (12) |
where CD denotes center distance.
For the third metric, we compute an approximate radius
| (13) |
We finally compute the normalized average square difference between the distance of each point pi from the center and the approximate radius
| (14) |
where RD has been used as an abbreviation for radius difference. We develop our automated quality control system by specifying threshold values for CP, CD, and RD beyond which segmentations are rejected.
3. Experimental setup
We want to determine if the FCNN cardiovascular model building workflow provides an improved user-experience over current approaches. Therefore, our first experiment is designed to evaluate the segmentation accuracy of each algorithm in isolation. In particular, we also investigate different combinations of the neural network architectures and loss functions. The networks were trained and evaluated using a desktop computer with an i7 3.0GHz 8-core CPU, 64Gb of DDR4 RAM and 3 Nvidia Titan X GPUs with 12Gb of RAM each. With this hardware and the chosen training parameters, training each network takes approximately 24 h.
The ground-truth data that we use to measure segmentation accuracy is subject to both measurement and human sources of uncertainty. Therefore, we conducted experiments to measure the degree of uncertainty in our ground-truth data.
Finally we performed end-to-end user experiments in SimVascular, comparing the proposed approach and current approaches when constructing full cardiovascular models. Here, we measure the degree of user interaction needed to produce acceptable models so that we can determine which method reduced user interaction.
3.1. Dataset and vascular model repository
We evaluate our method using 104 contrast-enhanced medical image volumes, evenly split between CT and MR acquisition. All medical image volumes are publicly available from the Vascular Model Repository (VMR)2 [51]. This dataset contains image data, pathlines, segmentations, models, and simulation results for a range of anatomic regions. All segmentations were created in SimVascular, by expert curators, using the pathline-based model building approach in Fig. 1, and verified by clinical experts. Most image volumes in the VMR have anisotropic pixel spacing. Here, we resampled all volumes to a spacing of 0.029 cm in all directions. The volumes are split into mutually exclusive training, validation, and testing sets, of 86, 4, and 14 volumes, respectively.
2D training, validation, and testing image patches were extracted using the process described in Section 2.4. We selected 160 × 160 pixels as the window size as this size allowed the full range of vessel sizes in our dataset to be fully visible. In total, 16,004 training, 239 validation, and 6317 input and label images were extracted.
3.2. Reference segmentation methods
We compared the proposed FCNN method against two reference 2D segmentation algorithms. The first is a thresholding algorithm, which is widely used in many existing medical imaging software applications. Active contour methods such as level sets are also widely used. Due to availability of recent open-source implementations, the distance regularized level set [28] (DRLS) is used here. For both algorithms, input images are preprocessed to have zero mean and unit-variance pixel values as described in Section 2.1. We note that we attempted to compare against multiscale vessel enhancement filters [12] as a third reference segmentation method, but were unable to obtain acceptable performance despite investigating a range of different scale parameters.
Threshold:
Given a 2D input image , and a specified threshold value t, the threshold algorithm outputs a segmented binary image where
| (15) |
The threshold value t is optimized for segmentation accuracy using the training dataset.
Level set method:
Level sets define a segmentation boundary as the zero level set of a function and then evolve the function according to a partial differential equation. The DRLS further regularizes the length of the zero level set to prevent large fluctuations in segmentation boundaries. In particular, given an initial level set ϕ(x, 0), DRLS solves the equation
| (16) |
where ϕ(x,t)is the level set function, δϵ is an approximate Dirac delta function, g is an approximate image edge-indicator function, and dp is a derivative function defined using a potential function p. μ, λ, and α are tunable constants. The first term in Eq. 16 regularizes the length of the zero level set boundary. The second term regularizes the curvature. The third term attracts the level set function to edges in the image. Parameter values for the DRLS were found empirically using the training dataset; these were α = 0.25, λ = 1, ϵ = 1.5, μ = 0.2, and 100 iterations.
3.3. Performance metrics
Segmentations generated by the above methods, and by the users, were compared using the following metrics.
DICE
The DICE coefficient values range from 0 (no overlap) to 1 (no error) which measures the similarity between two segmentations and is given by:
| (17) |
Hausdorff distance (HD)
The Hausdorff distance has a lower bound of 0 (perfect match) with no upper bound. This metric measures the maximum minimum distance between two sets of points and is given by:
| (18) |
where d(a, b) is a distance function, for which we use the euclidean norm .
Average symmetric surface distance (ASSD)
The average symmetric surface distance computes the average minimal distance between the surface points of two sets A and B. Let and be sets of the surface points in A and B, respectively. The ASSD is then:
| (19) |
where d is again the Euclidean norm.
3.4. Neural network hyperparameters and nomenclature
The neural networks and training procedures require specification of a number of so-called hyperparameters. For our training process, we used L2 regularization with a coefficient of 0.0001, and a starting learning rate of 0.0001, with the learning rate decreased stepwise by a factor of 10 every 10,000 batches. Training was run for 35,000 batches with a batch size of 4. No pretraining was performed. The ADAM [21] algorithm was used to minimize the prescribed loss function. For the masked loss function, was computed by dilating y by 30 pixels.
In our experiments, we investigate the influence of the chosen loss functions and neural network architectures. The used neural network architectures employed the previously described modified I2INet, UNet, and DeepLab-ASPP networks. For loss functions, we compared sigmoid cross-entropy, balanced sigmoid cross-entropy, and the proposed masked loss function with sigmoid cross-entropy. The labels for each network and loss function we compared are listed in Table 1.
Table 1.
FCNN naming conventions
| Name | Architecture | Loss function |
|---|---|---|
| I2I | I2INet | Sigmoid Cross-Entropy |
| I2I-B | I2INet | Balanced Cross-Entropy |
| I2I-M | I2INet | Masked Cross-Entropy |
| UNet | UNet | Sigmoid Cross-Entropy |
| UNet-B | UNet | Balanced Cross-Entropy |
| UNet-M | UNet | Masked Cross-Entropy |
| DeepLab | DeepLab-ASPP | Sigmoid Cross-Entropy |
| DeepLab-B | DeepLab-ASPP | Balanced Cross-Entropy |
| DeepLab-M | DeepLab-ASPP | Masked Cross-Entropy |
The name refers to the network used and selected loss function. -B and -M appended to the name of the network indicate use of the balanced sigmoid cross-entropy loss function and masked sigmoid cross-entropy loss function respectively
3.5. Automated segmentation quality control
To perform quality control experiments, we further split the testing dataset into two mutually exclusive sets of equal size. On the first half, we examined the effectiveness of different statistics of the input image and neural network prediction as an indicator of produced segmentation quality. Once we identified a suitable set of statistics and cutoff values, the second test set was used to determine the percentage of accepted versus discarded segmentations and corresponding improvement in metric scores.
3.6. Measuring ground-truth segmentation uncertainty
As the ground-truth images were labeled by human experts, they are subject to a certain amount of error. Despite expert knowledge of anatomy, users may have different interpretations of the image due to factors such as low image resolution or measurement noise. To measure the uncertainty in ground-truth segmentation images, an additional experiment was performed. One hundred eighty-seven cross-sectional images were selected from the model of a Coronary Artery Bypass Graft patient. This model was selected as it contains vessels across a range of sizes. Each image was segmented by three expert users of SimVascular. The segmentations were then compared using the DICE, HD, and ASSD metrics to measure variation between users. The results of this experiment will quantify the limit of attainable accuracy in our dataset. Assuming that users will expect segmentation algorithms to produce comparably accurate segmentations, we can measure the number of segmentations produced by each algorithm that were at or above the threshold of human accuracy. This measurement can be used to indicate of the percentage of useful segmentations produced by each algorithm.
3.7. End-to-end model building workflow testing
To fully assess the end-to-end accuracy of the proposed FCNN-based model building method in practice, an experiment was performed with three expert users of the SimVascular software. Each user was assigned one of a cerebrovascular MR image, MR image of patient with Kawasaki disease, and a CT image of a coronary artery bypass graft patient (Fig. 7). For each image, vessel pathlines were created and locations marked for segmentation. Segmentations were generated using the three best performing neural networks and the best performing reference segmentation algorithm. Users inspected all automatically generated segmentations and corrected them if necessary. Comparing the number of segmentations that were accepted by users to the total then indicates the acceptance probability for each method.
Fig. 7.

Comparison of cardiovascular models built using I2I-M to manually built models. First two columns are frontal views, third and fourth columns are side views. First and third columns: models built with I2I-M. Second and fourth columns: manually built models. Top to bottom: coronary artery bypass graft case (CT), carotid arteries and branch vessels (MR), and aorta and coronary arteries for a patient with Kawasaki disease (CT)
4. Results
We compare the DRLS, threshold, and each FCNN architecture (listed in Table 1) via the average DICE, HD, and ASSD scores on the test set (Table 2). All p values were calculated using a one-sided t test for paired samples. We also measure results on small and large vessels separately by splitting the test dataset on vessel radius. The split point is chosen at a vessel radius of 0.55 cm, where vessels with a smaller radius are designated as small vessels and those with a larger radius as large vessels. The splitting point was chosen at 0.55 cm as it represents a middle point between radius measurements for typical small and large vessels such as coronary arteries and the aorta [9, 31].
Table 2.
(Test set) Mean DICE, Hausdorff distance (HD), and average symmetric surface distance (ASSD) for each method. r denotes vessel radius (cm)
| DICE | HD (cm) | ASSD (cm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| r > 0.55 | r ≤ 0.55 | r > 0.55 | r ≤ 0.55 | r > 0.55 | r ≤ 0.55 | ||||
| I2I | 0.53 | 0.91 | 0.50 | 0.32 | 0.23 | 0.32 | 0.17 | 0.07 | 0.17 |
| I2I-B | 0.45 | 0.88 | 0.42 | 0.51 | 0.36 | 0.52 | 0.24 | 0.11 | 0.25 |
| I2I-M | 0.58 | 0.91 | 0.56 | 0.30 | 0.26 | 0.31 | 0.13 | 0.07 | 0.13 |
| UNet | 0.52 | 0.81 | 0.50 | 0.34 | 0.51 | 0.32 | 0.18 | 0.17 | 0.18 |
| UNet-B | 0.36 | 0.81 | 0.33 | 0.70 | 0.46 | 0.72 | 0.40 | 0.16 | 0.42 |
| UNet-M | 0.58 | 0.92 | 0.56 | 0.31 | 0.24 | 0.31 | 0.13 | 0.07 | 0.13 |
| DeepLab | 0.51 | 0.88 | 0.48 | 0.43 | 0.38 | 0.43 | 0.19 | 0.10 | 0.19 |
| DeepLab-B | 0.49 | 0.89 | 0.46 | 0.48 | 0.32 | 0.49 | 0.23 | 0.10 | 0.24 |
| DeepLab-M | 0.59 | 0.91 | 0.57 | 0.25 | 0.26 | 0.25 | 0.12 | 0.08 | 0.12 |
| Threshold | 0.46 | 0.86 | 0.43 | 0.71 | 0.48 | 0.72 | 0.22 | 0.12 | 0.22 |
| DRLS | 0.43 | 0.85 | 0.40 | 0.78 | 0.47 | 0.80 | 0.28 | 0.12 | 0.29 |
UNet-M and DeepLab-M scored better than UNet and DeepLab respectively across all metrics (p < 0.001). I2I-M produced better scores than I2I for all metrics when measured on small vessels (r ≤ 0.55cm, p < 0.001). Furthermore I2I-B and UNet-B produced consistently worse average scores across all metrics when compared with I2I and UNet (p < 0.001). DeepLab-B and DeepLab did not produce significantly different DICE scores, but DeepLab-B produced worse HD and ASSD scores for small vessels but improved HD for large vessels (p < 0.001). I2I-M and UNet-M did not produce significantly different scores (p < 0.05). DeepLab-M significantly improved HD for small vessels when compared with I2I-M and UNet-M (p < 0.001). Compared with reference methods, I2INet-M, UNet-M, and DeepLab-M produced better average scores than DRLS and Threshold across all metrics (p < 0.001).
From a cardiovascular model building perspective, we also examine the number of usable segmentations produced by each method (Fig. 8). Here, usable is defined as segmentations with a DICE score exceeding the average DICE agreement between segmentations produced by expert users (0.94 for large vessels, r ≥ 0.55cm, and 0.78 for small vessels, r < 0.55cm). The percentage of usable segmentations produced using I2I-M, UNet-M, and DeepLab-M were 54.6%, 54.9%, and 50.4% respectively for large vessels and 26.5%, 25.6%, and 28.8% respectively for small vessels. I2I-M and UNet-M produced more usable segmentations than all other methods for large vessels (p < 0.001), but did not differ significantly from each other (p > 0.05). When considering small vessels, DeepLab-M produced more usable segmentations than all other methods (p < 0.001). Additionally I2INet-B, UNet-B, and DeepLab-B produced fewer usable segmentations than their masked loss counterparts. This demonstrates the importance of the choice of network architecture and loss function as well as the fact that classical image segmentation algorithms tend to perform better when the structures to be segmented are well-resolved, such as with large vessels. For small vessels, the threshold, DRLS, and methods produced comparably fewer usable segmentations, showing that without specific parameter tuning, the performance of classical segmentation methods degrades. I2INet-B, UNet-B, and DeepLab-B similary produced fewer usable segmentations for small vessels, highlighting the oversegmentation effect of balanced loss functions.
Fig. 8.
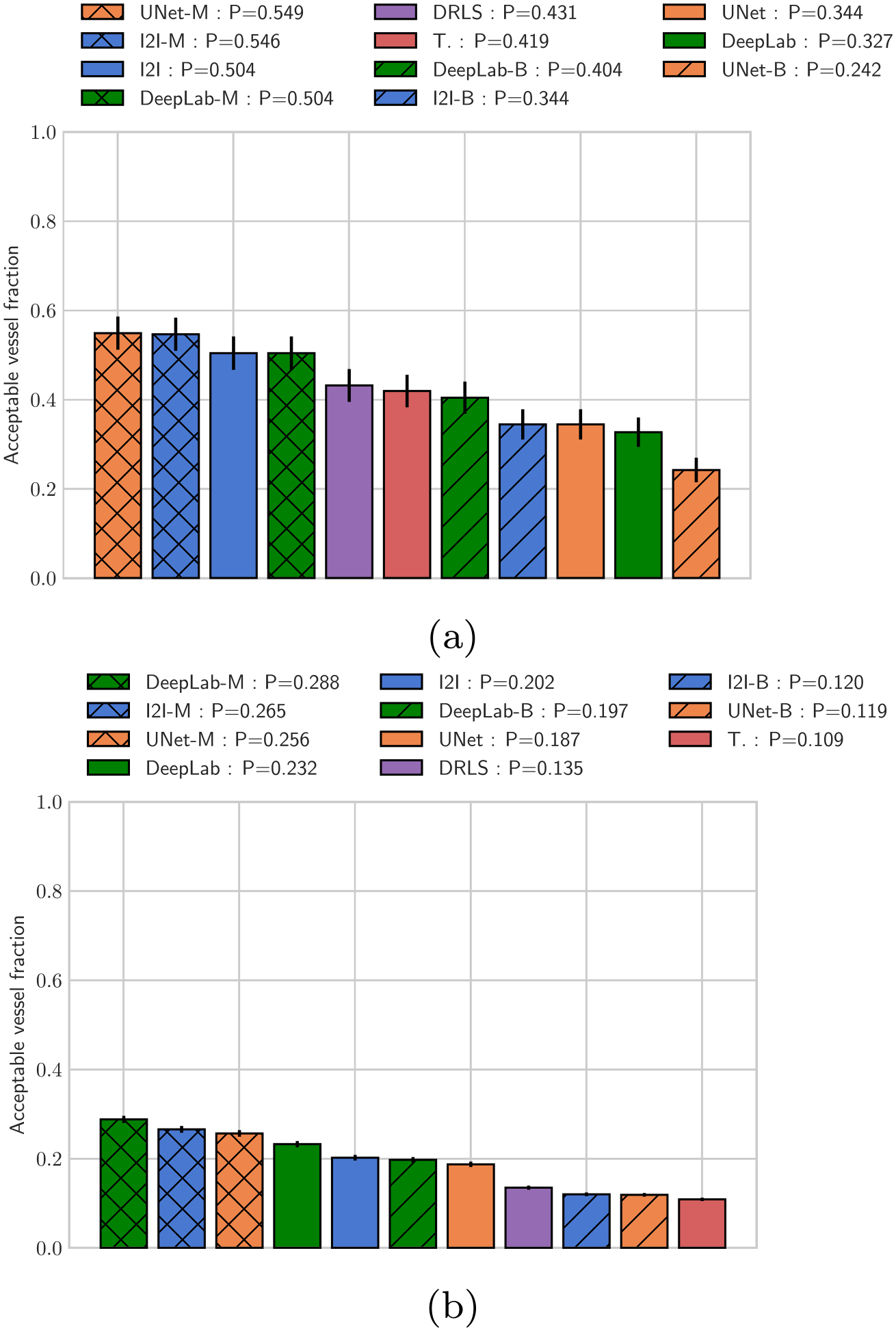
Fraction of usable vessel segmentations produced. a Fraction of segmentations with DICE > 0.94 for large vessels with radius >= 0.55 cm. b Fraction of segmentations with DICE > 0.78 for small vessels with radius< 0.55 cm, cutoff DICE values were determined from the user uncertainty test. Note that P in the legend indicates the fraction of segmentations produced by each method on the test set that were considered usable
In Fig. 6, we examine example vessel surfaces produced by each algorithm; in general the neural network methods resemble the user ground truth in all cases presented. Additionally, the common failure mode of the threshold and level set algorithm occurred when the algorithms segmented additional surrounding structures, or bright spots that are not part of the vessel. Both neural network methods are more robust and do not exhibit a similar failure mode. The typical failure mode for the neural networks was failure to identify the central vessel to be segmented, leading to misplaced segmentations. When the neural networks failed, it was typically for smaller vessels with poor resolution.
4.1. Ground-truth segmentation uncertainty
Comparisons of segmentations produced by users is reported in Table 3. The degree of uncertainty depends on the size of the vessel being segmented by the user. For large vessels, the average DICE between users was 0.94, whereas for smaller vessels there is more uncertainty with the DICE dropping to 0.79. Similar trends were observed for all other metrics. Figure 9 shows that the variation in uncertainty increases substantially as the vessel size decreases.
Table 3.
(Uncertainty test) Mean inter-user DICE, Hausdorff distance (HD), and average symmetric surface distance (ASSD)
| DICE | HD (cm) | ASSD (cm) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| r > 0.55 | r ≤ 0.55 | r > 0.55 | r ≤ 0.55 | r > 0.55 | r ≤ 0.55 | ||||
| User | 0.81 | 0.94 | 0.78 | 0.08 | 0.13 | 0.07 | 0.03 | 0.05 | 0.03 |
r denotes vessel radius (cm)
Fig. 9.
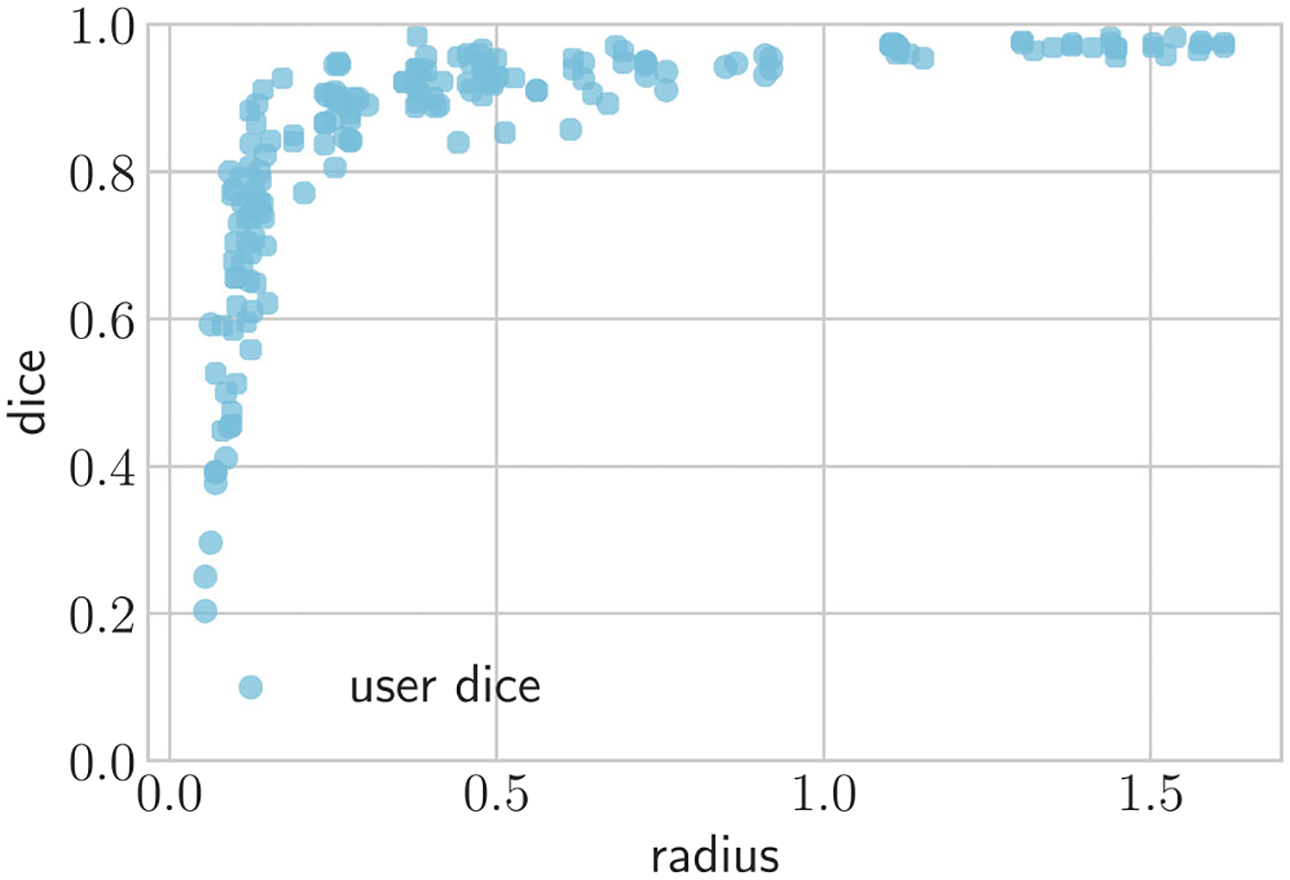
Scatter plot analyzing segmentation agreement between users as a function of vessel radius
4.2. Automated quality control results
To perform quality control experiments, we selected the I2I-M segmentations and computed the CP, CD, and RD metrics, testing various acceptance threshold values. Our results (Table 4) show that using different numbers of quality metrics and cutoff values affects the fraction of segmentations accepted and corresponding quality improvement. For example, using the CP metric and accepting only segmentations with CP > 0.3, the average DICE across all vessel sizes improved to 0.68, and 80.8% of the segmentations were accepted. The average DICE can be improved by 25.8% to 0.73, by restricting to CP > 0.5; however, now only 59.3% of segmentations are accepted. Combining all three metrics, the same DICE improvement can be reached while accepting 74.8% of segmentations.
Table 4.
DICE improvement and fraction of accepted segmentations under different quality control metrics and thresholds
| CP | CD | RD | Acceptance fraction (%) | DICE |
|---|---|---|---|---|
| > 0.3 | 80.8 | 0.68 | ||
| > 0.5 | 59.3 | 0.73 | ||
| < 0.65 | 88.7 | 0.62 | ||
| < 0.3 | 92.7 | 0.62 | ||
| > 0.2 | < 0.75 | < 0.4 | 82.6 | 0.68 |
| > 0.3 | < 0.65 | < 0.3 | 74.8 | 0.73 |
CP is the value of the center pixel of the predicted segmentations, CD is the offset distance of the center of the predicted vessel lumen from the pathline, RD is the normalized radius variance of the predicted lumen surface points
4.3. User-testing results
When testing our complete proposed model building workflow, users corrected significantly fewer segmentations, when using the FCNN-based methods, than with the threshold algorithm (p < 0.001) (Table 5). Users accepted a similar percentage of large vessel segmentations for I2I-M, UNet-M, and DeepLab-M. However, for smaller vessels, more segmentations were accepted for DeepLab-M, 71%, versus 65% for I2I-M and 58% for UNet-M. Using our quality control system to screen for unsuitable segmentations, it improved the acceptance fraction for each algorithm. Using the I2I-M network, the acceptance fractions for smaller vessels improved more than for larger vessels, e.g., increasing from 65 to 79% for small vessels compared with 83 to 85% for larger vessels. For DeepLab-M, the acceptance probability improvement with quality control was not as large as for I2I-M, 0.04 vs 0.11 increase, respectively.
Table 5.
(User test) Mean user acceptance probability for segmentations produced by each method
| Acceptance probability | |||
|---|---|---|---|
| r > 0.55 | r ≤ 0.55 | ||
| I2I-M | 0.69 | 0.83 | 0.65 |
| UNet-M | 0.62 | 0.81 | 0.58 |
| DeepLab-M | 0.74 | 0.83 | 0.71 |
| Threshold | 0.34 | 0.68 | 0.26 |
| Acceptance probability with quality control | |||
| I2I-M | 0.80 | 0.85 | 0.79 |
| UNet-M | 0.70 | 0.85 | 0.67 |
| DeepLab-M | 0.78 | 0.84 | 0.76 |
| Threshold | 0.50 | 0.84 | 0.40 |
Acceptance means the user did not edit the predicted segmentation
As a final test, users were allowed to edit segmentations and add segmentations to construct final cardiovascular models in SimVascular. The ground-truth models and those built using the proposed FCNN method with I2I-M are visually similar (Fig. 7). Inspecting the kawasaki disease case, we see that essential features of the model such as aneurysms in the coronary arteries are preserved. Furthermore, both small and large vessels were accurately captured. For the coronary artery bypass graft patient, when using the FCNN method, 125 segmentations were used for the final model, 34 of which were produced through manual segmentation. For the cerebrovascular MR case, 107 segmentations were produced, 47 of which were manual. For the kawasaki disease case, 68 total segmentations were produced, 20 of which were manually produced. As such using the FCNN method resulted in reductions of manual segmentations required of 73%, 57%, and 71%, respectively.
4.4. Runtime performance and segmentation time savings
On a laptop with a 2.4Ghz i7 CPU, computing 100 segmentations, without use of a GPU, with I2I-M took, on average, 13.6 s. As such the time to compute a single segmentation is on the order of 0.1 s. Manual segmentation takes on average, an order of 5–10 s for a single segmentation. As such the FCNN computation time is not a bottleneck even with standard computer hardware.
Assuming an average manual segmentation time of 5 s, considering the user-testing results (Fig. 7), use of I2I-M thus saved 432.5 s, 290.3 s, and 233.2 s for each of the three cases, respectively. The cases considered for the user test were limited to a small number of vessels. In more realistic simulation scenarios, models can contain 10–30 times more vessels (100–300 vessels), showing that our FCNN segmentation approach can save on the order of hours of manual segmentation effort.
5. Conclusion
Comparisons of the FCNN segmentation methods and the reference Threshold and DRLS algorithms demonstrated that neural networks improved overall performance. All FCNN methods significantly improved average metric scores over the reference methods, illustrating that standard algorithms such as thresholding and level sets need to be recalibrated for each image, whereas neural networks provide more automated approaches.
Our results further showed that the proposed masked loss function did indeed improve the performance of all neural networks, in particular the improvement was larger for small vessels than for large vessels, achieving more precise vessel delineation in regions that are typically difficult to segment.
We further validated our hypothesis that balanced loss functions lead to oversegmentation. Here the balanced loss function significantly degraded average metric scores, especially for small vessels.
The automated quality control experiments showed that the output information from the neural networks is a useful metric to identify good segmentations. We further showed that a combination of metrics rejects fewer segmentations, compared with using a single metric, for the same degree of accuracy improvement. Substantial performance improvement was obtained with a handful of relatively simple metrics, requiring only incrementally additional computational cost. However, the improvement with quality control varied depending on the used neural network architecture, showing that optimal improvement requires network specific tuning of the quality metric threshold levels.
Our results demonstrated that FCNNs are an effective method for automated cardiovascular segmentation and reduce the user interaction needed to build cardiovascular models.
Acknowledgments
The authors acknowledge funding from NSF SI2-SSI grants 1562450 and 1339824 and the American Heart Association. The authors would like to Daniel Rubin and Assaf Hoogi for their insightful discussions and comments related to this work. We also thank Jameson Merkow and David Kriegman for their assistance in implementation of I2I, as well as Noelia Grande Gutierrez, Justin Tran, Casey Fleeter, Melody Dong, Aekaansh Verma, Suhaas Anbazhakan, and Weiguang Yang for performing user tests.
Funding information This study was financially supported by the NSF SI2-SSI grants 1562450 and 1339824 and the American Heart Association.
Biographies

Gabriel Maher is a PhD student at the Institute for Computational and Mathematical Engineering (ICME) at Stanford University. Gabriel has a background in both fluid dynamics and deep learning.

Nathan Wilson (Ph.D.) has 15 years of experience in biomedical research and has presented at international conferences on medical imaging, bioengineering, and computer modeling of micro-electro-mechanical systems.

Alison Marsden (Ph.D.) is an associate professor in the departments of Pediatrics, Bioengineering, and, by courtesy, Mechanical Engineering at Stanford University.
Appendix: Neural networks and deep learning
Neural networks are nonlinear function approximators. In their most general form, neural networks are constructed as computational graphs, where each edge in the graph is a parametrized function that operates on a subset of the nodes in the graph. However, typically a simplified form of neural network, known as a feedforward neural network, is used. Feedforward neural networks are created by composing a sequence of parameterized functions into a chain, where each subsequent function operates on the output of the previous function in the chain. The parameterized functions are often referred to as layers, and the parameters as the weights of the network. The particular choice of layers is what denotes the neural network, or network architecture. It can be shown that feedforward networks can approximate any function to arbitrarily small error, given enough weights [17]
Developing a neural network for a particular application then involves determining a suitable network architecture, and finding weight values that lead to good performance. Typically performance is measured on a sample of input-output pairs using metrics that measure the error between predicted outputs and ground-truth outputs. Values for the network weights are found using optimization algorithms that minimize a specified, often differentiable, loss function and a training set of input-output pairs. The training set is separate from the set that is used to measure performance so that the measured performance represents an accurate measurement of out-of-sample performance.
Determining suitable network architectures is the subject of a large body of research. For a feedforward network, the number of layers can be varied, as well as the type of layer to be used at each step. Developing neural network layers is an active research area; however, the most commonly used layers for image segmentation purposes are convolutional layers. Typically a layer will perform an operation on its input followed by an elementwise nonlinear function known as an activation function. Using nonlinear activation, functions are essential as it allow the neural network to become a universal function approximator [17]. In this work, we used the leaky rectified linear unit (leaky-RELU) for all except the final layer. For the final layer, we used a sigmoid activation function to ensure the output values of the network lie between 0 and 1. The leaky-RELU and sigmoid activation functions are given by
| (20) |
and
| (21) |
We can then formulate a typical layer as
| (22) |
| (23) |
where l denotes the layer index, θl are the weights of layer l, is the operation applied by layer l, parameterized by θl, σ(l) is the activation function of layer l, and a(l) is the final output of layer l.
A 2D convolutional layer uses a 4D tensor of weights , where Hl, Wl, Cl, and Fl are the height, width, number of channels, and number of filters, respectively. Intuitively weights for a convolutional layer can be thought of as Fl filters with a shape of Hl × Wl × Cl stacked on top of each other. The input to a 2D convolutional layer is a 3D tensor , where C = Cl is necessary to ensure the convolution is compatible. The output of a convolutional layer is the result of the chosen activation function applied to the cross-correlation of Θl and a(l−1):
| (24) |
The outputs of a convolutional layer are again 3D tensors, which allows convolutional layers to be chained to form a convolutional network.
Pooling layers are used to subsample network layer inputs, typically to reduce computational burden or to allow processing inputs at different resolutions. A max-pooling layer subsamples its input by using a strided cross-correlation where each output element is the maximum of all elements within the domain of the filter for that step of the cross-correlation. That is, given a filter size of Hl × Wl and a stride K, a max-pooling layer outputs
| (25) |
An average-pooling layer will output the empirical mean of all elements within the filter domain
| (26) |
Note that typically the activation function is omitted for pooling layers.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Antiga L, Piccinelli M, Botti L, Ene-Iordache B, Remuzzi A, Steinman DA (2008) An image-based modeling framework for patient-specific computational hemodynamics. Med Biol Eng Comput, 46 [DOI] [PubMed] [Google Scholar]
- 2.Becker C, Rigamonti R, Lepetit V, Fua P (2013) Supervised feature learning for curvilinear structure segmentation. Medical Image Computing and Computer Assisted Intervention [DOI] [PubMed]
- 3.Benmansour F, Cohen LD (2011) Tubular structure segmentation based on minimal path method and anisotropic enhancement. Int J Comput Vis, 92 [Google Scholar]
- 4.Charbonnier JP, van Rikxoort EM, Setio AAA, Schaefer-Prokop CM, van Ginneken B, Ciompi F (2017) Improving airway segmentation in computed tomography using leak detection with convolutional networks. Medical Image Analysis [DOI] [PubMed]
- 5.Chen H, Dou Q, Yu L, Qin J, Heng PA (2018) VoxResNet: deep voxelwise residual networks for brain segmentation from 3d MR images. Neuroimage 170:446–455. 10.1016/j.neuroimage.2017.04.041 [DOI] [PubMed] [Google Scholar]
- 6.Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL (2016) DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. arXiv [DOI] [PubMed]
- 7.Christ PF, Ettlinger F, Grun F, Elshaer MEA, Lipkova J, Schlecht S, Ahmaddy F, Tatavarty S, Bickel M, Bilic P, Rempfler M, Hofmann F, D’Anastasi M, Ahmadi S, Kaissis G, Holch J, Sommer W, Braren R, Heinemann V, Menze B (2017) Automatic liver and tumor segmentation of ct and mri volumes using cascaded fully convolutional neural networks. Medical Image Analysis
- 8.Cicek O, Abdulkadir A, Lienkamp SS, Ronneberger O (2017) 3D U-net: learning dense volumetric segmentation from sparse annotation. Medical Image Computing and Computer Assisted Intervention
- 9.Dodge JT, Brown BG, Bolson EL, Dodge HT (1992) Lumen diameter of normal human coronary arteries. Influence of age, sex, anatomic variation, and left ventricular hypertrophy or dilation. Circulation, 86(1) [DOI] [PubMed] [Google Scholar]
- 10.Doost SN, Ghista D, Su B, Zhong L, Morsi YS (2016) Heart blood flow simulation: a perspective review. Biomed Eng Online, 15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dou Q, Yu L, Chen H, Jin Y, Yang X, Qin J, Heng PA (2017) 3d deeply supervised network for automated segmentation of volumetric medical images. Med Image Anal 41:40–54. 10.1016/j.media.2017.05.001 [DOI] [PubMed] [Google Scholar]
- 12.Frangi AF, Niessen WJ, Vincken KL, Viergever MA (1998) Multiscale vessel enhancement filtering. Medical Image Computing and Computer-Assisted Intervention
- 13.Friman O, Hindennach M, Kühnel C, Peitgen HO (2010) Multiple hypothesis template tracking of small 3D vessel structures. Med Image Anal, 14 [DOI] [PubMed] [Google Scholar]
- 14.Grady L (2005) Multilabel random walker image segmentation using prior models In: 2005 IEEE computer society conference on computer vision and pattern recognition (CVPR’05), vol 1 IEEE, San Diego, pp 763–770, 10.1109/CVPR.2005.239 [DOI] [Google Scholar]
- 15.He K, Zhang X, Ren S, Sun J (2016) Deep residual learning for image recognition In: The IEEE conference on computer vision and pattern recognition (CVPR) [Google Scholar]
- 16.Heidenreich PA, Trogdon JG, Khavjou OA, Butler J, Dracup K, Ezekowitz MD, Finkelstein EA, Hong Y, Johnston SC, Khera A, Lloyd-Jones DM, Nelson SA, Nichol G, Orenstein D, Wilson PWF, Woo YJ (2011) Forecasting the future of cardiovascular disease in the United States: a policy statement from the American Heart Association. Circulation, 123 [DOI] [PubMed] [Google Scholar]
- 17.Hornik K (1991) Approximation capabilities of multilayer feedforward networks. Neural Netw, 4 [Google Scholar]
- 18.Kamnitsas K, Ledig C, Newcombe VFJ, Simpson JP, Kane AD, Menon DK, Rueckert D, Glocker B (2016) Efficient multi-scale 3d cnn with fully connected crf for accurate brain lesion segmentation. Medical Image Analysis [DOI] [PubMed]
- 19.Kerrien E, Yureidini A, Dequidt J, Duriez C, Anxionnat R, Cotin S (2017) Blood vessel modeling for interactive simulation of interventional neuroradiology procedures. Med Image Anal, 35 [DOI] [PubMed] [Google Scholar]
- 20.Khlebnikov R, Figueroa CA (2016) Crimson: towards a software environment for patient-specific blood flow simulation for diagnosis and treatment. Clinical Image-Based Procedures Translational Research in Medical Imaging
- 21.Kingma D, Ba J (2015) Adam: a method for stochastic optimization In: International conference on learning representations [Google Scholar]
- 22.Kretschmer J, Godenschwager C, Preim B, Stamminger M (2013) Interactive patient-specific vascular modeling with sweep surfaces. IEEE Trans Vis Comput Graph, 19 [DOI] [PubMed] [Google Scholar]
- 23.Krissian K, Malandain G, Nicholas A (2000) Model-based detection of tubular structures in 3D images. Comput Vis Image Underst, 80 [Google Scholar]
- 24.Law MWK, Chung ACS (2008) Three dimensional curvilinear structure detection using optimally oriented flux. European Conference on Computer Vision
- 25.Law MWK, Chung ACS (2010) An oriented flux symmetry based active contour model for three dimensional vessel segmentation. European Conference on Computer Vision
- 26.LeCun Y, Bengio Y, Hinton G (2015) Deep learning. Nature 521(7553):436–444. 10.1038/nature14539 [DOI] [PubMed] [Google Scholar]
- 27.Lesage D, Angelini ED, Bloch I, Funka-Lea G (2009) A review of 3D vessel lumen segmentation techniques: models, features and extraction schemes. Med Image Anal, 13 [DOI] [PubMed] [Google Scholar]
- 28.Li C, Xu C, Gui C, Fox MD (2010) Distance regularized level set evolution and its application to image segmentation. IEEE Trans Image Process, 19 [DOI] [PubMed] [Google Scholar]
- 29.Long J, Shelhamer E, Darrell T (2015) Fully convolutional networks for semantic segmentation, 3431–3440 [DOI] [PubMed] [Google Scholar]
- 30.Lorigo LM, Faugeras OD, Grimson WEL, Keriven R, Kikinis R, Nabavi A, Westin CF (2001) CURVES: curve evolution for vessel segmentation. Med Image Anal, 5 [DOI] [PubMed] [Google Scholar]
- 31.Mao SS, Ahmadi N, Shah B, Beckmann D, Chen A, Ngo L, Flores FR, Gao YL, Budoff MJ (2008) Normal thoracic aorta diameter on cardiac computed tomography in healthy asymptomatic adult; impact of age and gender. Acad Radiol, 15(7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Marsden A (2013) Simulation based planning of surgical interventions in pediatric cardiology. Phys Fluids, 25 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Merkow J, Marsden A, Kriegman D, Tu Z (2016) Dense volume-to-volume vascular boundary detection In: Medical image computing and computer-assisted intervention. Springer International Publishing, Cham [Google Scholar]
- 34.Merkow J, Tu Z, Kriegman D, Marsden A (2015) Structural edge detection for cardiovascular modeling In: MICCAI 2015. Springer, pp 735–742 [Google Scholar]
- 35.Moreno R, Smedby O (2015) Gradient-based enhancement of tubular structures in medical images. Med Image Anal, 26 [DOI] [PubMed] [Google Scholar]
- 36.Parker D, Taylor CA, Wang K (1998) Imaged based 3D solid model construction of human arteries for blood flow simulations In: International conference of the IEEE engineering in medicing and biology society, 20 [Google Scholar]
- 37.Petersen K, Schaap M, Lesage D, Lee M, Grady L (2017) Fast and accurate segmentation of coronary arteries for improved cardiovascular care. GPU Technology Conference, 55 [Google Scholar]
- 38.Pezold S, Horvath A, Fundana K, Tsagkas C, Andelova M, Weier K, Amann M, Cattin PC (2016) Automatic, robust, and globally optimal segmentation of tubular structures. Medical Image Computing and Computer Assisted Intervention
- 39.Rigamonti R, Lepetit V (2012) Accurate and efficient linear structure segmentation by leveraging Ad Hoc features with learned filters In: Medical image computing and computer-assisted intervention - MICCAI 2012, lecture notes in computer science. Springer, Berlin, pp 189–197, 10.1007/978-3-642-33415-3_24 [DOI] [PubMed] [Google Scholar]
- 40.Ronneberger O, Fischer P, Brox T (2015) U-net: convolutional networks for biomedical image segmentation. Medical Image Computing and Computer Assisted Intervention
- 41.Rudyanto RD, Kerkstra S, van Rikxoort EM, Fetita C, Brillet PY, Lefevre C, Xue W, Zhu X, Liang J, Oksuz I, Unay D, Kadipaşaoglu K, Estepar RSJ, Ross JC, Washko GR, Prieto JC, Hoyos MH, Orkisz M, Meine H, Hullebrand M, Stocker C, Mir FL, Naranjo V, Villanueva E, Staring M, Xiao C, Stoel BC, Fabijanska A, Smistad E, Elster AC, Lindseth F, Foruzan AH, Kiros R, Popuri K, Cobzas D, Carretero DJ, Santos A, Carbayo MJL, Helmberger M, Urschler M, Pienn M, H BDG, Campo A, Prokop M, de Jong PA, Ortiz-de Solorzano C, Munoz-Barrutia A, van Ginneken B (2014) Comparing algorithms for automated vessel segmentation in computed tomography scans of the lung: the vessel12 study. Med Image Anal, 18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sankaran S, Kim HJ, Choi G, Taylor CA (2016) Uncertainty quantification in coronary blood flow simulations: impact of geometry, boundary conditions and blood viscosity. J Biomech, 49 [DOI] [PubMed] [Google Scholar]
- 43.Schaap M, Metz CT, van Walsum T, van der Giessen AG, Weustink AC, Mollet NR, Bauer C, Bogunovic H, Castro C, Deng X, Dikici E, O’Donnell T, Frenay M, Friman O, Hoyos MH, Kitslaar PH, Krissian K, Kuhnel C, Luengo-Oroz MA, Orkisz M, Smedby O, Styner M, Szymczak A, Tek H, Wang C, Warfield SK, Zambal S, Zhang Y, Krestin GP, Niessen WJ (2009) Standardized evaluation methodology and reference database for evaluating coronary artery centerline extraction algorithms. Med Image Anal, 13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Schmidhuber J (2015) Deep learning in neural networks: an overview. Neural Netw 61:85–117. 10.1016/j.neunet.2014.09.003 [DOI] [PubMed] [Google Scholar]
- 45.Schumann C, Neugebauer M, Bade R, Preim B, Peitgen HO (2008) Implicit vessel surface reconstruction for visualization and CFD simulation. Int J Comput Assist Radiol Surg, 2 [Google Scholar]
- 46.Taylor CA, Figueroa CA (2009) Patient-specific modeling of cardiovascular mechanics. Annu Rev Biomed Eng, 11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Turetken E, Benmansour F, Andres B, Pfister H, Fua P (2013) Reconstructing loopy curvilinear structures using integer programming. In: IEEE Conference on computer vision and pattern recognition [DOI] [PubMed]
- 48.Updegrove A, Wilson N, Merkow J, Lan H, Marsden A, Shadden SC (2013) SimVascular: an open source pipeline for cardiovascular simulation. Ann Biomed Eng, 61 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Updegrove A, Wilson NM, Shadden SC (2016) Boolean and smoothing of discrete surfaces. Adv Eng Softw, 95 [Google Scholar]
- 50.Wang KCY (2001) Level set methods for computational prototyping with application to hemodynamic modeling. Stanford University, Ph.D. thesis [Google Scholar]
- 51.Wilson NM, Ortiz AK, Johnson AB (2013) The vascular model repository: a public resource of medical imaging data and blood flow simulation results. J Med Dev, 7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wu X, Luboz V, Krissian K, Cotin S, Dawson S (2011) Segmentation and reconstruction of vascular structures for 3D real-time simulation. Med Image Anal, 15 [DOI] [PubMed] [Google Scholar]
- 53.Xie S, Tu Z (2015) Holistically-nested edge detection ICCV
- 54.Zhang H, Frits J, Sally A (2008) Multi-scale gaussian normalizaton for solar image processing. Comput Vis Image Underst, 110 [Google Scholar]
- 55.Zhang Y, Bazilevs Y, Goswami S, Bajaj CL, Hughes TJR (2007) Patient-specific vascular NURBS modeling for isogeometric analysis of blood flow. Comput Methods Appl Mech Eng, 196 [DOI] [PMC free article] [PubMed] [Google Scholar]


