Abstract
The effect of urine pH on renal excretion and systemic disposition has been observed for many drugs and metabolites. When urine pH is altered, tubular ionization, passive reabsorption, renal clearance, and systemic exposure of drugs and metabolites may all change dramatically, raising clinically significant concerns. Surprisingly, the urine pH effect on drug disposition is not routinely explored in humans, and regulatory agencies have neither developed guidance on this issue nor required industry to conduct pertinent human trials. In this study, we hypothesized that physiologically based pharmacokinetic (PBPK) modeling could be used as a cost-effective method to examine potential urine pH effect on drug and metabolite disposition. Our previously developed and verified mechanistic kidney model was integrated with a full-body PBPK model to simulate renal clearance and area under the plasma concentration-time curve (AUC) with varying urine pH statuses using methamphetamine and amphetamine as model compounds. We first developed and verified drug models for methamphetamine and amphetamine under normal urine pH condition [absolute average fold error (AAFE) < 1.25 at study level]. Then, acidic and alkaline urine scenarios were simulated. Our simulation results show that the renal excretion and plasma concentration-time profiles for methamphetamine and amphetamine could be recapitulated under different urine pH (AAFE < 2 at individual level). The methamphetamine-amphetamine parent-metabolite full-body PBPK model also successfully simulated amphetamine plasma concentration-time profiles (AAFE < 1.25 at study level) and amphetamine/methamphetamine urinary concentration ratios (AAFE < 2 at individual level) after dosing methamphetamine. This demonstrates that our mechanistic PBPK model can predict urine pH effect on systemic and urinary disposition of drugs and metabolites.
SIGNIFICANCE STATEMENT
Our study shows that integrating mechanistic kidney model with full-body physiologically based pharmacokinetic model can predict the magnitude of alteration in renal excretion and area under the plasma concentration-time curve (AUC) of drugs and metabolites when urine pH is changed. This provides a cost-effective method to evaluate the likelihood of renal and systemic disposition changes due to varying urine pH. This is important because multiple drugs and diseases can alter urine pH, leading to quantitatively and clinically significant changes in drug and metabolite disposition that may require adjustment of therapy.
Introduction
The effect of urine pH on renal clearance of weak acids and bases was discovered more than half a century ago in studies with salicylic acid (Macpherson et al., 1955) and methamphetamine (Beckett and Rowland, 1965c). The mechanism behind this phenomenon is believed to be the altered ionization status of weak acids and bases with changes in renal tubular filtrate pH and the subsequent alterations in renal passive reabsorption of unionized drugs (Milne et al., 1958; Tucker, 1981). Changes in renal passive reabsorption can have a drastic impact on renal clearance. For example, when urine pH decreased from alkaline (pH ≈ 7.5–8.5) to acidic (pH ≈ 4.5–5.5), the amount of drug excreted unchanged in urine for weak bases, such as pethidine, methamphetamine, and mexiletine, increased up to 21-fold (Chan, 1979), 48-fold (Beckett and Rowland, 1965c), and 87-fold (Kiddie et al., 1974), respectively, whereas the renal clearance of weak acids, such as chlorpropamide (Neuvonen and Kärkkäinen, 1983) and salicylic acid (Macpherson et al., 1955), decreased by 99% and 97%, respectively. Also, after dosing of imipramine, methamphetamine, and amitriptyline, their respective metabolites, desipramine, amphetamine, and nortriptyline, have shown up to 5-fold (Gram et al., 1971), 11-fold (Beckett and Rowland, 1965b), and 93-fold (Kärkkäinen and Neuvonen, 1986) increases in urinary excretion, respectively, in acidic urine condition in comparison with alkaline urine condition. These findings demonstrate the pronounced and broad significance of the urine pH effect on both drugs and metabolites.
Overall, approximately 31% of marketed drugs are significantly excreted unchanged via the kidney (Varma et al., 2009), and 70% of marketed drugs are either monoprotic weak acids or monoprotic weak bases (Manallack, 2007) that may have varying ionization statuses in the tubular lumen. In addition, the mean LogP of patented compounds across 18 pharmaceutical companies ranged from 3.5 to 4.5 (Leeson and St-Gallay, 2011), suggesting that the majority of drugs have a moderate to high intrinsic lipophilicity and therefore transcellular permeability. Together, these data suggest that many drugs are potentially subject to significant renal clearance and effective renal passive reabsorption that can be altered because of urine pH changes. As such, the variability of renal clearance with urine pH can be surprisingly common. Indeed, more than a dozen drugs have been shown to have urine pH-dependent renal excretion (Macpherson et al., 1955; Beckett and Rowland, 1965a,c; Gerhardt et al., 1969; Sharpstone, 1969; Sjöqvist et al., 1969; Gram et al., 1971; Kiddie et al., 1974; Chan, 1979; Neuvonen and Kärkkäinen, 1983; Muhiddin et al., 1984; Benowitz and Jacob, 1985; Aoki and Sitar, 1988; Freudenthaler et al., 1998). If renal excretion is an important elimination pathway for the drug of interest, the systemic drug disposition will also be affected by altered urine pH. For example, for weak bases memantine and flecainide, the area under the plasma concentration-time curve (AUC0-inf) increased by 5.3-fold (Freudenthaler et al., 1998) and 3.6-fold (Muhiddin et al., 1984), respectively, whereas for weak acids cinoxacin and chlorpropamide, the plasma AUC0-inf decreased by 67% (Barbhaiya et al., 1982) and 81% (Neuvonen and Kärkkäinen, 1983), respectively, in alkaline urine condition in comparison with acidic urine condition. This demonstrates that the magnitude of urine pH effect on plasma AUC could be as significant as drug-drug interactions resulting from coadministration with a strong inhibitor or inducer (i.e., AUC increased by 5-fold or decreased by 80%).
Given the number of known drugs affected by urine pH and the substantial magnitude of observed urine pH effects on drug and metabolite disposition, it is striking that urine pH effects on drug and metabolite renal and systemic disposition are not routinely examined for weak acids and bases in clinical studies, and regulatory agencies have not developed guidelines to assess drug safety under different urine pHs. In contrast, characterization of drug-drug interactions, food effects, and disease effects on drug disposition are required by regulatory agencies as essential components of drug approval process, and these interactions and effects have been explored extensively in human subjects and simulated by models (Shebley et al., 2018) to support regulatory decision making.
In this study, we hypothesized that modeling techniques could be leveraged to understand and predict urine pH effect on drug and metabolite disposition. To test this hypothesis, a recently developed and verified dynamic physiologically based mechanistic kidney model (Huang and Isoherranen, 2018) was integrated into a parent-metabolite full-body physiologically based pharmacokinetic (PBPK) model (Huang and Isoherranen, 2020) to simulate urine pH-dependent parent-metabolite systemic disposition and urinary excretion using methamphetamine and amphetamine as model compounds.
Materials and Methods
Development of Parent-Metabolite Full-Body PBPK Structural Model with Mechanistic Kidney Model and Peripheral Arm Vein Sampling Site.
A 104-compartment parent-metabolite (52 compartments for each) full-body PBPK model was developed using MATLAB and Simulink platform (R2018a; MathWorks, Natick, MA) by merging our previously published mechanistic kidney model (Huang and Isoherranen, 2018) with the parent-metabolite full-body PBPK model (Huang and Isoherranen, 2020), as shown in Fig. 1. This model contains 10 physiologically important tissue/organ compartments modeled as perfusion rate-limited organs, two blood circulation compartments (i.e., central venous compartment and central arterial compartment), a peripheral arm vein sampling site as previously described (Huang and Isoherranen, 2020), a two-compartment permeability rate-limited liver model, and a 35-compartment mechanistic kidney model (Huang and Isoherranen, 2018). The mechanistic kidney model was incorporated to replace the conventional perfusion rate–limited kidney compartment and to capture the unbound filtration, active secretion, and tubular filtrate/urine pH-dependent passive reabsorption. The mechanistic kidney model was merged with the PBPK model by connecting the central arterial compartment to the glomerulus to create the renal inflow and connecting the vascular compartment of the last subsegment of collecting duct to the central venous compartment to create the renal outflow. The model file and the code script are provided as Supplemental Material.
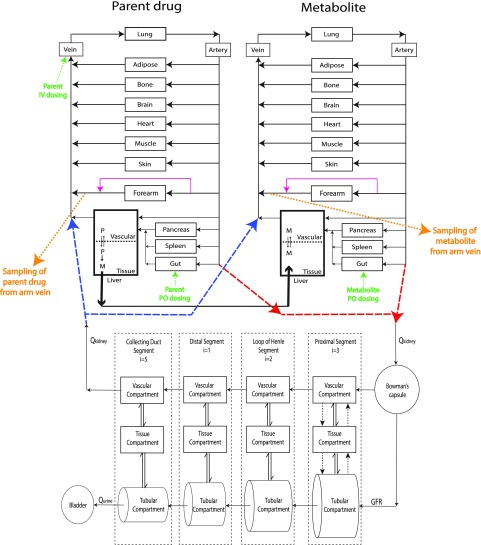
Fig. 1.
Structure of the developed mechanistic kidney-integrated parent-metabolite full-body PBPK model. Schematic presentation of the physiologically based parent-metabolite pharmacokinetic model with a mechanistic kidney model and peripheral arm vein sampling site incorporated. The renal artery that connects central artery to the entrance of the mechanistic kidney model is shown in red dashed lines. The renal vein that connects the exit of the mechanistic kidney model to the central venous compartment is shown in blue dashed lines. The transporter-mediated active secretion or active reabsorption is shown in black dotted arrows. The bidirectional pH-dependent passive diffusion is shown in double arrows. The peripheral arm vein sampling sites are shown in orange with forearm anastomoses shown in magenta. The intravenous and oral dosing are shown in green. GFR, glomerular filtration rate; i, number of subsegment each segment is divided into; M, metabolite; P, parent; Qkidney, renal blood flow; Qurine, urine formation flow.
Physicochemical Parameters for Methamphetamine and Amphetamine.
In this study, only dextrorotary isomers of methamphetamine and amphetamine [i.e., S(+)-methamphetamine and S(+)-amphetamine] are discussed because of their greater psychoactive activity compared with the l-isomers. The molecular weight, pKa, and LogP values of methamphetamine (Meth) and amphetamine (Amph) were collected from www.drugbank.ca. The plasma unbound fractions (fu,p) of methamphetamine and amphetamine were determined in pooled human plasma by ultracentrifugation as previously described (Shirasaka et al., 2013). In brief, pooled human plasma was spiked with methamphetamine and amphetamine to a final concentration of 0.2 µM. Three 200-µl aliquots were centrifuged in 435,000 g for 90 minutes at 37°C, and another three 200-µl aliquots were incubated at 37°C for 90 minutes. The supernatant (50 µl) from the ultracentrifugation and the incubated samples (50 µl) were then quenched with 250 µl of 3:1 (v/v) acetonitrile:methanol containing 100 nM methamphetamine-d11 and amphetamine-d11 as internal standards and analyzed by LC-MS/MS as previously described (Wagner et al., 2017). The experiments were conducted in triplicate on two separate days. The plasma unbound fraction for each day was calculated as the ratio of mean free concentration (Cu) in supernatant (after ultracentrifugation) over mean total concentration (C) in plasma (after incubation). The average value of the two experiments was used as the final fu,p.
The blood-to-plasma ratio of methamphetamine and amphetamine were experimentally determined as described previously (Sager et al., 2016). Methamphetamine and amphetamine were spiked into 3 ml of fresh human blood to a final concentration of 0.2 µM. Three 700 µl aliquots were collected and incubated for 2 hours at 37°C to equilibrate blood partitioning. Blood samples (60 µl) were collected after incubation to measure blood concentration, remaining samples were centrifuged in 1000g for 10 minute to separate plasma and a plasma sample (60 µl) was collected to measure plasma concentration. Both blood and plasma samples (60 µl) were then quenched with 120 µl of methanol containing 100 nM methamphetamine-d11 and amphetamine-d11 as internal standards and analyzed by LC-MS/MS as previously described (Wagner et al., 2017). The experiments were conducted in triplicate on two separate days and the blood-to-plasma ratio was calculated as the ratio of concentration in blood sample over concentration in plasma sample. The average value of the two experiments was used as the final blood-to-plasma ratio.
The cellular permeabilities of methamphetamine and amphetamine were measured using Madin-Darby canine kidney (MDCK) cells (American Type Culture Collection CCL-34 passage 10–15). The cells were cultured in Dulbecco’s modified Eagle’s medium supplemented with 10% FBS, 4.5 g/l glucose, and 1% penicillin/streptomycin at 37°C with 5% CO2 in a humidified atmosphere. Cells were seeded at a density of approximately 6.5 × 104 cells/cm2 on 24-well Transwell plates with 0.4-µm pore size inserts. Ninety-six hours after seeding, cells were used for permeability assays. For the preincubation, the apical and basolateral chambers were first rinsed twice with warm Hank’s Balanced Salt Solution (HBSS) pH 7.2, and this was followed by acclimation to HBSS for 15 minutes. Membrane integrity was confirmed by transepithelial electrical resistance measurements, and monolayers with values below 200 Ω × cm2 were excluded from the study. Transport assay was initiated by replacing the buffer on either apical or basolateral side with test solutions (200 µl apical, 800 µl basolateral donor chambers) containing 1 µM of methamphetamine or amphetamine in HBSS (pH 7.2). Samples of 100 µl medium from the receiver chamber were collected at 0, 20, 40, 60, 90, and 120 minutes for analysis by LC-MS/MS using a previously published method (Wagner et al., 2017). The apparent permeability (Papp) of methamphetamine and amphetamine across cell monolayers was calculated using eq. 1:
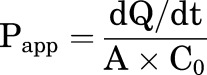 |
(1) |
in which A is the membrane surface area (cm2) of the insert filter, C0 is the initial concentration of compound in the donor chamber (micromolars), and dQ/dt (micromoles per second) is the slope of the linear regression line of measured drug amount in receiver chamber (Q) as a function of time (t) and represents the amount of methamphetamine or amphetamine that crossed the monolayer per unit time. The experiments were conducted for both apical-to-basolateral and basolateral-to-apical directions in duplicates on three separate days. The average value of Papp measured in both directions in three experiments was used as the final apparent permeability. Detailed results are shown in Supplemental Figs. 1 and 2.
PBPK Model Development for Methamphetamine and Amphetamine.
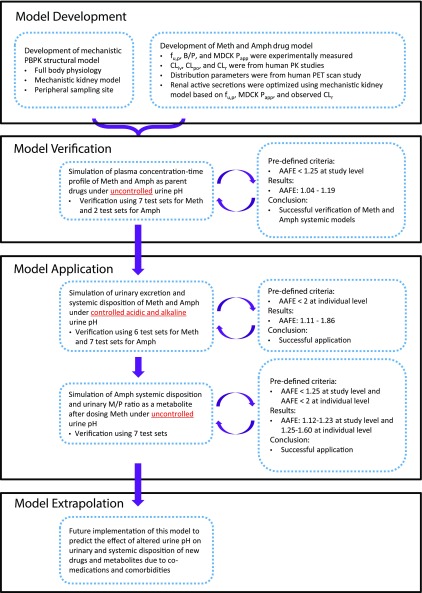
The overall workflow for model development and verification is shown in Fig. 2. For the drug model development, the clinical pharmacokinetic data of methamphetamine and amphetamine in humans were collected from the National Center for Biotechnology Information data base (http://www.ncbi.nlm.nih.gov/pubmed) accessed on January 1, 2019. Search keywords were “methamphetamine OR amphetamine AND pharmacokinetics.” One intravenous (Li et al., 2010) and two po (Rowland, 1969; CDER, 2001) data sets were used as training sets for methamphetamine and amphetamine model development, respectively. Seven (six intravenous and one po) and two (both po) data sets published in six studies (Perez-Reyes et al., 1991; Cook et al., 1993; Mendelson et al., 1995, 2006; CDER, 2002; Harris et al., 2003) were used as test sets to verify the developed PBPK models for methamphetamine and amphetamine, respectively. The detailed information of study populations and study designs for all the data sets used are summarized in Supplemental Table 1. Plasma concentration-time curves and urinary excretion profiles from these studies were digitized using WebPlotDigitizer (version 4.2, https://automeris.io/WebPlotDigitizer).
Fig. 2.
The overall workflow for developing and verifying the full-body parent-metabolite PBPK model of methamphetamine and amphetamine for the simulation of urine pH-dependent systemic disposition and urinary excretion. AAFE, absolute average fold error; B/P, blood-to-plasma ratio; CLiv, total body clearance measured after intravenous dosing; CLpo, total body clearance measured after oral dosing; CLr, renal clearance; M/P, metabolite-to-parent ratio; Papp, experimentally determined apparent cellular permeability; PET, positron emission tomography.
For oral drug absorption of both methamphetamine and amphetamine, compounds in the gastrointestinal lumen were assumed to be completely dissolved and evenly distributed inside the lumen compartment immediately upon oral administration. The drug absorption from lumen into intestinal blood was assumed to be governed by a single absorption rate constant, which was set to be a sufficiently high value such that the overall absorption was intestinal blood flow-limited. This was based on the high aqueous solubility [928 and 1740 mg/l (www.drugbank.ca)] and high permeability of methamphetamine and amphetamine. The gut metabolism of methamphetamine and amphetamine was assumed to be negligible because both drugs have low extraction ratios in the liver primarily mediated by CYP2D6, and CYP2D6 is not highly expressed in the intestine (Paine et al., 2006). As such, the fraction absorbed (Fa) and fraction escaping gut clearance (Fg) were assumed to be 1.
For the physiologic model, the system-specific parameters, including the physical volume and the blood flow to each organ/tissue, were collected from literature (Brown et al., 1997). The tissue-to-plasma partition coefficients (Kp) for brain, gastrointestinal tract, heart, kidney, liver, lung, pancreas, and spleen for methamphetamine were calculated based on a published human positron emission tomography study (Volkow et al., 2010), whereas the Kp values for adipose, bone, muscle, and skin were optimized because Kp = 3 based on observed methamphetamine volume of distribution at steady state (Vss) of 4.02 l/kg (Harris et al., 2003). Because of the structural similarity between methamphetamine and amphetamine, the visceral organ-specific Kp values (i.e., Kp for brain, gastrointestinal tract, heart, kidney, liver, lung, pancreas, and spleen) for amphetamine were set the same as for methamphetamine. Based on the higher polarity of amphetamine in comparison with methamphetamine, the tissue-specific Kp values of adipose, bone, muscle, and skin were set as 2 for amphetamine, resulting in a predicted Vss of 3.14 l/kg versus an observed apparent Vss ranging from 3.2 to 5.6 l/kg after oral dosing (Randall, 2004).
The hepatic clearances of methamphetamine and amphetamine were modeled based on in vivo human data. Methamphetamine has an observed systemic clearance of 18.0 l/h (Li et al., 2010) and an observed renal clearance of 8.09 l/h (Li et al., 2010) after intravenous administration. Amphetamine has an observed oral clearance of 15.8 l/h (CDER, 2001) and an observed renal clearance of 7.14 l/h (Rowland, 1969). As a result, the hepatic clearances of methamphetamine and amphetamine were calculated as 9.91 and 7.41 l/h, respectively, based on the assumption that Fa and Fg are equal to 1 for amphetamine. The intrinsic metabolic clearances of methamphetamine and amphetamine were back-calculated as 14.4 and 9.87 l/h, respectively, based on measured plasma unbound fraction, blood-to-plasma ratio, and the well-stirred hepatic clearance model (Wilkinson and Shand, 1975).
The mechanistic kidney model was used to simulate the renal clearance of methamphetamine and amphetamine. The experimentally determined human fu,p and the permeability in the MDCK cells were used as model inputs to simulate unbound filtration and passive reabsorption processes as previously described (Huang and Isoherranen, 2018). Without incorporating active secretion, the mechanistic kidney model predicted renal clearance values of 2.9 and 3.2 l/h for methamphetamine and amphetamine, respectively, which were significantly below the observed values [8.09 l/h for methamphetamine (Li et al., 2010) and 7.14 l/h for amphetamine (Rowland, 1969)]. Therefore, an active secretion component was added to the mechanistic kidney model to simulate methamphetamine and amphetamine renal clearances based on the previous characterization of methamphetamine and amphetamine as organic cation transporter 2 and multidrug and toxin extrusion substrates (Wagner et al., 2017). Because of the low confidence of in vitro and in vivo renal transporter quantification and expression, the active secretion clearances of methamphetamine and amphetamine were optimized with respect to the observed renal clearance [i.e., 8.09 l/h for methamphetamine (Li et al., 2010) and 7.14 l/h for amphetamine (Rowland, 1969)], assuming equal apical and basolateral secretion and uniform distribution of active secretion among the three subsegments of proximal tubule in the model. All the detailed physicochemical and pharmacokinetic values used in the models are listed in Table 1.
TABLE 1.
Physicochemical and pharmacokinetic parameters of methamphetamine and amphetamine used in the full-body parent-metabolite PBPK model with the integrated mechanistic kidney model and peripheral arm vein sampling site
| Parameter | Methamphetamine | Amphetamine |
|---|---|---|
| Physicochemical | ||
| Molecular weight (g/mol) | 149.23a | 135.21a |
| Compound type | Basea | Basea |
| pKa | 10.21a | 10.01a |
| LogP | 2.23a | 1.85a |
| fu,p | 0.77b | 0.82b |
| B/P | 1.04b | 1.04b |
| MDCK cellular permeability (10−6 cm/s) | 29.1b | 26.9b |
| Absorption | ||
| ka (h−1) | 5c | 5c |
| Fa | 1c | 1c |
| Fg | 1c | 1c |
| Distribution | ||
| Kp,adipose | 3d | 2d |
| Kp,bone | 3d | 2d |
| Kp,brain | 9.67e | 9.67e |
| Kp,gastrointestinal tract | 25.2e | 25.2e |
| Kp,heart | 5.21e | 5.21e |
| Kp,kidney | 14.5e | 14.5e |
| Kp,liver | 25e | 25e |
| Kp,lung | 6.94e | 6.94e |
| Kp,muscle | 3d | 2d |
| Kp,pancreas | 12.7e | 12.7e |
| Kp,skin | 3d | 2d |
| Kp,spleen | 11e | 11e |
| Metabolism (l/h) | ||
| CLtotal | 18.0f (i.v.) | 15.8g (p.o.) |
| CLh | 9.91h | 7.41h |
| CLintrinsic | 14.4h | 9.87h |
| CLf | — | 3.29i |
| Excretion (l/h) | ||
| CLr | 8.09f | 7.14j |
| CLsecretion | 48k (16 × 3) | 30k (10 × 3) |
B/P, blood-to-plasma ratio; CLf, formation clearance; CLh, hepatic clearance; CLintrinsic, metabolic intrinsic clearance; CLr, renal clearance; CLsecretion, renal active secretion clearance at proximal tubule (clearance value of each proximal subsegment S1, S2, and S3); CLtotal, total body clearance (intravenous administration for methamphetamine; oral administration for amphetamine); Fa, fraction absorbed; Fg, fraction passed the enterocyte; ka, absorption rate constant from gut lumen to blood.
Collected from www.drugbank.ca.
Measured from experiments.
Assumed as described in Materials and Methods.
Optimized as described in Materials and Methods.
Derived as described in Materials and Methods.
Derived based on Lane and Levy (1980), CDER (2001), Newton et al. (2005).
Optimized as described in Materials and Methods.
Verification of Methamphetamine and Amphetamine PBPK Models.
All simulations were performed using MATLAB and Simulink platform (R2018a; MathWorks) with the same route of administration and the same dosage regimen as reported in the corresponding clinical studies (Supplemental Table 1), assuming a representative population with average physiology. The renal tubular filtrate pH gradient for a representative population is shown in Supplemental Table 2 with a urine pH value of 6.5 under uncontrolled (i.e., normal) conditions. The overall model development and verification workflow was adapted from previous studies (Huang et al., 2017; Cheong et al., 2019) and is shown schematically in Fig. 2. To verify the methamphetamine model, methamphetamine plasma concentration-time profiles were simulated after intravenous and oral dosing and compared with the observed data from seven test sets (six intravenous and one po dosing) published in five studies (Perez-Reyes et al., 1991; Cook et al., 1993; Mendelson et al., 1995, 2006; Harris et al., 2003). These studies were not used in model development. For amphetamine model verification, the amphetamine plasma concentration-time profiles were simulated after oral dosing and compared with the observed data from two test data sets (CDER, 2002) that were not used in model development. All simulated plasma concentrations were sampled from peripheral arm vein sampling site that was developed and verified previously (Huang and Isoherranen, 2020) to match with the sampling site in the observed pharmacokinetic studies. To assess model performance, absolute average fold error (AAFE) was calculated according to eq. 2. Furthermore, the AUC was calculated using trapezoidal method and compared with the observed AUC. The ratio between the simulated and observed AUC was calculated to assess the fold difference between the two. The calculated AAFE had to be within 1.25-fold and the AUC ratio within 0.8-1.25- fold (model acceptance criterion) for the simulation to be considered successful.
| (2) |
Simulation and Verification of Urine pH Effect on Renal Excretion and Systemic Disposition of Methamphetamine and Amphetamine.
To evaluate whether the verified full-body PBPK model could be applied to predict urine pH effect on plasma concentration-time profile and urinary drug excretion of methamphetamine and amphetamine, methamphetamine disposition was simulated under two different urine pH conditions in contrast to the default uncontrolled urine pH (i.e., urine pH = 6.5). For acidic urine pH, the tubular filtrate pH was set to decrease in a stepwise manner from 7.2 at the first proximal tubule subsegment to 5.0 at the last collecting duct subsegment. For alkaline urine pH, the tubular filtrate pH was set to increase in a stepwise manner from 7.4 at the first proximal tubule subsegment to 8.0 at the last collecting duct subsegment. Detailed renal tubular filtrate pH gradient setups used in the modeling are shown in Supplemental Table 2.
The amount of drug excreted in urine with time and the plasma concentration-time profile for methamphetamine was simulated at each of the three urine pH conditions after oral dosing of 11 mg methamphetamine base. The simulated urinary excretion-time profiles were compared with observed data from three test sets corresponding to the three urine pH conditions (Beckett and Rowland, 1965c). Because of the limited number of subjects in the observed data (n = 1), a 2-fold acceptance criterion of AAFE was used as the acceptance criterion when the simulated population representative was compared with the individual observed data. The 2-fold criterion was selected given the reported interindividual variability (coefficient of variance: 56%) in methamphetamine renal clearance (Kim et al., 2004). The 2-fold range is a conservative criterion provided renal clearance follows log-normal distribution, in which 95% of individuals have a renal clearance within 2.53-19.5 l/h, yielding a 2.77-fold difference between the upper/lower limit and the geometric mean. The simulation results of the urine pH effect on methamphetamine urinary excretion were also compared with another clinical study (Beckett and Rowland, 1965b) as a second set of verification. Because the observed plasma concentration-time data for methamphetamine were not available under the basic and acidic urine pH conditions, simulated and observed plasma concentrations were not compared.
The urinary excretion and plasma concentration-time profile for amphetamine were simulated similarly under uncontrolled, acidic, and alkaline urine conditions after oral dosing of 11 mg amphetamine base. The percentage of amphetamine dose excreted into urine was calculated by dividing the cumulative amount excreted into urine by dose. The amount excreted into urine was considered over 48 hours for uncontrolled urine pH and 16 hours for acidic and alkaline urine pH as described in the observed study and compared with observed data from respective test data sets (Beckett and Rowland, 1965a). The effect of altered urine pH on amphetamine urinary excretion was evaluated based on the percent change in urinary excretion (amount of amphetamine excreted) under either acidic or alkaline urine in comparison with the urinary excretion when urine pH was not controlled (simulated urine pH = 6.5). The ratio of the predicted to observed percent change in urinary excretion with altered urine pH was calculated. A 2-fold acceptance criterion, similar to what has been used for drug-drug interaction studies (Sager et al., 2015), was applied to this ratio to determine whether the simulation was successful. Additionally, simulated plasma concentration-time profile for amphetamine under uncontrolled and acidic urine conditions was compared with the observed data from four test data sets (Beckett et al., 1969). Because of the limited number of subjects in the observed data (n = 2), a 2-fold acceptance criterion of AAFE was used when comparing the simulated population mean results to the individual observed data.
Verification of Methamphetamine-Amphetamine Parent-Metabolite Model.
The methamphetamine-amphetamine parent-metabolite model was established based on the individual compound models using previously developed PBPK model (Huang and Isoherranen, 2020). Amphetamine formation from methamphetamine was modeled to occur within the liver compartment. The hepatic formation clearance of amphetamine from methamphetamine was calculated as 3.29 l/h using the data from a clinical study reporting the AUC ratio of amphetamine to methamphetamine (ratio = 0.208) after intravenous dosing of methamphetamine (Newton et al., 2005) and observed amphetamine oral clearance of 15.8 l/h (CDER, 2001) based on a previous method (Lane and Levy, 1980).
To verify the methamphetamine-amphetamine parent-metabolite kinetic model, amphetamine plasma concentration-time profiles as a metabolite of methamphetamine after intravenous administration of methamphetamine were simulated and compared with the observed data from four test sets (Cook et al., 1993; Harris et al., 2003; Mendelson et al., 2006). To evaluate the model, a 1.25-fold acceptance criterion was applied to the AAFE to determine whether the simulation was successful. All simulations were performed with the same route of administration and same dosage as reported in the corresponding studies (Supplemental Table 1), and all simulated plasma concentrations were sampled from the peripheral arm vein sampling site.
To test whether the verified parent-metabolite model can capture the methamphetamine-amphetamine urinary kinetics under different urine pH conditions, simulation results were compared with observed urinary concentration ratio (Oyler et al., 2002) and excretion data (Kim et al., 2004). First, the urinary concentration of methamphetamine and amphetamine were simulated under uncontrolled urine pH (urine pH = 6.5) after four consecutive oral doses of 10 or 20 mg methamphetamine. The urinary metabolite/parent concentration ratio was calculated as the ratio of amphetamine to methamphetamine urinary concentration, and the ratio was compared with the observed data (Oyler et al., 2002). Since the observed data were reported only from a single subject after 10- or 20-mg doses, a 2-fold acceptance criterion for the calculated AAFE was used to determine whether the simulation was successful. For extrapolation, we also simulated the urinary metabolite/parent concentration ratio under acidic and alkaline urine conditions. Because the observed urinary metabolite/parent ratio data were not available under the acidic and alkaline urine pH conditions, no comparisons between simulated and observed urinary concentrations were done for these two conditions. Second, the amount of methamphetamine and amphetamine excreted in urine was simulated under uncontrolled urine pH (urine pH = 6.5) after four consecutive doses of 10 mg methamphetamine. The percentage of methamphetamine dose excreted into urine as methamphetamine or amphetamine was calculated by dividing cumulative amount of methamphetamine and amphetamine excreted into urine over 16 days by methamphetamine dose. The urinary metabolite/parent excretion ratio was calculated by dividing the urinary excretion of amphetamine with the urinary excretion of methamphetamine. The simulated percentage of urinary excretion of methamphetamine and amphetamine and the metabolite/parent ratio were compared with observed data from 13 individuals (Kim et al., 2004).
Results
Development and Verification of Methamphetamine and Amphetamine Drug Models.
Human plasma unbound fraction, blood-to-plasma ratio, and MDCK cellular permeability were experimentally determined for methamphetamine and amphetamine and used in the PBPK model. The fu,p value was 0.77 (±0.03) for methamphetamine and 0.82 (±0.09) for amphetamine. The blood-to-plasma ratio was 1.04 (±0.07) for methamphetamine and 1.04 (±0.06) for amphetamine, suggesting some distribution into the red blood cells. The MDCK cellular permeability was 29.1 × 10−6 (±5.75) cm/s for methamphetamine and 26.9 × 10−6 (±4.42) cm/s for amphetamine (Supplemental Figs. 1 and 2), indicating a high permeability for both compounds.
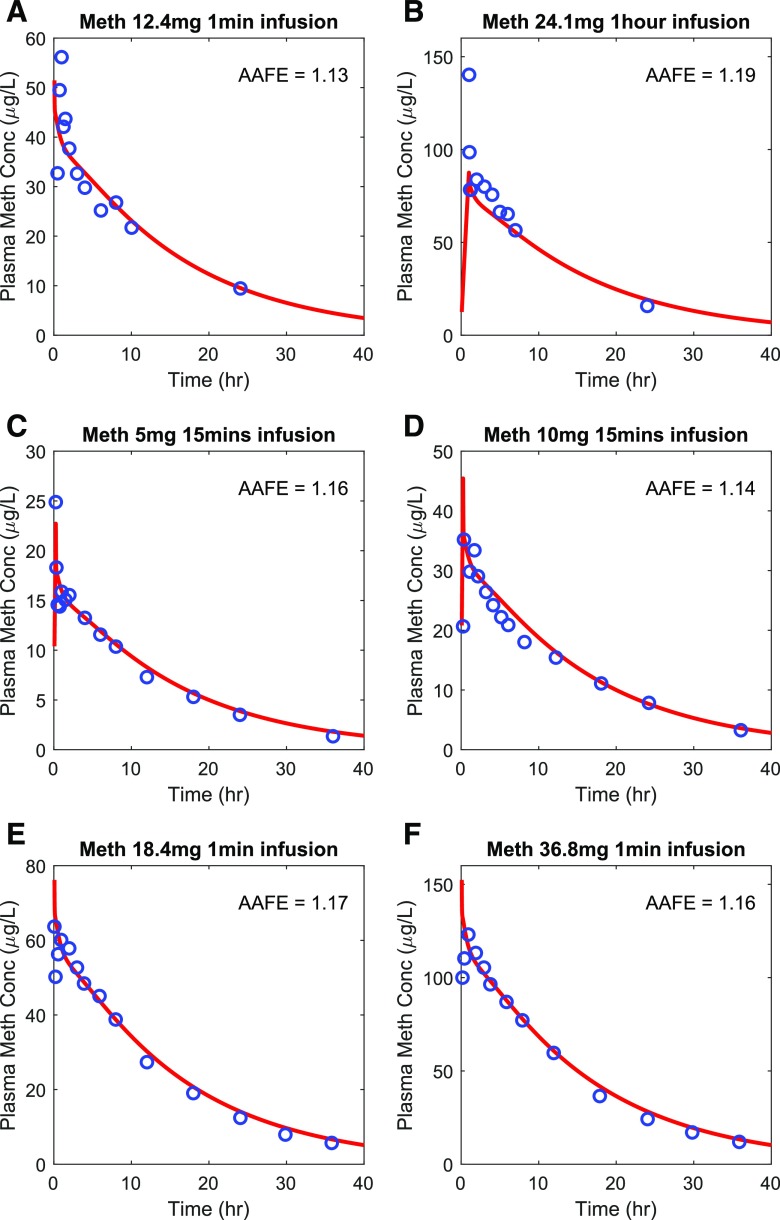
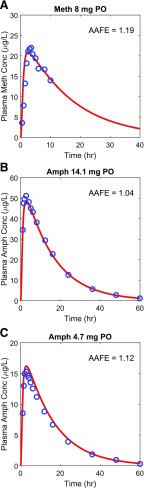
The methamphetamine (Fig. 3) and amphetamine (Fig. 4) drug models were independently verified using the observed plasma concentration-time data from seven methamphetamine test sets (six intravenous dosing and one oral dosing) (Perez-Reyes et al., 1991; Cook et al., 1993; Mendelson et al., 1995, 2006; Harris et al., 2003) and two amphetamine oral dosing test sets (CDER, 2002), respectively. The AAFE values for methamphetamine (Fig. 3) and amphetamine (Fig. 4) plasma concentration-time data in the test sets ranged from 1.04 to 1.19, and the predicted/observed AUC ratios ranged from 0.87 to 1.11 (Supplemental Fig. 3; Supplemental Table 1). The relationship between predicted and observed concentrations for the simulated studies is also shown in Supplemental Fig. 3. Both evaluation metrics met the stringent model acceptance criterion demonstrating successful model verification and high confidence on the model parameter inputs for both methamphetamine and amphetamine.
Fig. 3.
Simulation of methamphetamine (Meth) plasma concentration-time profiles after intravenous dosing. The simulated plasma concentrations (shown in red) were compared to the observed data (shown in blue) from six different test sets. The calculated AAFE value for each dataset is shown in each panel. The observed data for methamphetamine are from (A) (Cook et al., 1993), (B) (Mendelson et al., 1995), (C) (Harris et al., 2003), (D) (Harris et al., 2003), (E) (Mendelson et al., 2006), and (F) (Mendelson et al., 2006).
Fig. 4.
Simulation of methamphetamine (Meth) and amphetamine (Amph) plasma concentration-time profiles after oral dosing. The simulated plasma concentrations (red lines) were compared to the observed data (blue circles) from three different test sets. The calculated AAFE value for each data set is shown in each panel. The observed data for methamphetamine (A) are from Perez-Reyes et al. (1991), and the observed data for amphetamine (B and C) are from CDER (2002).
Simulation and Verification of Urine pH Effect on Renal Excretion and Systemic Disposition of Methamphetamine and Amphetamine.
After the successful verification of the methamphetamine systemic model, methamphetamine urinary excretion was simulated as a function of time under different urine pH conditions. The goal of these simulations was to test whether the effect of urine pH on methamphetamine excretion could be simulated using the full-body PBPK model coupled with the mechanistic kidney model. Our simulations show that methamphetamine urinary excretion when urine is acidic (Fig. 5A red dashed curve) significantly exceeds the excretion when urine is alkaline (Fig. 5A blue dotted curve) and that the simulated urinary excretion profile of methamphetamine under alkaline or acidic urine agrees with the observed data in humans (Beckett and Rowland, 1965c). The simulated excretion of methamphetamine with urine pH of 6.5 (Fig. 5A black solid curve) is in between the acidic and alkaline urine conditions (Fig. 5A red and blue). The urine pH of 6.5 was selected to represent the estimated urine pH in individuals when urine pH is not controlled. The calculated AAFE values met the 2-fold model acceptance criterion under all three urine pH conditions (Fig. 5A). The urine pH effect on urinary excretion was also simulated and compared with a second observed study, shown in Supplemental Fig. 4. The percent dose excreted in urine as methamphetamine was successfully captured under all three urine pH conditions, with all calculated AAFE values meeting the 2-fold model acceptance criterion (Supplemental Fig. 4).
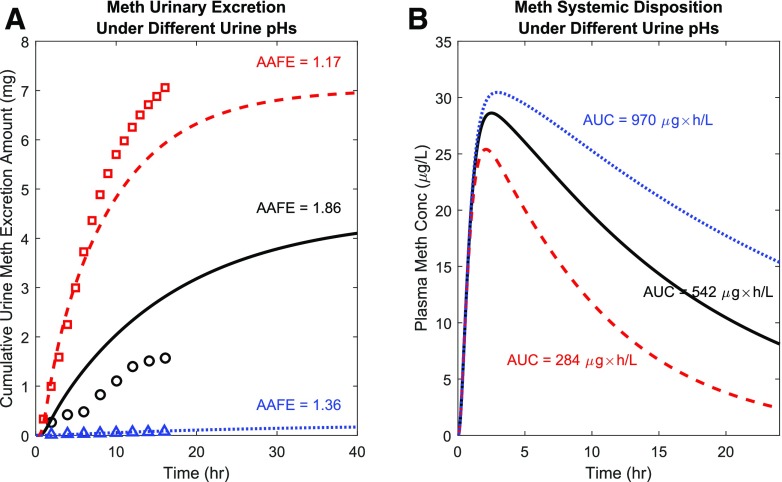
Fig. 5.
Simulation of the urine pH effect on methamphetamine (Meth) urinary excretion and plasma concentration-time profile. Methamphetamine urinary excretion profiles (A) and plasma concentration-time profiles (B) were simulated after 11 mg methamphetamine oral administration under acidic urine pH condition (red dashed curves), uncontrolled urine pH condition (black solid curves), and alkaline urine pH condition (blue dotted curves). Simulated Meth urinary excretion as a function of time was compared to observed data (N = 1) under three different urine pH conditions (Beckett and Rowland, 1965c) shown in red squares (acidic urine), black circles (uncontrolled pH urine), and blue triangles (alkaline urine). The calculated AAFE values for all three urine conditions are shown in the insets.
The urine pH effect on methamphetamine systemic disposition was also simulated (Fig. 5A) to explore the effect of changes in urine pH on methamphetamine exposure and half-life. The calculated plasma methamphetamine AUC0-inf values under alkaline, uncontrolled, and acidic urine conditions were 970, 542, and 284 μg × h/l, respectively, after an oral dose of 11 mg methamphetamine base, illustrating a dramatic impact of urine pH on methamphetamine systemic exposure. The simulated plasma concentrations of methamphetamine were highest when urine was alkaline, followed by uncontrolled urine pH (urine pH = 6.5), and the plasma concentrations of methamphetamine were the lowest when urine was acidic (Fig. 5B).
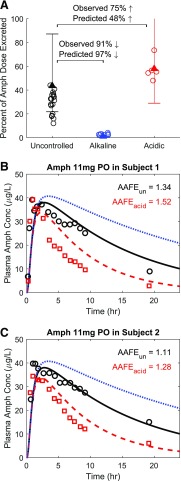
Similar to methamphetamine, urine pH also plays a significant role in amphetamine urinary excretion (Beckett and Rowland, 1965a). To recapitulate the urine pH effect on amphetamine renal disposition, the urinary excretion of amphetamine was simulated under three different urine pH conditions (Fig. 6A). Compared with uncontrolled urine pH condition (urine pH = 6.5), alkaline urine condition was predicted to result in a 97% decrease of urinary excretion of amphetamine, whereas the observed decrease was 91%, resulting in a predicted over observed ratio of 1.07-fold meeting the acceptance criterion of 2-fold. On the other hand, urine acidification was predicted to result in a 48% increase of urinary excretion of amphetamine when compared with uncontrolled urine pH condition, whereas the observed increase was 75%, resulting in a predicted/observed ratio of 0.64-fold meeting the acceptance criterion of 2-fold.
Fig. 6.
Simulation of the effect of urine pH on the urinary excretion and plasma concentration-time profile of amphetamine (Amph). Amphetamine urinary excretion over 48 hours (uncontrolled urine pH shown in black), 16 hours (alkaline urine pH shown in blue), and 16 hours (acidic urine pH shown in red) was simulated after 11 mg amphetamine oral administration (A). The observed individual data of amphetamine excretion are shown in circles (Beckett and Rowland, 1965a). The mean simulated amount (as percent of dose) of amphetamine excreted in urine under each urine pH condition is shown in triangles with 2-fold error bars. Simulated (curves) amphetamine plasma concentration-time profiles (B and C) are shown in comparison with the observed [open symbols, (Beckett et al., 1969)] data in two individual subjects under uncontrolled urine pH (black symbols and solid curve), acidic urine pH (red symbols and dashed curve), and alkaline urine pH (blue dotted curve) after 11 mg oral administration of amphetamine. The calculated AAFE values for each individual subject are shown. AAFEun represents the calculated AAFE comparing simulated and observed amphetamine plasma concentrations under uncontrolled urine pH. AAFEacid represents the calculated AAFE comparing simulated and observed amphetamine plasma concentrations under acidic urine pH.
The urine pH effect on amphetamine systemic disposition was also simulated (Fig. 6, B and C) and compared with the observed data (Beckett et al., 1969). The AAFE values for the simulations of acidic and uncontrolled urine pH met the 2-fold model acceptance criterion (Fig. 6, B and C). The 2-fold criterion was used because of the small sample size in the observed studies (n = 2). Unfortunately, clinical data regarding the alkaline urine pH effect on amphetamine systemic disposition were not available, and hence no verification was conducted for this condition. Based on the simulations using the verified amphetamine model, the plasma amphetamine AUC0-inf values under alkaline, uncontrolled, and acidic urine conditions were 1325, 692, and 361 μg × h/l, respectively, after an oral dose of 11 mg amphetamine base, demonstrating a dramatic impact of urine pH on amphetamine systemic exposure.
Simulation and Verification of Plasma and Urinary Methamphetamine-Amphetamine Parent-Metabolite Kinetics.
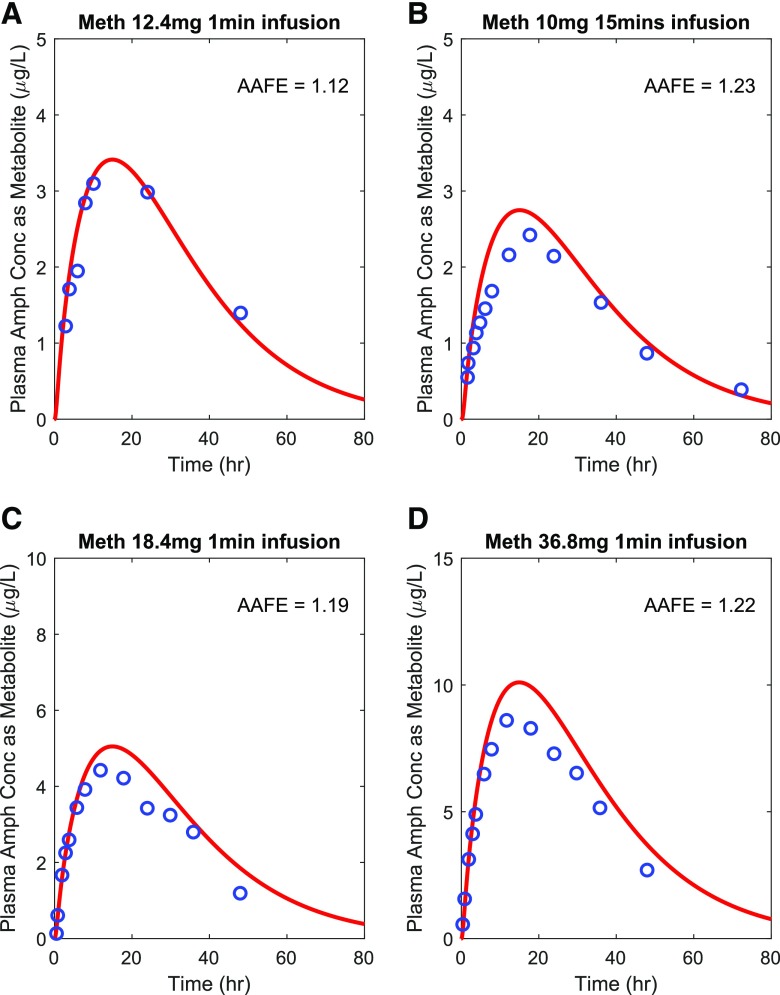
After the successful verification of methamphetamine (Fig. 3) and amphetamine (Fig. 4) models, the parent-metabolite link was established to allow for simulation of amphetamine disposition as a metabolite of methamphetamine. To verify the methamphetamine-amphetamine parent-metabolite model, amphetamine plasma concentration-time profiles were simulated as a metabolite after intravenous dosing of methamphetamine and compared with observed data. As shown in Fig. 7, all AAFE values were within 1.25-fold acceptance criterion, indicating the parent-metabolite linkage between methamphetamine and amphetamine was successfully established and verified.
Fig. 7.
Simulation of plasma amphetamine (Amph) concentration-time profile as a metabolite after intravenous dosing of methamphetamine (Meth). Amphetamine plasma concentration-time profiles were simulated (shown in red curves) as the metabolite of methamphetamine after intravenous dosing of methamphetamine and compared with the observed data (shown in blue circles) from four test sets. The calculated AAFE values were all within the 1.25-fold range. The observed data of amphetamine are from (A) (Cook et al., 1993), (B) (Harris et al., 2003), (C) (Mendelson et al., 2006), and (D) (Mendelson et al., 2006).
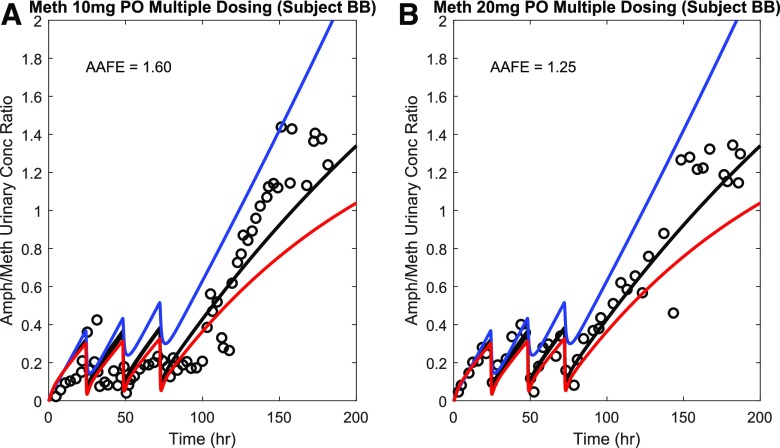
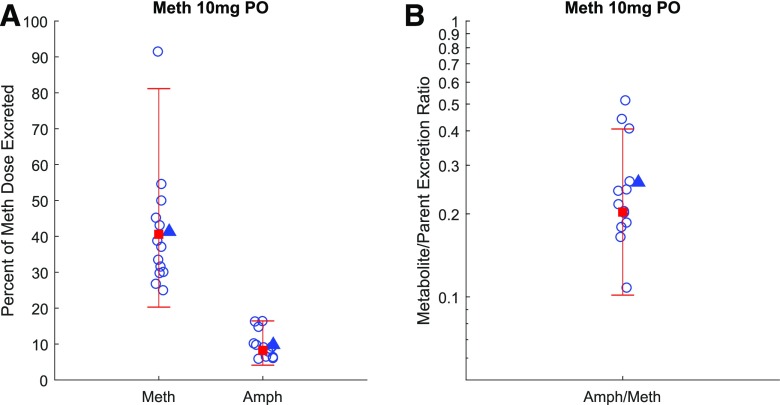
To evaluate the applicability of the verified parent-metabolite model to capture the methamphetamine-amphetamine urinary kinetics, the urinary metabolite/parent concentration ratio was simulated under uncontrolled urine pH (urine pH = 6.5) and compared with the observed data (Oyler et al., 2002) from a single subject after four consecutive doses of 10 or 20 mg methamphetamine (Fig. 8). The AAFE values for these simulations were within the 2-fold acceptance criterion, which was used because of the small sample size (n = 1). The urinary metabolite/parent concentration ratio was also simulated under acidic and alkaline urine conditions to explore the impact of varying urine pH on this measure. The simulation results show that the urinary metabolite/parent concentration ratio can be affected by urine pH. Particularly, alkaline urine resulted in a higher urinary Amph/Meth ratio. In addition, the percent dose excreted in urine as methamphetamine and amphetamine was also simulated under uncontrolled urine pH (urine pH = 6.5) and compared with the observed data (Fig. 9). The observed mean percent dose excreted in urine as methamphetamine and amphetamine were 41.3% and 9.8%, respectively, whereas the predicted values were 40.6% and 8.2% respectively. The observed amphetamine/methamphetamine ratio in urine was 0.26, whereas the predicted ratio was 0.20. The predicted/observed values were all within the 2-fold acceptance criterion. Together, these data suggest successful application of the model to simulate systemic and urinary parent-metabolite kinetics.
Fig. 8.
Simulation of the time course of metabolite to parent (amphetamine/methamphetamine) urinary concentration ratio after multiple oral doses of methamphetamine (Meth). Amphetamine/methamphetamine (Amph/Meth) urinary ratio was simulated under acidic urine pH condition (red curves), uncontrolled urine pH condition (black curve), and alkaline urine pH condition (blue curve) after four consecutive oral doses of methamphetamine, and compared with the observed urinary ratio (black circles) from two test sets (Oyler et al., 2002) with 10 mg dose (A) and 20 mg dose (B) under uncontrolled urine pH condition. The calculated AAFE values comparing simulation and observation under uncontrolled urine pH condition are shown in insets.
Fig. 9.
Simulation of the amount of methamphetamine (Meth) and its metabolite amphetamine (Amph) excretion into urine (as a percent of methamphetamine dose) after multiple oral dosing of methamphetamine. (A) shows the simulated fraction (in red square with 2-fold error bars) of methamphetamine dose excreted into urine as methamphetamine and amphetamine (expressed as a percent of methamphetamine dose) after four oral doses of 10 mg methamphetamine and assuming urine pH of 6.5 to mimic uncontrolled urine pH. The simulated Amph/Meth urinary excretion ratio (in red square with 2-fold error bars) based on the data presented in (A) is shown in (B). The observed data (Kim et al., 2004) for individual subjects are shown in blue circles and observed means are shown in blue triangles.
Discussion
The effect of urine pH on renal excretion of drugs has been observed for a multitude of drugs in humans (Macpherson et al., 1955; Beckett and Rowland, 1965a,c; Gerhardt et al., 1969; Sharpstone, 1969; Sjöqvist et al., 1969; Gram et al., 1971; Kiddie et al., 1974; Chan, 1979; Muhiddin et al., 1984; Benowitz and Jacob, 1985; Aoki and Sitar, 1988; Freudenthaler et al., 1998). In addition, a plethora of medications and disease states have been reported to cause changes in urine pH (Cook et al., 2007). For example, acetazolamide, which was indicated for glaucoma and edema, has been shown to increase urinary pH in humans from 5.5 to 7.6 (Moviat et al., 2006). In contrast, cholestyramine, indicated for hypercholesterolemia, was shown to induce metabolic acidosis and therefore can decrease urinary pH to as low as 4.8 (Eaves and Korman, 1984). Furthermore, urine acidification is observed with diabetes, obesity, and chronic kidney disease (Maalouf et al., 2004, 2010; Nakanishi et al., 2012), and urine alkalinization is observed with vomiting and urinary tract infection (Yi et al., 2012; Lai et al., 2019). Therefore, the potential impact of comedications and comorbidities on urine pH and consequently renal drug clearance can be commonplace and profound. Nonetheless, the overall effect of altered urine pH on urinary drug concentrations, excretion profiles, systemic exposure, and subsequent clinical consequences has been underappreciated. In this study, we hypothesized that in silico modeling could be used to understand and predict the effects of altered urine pH on drug and metabolite renal and systemic disposition. The goal of this study was to integrate the verified mechanistic kidney model (Huang and Isoherranen, 2018) with a parent-metabolite full-body PBPK model (Huang and Isoherranen, 2020) to examine the applicability of the final model to predict the effect of varying urine pH on renal clearance and systemic exposure, to assess the potential clinical consequences using methamphetamine and amphetamine as model compounds.
Currently, the urine pH effect on renal clearance and systemic disposition have rarely been considered when using in silico techniques to simulate drug and metabolite disposition. For studies that specifically explore urinary excretion as a function of time, the urinary excretion profiles were mostly simulated using simple first-order urinary kinetics (Heredia Ortiz et al., 2014; Phillips et al., 2014; Adachi et al., 2015; Marchand et al., 2015; Yang et al., 2015) governed by a fixed observed value, such as elimination rate constant. Although these models may have successfully recapitulated the observed data, they cannot be extrapolated to untested or altered scenarios because of their non-mechanistic nature when simulating urinary kinetics. In contrast, mechanistic modeling can be used to extrapolate drug disposition from known settings to unstudied scenarios, such as unstudied populations and unstudied drug coadministration (Wagner et al., 2015; Huang et al., 2017; Zhang et al., 2017; Hanke et al., 2018) and likely unstudied urine pH conditions.
Recently, the MechKiM model embedded in the Simcyp platform was used to predict renal clearance and urine pH effects on renal clearance (Matsuzaki et al., 2019). In that study, seven compounds were used as the test set to examine model performance, and the simulations were conducted assuming uniform renal tubular filtrate pH throughout all renal segments. The overall simulation results under the uncontrolled urine pH condition showed AAFE values ranging from 2.87 (assuming uniform tubular filtrate pH = 6.2) to 3.62 (assuming uniform tubular filtrate pH = 7.4). In comparison, our mechanistic kidney modelwhich assumes a tubular pH gradient across different tubular segments, showed superior performance for a set of 35 non-neutral test compounds with AAFE values of 1.83, 1.82, and 1.46 for weak bases, weak acids, and zwitterions, respectively (Huang and Isoherranen, 2018). This better performance could be because of our strategy to use a stepwise gradient for renal tubular filtrate pH to account for the naturally continuous acidification process of tubular filtrate, although other differences, such as microvilli consideration and a larger number (11 vs. 7) of tubular compartments in our model, may also contribute to the better performance. Furthermore, the previous study (Matsuzaki et al., 2019) showed a relatively insensitive response of simulated renal clearance to urine pH changes. For example, their simulated amphetamine renal clearance did not change with urine pH between 5 and 8, which is inconsistent with the observed dramatic changes (Beckett and Rowland, 1965a; Beckett et al., 1969). Conversely, our model accurately recapitulated the renal excretion of methamphetamine and amphetamine under acidic (urine pH = 5.0), uncontrolled (urine pH = 6.5), and alkaline (urine pH = 8.0) urine conditions (Fig. 6) and was previously shown to capture the varying renal clearance of salicylic acid and memantine as a function of urine pH (Huang and Isoherranen, 2018). We confirmed the importance of the stepwise gradient via an in-house head-to-head comparison of the urinary methamphetamine excretion using our stepwise pH gradients and the previously published (Matsuzaki et al., 2019) constant pH value. The constant pH value approach failed to recapitulate the observed data under uncontrolled (AAFE = 2.2 or 6.5) and alkaline urine condition (AAFE = 13.6) (Supplemental Fig. 5), whereas the stepwise pH gradient approach successfully (AAFE < 2) simulated methamphetamine urinary excretion (Supplemental Fig. 4). Together, these results support that our PBPK model and strategy can capture the mathematical relationship between urine pH and the corresponding apparent permeability, passive reabsorption, and renal clearance successfully. More examination using additional data sets is warranted for further validation of the full model.
Altered urine pH may also affect the systemic exposure of drugs and their metabolites if renal clearance is an important elimination pathway. For example, amphetamine plasma AUC was decreased by approximately 50% under acidic urine pH condition compared with uncontrolled urine pH condition (Beckett et al., 1969), and because urine pH is known to affect the renal clearance for many drugs, such effects on drug AUC can be common. The modeling and simulation workflow presented here offers a feasible approach to predict whether the drug exposure is sensitive to changes in urine pH. To do this, it is important to construct both a urine pH-sensitive mechanistic kidney model and a full-body PBPK model that captures drug absorption, distribution, and other pathways of elimination, such as hepatic metabolism and biliary excretion. In this study, we first verified the full-body PBPK model for methamphetamine (Fig. 3) and amphetamine (Fig. 4) and then verified the urine pH effect on renal excretion (Figs. 5A and 6A) to ultimately simulate the urine pH effect on plasma AUC for methamphetamine (Fig. 5B) and amphetamine (Fig. 6, B and C). Based on the simulations, we also predicted that urine alkalinization can increase plasma AUC of methamphetamine and amphetamine by about 100 % in comparison with uncontrolled urine pH because of increased passive reabsorption and decreased renal clearance (Figs. 5 and 6). Collectively, we show a modeling workflow that can serve as a robust and cost-effective method to assess how drug AUC is altered when urine pH is changed because of comedications or disease states.
The urine pH effect also impacts the interpretation of urinary concentration data. At present, the urinary concentrations of drugs and metabolites have been widely used for understanding drug pharmacokinetics, for phenotyping human subjects for certain metabolizing enzymes (Wedlund et al., 1984; Chládek et al., 2000; Vogl et al., 2015), and for testing and screening for illicit drug use (Fabbri et al., 2003; Moeller et al., 2017). As shown in Figs. 5 and 6, the changes in urine pH will change the renal excretion and, therefore, the urinary concentration-time profile. Furthermore, simulations in Fig. 8 suggest that urinary metabolite/parent ratio can also be influenced by urine pH changes. Currently, urine samples collected at a single time point often serve as the direct proxy for data interpretation, without the quantitative consideration of the confounding effect of different urine pHs on urinary disposition. As such, analysis of drug concentrations in the collected urine samples may lead to misinterpretation and suboptimal decision making. The modeling and simulation approach described here, together with the measurement of urine pH values, can aid in interpreting urinary excretion data and help minimize false negative and false positive readings.
In conclusion, this study shows that the previously developed and verified mechanistic kidney model together with the full-body parent-metabolite PBPK model can accurately predict the effect of urine pH on methamphetamine and amphetamine renal clearance, plasma concentration-time profile and systemic and urinary parent-metabolite kinetics. These results suggest that mechanistic PBPK models can be generally applied to predict the potential impact of comedications and comorbidities on parent-metabolite renal and systemic disposition due to altered urine pH. The modeling workflow and approach established here is likely to be useful in assessing the sensitivity of new compounds’ disposition to changes in urine pH, especially for weak acids and bases that have substantial permeability.
Acknowledgments
The authors would like to thank Dr. David J. Wagner for his skillful assistance in preliminary permeability experiments.
Abbreviations
- AAFE
absolute average fold error
- Amph
amphetamine
- AUC
area under the plasma drug concentration-time curve
- fu,p
unbound fraction in plasma
- HBSS
Hank’s Balanced Salt Solution
- Kp
tissue-to-plasma partition coefficient for the drug
- LC-MS/MS
liquid chromatography with tandem mass spectrometry
- MDCK
Madin-Darby canine kidney
- Meth
methamphetamine
- PBPK
physiologically based pharmacokinetics
- po
by mouth
- Vss
volume of distribution at steady state
Authorship Contributions
Participated in research design: Huang, Czuba, Isoherranen.
Conducted experiments: Huang, Czuba.
Performed data analysis: Huang, Czuba, Isoherranen.
Wrote or contributed to the writing of the manuscript: Huang, Czuba, Isoherranen.
Footnotes
This work was supported by National Institutes of Health Grant P01 DA032507. W.H. was supported by Warren G. Magnuson Scholarship and William E. Bradley Fellowship from the University of Washington, Seattle, WA.
 This article has supplemental material available at jpet.aspetjournals.org.
This article has supplemental material available at jpet.aspetjournals.org.
References
- Adachi K, Suemizu H, Murayama N, Shimizu M, Yamazaki H. (2015) Human biofluid concentrations of mono(2-ethylhexyl)phthalate extrapolated from pharmacokinetics in chimeric mice with humanized liver administered with di(2-ethylhexyl)phthalate and physiologically based pharmacokinetic modeling. Environ Toxicol Pharmacol 39:1067–1073. [DOI] [PubMed] [Google Scholar]
- Aoki FY, Sitar DS. (1988) Clinical pharmacokinetics of amantadine hydrochloride. Clin Pharmacokinet 14:35–51. [DOI] [PubMed] [Google Scholar]
- Barbhaiya RH, Gerber AU, Craig WA, Welling PG. (1982) Influence of urinary pH on the pharmacokinetics of cinoxacin in humans and on antibacterial activity in vitro. Antimicrob Agents Chemother 21:472–480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckett AH, Rowland M. (1965a) Urinary excretion kinetics of amphetamine in man. J Pharm Pharmacol 17:628–639. [DOI] [PubMed] [Google Scholar]
- Beckett AH, Rowland M. (1965b) Urinary excretion kinetics of methylamphetamine in man. J Pharm Pharmacol 17:109S–114S. [DOI] [PubMed] [Google Scholar]
- Beckett AH, Rowland M. (1965c) Urinary excretion of methylamphetamine in man. Nature 206:1260–1261. [DOI] [PubMed] [Google Scholar]
- Beckett AH, Salmon JA, Mitchard M. (1969) The relation between blood levels and urinary excretion of amphetamine under controlled acidic and under fluctuating urinary pH values using [14C] amphetamine. J Pharm Pharmacol 21:251–258. [DOI] [PubMed] [Google Scholar]
- Benowitz NL, Jacob P., III (1985) Nicotine renal excretion rate influences nicotine intake during cigarette smoking. J Pharmacol Exp Ther 234:153–155. [PubMed] [Google Scholar]
- Brown RP, Delp MD, Lindstedt SL, Rhomberg LR, Beliles RP. (1997) Physiological parameter values for physiologically based pharmacokinetic models. Toxicol Ind Health 13:407–484. [DOI] [PubMed] [Google Scholar]
- CDER (2001) Application number 21-303. Clinical Pharmacology and biopharmaceutics review(s). https://www.accessdata.fda.gov/drugsatfda_docs/nda/2001/21303_Adderall_biopharmr.pdf
- CDER (2002) Application number 11-522. Clinical Pharmacology and biopharmaceutics review(s).https://www.accessdata.fda.gov/drugsatfda_docs/nda/2002/11-522S030_Adderall_BioPharmr.pdf
- Chan K. (1979) The effects of physiocochemical properties of pethidine and its basic metabolites on their buccal absorption and renal elimination. J Pharm Pharmacol 31:672–675. [DOI] [PubMed] [Google Scholar]
- Cheong EJY, Teo DWX, Chua DXY, Chan ECY. (2019) Systematic development and verification of a physiologically based pharmacokinetic model of rivaroxaban. Drug Metab Dispos 47:1291–1306. [DOI] [PubMed] [Google Scholar]
- Chládek J, Zimová G, Beránek M, Martínková J. (2000) In-vivo indices of CYP2D6 activity: comparison of dextromethorphan metabolic ratios in 4-h urine and 3-h plasma. Eur J Clin Pharmacol 56:651–657. [DOI] [PubMed] [Google Scholar]
- Cook CE, Jeffcoat AR, Hill JM, Pugh DE, Patetta PK, Sadler BM, White WR, Perez-Reyes M. (1993) Pharmacokinetics of methamphetamine self-administered to human subjects by smoking S-(+)-methamphetamine hydrochloride. Drug Metab Dispos 21:717–723. [PubMed] [Google Scholar]
- Cook JD, Strauss KA, Caplan YH, Lodico CP, Bush DM. (2007) Urine pH: the effects of time and temperature after collection. J Anal Toxicol 31:486–496. [DOI] [PubMed] [Google Scholar]
- Eaves ER, Korman MG. (1984) Cholestyramine induced hyperchloremic metabolic acidosis. Aust N Z J Med 14:670–672. [DOI] [PubMed] [Google Scholar]
- Fabbri A, Marchesini G, Morselli-Labate AM, Ruggeri S, Fallani M, Melandri R, Bua V, Pasquale A, Vandelli A. (2003) Comprehensive drug screening in decision making of patients attending the emergency department for suspected drug overdose. Emerg Med J 20:25–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freudenthaler S, Meineke I, Schreeb KH, Boakye E, Gundert-Remy U, Gleiter CH. (1998) Influence of urine pH and urinary flow on the renal excretion of memantine. Br J Clin Pharmacol 46:541–546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerhardt RE, Knouss RF, Thyrum PT, Luchi RJ, Morris JJ., Jr (1969) Quinidine excretion in aciduria and alkaluria. Ann Intern Med 71:927–933. [DOI] [PubMed] [Google Scholar]
- Gram LF, Kofod B, Christiansen J, Rafaelsen OJ. (1971) Imipramine metabolism: pH-dependent distribution and urinary excretion. Clin Pharmacol Ther 12:239–244. [DOI] [PubMed] [Google Scholar]
- Hanke N, Frechen S, Moj D, Britz H, Eissing T, Wendl T, Lehr T. (2018) PBPK models for CYP3A4 and P-gp DDI prediction: a modeling network of rifampicin, itraconazole, clarithromycin, midazolam, alfentanil, and digoxin. CPT Pharmacometrics Syst Pharmacol 7:647–659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris DS, Boxenbaum H, Everhart ET, Sequeira G, Mendelson JE, Jones RT. (2003) The bioavailability of intranasal and smoked methamphetamine. Clin Pharmacol Ther 74:475–486. [DOI] [PubMed] [Google Scholar]
- Heredia Ortiz R, Maître A, Barbeau D, Lafontaine M, Bouchard M. (2014) Use of physiologically-based pharmacokinetic modeling to simulate the profiles of 3-hydroxybenzo(a)pyrene in workers exposed to polycyclic aromatic hydrocarbons. PLoS One 9:e102570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang W, Isoherranen N. (2018) Development of a dynamic physiologically based mechanistic kidney model to predict renal clearance. CPT Pharmacometrics Syst Pharmacol 7:593–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang W, Isoherranen N. (2020) Sampling site has a critical impact on physiologically based pharmacokinetic modeling. J Pharmacol Exp Ther 372:30–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang W, Nakano M, Sager J, Ragueneau-Majlessi I, Isoherranen N. (2017) Physiologically based pharmacokinetic model of the CYP2D6 probe atomoxetine: extrapolation to special populations and drug-drug interactions. Drug Metab Dispos 45:1156–1165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kärkkäinen S, Neuvonen PJ. (1986) Pharmacokinetics of amitriptyline influenced by oral charcoal and urine pH. Int J Clin Pharmacol Ther Toxicol 24:326–332. [PubMed] [Google Scholar]
- Kiddie MA, Kaye CM, Turner P, Shaw TR. (1974) The influence of urinary pH on the elimination of mexiletine. Br J Clin Pharmacol 1:229–232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim I, Oyler JM, Moolchan ET, Cone EJ, Huestis MA. (2004) Urinary pharmacokinetics of methamphetamine and its metabolite, amphetamine following controlled oral administration to humans. Ther Drug Monit 26:664–672. [DOI] [PubMed] [Google Scholar]
- Lai HC, Chang SN, Lin HC, Hsu YL, Wei HM, Kuo CC, Hwang KP, Chiang HY. (2019) Association between urine pH and common uropathogens in children with urinary tract infections. J Microbiol Immunol Infect DOI: 10.1016/j.jmii.2019.08.002 [published ahead of print]. [DOI] [PubMed] [Google Scholar]
- Lane EA, Levy RH. (1980) Prediction of steady-state behavior of metabolite from dosing of parent drug. J Pharm Sci 69:610–612. [DOI] [PubMed] [Google Scholar]
- Leeson PD, St-Gallay SA. (2011) The influence of the ‘organizational factor’ on compound quality in drug discovery. Nat Rev Drug Discov 10:749–765. [DOI] [PubMed] [Google Scholar]
- Li L, Everhart T, Jacob Iii P, Jones R, Mendelson J. (2010) Stereoselectivity in the human metabolism of methamphetamine. Br J Clin Pharmacol 69:187–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maalouf NM, Cameron MA, Moe OW, Sakhaee K. (2010) Metabolic basis for low urine pH in type 2 diabetes. Clin J Am Soc Nephrol 5:1277–1281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maalouf NM, Sakhaee K, Parks JH, Coe FL, Adams-Huet B, Pak CYC. (2004) Association of urinary pH with body weight in nephrolithiasis. Kidney Int 65:1422–1425. [DOI] [PubMed] [Google Scholar]
- MacPherson CR, Milne MD, Evans BM. (1955) The excretion of salicylate. Br J Pharmacol Chemother 10:484–489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manallack DT. (2007) The pK(a) distribution of drugs: application to drug discovery. Perspect Medicin Chem 1:25–38. [PMC free article] [PubMed] [Google Scholar]
- Marchand A, Aranda-Rodriguez R, Tardif R, Nong A, Haddad S. (2015) Human inhalation exposures to toluene, ethylbenzene, and m-xylene and physiologically based pharmacokinetic modeling of exposure biomarkers in exhaled air, blood, and urine. Toxicol Sci 144:414–424. [DOI] [PubMed] [Google Scholar]
- Matsuzaki T, Scotcher D, Darwich AS, Galetin A, Rostami-Hodjegan A. (2019) Towards further verification of physiologically-based kidney models: predictability of the effects of urine-flow and urine-pH on renal clearance. J Pharmacol Exp Ther 368:157–168. [DOI] [PubMed] [Google Scholar]
- Mendelson J, Jones RT, Upton R, Jacob P., III (1995) Methamphetamine and ethanol interactions in humans. Clin Pharmacol Ther 57:559–568. [DOI] [PubMed] [Google Scholar]
- Mendelson J, Uemura N, Harris D, Nath RP, Fernandez E, Jacob P, III, Everhart ET, Jones RT. (2006) Human pharmacology of the methamphetamine stereoisomers. Clin Pharmacol Ther 80:403–420. [DOI] [PubMed] [Google Scholar]
- Milne MD, Scribner BH, Crawford MA. (1958) Non-ionic diffusion and the excretion of weak acids and bases. Am J Med 24:709–729. [DOI] [PubMed] [Google Scholar]
- Moeller KE, Kissack JC, Atayee RS, Lee KC. (2017) Clinical interpretation of urine drug tests: what clinicians need to know about urine drug screens. Mayo Clin Proc 92:774–796. [DOI] [PubMed] [Google Scholar]
- Moviat M, Pickkers P, van der Voort PHJ, van der Hoeven JG. (2006) Acetazolamide-mediated decrease in strong ion difference accounts for the correction of metabolic alkalosis in critically ill patients. Crit Care 10:R14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muhiddin KA, Johnston A, Turner P. (1984) The influence of urinary pH on flecainide excretion and its serum pharmacokinetics. Br J Clin Pharmacol 17:447–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakanishi N, Fukui M, Tanaka M, Toda H, Imai S, Yamazaki M, Hasegawa G, Oda Y, Nakamura N. (2012) Low urine pH Is a predictor of chronic kidney disease. Kidney Blood Press Res 35:77–81. [DOI] [PubMed] [Google Scholar]
- Neuvonen PJ, Kärkkäinen S. (1983) Effects of charcoal, sodium bicarbonate, and ammonium chloride on chlorpropamide kinetics. Clin Pharmacol Ther 33:386–393. [DOI] [PubMed] [Google Scholar]
- Newton TF, Roache JD, De La Garza R, II, Fong T, Wallace CL, Li S-H, Elkashef A, Chiang N, Kahn R. (2005) Safety of intravenous methamphetamine administration during treatment with bupropion. Psychopharmacology (Berl) 182:426–435. [DOI] [PubMed] [Google Scholar]
- Oyler JM, Cone EJ, Joseph RE, Jr, Moolchan ET, Huestis MA. (2002) Duration of detectable methamphetamine and amphetamine excretion in urine after controlled oral administration of methamphetamine to humans. Clin Chem 48:1703–1714. [PubMed] [Google Scholar]
- Paine MF, Hart HL, Ludington SS, Haining RL, Rettie AE, Zeldin DC. (2006) The human intestinal cytochrome P450 “pie”. Drug Metab Dispos 34:880–886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Reyes M, White WR, McDonald SA, Hicks RE, Jeffcoat AR, Hill JM, Cook CE. (1991) Clinical effects of daily methamphetamine administration. Clin Neuropharmacol 14:352–358. [DOI] [PubMed] [Google Scholar]
- Phillips MB, Yoon M, Young B, Tan Y-M. (2014) Analysis of biomarker utility using a PBPK/PD model for carbaryl. Front Pharmacol 5:246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randall B. (2004) Disposition of Toxic Drugs and Chemicals in Man, 7th ed, Biomedical Publications, Foster City, CA. [Google Scholar]
- Rowland M. (1969) Amphetamine blood and urine levels in man. J Pharm Sci 58:508–509. [DOI] [PubMed] [Google Scholar]
- Sager JE, Price LSL, Isoherranen N. (2016) Stereoselective metabolism of bupropion to OH-bupropion, threohydrobupropion, erythrohydrobupropion, and 4′-OH-bupropion in vitro. Drug Metab Dispos 44:1709–1719. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sager JE, Yu J, Ragueneau-Majlessi I, Isoherranen N. (2015) Physiologically based pharmacokinetic (PBPK) modeling and simulation approaches: a systematic review of published models, applications, and model verification. Drug Metab Dispos 43:1823–1837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharpstone P. (1969) The renal handling of trimethoprim and sulphamethoxazole in man. Postgrad Med J 45 (Suppl):38–42. [PubMed] [Google Scholar]
- Shebley M, Sandhu P, Emami Riedmaier A, Jamei M, Narayanan R, Patel A, Peters SA, Reddy VP, Zheng M, de Zwart L, et al. (2018) Physiologically based pharmacokinetic model qualification and reporting procedures for regulatory submissions: a consortium perspective. Clin Pharmacol Ther 104:88–110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirasaka Y, Sager JE, Lutz JD, Davis C, Isoherranen N. (2013) Inhibition of CYP2C19 and CYP3A4 by omeprazole metabolites and their contribution to drug-drug interactions. Drug Metab Dispos 41:1414–1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sjöqvist F, Berglund F, Borgå O, Hammer W, Andersson S, Thorstrand C. (1969) The pH-dependent excretion of monomethylated tricyclic antidepressants. Clin Pharmacol Ther 10:826–833. [DOI] [PubMed] [Google Scholar]
- Tucker GT. (1981) Measurement of the renal clearance of drugs. Br J Clin Pharmacol 12:761–770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varma MVS, Feng B, Obach RS, Troutman MD, Chupka J, Miller HR, El-Kattan A. (2009) Physicochemical determinants of human renal clearance. J Med Chem 52:4844–4852. [DOI] [PubMed] [Google Scholar]
- Vogl S, Lutz RW, Schönfelder G, Lutz WK. (2015) CYP2C9 genotype vs. metabolic phenotype for individual drug dosing-A correlation analysis using flurbiprofen as probe drug. PLoS One 10:e0126329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volkow ND, Fowler JS, Wang GJ, Shumay E, Telang F, Thanos PK, Alexoff D. (2010) Distribution and pharmacokinetics of methamphetamine in the human body: clinical implications. PLoS One 5:e15269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner C, Zhao P, Pan Y, Hsu V, Grillo J, Huang SM, Sinha V. (2015) Application of physiologically based pharmacokinetic (PBPK) modeling to support dose selection: report of an FDA public workshop on PBPK. CPT Pharmacometrics Syst Pharmacol 4:226–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner DJ, Sager JE, Duan H, Isoherranen N, Wang J. (2017) Interaction and transport of methamphetamine and its primary metabolites by organic cation and multidrug and toxin extrusion transporters. Drug Metab Dispos 45:770–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wedlund PJ, Aslanian WS, McAllister CB, Wilkinson GR, Branch RA. (1984) Mephenytoin hydroxylation deficiency in Caucasians: frequency of a new oxidative drug metabolism polymorphism. Clin Pharmacol Ther 36:773–780. [DOI] [PubMed] [Google Scholar]
- Wilkinson GR, Shand DG. (1975) Commentary: a physiological approach to hepatic drug clearance. Clin Pharmacol Ther 18:377–390. [DOI] [PubMed] [Google Scholar]
- Yang X, Doerge DR, Teeguarden JG, Fisher JW. (2015) Development of a physiologically based pharmacokinetic model for assessment of human exposure to bisphenol A. Toxicol Appl Pharmacol 289:442–456. [DOI] [PubMed] [Google Scholar]
- Yi JH, Han SW, Song JS, Kim HJ. (2012) Metabolic alkalosis from unsuspected ingestion: use of urine pH and anion gap. Am J Kidney Dis 59:577–581. [DOI] [PubMed] [Google Scholar]
- Zhang Z, Imperial MZ, Patilea-Vrana GI, Wedagedera J, Gaohua L, Unadkat JD. (2017) Development of a novel maternal-fetal physiologically based pharmacokinetic model I: insights into factors that determine fetal drug exposure through simulations and sensitivity analyses. Drug Metab Dispos 45:920–938. [DOI] [PMC free article] [PubMed] [Google Scholar]