Rotational spectroscopy and astronomical search for glutaronitrile^★

Abstract

Context

Nitriles constitute almost 15% of the molecules observed in the interstellar medium (ISM), surprisingly only two dinitriles have been detected in the ISM so far. The lack of astronomical detections for dinitriles may be partly explained by the absence of laboratory rotational spectroscopic data.

Aims

Our goal is to investigate the rotational spectrum of glutaronitrile, N≡C−CH₂−CH₂−CH₂−C≡N, in order to allow its possible detection in the ISM.

Methods

The rotational spectrum of glutaronitrile was measured using two different experimental setups. A Fourier transform microwave spectrometer was employed to observe the supersonic jet rotational spectrum of glutaronitrile between 6 and 20 GHz. In addition, the mmW spectrum was observed in the frequency range 72−116.5 GHz using a broadband millimetre-wave spectrometer based on radio astronomy receivers with fast Fourier transform backends. The spectral searches were supported by high-level ab initio calculations.

Results

A total of 111 rotational transitions with maximum values of J and K_a quantum numbers 54 and 18, respectively, were measured for the gg conformer of glutaronitrile. The analysis allowed us to accurately determine the rotational, nuclear quadrupole coupling, quartic and sextic centrifugal distortion constants. These rotational parameters were employed to search for glutaronitrile in the cold and warm molecular clouds Orion KL, Sgr B2(N), B1-b and TMC-1, using the spectral surveys captured by IRAM 30m at 3mm. Glutaronitrile was not detected, and the upper limits’ column densities were derived. Those are a factor of 1.5 and 5 lower than those obtained for the total column densities of the analogous succinonitrile in Orion KL and Sgr B2, respectively.

1. Introduction

The chemical complexity of the interstellar medium (ISM) has been demonstrated by detecting more than 200 different chemical species¹. The list of observed molecules includes very simple species like methylidyne (CH), the first molecule detected in the ISM (Swings & Rosenfeld 1937; Dunham 1937; McKellar 1940), or more complex structures like c-C₆H₅CN (McGuire et al. 2018). The emergence of radio astronomy in the middle of the last century enabled the detection of many new molecules, and, thanks to the increased sensitivity and angular resolution, this trend has continued at a nearly linear rate ever since. The identification of most of these molecules has been done through an interplay between rotational spectroscopy and radio astronomy by the direct comparison of the emission frequencies from the ISM with laboratory spectroscopic measurements of known species. Since astronomical searches for new molecules are carried out for even more complicated molecules that show very weak emission spectral signals, it is of utmost importance to provide very precise laboratory data of molecules as likely candidates based on astronomically modelled reactions.

About 15% of the chemical species detected in the ISM contain a nitrile group. For example, simple molecular species like the CN⁻ anion (Agúndez et al. 2010), alkyl nitriles like CH₃CN (Solomon et al. 1971) or metal-bearing species like AlNC (Ziurys et al. 2002). Surprisingly, the number of dinitriles detected in the ISM is very low compared to the number of nitriles, and, to date, only two - the protonated cyanogen (NCCNH⁺) (Agúndez et al. 2015) and isocyanogen (CNCN) (Agúndez et al. 2018) - have been detected in the ISM. This can be easily explained by the fact that the most stable dinitriles, dicyanopolyynes N≡C−(C≡C)_n−C≡N, have no permanent electric dipole moment and therefore cannot be detected through their rotational spectra. In contrast, dinitriles with a saturated hydrocarbon skeleton ended by a −C≡N group at each edge, that is to say, N≡C−(CH₂)_n−C≡N, can be considered as good candidates to be observed in the ISM since they present large electric dipole moments. These dinitriles can also be important molecules in the chemistry of planetary bodies, particulary in Titan. Titan’s atmosphere is composed of nitrogen (95-98%), methane (1.8-5.0%), hydrogen (0.1-0.2%), and carbon monoxide (0.005%), with trace amounts of ethane, acetylene, propane, ethylene, hydrogen cyanide, cyanoacetylene, carbon dioxide, and water vapor. The photochemistry of these species, initiated by absorption of solar radiation in the vacuum ultraviolet (VUV) region, produces a rich variety of large organic molecules including hydrocarbons, nitriles, or tholins (Sagan & Khare 1979; Cable et al. 2012).

In order to provide precise data that allow the astronomical detection of dinitriles, laboratory investigations of some of them have been carried out recently. Motiyenko et al. (2019, 2012) observed the rotational spectrum of the simplest molecule of this family of dinitriles, malononitrile (N≡C−CH₂−C≡N) and its isomers isocyanoacetonitrile (N≡C−CH₂−N≡C) and diisocyanomethane (C≡N−CH₂−N≡C) in the frequency range 120-620 GHz. They determined the rotational parameters for these molecules in the ground and in the first vibrational excited states providing accurate frequency predictions to meet astronomical searches for the three molecules. However, their detection in the ISM has not been achieved so far. Succinonitrile, N≡C−CH₂−CH₂−C≡N, a dinitrile with one more atom carbon in the hydrocarbon skeleton than malononitrile was investigated by Cabezas et al. (2019) in the frequency range 72−116.5 GHz. They identified the ground state and eleven vibrationally excited states and determined their rotational parameters which were employed to unsuccessfully search for succinonitrile in the cold and warm molecular clouds Orion KL, Sgr B2(N), B1-b and TMC-1.

In the present work, we report the rotational investigation of a larger dinitrile, glutaronitrile, with one more atomic carbon in the hydrocarbon skeleton than succinonitrile. To record the rotational spectrum of glutaronitrile, we have employed two different spectroscopic techniques; a high resolution Fourier transform microwave pulsed supersonic jet spectrometer operating in the centimetre wave region and a broadband millimetre-wave spectrometer based on radio astronomy receivers with fast Fourier transform backends. The rotational parameters derived from the analysis of the rotational spectrum for the ground state were employed to search for glutaronitrile in the cold and warm molecular clouds Orion KL, Sgr B2(N), B1-b, and TMC-1, using the spectral surveys captured by IRAM 30m at 3mm.

2. Quantum chemical calculations

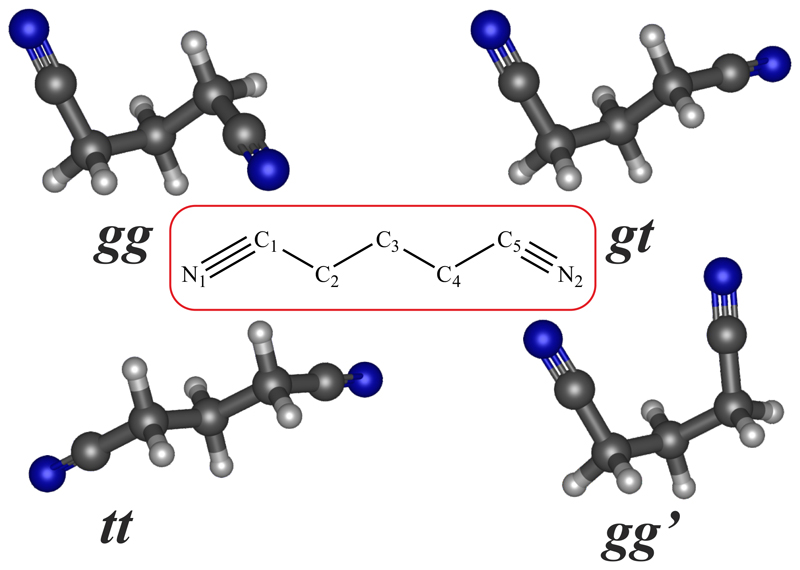
Quantum chemical calculations for the glutaronitrile molecule were carried out at the MP2/cc-pVTZ and CCSD/cc-pVTZ levels of theory using the Molpro 2018.1 quantum chemistry programme package (Werner et al. 2018). Initial searches for minimum energy structures for the glutaronitrile were conducted using the MP2/cc-pVTZ level of theory. The conformational minima found were then optimised at the CCSD/cc-pVTZ level of theory to ascertain their relative stabilities as well as the rotational parameters necessary to predict rotational transition frequencies before the spectral searches. Four conformers were found within an energy window of 4 kcal/mol. Gaussian 16 programme package (Frisch et al. 2016) was employed to calculate the ¹⁴N electric nuclear quadrupole coupling constants and the centrifugal distortion constants by harmonic and anharmonic frequency calculations at MP2/cc-pVTZ level of theory. The conformers have been labelled according to the dihedral angles of their carbon atom skeleton, in particular the dihedral angles ∠ C₁C₂C₃C₄ and ∠ C₂C₃C₄C₅ (See Figure 2). In this manner, we used the label g or t to denote dihedral angles close to ±60° or ±180°, respectively, and the conformers were labelled as gg, gt, tt, and ggʹ. The rotational constants, electric dipole moment cmponents and the relative energies for these four species are summarised in Table 1.

Fig. 2.

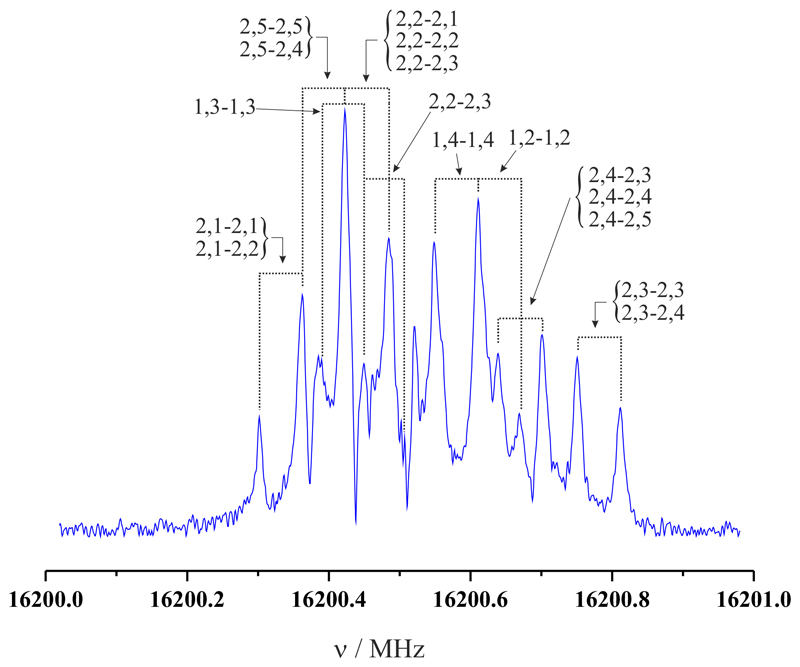
The 3_3,1-3_2,2 rotational transition of gg conformer of glutaronitrile showing the multiple hyperfine components completely resolved by FTMW spectrometer. The coaxial arrangement of the adiabatic expansion and the resonator axis produces an instrumental Doppler doubling, which is marked with the dashed lines. The resonances frequencies are calculated as the average of the two Doppler components. Each hyperfine component is labelled with the corresponding values of quantum numbers I′, F′ -I″, F″.

Table 1. Theoretical spectroscopic constants, electric dipole moment components and relative energies for the four conformers of glutaronitrile calculated at the CCSD/cc-pVTZ level of theory.

Constants/Units	gg	gt	tt	gg′
A/MHz	4767.1	7417.1	11932.6	3461.8
B/MHz	1571.6	1198.5	961.3	2282.7
C/MHz	1439.5	1084.0	904.5	1454.7
|μa|/Da	0.0	1.6	0.0	0.0
|μb|/D	4.4	3.5	3.9	7.1
|μc|/D	0.0	1.3	0.0	0.7
ΔE/cm−1	0.0	247.7	587.3	1363.4

Notes.

^a1D≈3.3356x10⁻³⁰ C·m

3. Experimental

Firstly, the rotational spectrum of glutaronitrile was investigated using a Balle-Flygare (Balle & Flygare 1981) narrow-band-type Fourier transform microwave (FTMW) spectrometer (Cabezas et al. 2016) operating in the frequency region of 4-40 GHz. A commercial sample of glutaronitrile (Sigma-Aldrich, 99%, b.p. 282°C) was used without any further purification. A small amount of glutaronitrile sample was placed in a liquid reservoir which was heated at around 75°C to obtain sufficient vapor pressure. A flow of Ar at a pressure of 0.8 bar was passed through the reservoir, placed immediately before the pulsed valve. In this way, the highly diluted mixture of glutaronitrile in Ar was supersonically expanded between the two mirrors of the Fabry-Pérot resonator cavity through a pulsed valve, which is arranged parallel to the resonator in order to resolve small hyperfine splittings. The glutaronitrile molecules are then rapidly cooled to a rotational temperature of ∼2 K to be probed by FTMW spectroscopy. The estimated accuracy of the frequency measurements is better than 3 kHz, and the resolution better than 5 kHz.

In the second part of the experiment, the emission rotational spectrum of glutaronitrile was recorded from 72 to 116.5 GHz at room temperature using the GACELA (GAS CEll for Laboratory Astrophysics) spectrometer constructed at the Yebes Observatory (Spanish National Geographic Institute (IGN)). The detailed description can be found in Cernicharo et al. (2019). The broad-band high resolution rotational spectrometer is equipped with radio receivers similar to those used in radio astronomy to search for molecular emission in space. The receivers are equipped with 16 x 2.5 GHz fast Fourier transform spectrometers (FFTs) with a spectral resolution of 38.14 kHz allowing the observation of the rotational transitions in the W band (72-116.5 GHz). The spectrometer’s cell consists of a stainless steel cylinder of 890 mm length and 490 mm diameter positioned with the long axis horizontally. The glutaronitrile sample was placed into a Pyrex™ vacuum Schlenk, which was heated to 80°C using a dry heating tape and a PID (proportional integral derivative) temperature controller. In order to avoid sample condensation during the experiment, the temperature of the injection line was kept at 80°C. Prior to the sample introduction, the pressure inside the vacuum chamber was 2.0x10⁻⁴ mbar and during the experiment, carried out in continuous flow mode, the pressure was kept at 7.0x10⁻³ mbar, because higher pressures produce undesirable line broadenings. With the selected working pressure, the rotational lines of glutaronitrile have a HWHM of 0.3−0.45 MHz, which is well adapted to frequency measurements with high accuracy. In all these experiments, frequency switching with a throw of 25 MHz was selected as the observing procedure.

4. Rotational spectrum and analysis

Glutaronitrile can adopt four conformers in the gas phase, being the gg species, the global minimum, and thus the most probable candidate to be detected through its rotational spectrum. We used the theoretical rotational constants from Table 1 to predict the frequency transitions for this conformer in the 6 to 20 GHz interval. This conformer is a near prolate molecule that has a C₂ symmetry axis, which coincides with its molecular b axis, and thus it has only one dipole moment component. We found b-type R-branch rotational transitions with K_a=0,1 very close to the predictions. They were assigned to improve the transition frequency predictions and search for new ones. In this manner, we extended our measurements to b-type R-branch transitions with K_a=2 and b-type Q-branch transitions with K_a=1,2 and 3. Each rotational transition is split into several hyperfine components because of the nuclear quadrupole coupling effects produced by the presence of two equivalent nitrogen atoms, as can be seen in Figure 2 for the 3_3,1-3_2,2 rotational transition. The interaction at the nuclei of these quadrupole moments with the electric field gradient created by the rest of the molecular charges causes the coupling of the nuclear spin moments to the overall rotational momentum (Gordy & Cook 1984). In total we observed 228 hyperfine components corresponding to 24 pure rotational transitions (see Table 2). Rotational, centrifugal, and nuclear quadrupole coupling constants were determined fitting the transition frequencies, using the SPFIT programme (Pickett 1991), to a Watson’s A-reduced ¹A’ Hamiltonian for asymmetric top molecules, with the following form (Watson 1977): H = H_R + H_Q, where H_R contains rotational and centrifugal distortion parameters and HQ the quadrupole coupling interactions. The energy levels involved in each transition are labelled with the quantum numbers J, K_a, K_c, I, and F, where I = I_N1 + I_N2 and F = J + I, where I = 0, 1, and 2. The analysis rendered the experimental constants listed in Table 3 together with theoretical data. Comparison of the experimentally determined rotational constants with those predicted ab initio leads to the unambiguous identification of conformer gg. The calculated constants of Table 3 show deviations from experimental values lower than 0.7 %, indicating that the calculated ab initio geometry is fairly accurate. In spite of the fact that larger discrepancies can be found between the experimental and theoretical centrifugal distortion constants, the accordance can be considered satisfactory since the estimation procedure of these parameters is not trivial. Finally, it can be seen that the nuclear quadrupole coupling constants agree very well with those predicted theoretically.

Table 2. Rotational transitions ^a for glutaronitrile observed by FTMW spectroscopy.

J′ b	$K_a^{\prime }$	$K_c^{\prime }$	I′	F′	J″	$K_a^{″}$	$K_c^{″}$	I″	F″	Freq. meas. c (MHz)	Uncert. d (MHz)	Obs.-calc.e (MHz)
2	2	0	2	4	2	1	1	2	4	9523.644	0.005	0.000
2	2	0	1	3	2	1	1	1	3	9523.754	0.005	-0.000
2	2	0	1	1	2	1	1	1	1	9523.848	0.005	0.001
2	2	0	2	3	2	1	1	2	3	9523.866	0.005	0.001
2	2	0	2	2	2	1	1	2	2	9523.943	0.005	0.001
2	2	1	0	2	2	1	2	0	2	9919.754	0.005	-0.000
2	2	1	1	2	2	1	2	1	2	9919.807	0.005	-0.003
2	2	1	2	4	2	1	2	2	4	9919.886	0.005	-0.003
2	2	1	1	3	2	1	2	1	3	9920.044	0.005	-0.000
2	2	1	1	1	2	1	2	1	1	9920.178	0.005	0.004
2	2	1	2	3	2	1	2	2	3	9920.199	0.005	-0.001
2	2	1	2	2	2	1	2	2	2	9920.309	0.005	0.001
2	1	2	2	1	1	0	1	2	1	9103.868	0.005	0.002
2	1	2	1	1	1	0	1	1	1	9103.879	0.005	0.002
2	1	2	0	2	1	0	1	2	1	9103.891	0.005	0.001
2	1	2	2	3	1	0	1	2	3	9103.926	0.005	-0.001
2	1	2	1	3	1	0	1	1	2	9104.052	0.005	-0.003

Notes.

^aThe complete table (Table A.1) is available at the CDS.

^bJ′, $K_a^{\mathrm{\prime }},$$K_c^{\mathrm{\prime }},$ I′, and F′, represent the quantum numbers associated with the upper rotational level. J″, $K_a^{″}$, $K_c^{″}$, I″, and F″, represent the quantum numbers associated with the lower rotational level.

^cObserved experimental frequency.

^dUncertainty in the observed frequency.

^eDifference between the observed frequency and that derived from the fit.

Table 3. Molecular constants for glutaronitrile.

Constants/Units	FTMW fit	Global fit	mmW fit	Theorya
A/MHz	4756.13738(24)	4756.1397(30)	4755.60(11)	4767.1
B/MHz	1582.79295(64)	1582.7606(25)	1582.7530(84)	1571.6
C/MHz	1449.29522(55)	1449.27921(65)	1449.28150(85)	1439.5
ΔJ /kHz	2.4036(64)	2.3447(16)	2.3555(52)	2.2839
ΔK /kHz	56.221(24)	59.787(41)	57.89(39)	35.8181
ΔJK /kHz	-19.905(21)	-20.4772(93)	-20.486(11)	-21.7187
δJ /kHz	0.5920(32)	0.54303(77)	0.5477(25)	0.3213
δK /kHz	4.54(26)	4.282(45)	4.78(14)	5.3779
ΦK /Hz	-	6.680(87)	4.40(47)	1.3457
ΦKJ /Hz	-	-1.834(17)	-1.804(21)	-1.2627
φJK /Hz	-	-0.112(17)	-0.110(30)	-0.5042
χaa/MHz	-0.4123(10)	-	-	-0.4126
χbb/MHz	0.0989(15)	-	-	0.1045
σrms/kHz	3.44	38.10	42.33	-
σwrms	0.60b	0.76c	0.84c	-
Nlines	228d	111	89	-
Jmin/Jmax	0/5	0/54	24/54	-
Ka,min/Ka,max	0/3	0/18	0/18	-

Notes. Numbers in parentheses represent the derived uncertainty (1 σ) of the parameter in units of the last digit.

^aRotational and nuclear quadrupole coupling constants derived from the optimisation calculations at CCSD/cc-pVTZ level of theory. The distortion constants were obtained from anharmonic frequency MP2/cc-pVTZ calculations.

^bThe uncertainty associated with the lines is 5 kHz.

^cThe uncertainty associated with the lines is 50 kHz.

^dNumber of hyper-fine components included in the fit.

Once the gg conformer was assigned, we looked for the rotational transitions of higher energy conformers, in particular gt species. According to its relative energy, its estimated population (at the cell’s temperature, 300K) is ∼1/3 of that of gg conformer but taking into account the values of dipole moment components predicted by ab initio calculations, the expected intensity of its rotational transitions is ∼1/5 of those observed for gg conformer. We scanned the predicted frequency regions, but no lines attributable to gt conformer were found. Given the good signal-to-noise ratio for the rotational transitions of the gg conformer observed by FTMW spectroscopy, it seems that gt should be also detected. The absence of the gt conformer in the supersonic jet can be associated with a collisional relaxation of this conformer to the gg conformer through a low-energy interconversion barrier. This process takes place in the early stages of the supersonic expansion by collisions between the different conformers and the buffer gas molecules (Ruoff et al. 1990). It has been shown that collisional removal of a higher energy conformer is possible when the isomerisation barrier is around 500-600 cm−1 and Ar is used as carrier gas (Cabezas et al. 2018). To gain some insight, we calculated the potential energy profile between the gt and gg conformers by scanning the dihedral angle ∠ C₁C₂C₃C₄. An energy barrier of 698 cm⁻¹ was found, at the CCSD/cc-pVTZ level of theory, suggesting a collisional relaxation, at least partial, from gt to gg conformer. This fact makes the gt conformer population smaller than the expected one, preventing the observation of its rotational transitions.

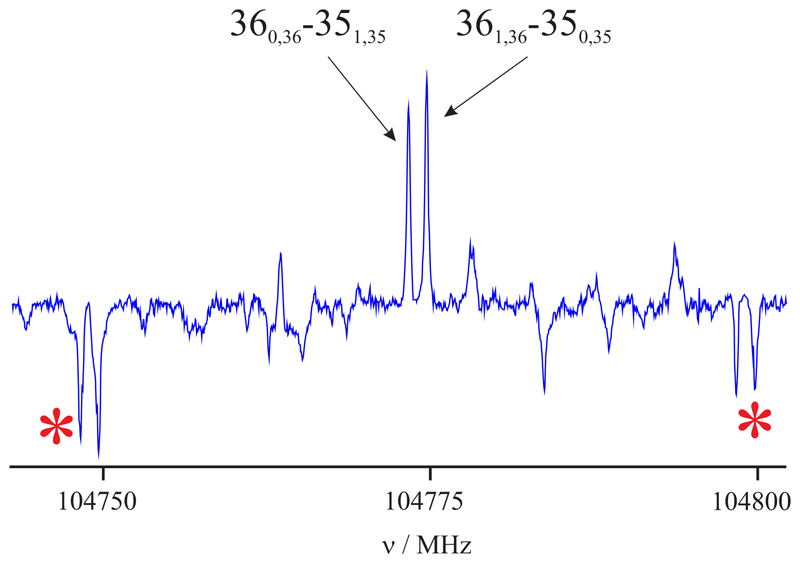
Using the rotational and centrifugal distortion constants determined by FTMW measurements, we predicted the transition frequencies for the gg conformer of glutaronitrile in the mmW frequency region. An initial assignment was obtained simply by locating the b-type R-branch transitions with K_a=0,1 as those depicted in Figure 3. Measurements were extended to b-type R-branch rotational transitions up to K_a=3 and Q-branch transitions with K_a=17,18. A total of 89 rotational transitions, see Table 4, were observed in the mmW range and fitted (Pickett 1991) to a Watson’s A-reduced ¹A’ Hamiltonian. The analysis rendered the experimental data listed in Table 3. In addition to the rotational and quartic centrifugal distortion constants previously determined by FTMW measurements, the sextic centrifugal distortion constants Φ_K, Φ_KJ, and φ_JK were determined. The inclusion of these parameters in the fit slightly affects the value of the rest of the floated parameters, as can be seen if data for the FTMW and mmw fits are compared (Table 3).

Fig. 3.

Section of broadband rotational spectrum of glutaronitrile showing the R-branch rotational transitions 36_0,36−35_1,35 and 36_1,36−35_0,35 of gg conformer of glutaronitrile. The negative features marked with an asterisk are produced by the folding of the frequency switched data and appear at ±25MHz of each rotational transition.

Table 4. Rotational transitions ^a for glutaronitrile observed in the mmW region.

J′ b	$K_a^{\prime }$	$K_c^{\prime }$	J″	$K_a^{″}$	$K_c^{″}$	Freq. meas. c (MHz)	Uncert. d (MHz)	Obs.- calc. e (MHz)
40	1	40	39	0	39	116272.079	0.050	-0.010
40	0	40	39	1	39	116271.949	0.050	0.016
39	2	38	38	1	37	114711.079	0.050	-0.038
39	1	38	38	2	37	114700.167	0.050	-0.033
39	1	39	38	0	38	113397.853	0.050	0.018
39	0	39	38	1	38	113397.669	0.050	0.041
38	2	37	37	1	36	111839.559	0.050	-0.023
38	1	37	37	2	36	111824.587	0.050	-0.021
38	1	38	37	0	37	110522.432	0.050	0.023
38	0	38	37	1	37	110522.139	0.050	0.023
36	1	36	35	0	35	104768.151	0.050	-0.009
36	0	36	35	1	35	104767.553	0.050	-0.020

Notes.

^aThe complete table (Table A.2) is available at the CDS.

^bJ′, $K_a^{\mathrm{\prime }},$ and $K_c^{\prime }$ represent the quantum numbers associated with the upper rotational level. J″, $K_a^{″}$, and $K_c^{″}$ represent the quantum numbers associated with the lower rotational level.

^cObserved experimental frequency.

^dUncertainty in the observed frequency.

^eDifference between the observed frequency and that derived from the fit.

Collisional relaxation between conformers is not possible in the GACELA experiments since they are not performed in a supersonic expansion environment. Hence, the rotational transitions for gt conformer should be observed in our mmW spectrum with intensity five times smaller than those for the gg conformer. However, the signal-to-noise ratio of the gg conformer is much smaller in the mmW region than that found in the FTMW experiments, and then, the rotational lines for gt conformer could not be distinguished from the noise level.

As mentioned before, glutaronitrile has two equivalent ¹⁴N nuclei with a spin of I = 1, so that nuclear quadrupole coupling hyperfine splittings were observed using the FTMW spectrometer. However, in the mmW range, all the measured lines were observed as single lines, and no hyperfine splittings could be noticed (Figure 3) because they are smaller than the experimental broadening of the lines. The rotational spectrum in the mmW region, yet, shows the influence of nuclear spin statistics on the transition intensities. This is due to the geometry of the molecule, which allows an interchange of identical particles by the rotation around one of the principal axes. The C_2b operation of the C₂ symmetry point group, which corresponds to the rotation about the b axis by π radians, simultaneously exchanges the positions of three non-equivalent pairs of hydrogen (fermions with I = 1/2) and two nitrogen atoms (bosons with I = 1) in the molecule. Fermi-Dirac statistics must be considered due to the presence of three pairs of fermions and the bosons. Hence, the total wavefunction, expressed as ψ_tot =ψ_eleψ_vibψ_rotψ_ns, must be antisymmetric with respect to the C_2b operation. The corresponding wavefunctions ψ_ele and ψ_vib for the ground electronic and vibrational states are symmetric. The parity of the rotational wavefunction ψ_rot depends on the K_a and K_c values, and it is symmetric for the levels with K_a + K_c = even, while for the levels with K_a + K_c = odd it is antisymmetric. Hence, to satisfy Fermi-Dirac statistics, symmetric and antisymmetric nuclear spin functions must be combined with antisymmetric and symmetric rotational wavefunctions, respectively. As shown in Bunker & Jensen (1998), the total nuclear statistics weights are (2I_H + 1)²(2I_H + 1)²(2I_H + 1)²(2I_N + 1)² = 576, and the nuclear statistical weight for the rotational levels with K_a + K_c = even and odd is 23 and 25, respectively. Figure 3 shows the 36_0,36−35_1,35 and 36_1,36−35_0,35 rotational transitions and their relative intensity ratio of 23-to-25.

A combined fit using all the transition frequencies from both FTMW and mmW measurements was done. The spectroscopic constants derived for the gg conformer are shown in Table 3 together with the other fits and the theoretical calculations. In order to search for glutaronitrile in the space, we implemented the constants derived from the combined fit into the MADEX code (Cernicharo 2012) and simulated the spectra of glutaronitrile at higher frequencies. The frequency predictions for glutaronitrile up to 300 GHz calculated at T = 300 K are given in Table A.3 available at CDS. To estimate the column density of glutaronitrile, we used the partition function values shown in Table 5, which were calculated including rotational levels at maximum value of J = 90. The results of the astronomical search are shown in the next section.

Table 5. Rotational partition functions for glutaronitrile at different temperatures.

Temperature/K	Qr
300.000	223332.4
225.000	158807.8
150.000	92210.4
75.000	33259.6
37.500	11747.9
18.750	4152.4
9.375	1469.2

5. Search for glutaronitrile in space

Using the rotational parameters for the observed gg conformer of glutaronitrile and the MADEX code (Cernicharo 2012), we searched for it in space. We searched for glutaronitrile in the two high-mass star-forming regions, Orion KL and Sagittarius (Sgr) B2 using the IRAM 30m data at 3 mm provided by Tercero et al. (2010) and Belloche et al. (2013), respectively. In addition, we extended our search to the starless core in the Taurus Molecular Cloud (TMC-1) and the cold dark cloud Barnard 1 (B1-b) using 3 mm data of the IRAM 30m telescope (Marcelino et al. 2007; Cernicharo 2012). We focused on data at frequencies below 200 GHz to assess a potential detection and prevent non-reliable frequency predictions.

firstly, we searched for glutaronitrile using the IRAM 30m data at 3 mm of TMC-1 and B1-b sources. For these cold cores, we focused the search on unresolved doublets with energies of the upper level of about 20 K such as 10_9,2-9_8,1 and 10_9,1-9_8,2 at 85307 MHz and 11_9,3-10_8,2 and 11_9,2-10_8,3 at 88347 MHz. We did not detect glutaronitrile above the 3σ detection limit of our data. The derived upper limits for glutaronitrile column densities, considering local thermodynamic equilibrium (LTE), and the assumed physical parameters are summarised in Table 6. For the high-mass star-forming regions, we built a synthetic spectrum of glutaronitrile adopting the physical parameters derived for CH₂CHCN by Lopez et al. (2014) in Orion KL, and those derived for CH₃CN by Belloche et al. (2013) in Sgr B2.

Table 6. Physical parameters of the considered cloud cores in the astronomical search of glutaronitrile.

Source	Coordinates J2000.0	HPBW(a) (″)	Frequencies(b) (GHz)	vLSR(c) (km s−1)	∆vFWHM(d) (km s−1)	dsou(e) (″)	Trot(f) (K)	N(g) ×1015 (cm−2)
Orion KL	α=5h35m14.5s δ=−05°22′ 30.0″	30-21	80-115.5	5.0	6.0	10	320	≤(1.0±0.5)
				5.0	6.0	15	100	≤(0.50±0.25)
				3.0	20	10	200	≤(0.20±0.10)
				3.0	20	15	90	≤(0.20±0.10)
Sgr B2(N)	α=17h47m20.0s δ=−28°22′ 19.0″	30-21	80-115.5	63	6.5	2.7	200	≤(100±50)
				73	6.5	2.7	200	≤(50±25)
				53	8	2.7	200	≤(50±25)
B1-b	α=03h33m20.0s δ=31°07′ 34.0″	30-21	82.5-115.5	6.7	0.7	60	12	≤(0.002±0.001)
TMC-1	α=04h41m41.9s δ=25°41′ 27.0″	30-21	82.5-115.5	6.0	0.7	60	10	≤(0.002±0.001)

Notes

^(a)Half power beam width.

^(b)Range of frequencies considered in the analysis.

^(c)Radial velocity with respect the Local Standard of Rest.

^(d)Full width at half maximum.

^(e)Source diameter assuming a uniform disc-type model.

^(f)Rotational Temperature.

^(g)Column density for glutaronitrile .

These results are not totally unexpected, since in a previous work (Cabezas et al. 2019) we were not able to detect the simpler succinonitrile. However, the negative result for the detection of succinonitrile may be related to the fact that the search was limited to the gauche conformer which is 321 cm⁻¹ above the most stable conformer, the trans one, which is a non-polar species. Therefore, the search for a more complex species like glutaronitrile is required in order to constrain the production of complex nitriles in space. A general discussion related to the source selection and the production of dinitriles in space can be found in our previous work on succinonitrile (Cabezas et al. 2019). Here, we only provide upper limits for the glutaronitrile column density in these sources. Like in the case of succinonitrile, the derived upper limits are only a factor ≤10 lower than the column density derived for CH₃CN in Orion KL (Lopez et al. 2014) and Sgr B2 (Belloche et al. 2013). This suggests that the high level of line confusion in the considered surveys produces very high upper limits for the column densities of the nondetected species. We also note that the derived upper limits are only a factor of 1.5 and 5 lower than those obtained for the total column densities of succinonitrile (including the lowest energy conformer) provided by Cabezas et al. (2019) for Orion KL and Sgr B2, respectively.

6. Conclusions

The present work reports the investigation of the rotational spectra of a new dinitrile, glutaronitrile. The microwave and millimetre-wave spectra were measured using two different spectroscopic techniques: a FTMW spectrometer at low frequencies, and a broadband millimetre-wave spectrometer in the frequency range 72-116.5 GHz. From the analysis of the spectra, we obtain accurate rotational parameters for the most stable conformation, named the gg species, which were used to unsuccessfully search for glutaronitrile in the cold and warm molecular clouds Orion KL, Sgr B2(N), B1-b, and TMC-1, using the spectral surveys captured by IRAM 30m at 3mm.

Fig. 1.

Molecular structures for the four possible conformers of glutaronitrile obtained from ab initio calculations at the CCSD/cc-pVTZ level of theory.