Establishment of Best Practices for Evidence for Prediction A Review

Abstract

IMPORTANCE

Great interest exists in identifying methods to predict neuropsychiatric disease states and treatment outcomes from high-dimensional data, including neuroimaging and genomics data. The goal of this review is to highlight several potential problems that can arise in studies that aim to establish prediction.

OBSERVATIONS

A number of neuroimaging studies have claimed to establish prediction while establishing only correlation, which is an inappropriate use of the statistical meaning of prediction. Statistical associations do not necessarily imply the ability to make predictions in a generalized manner; establishing evidence for prediction thus requires testing of the model on data separate from those used to estimate the model’s parameters. This article discusses various measures of predictive performance and the limitations of some commonly used measures, with a focus on the importance of using multiple measures when assessing performance. For classification, the area under the receiver operating characteristic curve is an appropriate measure; for regression analysis, correlation should be avoided, and median absolute error is preferred.

CONCLUSIONS AND RELEVANCE

To ensure accurate estimates of predictive validity, the recommended best practices for predictive modeling include the following: (1) in-sample model fit indices should not be reported as evidence for predictive accuracy, (2) the cross-validation procedure should encompass all operations applied to the data, (3) prediction analyses should not be performed with samples smaller than several hundred observations, (4) multiple measures of prediction accuracy should be examined and reported, (5) the coefficient of determination should be computed using the sums of squares formulation and not the correlation coefficient, and (6) k-fold cross-validation rather than leave-one-out cross-validation should be used.

The development of biomarkers for disease is attracting increasing interest in many domains of biomedicine. Interest is particularly high in neuropsychiatry owing to the current lack of biologically validated diagnostic or therapeutic measures.¹ An essential aspect of biomarker development is demonstration that a putative marker is predictive of relevant behavioural outcomes,² disease prognosis,³ or therapeutic outcomes.⁴ As the size and complexity of data sets have increased (as in neuroimaging and genomics studies), it has become increasingly common that predictive analyses have been performed using methods from the field of machine learning, with techniques that are purpose-built for generating accurate predictions on new data sets.

Despite the potential utility of prediction-based research, its successful application in neuropsychiatry—and medicine more generally—remains challenging. In this article, we review a number of challenges in establishing evidence for prediction, with the goal of providing simple recommendations to avoid common errors. Although most of these challenges are well known within the machine learning and statistics communities, awareness is less widespread among research practitioners.

We begin by outlining the meaning of the concept of prediction from the standpoint of machine learning. We highlight the fact that predictive accuracy cannot be established by using the same data both to fit and test the model, which our literature review found to be a common error in published claims of prediction. We then turn to the question of how accuracy should be quantified for categorical and continuous outcome measures. We outline the ways in which naive use of particular predictive accuracy measures and cross-validation methods can lead to biased estimates of predictive accuracy. We conclude with a set of best practices to establish valid claims of successful prediction.

Code to reproduce all simulations and figures is available at https://github.com/poldrack/PredictionCV.

Association vs Prediction

A claim of prediction is ultimately judged by its ability to generalize data to new situations; the term implies that it is possible to successfully predict outcomes in data sets other than the one used to generate the claim. When a statistical model is applied to data, the goodness of fit of that model to those data will in part reflect the underlying data-generating mechanism, which should generalize to new data sets sampled from the same population, but it will also include a contribution from noise (ie, unexplained variation or randomness) that is specific to the particular sample.⁵ For this reason, a model will usually fit better to the sample used to estimate it than it will to a new sample, a phenomenon known in machine learning as overfitting and in statistics as shrinkage.

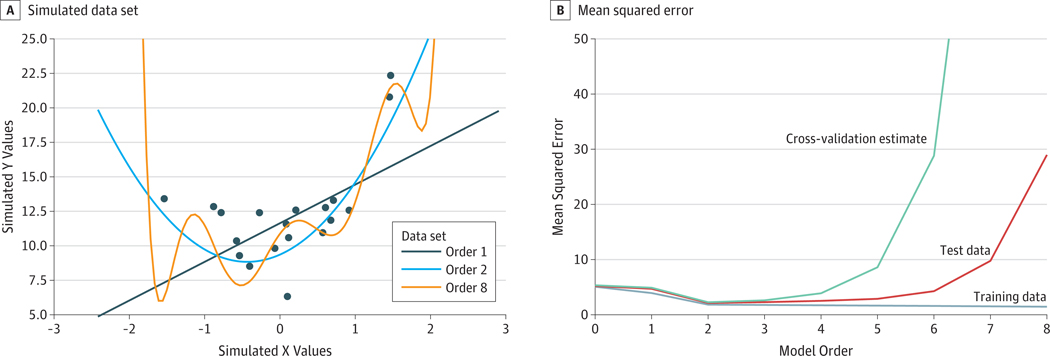
Because of overfitting, it is not possible to draw useful estimates of predictive accuracy simply from a model’s goodness of fit to a data set; such estimates will necessarily be inflated, and their degree of optimism will depend on many factors, including the complexity of the statistical model and the size of the data set. The fit of a model to a specific data set can be improved by increasing the number of parameters in the model; any data set can be fit with 0 error if the model has as many parameters as data points. However, as the model becomes more complex than the process that generates the data, the fit of the model starts to reflect the specific noise values in the data set. A sign of overfitting is that the model fits well to the specific data set used to estimate the model but fits poorly to new data sets sampled from the same population. Figure 1 presents a simulated example, in which increasing model complexity results in decreased error for the data used to fit the model, but the fit to new data becomes increasingly poor as the model grows more complex than the true data-generating process.

Figure 1. Depiction of Overfitting.

A, Simulated data set. The data set was generated from a quadratic model (ie, polynomial order 2). The best-fitting models are depicted: polynomial order 1 (linear), polynomial order 2 (quadratic), and polynomial order 8 (complex). The complex model overfits the data set, adapting itself to the noise evident in specific data points, with its predictions oscillating at the extremes of the x-axis. B, Mean squared error. Mean squared error for the model was assessed against the data set used to train the model and against a separate test data set sampled from the same generative process with different random measurement error. Results reflect the median over 1000 simulation runs. Order 0 indicates no model complexity, and order 8 indicates maximum model complexity. The mean squared error decreases for the training data set as the complexity of the model increases. The mean squared error estimated using 4-fold cross-validation (green) is also lowest for the true model.

Because we do not generally have a separate test data set to assess generalization performance, the standard approach in machine learning to address overfitting is to assess model fit via cross-validation, a process that uses subsets of the data to iteratively train and test the predictive performance of the model. The simplest form of cross-validation is known as leave-one-out, in which the model is successively fit on every data point but 1 and is then tested on that left-out point. A more general cross-validation approach is known as k-fold cross-validation, in which the data are split into k different subsets, or folds. The model is successively trained on every subset but 1 and is then tested on the held-out subset. Cross-validation can also help discover the model that will provide the best predictive performance on a new sample (Figure 1).

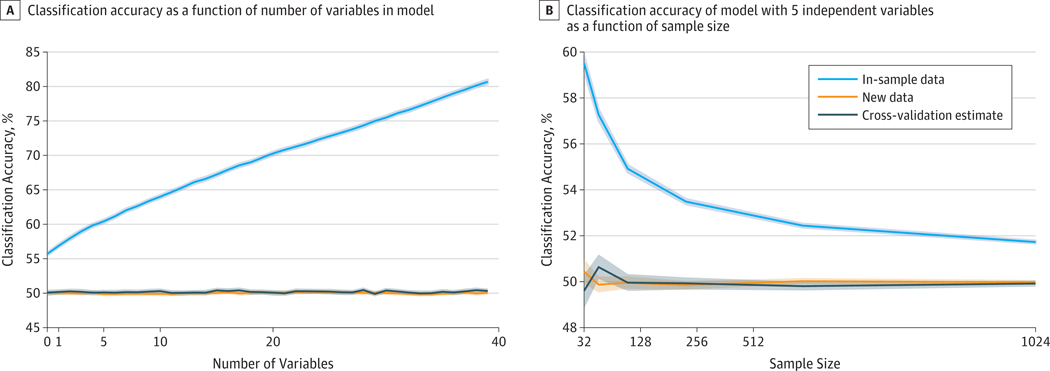
One might ask how poorly inflated the in-sample association is as an estimate of out-of-sample prediction; if the inflation is small, or only occurs with complex models, then perhaps it can be ignored for practical purposes. Figure 2 shows an example of how the optimism of in-sample fits depends on the complexity of the statistical model; in this case, we use a simple linear model but vary the number of irrelevant independent variables in the model. As the number of variables increases, the fit of the model to the sample increases owing to overfitting. However, even for a single predictor in the model, the fit of the model is inflated compared with new data or cross-validation. The optimism of in-sample fits is also a function of sample size (Figure 2). This example demonstrates the utility of using cross-validation to estimate predictive accuracy on a new sample.

Figure 2. Classification Accuracy.

A, Classification accuracy as a function of number of variables in model. For each of 1000 simulation runs, a completely random data set (comprising a set of normally distributed independent variables and a random binary dependent variable) was generated, and logistic regression was fitted to both the data as a whole and the data estimated using 4-fold cross-validation. In addition, a second data set was generated using the same mechanism to serve as an unseen test data set. The orange and gray lines show that cross-validation is a good proxy for testing the model on new data, with both showing chance accuracy. The blue line shows that in-sample classification accuracy is inflated compared with the true value of 50% because of the fitting of noise in those variables. B, Classification accuracy of model with 5 independent variables as a function of sample size. Optimism (the difference in accuracy between in-sample and cross-validated or new data) is substantially higher for smaller sample sizes. Shaded areas indicate 95%CIs estimated with the bootstrapping method.

Statistical Significance vs Useful Prediction

A second reason that significant statistical association does not imply practically useful prediction is exemplified by the psychiatric genetic literature. Large genome-wide association studies have now identified significant associations between genetic variants and mental illness diagnoses. For example, Ripke et al⁶ compared more than 21 000 patients with schizophrenia with more than 38 000 patients without schizophrenia and found 22 genetic variants significant at a genome-wide level (P = 5 × 10⁻⁸), the strongest of which (rs9268895) had a combined P value of 9.14 × 10⁻¹⁴. However, this strongest association would be useless on its own as a predictor of schizophrenia. The combined odds ratio for this risk variant was 1.167; assuming a population prevalence of schizophrenia of 1 in 196 individuals as the baseline risk,⁷ possessing the risk allele for this strongest variant would raise an individual’s risk to 1 in 167. Such an effect is far from clinically actionable. In fact, the increased availability of large samples has made clear the point that Meehl⁸ raised more than 50 years ago, which stated that in the context of null hypothesis testing, as samples become larger, even trivial associations become statistically significant.

A more general challenge exists regarding the prediction of un-common outcomes, such as a diagnosis of schizophrenia. Consider the case in which a researcher has developed a test for schizophrenia that has 99% sensitivity (ie, a 99% likelihood that the test will return a positive result for someone with the disease) and 99% specificity (ie, a 99% likelihood that the test will return a negative result for someone without the disease).These are performance levels that any test developer would be thrilled to obtain; in comparison, mammography has a sensitivity of 87.8% and a specificity of 90.5% for the detection of breast cancer.⁹ If this test for schizophrenia were used to screen 1 million people, it would detect 99% of those with schizophrenia (5049 individuals) but would also incorrectly detect 9949 individuals without schizophrenia; thus, even with exceedingly high sensitivity and specificity, the predictive value of a positive test result remains well below 50%. As we can straightforwardly deduce from the Bayes theorem, false alarm rates will usually be high when testing for events with low baseline rates of occurrence.

Misinterpretation of Association as Prediction

A significant statistical association is insufficient to establish a claim of prediction. However, in our experience, it is common for investigators in the functional neuroimaging literature to use the term prediction when describing a significant in-sample statistical association. To quantify the prevalence of this practice, we identified 100 published studies between December 24, 2017, and October 30, 2018, in PubMed by using the search terms fMRI prediction and fMRI predict. For each study, we identified whether the purported prediction was based on a statistical association, such as a significant correlation or regression effect, or whether the researchers used a statistical procedure specifically designed to measure prediction, such as cross-validation or out-of-sample validation. We only included studies that purported to predict an individual-level outcome based on fMRI data and excluded other uses of the term prediction, such as studies examining reward prediction error. A detailed description of these studies is presented in the eTable in the Supplement.

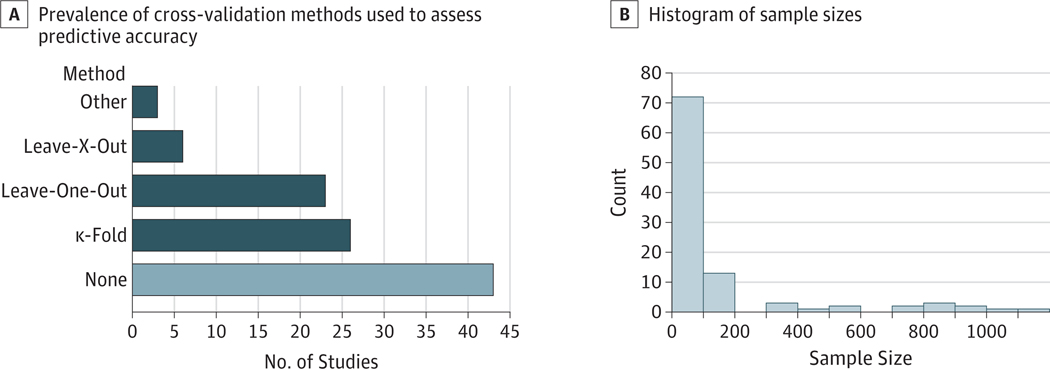
Of the 100 studies assessed, 45 reported an in-sample statistical association as the sole support for the claims of prediction, suggesting that the conflation of statistical association and predictive accuracyiscommon.¹⁰The remaining studies used a mixture of cross-validation strategies, as shown in Figure 3.

Figure 3. Results From Review of 100 Most Recent Studies (2017–2019) Claiming Prediction on the Basis of fMRI Data.

A, Prevalence of cross-validation methods used to assess predictive accuracy. B, Histogram of sample sizes.

Factors That Can Bias Assessment of Prediction

Although performing some type of assessment of an out-of-sample prediction is essential, it is also clear that cross-validation still leaves room for errors when establishing predictive validity. We now turn to issues that can affect the estimation of predictive accuracy even when using appropriate predictive modeling methods.

Small Samples

The use of cross-validation with small samples can lead to highly variable estimates of predictive accuracy. Varoquaux¹¹ noted that a general decrease in the level of reported prediction accuracy can be observed as sample sizes increase. Given the flexibility of analysis methods¹² and publication bias for positive results, such that only the top tail of accuracy measures is reported, the high variability of estimates with small samples can lead to a body of literature with inflated estimates of predictive accuracy.

Our literature review found a high prevalence of small samples, with more than half of the samples comprising fewer than 50 people and 15% of the studies with samples comprising fewer than 20 people (Figure 3). Most studies that use small samples are likely to exhibit highly variable estimates. This finding suggests that many of the claims of predictive accuracy in the neuroimaging literature may be exaggerated and/or not valid.

Leakage of Test Data

To give a valid measure of predictive accuracy, cross-validation needs to build on a clean isolation of the test data during the fitting of models to the training data. If information leaks from the testing set into the model-fitting procedure, then estimates of predictive accuracy will be inflated, sometimes wildly. For example, any variable selection that is applied to the data before application of cross-validation will bias the results if the selection involves knowledge of the variable being predicted. Of the 57 studies in our review that used cross-validation procedures, 10 may have applied dimensionality reduction methods that involved the outcome measure (eg, thresholding based on correlation) to the entire data set. This lack of clarity raises concerns regarding the level of methodological reporting in these studies.¹³

In addition, any search across analytic methods, such as selecting the best model or the model parameters, must be performed using nested cross-validation, in which a second cross-validation loop is used within the training data to determine the optimal method or parameters. The best practice is to include all processing operations within the cross-validation loop to prevent any potential for leakage. This practice is increasingly possible using cross-validation pipeline tools, such as those available within the scikit-learn software package (scikit-learn Developers).¹⁴

Model Selection Outside of Cross-validation

Selecting a predictive method based on the data creates an opportunity for bias that could involve the potential use of a number of different classifiers, hyperparameters for those classifiers, or various preprocessing methods. As in standard data analysis, there is a potential garden of forking paths,¹⁵ such that data-driven modeling decisions can bias the resulting outcomes even if there is no explicit search for methods providing the best results. The outcomes are substantially more biased if an explicit search for the best methods is performed without a held-out validation set.

As reported in studies by Skocik et al¹⁶ using simulations and Varoquaux¹¹ using fMRI data, it is possible to obtain substantial apparent predictive accuracy from data without any true association if a researcher capitalizes on random fluctuations in classifier performanceandsearchesacrossalargeparameterspace.Atrueheldoutvalidationsampleisagoodsolutiontothisproblem.Amoregeneralsolutiontotheproblemofanalyticflexibilityisthepreregistration of analysis plans before any analysis, as is increasingly common in other areas of science.¹⁷

Nonindependence Between Training and Testing Sets

Like any statistical technique, the use of cross-validation to estimate predictive accuracy involves assumptions, the failure of which can undermine the validity of the results. An important assumption of cross-validation is that observations in the training and testing sets are independent. While this assumption is often valid, it can break down when there are systematic relationships between observations. For example, the Human Connectome Project data set includes data from families, and it is reasonable to expect that family members will be closer to each other in brain structure and function than will individuals who are not biologically related.

Similarly, data collected as a time series will often exhibit autocorrelation, such that observations closer in time are more similar. In these cases, there are special cross-validation strategies that must be used to address this structure. For example, in the presence of family structure, such as the sample used in the Human Connectome Project, a researcher might cross-validate across families (ie, leave-k-families-out) rather than individuals to address the nonindependence potentially induced by family structure.¹⁸

Quantification of Predictive Accuracy

Two main categories of problems occur in predictive modeling. The first, classification accuracy, involves the prediction of discrete class membership, such as the presence or absence of a disease diagnosis; the second, regression accuracy, involves the prediction of a continuous outcome variable, such as a test score or disease severity measure. In our literature review, we found that 37 studies performed classification while 64 performed regression to determine predictive accuracy. These strategies generally involve different methods for quantification of accuracy, but in each case, potential problems can arise through the naive use of common methods.

Quantifying Classification Accuracy

In a classification problem, we aim to quantify our ability to accurately predict class membership, such as the presence of a disease or a cognitive state. When the number of members in each class is equal, then average accuracy (ie, the proportion of correct classifications, as used in the examples in Figure 2) is a reasonable measure of predictive accuracy. However, if any imbalance exists between the frequencies of the different classes, then average accuracy is a misleading measure. Consider the example of a predictive model for schizophrenia, which has a prevalence of 0.5% in the population; the classifier can achieve average accuracy of 99.5% across all cases by predicting that no one has the disease, simply owing to the low frequency of the disease.

A standard method to address the class imbalance problem is to use the receiver operating characteristic curve from signal detection theory.¹⁹ A receiver operating characteristic curve can be constructed given any continuous measure of evidence, as provided by most classification models. A threshold is then applied to this measure of evidence, systematically ranging from low (in which most cases will be assigned to the positive class, and the number of false positives will be high) to high (in which most cases will be assigned to the negative class, and the number of false positives will be low). The area under the curve can then be used as an integrated measure of classification accuracy. A perfect prediction leads to an area under the curve of 1.0, while a fully random prediction leads to an area under the curve of 0.5. Importantly, the area under the curve value of 0.5 expected by chance is not biased by imbalanced frequencies of positive and negative cases in the way that simple measures of accuracy would be. It is also useful to separately present the sensitivity (ie, the proportion of positive cases correctly identified as positive) and specificity (ie, the proportion of negative cases correctly identified as negative) of the classifier, to allow assessment of the relative balance of false positives and false negatives.

Quantifying Regression Accuracy

It is increasingly common to apply predictive modeling in cases in which the outcome variable is continuous rather than discrete—that is, in regression rather than classification problems. For example, a number of studies in cognitive neuroscience have attempted to predict phenotypic measures, such as age,²⁰ personality,²¹ or behavioral outcomes.²² For continuous predictions, accuracy can be quantified either by the relation between the predicted and actual values, relative to perfect prediction, or by a measure of the absolute difference between predicted and actual values (ie, the error). A relative measure is useful because its value can easily be related to the success of the prediction. For this purpose, a useful measure is the fraction of explained variance, often called the coefficient of determination or R². If a model makes perfect predictions, its associated R² value will be 1.0, whereas a model making random predictions should have an R² value of approximately 0. If a model is particularly poor, to the point that its predictions are less accurate than they would be if the model simply returned the mean value for the data set, the R² value can be negative, despite the fact that it is called R². The disadvantage of this measure is that it does not support comparisons of the quality of predictions across different data sets because the variance of the outcome variable may differ between one data set and another. For this purpose, absolute error measurements, such as the mean absolute error, which has the benefit of quantifying error in the units of the original measure (such as IQ points), are useful.

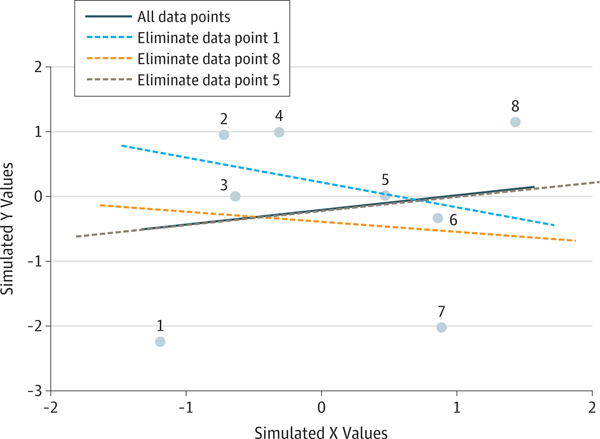
It is common in the literature to use the correlation between predicted and actual values as a measure of predictive performance; of the 64 studies in our literature review that performed prediction analyses on continuous outcomes, 30 reported such correlations as a measure of predictive performance. This reporting is problematic for several reasons. First, correlation is not sensitive to scaling of the data; thus, a high correlation can exist even when predicted values are discrepant from actual values. Second, correlation can sometimes be biased, particularly in the case of leave-one-out cross-validation. As demonstrated in Figure 4, the correlation between predicted and actual values can be strongly negative when no predictive information is present in the model. A further problem arises when the variance explained (R²) is incorrectly computed by squaring the correlation coefficient. Although this computation is appropriate when the model is obtained using the same data, it is not appropriate for out-of-sample testing²³; instead, the amount of variance explained should be computed using the sum-of-squares formulation (as implemented in software packages such as scikit-learn).

Figure 4. Example of Anticorrelated Regression Predictions Using Leave-One-Out Cross-validation.

The regression line fit to the full data set (solid gray line) has a slightly positive slope. Dropping data points near the overall regression line has little effect on the resulting slope (eg, dashed gray line showing slope after dropping data point 5), but dropping high-leverage data points at the extremes of the X distribution has major effect on the resulting regression lines (eg, dashed blue and orange lines showing effect of dropping points 1 and 8, respectively), changing the slope from positive to negative. In the context of leave-one-out cross-validation, this instability implies that a regression fit on the train set is negatively correlated with the value of the testing set, even for purely random data.

As discussed previously in this section, leave-one-out cross-validation is problematic because it allows for the possibility of negative R² values. For classification settings, the effect is the same; in a perfectly balanced data set, leave-one-out cross-validation creates a testing set comprising a single observation that is in the minority class of the training set. A simple prediction rule, such as majority vote, would thus lead to predictions that would be incorrect.²⁴ Rather, the preferred method of performing cross-validation is to leave out 10% to 20% of the data, using k-fold or shuffle-split techniques that repeatedly split the data randomly. Larger testing sets enable a good computation of measurements, such as the coefficient of determination or area under the receiver operating characteristic curve.

Best Practices for Predictive Modeling

We have several suggestions for researchers engaged in predictive modeling to ensure accurate estimates of predictive validity:

• In-sample model fit indices should not be reported as evidence for predictive accuracy because they can greatly overstate evidence for prediction and take on positive values even in the absence of true generalizable predictive ability.

• The cross-validation procedure should encompass all operations applied to the data. In particular, predictive analyses should not be performed on data after variable selection if the variable selection was informed to any degree by the data themselves (ie, post hoc cross-validation). Otherwise, estimated predictive accuracy will be inflated owing to circularity.²⁵

• Prediction analyses should not be performed with samples smaller than several hundred observations, based on the finding that predictive accuracy estimates with small samples are inflated and highly variable.²⁶

• Multiple measures of prediction accuracy should be examined and reported. For regression analyses, measures of variance, such as R², should be accompanied by measures of unsigned error, such as mean squared error or mean absolute error. For classification analyses, accuracy should be reported separately for each class, and a measure of accuracy that is insensitive to relative class frequencies, such as area under the receiver operating characteristic curve, should be reported.

• The coefficient of determination should be computed by using the sums-of-squares formulation rather than by squaring the correlation coefficient.

• k-fold cross-validation, with k in the range of 5 to 10,²⁷ should be used rather than leave-one-out cross-validation because the testing set in leave-one-out cross-validation is not representative of the whole data and is often anticorrelated with the training set.