Determining the unbinding events and conserved motions associated with the pyrazinamide release due to resistance mutations of Mycobacterium tuberculosis pyrazinamidase

Graphical abstract

Highlights

• •WT and 82 Mtb PZase-PZA complexes were established using molecular modelling.
• •AMBER force field parameters for the PZase Fe²⁺ cofactor were established.
• •Statistically guided network analysis described late PZA unbinding events.
• •MBS and nearby residue mutations lead to premature PZA release from PZase.
• •Cofactor destabilisation was found in only some PZase mutants.

Abstract

Pyrazinamide (PZA) is the only first-line antitubercular drug active against latent Mycobacterium tuberculosis (Mtb). It is activated to pyrazinoic acid by the pncA-encoded pyrazinamidase enzyme (PZase). Despite the emergence of PZA drug resistance, the underlying mechanisms of resistance remain unclear. This study investigated part of these mechanisms by modelling a PZA-bound wild type and 82 mutant PZase structures before applying molecular dynamics (MD) with an accurate Fe²⁺ cofactor coordination geometry. After observing nanosecond-scale PZA unbinding from several PZase mutants, an algorithm was developed to systematically detect ligand release via centre of mass distances (COM) and ligand average speed calculations, before applying the statistically guided network analysis (SGNA) method to investigate conserved protein motions associated with ligand unbinding. Ligand and cofactor perspectives were also investigated. A conserved pair of lid-destabilising motions was found. These consisted of (1) antiparallel lid and side flap motions; (2) the contractions of a flanking region within the same flap and residue 74 towards the core. Mutations affecting the hinge residues (H51 and H71), nearby residues or L19 were found to destabilise the lid. Additionally, other metal binding site (MBS) mutations delocalised the Fe²⁺ cofactor, also facilitating lid opening. In the early stages of unbinding, a wider variety of PZA poses were observed, suggesting multiple exit pathways. These findings provide insights into the late events preceding PZA unbinding, which we found to occur in some resistant PZase mutants. Further, the algorithm developed here to identify unbinding events coupled with SGNA can be applicable to other similar problems.

1. Introduction

Tuberculosis (TB) due to Mycobacterium tuberculosis (Mtb) infection remains a global health concern with recent reports indicating high morbidity and mortality [1]. The World Health Organization (WHO) reported approximately 1.6 million TB-related deaths in 2018 [1] despite the availability of therapeutic options. Approximately one third of the global population is latently infected with Mtb [2]. Since its discovery, the pyrazinamide (PZA) drug has become an essential component in first-line TB treatment [3], showing activity against primary TB, multidrug-resistant TB (MDR-TB), and even preventing relapse of the disease [4]. It is frequently combined with isoniazid (INH) and rifampicin (RIF) during the initial phase of therapy [4].

1.1. Mechanism of action of PZA

PZA is a prodrug that requires intracellular activation by the pncA-encoded bacterial enzyme pyrazinamidase (PZase) [4] to form bacteriostatic pyrazinoic acid (POA). Improved efficacy of PZA is due to its increased specificity on latent tubercle cells, which shortens the course of treatment to six months, instead of the standard period of nine to twelve months [5]. Additionally, studies on murine models have shown that the omission of PZA in TB therapeutic regimens not only lengthens the treatment duration but also compromises the efficacy of the other drugs to clear the bacterial cells [6], [7]. Hitherto, the underlying mechanism of action of PZA remains elusive [8]. Natively, PZase hydrolyses nicotinamide to nicotinic acid, a precursor of nicotinamide adenine dinucleotide (NAD⁺) in the NAD salvage pathway [4], through a cysteine-based catalytic mechanism [9].

1.2. Structure of the drug target and resistance mutations

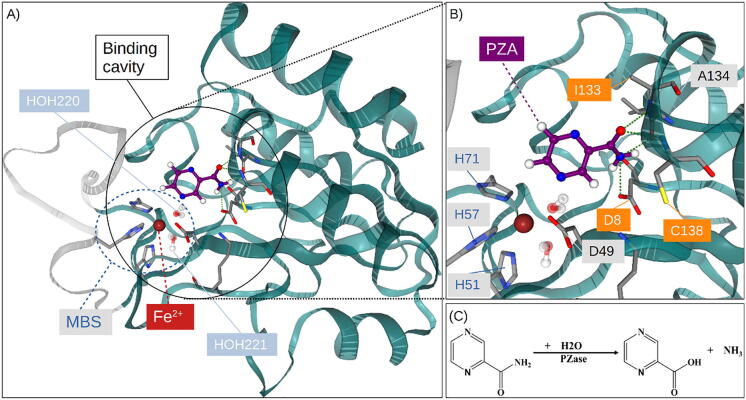
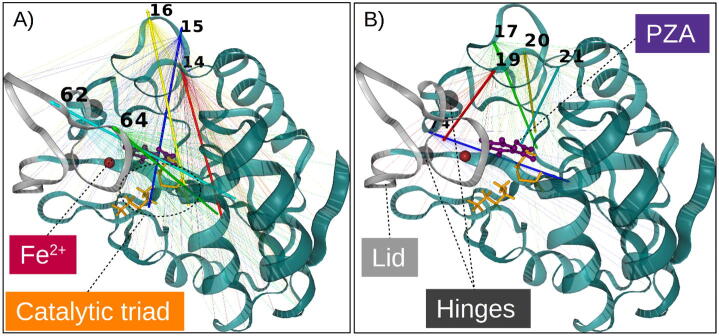
The monomeric structure of PZase consists of six parallel beta-sheets with helices packed on either side to form a single α/β domain (Fig. 1) [9]. PZase has a metal binding site (MBS) consisting of a ferrous ion (Fe²⁺) coordinated by the NE2 atom of H51 (H51_NE2), H57 (H57_NE2), H71 (H71_NE2) and OD2 of D49 (D49_OD2). Adjacent to the MBS are three substrate-binding residues (D8, K96 and C138), which form a catalytic triad [9]. Access to the active pocket is controlled by a lid (residue positions 52–70) [10], which is tethered at the base by two of the MBS residues H51 and H71. The exact catalytic mechanism for PZA activation is not known. According to Petrella et al, Mtb PZase shares an addition–elimination mechanism with PZase from Acinetobacter baumannii in which the C138 nucleophilic thiolate, assisted by D8, attacks the PZA carbonyl carbon atom to release ammonia and an acyl-enzyme intermediate [9], [11].

Fig. 1.

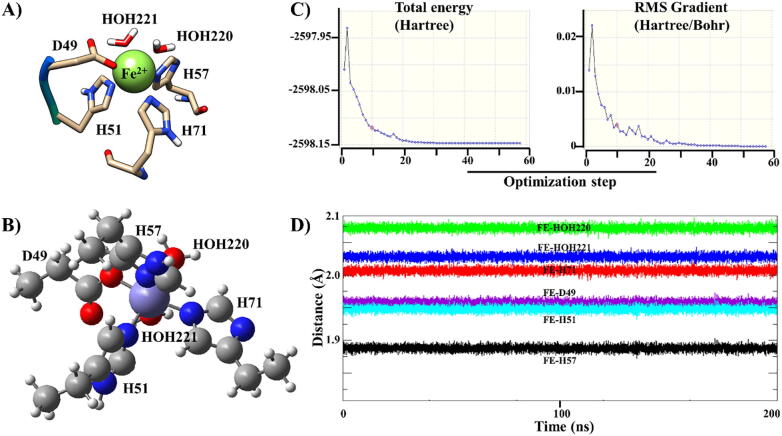
Cartoon representation of (A) the Mtb PZase-PZA complex and (B) the catalytic residue interactions within the MBS. The metal ion (Fe²⁺) is coordinated by D49, H51/57/71 and two water (HOH220/221) molecules. (C) The hydrolytic activation of PZA to POA and ammonia by PZase.

Although current TB therapeutics are effective for drug-susceptible TB strains, the emergence of drug-resistant Mtb has raised the level of difficulty in the control of MDR-TB globally, leading to increased TB-related morbidity and mortality [12]. In 2018, the WHO reported 556,000 cases of MDR to the first-line anti-TB drugs RIF and INH, leading to 251,000 fatalities [1]. Phenotypic resistance to PZA is associated with mutations in the pncA gene, leading to the reduced or complete loss of PZase activity [13], [14], [15]. These mutations include indels and missense/nonsense mutations [16], [17], and confer varying degrees of PZA resistance in patients within different geographical locations [18]. Although mutations are distributed throughout the PZase structure, previous studies have shown that the majority of them are located in the following regions: residues 3–17, 61–85 and 132–142 [13], [19]. These positions account for 54% of all mutations conferring PZA-resistance. Proteins are dynamic entities displaying a set of diverse movements, which are greatly influenced by the inter- and intra-residue interactions. This in turn defines the overall stability, folding and functioning of enzymes in 3D space [20]. Thus, a residue substitution might drastically affect the ligand overall binding and unbinding process.

1.3. The importance of understanding the ligand unbinding events in drug discovery

Exploring the effect of mutations on the (drug) binding/unbinding processes is an essential step in deciphering the underlying molecular mechanism of drug resistance. A growing body of work suggests the importance of ligand residence times and their characterisation for assessing drug performance in silico [21], [22], [23], [24], [25], [26]. Whilst playing an important role in determining drug performance, the time-scales required to sample and observe ligand exit can vary by several orders of magnitude across protein systems, ranging from a few nanoseconds (as seen in our work) to hours [27], [28], [29]. A long retention time for instance, partly explains the effectiveness of several marketed long-acting drugs [24], [30]. Several computational approaches have thus been developed to expedite and characterise the observation of ligand unbinding events in silico, some of which are discussed below.

Hu and co-workers determined possible unbinding routes for the insecticide TMG-chitotriomycin from the target β-N-Acetyl-d-hexosaminidase, by applying steered MD to a list of CAVER 3.0-generated pathway predictions [23], [31]. By pulling the ligand along defined pathways, one can determine the directionality of unbinding [24], while also approximately determining the ease of ligand dissociation [32]. As the force bias ushers the ligand along a predefined path, the process is computationally faster, but needs to be assisted by more rigorous methods to confirm the results [32]. Tiwary et al. have used metadynamic simulations to monitor various properties around ligand unbinding, such as the effect of water and steric constraints [29], and drug association/dissociation kinetics [21], [33]. In metadynamics, the efficiency of conformational sampling rate along the free energy surface is increased by introducing a history-dependent potential term [34]. This entails the predefinition of a set of collective variables (CVs) around which repulsive Gaussians are added whenever a conformation visits that CV [29], which discourages the system from visiting previously explored energy surfaces [34]. The choice of collective variables (CVs) thus is essential for the success of these simulations. A scaled MD approach was used with replication for several modulators of the glucokinase isoform 1 – a type 2 diabetes mellitus target – to determine their residence times [26]. Scaling the potential energy function expedites conformational transition rates by weakening stabilising interactions, thus facilitating ligand dissociation [26]. While reducing the level of detail for the energy landscape, the method is computationally cheaper to compute, and benefits from the statistical significance derived from replication. Rational sampling is a recent approach proposed by Sohraby et al. where human intuition was used to selectively guide MD simulations through the desired unbinding path for the anticancer drug dasatinib from its drug target c-Src kinase by selecting certain sampled conformations and extending the MD runs, under replication [28]. Doing so avoided the need for introducing pseudo forces via modified potential functions, and also avoided the application of additional external forces into the system.

1.4. The study

Due to the diversity of mutations in Mtb PZase and their clinical significance, a comprehensive study to understand the mechanism of drug resistance is of paramount importance. Previous studies have focused on a small subset of mutations, mostly using sequenced based approaches [35] or wet laboratory-based assays [36], such as the PZA-susceptibility test [37]. The fundamental mechanism of PZA resistance is yet to be determined. Recent efforts in understanding the molecular mechanism of resistance against PZA using computational approaches focused on the mutations that destabilize the metal ion and affect PZA binding [38], [39]. PZA unbinding would be a sure determinant of decreased drug performance. However, there is no literature describing such mechanisms. Such information would provide invaluable insights to our understanding of the resistance mechanisms.

In the current study, we aimed to identify the unbinding events of PZA due to resistance mutations of Mtb PZase as well as determine if there is a common mechanism at the molecular level for the PZA release. For that, we developed a new algorithm and utilized a range of existing in silico approaches. Due to the presence of the Fe²⁺ cofactor in the MBS, forcefield parameters defining the coordination environment were calculated for use in high throughput molecular dynamics (HTMD) simulations. As there was no crystal structure data for PZA-bound PZase, docking was performed using the wild type (WT) crystal structure, which was then used to model the mutant PZA-bound complexes for each of the 82 high confidence drug resistance mutations. Statistically guided network analysis (SGNA), as proposed in our earlier study [40], [41], was used to determine the conserved movements associated with ligand exit as part of the resistance mechanism. A different dynamical behaviour between the WT complex and the mutant complexes was observed with the ligand being released from the active pocket of ~30 mutant-PZA complexes during simulations. Further analysis revealed that the lid region residues exhibited increased flexibility in the mutant complexes as compared to the WT complex. SGNA results identified two hinge residues (H51 and H71) that act like a fulcrum and are responsible for regulating the dynamics of the lid region. Residue interaction data showed a rich network of inter-residue bonding contacts between these two residues and neighbouring ones in the MBS and the catalytic pocket. Mutations affecting both the hinge and neighbouring residues around the MBS and PZA binding pocket led to the loss of the bonding contacts leading to opening of the lid and collapsing of the side flaps. Mutations within the α/β core were also found to adversely affect the stability of the domain either by a loss or gain of bonding contacts, as well as the introduction of steric clashes, which ultimately compromise protein structural integrity. The overall analysis reveals an inter residue network affected by mutations that together contribute to PZA release in resistant Mtb PZase.

2. Material and methods

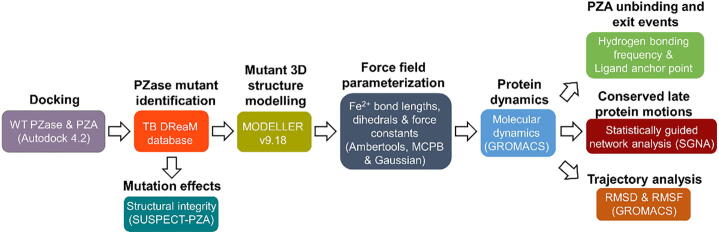
A graphical representation of the methodology applied to this study is presented in Fig. 2.

Fig. 2.

Flow diagram of methods and tools used in the identification of mutant PZase motions and associated events leading to PZA release.

2.1. Retrieval of WT Mtb PZase and identification of its high confidence mutations

The crystal structure of WT Mtb PZase (PDB ID: 3PL1) [9] was retrieved from the RCSB Protein Data Bank (PDB) [42]. From the TB Drug Resistance Mutation Database [43], a total of 87 high confidence single point mutations previously identified by genomic approaches and PZA susceptibility assays were selected (Table S1). Additional filtering was performed to exclude five nonsense mutations that would otherwise cause premature termination of protein translation; hence the final dataset had only 83 missense mutations.

2.2. Establishment of WT Mtb PZase protein-drug complex and the mutants

Due to the unavailability of 3D structural data of Mtb PZase containing co-crystallised PZA, molecular docking was performed using the WT crystal structure (3PL1) and PZA. Prior to docking, all the crystal waters were deleted with an exception of HOH220 and HOH221 as they are important in the coordination and stabilization of the Fe²⁺ found in the catalytic pocket of the enzyme. The structure of PZA was downloaded from the PubChem Database (compound ID: 1046) [44]. Using Discovery Studio (DS) [45], the 3D structure of PZA was minimized to a stable conformation. AutoDockTools (version 1.5.6) [46] was used to prepare the protein (receptor) and PZA pdbqt input files where non-polar hydrogen atoms were merged, and partial charges were assigned using the Gasteiger-Huckel method. A cubic box of 40x40x40 grid points was centered at coordinates (9.88, −26.6, 0.35) to surround the active pocket. A grid spacing of 0.375 Å was used and 100 conformational searches were performed using AutoDock4.2 with the Lamarckian genetic algorithm [47]. The maximum number of generations per run was set at 27,000 while the maximum number of energy evaluations at 450,000. The interaction energy for each pose was calculated using the semi-empirical scoring algorithm in AutoDock4.2, and the best pose was selected based on the lowest energy and the largest cluster. To generate the different PZase mutant structures, homology modelling was performed using MODELLER (version 9.18) [48] and the best docked WT PZase-PZA complex was used as template. For each mutant protein, 100 models were calculated using the slow refinement approach before ranking them in increasing order of the z-DOPE (normalised Discrete Optimized Protein Energy) score [49] to obtain the best model. The PZase-PZA interaction fingerprint for each of the 82 selected models and the WT complex were determined using DS.

2.3. Establishment of AMBER force field compatible coordination parameters for Fe²⁺

A key requirement for PZase activity is the presence of Fe²⁺ in the active pocket. In the WT, one aspartate (D49), two water molecules (H220 and H221) and three histidine (H51, H57 and H71) residues coordinate the Fe²⁺, forming an octahedral (distorted) geometry. However, the presence of the metal ion presents a challenge in the implementation of classical molecular dynamics (MD) simulations. Thus, in order to perform all-atom MD simulations, it is necessary to establish accurate force-field parameters describing the geometric interactions within the metal binding site (MBS) in both the WT and mutant systems. A few of the mutations affected the MBS coordinating residues, resulting in a different coordination environment compared to that of the WT (D49_OD2, H51_NE2, H57_NE2 and H71_NE2). Thus, additional parameters describing these unique geometries were required. Firstly, the, PZase WT and mutant apo proteins were protonated using the H++ web server [50] at pH 6.5 [51], with a salinity of 0.15 M and default dielectric values. The generated AMBER topology and coordinate (top and crd) files were used to build protonated protein structure files. In Schrödinger Maestro (version 11.8), the correct protonation states (HID) for each of the histidine coordinating residues were evaluated. Using the AMBER bonded model approach and the Metal Center Parameter Builder (MCPB) [52], Gaussian 09 com input files were generated and quantum mechanics (QM) approaches (structure optimization, force constant and the Merz-Kollman RESP charge calculations) were performed by the B3LYP/6-31G basis set [53] as described by Li and Merz [52]. All calculations were performed using 72 cores and a memory of 10,000 MB on a Linux cluster at the Center for High Performance Computing (CHPC) cluster, Cape Town South Africa. Finally, MCPB was used to calculate the geometric force field parameters (bond lengths, angles and dihedrals) between the Fe²⁺ and the coordinating residues in each system. The generated parameters were then evaluated by fitting the molecular mechanics-derived normal mode frequencies to the QM frequencies, followed by MD simulations.

2.4. High-throughput molecular dynamics (HTMD) and trajectory analysis

To evaluate the conformational changes in the different PZA-bound systems, all-atom MD simulations of 150 ns (ns) were performed using the GROMACS tool (version 2016.1) [54] utilizing the generated force field parameters. Firstly, AMBER topologies for each of the systems were generated by Leap modelling with the AMBER ff14SB force field [55] to incorporate the generated force field parameters. Using the AnteChamber Python Parser interface (ACPYPE) tool [56], the resulting topologies were converted to GROMACS-compatible input files for the structure (gro) and the topology (top), with the correct atom types and charges. Subsequently, these systems were solvated using the TIP3P water model [57] in a cubic box with a minimal padding distance of 1.0 nm between each complex system and box edges. The resulting infinite systems were neutralized by adding 0.15 M NaCl, and were subsequently relaxed using the steepest descent algorithm for energy minimization (without constraints) until a maximum force of 1000.0 kJ/mol/nm was attained. A key step in MD simulations is the equilibration phase, which ensures the solvated protein system is at the correct temperature and pressure. A two-step approach was used (each 200 ps), starting with a 300 K temperature equilibration (NVT – constant number of particles, volume, and temperature) using the Berendsen thermostat. This was followed by a pressure equilibration at 1 atm (NPT – constant number of particles, pressure and temperature) step using the Parrinello-Rahman barostat [58]. By setting a uniform temperature and pressure, the biological environment conditions necessary for the functioning of the protein are mimicked. After equilibration, all systems were subjected to 150 ns MD production runs with an integration time step of 2 fs (fs) at the equilibrated temperature and pressure. All bonds were constrained under the LINCS algorithm [59] during the equilibration and production processes. A Particle-mesh Ewald (PME) algorithm [60] with a Fourier grid spacing of 0.16 nm was used for long-range electrostatics calculations, and a 1.4 nm cut-off distance was used for the Coulomb and van der Waals interactions. Each MD simulation was run on a Linux cluster using 120 cores with ~478,080 CPU time at the CHPC. Structure coordinates were written to a file after every 10 ps. Resulting trajectories were stripped of all periodic boundary conditions (PBC) and centred prior to any analysis. Using the GROMACS tools gmx rms and gmx rmsf, the global stability and local residue fluctuations for PZA-bound systems were evaluated. The MD of each system was visualised using the Visual Molecular Dynamics program (VMD) [61]. This was also necessary to ensure that the defined force field parameters correctly described the MBS coordination geometry by maintaining Fe²⁺ in place throughout the simulations. R and Python packages were used for data analysis and plotting.

2.5. Determining unbinding events from ligand exit points

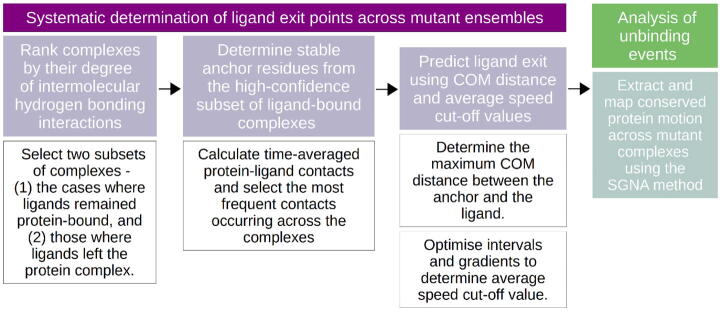
In the course of MD simulations, dissociation of PZA from the binding pocket of some mutant PZase systems was observed, prompting additional analysis to understand the ligand unbinding process. In order to extract and investigate PZA unbinding events, ligand exit points were first determined using a three-step algorithm, as explained below (Fig. 3).

Fig. 3.

Work-flow used to investigate ligand unbinding events from MD simulations.

2.5.1. Ranking of protein–ligand complexes by their hydrogen bonding propensities

The total number of strong hydrogen bonds was estimated at each time step using the gmx hbond tool from the GROMACS software (version 2019.4) with default parameters, for all the PZA-bound protein complexes. The results were then ranked in ascending order of frequency of absence of hydrogen bonding and summarized as a heat map. This resulted in a sorted array of trajectory labels, whereby top ones would most likely comprise trajectories with retained ligands while bottom ones would include complexes where the ligands would have most likely been released. After visually confirming the “retention – the ligand-bound state” and “release – ligand-unbinding state” and removing any ambiguous cases, this information was used as a reference depicting the mechanistic(s) of PZA release and retention within PZase. Ambiguous cases comprised mutant complexes where the computational prediction of ligand exit points did not reasonably correspond to the visually determined release time points (Section 3.4.3.).

2.5.2. Determination of stable anchor residues for the ligand

In order to increase our likelihood of finding a ligand exit point, the most stable ligand anchor points within the top 15 complexes with the highest hydrogen bonding frequencies were shortlisted. Protein-ligand atomic contacts were inferred using an in-house Python script that estimates atomic contacts at a maximum interatomic distance of 4 Å and averages them, using MD data as input. From the resulting analysis, any residue with atomic contact frequencies greater than 0.8 over the MD simulation were recorded for each complex before ranking the complete list in descending order to retain a consensus comprising the top six most frequent residues.

2.5.3. Combining COM and the estimated average rate of motion to predict the ligand exit time

The COM distance was subsequently calculated between the set of previously determined anchor point residues and PZA for each time point for all complexes. The maximum recorded COM distance obtained from the high frequency ligand-contacting residues (the anchor point) in the top 15 hydrogen-rich complexes was recorded as one of the criteria required to characterise ligand retention. More specifically, any subsequent distance should always be above that value, i.e. from that event until the end of a simulation for a given complex. In order to increase the likelihood of finding a most likely exit point, a gradient was estimated from the linear regression of COM distance against a set of time scales. Given the ligand masses were identical across all complexes, the estimated average speed was deemed a reasonable measure of ligand behaviour. A series of minimum gradients (0.1, 0.2, 0.3, 0.4, 0.6, 0.8 and 1.0 nm/ps) was thus evaluated against a series of time scales (50, 100, 200, 500, 600, 700, 800, 900, 1000 and 2000 ps) to visually determine an interval in which varying the minimum gradient did not result in greatly shifted time points. From this observation, a 2 ns window was extracted prior to the estimated ligand exit time point. For comparison, the final 2 ns were selected from the trajectories where the ligand was retained.

2.6. Estimating conserved protein motion using statistically guided network analysis (SGNA)

In order to identify conserved late motions associated with the release of PZA in mutant proteins, two ensembles were defined based on the observed PZA dynamics during simulations, namely the “retention – the ligand-bound state” and “release – ligand-unbinding state” events. The approach designed previously by Sheik Amamuddy [40] was then applied to the ensembles, and the result was mapped onto a WT static structure. The original code used for mapping the differential effects was updated to show arrows connecting the high degree nodes to their neighbours’ respective centroids. For larger distances, the arrowheads point in the direction of the high degree nodes, while for smaller distances they point towards the nodes’ corresponding neighbour centroids.

2.7. Determining changes in inter-residue interaction and structural integrity due to mutations

To further evaluate the effect of mutations on PZase stability and residue bonding network, all single point missense mutations exhibiting PZA release were analysed using the SUSPECT-PZA (StrUctural Susceptibility PrEdiCTion for PZA) web server [17]. The SUSPECT-PZA webserver utilises a combination of sequence and structure-based tools and machine learning approaches to predict PZase drug resistance and changes in inter-residue interaction in comparison to the WT protein. These tools include SDM (Site-Directed Mutator) [62], mCSM (mutation Cutoff Scanning Matrix) [62], SNAP2 (Screening for Non-Acceptable Polymorphisms) and PROVEAN (Protein Variation Effect Analyzer) [63]. A comparison of the predictions was made with those from the Variant Analysis Portal (VAPOR) [64] for a consensus.

3. Results and discussion

3.1. Global distribution of the selected PZA drug resistance mutations in Mtb PZase

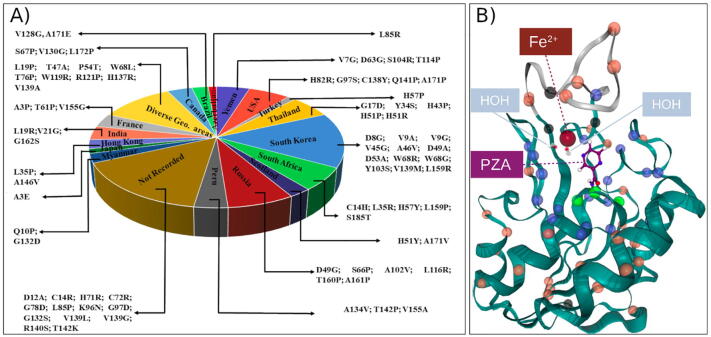
A total of 82 high confidence missense mutations were retrieved from the TB Drug Resistance Mutation Database [43]. These mutations have been identified in different geographical regions (Fig. 4A), and their effects have been rigorously studied using DNA sequencing and PZA susceptibility assays (Table S1). In this study, the mutations were separated into four groups based on the distance between the C_α atoms of each mutation and the PZA COM using the WT complex as reference (Fig. 4B and Table 1). Group 1 (green spheres) comprised all mutations within a radius of ≤6.7 Å from the ligand COM; Group 2 (blue spheres) consisted of mutations within the range 6.7 Å < X ≤ 11.0 Å; Group 3 (orange spheres) comprised all mutations whose distance were >11.0 Å. The remaining mutations coordinating the MBS formed Group 4 (black spheres). This way of grouping was designed to investigate the effect of the location of drug resistance mutations on the dynamics of PZA-bound PZase.

Fig. 4.

(A) The geographical distribution of high confidence PZA drug resistance mutations. (B) Distance-based grouping of the mutations, using the PZA COM as origin. Mutation positions are represented as spheres, where Group 1 residues (≤6.7 Å) are coloured green, Group 2 residues (6.7 Å < X ≤ 11.0 Å) are coloured orange and Group 3 residues (>11.0 Å) are in blue. Group 4 mutations that coordinate the Fe²⁺ cofactor in the MBS are in black. The Fe²⁺-coordinating water molecules (HOH220 and HOH221) are depicted as sticks. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 1.

List of Mtb PZase missense mutations for each group.

Missense Mutations
Group 1	Group 2	Group 3	Group 4
A134V, H137R, C138Y	V7G, V9A, V9G, D8G, Q10P, D12A, C14H, C14R L19P, L19R, V21G, T47A, W68G, W68L, W68R, C72R, G97D, G97S, A102V, Y103S, S104R, G132D, G132S, V139A, V139G, V139L, V139M, R140S, Q141P, T142P, T142K, A161P, G162D	A3P, A3E, G17D, Y34S, L35P, L35R, H43P V45G, A46V, D53A, P54T, T61P, D63G, S66P, S67P, T76P, G78D, H82R, L85P, L85R, K96N, T114P, L116R, W119R, R121P, V128G, V130G, A146V, V155A, V155G, L159P, L159R, T160P, A171E, A171P, A171V, L172P, S185T	D49G, D49A, H51P, H51R, H51Y, H57P, H57Y, H71R

3.2. PZA docking against WT PZase and homology modelling of mutant PZA-bound complexes

From 100 conformational searches performed in an exhaustive docking experiment, the most stable PZA conformation was selected as a representative of the PZase-PZA complex, based on the lowest binding energy (−4.48 kcal/mol) and the highest clustering percentage (83%). Key protein–ligand interactions consisted of hydrogen bonds involving residues D8, I133, A134 and C138, and van der Waals interactions with residues V7, F13, L19, D49, W68, H71, K96 and H137. In a previous crystallographic experiment performed by Petrella et al. aimed at obtaining the PZA-bound PZase complex [9], a nearly identical interaction fingerprint was obtained, with the exception of residues V7, L19 and H71, which formed hydrophobic contacts in our in silico study. Due to the lack of 3D mutant structures in PDB, the mutant PZA-bound complexes were modelled by MODELLER (v9.18) using the docked WT complex as template. Prior to modelling, the quality of the template structure was assessed and validated using the z-DOPE score, ProSA [65] and PROCHECK [66]. A z-DOPE score of −1.69 was obtained, with a ProSA z-score of −7.34 and 96.8% of the residues being in allowed regions of the Ramachandran plot, for the WT.

3.3. Derivation and validation of QM-based AMBER force field parameters describing the MBS environment in Mtb PZase

Molecular mechanical force fields are integral tools used to investigate the dynamic properties of biomolecules at an atomistic level [67], [68]. However, existing classical force fields in GROMACS simulation package lack the required parameters to accurately model the dynamic polarization effects around the Fe²⁺ MBS in PZase, leading to the complete dissociation of the metal ion cofactor during simulations. The metal ion is key for the hydrolytic activity of PZase, which is carried out through the deprotonation of coordinated water molecules, creating a nucleophile required for the acidic activation of PZA. Consequently, reliable parameters are required to ensure an intact active site and an accurate coordination geometry is maintained during simulations. We derived new force field parameters (Table 2) for both PZA unbound WT PZase, as well as for eight mutants in Group 4 (with different Fe²⁺ coordinating residues as a result of the single point mutations D49, H51, H57 and H71) using the AMBER bonded approach scheme.

Table 2.

Optimised parameters (bond lengths, force constants, charges) and geometry in WT and the eight mutant systems in Group 4. In brackets are values from the crystal structure. * values are in kcal/mol, and ** indicates parameter values from Tyr (mutation) in the MBS enviroment.

	System	WT	D49A	D49G	H51P	H51R	H51Y	H57P	H57Y	H71R
bo (Å)	D49OD2	1.96 (2.15)	–	–	1.92	1.92	1.90	1.90	1.95	1.92
	H51NE2	1.95 (2.30)	1.94	1.94	–	–	2.00**	1.90	1.96	1.95
	H57NE2	1.88 (2.32)	1.96	1.96	1.95	1.95	2.00	–	2.01**	1.95
	H71NE2	2.01 (2.23)	1.92	1.92	1.95	1.95	1.96	1.93	1.97	–
Kb *	D49OD2	70.30	–	–	138.30	138.20	129.00	132.20	110.80	136.9
	H51NE2	108.59	124.60	124.60	–	–	65.80**	129.50	91.20	114.2
	H57NE2	132.70	108.30	108.30	104.70	104.70	74.30	–	48.00**	106.4
	H71NE2	82.60	124.00	124.00	110.10	110.10	103.40	112.00	78.80	–
Charge	Fe2+	0.59 (2.00)	1.13	1.14	1.04	1.03	0.62	1.08	0.33	1.07
	D49OD2	−0.47	–	–	−0.64	−0.63	−0.52	−0.68	−0.55	−0.56
	H51NE2	0.01	−0.34	−0.35	–	–	−0.57**	−0.36	−0.04	−0.59
	H57NE2	−0.15	−0.84	−0.84	−0.54	0.10	−0.34	–	−0.57**	−0.56
	H71NE2	−0.18	−0.43	−0.43	−0.57	−049	−0.25	−0.31	−0.17	–
Geometry	MBS	Octahedral (distorted)	Square pyramidal		Square planar	Trigonal bi-pyramidal	Square planar	Square pyramidal

A 200 ns MD validation run was performed for each of these systems to evaluate the reliability and accuracy of the derived parameters. This revealed that the bonds between the coordinating residues and the metal centre remained intact throughout the simulations (Fig. 5). In each of these systems, the bond lengths between the Fe²⁺ and the coordinating atoms in each of the MBS residues were compared to those previously reported by Harding [50] and found to be in agreement. Mutations occurring in the MBS modified the coordination geometry of Fe²⁺ compared to the distorted octahedral arrangement found in the WT. The distorted geometry comprises of (1) a square pyramidal geometry involving D49A/G, H57P/Y and H71R, (2) a square planar geometry including H51P/Y; and a trigonal bi-pyramidal shape including H51R. In H51Y and H57Y, the TYR_O atom interacted with Fe²⁺. WT-derived parameters were extrapolated to the proteins bearing mutations belonging to Groups 1–3.

Fig. 5.

Parameterization of the Fe²⁺ MBS in Mtb PZase. (A) The Fe²⁺ coordination environment in the Mtb PZase crystal structure. (B) The optimised geometry of the MBS subset according to the B3LYP/6-31G level of theory, and (C) the energy potential for the geometry as visualised in gview. (D) Bond distances of Fe²⁺ coordinating residues during a 200 ns MD simulation.

3.4. Determining “ligand-unbinding - release” events

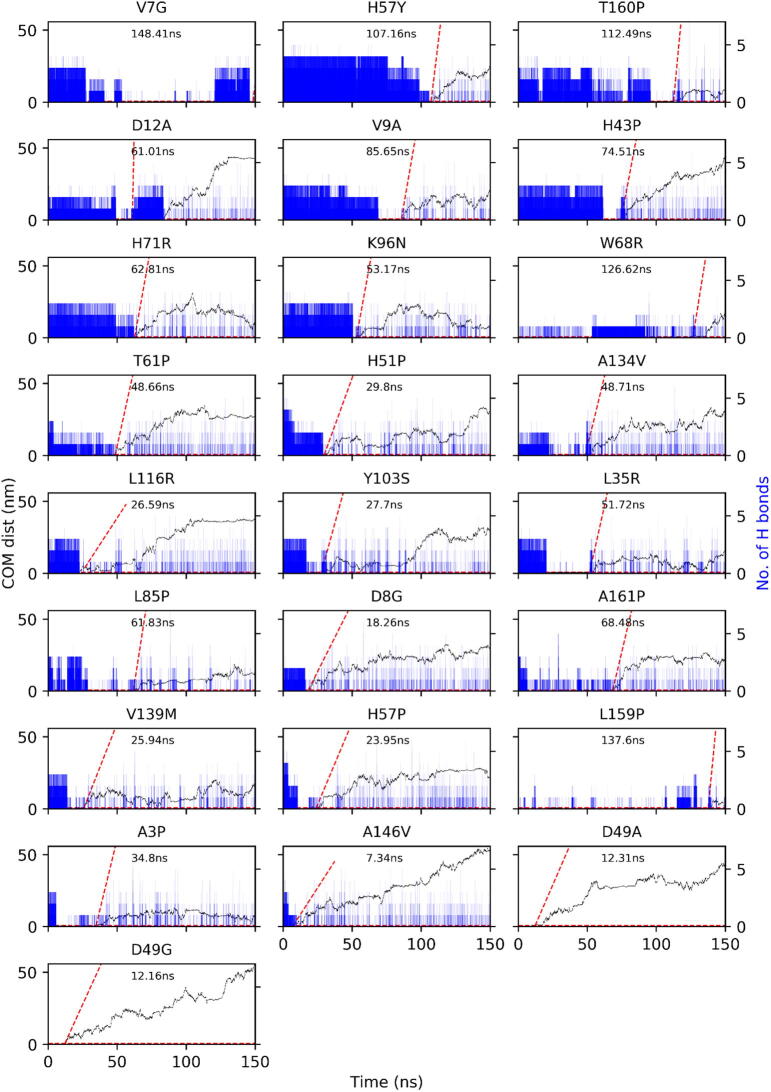
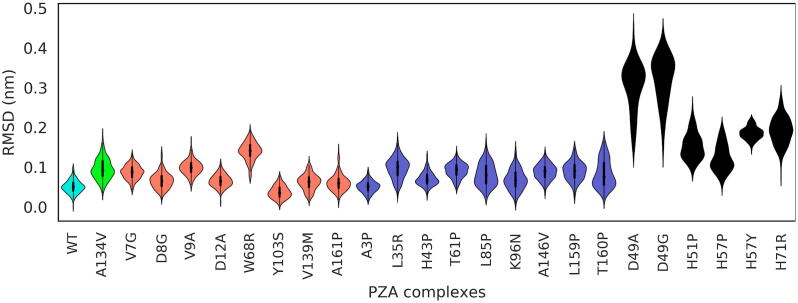
83 PZA-bound PZase complexes were MD simulated for a period of 150 ns each, totalling to about 478,080 h of CPU time. Over the course of MD, rapid dissociation of the ligand from the protein binding site was observed in some of the mutants at different time points, in the nanosecond scale (Table 3). These included the mutants A3P, D8G, V9A, D12A, L19P, L35R, D49A/G, H51P/R/Y, H57Y, T61P, W68R, H71R, G78D, L85P, K96N, L116R, A134V, V139M, Q141P, A146P, A146V and T160P. The observed dissociation times of PZA from the binding pocket ranged from 7.34 ns to 148.41 ns with a median of 51.72 ns, which prompted further analysis to explore the dynamics of the ligand unbinding mechanism(s). Understanding drug unbinding mechanisms is very important for the design of better drugs as the retention (rather than the equilibrium binding affinity) tends to be a better predictor of in vivo pharmacological action [22]. A growing body of computational studies is indeed motivating the importance of ligand residence times and the characterisation of unbinding for assessing drug performance in silico [21], [22], [23], [24], [26], [28]. These approaches generally aim to increase the conformational sampling efficiency to avoid getting stuck in local minima or to expedite the sampling of unbinding events [28], [69], [70]. A long retention time for instance, partly explains the effectiveness of several marketed long-duration drugs [24], [30].

Table 3.

Estimated exit time points for the initially PZA-bound protein complexes.

Mutant	Estimated exit time (ns)	Group	Mutant	Estimated exit time (ns)	Group
A134V (test)	48.71	1	T61P (test)	48.66	3
V7G (test)	148.41	2	L85P (reference)	61.83	3
D8G (reference)	18.26	2	K96N (test)	53.17	3
V9A (test)	85.65	2	A146V (reference)	7.34	3
D12A (test)	61.01	2	L159P (reference)	137.60	3
W68R (test)	126.62	2	T160P (test)	112.49	3
Y103S (test)	27.70	2	D49A (reference)	12.31	4
V139M (reference)	25.94	2	D49G (reference)	12.16	4
A161P (reference)	68.48	2	H51P (test)	29.80	4
A3P (reference)	33.80	3	H57P (reference)	23.95	4
L35R (test)	51.72	3	H57Y (test)	107.16	4
H43P (test)	74.51	3	H71R (test)	62.81	4
L116R (test)	26.59	3

In the case of PZA, rapid release of the prodrug from PZase would be a clear indication of a reduced efficiency of catalysis. Thus, the main aim was to find a systematic and unbiased way of determining the ligand exit time point such that analogous events would be detected across similarly behaving PZA-bound complexes. It was crucial to sample the PZase dynamics as soon as the PZA unbinding was about to happen, such that the protein would not revert to its holo state dynamics once the ligand had left. Hence, a model of estimating the ligand exit time was calculated based on the COM distance and an estimated minimum average speed, using a smaller reference subset of complexes to test our model before applying the method to the entire set of trajectories. The results for our proposed three-step algorithm are elaborated below.

3.4.1. Evaluation of hydrogen bonding frequencies for the PZase-PZA complexes

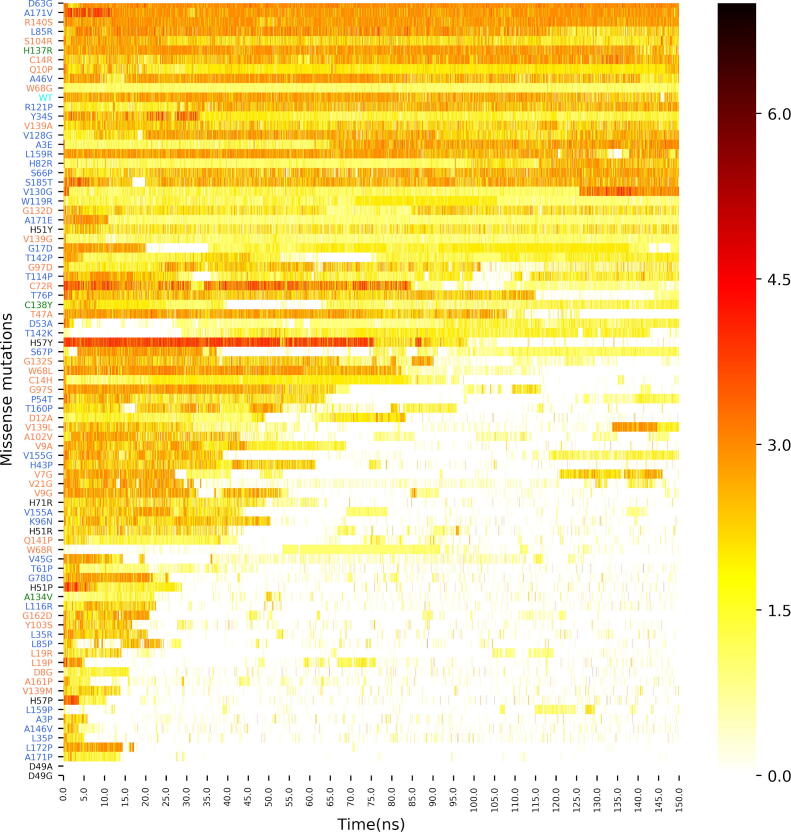
Hydrogen bonding analysis was performed as a first investigation of the exact moment of bond breakage between the PZA head region and the catalytic residue triad of the protein. As seen in Fig. 6, an initial interruption in H-bonding was not a persistent event. The protein–ligand dynamics rather resulted in transient interactions that were accompanied by partly erratic ligand motions. This was closely associated with the irregularity of H-bonding distributions. Upon closer inspection, PZA could be seen establishing H-bonds of differing number and duration with varying residues within the binding site. The mutant proteins were therefore sorted in ascending order of H-bonding absence as a way to partition the extremes of ligand behaviour, corresponding to subsets of the mutant complexes to most likely retain or release PZA, respectively. The top and bottom subsets were visualised in VMD [61] to confirm the presence of ligand retention and exit events. As seen in Fig. 6, no clear relationship could be found between the distance of the mutation and the H-bonding ability in MD.

Fig. 6.

Hydrogen bonding counts for the PZase-PZA complexes sorted according to the frequency of absence of H-bonds, obtained from MD runs. The different mutants are coloured according to their groups: Group 1 (green), Group 2 (orange), Group 3 (blue) and Group 4 (black), while the WT complex is in cyan. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.4.2. Determination of a PZA anchor point in PZase for predicting the ligand exit time

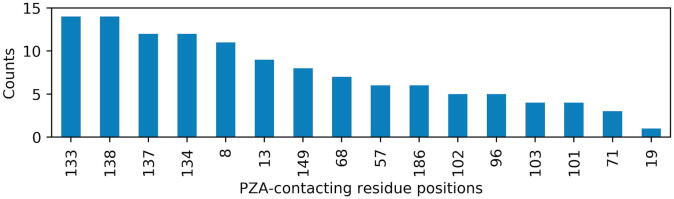
A stable PZA binding surface was subsequently determined from the MD trajectories of the ligand-bound protein complexes. An in-house Python script was written to carry out weighted atomic contact mapping between PZA atoms and those of the protein, similarly to how the contact mapping script from MD-TASK assigns the contact frequencies to the edge widths of the network graph [71]. In this case, a cut-off distance of 4 Å was used to infer inter-atomic contacts. In order to obtain the residues that were most likely involved in ligand retention, residues that had any unique contact frequency above an arbitrarily chosen cut-off value of 0.8 were selected for each complex. To obtain a consensus, the top six residue positions with the highest value counts were retained, containing the positions 133, 138, 137, 134, 8 and 13 (in descending order of frequency for unique contacts), as seen in Fig. 7.

Fig. 7.

PZA-contacting residue positions with contact frequencies ≥0.8 from the top 15 PZA-bound complexes.

Catalytic triad residue position 96 was not part of the top PZA contacting residues (being shortlisted only in 5 out of 15 cases), indicating that its role may be less important for maintaining ligand stability, in contrast to C138 and D8. More generally, a too large number of residues used as the PZA anchor point would increase the variability in the predictions and tend to overestimate ligand retention. A too low number would increase predictive bias by only considering a smaller portion of the ligand motions, thus wrongly predicting a higher number of ligand exit cases. These top residue positions were used to compute a stable anchor point COM to be used in ligand COM distance calculations in all samples. The COM metric was used instead of RMSD calculations based on earlier work, which showed the stability of COM distance towards bond rotational movements, especially for the case of long flexible compounds that may still be retained within an active site [72]. This is due to the fact that distances computed at each point in the time series between two moving COM vectors accounts for both protein and ligand motions, compared to computing the RMSD at each time step from a fixed reference frame for the ligand only. The maximum recorded COM distance for the PZA bound complexes was 7 Å, a number coincidentally very close to the commonly used residue contact distance cut-off value in dynamic residue network (DRN) calculations [71], [73], [74].

3.4.3. Designing an algorithm to estimate PZA exit times from mutant proteins

Determining an exact point of exit over a short time scale may not be a well-defined problem, mostly due to the entropic contributions coming from the ligand, the protein and the system they are surrounded in, which influence ligand dynamics. It may also depend on what an experimenter defines as the exit point, which can make a systematic detection difficult. For instance, a ligand may leave the catalytic triad but linger at the opening of the binding site before complete dissociation. From visualisations of PZA leaving its binding site, we observed numerous ways in which it PZA navigates when unstably maintained in the catalytic pocket, such as flipping in various axes of rotation, translational motions, forming transient interactions with the edge of the receptor surface, and also back-and-forth motions. It was on the basis of these factors that we chose to focus on a subset of the PZA drug resistance mechanism, a late event that was observed from MD simulations for certain PZA-resistant PZases. To do so, we visually assessed the top and bottom fifteen complexes that had been sorted according to H-bonding frequency (Fig. 6) to verify the PZA had remained or left its receptor. In order to build reference subsets, the PZase mutants L19R, L19P, L35P, A171P and L172P were removed as they were deemed ambiguous for our purposes. In these cases, PZA either stayed with poor hydrogen bonding or flipped in a manner that does not coincide with the proposed mechanism of action, i.e. with the amide group pointing away from the catalytic triad. There was no relationship between the position of the retained mutations in the two defined ensembles and ligand behaviour in terms of surface exposure, propensity towards secondary structural elements, or in the physicochemical properties of the amino acids in the two groups [74].

Once the anchor point for the PZA-bound state was defined, an approach was designed to estimate the moment of ligand exit in each of the shortlisted protein receptor complexes (Table 3 reference complexes). The previously computed maximum distance from the anchor point COM and the ligand COM (Section 3.4.2) was chosen as the minimum distance criterion for deciding on the ligand exit event. As the ligands could rotate and translate to a certain extent before coming back to the anchor point under the constraints of the binding cavity, the COM distance alone was deemed insufficient to define a moment of exit and was supplemented by the speed of movement. Due to the frequency of the partially erratic ligand motion, the instantaneous speed was deemed too variable, and we thus decided to estimate the speed as an average taken over increasing time intervals via a regression line, as specified in the methods section. We then optimised the parameters by varying the time scales and the minimum gradients, with the aim of minimising variability of our exit point predictions. As there were several optima, we chose a minimum gradient of 0.3 nm/ps for a time frame of 1 ns as our optimal parameters, as we found that our predictions tended to be more stable when the minimum gradient was not very high and the window size was not too small. A gradient that was too small tended towards non-specificity of predictions. Due to time constraints, the algorithm and scripts developed were semi-automated and applied to investigate only part of the resistance-associated mechanistic processes of PZase and will be further developed in a follow-up study catering for the earlier phase of the resistance-driven motions.

By applying our method to the entirety of the trajectories and ignoring the ambiguous cases, the following time points were obtained, as shown in Table 3. The “reference” subset consisted firstly of complexes used to calibrate the ligand release time point estimation and secondly, of the retained ligands. The “test” set consisted of the ones where the method was applied. From results in Table 3, we conclude that the radial distance (defined by the Groups) of the mutation with respect to the bound PZA does not have an effect on exit time. However, such a comparison may not be entirely correct as the atomic velocities are instantiated from random numbers selected from a Maxwell-Boltzmann distribution [54], applied at the beginning of equilibration, using initial conformations that slightly differ in each case. The graphical output for the PZA exit predictions is presented in Fig. 8.

Fig 8.

Predictions of PZA exit times from the complete MD data set, with the exception of mutations L19R, L19P, L35P, A171P and L172P. The H-bond frequencies are in blue, while the PZA COM distance to the anchor point is in black. The red dotted line points to the exit time. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

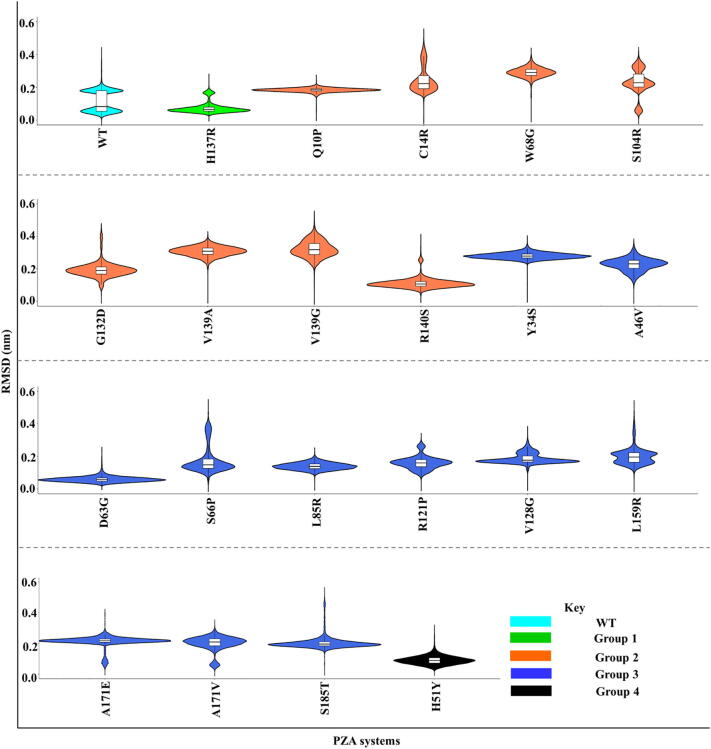
For the remainder of the HTMD dataset, PZA was predicted as being retained within the binding pocket of PZase systems. The 15 PZA-bound complexes were used as “reference” for the PZA-bound ensemble, and comprised the mutants Q10P, C14R, Y34S, A46V, D63G, W68G, L85R, S104R, R121P, V128G, H137R, V139A, R140S and A171V, in addition to the WT. The graphical output for the predictions of PZA retention is presented in Fig. S1. From the figure, it can be observed that the COM distance is generally <~6 Å and has a very low variance in each of the reference samples. For the 37 test cases (A3E, V9G, C14H, G17D, L19R, V45G, T47A, H51Y, P54T, D53A, S66P, S67P, W68L, C72R, T76P, H82R, G97D, G97S, A102V, T114P, W119R, V130G, G132D, G132S, C138Y, V139G, V139L, T142P, T142K, V155G, V155A, L159R, G162D, A171E, A171P, L172P and S185T) the variability was higher, and visibly negatively affected by the decrease in the instantaneous number of hydrogen bonds and their frequency of occurrence. During the simulations, PZA displayed various motions inside the binding cavity, leading to either ligand release or retention, as recorded in Table S2. These important characteristics influencing PZA stability within PZase were further examined to track the events preceding the drug’s release in the case of resistance to PZA.

3.5. Analysis of PZA unbinding events: the ligand/cofactor perspective

In order to have a more global picture of the events from the PZA-bound PZase, separate attention was given to each of the protein and the ligand dynamics, to search for any possibility of coupled events between the enzyme and PZA. Further, both early (up to 2 ns before ligand release) and late events (2 ns before ligand release) were examined for the ligand.

3.5.1. Early PZA unbinding events

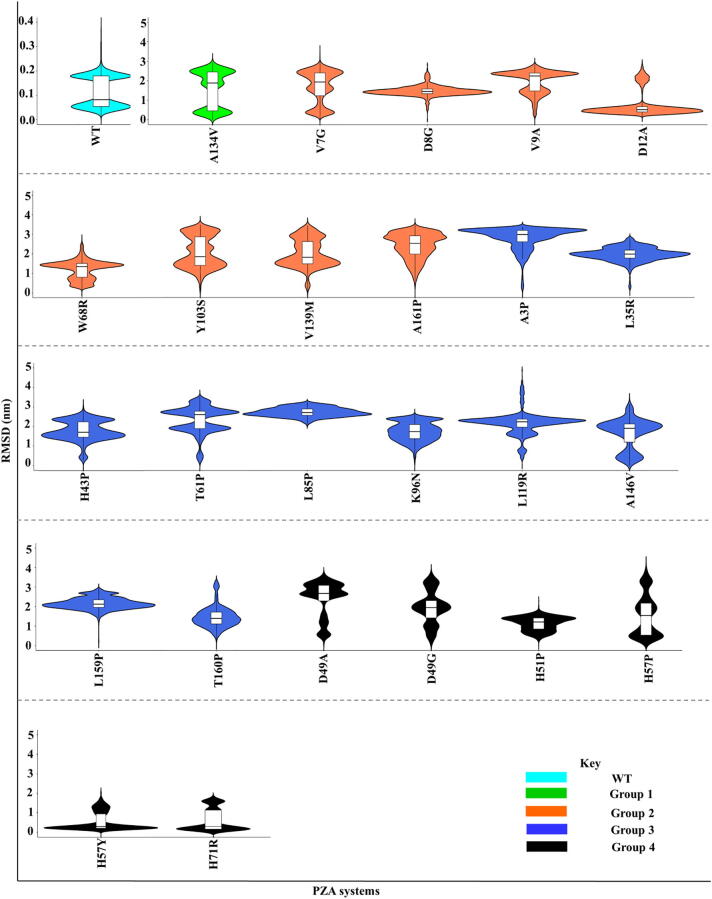
While the analysis of late protein dynamics revealed a conserved pair of motions involving the lid and one of the side flaps (Section 3.6), the systematic behaviour triggered from the early stages was analysed. Ligand RMSDs were calculated for the ligand release and ligand retention systems. Fig. 9 shows the distribution of ligand RMSD from the start of simulations until 2 ns before ligand release from PZase. In the WT protein, PZA displayed a bimodal (two peaks) RMSD distribution with modes around 0.05 and 0.20 nm. This suggests that contrary to what would be expected, the ligand adopts two conformational equilibria, instead of staying immobile, awaiting hydrolytic cleavage. It can be observed that in the WT, the pyrazine moiety (PZA head) region is anchored to the catalytic triad, resulting in more subtle oscillations. In mutant systems, where PZA release was observed at different simulation times, multimodal ligand RMSD distributions were recorded in Groups 1–4 (3rd quartile RMSD above 3.0 nm). This suggests that these mutations destabilised PZase-PZA interactions. No conserved distribution pattern was observed across the groups, suggesting a weak correlation between mutation distance and ligand dynamics. Interestingly, PZA bound to Group 2 mutants (A3P and L85P) showed a more spread out distribution with standard deviations of 0.55 nm and 0.23 nm respectively, indicative of increased mobility. However, in mutants exhibiting ligand retention, most systems displayed one or two peaks with RMSD values around 0.4 nm, an indication of ligand stability (Fig. 10). In Group 2, Q10P displayed a tighter distribution, representing a more stable equilibrium. This may be due to the anchoring of the pyrazine moiety of PZA to residues within the binding pocket. Group 3 mutant (D63G) showed a similar behaviour, indicative of stability. However, C14R showed a wider distribution coupled with a skinnier section. This observation is attributed to the linear flipping of the pyrazine moiety.

Fig. 9.

Ligand RMSD violin plots for stages of simulation until a 2 ns window before ligand release. RMSD values for the mutants are presented, including the WT as reference. Kernel density traces were plotted around the boxplots, whereby the width corresponds to frequencies of occurrence. The box plot shows the first, second and third quartile.

Fig. 10.

Violin plots showing RMSDs of ligand retention for the PZA-bound systems, in the early stages (from the beginning to 2 ns before ligand release). The width of the kernel density plot is proportional to the frequency of RMSD occurrence, while the top and bottom lines of the box plots illustrate the 3rd and 1st quartile. The middle bar shows the median (2nd quartile).

3.5.2. Late PZA unbinding events (preceding release)

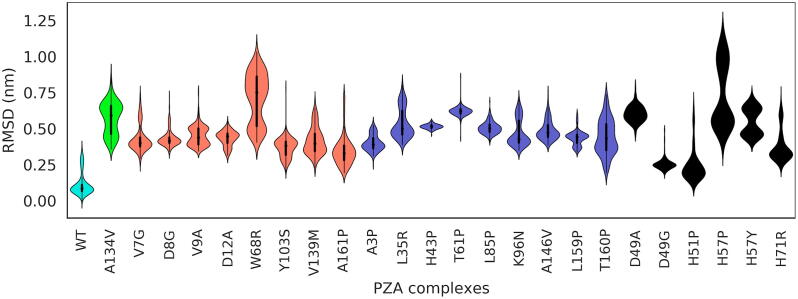
In order to examine the underlying ligand events associated with the SGNA-determined late protein motions preceding ligand release (Section 3.6), the corresponding ligand poses were compared to the analogous region from the WT trajectory. Ligand poses from the mutant PZases were analysed by superimposing the mutant proteins against the first frame from the 2 ns window for the WT before calculating the ligand RMSD, without aligning the ligands themselves. From the skewed distribution of the PZA-bound WT in Fig. 11, it can be inferred from the area under the curve that a large part of the ligand motion comprised of subtle vibrations, due to the anchoring of the PZA head to the catalytic triad, under the constraints of the binding cavity. The lowest RMSD mode for the WT PZA system is lower than those observed for all of the mutants that displayed the ligand release event. As highlighted by the flatter distribution of the higher RMSD mode in the WT PZA, the ligand seldom visits the other conformations that are otherwise more enriched in the mutants. The higher RMSD mode in the WT PZA is due to a shift in the plane of the amide moiety of PZA, whilst being anchored to the catalytic triad residues. The lack of a consistent ligand RMSD distribution pattern across the groups of mutants suggests a poor correlation between the distance of the mutation from the PZA COM and the sampled RMSD distribution for Groups 1–4. Collectively, the mutants can be seen to enrich populations of ligand conformations with generally larger distances, compared to the WT PZA equilibria. Ligands with the highest RMSD modes before drug release were observed from mutants H57P (Group 4) and W68R (Group 2), followed by A134V (Group 2). L116R was discarded from this comparison as the exact release time could not be determined with a higher degree of accuracy.

Fig. 11.

Ligand RMSD violin plots for the 2 ns window preceding ligand release (late stages) for the PZase mutants, including the WT as reference. The WT PZA complex is in cyan while the mutant ones (Groups 1–4) are coloured green, orange, blue and black. Both the reference and the test sets are included. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.5.3. Late PZA unbinding events: the cofactor (Fe²⁺) dynamics

As done for determining the late ligand unbinding events, the protein complexes were aligned to the WT protein, before computing the violin plots for the cofactor RMSD using the first frame of the WT as reference for the metal. It is clear from Fig. 12 that Group 4 mutations lead to a greater shift in the position of the metal from the catalytic triad, with mutants D49A/G showing the highest displacements with respect to those of the WT complex. This is followed by H71R and H57P from the same group. As residue 49 forms an integral part of the MBS and is thus in close proximity to both H51 and H71, its mutation is very detrimental to hinge stability, which explains the rapid PZA release for these MBS mutations. Mutant W68R displayed the highest mode for Group 2 mutants.

Fig. 12.

Fe²⁺ RMSD violin plots for the 2 ns window preceding ligand release for the PZase mutants, including the WT as reference. The WT PZA complex is in cyan while the mutant ones (Groups 1–4) are coloured green, orange, blue and black. Both the reference and the test sets are included. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

3.6. Analysis of PZA unbinding events: the protein perspective

3.6.1. Detecting conserved protein motions by constructing a statistically guided network

As a first demonstration of the application of SGNA, the approach was successfully used to determine distinct early motions from HIV-1 protease conserved across 8 FDA-approved inhibitors [40]. For the HIV drug target, these comprised a lateral expansion and a compaction stemming from the base of the drug target towards the catalytic region, preparing for drug expulsion. The requirements for the analysis are two comparable ensembles of alternating characteristics.

With the exit time points systematically defined in the case of the PZase complexes, their trajectories were visually assessed before extracting the immediate events preceding ligand release from a 2 ns window. The SGNA algorithm was then applied to the dataset to compare the PZA-bound against the PZA-unbinding event (just before the detected ligand release) to seek for conserved motions buried within the HTMD data. The main algorithm is unchanged from its original version [40], however arrows were added to the output figure (Fig. 13), as explained in the methods section, to more clearly show the overall direction of the conserved movements. While not all motions may be unidirectional or of similar magnitudes, we infer that there is a very high likelihood for an overall resultant direction. This is especially the case if each top single residue is distant to a community of neighbours (larger distances) or closer (smaller distances), via the degree centrality, as explained in [40]. In social network analysis, the degree centrality (or the connectivity) corresponds to the average number of connections an individual has, which in graph theory terms corresponds to the row (or column) sum of an adjacency matrix [75].

Fig. 13.

3D mapping of SGNA results using a WT PZase conformation as template, showing the conserved (A) lid opening and (B) flap contractions extracted from the PZA-unbinding event from PZase. Hinge residues (H51 and H71) are represented as black spheres, which connect the lid (residue positions 52–70). The arrows show the general direction of movement, inferred for each of the highest degree residues and their corresponding neighbourhood of differential residues. 3D images were generated using MDTraj and NGLView.

The SGNA algorithm capitalises on the ability to extract conserved differences within related groups of phenotypes, offering increased sensitivities by performing statistical tests on pairs of multiple averaged distance values. This makes the data more normal, before using the degree centrality to support residue pairs with the most systematically differential distances. The following hypotheses are used for the t-tests:

$${\text{H}}_0:{\text{D}}_{\text{ij},\text{PZA-unbinding}}={\text{D}}_{\text{ij},\text{PZA-bound}}$$

$${\text{H}}_{\text{A}}:{\text{D}}_{\text{ij},\text{PZA-unbinding}}>{\text{D}}_{\text{ij},\text{PZA-bound}}$$

$${\text{H}}_{\text{A}}:{\text{D}}_{\text{ij},\text{PZA-unbinding}}<{\text{D}}_{\text{ij},\text{PZA-bound}}$$

where D_ij is the collection of time-averaged distances observed for the residue pair (i, j). H₀ and H_A are the null and alternate hypotheses respectively. The subscripts “PZA-bound” and “PZA-unbinding” refer to the alternate states. The significant p-values for the one-tailed tests conducted at the default 99% confidence level were used with Bonferroni correction to construct a robust network in each alternate case.

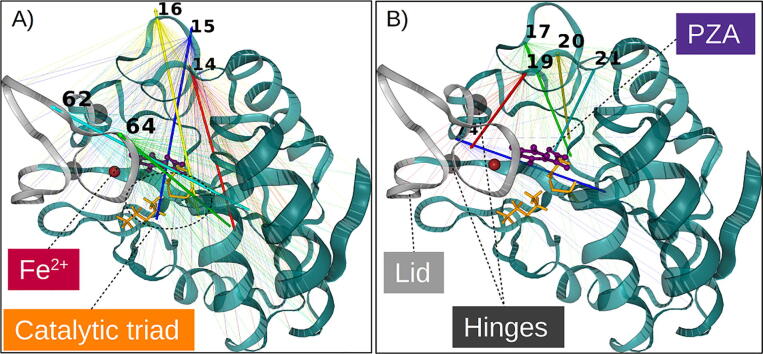
Petrella and co-workers define a lid region in the form of a loop spanning residues 52–70, which controls the closure of the binding cavity [9], as shown in Fig. 13. This lid is tethered to the protein by two residues (H51 and H71) that act as a hinge and form part of the metal ion chelators together with H57. From Fig. 13, two associated but distinct motions were observed from the HTMD simulations, comprising (1) an expansion involving the antiparallel motion of the lid (residue positions 62 and 64) and a side flap (residue positions 14–16) (Fig. 13A); (2) an associated contraction of a flanking region of the same side flap (residue positions 17,19–21), together with residue 74, towards the α/β core area (Fig. 13B). The coupled expansion event in (1) clearly depicts the preparations for the lid opening. Coupled contraction events in (2) were less expected, as a flanking region of the flap involved in expansion drives inwards to the core. From the 3D structure visualisation, the contracting flap segment (residue positions 17,19–21) and the expanding flap segment (residue positions 14–16) were found to coil over each other. They actually form a dense, hydrophobically-connected network, which may rely on the length and charge of residue 19 for lid interaction and closure. The physicochemical implications around residue 19 are discussed in Section 3.6.3. Surface residue 74, which is adjacent to the lid hinge residue 51, brings the lid base from an angled position, towards the core, and may thus be a key mediator for lid opening. In all, these suggest that the side flap dynamics around residue 19 may form part of a switch that tunes lid dynamics to allow PZA release, with assistance from the hinge base residue 74 across all PZase mutants that showed ligand release.

While giving important insights about the late events leading to the release of PZA from the PZase active site, this experiment shows once more its effectiveness at detecting conserved motions from noisy MD data, as was the case earlier with HIV-1 protease [40]. Careful data preparation according to a given experimental objective makes the technique more likely to extract relevant signals. Coincidentally, during our experimentation it was found that the SGNA predictions were consistent at extracting and showing conserved motions for the highest degree nodes, even in the presence of few wrongly labelled samples for a given ensemble, which hints at some form of robustness of the method.

3.6.2. Identifying PZase residue flexibility changes linked to the release of PZA

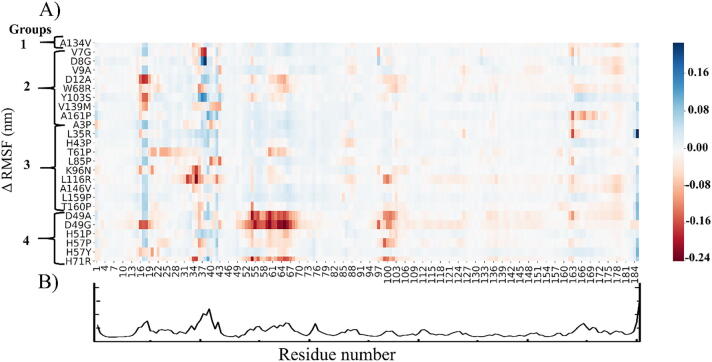
Root mean square fluctuation (RMSF) is an important dynamics metric to identify per-residue flexibility changes during MD simulations. To further characterise the events leading to PZA release, the difference in local residue flexibility fluctuations from the start of simulation to the time when the ligand exit event occurred (Table 3) were calculated by subtracting RMSF for the mutant PZA complexes from that of the WT PZA-bound system (Fig. 14). Thus, in ΔRMSF, a negative value (red) indicates increased flexibility as a result of mutation, while positive value (blue) represents more flexible regions in the WT with respect to mutant protein.

Fig. 14.

(A) A heat map showing the change in local residue fluctuations between the WT and mutants in PZA-bound systems exhibiting PZA release. Change in RMSF was calculated by subtracting the RMSF of each mutant PZA complex from the WT PZA-bound system. A negative change (red) indicates highly flexible regions as a result of mutation while positive change (blue) represents flexible regions in the WT. Heat map was plotted using the JupyterLab tool. (B) The raw RMSF values of WT PZA-bound complex. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

From Fig. 14B, residues 17–19 and 38–41 show higher flexibility in the WT PZA-bound system. These residues form part of the side flap. In comparison to the mutants, highly flexible residue positions are noted across the Groups 1–4. Several regions (16–21, 33–43, 49–72, 97–103 and 162–163) were generally flexible. These regions are located at the lid and the side flaps, an indicative of lid and flap opening causing the release of PZA. In Group 3, D12A exhibited the highest fluctuations. Additionally, RMSF of Group 2 mutations (T61P, K96N and L116R) were higher in multiple regions compared to the WT, an indication of increased flexibility in these protein segments. As expected, mutations occurring around the MBS (Group 4) showed the highest flexibility especially around the lid (residue 49–72) and side flap (residue 100–103) regions. The high flexibility observed in D49A/G could be associated with the observed rapid release of PZA during the simulation. (~12 ns).

3.6.3. Residue-residue interactions of the hydrophobic core, the MBS, binding pocket and their influence on PZA release

Maintaining the active pocket structural integrity of a protein is of crucial importance during the molecular recognition process between a biological macromolecule and their cognate ligands. This is highly determined by the residue-residue interactions within the protein. A change in the protein residue composition can drastically affect its binding pocket structural as well as its chemical features which are key in determining the affinity and specificity for a particular ligand. Thus, assessment of the residue-residue interaction changes as a result of a mutation can provide valuable insights about the ligand binding process as well as the drug resistance mechanism. From SGNA and dynamics results, several plausible links associated with the unbinding and release of PZA in several PZase mutant protein systems have been established. These included higher lid and side flap flexibility (Fig. 13) as well as additional mutation-driven changes around the PZA binding pocket that create internal stresses (interatomic clashes) that may contribute to ligand release (Table S3). These clashes were identified using the SUSPECT-PZA web server (Table S3).

Besides the identified hinge residues (H51 and H71) facilitating the lid dynamics, the interactions of the residue involved in the two distinct ligand release motions determined by SGNA [flap contraction (residues 17, 19, 20, 21 and 74) and lid opening-expansion (residues 14, 15, 16, 62, and 64)] were analysed. In the WT, residues L19 and S74 both formed strong interactions with the two hinge residues. Additionally, L19 which is located in one of the side flaps also formed a network of hydrophobic contacts with Y64, W68, and P69 lid residues. A complete loss of the bonding network between L19 and the hinge residues as well as the lid residues was observed with the introduction of a mutation in position 19 (L19/P/R) which may explain the observed inward movement of the side flap. The observed inward movement of S74 and associated outward movement by P62 and Y64 may be an integral requirement for the lid opening and release of PZA.

An intricate bonding network composed mainly of polar, hydrogen, and aromatic interactions was observed around both the MBS (D49, H51, H51 and H71) and binding pocket residues (V7, D8, F13, L19, D49, W68, K96, I133, A134 and C138) of the WT. However, residue changes in any of these positions led to the disruption of the bonding network either through a loss of bonding contacts or by the introduction of steric clashes with other neighbouring residues possibly causing a destabilization effect of the binding pocket. Introduction of a mutation in the catalytic triad residues (D8 and/or K96) resulted in loss of polar contacts formed with D49 and either of them. Investigations of the possible consequences of these mutations (D8 and K96) using the SUSPECT-PZA web server indicated both to cause damaging effects. In the WT, the MBS residues formed a rich contact network with each other, as well as with residues forming the lid (residues 54–74) and side flaps (residues S18, L19 and G97). This is a probable indication that these are an integral functional unit regulating ligand access to or exit from the binding site. In addition, each of the histidine residues in the MBS region forms aromatic interactions with each other as well as with F58 and F68 which are both in the lid loop. However, mutations affecting the MBS residues led to a significant loss of interaction in the bonding network, possibly leading to the opening of the lid and exit of the ligand (Table S3). In the WT, D49 forms a bonding interaction of polar contacts with catalytic triad residues D8 and K96, as well as with the hinge residues. From the interaction results, D49 mutations were found to lead to a loss of the Fe²⁺ coordinating interactions through reduced polar interactions and hydrophobic contacts" (Table S3). The loss of the bonding network around the MBS may explain the metal cofactor delocalization seen in Group 4 mutations (Fig. 12). In the WT system, the lid region and one of the side flaps are stabilised by hydrophobic interactions between W68 and L19, and a substitution of the tryptophan with a polar residue leads to a loss of the interaction besides those established with H57 and other lid residues. Interestingly, in W68R, a similar delocalization of the Fe²⁺ is also observed mainly due to the disrupted interaction with H57 MBS residue. In Group 3 mutations (mainly located in the α/β core domain), no interactions were detected between the mutation and the active site residue (including the lid, side flaps and MBS). This may hint to the existence of additional mechanisms through which ligand exit is triggered. However, an altered interaction network (Table S3), as well as steric clashes were observed in these mutants, which may compromise protein integrity, thus leading to the ultimate release of the ligand.

4. Conclusion

TB drug resistance remains a serious global problem and a major obstacle towards the proposed WHO and the United Nations commitment to achieve a TB-free world by 2035 [68], [69]. PZA is the only first-line anti-tubercular drug possessing bactericidal effects against latent Mtb, and as such can shorten the TB treatment period to six months. However, its effectiveness has lately been reduced due to the development of numerous drug resistance mutations in its target enzyme PZase. The exact molecular mechanism of PZA resistance is still incompletely understood, and an improved knowledge of the drug resistance mechanism in PZase is vital for the development of more efficacious anti-tubercular agents. To do so, a range of in silico tools was used to determine conserved dynamics associated with PZA release in Mtb PZase mutants.

The limited literature on structure-based computational studies involving Mtb PZases is mainly due to the unavailability of a 3D PZase-PZA complex. Herein, molecular docking and homology modelling techniques were successfully applied to establish native-like protein–ligand complexes, highlighting the importance of computer-aided drug discovery. Due to the importance of the metal ion cofactor for PZase, a highly accurate description of the coordination geometry was developed using QM for use in MD with the AMBER force field for 82 PZA-bound mutants and the PZA-bound WT. Mutations affecting the MBS were found to drastically alter the inherent octahedral coordination geometry of Fe²⁺ found in the WT. Analysis of MD simulations revealed the unbinding of PZA in some mutants, which were then investigated from the protein, ligand and metal perspectives. An algorithm was designed to systematically determine ligand exit times to compare late PZA unbinding events against the PZA-bound states. The exit times varied widely in the nanosecond range. Using this information, the SGNA algorithm was applied to characterise late PZA-unbinding events derived from ensembles of PZA unbinding and PZA- bound trajectory segments. This revealed coupled expansions (involving the antiparallel motion of the lid and one side flap) and contractions (contraction of a flanking region of the same side flap, together with residue 74, towards the α/β core) happening in PZA unbinding. The flap residues formed a dense network of hydrophobic contacts, which may rely on the length and charge of residue 19 for lid interaction and closure. Destabilisation of the hinge residues (or nearby residues) facilitated lid opening and PZA release from the active site. RMSF showed increased fluctuations of the lid and the other flap (position 100–103) during early stages. From the ligand perspective, in the early stages, generally higher modes and differing distributions of RMSD values were found, hinting at larger ligand conformational changes and multiple unbinding dynamics. Later events showed a generally higher range of ligand RMSD values preceding ligand release from mutants, compared to the WT complex. The Fe²⁺ cofactor was generally destabilised in the Group 4 mutants. The SUSPECT-PZA server identified residue-residue interactions that were linked to the PZA unbinding dynamics that were characterised in detail through dynamics analysis and SGNA. Although our molecular mechanics-based approaches were able to describe the PZA unbinding events for a subset of resistant PZases, additional methods such as QM simulations, protein–protein interactions and longer simulation times may be explored to obtain a better description of atomistic behaviour that may be occurring in drug resistant mutants where PZA remained stably bound.

These findings provide valuable insights which may be used for the development of newer anti-tubercular agents with improved activities. Compared to the existing tools which aim at increasing the probability of sampling ligand dissociation events, our work-flow focuses on the systematic identification of the ligand exit time points. Coupled to SGNA, this approach revealed robust and sensitive to extract conserved protein motions within the chaotic protein dynamics across collections of alternate states. As a way to explore further details of PZA drug resistance, follow-up studies will be done to improve the algorithm efficiencies and study other facets of drug resistance in PZase. The approaches and algorithms used here can be applicable to any other similar scientific problems.

Conflicts of interest

The authors declare no competing financial interests.

Appendix A. Supplementary data

The following are the Supplementary data to this article: