Generalized Z-numbers with hesitant fuzzy linguistic information and its application to medicine selection for the patients with mild symptoms of the COVID-19

Highlights

• •We extend the Z-number to a generalized form based on hesitant fuzzy linguistic term sets.
• •The identification framework in the Dempster-Shafer (DS) theory is used to describe generalized Z-numbers.
• •Z-numbers is used to derive the basic probability assignment of evidence.
• •The synthetic rules in the DS theory are used to integrate evaluations.
• •A case of medicine selection for the patients with mild symptoms of the COVID-19 is provided.

Abstract

Fuzzy set theory and a series of theories derived from it have been widely used to deal with uncertain phenomena in multi-criterion decision-making problems. However, few methods except the Z-number considered the reliability of information. In this paper, we propose a multi-criterion decision-making method based on the Dempster-Shafer (DS) theory and generalized Z-numbers. To do so, inspired by the concept of hesitant fuzzy linguistic term set, we extend the Z-number to a generalized form which is more in line with human expression habits. Afterwards, we make a bridge between the knowledge of Z-numbers and the DS evidence theory to integrate Z-valuations. The identification framework in the DS theory is used to describe the generalized Z-numbers to avoid ambiguity. Then, the knowledge of Z-numbers is used to derive the basic probability assignment of evidence and the synthetic rules in the DS theory are used to integrate evaluations. An illustrative example of medicine selection for the patients with mild symptoms of the COVID-19 is provided to show the effectiveness of the proposed method.

1. Introduction

For each decision-making problem, there is more or less uncertainty including hesitation, incompleteness or imprecision. These uncertainties are hard to depict by crisp numbers. Initially, Zadeh (1965) proposed the fuzzy set theory to deal with uncertain problems. Later, scholars put forward the concepts of intuitionistic fuzzy sets, hesitant fuzzy sets, probabilistic linguistic term sets and their extended forms to deal with uncertain problems (Liao, Xu, Herrera-Viedma, & Herrera, 2018). However, none of these methods except the Z-number (Zadeh, 2011) can reflect the reliability of information. A Z-number is an order pair of fuzzy numbers $(A,B)$, where $A$ represents the fuzzy restriction of information and $B$ represents the probability measure of the reliability of $A$. Since Zadeh put forward the concept of Z-numbers, there has been an endless stream of research on Z-numbers. For example, Aliev and Alizadeh (2015) combined possibilistic and probabilistic distributions to propose a calculation model of discrete Z-numbers. After that, Aliev and Huseynov (2016) continued the discrete Z-numbers on the basis of discrete Z-numbers, and proposed the arithmetic operations of continuous Z-numbers. Li and Deng (2020) proposed a new uncertainty measure of Z-numbers by estimating the potential probability distribution with a maximum entropy method. Yaakob and Gegov (2016) extended the TOPSIS approach to deal with group decision making problems with Z-numbers. Wang and Cao (2017) calculated the score and accuracy functions of linguistic Z-numbers based on a distance measure and then ranked Z-numbers with an extended TODIM method. Shen and Wang (2018) proposed a distance measure considering the randomness and fuzziness of Z-numbers and then improved the classical VIKOR method.

In traditional Z-numbers, the restriction $A$ and reliability $B$ are expressed as single linguistic terms, for instance, “the air quality is good, very certain”. To represent human cognition more flexible, in this study, we use the hesitant fuzzy linguistic term sets (HFLTSs) (Liao et al., 2015, Rodríguez et al., 2012) rather than single linguistic terms to describe the restriction $A$ and reliability $B$ of a Z-number and call this extended form as a generalized Z-number. For example, “the air quality is good or above, not very certain”. In this case, if there are three degrees of certainty such as “generally certain”, “certain”, “very certain”, then “not very certain” means “certain” or “generally certain”. Compared with the classical Z-number, the description of the generalized Z-number is not only more consistent with human cognition, but also more able to reflect the uncertainty in decision-making problems.

For a Z-number, implicitly, we have $Z=(A,u_A\left(x\right)·p_{X}isB)$, where $u_A\left(x\right)$ represents the membership function of $A$ and $p_X$ represents the probability distribution function of $A$ (Zadeh, 2011). In this sense, when we get the evaluation information $Z=(A,B)$, we can obtain the probability distribution of $A$ if the membership function of $A$ is given according to the expert preferences. But, in practice, the membership functions associated with an HFLTS are not easy to determine and the process of integrating HFLTSs is complicated. The most common method to integrate classical Z-numbers is to convert Z-numbers into classical fuzzy numbers, and then use the aggregation method of fuzzy numbers to make decisions. With the arithmetic operations of Z-numbers, Kang (2012) proposed a new multi-criterion decision-making (MCDM) method in which the restriction $A$ and reliability $B$ are combined according to the canonical representation of multiplication operation of triangular fuzzy numbers. Later, Kang, 2020, Kang, 2018) applied Z-numbers to the environmental assessment under uncertainty and the stable strategies analysis in evolutionary games; Aboutorab, Saberi, and Rajabi (2018) extended the Z-numbers to the best-worst method and its application in supplier development; Peng and Wang (2018) developed an outranking method in which the cognitive information was represented by Z-numbers. In a Z-number, a connection is established between the restriction and reliability through the membership function and probability distribution function. However, since the restriction $A$ and reliability $B$ are two different concepts, direct converting Z-numbers to classical fuzzy numbers may result in distortion and loss of the original information.

Considering these challenges, in this paper, we use the Dempster-Shafer (DS) theory to integrate the generalized Z-numbers. Not only is the DS theory a powerful tool for integrating uncertain information, but the identification framework in the DS theory also provides appropriate technique for constructing the generalized Z-numbers. Since the elements in the identification framework are exhaustive and mutually exclusive, when we give the evaluation information of Z-numbers, it is convenient and easy to explain whether it is restriction $A$ or reliability $B$. In addition, after generalizing Z-numbers with HFLTSs, both the restriction $A$ and reliability $B$ may be expressed as a collection of linguistic terms. In this regard, we substitute the membership function with the utility function in the DS theory and generalize the probability distribution to the basic probability assignment (BPA). In other words, in this paper, $u_A\left(x\right)$ represents the utility function of $A$ and $p_X$ represents the BPA function of $A$. Then we can integrate the evaluation according to the synthesis rules of the DS theory.

To sum up, the study dedicates to achieving the following innovative contributions:

• (1)The elements of Z-numbers are generalized from classical fuzzy numbers or linguistic terms to HFLTSs and the generalized Z-number is introduced. In this way, we can enrich the representation form for uncertain information.
• (2)The identification framework in the DS theory is used to describe the generalized Z-numbers to avoid ambiguity.
• (3)The knowledge of Z-numbers is used to derive the BPA of evidence, and the synthetic rules of the DS theory are used to integrate Z-numbers.

Since the beginning of 2020, novel coronavirus outbreaks have occurred in various parts of the world. Although the state and government have invested a lot of money and time in the treatment of novel coronavirus, there is still no recognized effective medicine available for public use. In this paper, a case study concerning the medicine selection for coronavirus patients is given to validate the information fusion method with generalized Z-numbers.

The paper is organized as follows: The basic concepts are reviewed in Section 2. Then, how to generate the BPA of evidence is discussed in Section 3. A multi-criterion decision-making method based on the DS theory and generalized Z-numbers is proposed in Section 4. In Section 5, an illustrative example of the medicine selection for coronavirus patients is provided to show the effectiveness of the proposed method. The paper ends with concluding remarks in Section 6.

2. Preliminaries

In this section, some concepts involved are introduced.

2.1. Hesitant fuzzy linguistic term set

To express uncertain evaluation information, Zadeh (1965) proposed the fuzzy set theory. Since there is not only fuzzy uncertainty but also hesitation uncertainty in human cognition, Rodríguez et al. (2012) proposed the HFLTS to represent the hesitancy of experts with a set of possible linguistic terms. Later, Liao et al. (2015) mathematically redefined the HFLTS and introduced the hesitant fuzzy linguistic elements. The HFLTS is effective to describe both simple and complex linguistic evaluations. Therefore, it has aroused great interest of many scholars (Liao et al., 2018) and many studies on HFTLSs have been developed, such as the distance and similarity measures (Liao, Xu, & Zeng, 2014), correlation measures (Liao, Gou, & Xu, 2020), score function (Liao et al., 2019) and aggregation in group decision making (Rodríguez, Martínez, & Herrera, 2013).

Definition 1 (Liao et al., 2015, Rodríguez et al., 2012) —

Let $S$ be a linguistic term set. An HFLTS $H_S=\{<x,h_S\left(x\right)>|x\in X\}$ is an ordered finite subset of the consecutive linguistic terms of $S$, where

$$h_S\left(x\right)=\left\{s_{{\varphi }_l}\left(x\right)\right|s_{{\varphi }_l}\left(x\right)\in S,{\varphi }_l\in \{-\tau ,\cdots ,0,\cdots ,\tau \},l=1,2,\cdots ,L\left(x\right)\}$$

$L\left(x\right)$ is the number of elements in $h_S\left(x\right)$ and $s_{{\varphi }_l}\left(x\right)$ is the continuous terms in $S$. $h_S\left(x\right)$ is a hesitant fuzzy linguistic element which indicates a set of possible degrees of the linguistic variable to $S$.

For human expression to be highly consistent with hesitant fuzzy linguistic elements, (Rodríguez et al., 2012) proposed a translation function $E_{G_H}$, which can handle most types of linguistic expressions, shown as:

• (1) $E_{\mathit{GH}}\left(s_t\right)=\left\{s_t\right|s_t\in S\}$;
• (2) $E_{\mathit{GH}}\left(atmost{s}_i\right)=\left\{s_t\right|s_t\in Sand{s}_t⩽s_i\}$;
• (3) $E_{\mathit{GH}}\left(lessthan{s}_i\right)=\left\{s_t\right|s_t\in Sand{s}_t<s_i\}$;
• (4) $E_{\mathit{GH}}\left(atleast{s}_i\right)=\left\{s_t\right|s_t\in Sand{s}_t⩾s_i\}$;
• (5) $E_{\mathit{GH}}\left(morethan{s}_i\right)=\left\{s_t\right|s_t\in Sand{s}_t>s_i\}$;
• (6) $E_{\mathit{GH}}\left(between{s}_{i}and{s}_j\right)=\left\{s_t\right|s_t\in Sand{s}_i⩽s_t⩽s_j\}$.

2.2. Z-number

A Z-number (Zadeh, 2011) is an ordered pair composed of two fuzzy numbers expressed as $Z=(A,B)$. The first component, $A$, represents a constraint on the value of an uncertain variable $X_A$. The second component, $B$, represents the probability measure of the reliability of the first component, $A$. In particular, if the variable $X_A$ is a random variable for $A$, a further definition of a Z-number can be denoted as (Zadeh, 2011):

$$Z=(A,B)=Z^{+}(A,u_A\left(x\right)·p_{X}isB)$$

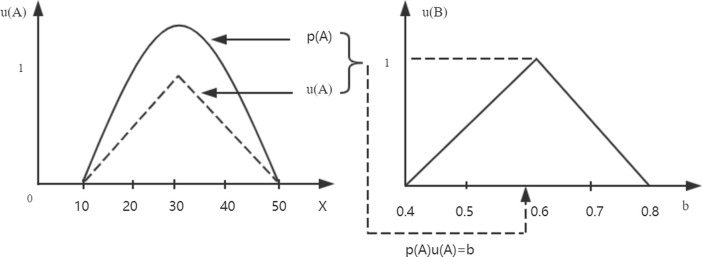
where $u_A\left(x\right)$ represents the membership function of the fuzzy set $A$ and $p_X$ represents the probability distribution function of the random variable $X_A$ to the fuzzy set $A$. $x\in X_A\subset R$ and $R$ is the real value domain. The membership function of the fuzzy set $B$ is denoted as $u_B\left(x\right)$, $x\in X_B\subset R$. In addition, $u_A\left(x\right)·p_X$ is $B$ and thus the membership degree of the Z-number $(A,B)$ is $u_B(\int u_A\left(x\right)·p_{X}dx)$. A simple Z-number is shown as Fig. 1 .

Fig. 1.

Demonstration of a simple Z-number.

Due to the richness of information contained in Z-numbers, a large number of studies on Z-numbers have been carried out. Shen and Wang (Shen & Wang, 2018) proposed the Z-VIKOR method based on the distance measure of Z-numbers for selecting regional circular economy development plan. Kang (2020) applied Z‑numbers to environmental assessment problem based on the DS evidence theory under uncertainty. Aboutorab et al. (2018) proposed an integration of Z-numbers with the best-worst method and applied it to supplier development. Peng and Wang (2018) proposed an outranking decision-making method with Z-numbers combining ELECTRE III and QUALIFLEX for job-satisfaction evaluation. Yang and Wang (2018) combined the stochastic multi-criteria acceptability analysis (SMAA) with Z-numbers to deal with decision-aiding problems. To generate Z-numbers, Kang, Deng, and Hewage (2018) used the maximum entropy based on the ordered weight averaging (OWA) operator inspired by Yager (1988). Liu, Tian, and Kang (2019) derive knowledge of Z-numbers from the perspective of DS evidence theory. Liu et al. (2019) used the DS evidence theory and fuzzy set theory to get Z-numbers. In this study, contrary to Liu et al.’s ideas, we generate the BPA of evidence from the knowledge of the generalized Z-numbers with HFLTS.

2.3. The Dempster-Shafer theory

The DS theory, also called the DS evidence theory, was first proposed by Dempster (1967) and then developed by Shafer (1976) to handle uncertain information. It promotes the traditional Bayes reasoning approach by allowing weaker conditions than the traditional Bayes reasoning approach. The DS evidence theory has been widely used in various fields. Yang and Xu (2013) proposed the evidential reasoning rule to deal with MCDM problems. Chen and Deng (2018) combined the AHP and DS evidence theory to evaluate sustainable transport solutions. Jiroušek and Shenoy (2018) introduced a new entropy of belief functions in the DS theory to measure the total uncertainty of BPA. Zhang and Deng (2018) and Dong, Zhang, and Li (2019) used the DS evidence theory to analysis fault diagnosis problems in uncertain environment. Yuan and Luo (2019) proposed a novel intuitionistic fuzzy entropy to determine the weights of evidence. Fang and Liao (2020) proposed a generalized probabilistic linguistic evidential reasoning approach considering to reassign the remaining belief degree to an envelopment of focal elements. Fu and Chang (2020) proposed a group satisfaction concept to analysis multiple criteria group decision making problems with evidential reasoning approach. Ng and Law (2020) used the evidential reasoning to analysis sentiment words in social networks to investigate consumer preferences.

Let $\mathrm{\Omega }=\{H_1,H_2,\cdots H_n\}$ be a set of mutually exclusive and collectively exhaustive events. We call the set $\mathrm{\Omega }$ a frame of discernment and denote $P\left(\mathrm{\Omega }\right)$ as the power set composed of $2^n$ elements of $\mathrm{\Omega }$, that is $P\left(\mathrm{\Omega }\right)=\{\mathrm{\varnothing },\left\{H_1\right\},\left\{H_2\right\},\cdots ,\left\{H_n\right\},\{H_1\cup H_2\},\{H_1\cup H_3\},\cdots ,\mathrm{\Omega }\}$. For a frame of discernment $\mathrm{\Omega }=\{H_1,H_2,\cdots H_n\}$, the mass function $m(·)$ is a mapping from $2^{\mathrm{\Omega }}$ to the number between 0 and 1. $m(·)$ satisfies the following conditions:

$$m\left(\mathrm{\varnothing }\right)=0\text{and}\sum _{A\in 2^{\mathrm{\Omega }}}m\left(A\right)=1$$ (1)

The elements of $P\left(\mathrm{\Omega }\right)$ or the subset of $\mathrm{\Omega }$ are called propositions. In other words, if $A\in$ $P\left(\mathrm{\Omega }\right)$, then, $A$ is a proposition. The mass function is also called the BPA or belief function, which represents how strongly the evidence supports $A$. If $m\left(A\right)>0$, then, $A$ is called a focal element.

In the DS theory, for two evidences $m_1$ and $m_2$, the synthesis rule is denoted as $m=m_1\oplus m_2$ with Dempster’s rule of combination defined as:

$$m\left(A\right)=\left\{\begin{array}{c}\frac{1}{1-K}\sum _{B\cap C=A}{m}_1\left(B\right)m_2\left(C\right),A\ne \mathrm{\varnothing }\\ 0,A\ne \mathrm{\varnothing }\end{array}\right\}$$ (2)

with

$$K=\sum _{B\cap C=\mathrm{\varnothing }}{m}_1\left(B\right)m_2\left(C\right)$$ (3)

To avoid the conflict between evidences, a discount coefficient could be introduced. A discounting coefficient $\beta \in \left[0,1\right]$ represents the weight (reliability) of the evidence. Then, the updated evidence $m_{\beta }$ is represented as follow:

$$m_{\beta }\left(A\right)=\beta m\left(A\right),\forall A\in \mathrm{\Omega }andA\ne \mathrm{\Omega }$$ (4)

$$m_{\beta }\left(\mathrm{\Omega }\right)=\beta m\left(\mathrm{\Omega }\right)+(1-\beta )$$ (5)

In Eq. (5), $m_{\beta }\left(\mathrm{\Omega }\right)$ can be divided into two parts ${\tilde{m}}_{\beta }\left(\mathrm{\Omega }\right)=\beta m\left(\mathrm{\Omega }\right)$ and ${\overline{m}}_{\beta }\left(\mathrm{\Omega }\right)=1-\beta$. Then, the belief degree of a focal element can be gained by:

$$p\left(A\right)=m_{\beta }\left(A\right)/1-{\overline{m}}_{\beta }\left(\mathrm{\Omega }\right)$$ (6)

$$p\left(\mathrm{\Omega }\right)={\tilde{m}}_{\beta }\left(\mathrm{\Omega }\right)/1-{\overline{m}}_{\beta }\left(\mathrm{\Omega }\right)$$ (7)

According to the utility theory (Yang & Xu, 2013), we can get the upper and lower bounds of the utility of alternative $x_i$, and then rank the alternatives:

$$\begin{array}{c}u{\left(x_i\right)}_{max}={\sum }_{n=1}^{N}u\left(H_n\right)p_n\left(x_i\right)+u\left(H_N\right)p_{\mathrm{\Omega }}\left(x_i\right)\\ u{\left(x_i\right)}_{min}={\sum }_{n=1}^{N}u\left(H_n\right)p_n\left(x_i\right)+u\left(H_1\right)p_{\mathrm{\Omega }}\left(x_i\right)\end{array}$$ (8)

$$u{\left(x_i\right)}_{min}={\sum }_{n=1}^{N}u\left(H_n\right)p_n\left(x_i\right)+u\left(H_1\right)p_{\mathrm{\Omega }}\left(x_i\right)$$ (9)

$$u\left(x_i\right)=\left(u{\left(x_i\right)}_{max}+u{\left(x_i\right)}_{min}\right)/2$$ (10)

3. Generate basic probability assignment based on the knowledge of Z-numbers

In a classical Z-number $Z=(A,B)$, the constraint $A$ and reliability $B$ are represented by single linguistic terms. When the constraint $A$ and reliability $B$ become complicated and are expressed in more than one linguistic term, we can use HFLTSs to represent the hesitancy information of experts. To make the meaning of the expression unambiguous, we use the identification framework of the DS theory to represent the constraint $A$ and reliability $B$ in Z-numbers. There are two problems to be solved. The evaluation grades in the identification framework are indeed not independent. In this regard, we introduce the Shapley value to assign a reasonable utility value to each evaluation grade. Additionally, it is also an important problem to translate the evaluations of reliability given by experts into crisp values. To this point, the score function of HFLTSs can be used to handle this problem.

3.1. Determine the utility values of non-independent evaluation grades

A fuzzy measure $\mu$ is a set function on the set of $H=\{H_1,H_2,\cdots ,H_n\}$: $2^n\to [0,1]$, satisfying the follow conditions: 1) $\mu \left(\mathrm{\varnothing }\right)=0,\mu \left(H\right)=1$; 2) $A\subseteq B$ implies $\mu \left(A\right)⩽\mu \left(B\right)$, for all $A,B\subseteq H$ (Shapley & Shubik, 1953). $\mu \left(\left\{H_j\right\}\right)$ represents the weight or utility of the element $H_j$. If the elements in $H$ are independent, then, $\mu \left(B\right)=\sum _{h_j\in B}\mu \left(\left\{H_j\right\}\right)$, for all $B\subseteq H$.

In fact, the elements in the set $H$ are usually not independent. To determine the expected marginal contribution of a particular element to the set $H$, the Shapley value can be introduced. The Shapley index for each $j\in H$ is defined as (Shapley & Shubik, 1953):

$$\varphi \left(H_j\right)=\sum _{K\subset H\backslash H_j}\frac{(n-\left|K\right|-1)!\left|K\right|!}{n!}\left[\mu \left(K\cup \left\{H_j\right\}-\mu \left(K\right)\right)\right],(j=1,2,\cdots ,n)$$ (11)

The Shapley value ${\varphi }_j$ can be interpreted as a kind of average value of marginal contribution of a single element in all possible coalitions. In the DS theory, the elements of identification framework are mutually exclusive and exhaustive but not necessarily independent. In Yang and Xu (2013)’s evidential reasoning approach, all evaluation grades are considered to be independent. This is not realistic. For example, “good” and “very good” are actually not independent. Suppose that the utility of “good” is 0.25 and the utility of “very good” is 0.5, according to Yang and Xu (2013)’s approach, the utility of “at least good” is equal to 0.75. However, if the decision-maker has a certain preference, the result will be greater than or less than 0.75. The Shapley value can be used to handle this problem well when evaluation grades are considered to be non-independent. In fact, the Choquet integral is a more widely used tool for the non-additive fuzzy measure. However, the Choquet integral is usually used to solve the interactions of weighted criteria, and this study is intended to analyze the effectiveness of non-mutually exclusive evaluation levels. So, the Shapley value may not be a better approach but it may be a more appropriate way to do it.

3.2. Quantify reliability and determine the discount coefficient

Although experts give the evaluation of reliability $B$, it is not easy to quantify especially if it is expressed in more than one linguistic term. Gou and Xu (2016) proposed two transformation functions to explain the meanings of hesitant fuzzy linguistic term sets. Further, Liao et al. (2019) proposed a score function of HFLTS based on the hesitancy degree and linguistic scale function. This score function mainly considers the positions of linguistic terms and the number of linguistic terms. It can be used to measure the reliability $B$ expressed by HFLTS reasonably.

Definition 2 Liao et al., 2019 —

Let $S=\left\{s_{\alpha }\right|\alpha =-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}$ be a linguistic term set. The score function of the HFLTS $h_S=\left\{s_{{\phi }_l}\right|s_{{\phi }_l}\in S;l=1,\cdots ,L;{\phi }_l\in \{-\tau ,\cdots ,-1,0,1,\cdots ,\tau \}\}$ can be defined as:

$$E\left(h_S\right)=(1-HD\left(h_S\right))\times \left(\frac{1}{L}\sum _{l=1}^{L}g\left(s_{{\phi }_l}\right)\right)$$ (12)

where $\mathit{HD}\left(h_S\right)$ is the hesitancy degree of $h_S$, and $g\left(s_{{\phi }_l}\right)$ is the semantic of $s_{{\phi }_l}$, which can be calculated as follows:

$$g\left(s_{\alpha }\right)=(\alpha +\tau )/2\tau$$ (13)

$$\mathit{HD}\left(h_s\right)=\frac{L\left(h_s\right)ln\left(L\left(h_s\right)\right)}{(2\tau +1)ln\left(\right(2\tau +1\left)\right)}$$ (14)

In addition, how to deal with the conflict between evidences is a long-standing research topic in the DS theory. One of the common methods is to assign different discount coefficients to different pieces of evidences. In recent studies (Dong et al., 2019, Murofushi and Sugeno, 1989, Zhang and Deng, 2018), the discount coefficient was obtained by measuring the distance between evidences. The smaller the total distance between one evidence and another is, the more reliable the evidence is, and the larger the discount coefficient should be given. When we use Z-numbers to give evaluations, the reliability is measurable. Given that a piece of evidence may be made up of several Z-numbers, the function of discount coefficient can be given by the reference score function as follow:

$$\beta =(1-HD\left(e_{\mathit{ij}}\right))\times \left(\frac{1}{n}\sum _{l=1}^{n}E\left(h_{S_l}\right)\right)$$ (15)

where $\mathit{HD}\left(e_{\mathit{ij}}\right)$ is the hesitancy degree of a piece of evidence $e_{\mathit{ij}}$, $E\left(h_{S_l}\right)$ is the score of the reliability $B$ in a Z-number, and $n$ is the number of the Z-number in a piece of evidence.

3.3. Generate the basic probability assignment

According to the definition of a Z-number, $u_A\left(x\right)·p_{X}isB$. In this paper, we substitute the membership function $u_A\left(x\right)$ with the utility function $\mu \left(H_j\right)$ in the DS theory and generalize the probability distribution $p_X$ to the BPA $m\left(H_j\right)$. According to Eq. (12), the reliability $B$ can be translated to $E\left(h_S\right)$ by the score function. Thus, we can derive the BPA $m\left(H_j\right)$ as follow:

$$m\left(H_j\right)=E\left(h_S\right)/\mu \left(H_j\right)$$ (16)

After normalization, it follows

$$m^{\prime }\left(H_j\right)=\frac{m\left(H_j\right)}{\sum _j^{n}m\left(H_j\right)}$$ (17)

It is easy to understand why we derive the result of a basic probability allocation rather than probability. After we extend the Z-numbers with HFLTS, the focal element of the Z- evaluation information is likely to be made up of an envelope of evaluation levels rather than a single linguistic term. Considering that there are multiple Z-evaluations due to the hesitancy of decision makers, it is necessary to normalize $m\left(H_j\right)$. Next, we can integrate the Z-evaluation with $m^{\prime }\left(H_j\right)$ according to the DS evidence synthesis rules.

4. A multi-criterion decision-making method based on the DS theory and generalized Z-numbers

Suppose that there is an MCDM problem with $I$ alternatives $x_i(i=1,2,\cdots ,I)$ being evaluated on $J$ criteria $c_j(j=1,2,\cdots ,J)$. The alternatives are evaluated under the identification framework $H=\left\{H_n\right|n=1,2,\cdots ,N\}$ and $R=\left\{R_n\right|n=1,2,\cdots ,N\}$ which are collectively exhaustive and mutually exclusive, where $H$ represents the evaluation grade and $R$ represents the reliability of information. Based on $H$ and $R$, an expert can evaluate alternative $x_i$ on criterion $c_j$ and give a distributed evaluation as $e_{\mathit{ij}}=$ $\left(\{H_p,\cdots ,H_q\},\{R_p,\cdots ,R_q\}\right),p,q=1,2,\cdots ,N$, where $e_{\mathit{ij}}$ is a generalized Z-number. In addition, the utility of $H_n$, $\mu \left(H_n\right)$, satisfies $\mu \left(H_1\right)⩽\mu \left(H_2\right)⩽\cdots ⩽\mu \left(H_N\right)$ and $\mu \left(\mathrm{\varnothing }\right)=0,\mu \left(H\right)=1$. The score of $R_n$, $E\left(R_n\right)$, is used to quantify the reliability of information. The greater the $E\left(R_n\right)$ is, the greater the reliability of information should be.

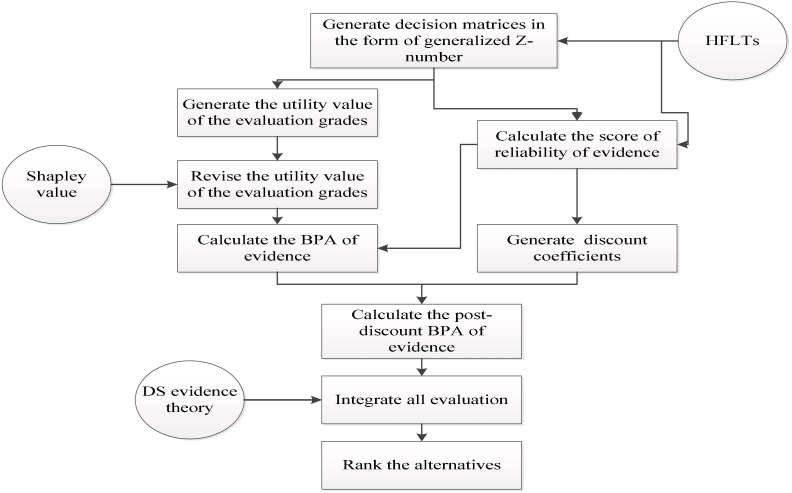
According to the analysis in the previous section, we propose an MCDM method based on the DS theory and generalized Z-numbers. To facilitate the application, we summarize the algorithm of this method below. The flow chart of this algorithm is illustrated in Fig. 2 .

Fig. 2.

The algorithm flow chart of the proposed method.

Step 1. (Generate decision matrices in the form of generalized Z-numbers) For an MCDM problem with $I$ alternatives and $J$ criteria, according to sensor records and expert opinions, $I\times J$ pieces of evidences are given. Each piece of evidence is represented as $e_{\mathit{ij}}=\left(\{H_p,\cdots ,H_q\},\{R_p,\cdots ,R_q\}\right),p,q=1,2,\cdots ,N$, and $e_{\mathit{ij}}$ is the evaluation of the $j\text{- th}$ criterion for the $i\text{- th}$ alternative. Then, all those evidences form a $I\times J$ decision matrix $D_{I\times J}$.

Step 2. (Revise the utility value of the evaluation grades by Shapley value) According to the preference of experts, the utility value of the evaluation grade $H_j$ and all of the subsets of $H$ are given. By Eq. (11), the utility value of the evaluation grade $H_j$ is revised by the corresponding Shapley value.

Step 3. (Generate the BPA) By Eqs. (12)-(14), the score of the reliability of evidence can be calculated. Then, the BPA $m\left(H_j\right)$ can be calculated by Eq. (16). Because there may be more than one evaluation in one piece of evidence, sometimes we need to normalize the BPA.

Step 4. (Generate the discount coefficient) In Step 3, we generate the score of the reliability. In this step, we still use this method to calculate the comprehensive reliability of a piece of evidence as a discount coefficient by Eq. (15). Again, the discount coefficient needs to be normalized by Eq. (17).

Step 5. (Integrate all evaluations by the DS theory) After obtaining the BPA for each piece of evidence, the decision matrix can be integrated by the evidential reasoning method (Yang & Xu, 2013).

Step 6. (Rank the alternatives) We finally rank the alternatives according to their utilities.

As shown in the steps above, our approach is simple and easy to understand. The highlight is that we consider the reliability of information when constructing the Z-evaluation decision matrices. In addition, when calculating the utility values of evaluation levels, we introduce the Shapley value to deal with the non-exclusive relationships between evaluation levels. All of these are the shortcomings of traditional evidential reasoning approach. These illustrate that our approach is more suitable in dealing with uncertain decision problems.

5. An illustrative example: Medicine options for the patients with mild symptoms of the COVID-19

In this section, an illustrative example concerning the medicine selection for the patients with mild symptoms of the COVID-19 is given to show the effectiveness of the proposed method.

5.1. Case description

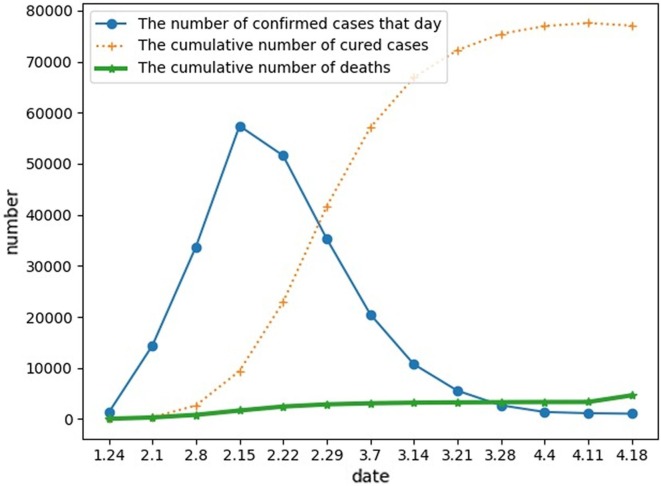
In December 2019, a new type of coronavirus pneumonia broke out in Wuhan, China, which wreaked havoc across the country and seriously threatened human health, drawing worldwide attention. The COVID-19 is a B type infectious disease similar to the SARS coronavirus in 2003, causing severe symptoms of pneumonia. Coronaviruses belong to the Coronaviridae family in the Nidovirales order. Corona represents crown-like spikes on the outer surface of the virus; thus, it was named as a coronavirus (Shereen & Khan, 2020). The virus is transmitted through droplets, close contact and other means, and patients in the incubation period could potentially transmit the virus to other persons. According to current observations, the new coronavirus is weaker than SARS in pathogenesis, but has stronger transmission competence (Tian, 2020). According to the data from the official website of National Health Commission of the People’s Republic of China (http://www.nhc.gov.cn/), there was a clear trend of the epidemic spreading after January 24, 2020. By April 18, 2020, China had a total of 4632 deaths, 1041 confirmed cases and 77,062 cured cases. Since mid-February, the number of confirmed cases has been on a downward trend. In addition, the number of people cured has been increased and the number of deaths was small and stable. The spread is illustrated in Fig. 3 .

Fig. 3.

The spread of COVID-19 in China (from January 24 to April 18, 2020).

Unfortunately, no drugs or vaccines have been approved for the treatment of human coronaviruses. Several approaches for the control or prevention of the COVID-19 infections can be envisaged, including vaccines, monoclonal antibodies, oligonucleotide-based therapies, peptides, interferon therapies, and small-molecule drugs (Li & Clercq, 2019). However, in terms of antiviral medicine, there is still no specific medicine. Ribavirin combined with interferon is still recommended for the diagnosis and treatment of the COVID-19 in China due to its effectiveness in treating Middle East respiratory syndrome (MERS). Lopinavir is one kind of protease inhibitor used to treat HIV infection, with ritonavir as a booster. Lopinavir/Ritonavir have anti coronavirus activity in vitro. Besides, Remdesivir may be the best potential medicine for the treatment of the COVID-19. As a drug undergoing a clinical trial, Remdesivir has been shown to have highly proofreading ability, and mutated drug resistance can effectively reduce virulence (Liu & Morse, 2020). In addition, Chinese medicine, such as Lianhuaqingwen Capsules, has also played an important role in the prevention and treatment of new respiratory infectious diseases (Lu, 2020). However, it is worth noting that there are no specific antiviral medicines or vaccines for the COVID-19. All medicine need to be further confirmed in clinical trials.

The most detailed breakdown of symptoms of the disease comes from a recent World Health Organization analysis of more than 55,000 confirmed cases in China (World Health Organization, 2019). According to the statistics, here are the most common symptoms and the percentage of people who had them: fever: 88%, dry cough: 68%, fatigue: 38%, Coughing up sputum, or thick phlegm, from the lungs: 33%, Shortness of breath: 19%, Bone or joint pain: 15% and the rest are small enough to ignore (World Health Organization, 2019).

In this study, we select four medicine as candidates for patients of the COVID-19. They are Ribavirin, Lopinavir/Ritonavir, Remdesivir and Lianhuaqingwen Capsules. Medicine should be selected not only for their effect on symptoms, but also for their antiviral activity and their possible side effects. Thus, we select four indicators antiviral activity, coolify, ease breathing and side effect as criteria for expert evaluation. To find the best medicine for the patients with mild symptoms of the COVID-19, we suppose that the evaluation grades of constraint $A$ is predetermined as $H=$ $H_3=verygood\left(VG\right),H_4=extremelygood\left(EG\right)\}$ and that of reliability $B$ is predetermined as $R=\{R_1=normal\left(M\right),$ $R_2=$ $alittlecertain\left(ALC\right),$ $R_3=verycertain\left(VC\right),$ $R_4=$ $\mathit{extremely}certain\left(EC\right)\}$. According to the experience and opinions of experts, the performances of the four medicine on four criteria are given in Table 1 .

Table 1.

The evaluation matrix regarding four medicines.

Medicine	Antiviral activity	Coolify	Ease breathing	Side effect
Ribavirin	(at least VG, ALC or VC), (EG, ALC)	(ALG, at most ALC), (at least VG, M)	(M, M), (ALG, between ALC or VC)	(M, VC), (ALG, ALC)
Lianhuaqingwen Capsules	(VG, VC), (EG, ALC)	(at least VG, EC), (EG, ALC)	(M, ALC), (VG, at most ALC)	(ALG, at least VC), (VG, VC)
Lopinavir/Ritonavir	(VG, at least VC), (EG, VC)	(ALG, at least VG), (VG, VC)	(at least ALG, VC), (VG, ALC)	(VG, VC), (EG, ALC)
Remdesivir	(at least VG, VC), (EG, M)	(at least VG, VC), (EG, between M or ALC)	(ALG, ALC or VC), (VG, ALC)	(VG, VC), (EG, ALC)

5.2. Solve the case by the proposed method

Below we use our proposed decision-making method to help the patients with mild symptoms of the COVID-19 to select the most suitable medicine.

Step 1. (Generate decision matrices in the form of Z-numbers) We can translate these initial linguistic expressions into generalized Z-numbers. The decision matrix is obtained as Table 2 .

Table 2.

The decision matrix regarding four medicines.

Medicine	Antiviral activity	Coolify	Ease breathing	Side effect
Ribavirin	$\begin{array}{c}\left(\{H_3,H_4\},\{R_2,R_3\}\right),\\ \left(\left\{H_4\right\},\left\{R_2\right\}\right)\end{array}$	$\begin{array}{c}\left(\left\{H_2\right\},\{R_1,R_2\}\right),\\ (\{H_3,H_4\},\left\{R_1\right\})\end{array}$	$\begin{array}{c}\left(\left\{H_1\right\},\left\{R_1\right\}\right),\\ (\left\{H_2\right\},\{R_2,R_3\})\end{array}$	$\begin{array}{c}\left(\left\{H_1\right\},\left\{R_3\right\}\right),\\ \left(\left\{H_2\right\},\left\{R_2\right\}\right)\end{array}$
Lianhuaqingwen Capsules	$\begin{array}{c}(\left\{H_3\right\},\left\{R_3\right\}),\\ (\left\{H_4\right\},\left\{R_2\right\})\end{array}$	$\begin{array}{c}\left(\{H_3,H_4\},\left\{R_4\right\}\right),\\ (\left\{H_4\right\},\left\{R_2\right\})\end{array}$	$\begin{array}{c}(\left\{H_1\right\},\left\{R_2\right\}),\\ (\left\{H_3\right\},\{R_1,R_2\})\end{array}$	$\begin{array}{c}\left(\left\{H_2\right\},\{R_3,R_4\}\right),\\ \left(\left\{H_3\right\},\left\{R_3\right\}\right)\end{array}$
Lopinavir/Ritonavir	$\begin{array}{c}\left(\left\{H_3\right\},\{R_3,R_4\}\right),\\ (\left\{H_4\right\},\left\{R_3\right\})\end{array}$	$\begin{array}{c}(\left\{H_2\right\},\{R_3,R_4\}),\\ (\left\{H_3\right\},\left\{R_3\right\})\end{array}$	$\begin{array}{c}\left(\{H_2,H_3,H_4\},\left\{R_3\right\}\right),\\ (\left\{H_3\right\},\left\{R_2\right\})\end{array}$	$\begin{array}{c}\left(\left\{H_3\right\},\left\{R_4\right\}\right),\\ \left(\left\{H_4\right\},\left\{R_2\right\}\right)\end{array}$
Remdesivir	$\begin{array}{c}\left(\{H_3,H_4\},\left\{R_3\right\}\right),\\ (\left\{H_4\right\},\left\{R_1\right\})\end{array}$	$\begin{array}{c}\left(\{H_3,H_4\},\left\{R_3\right\}\right),\\ \left(\left\{H_4\right\},\{R_1,R_2\}\right)\end{array}$	$\begin{array}{c}\left(\left\{H_2\right\},\{R_2,R_3\}\right),\\ (\left\{H_3\right\},\left\{R_2\right\})\end{array}$	$\begin{array}{c}\left(\left\{H_3\right\},\left\{R_4\right\}\right),\\ \left(\left\{H_4\right\},\left\{R_2\right\}\right)\end{array}$

Step 2. (Revise the utility values of the evaluation grades by the corresponding Shapley values) Suppose that the utility of evaluation grades $H_n(n=1,2,3,4)$ and coalitions of $H_n$ are as follows:

$$\mu \left(\mathrm{\varnothing }\right)=0,\mu \left(H_1\right)=0.1,\mu \left(H_2\right)=0.2,\mu \left(H_3\right)=0.3,\mu \left(H_4\right)=0.4$$

$$\mu (H_1,H_2)=0.26,\mu (H_1,H_3)=0.34,\mu (H_1,H_4)=0.42$$

$$\mu (H_2,H_3)=0.52,\mu (H_2,H_4)=0.63,\mu (H_3,H_4)=0.72$$

$$\mu (H_1,H_2,H_3)=0.56,\mu (H_1,H_2,H_4)=0.67,\mu (H_1,H_3,H_4)=0.76,\mu (H_2,H_3,H_4)=0.92$$

$$\mu (H_1,H_2,H_3,H_4)=1$$

By Eq. (11), the Shapley values for criteria can be calculated as follows:

• (1)When $K$ is $\mathrm{\varnothing }$, we have

$$\varphi {\left(H_1\right)}_0=\frac{1}{4}\times [\mu \left(H_1\right)-\mu \left(\mathrm{\varnothing }\right)]=0.025$$

• (2)When $K$ is the combination of $\{H_1,H_2\},\{H_1,H_3\}$ and $\{H_1,H_4\}$, we have

$$\varphi {\left(H_1\right)}_1=\frac{1}{12}\times [(\mu (H_1,H_2)-\mu \left(H_2\right))+(\mu (H_1,H_3)-\mu \left(H_3\right))+(\mu (H_1,H_4)-\mu \left(H_4\right))]=0.01$$

• (3)When $K$ is the combination of $\{H_1,H_2,H_3\},\{H_1,H_2,H_4\}$ and $\{H_1,H_3,H_4\}$, we have

$$\begin{array}{cc}\hfill \varphi {(H_1)}_2& =\frac{1}{12}\times \left[\begin{array}{c}(\mu (H_1,H_2,H_3)-\mu (H_2,H_3))+(\mu (H_1,H_2,H_4)-\mu (H_2,H_4))\\ +(\mu (H_1,H_3,H_4)-\mu (H_3,H_4))\hfill \end{array}\right]\hfill \\ & =0.01\hfill \end{array}$$

• (4)When $K$ is the combination of $\{H_1,H_2,H_3,H_4\}$, we have

$$\varphi {\left(H_1\right)}_3=\frac{1}{4}\times \left[(\mu (H_1,H_2,H_3,H_4)-\mu (H_2,H_3,H_4))\right]=0.02$$

Thus, the Shapley value of the evaluation grade can be obtained as:

$$\varphi \left(H_1\right)=\varphi {\left(H_1\right)}_0+\varphi {\left(H_1\right)}_1+\varphi {\left(H_1\right)}_2+\varphi {\left(H_1\right)}_3=0.065$$

Then, we can get the Shapley value for the rest of evaluation grades:

$$\varphi \left(H_2\right)=0.215,\varphi \left(H_3\right)=0.31,\varphi \left(H_4\right)=0.41$$

Step 3. (Generate the BPA) First, we calculate the score of the reliability of evidence. By Eqs. (12)–(14), the score of the reliability for evidence $e_{11}$ is calculated as:

$$\begin{array}{c}E{\left(e_{11}\right)}_1=\left(1-HD{\left(e_{11}\right)}_1\right)\times \left(\frac{1}{2}\times \left[g\left(R_2\right)+g\left(R_3\right)\right]\right)=0.756\hfill \\ E{\left(e_{11}\right)}_2=\left(1-HD{\left(e_{11}\right)}_2\right)\times g\left(R_2\right)=0.75\hfill \end{array}$$

The score of the reliability for the rest evidences can be calculated as:

$$E{\left(e_{12}\right)}_1=0.639,E{\left(e_{12}\right)}_2=0.625,E{\left(e_{13}\right)}_1=0.625,E{\left(e_{13}\right)}_2=0.756,$$

$$E{\left(e_{14}\right)}_1=0.875,E{\left(e_{14}\right)}_2=0.75$$

$$\begin{array}{c}E{\left(e_{21}\right)}_1=0.875,E{\left(e_{21}\right)}_2=0.75,E{\left(e_{22}\right)}_1=1,E{\left(e_{22}\right)}_2=0.75,\hfill \\ E{\left(e_{23}\right)}_1=0.75,E{\left(e_{23}\right)}_2=0.639,E{\left(e_{24}\right)}_1=0.872,E{\left(e_{24}\right)}_2=0.875\hfill \end{array}$$

$$\begin{array}{c}E{\left(e_{31}\right)}_1=0.872,E{\left(e_{31}\right)}_2=0.875,E{\left(e_{32}\right)}_1=0.872,E{\left(e_{32}\right)}_2=0.875,\hfill \\ E{\left(e_{33}\right)}_1=0.875,E{\left(e_{33}\right)}_2=0.75,E{\left(e_{34}\right)}_1=1,E{\left(e_{34}\right)}_2=0.75\hfill \end{array}$$

$$\begin{array}{c}E{\left(e_{41}\right)}_1=0.875,E{\left(e_{41}\right)}_2=0.625,E{\left(e_{42}\right)}_1=0.875,E{\left(e_{42}\right)}_2=0.639,\hfill \\ E{\left(e_{43}\right)}_1=0.756,E{\left(e_{43}\right)}_2=0.75,E{\left(e_{44}\right)}_1=1,E{\left(e_{44}\right)}_2=0.75\hfill \end{array}$$

Then, by Eq. (16) and (17), the BPA can be obtained by dividing the score of the reliability by the utilities of evaluation grades. Thus, the new decision matrix is translated to Table 3 .

Table 3.

The new decision matrix regarding four medicines.

Medicine	Antiviral activity	Coolify	Ease breathing	Side effect
Ribavirin	$\begin{array}{c}m\left(H_3,H_4\right)=0.36,\\ m\left(H_4\right)=0.64\end{array}$	$\begin{array}{c}m\left(H_2\right)=0.77,\\ m\left(H_3,H_4\right)=0.23\end{array}$	$\begin{array}{c}m\left(H_1\right)=0.73,\\ m\left(H_2\right)=0.27\end{array}$	$\begin{array}{c}m\left(H_1\right)=0.79,\\ m\left(H_2\right)=0.21\end{array}$
Lianhuaqingwen Capsules	$\begin{array}{c}m\left(H_3\right)=0.61,\\ m\left(H_4\right)=0.39\end{array}$	$\begin{array}{c}m\left(H_3,H_4\right)=0.43,\\ m\left(H_4\right)=0.57\end{array}$	$\begin{array}{c}m\left(H_1\right)=0.85,\\ m\left(H_3\right)=0.15\end{array}$	$\begin{array}{c}m\left(H_2\right)=0.59,\\ m\left(H_3\right)=0.41\end{array}$
Lopinavir/Ritonavir	$\begin{array}{c}m\left(H_3\right)=0.57,\\ m\left(H_4\right)=0.43\end{array}$	$\begin{array}{c}m\left(H_2\right)=0.59,\\ m\left(H_3\right)=0.41\end{array}$	$\begin{array}{c}m\left(H_2,H_3,H_4\right)\\ =0.28,\end{array}$ $m\left(H_3\right)=0.72$	$\begin{array}{c}m\left(H_3\right)=0.64,\\ m\left(H_4\right)=0.36\end{array}$
Remdesivir	$\begin{array}{c}m\left(H_3,H_4\right)=0.45,\\ m\left(H_4\right)=0.55\end{array}$	$\begin{array}{c}m\left(H_3,H_4\right)=0.45,\\ m\left(H_4\right)=0.55\end{array}$	$\begin{array}{c}m\left(H_2\right)=0.59,\\ m\left(H_3\right)=0.41\end{array}$	$\begin{array}{c}m\left(H_3\right)=0.64,\\ m\left(H_4\right)=0.36\end{array}$

Step 4. (Generate the discount coefficients) By Eq. (15), the discount coefficient of each criterion can be calculated as: ${\beta }_1=0.25,{\beta }_2=0.25,{\beta }_3=0.23,{\beta }_4=0.27$.

Step 5. (Integrate all evaluations by the DS theory) By Eqs. (2)-(7), the decision matrix can be integrated with the synthesis rules of the DS theory. The results are listed in Table 4 .

Table 4.

The comprehensive evaluations of four medicines.

Medicine	BPA
Ribavirin	$m\left(H_1\right)=0.23,m\left(H_2\right)=0.19,m\left(H_4\right)=0.1,m\left(H_3,H_4\right)=0.08,m\left(H\right)=0.4$
Lianhuaqingwen Capsules	$m\left(H_1\right)=0.1,m\left(H_2\right)=0.09,m\left(H_3\right)=0.2,m\left(H_4\right)=0.15,m\left(H_3,H_4\right)=0.06,m\left(H\right)=0.4$
Lopinavir/Ritonavir	$m\left(H_2\right)=0.08,m\left(H_3\right)=0.4,m\left(H_4\right)=0.12,m\left(H_2,H_3,H_4\right)=0.03,m\left(H\right)=0.37$
Remdesivir	$m\left(H_2\right)=0.07,m\left(H_3\right)=0.18,m\left(H_4\right)=0.26,m\left(H_3,H_4\right)=0.12,m\left(H\right)=0.37$

Step 6. (Rank the alternatives) By Eqs. (8)-(10), based on the utility values and the belief degrees obtained in previous steps, we can calculate $u\left(x_i\right)$ for each alternative:

$$u\left(x_1\right)=0.257,u\left(x_2\right)=0.32,u\left(x_3\right)=0.347,u\left(x_4\right)=0.418$$

So, $u\left(x_1\right)<u\left(x_2\right)<u\left(x_3\right)<u\left(x_4\right)$, that is, the most effective medicine for patients with mild symptoms of the COVID-19 is Remdesivir.

5.3. Comparing with Liu et al. (2019)’s model

Both of our method and Liu et al. (2019)’s model establish the connection between Z-numbers and the DS evidence theory through the knowledge of fuzzy set theory. By this connection, the reliability of information is well considered in MCDM problems with incomplete information. At present, how to handle incomplete and uncertain information is still an open and worthy issue.

The difference between our method and Liu et al. (2019)’s model is that the research idea of this paper is just from different direction of Liu et al. (2019)’s model. The motivation of Liu et al. (2019)’s model is to derive the membership degree of reliability of information from the perspective of information fusion. The purpose is to use the existing evaluation information to generate Z-numbers. By contrast, in this paper, we use the reliability of information to integrate information indirectly instead of directly relying on the probability distribution, so as to sort and select the best alternative. Obviously, our method provides a solution to uncertain MCDM problem with reliability. On the other hand, the membership function in the form of triangular fuzzy number used by Liu et al. (2019) is too simple to present complex evaluation information. In addition, transforming the reliability part of Z-numbers into triangular fuzzy numbers will lead to the distortion and loss of the original Z-evaluation information. In this respect, we generalize the elements of Z-numbers from classical fuzzy numbers or linguistic terms to HFLTSs, which enriches the representation form of uncertain information. In addition, the utility function is used to replace the membership function, which not only well conforms to the knowledge of the DS evidence theory, but also considers the mutual influence between evaluation levels. In general, the method we proposed makes full use of the original definition of Z-numbers, and it is easier to integrate Z-evaluation information by using the evidence aggregation rules of the DS theory than to convert Z-numbers into classical fuzzy numbers.

Due to the destructive power of novel coronavirus, there are no effective drugs that can be used in clinical trials to protect against and treat symptoms caused by the coronavirus. In this case, unlike conventional drug selection issues, the expert's opinion is especially important to medicine options for the patients with mild symptoms of the COVID-19. The generalized Z-numbers evaluation model proposed in this paper fully considers the reliability of information when evaluating information under multiple criteria, so it fits well with the drug selection of patients in this outbreak.

6. Conclusions

Although many theories are devoted to describing uncertain phenomena include hesitation, incompleteness or imprecision for MCDM problems, none of these except the Z-number can well describe the reliability of information. The traditional Z-number is represented by a single linguistic term or uncertain linguistic terms. In this paper, we generalized the form of Z-number to hesitant fuzzy linguistic environment from fuzzy sets. Because the expression form of the generalized Z-numbers is more complex, to avoid ambiguity, the generalized Z-numbers were described by the identification framework of the DS theory. Then, the knowledge of Z-numbers was used to derive the BPA of evidence, and the synthetic rules in the DS theory were used to integrate evaluations. In this process, considering that the evaluation grades may be not independent of each other, the Shapley value was introduced to determine the utility values of evaluation grades. Finally, the effectiveness of this proposed method was illustrated by the selection of medicine for patients with mild symptoms of the COVID-19.

In this study, we used the Shapley value to deal with non-dependent evaluation grades. In fact, the D-number, as an extension of the DS theory, is based on the premise that evaluation levels in the identification framework are not mutually exclusive. So, we are going to investigate the generalized Z-numbers based on the knowledge of D-numbers in the future. On the other hand, although we considered that evaluation levels are not independent of each other, the dependency between criteria was not considered. In the future research, we will try to introduce the interactions of criteria into this process and get a more perfect decision-making method.

CRediT authorship contribution statement

Zongyuan Ren: Conceptualization, Formal analysis, Writing - original draft. Huchang Liao: Supervision, Writing - original draft. Yuxi Liu: Data curation.