Risk of the Brazilian health care system over 5572 municipalities to exceed health care capacity due to the 2019 novel coronavirus (COVID-19)

Abstract

The spread of the 2019 novel coronavirus (COVID-19) has challenged governments to develop public policies to reduce the load of the COVID-19 on health care systems, which is commonly referred to as “flattening the curve”. This study aims to address this issue by proposing a spatial multicriteria approach to estimate the risk of the Brazilian health care system, by municipality, to exceed the health care capacity because of an influx of patients infected with the COVID-19. We estimated this risk for 5572 municipalities in Brazil using a combination of a multicriteria decision-making approach with spatial analysis to estimate the exceedance risk, and then, we examined the risk variation by designing 5 control intervention scenarios (3 scenarios representing reduction on social contacts, and 2 scenarios representing investment on health care system). For the baseline scenario using an average infection rate across Brazil, we estimated a mean Hospital Bed Capacity (HBC) value of −16.73, indicating that, on average, the Brazilian municipalities will have a deficit of approximately 17 beds. This deficit is projected to occur in 3338 municipalities with the north and northeast regions being at the greatest risk of exceeding health care capacity due to the COVID-19. The intervention scenarios indicate across all of Brazil that they could address the bed shortage, with an average of available beds between 23 and 32. However, when we consider the shortages at a municipal scale, bed exceedances still occur for at least 2119 municipalities in the most effective intervention scenario. Our findings are essential to identify priority areas, to compare populations, and to provide options for government agencies to act. This study can be used to provide support for the creation of effective health public policies for national, regional, and local intervention.

Graphical abstract

Highlights

• •On average, the Brazilian municipalities will have a deficit of approximately 17 beds.
• •Bed exceedances still occur for at least 2,119 municipalities in the most effective intervention scenario.
• •If there is a 50% increase in the hospital services, there will be an oversupply of 27 beds.

1. Introduction

According to the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University, on March 30th 2020, an outbreak of the 2019 novel coronavirus (COVID-19) has resulted in 741,030 confirmed cases and 35,114 deaths in >150 countries (CSSE, 2020). The first case was identified in Wuhan, China, in December 2019 (Guan et al., 2020). Since then, the spread of the COVID-19 has been challenging governments to create public policies to minimize the load of COVID-19 cases on health care systems (Chinazzi et al., 2020; Kraemer et al., 2020), often described as “flattening the curve”.

Although most of the mitigation strategies to slow transmission of the COVID-19 are recommended for all countries, regions, cities, and communities (e.g., reduce social contacts), it is crucial to examine areas with community attributes that may require enhanced public policies. These attributes include demographic variation, economic aspects, transportation infrastructure, health condition of the population (e.g. rates of co-morbidities), and characteristic of the health care system (CDC, 2020). For example, while the Chines government reports that control intervention measures in China may have reduced new cases by approximately 90%, Italy and Iran have not achieved this success (Remuzzi and Remuzzi, 2020).

According to the Brazilian Health Agency (Ministério da Saúde, 2020), Brazil has been facing the impacts of the COVID-19 since February 2020, when the first case was reported in the city of São Paulo. As of March 30, 2020, COVID-19 in Brazil has resulted in 4256 confirmed cases and 136 deaths (Ministério da Saúde, 2020) and is present in all Brazilian states. Currently, the Brazilian Government has implemented mitigation strategies to slow the transmission of COVID-19 by restricting social contacts in several municipalities. If COVID-19 infection rates in Brazil parallel those observed in China, a 0.20 proportion of the population (Guan et al., 2020; Zhou et al., 2020), the largest country in South America (200 million inhabitants in 8,515,767 km²) would be expected to see 10 million cases. Given the potential undocumented cases due to limited testing, the infection rate may be a low estimate and situation in Brazil could be far greater (Li et al., 2020).

Our study estimates which Brazilian municipalities will exceed their health care capacity under five different mitigation strategies that vary their approach and local outcomes based on municipalities' community attributes. The various attributes are implemented in a hierarchical framework and the importance of each aspect is assessed by expert opinion and combined in a multicriteria decision model. The model is applied along with existing infection and hospitalization rates to identify health care capacity exceedances. Understanding the variation of this risk over space is essential to identify priority areas, to monitor conditions on the ground, to calculate temporal changes, to compare populations, and to communicate to potentially affected people and governmental agencies.

2. Materials and methods

2.1. Study design

This study was conducted in five stages. First, we established the conceptual model composed by all the criteria related to the aim of our study. In the second stage, we used Geographic Information System (GIS) techniques to consolidate a geodatabase encompassing all the criteria at the municipality scale. In the third stage, we used a decision-making approach to assign weights for each criterion. In the fourth stage, we integrated the weights into the infection rate functions to estimate the risk of each municipality health care system to exceed capacity because of COVID-19. Finally, in the fifth stage, we examined the risk variation by implementing various control intervention scenarios.

2.2. Conceptual model

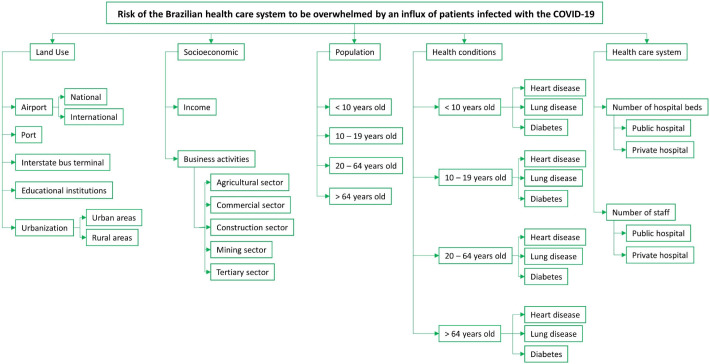
The hierarchical network characterizes the conceptual model, which is the cascading structure of criteria and measurable attributes needed for most multi-criteria models. We established the hierarchical network using five primary community attributes (criteria), including land use, socioeconomics, population, health conditions, and health care system. Each primary criterion decomposes into quantifiable sub-criteria. Fig. 1 presents the complete hierarchical network. Note that this hierarchical network does not capture all the complex interactions related to the risk of exceeding health care capacity because of COVID-19 infections; however, the variables represented by each criterion are those currently available. We highlight that our analysis was conducted at a fine spatial scale – municipality level. Data at municipal scale in Brazil are limited; however, it is important to analyze this scale because the health care system varies by local capacity. The 5572 municipalities are the smallest regions considered by the Brazilian political system.

Fig. 1.

Hierarchical network of community attributes with potential effects on COVID-19 transmission.

2.3. Geodatabase

We provide a description of each attribute by theme in Table 1 .

Table 1.

Description of the geodatabase.

Theme (primary criteria)	Attribute	Description
Land use	Airport	Count of national and international flights in each Brazilian airport in 2018 (proxy for the number of flights that would have entered Brazil prior to any reductions due to COVID-19). Source: The National Civil Aviation Agency (ANAC, 2018)
	Port	Quantity of goods movement by port aggregated by municipality. Source: National Inventory of Ports in 2018 (ANTAQ, 2018)
	Interstate bus terminal	The number of passengers that traveled to each municipality by interstate bus in 2019. Source: Brazilian Transportation Agency – National Transportation Database – BIT (https://www.infraestrutura.gov.br/bit.html)
Educational institutions	Address from each Brazilian educational institution. We accounted for the number of elementary schools, middle schools, high schools, colleges, and universities aggregated by municipality. Source: National Institute of Educational Studies (INEP, 2016)
Urbanization	Number of people living in urban areas and rural areas. Data were based on the national census in 2010. Source: Brazilian Institute of Geography and Statistics (IBGE, 2010)
Socioeconomic	Income	Per capita income (in Brazilian currency, real, R$) in each municipal district in Brazil in the year 2010. Source: The Institute for Applied Economic Research (IPEA, 2010).
Business activities	Information on the proportion of people above 18 years old in each Brazilian municipality that works in different sectors of the economy. We accounted for five sectors – agricultural, commercial, construction, mining, and tertiary. Source: Atlas of Human Development in Brazil (http://www.atlasbrasil.org.br/2013/en/download/)
Population	Age groups	Population data by age group at the municipality level. We considered four groups, including 0–9 years old, 10–19 years old, 20–64 years old, and above 64 years old. Source: National census in 2010, provided by the Brazilian Institute of Geography and Statistics (IBGE, 2010)
Health conditions	Age groups	Number of hospital admissions between January 2019 and January 2020 for heart diseases, lung diseases, and diabetes for each Brazilian municipality. Recent studies have shown that people with these diseases are the group more at risk of dying from an infection with the COVID-19 (Guan et al., 2020; Remuzzi and Remuzzi, 2020). The health data were aggregated by the same age groups defined in the previous primary criteria – Population. Source: National Health Database (Datasus, 2020)
Health care system	Hospital beds and number of staff	Number of hospital beds and staffs (e.g., doctors, nurses etc.) in each Brazilian municipality in January 2020. These data were grouped into two groups – private hospitals and public hospitals. Source: Datasus (2020)

2.4. Decision-making approach: multi-criteria decision analysis

Currently, it is unclear the mechanistic relationships between community attributes and the rate of COVID-19 infections. We developed a multi-criteria decision-making (MCDM) model to implement expert judgment to relate community attributes to the spread of infections (i.e. ranking of how each community attribute may influence disease spread or control at the municipal level). We applied the Analytic Hierarchy Process (AHP) developed by Saaty (1980) and frequently used in environmental and health studies (Fontana et al., 2013; Greening and Bernow, 2004; Requia et al., 2016; Tran et al., 2002). AHP is considered one of the best approaches for MCDM, because its flexibility enables decisions combining judgment and personal values in a pairwise comparison between criteria. In addition, it can be used to decompose a complex decision-making problem into simple sub problems (hierarchy network). It is a process for identifying, understanding, and assessing the interactions of a system as a whole by providing a scale for measuring intangibles and a method for establishing priorities (Saaty, 1980).

We used AHP to assign the weights in a stratified approach by obeying each level of the hierarchy defined in Stage 1. A total of 16 specialists in public health and stakeholders in the decision-making to reduce environmental health risks established the pair-wise comparison weights, which were on a scale from 1 to 9 developed by Saaty (1980). A value of one indicates equal importance. The reminder of the weights indicate greater importance of one criteria relative to the other, which include moderate importance (3); strong importance (5); very strong importance (7); extreme importance (9), and 2, 4, 6 and 8 representing intermediate values. The inverse comparison in the matrix is represented by one over the value. After assignment, we modeled the pair-wise comparison importance values using matrix A shown in Eq. (1).

$$A=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{a}_{11}\\ ⋮\end{array}\\ a_{i1}\end{array}\\ ⋮\\ a_{n1}\end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}\cdots \\ \ddots \end{array}\\ \cdots \end{array}\\ \ddots \\ \cdots \end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}{a}_{1j}\\ ⋮\end{array}\\ a_{\mathit{ij}}\end{array}\\ ⋮\\ a_{\mathit{nj}}\end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}\cdots \\ \ddots \end{array}\\ \cdots \end{array}\\ \ddots \\ \cdots \end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}{a}_{1n}\\ ⋮\end{array}\\ a_{\mathit{in}}\end{array}\\ ⋮\\ a_{\mathit{nn}}\end{array}\right]$$ (1)

where a _{ij =} α; a _ji = $\frac{1}{\alpha }$; a is a joint comparison; and α is the assigned importance value. We calculated the matrix (A) by the auto value V _i, as shown in Eq. (2).

$$V_i={\left(\prod _{j=1}^n{a}_{\mathit{ij}}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$n$}\right.}$$ (2)

Normalization of the Eq. (2) generates the vector W, which is the priorities vector (it represents the relative importance attributed for each criteria). We calculated W using Eq. (3):

$$W_{\mathit{nx}1}=\left[\begin{array}{c}{W}_1=\raisebox{1ex}{$V_1$}\!\left/ \!\raisebox{-1ex}{$\sum _{i=1}^n{V}_i$}\right.\\ W_2=\raisebox{1ex}{$V_2$}\!\left/ \!\raisebox{-1ex}{$\sum _{i=1}^n{V}_i$}\right.\\ \begin{array}{c}{W}_3=\raisebox{1ex}{$V_3$}\!\left/ \!\raisebox{-1ex}{$\sum _{i=1}^n{V}_i$}\right.\\ W_n=\raisebox{1ex}{$V_n$}\!\left/ \!\raisebox{-1ex}{$\sum _{i=1}^n{V}_i$}\right.\end{array}\end{array}\right]$$ (3)

The multiplication of the matrix (A) by the value for each weighing W = (W ₁, W ₂, …, W _n) generates the value Aw, which is represented by the Eq. (4).

$$\mathrm{A}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{W}_1/W_1\\ ⋮\end{array}\\ W_i/W_1\end{array}\\ ⋮\\ W_n/W_1\end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}\cdots \\ ⋮\end{array}\\ \cdots \end{array}\\ ⋮\\ \dots \end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}{W}_1/W_j\\ ⋮\end{array}\\ W_i/W_j\end{array}\\ ⋮\\ W_n/W_j\end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}\cdots \\ ⋮\end{array}\\ \cdots \end{array}\\ ⋮\\ \cdots \end{array}\begin{array}{c}\begin{array}{c}\begin{array}{c}{W}_1/W_n\\ ⋮\end{array}\\ W_i/W_n\end{array}\\ ⋮\\ W_n/W_n\end{array}\right]\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{W}_1\\ ⋮\end{array}\\ W_j\end{array}\\ ⋮\\ W_n\end{array}\right]=n\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{W}_1\\ ⋮\end{array}\\ W_j\end{array}\\ ⋮\\ W_n\end{array}\right]=\mathit{nW}$$ (4)

The relation Aw = nW cannot be calculated directly. Instead, Saaty (1980) suggests the use of Eq. (5):

$${\mathrm{\lambda }}_{\mathit{max}}=\frac{1}{n}\left(\frac{W_1}{W_1}+\frac{W_2}{W_2}+\dots +\frac{W_n}{W_n}\right)$$ (5)

Based on Eq. (5), we calculated the vector of priorities as shown in Eq. (6).

$$\mathrm{Aw}={\mathrm{\lambda }}_{\mathit{max}}w$$ (6)

The individual judgments were aggregated by calculating the geometric mean of all vectors of priorities (Aw). This is a common approach in AHP. We applied the geometric mean in order to obtain the central tendency of all judgments.

Saaty (1980) proposed a validation method for assigning weights using Inconsistency Rate (IR) values, which are calculated based on properties of reciprocal matrices. According to the author, IR should not exceed 0.10. Values lower than 0.10 indicate rational logic in the judgment process.

Finally, in order to establish a global value of each criterion, we used Eq. (7):

$$\mathrm{V}\left(\mathrm{a}\right)=\sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{W}}_{\mathrm{j}}{\mathrm{v}}_{\mathrm{j}}\left(\mathrm{a}\right)$$ (7)

where V(a) is the global value; W _j is the importance relative to the criteria j; V _j is the level of preference of the alternative for criterion j, which $\sum _{j=1}^n{W}_j=1v_j\left(a\right),$ and 0 < W_j < 1 (j = 1, …,n).

2.5. Risk modeling

First, we standardized all the sub-criteria consolidated in the second stage (described in the Section 2.3) to a scale of 0–1, where 0 represents the lowest risk of the health care system to be exceeded because of COVID-19, and 1 the highest risk. We used the following equation for the standardization of each observation (municipality m) of each variable (y).

$${\mathrm{y}}_{\text{standardized},\mathrm{m}}=\left(y_m-{\mathrm{y}}_{\text{minimum}}\right)/\left({\mathrm{y}}_{\text{maximum}}-{\mathrm{y}}_{\text{minimum}}\right)$$ (8)

Using the standardized variables, the final risk for each municipality x was estimated based on the weights (V) assigned to each criterion by obeying each level of the hierarchy that was established, as described in the following manner:

$$\text{Urbanization}{\text{Risk}}_{\mathrm{m}}=\left({\text{Urban areas}}_m\mathrm{x}{\mathrm{V}}_{\text{urban areas}}\right)+\left[\left(\frac{1}{{\text{Rural areas}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{rural areas}}\right]$$ (9)

$$\text{Airport}{\text{Risk}}_{\mathrm{m}}=\left({\text{International}}_m\mathrm{x}{\mathrm{V}}_{\text{international}}\right)+\left({\text{National}}_m\mathrm{x}{\mathrm{V}}_{\text{national}}\right)$$ (10)

$$\text{Land}\mathrm{Use}{\text{Risk}}_{\mathrm{m}}=\left({\mathit{Urbanization\; Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{urbanization}}\right)+\left({\mathit{Schools}}_m\mathrm{x}{\mathrm{V}}_{\text{schools}}\right)+\left(\mathit{Bus}{\mathit{terminal}}_m\mathrm{x}{\mathrm{V}}_{\mathrm{bus}\text{terminal}}\right)+\left({\mathit{Port}}_m\mathrm{x}{\mathrm{V}}_{\text{port}}\right)+\left({\mathit{Airport\; Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{airport}}\right)$$ (11)

$$\text{Business activities}{\text{Risk}}_{\mathrm{m}}=\left[\left(\frac{1}{{\text{Agricultural sector}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{agricultural sector}}\right]+\left({\text{Commercial sector}}_m\mathrm{x}{\mathrm{V}}_{\text{commercial sector}}\right)+\left({\text{Construction sector}}_m\mathrm{x}{\mathrm{V}}_{\text{construction sector}}\right)+\left[\left(\frac{1}{{\text{Mining sector}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{mining sector}}\right]+\left({\text{Tertiary sector}}_m\mathrm{x}{\mathrm{V}}_{\text{tertiary sector}}\right)$$ (12)

$$\text{Socioeconomic}{\text{Risk}}_{\mathrm{m}}=\left[\left(\frac{1}{{\text{Income}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{income}}\right]+\left(\text{Business}{\text{activities Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{Business activities}}\right)$$ (13)

$$\text{Population}{\text{Risk}}_{\mathrm{m}}=\left(<10\text{years}{\mathrm{old}}_m\mathrm{x}{\mathrm{V}}_{<10\text{years}\mathrm{old}}\right)+\left(10-19\text{years}{\mathrm{old}}_m\mathrm{x}{\mathrm{V}}_{10-19\text{years}\mathrm{old}}\right)+\left(20-64\text{years}{\mathrm{old}}_m\mathrm{x}{\mathrm{V}}_{20-64\text{years}\mathrm{old}}\right)+\left(>64\text{years}{\mathrm{old}}_m\mathrm{x}{\mathrm{V}}_{>64\text{years}\mathrm{old}}\right)$$ (14)

$$\text{Health conditions}<10\text{years}\mathrm{old}{\text{Risk}}_{\mathrm{m}}=\left(\text{Heart disease}<10{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{heart disease}<10\text{years}}\right)+\left(\text{Lung disease}<10{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{lung disease}<10\text{years}}\right)+\left(\text{Diabetes}<10{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{diabetes}<10\text{years}}\right)$$ (15)

$$\text{Health conditions}10-19\text{years}\mathrm{old}{\text{Risk}}_{\mathrm{m}}=\left(\text{Heart disease}10-19{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{heart disease}10-19\text{years}}\right)+\left(\text{Lung disease}10-10{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{lung disease}10-19\text{years}}\right)+\left(\text{Diabetes}10-19{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{diabetes}10-19\text{years}}\right)$$ (16)

$$\text{Health conditions}20-64\text{years}\mathrm{old}{\text{Risk}}_{\mathrm{m}}=\left(\text{Heart disease}20-64{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{heart disease}20-64\text{years}}\right)+\left(\text{Lung disease}20-64{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{lung disease}20-64\text{years}}\right)+\left(\text{Diabetes}20-64{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{diabetes}20-64\text{years}}\right)$$ (17)

$$\text{Health conditions}>64\text{years}\mathrm{old}{\text{Risk}}_{\mathrm{m}}=\left(\text{Heart disease}>64{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{heart disease}>64\text{years}}\right)+\left(\text{Lung disease}>64{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{lung disease}>64\text{years}}\right)+\left(\text{Diabetes}>64{\text{years}}_m\mathrm{x}{\mathrm{V}}_{\text{diabetes}>64\text{years}}\right)$$ (18)

$$\text{Health conditions}{\text{Risk}}_{\mathrm{m}}=\left(\text{Health conditions}<10\text{years}\mathrm{old}{\text{Risk}}_m\mathrm{x}{\mathrm{V}}_{<10\text{years}\mathrm{old}}\right)+\left(\text{Health conditions}10-19\text{years}\mathrm{old}{\text{Risk}}_m\mathrm{x}{\mathrm{V}}_{10-19\text{years}\mathrm{old}}\right)+\left(\text{Health conditions}20-64\text{years}\mathrm{old}{\text{Risk}}_m\mathrm{x}{\mathrm{V}}_{20-64\text{years}\mathrm{old}}\right)+\left(\text{Health conditions}>64\text{years}\mathrm{old}{\text{Risk}}_m\mathrm{x}{\mathrm{V}}_{>64\text{years}\mathrm{old}}\right)$$ (19)

$$\text{Hospital beds}{\text{Risk}}_{\mathrm{m}}=\left[\left(\frac{1}{{\text{Public hospital}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{public hospital}}\right]+\left[\left(\frac{1}{{\text{Private hospital}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{private hospital}}\right]$$ (20)

$$\text{Staff}{\text{Risk}}_{\mathrm{m}}=\left[\left(\frac{1}{{\text{Public hospital}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{public hospital}}\right]+\left[\left(\frac{1}{{\text{Private hospital}}_m}\right)\mathrm{x}{\mathrm{V}}_{\text{private hospital}}\right]$$ (21)

$$\text{Health care system}{\text{Risk}}_{\mathrm{m}}=\left(\text{Hospital}{\text{beds Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{hospital beds}}\right)+\left({\text{Staff Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{number of staff}}\right)$$ (22)

$${\text{FINAL RISK}}_{\mathrm{m}}=\left(\text{Land}\mathrm{Use}{\text{Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{land}\mathrm{use}}\right)+\left({\text{Socioeconomic Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{socioeconomic}}\right)+\left({\text{Population Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{population}}\right)+\left(\text{Health}{\text{conditions Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{health conditions}}\right)+\left(\text{Health care}{\text{system Risk}}_m\mathrm{x}{\mathrm{V}}_{\text{health care system}}\right)$$ (23)

Note that we applied an inverse function (1/x) for those criteria where 0 represented the highest risk and 1 the lowest risk. The criteria rural areas (Eq. (9)), income (Eq. (13)), agricultural sector (Eq. (12)), mining sector (Eq. (12)), number of hospital beds (Eq. (20)), and number of staff (Eq. (21)) present this concept. For example, the higher number of hospital beds (values close to 1) is the least risk that the health care system would be exceeded by the COVID-19.

Lastly, we integrated an infection rate in the model to estimate the Hospital Bed Capacity (HBC) to determine the Brazilian municipalities that will exceed bed capacity and those that should have enough supply, which is shown in Eq. (24). Here, the FINAL RISK _m calculated by Eq. (23) was defined as a “penalty”, where values close to 1 have minimal effect on HBC and values close to 0 have a greater effect on the availability of beds in each municipal district.

$${\mathrm{HBC}}_{\mathrm{m}}=\left({\mathrm{TB}}_{\mathrm{m}}\mathrm{x}\mathrm{BA}\right)-\left\{\left[\left({\mathrm{Pop}}_{\mathrm{m}}\mathrm{x}\mathrm{IR}\right)\mathrm{x}\mathrm{PC}\right]\mathrm{x}{\text{FINAL RISK}}_{\mathrm{m}}\right\}$$ (24)

where TB is the total beds available in each municipality m; BA is the percentage of beds that are available, which according to the Brazilian Health Agency, it is 70% (30% on average of the hospital beds are already occupied); Pop represents the total population in each municipal district m; IR is the infection rate (percentage of the population infected with the COVID-19), which we based on current studies at 0.20% overall (Guan et al., 2020; Zhou et al., 2020); and PC is the percentage of the infected population that will require hospitalization, which according to initial studies on COVID-19 is about 8% (China CDC, 2020; Zhou et al., 2020).

2.6. Control intervention scenarios

A baseline HBC scenario was assessed as a standard 0.20% infection rate for all municipalities in Brazil. We modeled 5 scenarios to examine HBC variation due to differences in the response to control intervention scenarios at the municipal scale in Brazil. Each scenario represents a different control intervention, including the creation of public policies related to social contacts and expansion of the health care system. With the scenarios, Brazil's overall infection rate does not change; however, the infection rates within municipalities are relocated based on the community attributes and the FINAL RISK calculation.

Scenario I included a 50% reduction in social contacts. Airport, port, interstate bus terminal, educational institutions, business activities, and population were defined as a proxy of social contact. The variables representing these criteria in the geodatabase were reduced by 50%, and then we repeated the steps described by Eqs. (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19), (20), (21), (22), (23), (24). Note that, in this scenario, the penalty of the FINAL RISK on HBC was reduced by 50%, increasing the availability of beds in each municipal district due to a flattening of the demand. Scenarios II and III, included a reduction of 75 and 100% of the social contacts, respectively. Scenario III is the most aggressive, where we try to simulate a quarantine that locks down the whole municipal district. Scenarios IV and V, the control intervention is an increase in resources in the health care system. We modeled an increase of 25% (Scenario IV) and 50% (Scenario V) resources in the health care system, which included the number of hospital beds and number of staff.

3. Results and discussion

3.1. Criteria weights

Table 2 presents the weights attributed to each criterion. Health care system was identified as the most important primary criteria (weight = 0.42), with number of hospital beds given a weight of 0.63, and number of staff a weight of 0.37. Since most Brazilians depend on the public health care system, private hospitals were prioritized with the highest weight for both number of beds and number of staff criteria. Health conditions, socioeconomic, population, and land use were assigned weights of 0.23, 0.15, 0.11, and 0.09, respectively (Table 2).

Table 2.

Weights attributed to each criterion.

Criteria and sub-criteria	Weight (V)
Land use	0.090
Airport	0.422
National	0.167
International	0.833
Port	0.120
Interstate bus terminal	0.074
Educational Institutions	0.213
Urbanization	0.171
Urban areas	0.861
Rural areas	0.139
Socioeconomic	0.146
Income	0.321
Business activities	0.679
Agricultural sector	0.072
Commercial sector	0.350
Construction sector	0.165
Mining sector	0.110
Tertiary sector	0.304
Population	0.114
<10 years old	0.053
10–19 years old	0.102
20–64 years old	0.235
>64 years old	0.610
Health conditions	0.229
<10 years old	0.053
Heart disease	0.247
Lung disease	0.512
Diabetes	0.241
10–19 years old	0.102
Heart disease	0.244
Lung disease	0.552
Diabetes	0.204
20–64 years old	0.235
Heart disease	0.244
Lung disease	0.552
Diabetes	0.204
>64 years old	0.610
Heart disease	0.205
Lung disease	0.595
Diabetes	0.199
Health care system	0.421
Number of hospital beds	0.625
Public hospital	0.625
Private hospital	0.375
Number of staff	0.375
Public hospital	0.708
Private hospital	0.292

The weights attributed by the specialists in public health in our study are in agreement with the studies on COVID-19. Kraemer et al. (2020) have shown that human mobility data explain a substantial part of the spatial distribution of COVID-19 in China. Control measures based on mobility can help mitigate the spread of COVID-19, which include travel restrictions (Chinazzi et al., 2020) and social distancing (Buckee et al., 2020).

3.2. Mapping municipal hospital bed capacity

In Table 3 , we present the descriptive statistics for the Hospital Bed Capacity (HBC), which in our study was defined as the Brazilian municipalities that will exceed beds (negative values) and those that should have sufficient beds (positive values) because of the patients infected with the COVID-19. For the baseline scenario, we estimated a mean HBC value of −16.73, indicating that, on average, each Brazilian municipality will have a deficit of approximately 17 beds during the period of infection. In contrast, the average value was positive for all mitigation scenarios. For example, if there is a 50% increase in the number of hospital beds and of nurses, doctors, etc. (scenario V), there will be an oversupply of 27 beds across all the municipal districts in Brazil. If we introduce the most aggressive scenario (scenario III), there will be an oversupply of about 46 beds.

Table 3.

Descriptive statistics of the Hospital Bed Capacity (HBC) in Brazil after the influx of patients infected with the COVID-19.

Statistical parameters	Baseline scenario	Scenario I	Scenario II	Scenario III	Scenario IV	Scenario V
Minimum	−64,371.12	−45,085.39	−10,551.56	−126.21	−59,495.45	−54,619.77
Quartile 1	−29.95	−16.92	−10.05	−5.39	−5.74	−11.10
Mean	−16.73	23.26	38.12	46.86	17.17	27.16
Quartile 3	9.40	23.39	25.68	27.95	24.47	32.05
Maximum	4687.27	9471.97	10,353.72	10,814.19	7463.99	10,240.72

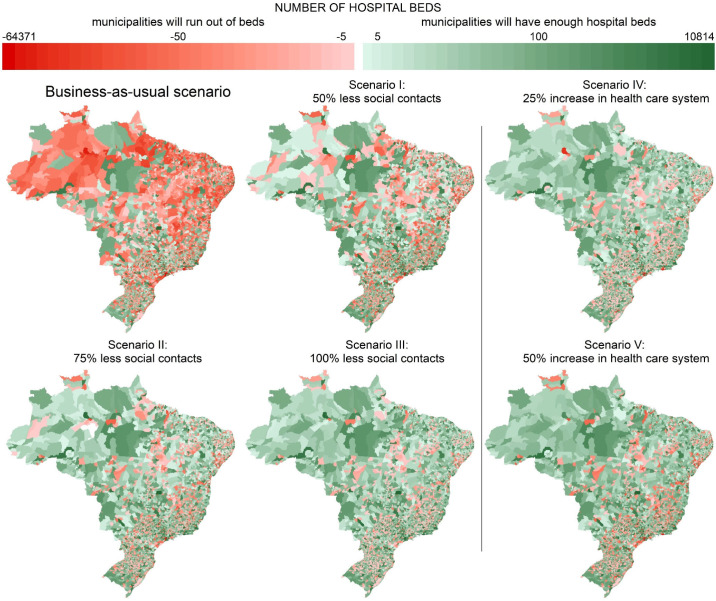
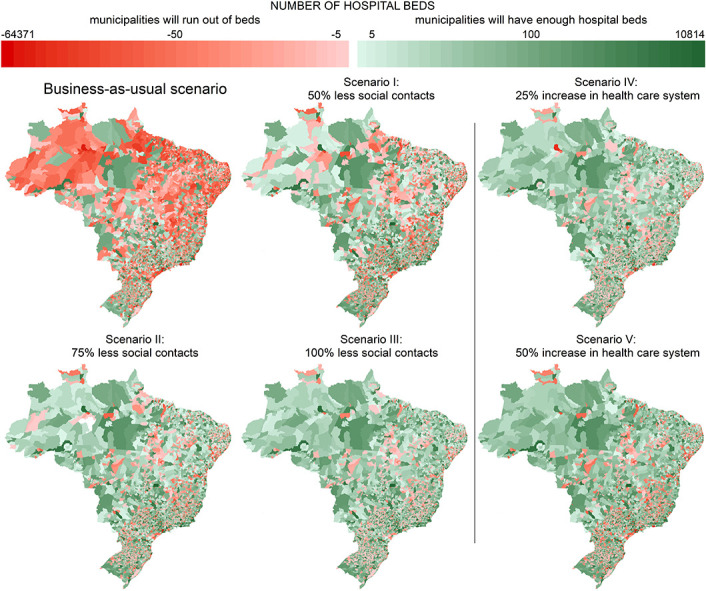
We illustrate the spatial distribution of HBC in Fig. 2 , including the baseline scenario and the five intervention control scenarios. The north and northeast are the Brazilian regions with the highest number of municipalities that will exceed bed capacity due to the COVID-19 when we consider the baseline scenario. Among the 5572 municipalities, 69% (3338) will not have enough hospital beds to receive the infected patients with the COVID-19. Among those 69% of the municipalities that will exceed hospital bed capacity, 52% (1962) municipalities are in the north and northeast. If we account for the five intervention control scenarios, the number of municipalities that will exceed bed capacity decreases to 2702 (scenario I), 2317 (scenario II), 2119 (scenario III), 2259 (scenario IV), and 2205 (scenario V).

Fig. 2.

Hospital Bed Capacity (HBC) in Brazil after the influx of patients infected with the COVID-19.

Currently, limited studies examine the risk of health care capacity, especially in Brazil. A recent report developed by the Brazilian Institute for Health Policy Studies (IEPS) has shown that 30% of the health regions in Brazil are vulnerable to the effects of the COVID-19 due to a deficit of hospital beds (Rache et al., 2020). In our study, this vulnerability was estimated to be 69% of the municipalities. This difference may be explained by spatial scale. While we accounted for the municipal districts, Rache et al. (2020) considered health regions (coarser scale compared with our spatial scale). We argue the finer spatial scale is important because of the challenges that would be faced in moving patients between municipal regions (e.g. impact on resources and increased exposures).

Our findings indicate that limitations on social contacts (scenarios I–III) and the investment on health care system (scenarios IV–V) should have a reasonable effect on reducing the number of municipalities that may run out of beds. We suggest that a larger reduction may be achieved by combining interventions related to social contacts, behavioral changes, and public health. The combination of these interventions has been suggested by initial studies on COVID-19. For example, Chinazzi et al. (2020) report that travel limitations of up to 90% of the traffic in China have a modest effect on reduction in the disease transmissibility. Emanuel et al. (2020) discuss looked at how medical resources can be allocated faily during a COVID-19 pandemic, suggesting that there are data that can be used to project resource demands. Given the challenging on modeling allocation of medical resources in the time of COVID-19, Emanuel et al. (2020) suggest the importance of some points that need to be considered, including the ethical values for rationing health resources and maximizing benefits. Our study may support these points considering that we used a multicriteira framework that can be easily adapted, depending on the local needs across cases.

3.3. Limitations

We recognize our study has some limitations. While we used a robust approach to assign weights to criteria that explain the spatial distribution of COVID-19, we did not account for temporal variation when we integrated the infection rate in the model to estimate the Hospital Bed Capacity (HBC) – described in Eq. (24). In other words, we assumed uniform infection rates over time (e.g., without incubation period, delay onset-to-confirmation), which does not capture all the transmission dynamics of COVID-19. Due to the lack of a temporal parameter in our model, we partially used the classical infection disease model – SEIR (susceptible, exposed, infected, and removed). Our research is also limited with the hierarchical network composed by criteria to represent the risk of the Brazilian health care system to exceed capacity by an influx of infected patients. As we mentioned previously, the variables represented by each criterion do not represent all the complex interactions related to the spread of the COVID-19. Those variables included were the most comprehensive list we could generate from the available data. An important criterion that should be considered in further studies relates to scenarios where not only do the numbers of sick patients increase rapidly, but also the number of sick health care workers. If workers do not have adequate clean Personal Protective Equipment (PPE), including N95 masks on COVID units or surgical masks on non-COVID units, they may get ill or, if they have COVID and are not symptomatic may inadvertently spread the disease. Thus, PPE becomes an essential part of protecting health care workers and patients and assuring that not only beds are available but healthy health care workers who know how to and have the equipment to care for these patients. Lastly, we assume the control strategies do not affect Brazil's infection rate, which was used because the findings are unclear if control strategies affect the long-term infection rate or modify the rates by region.

4. Conclusions

Our study provides a description of a potential multi-criteria decision-making approach to support the implementation of mitigation strategies to control the effects of the COVID-19 epidemic. The flexibility of our approach can guide the design of alternative interventions. In particular, our spatial estimates of the Brazilian municipalities that exceed bed capacity and those that can handle the patients infected with the COVID-19 provide an understanding of the future epidemiological situation in Brazil. We highlight that bed capacity is a starting point in terms of outcomes. In addition to bed capacity, as we mentioned above, there is also ventilator capacity, mask or mask recycling capacity and health care worker capacity, which should be considered in additional studies. We suggest that our study can guide these next investigations. Our estimates can also be used to provide support for the creation of effective health public policies for national, regional, and local intervention, since beds can be created and tents can be set up.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Editor: Dr Wei Huang