An acoustofluidic device for efficient mixing over a wide range of flow rates†

Abstract

Whether reagents and samples need to be combined to achieve a desired reaction, or precise concentrations of solutions need to be mixed and delivered downstream, thorough mixing remains a critical step in many microfluidics-based biological and chemical assays and analyses. To achieve complete mixing of fluids in microfluidic devices, researchers have utilized novel channel designs or active intervention to facilitate mass transport and exchange of fluids. However, many of these solutions have a major limitation: their design inherently limits their operational throughput; that is, different designs work at specific flow rates, whether that be low or high ranges, but have difficulties outside of their tailored design regimes. In this work, we present an acoustofluidic mixer that is capable of achieving efficient, thorough mixing across a broad range of flow rates (20–2000 μL min⁻¹) using a single device. Our mixer combines active acoustofluidic mixing, which is responsible for mixing fluids at lower flow rates, with passive hydrodynamic mixing, which accounts for mixing fluids at higher flow rates. The mechanism, functionality, and performance of our acoustofluidic device are both numerically and experimentally validated. Additionally, the real-world potential of our device is demonstrated by synthesizing polymeric nanoparticles with comparable sizes over a two-order-of-magnitude wide range of flow rates. This device can be valuable in many biochemical, biological, and biomedical applications. For example, using our platform, one may synthesize nanoparticles/nanomaterials at lower flow rates to first identify optimal synthesis conditions without having to waste significant amounts of reagents, and then increase the flow rate to perform high-throughput synthesis using the optimal conditions, all using the same single device and maintaining performance.

Introduction

Effectively mixing solutions and samples is a critical task for many industrial and biomedical applications.^1–3 As such, any successful lab equipment designed to accomplish these tasks must be able to thoroughly mix solutions in preparation for downstream use. For example, effectively and consistently combining reagents is critical for the self-assembly or nanoprecipitation of synthetic nanoparticles and nanomaterials; incomplete mixing of nanomaterial synthesis reagents can alter the physical properties of the particles that are generated, greatly affecting their effectiveness in their final application.² More specifically, the reason that nanomaterials have garnered so much attention in recent years is because of their unique and advantageous properties;^4,5 however, if these nanoparticles cannot be synthesized in a repeatable manner, then their advantages cannot be applied to real-world applications.

Microfluidic devices,⁶ with vast improvements in repeatability and precision compared to bulk methods,⁷ have been presented as optimal platforms for mixing reagents in a precise and controllable manner.^8,9 Over the last several decades, researchers have developed many novel methods for mixing in microfluidic settings. The simplest of these mixing methods are generally passive mixers,¹⁰ which traditionally rely on channel geometry to modify the flow profile and induce mixing; these devices use specialized structures,¹¹ expansions,¹² or bends¹³ in the channel to encourage and increase fluid interaction. These devices gained popularity due to their inherent simplicity and reduced reliance on external equipment.¹¹ That is, simply pumping the fluids through the channel achieves mixing through hydrodynamic interactions of the sample flows. While this simplicity provides benefits in cost, maintenance, and operational complexity, achieving mixing based on hydrodynamic or diffusion based interactions alone severely limits the use of this technology in many applications. With regards to nanoparticle synthesis, reliance on hydrodynamic forces usually entails the use of high flow rates that may waste expensive reagents during parametric optimizations; decreasing the channel dimensions to combat this high flow rate requirement can drive up fabrication costs, and increase the risk of clogging or pressure build up during fluid delivery. On the other hand, relying on diffusion alone results in extremely low production rates, and struggles to fully combine the samples, potentially generating more inconsistent and less desirable batches of nanoparticles.¹⁴ Researchers have made progress in designing passive mixers that function over wider ranges of flow rates,¹⁵ but obtaining complete mixing across a very broad spectrum of flow rates (three orders of magnitude from 1–1000 μL min⁻¹) using a single device presents a challenge for previous mixing methods.

Based on these deficiencies, researchers developed active mixing technologies such as optical,¹⁶ magnetic,¹⁷ electrokinetic,¹⁸ or acoustic^19–23 methods to mix or perturb samples. Some of these technologies have reported promising performance over a wide range of flow rates, such as a magnetic mixer which rotates steel balls within the channel;²⁴ however, the addition of steel balls in the channel, and use of a magnetic force for operation may prevent integration with alternative analysis methods, such as magnetic bead based assays.²⁵ One promising solution for active microfluidic mixing that avoids the presence of foreign objects, improving its integration potential, is the sharp-edge based acoustofluidic micromixer,^26,27 which relies on acoustic streaming to mix fluids.²⁸ In these devices, sharp protrusions in the channel sidewall geometry oscillate in response to excitation from a piezoelectric transducer. These oscillations have been shown to be extremely effective for mixing in numerous applications,²⁹ including reagent mixing,³⁰ biological sample preparation,^27,31 and nanoparticle/nanomaterial synthesis at low flow rates;¹⁴ however, the performance of this technology at higher flow rates has been shown to be diminished. Recently, researchers have designed a micromixer similar to the sharp-edge mixer which relies on exciting a sandwiched silicon oscillator which also has protrusions;³² this device focuses on the ability to successfully use acoustic technologies for high throughput mixing. While successful, the fabrication procedure for this device involves the alignment of multiple layers, complicating its fabrication. Additionally, while the high throughput performance is commendable, the nanoparticle size increased significantly as the flow rate was decreased to even moderate levels (250–500 μL min⁻¹). As a result of these observations, we believe that the design of a simple device that can effectively mix solutions at both low and high flow rates using a single device would be extremely beneficial to many applications, including nanoparticle/nanomaterial synthesis or multistep biological assays with complex protocols.

Here, we present a new acoustofluidic mixer which combines acoustic mixing effects with passive hydrodynamics to thoroughly mix solutions over a wide range of throughputs; this variable throughput performance is achieved using a one layer microfluidic chip design, which reduces its complexity compared to previous multi-layer devices,^33,34 and greatly simplifies the fabrication procedures. Our device functions based on the combination of hydrodynamic and acoustic effects, which serve to mix fluids in the channel through complimentary mechanisms. That is, the acoustic mixing mechanism is effective at combining solutions at low flow rates, whereas the hydrodynamic mixing effect is more successful at higher throughputs. Thus, combining these mechanisms yields a much more capable and versatile platform. In our combined acoustofluidic mixer, the system is effective at high flow rates with the acoustics OFF, and effective across the whole flow rate range with the acoustic signal ON when acoustic and hydrodynamic mixing is combined. In order to fully characterize the working mechanism of the device, we experimentally analyzed the device functionality using a laser Doppler vibrometer, and compared these results to numerical simulations.

Additionally, using numerical simulations, we explored the mixing performance of the device over a range of input flow rates. After exploring the computational domain, we tested the device’s mixing performance and demonstrated its potential real-world application by generating synthetic nanoparticles which have previously been shown as potential targeted drug carriers. Altogether, our results serve as a comprehensive analysis and presentation of the acoustofluidic mixer as a capable and effective microfluidic mixing solution for implementation in point-of-care and benchtop microfluidic platforms for biological testing and nanomaterial synthesis, amongst other mixing applications.

Device design and concept/mechanism

In this work, we sought to combine the active mixing benefits of acoustic technology with the high flow rate passive benefits of hydrodynamic mixing. To that end, Fig. 1a and b provide a schematic and photo of the assembled acoustofluidic mixing device, respectively. The foundation of the acoustofluidic device is a thin glass coverslip; this glass coverslip serves to transfer the vibration energy from the acoustic transducer (shown in the figure) into the PDMS chip via flexural waves that travel out from the transducer and along the glass coverslip. The channel also has two inlets, which allow for injection of separate samples, and a single outlet for collecting the mixture. The primary design of the microfluidic channel geometry (Fig. 1c) consists of repeated sharp-edge structures and Tesla structures. The sharp-edge structures oscillate in response to vibration from the transducer, producing acoustic streaming in the channel to mix the samples. The design of the Tesla structure region was guided by previous explorations into using so-called modified Tesla structures to achieve hydrodynamic mixing while staying within the geometric restrictions established by the design of the sharp-edge structures.³⁵ Specifically, the sharp-edge mixer is designed with a channel width of 600 μm and a height of 100 μm, which defined the channel size in the Tesla structure region. In total, there are eight sets of sharp-edge structures and recirculation zones along the length of the channel to ensure complete mixing across a range of inflow parameters.

Fig. 1.

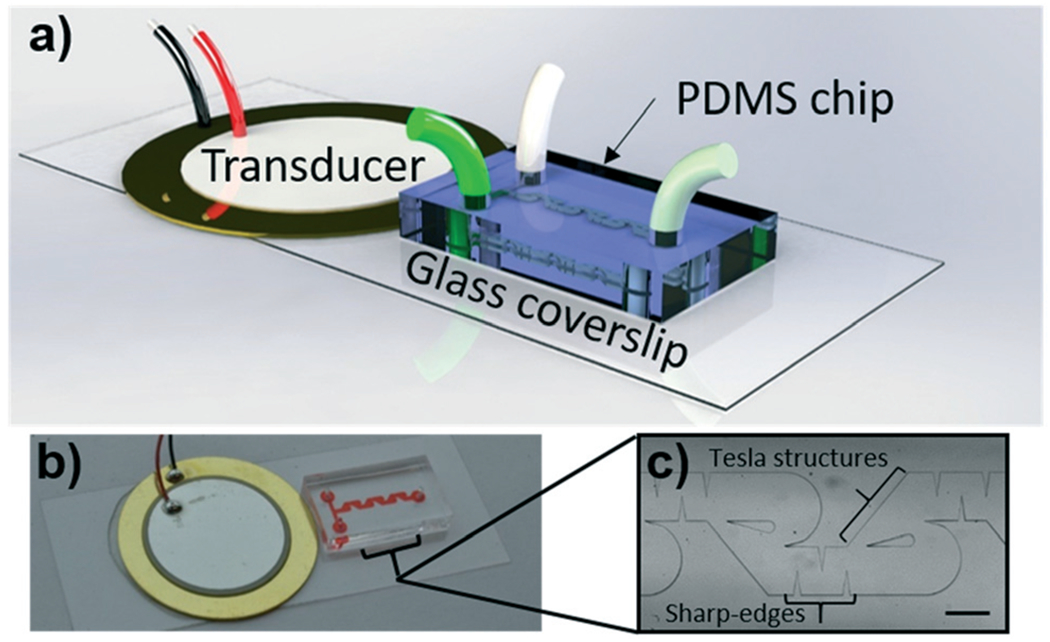
a) Schematic of the acoustofluidic mixing device. b) Photo of the acoustofluidic mixing device with a close-up (c) of the microfluidic channel design. Sharp-edge structures (vertical) and recirculation zones (rounded sections) can be seen in the channel. Scale bar: 500 μm.

As an overview of the technological components that contribute to the combined device, the sharp-edge based mixer is effective at low flow rates, but is less effective in the high flow rate region. At the same time, the Tesla mixer, in isolation, cannot effectively extend its influence to the low flow rate range, thus producing a gap in mixing performance. The combined acoustofluidic mixer, however, has the potential to bridge this gap. With the acoustic signal OFF, the mixer has performance similar to the Tesla mixer, where the channel geometry achieves mixing at high flow rates. Notably, the addition of the sharp-edges into a Tesla mixer design should add additional obstruction to the flow and slightly improve the moderate flow rate passive performance. When the acoustic signal is ON, the synergistic effect of the acoustic mixing and hydrodynamic forces can effectively combine solutions across the entire flow rate spectrum. An additional concern in the design of the device is channel clogging; while we did not experience clogging during our testing, alternative applications and experiments which utilize larger or more adhesive substances could increase the chance of clogging. If this is the case, then the overall dimensions of the device could be tailored to reduce this likelihood, similar to our previous experiments.²⁷

Materials and methods

Fabrication of the acoustofluidic mixer

To assemble the acoustofluidic mixer, the transducer is attached to the coverslip using an epoxy (PermaPoxy™ 5 Minute General Purpose, Permatex), and the PDMS chip is bonded onto the glass coverslip using an oxygen plasma treatment (BD-10AS, ElectroTechnic Products). The microfluidic channel is formed with the glass coverslip as its bottom, and PDMS for the other walls and channel features. The PDMS portion of the channel is fabricated using a deep reactive-ion etching (DRIE) technique.³⁶ Briefly, a hard silicon master mold is fabricated using DRIE, and this mold is used to form PDMS chips by combining Sylgard 184 silicone elastomer and curing agent (Dow Corning) at a ratio of 10 : 1. The PDMS chips are cured at 65 °C for one hour before being cut to size, punched with inlets and outlets, and bonded to the glass coverslip. Assembled chips are baked in the same oven overnight to ensure a stable bond and full curing of the polymer. The DRIE process is necessary to generate the high aspect ratio features of the microchannel, which can be seen in Fig. 1c. In order to ensure that there is a high level of repeatability across various devices (especially with regards to frequency response), care was taken in each step of the fabrication process. For example, alignment structures were designed into the photolithography mask, and a template was used for alignment during bonding of the channel and transducer; the template consisted of CAD sketch of the device components (glass coverslip, PDMS channel, and transducer) printed out and used as a visual reference beneath the glass coverslip for careful alignment during assembly. Together, these steps improved the consistency of device assembly and performance. As an additional consideration of the device performance, one must consider the device’s reusability in practical applications; depending on the application, this device may be reusable for simple, basic testing by thoroughly flushing the channel, or may be disposable for sensitive, critical biological assays to avoid cross contamination, given its low cost.

Experimental measurement of vibration patterns

During our investigation, we experimentally imaged the vibration patterns on the glass substrate using a laser Doppler vibrometer (PSV-400, Polytec). The acoustofluidic mixing device was secured in the custom microscope slide holder (Fig. S1†); the custom holder ensures that the chip is secured in the same manner for each test, reducing deviations in vibration patterns and improving performance consistency (this holder was utilized during all experimentation within this article). After securing the device to the holder, the back of the slide was sprayed with an aerosol of white developing particles (Spotcheck® SKD-S2 Developer, Magnaflux) that make the slide opaque for measurement using the laser Doppler vibrometer. During testing, we flipped the device holder upside down to expose the underside of the coverslip to the laser light; this ensured that we would have a clear, flat surface at a consistent distance from the laser source, as opposed to the crowded top side of the coverslip which holds the transducer and the PDMS chip. Next, using the software of the vibrometer, we established our testing region on the exposed area of the glass coverslip and assigned the scanning mesh density. For scanning, we analyzed transducer excitation frequencies from 0 kHz to 10 kHz with a step size of 50 Hz. The vibrometer would then sweep this frequency range and collect the wave pattern, and vibration amplitude for each point on the acoustofluidic device. Using a custom Matlab script, we were able to extract the vibrometer data and plot the wave patterns at any given frequency, as well as determine the overall frequency response at a selected point.

Modeling of vibration patterns in the mixing device

In order to explore the generation of vibration in the sharp-edges, we utilized a custom numerical simulation built in COMSOL Multiphysics® modeling software. The model was based around the piezoelectric multiphysics module of COMSOL, which couples the effects of the electrostatics and solid mechanics interfaces. Using these interfaces, a detailed model of the acoustofluidic mixing device was built, which included the piezoelectric disc, brass base of the transducer, a thin epoxy layer, the glass coverslip, and the PDMS chip; a detailed diagram of the model is provided in Fig. S2.† In order to reduce the complexity of the model, we used a simplified microfluidic channel design, which simply had one set of sharp-edge structures in it. We modeled the boundaries at the ends of the glass slide as low reflecting boundaries in an attempt to match the vibrometer measurements we previously analyzed. This model allows us to apply an oscillatory excitation signal to the transducer, and model the wave propagation on the glass slide.

Modeling of streaming and mixing behavior within the channel

The model outlined in the previous section investigated the vibration of the entire mixing device on a large scale; in this work, we also sought to simulate the mixing performance within the sharp-edge region of the acoustofluidic mixer during acoustic excitation; that is, transitioning to the micro-scale and investigating the fluid motion within the channel. Numerically, exploring the acoustic mixing effect in the fluid domain requires one to solve the mass and momentum balance equations for the fluid. For a compressible, Newtonian fluid, these equations can be written in the following form:

$$\frac{\partial \rho }{\partial t}+\rho (\nabla \cdot u)=0,$$ (1)

$$\rho \frac{\partial u}{\partial t}+\rho (u\cdot \nabla )u=-\nabla p+\mu {\nabla }^{2}u+\left({\mu }_b+\frac{1}{3}\mu \right)\nabla (\nabla \cdot u),$$ (2)

where eqn (1) represents the mass conservation equation, and eqn (2) provides the governing equation for momentum conservation. Here, ρ, u, p, μ, and μ_b represent the fluid density, velocity, pressure, and the shear and bulk dynamic viscosities, respectively. We also define a linear relationship between the fluid pressure and the density, as follows:

$$p=c_0^2\rho$$ (3)

where $c_0^2$ represents the speed of sound in the fluid at rest. Solving these equations will yield the motion in the fluid domain of the channel, but doing so is difficult because of the large disparities between the length (geometric dimensions of the channel vs. the acoustic wavelength) and time scales (characteristic time for mean fluid motion vs. acoustic signal time period);³⁷ additionally, due to viscous dissipation, the fluid response to a harmonic input is not traditionally harmonic itself,³⁸ further complicating the solution methodology. As such, a perturbation approach is utilized to solve for the acoustic response of the system. This approach, suggested by Nyborg³⁹ and utilized extensively in the research field,⁴⁰ splits eqn (1) and (2) into their zero, first, and second order components, where the three orders represent the background, oscillatory, and steady acoustic streaming flows, respectively. This is done by assuming the following form for the fluid velocity, pressure, and density:

$$\begin{gathered} u=u_0+\epsilon {\tilde{u}}_1+{\epsilon }^2{\tilde{u}}_2+O({\epsilon }^3) \\ p=p_0+\epsilon {\tilde{p}}_1+{\epsilon }^2{\tilde{p}}_2+O({\epsilon }^3) \\ \rho ={\rho }_0+\epsilon {\tilde{\rho }}_1+{\epsilon }^2{\tilde{\rho }}_2+O({\epsilon }^3), \end{gathered}$$ (4)

where ε is a smallness parameter defined as the ratio between the boundary displacement and the characteristic length. Utilizing this approach requires one to substitute the expansions from eqn (4) into eqn (1)–(3), and group terms of equal order; in doing so, equations that are successively coupled to the lower order solutions are obtained. That is, the equations in the first order of ε contain terms of order zero, and the second order equations contain terms of both lesser orders. Further detail on the derivation of these expansions, as well as the boundary conditions, can be found in our previous work.⁴¹ Converting these expanded equations into their weak form, and implementing them into COMSOL enables us to solve for the zero, first, and second order fluid velocities in the channel. Once calculated, these solutions can be combined and implemented in the convection-diffusion equation,

$$\frac{\partial c}{\partial t}+\nabla \cdot ({\mathit{cu}}_c)=D{\nabla }^{2}c,$$ (5)

for determining the mixing performance of the acoustofluidic mixer. In eqn (5), c, u_c, and D, represent the concentration of the sample, flow velocity, and diffusion coefficient, respectively. Further detail on the derivation and interpretation of the flow velocity to be used for this equation can be found in our previous work.⁴¹ This numerical model allows us to investigate the mixing performance of the device across a range of flow rates and input conditions.

Experimental operation of the mixer

To experimentally test the mixing performance of the device, we made a fluorescent solution by dissolving fluorescein powder into DI water; this provided us with a visual method for analyzing the mixing performance of the device. Equal volumes of the fluorescein solution and pure DI water were injected into the channel at varying flow rates through the two inlets using a syringe pump (Nemesys). An oscillatory signal was generated using a function generator (FG3011, Tektronix, USA), and amplified using a power amplifier (5A250A, Amplifier Research, USA) before being passed into the transducer. In some applications of acoustofluidic technology, the transducer used to induce vibrations may generate excessive heat that can negatively affect device performance or sample quality; however, previous testing with sharp-edge based acoustofluidic mixing chips has demonstrated that the temperature of the transducer does not rise above 30 °C, even after 20 minutes of continuous operation.⁴² During test, we first determined the optimal frequency of the mixer by visually examining which frequency excitation signal produced the best mixing performance; this was done by varying the frequency in steps of 100 Hz from 4 kHz to 6 kHz and visually assessing the level of uniformity achieved at the outlet. Notably, the need to sweep the frequency domain for the optimal excitation conditions is a significant hindrance to the widespread adoption of this technology; many factors including PDMS alignment, transducer bonding, and how the device is secured can affect the final operational efficiency at a given frequency. Additionally, the external equipment, tubing, and setup restricts its usage. As previously discussed, steps were taken to improve the repeatability of device operation through consistent manufacturing, and we have also recently taken efforts to improve the adoptability of the technology through the design of user friendly control platforms.^43,44

Results and discussions

Vibration profile investigation

Sharp-edge acoustofluidic technology relies on the vibration of the microscale sharp-edge structures within the channel to create acoustic streaming. Even though all previous sharp-edge platforms have relied on this phenomenon,^26,27,31 little work has been done to investigate the development of this actuation on a fundamental level. That is, research has yet to explore the wave patterns that are generated by the piezoelectric transducer to initiate sharp-edge vibration. In order to gain a better understanding of this principle, we experimentally investigated and numerically explored the generation of acoustic waves in the entirety of the mixer, and explored how these waves vibrate the sharp-edges to generate acoustic streaming.

Using a laser Doppler vibrometer, we explored the wave patterns generated within the acoustofluidic mixing device when an oscillatory signal is applied to the piezoelectric transducer. As seen in Fig. 2a and in Video S1,† successive waves propagate out from the transducer and travel towards the other end of the slide, where they are absorbed by the boundary; we believe it is the tape at the end of the slide that is able to absorb the energy from the wave with minimal reflection. We found that the wave motion on the glass slide is consistent with flexural wave theory, which predicts the speed of sound in the glass substrate using the following relationship:⁴⁵

$$c={\left(\frac{{\mathit{Ed}}^2}{3\rho (1-{\nu }^2)}\right)}^{\frac{1}{4}}\sqrt{\omega },$$ (6)

where E, d, ρ, v, and ω are the Young’s modulus, half thickness, density, Poisson’s ratio, and angular frequency, respectively. Substituting in property values from Table S1,† yields a theoretical wave speed of 88.4 m s⁻¹, whereas measurements extracted from the vibrometer data yielded a wave speed of 91.5 m s⁻¹. Also, similar to our previous experiments, the frequency response of the system as measured by the vibrometer (Fig. 2b) showed a peak at 5.3 kHz. This result is consistent with our previous experimental explorations, wherein the optimal device performance was determined by sweeping the frequency domain and finding the optimal pumping or mixing performance; that is, previous experimental investigation found that the optimal pumping or mixing frequency was located near 5–5.5 kHz, the same frequency peak as measured using the vibrometer data, which validates our previous experimental findings. Notably, we can see that the peak of the frequency spectrum measured using the vibrometer begins around 4 kHz, rises to its maximum at 5.3 kHz, and decreases through around 7 kHz. The breadth of this response is not unexpected given the damping nature of the PDMS elastomer and taped boundaries, which will act to damp the system and widen the resonance peak. Additionally, this is also consistent with experimental findings, where complete mixing can occur over a small range of flow rates; this range/breadth of frequency response makes the device more accommodating to slight errors in frequency selection while maintaining performance.

Fig. 2.

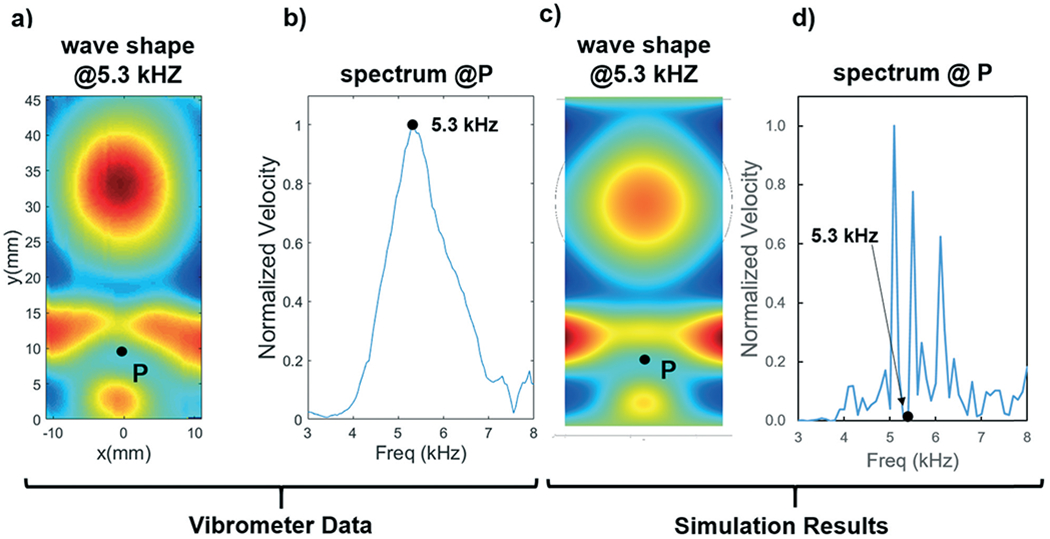
a) Plot showing the displacement of the glass coverslip measured using a laser Doppler vibrometer. b) Frequency response at the point P shown in (a), with a peak at 5.3 kHz. c) Simulated displacement profile generated using COMSOL Multiphysics®. d) Simulated frequency response for the glass slide. Simulation results qualitatively match with the vibrometer data for the wave shape, but predict a lower overall vibration speed at the given frequency; the peaks of the simulated frequency response, however, follow the same trend as the vibrometer data, with a maximum peak at 5.1 kHz.

Having experimentally studied the vibration profiles on the glass slide, we next sought to investigate the transmission of waves from the glass slide into the sharp edge tips in more detail. To do this, we constructed a model of the acoustofluidic mixer in COMSOL Multiphysics®. Using a time domain study, we first visualized the pattern of the vibration amplitude on the glass slide (Fig. 2c). Qualitatively, we noted that the vibration profile measured by the vibrometer and predicted by the model followed the same wave pattern. In both sources, the wavefronts leaving the transducers start out uniform, and then focus their energy towards the side of the glass substrate as they propagate towards the end of the coverslip. Notably, there are subtle differences between the simulation and experimental results, most readily seen in the lack of symmetry in the case of the vibrometer measurement. However, this result is to be expected seeing that the symmetry of the experimental device is going to have minor imperfections including the alignment of the PDMS chip, transducer, or even the application of the epoxy layer. Using the model and a frequency domain study, we were also able to plot the frequency response curve shown in Fig. 2d; a peak in the frequency spectrum plot at 5.1 kHz is consistent with our previous sharp-edge device testing, which has shown optimal device performance near this value (5.3 kHz ± 0.3 kHz).⁴³ However, the frequency spectrum produced by the numerical model predicts that the vibration speed with a 5.3 kHz excitation signal will be significantly lower than its excitation at 5.1 kHz. This is in disagreement with the experimental findings. However, the peaks of the simulated response curve follow the same downward trend as the experimental results; considering that the wave shape predicted by the model agrees with the experimental findings, this spectrum plot suggests that the model should be used for identifying a starting point for frequency and wave mode analysis/optimization, but that it should not be used to provide an exact value for the magnitude of vibration at a specific frequency.

Next, we sought to investigate the vibration of the sharp edge tips that results from the piezoelectric excitation. To do this, we utilized a time domain study which would enable us to visualize the dynamic movement of the sharp-edge tips as waves propagate past them. Using a time domain study, we generated a video of the wave propagation on the glass slide (Video S1†), and compared it to the pattern measured using the vibrometer. Examining this study, we found that the numerical model and the experimental findings qualitatively matched with regards to the wave propagation profile. Having visually validated the time domain study, we focused on analyzing the vibration in the sharp-edge tips of the PDMS chip. As shown in Fig. S3,† we can see that the tips oscillate from a positive to negative position. This is consistent with the oscillations seen during experimentation, thus validating and confirming the vibration mechanism in the acoustofluidic mixing device, and previous sharp-edge devices for that matter; while this investigation qualitatively shows the tips of the sharp-edges vibrating in an oscillatory manner, we have experimentally noted that the sharp edges will oscillate free of the glass substrate. We explored the microstructure of the sharp-edge (Fig. S4†), and found that the end of the tip has a slight curve, most likely a result of the high aspect ratio at the feature’s tip. We hypothesize that the curve in the sharp edge, in combination with the vibrational energy from the transducer, enable the sharp-edge to overcome bonding forces between the glass substrate and the PDMS achieved during fabrication. Notably, these observations suggest that it may be possible to encourage larger vibration amplitudes in the sharp edge tips by covering them during the plasma treatment phase of fabrication, thus creating a weaker bond with the glass substrate. Comprehensive modelling of this free vibration phenomenon, however, was beyond the scope of this work, and the presented simulations solely validate the working mechanism, in principle.

Computational streaming and mixing investigation

Knowing that previous research already explored the high flow rate fluid profiles in microfluidic channels with modified Tesla structures,^35,46 here, we sought to numerically explore the hydrodynamic and acoustic streaming patterns within the sharp-edge region of the mixing device. We started off by considering the flow profile produced without any acoustic actuation. In this investigation, we constructed a 3D model of the entire mixing device in COMSOL. Using the laminar flow interface, we qualitatively studied the streaming patterns through the sharp-edge region and compared them to experimental observations conducted with fluorescent tracer particles (Fig. 3). Flow rates reported in this figure provide the total flow rate for the channel, as a sum of the inputs from both inlets. As seen in both the numerical model and experimental image, the low (e.g., 20 μL min⁻¹) flow rate produces uniform, laminar streamlines that follow the curve of the sharp-edges, consistent with the Coanda effect.⁴⁶ Increasing the flow rate to 400 μL min⁻¹ yields slight flow separation on the back sides of the sharp-edges; this separation is seen in both computational and experimental figures, and is indicative of the onset of hydrodynamic mixing. At the high end of the flow rate spectrum, large areas of recirculation can be seen within and following the sharp-edge region, which aids in the thorough mixing of the solutions; capturing experimental images at these high flow rates is difficult, even using a fast camera, but nonetheless, the recirculation zones in the channel can be seen in the experimental image for 2000 μL min⁻¹. This investigation elucidated the hydrodynamic mixing profiles in the channel at various flow rates, but we still needed to explore the acoustic-assisted mixing performance. In order to properly model the acoustic streaming within the fluid domain, we experimentally measured the tip displacement so that we could utilize the proper vibration magnitude in the simulation; we found that the tips oscillated 30 μm from maximum to minimum and so we used this value in our numerical model. Although the design of the modified Tesla structures inherently creates additional “sharp-edges” in the channel that would be subject to acoustic excitation, our numerical model and experimental exploration showed that there is very little vibration in these tips (Fig. S3† provides experimental evidence of this diminished vibration); these structures are oriented perpendicular to the traditional sharp-edges, and our numerical model suggested that the vibration amplitude in this direction is 100 times smaller than the vibration that excites the sharp-edges.

Fig. 3.

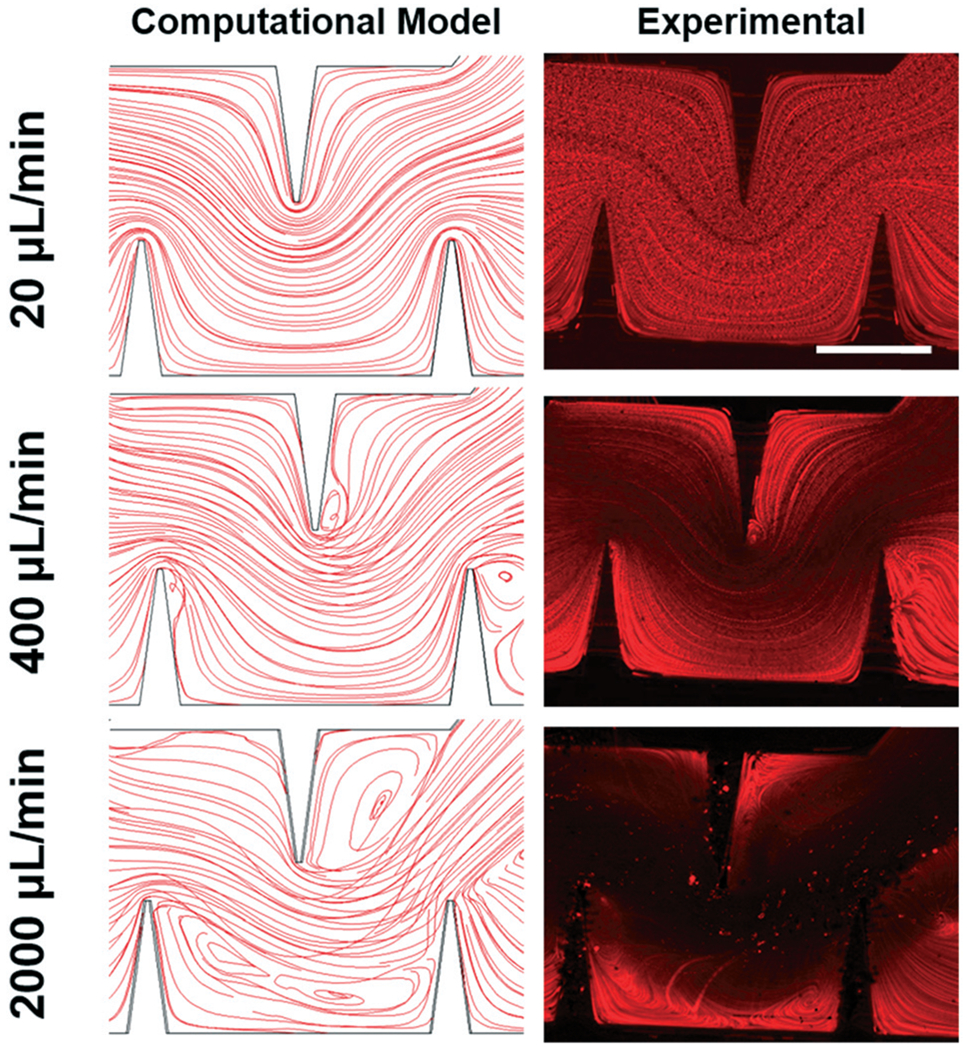
Simulated and experimental streaming patterns through the sharp-edge region. Both simulation and experimental results show uniform, laminar streamlines that follow the curve of the sharp-edges at the low (e.g., 20 μL min⁻¹) flow rate, flow separation at the 400 μL min⁻¹ flow rate condition, and larger vortexes produced at 2000 μL min⁻¹. Scale bar: 250 μm.

As such, we only considered the vibration of sharp-edges that were perpendicular to the flow path. In doing this simulation, we also attempted to avoid including the effects of hydrodynamic mixing by utilizing a similar background flow profile in each flow rate case. Fig. S5† provides a representative plot of the velocity magnitude and streamlines of the background flow (zero order solution) in the channel. This zero order velocity profile was calculated assuming Stokes flow, which ignores non-linearity in the governing equations that can cause the profile to deviate at higher flow rates. Utilizing this relatively consistent laminar flow profile reduces the effect of hydrodynamic mixing in the model, and enables us to probe how the acoustic streaming velocity is able to disrupt the varied background flow. Fig. 4a provides the results of the mixing simulation conducted at the same three flow rates shown in Fig. 3. It can be seen that at 20 μL min⁻¹, the acoustic streaming is strong enough to overcome the background flow and fully mix the samples in the channel. This concentration profile predicted in the computational result (Fig. 4a) is visually consistent with the low flow rate experimental result (Fig. 4b). However, at the higher flow rates, the acoustic streaming is not able to overcome the inertial forces of the strong background flow, and the solutions remain unmixed. We can see from the computational result that the acoustic streaming is only able to slightly disturb the flow near the sharp-edge tip in the 400 μL min⁻¹ condition. These results are visually consistent with previous experimentation where increasing the flow rate in the channel eventually overpowers the acoustic streaming and limits the effect of the sharp-edge acoustofluidic mixing platform.

Fig. 4.

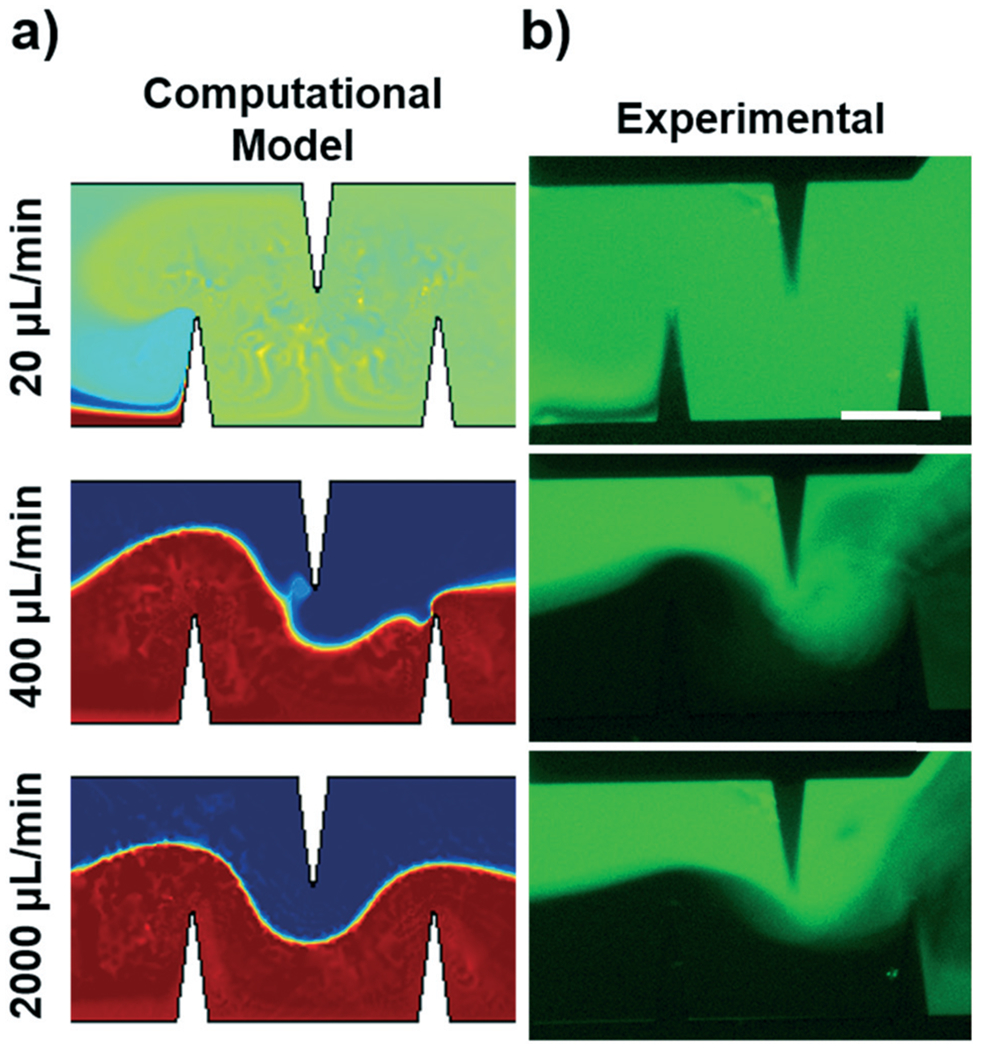
a) Simulated mixing performance in the acoustofluidic device across varied flow rates. The background flow (zero order) for each flow rate for each simulation was relatively unchanged except for the magnitude of the fluid velocity, so as to probe the acoustic mixing potential. b) Experimental mixing performance in the acoustofluidic device across various flow rates. A good comparison between the simulated and experimental data is seen for each flow rate. Further mixing can be seen as the fluid leaves the sharp-edge region due to hydrodynamic effects (right sides of the photos), but due to numerical complexity this hydrodynamic effect was not modelled in the COMSOL simulation. Scale bar: 250 μm.

We also experimentally observed the flow profiles using the new mixing device (Fig. 4b), and experimentally confirmed the findings from the simulation; the photos in Fig. 4b similarly show complete mixing at 20 μL min⁻¹, and reduced acoustic streaming effects as the flow rate is increased. However, these experimental results include hydrodynamic effects (unable to be decoupled), so the results are not a direct comparison to the simulations; this deviation can be seen in the photos directly after the sharp-edge region, where hydrodynamic mixing occurs at higher flow rates. Due to the complexity of the model, we have yet to model the entire system numerically with a high degree of accuracy. Nonetheless, we believe that when the recirculation and flow separation around the sharp-edges is combined with acoustic streaming effects and flow manipulation via the Tesla structures, the two mechanisms (acoustic streaming, hydrodynamic mixing) will be able to overcome viscous and inertial effects regardless of sample flow rate.

Mixing characterization experiments

Having simulated the mixing performance of the acoustofluidic device, we sought to experimentally validate its functionality across a range of flow rates. Based on a visual observation of the mixing performance at various input frequencies, we found that the frequency of 4.9 kHz provided optimal mixing performance, which was consistent with the location of the peak seen in the frequency response curve of the vibrometer data and COMSOL simulation. Using this frequency, and an applied voltage of 56 V, we then captured fluorescent images of the mixed solutions at the outlet of the device for various flow rates. We also captured images of the channel exit for various flow rates with the acoustic signal OFF. We characterized the mixing performance under these various parameters using the mixing index, and plotted all of the results in Fig. 5a; flow rate values in this figure are reported as the sum from both inlets. The mixing index is defined as the standard deviation of the normalized fluorescence intensity in the channel; a more homogenous solution will have a smaller standard deviation, which implies that a smaller mixing index is indicative of better mixing. A value of 0.1 is commonly used to define complete mixing.^26,41 As can be seen in Fig. 5a, when the acoustic signal is OFF, the mixing index follows the expected trend. At the lowest flow rates (20–100 μL min⁻¹), the mixing index actually worsens with an increase in flow rate. This can be attributed to the reduction in diffusion based mixing that occurs due to the shorter time the fluids spend in the channel. After this low flow rate regime, the mixing index begins to improve, with a sizeable decrease seen between 200 and 400 μL min⁻¹, which was identified as the start of the flow separation in the sharp-edge region during our simulations (Fig. 3). At the highest flow rates tested (1500–2000 μL min⁻¹), the mixing performances with and without the acoustic effect were indistinguishable from one another. Once the acoustic signal was turned ON, complete mixing was achieved across the entire flow rate spectrum (20–2000 μL min⁻¹). At the lowest and highest flow rates, the mixing index was well below the value for complete mixing, and even the middle of the flow rate range maintains complete mixing. Representative photos of this mixing have been provided in Fig. 5b and c, where low, middle, and high flow rate mixing photos are provided for when the acoustics are OFF (Fig. 5b) and ON (Fig. 5c). The vertical dashed line in Fig. 5b (right) provides the location that the fluorescent profile was collected in order to evaluate the mixing index. The large gradient in the channel at low flow rates is erased when the acoustic signal is activated. And, although there is a relatively large gradient in the fluorescence signal in the 400 μL min⁻¹ channel without acoustic actuation, this inhomogeneity is significantly improved with the addition of acoustic mixing. The high flow rate photos show that the hydrodynamic effects are sufficient to achieve mixing on their own, but that the acoustic streaming does remove some signal inconsistencies as well. Altogether, these results demonstrate the successful combination of acoustic and hydrodynamic effects to design a single device capable of mixing at a large range of flow rates (20–2000 μL min⁻¹).

Fig. 5.

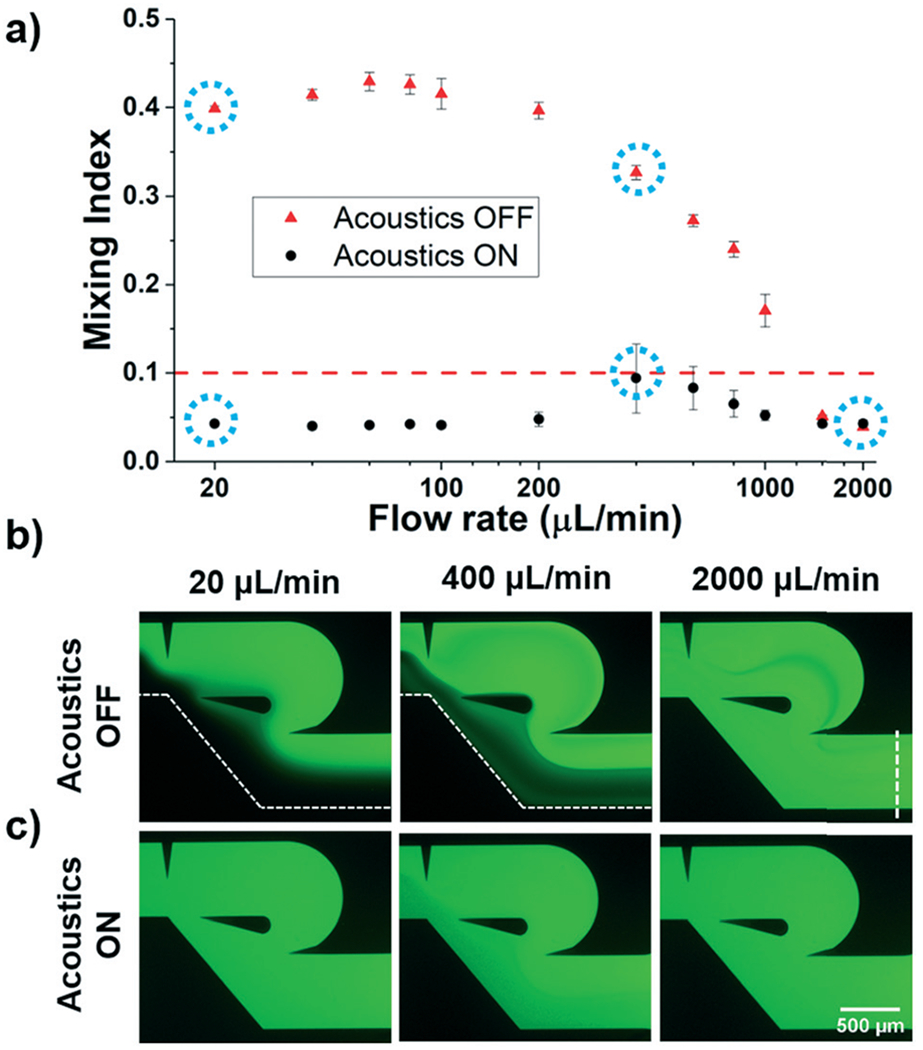
a) Plot showing the experimental performance of the acoustofluidic mixing device across a range of flow rates (20–2000 μL min⁻¹). Mixing performance is characterized using the mixing index, where 0.1 or lower indicated complete mixing (dashed red line). With the acoustic signal ON, uniform mixing was achieved across the entire flow rate range tested (n = 3). Blue dashed circles correspond to the fluorescent photos taken at the outlet of the device at various flow rates with the acoustic signal (b) OFF and (c) ON, respectively. The dashed line in the right photo of (b) indicates the line used to evaluate the mixing index shown in (a).

Nanoparticle generation over a wide range of flow rate

In order to demonstrate a practical application of our acoustofluidic mixing platform, we generated nanoparticles that have been shown to be good carriers for drug loading and other therapeutic applications. To form our nanoparticles, we chose the poly(lactic-co-glycolic acid)–poly(ethylene glycol) (PLGA-PEG) copolymer. As described in previous studies, this copolymer is well-suited for drug delivery since it is biodegradable and biocompatible;^2,34 the structures of the PLGA and PEG also improve drug loading and delivery performance as well. In order to synthesize the nanoparticles, a PEG methyl ether-block-PLGA (764752-1G, Sigma Aldrich) was dissolved in acetonitrile (26WD84, Grainger) at a concentration of 10 mg mL⁻¹. The dissolved polymer and acetonitrile were injected into the channel where they were mixed with DI water at a ratio of 3 : 7. Upon mixing with the water, the PLGA-PEG polymer strands form nanoparticle complexes such that the hydrophobic PLGA is protected by a shell of hydrophilic PEG; this process is illustrated by the schematic in Fig. S6a.†

With the acoustofluidic mixer outlined in this work, we were able to generate nanoparticles across a wide range of flow rates, from those used in our previous experiments (<100 μL min⁻¹) to much higher levels (up to 2000 μL min⁻¹). We analyzed the nanoparticles generated with and without acoustic actuation at total flowrates of 20, 400, and 2000 μL min⁻¹ using dynamic light scattering technology (Zetasizer Nano ZSP, Malvern). Table 1 provides a summary of nanoparticle sizes and polydispersity indices generated during testing (Fig. S6b† provides plots of the particle distributions as well). Notably, similar to the mixing performance shown in Fig. 5a, the difference in size distribution between samples with and without acoustic actuation decreased as the flow rate increased. This is expected since the mixing performance achieved by hydrodynamics alone approached the combined mixing performance as the flow rate was increased. Additionally, it can be seen that the average size of the nanoparticles generated at low flow rates was slightly higher than the increased flow rate samples; this could be attributed to the relatively higher mixing time that occurs due to the slow inlet flow rate. It may possible that by modifying the inlet region of the channel, we could prevent premature fluid interaction and create a more consistent mixing time across all flow rates, thus improving the consistency of nanoparticle size.

Table 1.

Summary of nanoparticle synthesis results (from DLS) across various flow rates using the acoustofluidic mixer

Flow rate (μL min−1)	Acoustics OFF		Acoustics ON
	Zavg (nm)	PDI	Zavg (nm)	PDI
20	177.64	0.076	93.76	0.163
400	110.46	0.052	65.76	0.070
2000	75.56	0.095	64.51	0.062

Nonetheless, the results presented here demonstrate the ability of the acoustofluidic mixer to synthesize nanoparticles across a range of flow rates (20–2000 μL min⁻¹), all using the same device. This is potentially beneficial in synthesis applications that involve expensive reagents; using a single device that offers similar performance across various flow rates would enable technicians to use smaller sample volumes during exploration, before increasing the throughput when experimental parameters are better defined.

Conclusions

In summary, the acoustofluidic mixing platform demonstrated here can provide a versatile and powerful mixing device that is capable of functioning across a wide range of flow rates. Altogether, we numerically and experimentally validated the performance of the platform and demonstrated its application in the real-world scenario of nanoparticle generation. Additionally, for the first time, we combined numerical simulations with experimental explorations into the mechanism of vibration generation in our sharp-edge acoustofluidic system; we were able to qualitatively model the vibration of our acoustofluidic mixer, and explore the generation of acoustic streaming through sharp-edge tip vibration. Future experiments will focus on expanding the scope of applications that the device can be used in, such as clinical sample preparation, or diagnostic testing; future work will also explore the customization that can be achieved when tailoring the balance between the acoustic and hydrodynamic mixing regimes. An additional challenge that remains is improving the consistency of device performance and operation; factors such as the connection of the device to external equipment, streamlining the determination of the working frequency, and improving the adoptability of the technology may be investigated in an attempt to improve the device. Altogether, we believe that this technology, with its versatile and thorough mixing capability, has the potential to be integrated into lab-on-a-chip systems in a variety of engineering and medical fields, with immediate cost savings and performance enhancements for many applications such as nanoparticle synthesis or complex biological assays that require precise sample mixtures.